Universidad de Santiago de Chile Autores: Miguel Martnez Concha

Facultad de Ciencia Carlos Silva Cornejo

Departamento de Matemtica y CC Emilio Villalobos Marn
.
1 Ejercicios Resueltos
1.1 Calculo de integrales dobles en coordenadas
1.2 rectngulares cartesianas
1.2.1 Problema
Calcular

1

r + ndrdn si 1 es la regin acotada por las respectivas rectas

n = r. n = r n r = 1
Solucin
Se tiene que la regin 1 =

(r. n) 11
2
0 _ r _ 1; r _ n _ r

r + ndrdn =

1
0

r
r

r + ndndr
=
2
3

1
0
(r + n)
3/2

r
r
dr
=
2
3

1
0
(2r)
3/2
dr
=
2
5/2
3
2
5
(r)
5/2

1
0
=
8

2
15
1.2.2 Problema
Calcular

1

r
2
n
2
drdn si 1 es el dominio limitado por el tringulo de
vrtices (0. 0) ,1(1. 1). C (1. 1) .
Solucin
Entonces se tiene que el dominio est delimitado por las rectas n = r.
n = r n r = 1.
Es decir 1 =

(r. n) 11
2
0 _ r _ 1; r _ n _ r

.
Integrando a franjas verticales, resulta
1

r
2
n
2
drdn =

1
0

r
r

r
2
n
2
dndr
=

1
0

r
r
r

n
r

2
dndr
Hacemos el cambio de variables
n
r
= :c:t == dn = rcos tdt y
determinemos los limites.
Para n = r == arc:c:

r
r

= arc:c:(1) =

2
.
Para n = r == arc:c:

r
r

= arc:c:(1) =

2
Por tanto

1
0

r
r
r

n
r

2
dndr =

1
0

2

2
r
2

1 :c:
2
tdtdr
=

1
0

2

2
r
2
cos
2
tdtdr
=

1
0

2

2
r
2
(
1 + cos 2t
2
)dtdr
=

1
0
r
2

t
2
+
:c:2t
4

2
dr
=

2

1
0
r
2
dr
=

2

r
3
3

1
0
=

6
1.2.3 Problema
Calcular

1

r
2
+ n
2

drdn si 1 =

(r. n) 11
2
r
2
+ n
2
_ 1

.Usando
coordenadas cartesianas
Solucin.
Usando coordenadas cartesianas, la regin de integracin es un crculo
centrado en el origen de radio uno
Por lo tanto
1 =

(r. n) 11
2
1 _ r _ 1.

1 r
2
_ n _

1 r
2

r
2
+ n
2

drdn =

1
1

p
1r
2

p
1r
2
(r
2
+ n
2
)dndr
=

1
1
(r
2
n +
n
3
3
)

p
1r
2

p
1r
2
dr
= 2

1
1
(r
2

1 r
2
+
1
3

(1 r
2
)
3
)dr
= 2

1
1
r
2

1 r
2
dr +
2
3

1
1

(1 r
2
)
3
dr
Con ayuda de una tabla de integrales obtenemos que:

1
1
r
2

1 r
2
dr = (
r
4

1 r
2
+
1
8
(r

1 r
2
+ arc:c:r)

1
1
=
1
8
(arc:c:(1) arc:c:(1) =
1
8
(

2
+

2
) =

8

1
1

(1 r
2
)
3
dr = (
r
4

(1 r
2
)
3
+
3r
8

(1 r
2
) +
3
8
arc:c:r)

1
1
=
3
8
Por lo tanto:

r
2
+ n
2

drdn =
2
8
+
2
3
3
8
=

2
Notese que la solucin del problema usando coordenadas cartesianas es
bastante compleja
1.2.4 Problema
Encontrar el rea de la regin determinada por las desigualdades: rn _ 4.
n _ r. 27n _ 4r
2
.
Solucin.
Sabemos que rn = 4 tiene por grca una hiprbola equiltera, n = r es la
recta bisectriz del primer cuadrante y 27n = 4r
2
corresponde a una parbola.
Veamos cuale son los puntos de interseccin de estas curvas con el proprosito
de congurar el dominio de integracin
rn = 4
n = r

== r
2
= 4 == r = 2 == n = 2
3
27n = 4r
2
n = r

== 27r = 4r
2
==
r = 0
r =
24
4

== n = 0. n =
27
4
rn = 4
27n = 4r
2

== r = 3. n =
4
3
Para calcular el rea (1) =

1
drdn. podemos escoger una particin del
dominio de tipo I de tipo II.
Consideremos dos subregiones de tipo I
1
1
=

(r. n) 11
2
2 _ r _ 3.
4
r
_ n _ r

1
1
=

(r. n) 11
2
3 _ r _
27
4
.
4
27
r
2
_ n _ r

Si proyectamos sobre eje x

(1) =

1
drdn =

11
drdn +

12
drdn
=

3
2

r
4
x
dndr +

27/4
3

r
4
27
r
2
dndr
=

3
2
n[
r
4
x
dr +

27/4
3
n[
r
4
27
r
2 dr
=

3
2

r
4
r

dr +

27/4
3

r
4
27
r
2

dr
=

r
2
2
4 lnr

3
2
+

r
2
2

4
81
r
3

27/4
3
=
5
2
4 ln
3
2
+
729
32

9
2

4
81
27
3
4
3
+
4
81
3
3
= 2 4 ln
3
2
+
729
32

243
16
+
4
3
=
665
96
4 ln
3
2
Si proyectamos sobre eje y
1
1
=

(r. n) 11
2

4
n
_ r _
3
2

3n.
4
3
_ n _ 2

1
1
=

(r. n) 11
2
n _ r _
3
2

3n. 2 _ n _
27
4

4
(1) =

1
drdn =

11
drdn +

12
drdn
=

2
4
3
3
2
p
3u
4
y
drdn +

27/4
2
3
2
p
3u
u
drdn
=

2
4
3

3n 4 lnn

dn +

27/4
2

3
2

3n n

dn
=

3
2

3n
3

4
n

2
4
3
+

3n
3

n
2
2

27/4
2
=
8
3
4 ln
3
2
+
9 27
8

729
32
+ 2
=
665
96
4 ln
3
2
1.3 Cambios de orden de Integracin
1.3.1 Problema
Invierta el orden de integracin y evale la integral resultante .
1 =

1
0

2
2r
c
u
2
dndr
Solucin.
El dominio de integracion dado es 1 =

(r. n) 11
2
0 _ r _ 1. 2r _ n _ 2

.
Si se invierte el orden de integracin tenemos que modicar la particin del
dominio. 1 =

(r. n) 11
2
0 _ r _
n
2
. 0 _ n _ 2

.entonces la integral
se puede escribir.
1 =

1
0

2
2r
c
u
2
dndr =

2
0
y
2
0
c
u
2
drdn
=

2
0
rc
u
2

y
2
0
dn
=

2
0
n
2
c
u
2
dn =
1
4
c
u
2

4
0
=
1
4

c
16
1

5
1.3.2 Problema
Invierta el orden de integracin y evale la integral resultante .
1 =

2
0

4
r
2

n cos ndndr
Solucin.
El dominio de integracion dado es 1 =

(r. n) 11
2
0 _ r _ 2. r
2
_ n _ 4

.
Si se invierte el orden de integracin tenemos que modicar la particin del
dominio.1 =

(r. n) 11
2
0 _ r _

n. 0 _ n _ 4

.entonces la integral
se puede escribir

2
0

4
r
2

n cos ndndr =

4
0

p
u
0

n cos ndrdn
=

4
0

n cos(n)r[
p
u
0
dn
=

4
0
n cos(n)dn
Integrando esta ltima integral por partes se tiene:

4
0
n cos(n)dn = n:c:(n)[
4
0

4
0
:c:(n)dn
= n:c:(n)[
4
0
+ cos(n)[
4
0
= 4:c:(4) + cos(4) 1
1.3.3 Problema
Encontrar el volumen de la regin acotada por los tres planos coordenados y el
plano r + 2n + 3. = 6
Solucin.
Usando integrales dobles y proyectando la regin sobre el plano xy tenemos:
\ =

1
6 r 2n
3
drdn , 1 =

(r. n) 11
2
0 _ r _ 6. 0 _ n _
6 r
2

6
\ =
1
3

6
0
6x
2
0
(6 r 2n) dndr
=
1
3

6
0

(6 r)n n
2

6x
2
0
dr
=
1
3

6
0

(6 r)
2
2

(6 r)
2
4

dr
=
1
12

6
0
(6 r)
2
dr
=

1
36
(6 r)
3

6
0
= 6
Usando integrales dobles y proyectando la regin sobre el plano yz tenemos:
\ =

1
(6 3. 2n) d.dn , 1 =

(n. .) 11
2
0 _ n _ 3. 0 _ . _
6 2n
3

\ =

3
0
62y
3
0
(6 2n 3.) d.dn
=

3
0

(6 2n).
3
2
.
2

62y
3
0
dn
=

3
0

(6 2n)
2
3

(6 2n)
2
6

dn
=
1
6

3
0
(6 2n)
2
dn
=

1
12
(6 r)
3
3

3
0
= 6
1.4 Cambios de variables: Coordenadas polares
1.4.1 Problema
Calcular

1

r
2
+ n
2

drdn si 1 =

(r. n) 11
2
r
2
+ n
2
_ 1

.usando
coordenadas polares
Solucin.
A partir de la coordenadas polares tenemos:
r = rco:0. n = r:c:0 == r
2
+ n
2
= r
2
El valor absoluto del Jacobiano de transformacion a polares es:

0 (r. n)
0 (r. 0)

= r
7

r
2
+ n
2

drdn =

1
r
2

0 (r. n)
0 (r. 0)

drd0
=

1
0

2t
0
r
3
d0dr
=

1
0

2t
0
r
3
0[
2t
0
dr
= 2

1
0
r
3
dr
= 2
r
4
4

1
0
=

2
Las coordenadas polares dieron una solucion ms simple del problema. La
simplicidad depende de la naturaleza del problema y de la simetria que presenta
el dominio.
1.4.2 Problema
Calcular el rea de la regin interior a la circunferencia r
2
+n
2
= 8n y exterior
a la circunferencia r
2
+ n
2
= 9.
Solucin.
Determinemos el centro y radio de la circunsferencia
r
2
+ n
2
= 8n == r
2
+ n
2
8n = 0 == r
2
+ (n 4)
2
= 16
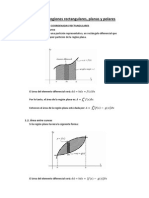
El rea de la regin D es: (1)

1
drdn
Por simetra, podemos calcular el rea de la regin D en el primer cuadrante
y multiplicar por 2.
A n de conocer los lmites de integracin en coordenadas polares
necesitamos conocer el ngulo que forma la recta OT con el eje x.
r
2
+ n
2
= 8n == r
2
= 8r:c:0 == r = 8:c:0
r
2
+ n
2
= 9 == r = 3
Como T pertenece a ambas circunferencias se cumple
8:c:0 = 3 == 0 = arc:c:
3
8
Luego, la mitad de la regin 1

=

(r. 0) 3 _ r _ 8:c:0; arc:c:
3
8
_ 0 _

2

1
drdn =

1

0 (r. n)
0 (r. 0)

drd0
= 2

t/2
o:cstn
3
8

8stn0
3
rdrd0
= 2

t/2
o:cstn
3
8
r
2
2

8stn0
3
d0
=

t/2
o:cstn
3
8

64:c:
2
0 9

d0
=

64

0
2

:c:20
4

9
2
0

t/2
o:cstn
3
8
=

55
2
0 16:c:20

t/2
o:cstn
3
8
=

55
4

55
2
arc:c:
3
8
+ 16:c:(2arc:c:
3
8
)

- 38. 42
1.4.3 Problema
Calcular

1
r
2
+ n
2
r +

r
2
+ n
2
drdn , si D es el interior del cardioide r = a (1 + cos 0)
Solucin.
Cambiando a cordenadas polares, tenemos:
9

1
r
2
+ n
2
r +

r
2
+ n
2
drdn =

1

r
2
r cos 0 + r

0 (r. n)
0 (r. 0)

drd0
=

1

r
2
r cos 0 + r
rdrd0
=

2t
0

o(1+cos 0)
0
r
2
1 + cos 0
drd0
=

2t
0
1
1 + cos 0
r
3
3

o(1+cos 0)
0
d0
=
a
3
3

2t
0
(1 + cos 0)
2
d0
=
a
3
3

2t
0

1 + 2 cos 0 + cos
2
0

d0
=
a
3
3

0 + 2:c:0 +
0
2
+
:c:20
4

2t
0
= a
3
Observacion si deseamos se rigurosos debemos hacer notar que la integral es
impropia cuando r _ 0. e n = 0. pues en tal caso el denominador es cero.
Luego:
1 = lim
o!t

:!0

o
0

o(1+cos 0)
:
r
2
1 + cos 0
drd0 + lim
o!t+
:!0

2t
o

o(1+cos 0)
:
r
2
1 + cos 0
drd0
= lim
o!t

a
3
3

o
0
(1 + cos 0)
2
d0 + lim
o!t+
a
3
3

2t
o
(1 + cos 0)
2
d0
= lim
o!t

a
3
3

3
2
c + 2:c:c +
:c:2c
4

+ lim
o!t+
a
3
3

3
3
2
2:c:
:c:2
4

= a
3
1.5 Cambios de variables. Coordenadas curvilineas
1.5.1 Problema
Calcular 1 =

1
3rndrdn. donde 1 es la regin acotada por por la rectas
r 2n = 0. r 2n = 4
r + n = 4. r + n = 1
(1)
Solucin.
Podemos usar el cambio de variables
10
n = r 2n
= r + n

(1) ==
r =
1
3
(2n + )
n =
1
3
(n )
(2)
Asi,r 2n = 4 se transforma en n = 4
r 2n = 0 se transforma en n = 0
r + n = 1 se transforma en = 1
r + n = 4 se transforma en = 4
Para calcular el Jacobiano

0 (r. n)
0 (n. )

tenemos dos posibilidades.

La primera, es usar la transformacin inversa (2) r e n en trminos de n y
.
La segunda, mucho ms simple, es calcular a partir de (1)

0 (n. )
0 (r. n)

y luego
usar la propiedad

0 (r. n)
0 (n. )

0 (n. )
0 (r. n)

1
.
En efecto

0 (n. )
0 (r. n)

1 2
1 1

= 1 + 2 = 3 ==

0 (r. n)
0 (n. )

=
1
3
Por lo tanto, del teorema del cambio e variables se deduce que:
1 =

1
3rndrdn =

1

1
3
(2n + )
1
3
(n )

0 (r. n)
0 (n. )

dnd
=

4
1

0
4
1
9

2n
2
n
2

ddn
=
1
9

4
1

2n
2

n
2
2


3
3

0
4
dn
=
1
9

4
1

8n
2
+ 8n
64
3

dn
=
1
9

8n
3
3
+ 4n
2

64
3
n

4
1
dn =
164
9
1.5.2 Problema
Calcular el rea de la regin 1. que esta acotada por las curvas
r
2
n
2
= 1. r
2
n
2
= 9
r + n = 4. r + n = 6
(1)
Solucin.
Teniendo en cuenta el cambio de variables que transforma la regin 1 en
la regin 1

n = r
2
n
2
= r + n

(1) ==
La regin 1

esta acotada por la rectas verticales;

r
2
n
2
= 1 se transforma en n = 1
11
r
2
n
2
= 9 se transforma en n = 9
y las rectas horizontales
r + n = 4 se transforma en = 4
r + n = 6 se transforma en = 6
Es decir, 1

= (n. ) 1 _ n _ 9. 4 _ _ 6
Vamos a calcular

0 (r. n)
0 (n. )

a partir de (1)

0 (n. )
0 (r. n)

y usar la propiedad

0 (r. n)
0 (n. )

0 (n. )
0 (r. n)

1
.
En efecto

0 (n. )
0 (r. n)

2r 2n
1 1

= 2 (r + n) = 2 ==

0 (r. n)
0 (n. )

=
1
2
El teorema del cambio variables arma que:
(1) =

1
drdn =

1

0 (r. n)
0 (n. )

dnd
=

9
1

6
4
1
3
ddn
=
1
2

9
1
[ln]
6
4
dn
=
1
2

ln
6
4

9
1
dn
=
1
2
ln
3
2
[n]
9
1
= 4 ln
3
2
1.5.3 Problema
Calcular 1 =

1
r
3
+ n
3
rn
drdn. donde 1 les la regin del primer cuadrante
acotada por:
n = r
2
. n = 4r
2
r = n
2
. r = 4n
2
(1)
Solucin.
El clculo de 1 sera bastante complejo si usamos coordenadas cartesianas
por la simetra que tiene el dominio.Sin embargo, una cambio de variables
simplica la regin 1 y la transforma en 1

.
Sean n =
r
2
n
. =
n
2
r
Luego 1

esta acotada por la rectas verticales;

n = r
2
se transforma en n = 1.
n = 4r
2
se transforma en n =
1
4
.
y las rectas horizontales
r = n
2
se transforma en = 1.
r = 4n
2
se transforma en =
1
4
.
12
Es decir, 1

=

(n. ) 1 _ n _
1
4
. 1 _ _
1
4

Para calcular

0 (r. n)
0 (n. )

tenemos dos posibilidades, la primera es despejar r

e n en trminos de n y a partir de (1) .
La segunda, es calcular

0 (n. )
0 (r. n)

y usar la propiedad

0 (r. n)
0 (n. )

0 (n. )
0 (r. n)

1
.
En efecto

0 (n. )
0 (r. n)

2r
n

r
2
n
2

n
2
r
2
2n
r

= 4 1 = 3 ==

0 (r. n)
0 (n. )

=
1
3
Calculemos ahora la integral
1 =

1
r
3
+ n
3
rn
drdn =

1

r
2
n
+
n
2
r

drdn
=

1
1/4

1
1/4
(n + )
1
3
ddn
=
1
3

1
1/4

n +

2
2

1
1/4
dn
=
1
3

1
1/4

3
4
n +
15
32

dn
=
1
3

3
8
n
2
+
15
32
n

1
1/4
=
1
3

3
8
15
16
+
15
32
3
4

=
15
64
1.6 Calculo de integrales triples en coordenadas
1.7 rectngulares cartesianas
1.7.1 Problema
Sea R la regin en IR
3
acotada por: . = 0. . =
1
2
n. r = 0; r = 1. n = 0. n = 2
Calcular

1
(r + n .) drdnd..
Solucin.
Del grco de la regin , tenemos que 0 _ . _
1
2
n.Proyectando la regin R
sobre el plano rn. As 1 =

(r. n) 11
2
0 _ r _ 1. 0 _ n _ 2

.
Por lo tanto;
13

1
(r + n .) drdnd. =

1
(
1
2
u
0
(r + n .) d.)drdn
=

1
0

2
0
(
1
2
u
0
(r + n .) d.)dndr
=

1
0

2
0

r. + n.
.
2
2

1
2
u
0
dndr
=

1
0

2
0

1
2
(r + n)n
n
2
8

dndr
=

1
0

2
0

1
2
rn +
3
8
n
2

dndr
=

1
0

1
4
rn
2
+
1
8
n
3

2
0
dr
=

1
0
[(r + 1)] dr =

1
2
r
2
+ r

1
0
=
3
2
Tambin es posible resolver el problema anterior proyectando la regin R
sobre el plano r..En tal caso, 2. _ n _ 2 y
1 =

(r. .) 11
2
0 _ r _ 1. 0 _ . _ 1

1
(r + n .) drdnd. =

1
0

1
0
(

2
2:
(r + n .) dn)d.dr
=

1
0

1
0

rn +
n
2
2
.n

2
2:
d.dr
= 2

1
0

1
0
[r + 1 . r.] d.dr
= 2

1
0

r. + .
.
2
2
r
.
2
2

1
0
dr
= 2

1
0

r + 1
1
2

r
2

dr
=

1
0
[(r + 1)] dr =

1
2
r
2
+ r

1
0
=
3
2
Una tercera posibilidad de solucin consiste en proyectar la regin R
sobre el plano yz.
Esta se deja como ejercicio.
14
1.7.2 Problema
Calcular

1
r
2
drdnd. si D es la regin acotada por n
2
+ .
2
= 4ar.
n
2
= ar. r = 3a
Solucin.
La supercie n
2
+ .
2
= 4ar corresponde a un paraboloide de revolucin
como el bosquejado en la gura.
En dos variables el graco de n
2
= ar es una parbola, pero es tres
variables es la supercie de un manto parablico.
Finalmente, el grco r = 3 es un plano paralelo al plano r. a la distancia
3a.
Luego el grco de la regin es
La proyeccin de la region sobre el plano xy es:
1 =

(r. n. .) 11
3
1
1
' 1
2
,

4ar n
2
_ . _

4ar n
2

Por simetra se tiene:

1 =

1
r
2
drdnd. = 2

11

4oru
2

4oru
2
r
2
d.drdn
= 2

3o
0

2
p
or
p
or

4oru
2

4oru
2
r
2
d.dndr
= 2

3o
0

2
p
or
p
or

r
2
.

4oru
2

4oru
2
dndr
= 4

3o
0

2
p
or
p
or
r
2

4ar n
2
dndr
De una tabla de integrales obtenemos

a
2
n
2
dn =
1
2
(n

a
2
n
2
+ a
2
arc:c:
n
a
)
1.8 Clculo de integrales triples usando cambio de vari-
ables
1.8.1 Problema
Resolver I=

r
2
+ n
2
+ .
2
c
(r
2
+u
2
+:
2
)
drdnd. si D es la regin de IR
3
limitada por las supercies r
2
+ n
2
+ .
2
= a
2
r
2
+ n
2
+ .
2
= /
2
con 0 < / < a anillo esfrico.
Solucin
15
Por la simetra del dominio usaremos coordenadas esfricas:
r = r:c:0 cos c
n = r:c:0:c:c
. = r cos 0

==
/
2
_ r
2
+ n
2
+ .
2
_ a
2
== / _ r _ a
to0 =
n
.
= 0 == 0 _ 0 _
toc =
n
r
= 0 == 0 _ c _ 2
Recordando que el valor absoluto del Jacobiano a esfricas es :

0 (r. n. .)
0 (r. 0. c)

= r
2
:c:0 se tiene:
1 =

2t
0

t
0

o
b
rc
:
2

0 (r. n. .)
0 (r. 0. c)

drd0dc
=

2t
0

t
0

o
b
r
3
c
:
2
:c:0 drd0dc
=

2t
0

t
0

1
2
r
2
c
:
2
c
:
2

o
b
:c:0 d0dc
=

1
2
/
2
c
b
2
+
1
2
c
b
2

1
2
a
2
c
o
2
c
o
2

2t
0

t
0
:c:0 d0dc
=

1
2
/
2
c
b
2
+
1
2
c
b
2

1
2
a
2
c
o
2
c
o
2

2t
0
cos 0[
t
0
dc
= 2

1
2
/
2
c
b
2
+
1
2
c
b
2

1
2
a
2
c
o
2
c
o
2

2t
0
dc
= 4

1
2
/
2
c
b
2
+
1
2
c
b
2

1
2
a
2
c
o
2
c
o
2

1.8.2 Problema
Usando integrales triples calcular el volumen de la regin acotada por . = r
2
+n
2
y . = 27 2r
2
2n
2
.
Solucin.
Por la simetra del volumen los resolveremos usando coordenadas cilndricas.
r = r cos 0
n = r:c:0
. = .

==
. = r
2
+ n
2
== . = r
2
.
. = 27 2r
2
2n
2
== . = 27 2r
2
r
2
+ n
2
= 9 == r = 3.
Como el Jacobiano de transformacin a cilndricas es:

0 (r. n. .)
0 (r. 0. .)

= r se tiene:
16
\ =

1
drdnd. =

2t
0

3
0

272:
2
:
2
rd.drd0
=

2t
0

3
0
r .[
272:
2
:
2 drd0
=

2t
0

3
0
r

27 3r
2

drd0
=

2t
0

27
2
r
2

3
4
r
4

3
0
d0
=
243
4

2t
0
d0 =
243
4
2 =
243
2

1.8.3 Problema
Encontrar el volumen de la regin determinada por r
2
+ n
2
+ .
2
_ 16 . .
2
_ r
2
+ n
2
.
Solucin
r
2
+ n
2
+ .
2
= 16 es una esfera con centro en el origen y radio 4
.
2
= r
2
+n
2
es un cono con vrtice en el origen y eje de simetra coincidente
con el eje z.
Como . _ 0 , slo debemos considerar slo la regin sobre el plano xy.
La interseccin de la esfera con el cono se obtiene mediante el sistema:
r
2
+ n
2
+ .
2
= 16
r
2
+ n
2
= .
2

==
. =

8
r
2
+ n
2
= 8
Usaremos coordenadas esfricas:
r = r:c:0 cos c
n = r:c:0:c:c
. = r cos 0

==
0 _ r
2
+ n
2
+ .
2
_ 16 == 0 _ r _ 4
to0 =
n
.
=

8
= 1 == 0 _ 0 _

4
toc =
n
r
= 0 == 0 _ c _ 2
Recordando que el valor absoluto del Jacobiano a esfricas es :

0 (r. n. .)
0 (r. 0. c)

= r
2
:c:0 se tiene:
\ =

1
drdnd. =

2t
0

4
0

4
0
r
2
:c:0 drd0dc
\ =

2t
0

4
0
r
3
3

4
0
:c:0 d0dc
\ =
4
3
3

2t
0
cos 0[

4
0
dc
\ =
4
3
3

2t
0

2
2

dc =
4
3
3

2
2

2
17
Otra opcin para resolver este problema es usar coordenadas cilndricas,en
tal caso
r = r cos 0
n = r:c:0
. = .

==
r
2
+ n
2
+ .
2
= 16 == . = 16 r
2
.
r
2
+ n
2
= .
2
== . = r
2
Tenamos que el Jacobiano de transformacin a cilndricas es:

0 (r. n. .)
0 (r. 0. .)

= r luego:
\ =

1
drdnd. =

2t
0

p
8
0

p
16:
2
:
2
rd.drd0
=

2t
0

p
8
0
r.[
p
16:
2
:
2 drd0
=

2t
0

p
8
0

16 r
2
r
2

drd0
=

2t
0

1
3

(16 r
2
)
3

r
3
3

p
8
0
d0
=
2
3

8
3

16
3

=
2
3

64 32

1.8.4 Problema
Calcular el volumen de la regin acotada por la esfera r
2
+ n
2
+ .
2
= 13 y el
cono (. 1)
2
= r
2
+ n
2
. . _ 1
Solucin.
Por la simetra del volumen los resolveremos usando coordenadas cilndricas.
r = r cos 0
n = r:c:0
. = .

==
Como el Jacobiano de transformacin a cilndricas es:

0 (r. n. .)
0 (r. 0. .)

= r se tiene:
18
\ =

1
drdnd. =

2
0

2t
0

p
13:
2
1+:
rd.d0dr
=

2
0

2t
0
r.
p
13:
2
1+:
d0dr
=

2
0

2t
0
r

13 r
2
(1 + r)

d0dr
= 2

2
0

13 r
2

r + r
2

dr
= 2

1
3

13 r
2

3/2

r
2
2
+
r
3
3

2
0
= 2

1
3

13
3/2
7
3/2

4
2
+
8
3

1.8.5 Problema
Calcular 1 =

1

r
2
a
2
+
n
2
/
2
+
.
2
c
2

drdnd..
En la regin 1 =

(r. n. .) 11
3

r
2
a
2
+
n
2
/
2
+
.
2
c
2
_ 1

a 0. / 0. c 0
Solucin.
La regin de integracin es un elipsoide de semieejes a,b,c.
Efectuemos un primer cambio de variables:
r = an. n = /. . = cn.
Con ello, 1 se transforma en la bola.
1

=

(n. . n) n
2
+
2
+ n
2
_ 1

yel valor absoluto del Jacobiano queda

:

0 (r. n. .)
0 (n. . n)

a 0 0
0 / 0
0 0 c

= a/c
Luego, aplicando el teorema del cambio de variables y obtenemos la integral
1 =

1

r
2
a
2
+
n
2
/
2
+
.
2
c
2

drdnd..
=

1

n
2
+
2
+ n
2

0 (r. n. .)
0 (n. . n)

dnddn
=

1

n
2
+
2
+ n
2

0 (r. n. .)
0 (n. . n)

dnddn
=

1

(n
2
+
2
+ n
2
) (a/c) dnddn
Ahora, transformamos a coordenadas esfricas.
19
n = r:c:0 cos c
= r:c:0:c:c
n = r cos 0

==
0 _ n
2
+
2
+ n
2
_ 1 == 0 _ r _ 1
to0 =

n
== 0 _ 0 _
toc =

n
== 0 _ c _ 2
Quedando, la region 1

= (r. 0. c) 0 _ r _ 1. 0 _ 0 _ . 0 _ c _ 2
a/c

(n
2
+
2
+ n
2
)dnddn = a/c

2t
0

t
0

1
0

r
2

r
2
:c:0 drd0dc
= a/c

2t
0

t
0
r
5
5

1
0
:c:0 d0dc
=
a/c
5

2t
0
cos 0[
t
0
dc
=
2a/c
5

2t
0
dc =
4a/c
5
Observacin
Es claro que la integracin se podra haber efectuado usando directamente
la trasformacin compuesta.
r = ar:c:0 cos c
n = /r:c:0:c:c
. = cr cos 0

==

0 (r. n. .)
0 (r. 0. c)

= a/cr
2
:c:0
1.8.6 Problema
Calcular 1 =

1
drdnd..

(r a)
2
+ (n /)
2
+ (. c)
2
.
en la regin 1 =

(r. n. .) 11
3
r
2
+ n
2
+ .
2
_ 1
2

. (a. /. c) es un punto
jo
no peteneciente a la esfera r
2
+ n
2
+ .
2
_ 1
2
.
Solucin.
Si usamos coordenadas cartesianas los lmites de integracin son
dicultosos, pues en tal caso tendramos.
1 =

1
drdnd..

(r a)
2
+ (n /)
2
+ (. c)
2
1 =

:
:

p
:
2
r
2

p
:
2
r
2

:
2
r
2
u
2

:
2
r
2
u
2
d.dndr.

(r a)
2
+ (n /)
2
+ (. c)
2
Es claro que si usamos este camino las cosas no sern fciles.
20
Sin embargo , dada la simetria esfrica del dominio y observando que el
integrando no es nada ms que el reciproco de la distancia desde (a. /. c) 1
hasta (r. n. .) 1.nos damos cuenta que el resultado no puede depender ms
que de la distancia d entre dichos puntos.Por ello, el resultado no puede variar
si ubicamos el eje z pasando por el punto (a. /. c). Si (0. 0. d) son las nuevas
coordenadas del punto jo tenemos.
1 =

1
drdnd..

r
2
+ n
2
+ (. d)
2
Observacin
El razonamiento anterior es muy usado el clculo de integrales que aparecen
aplicaciones a la Fsica pues en dicha Ciencia son comunes las leyes en que
aparece una distacia o el cuadrado de una distancia en el denominador del
integrando.
Para calcular 1 en (*) usamos coordenadas esfricas. Obtenemos:
1 =

1
0

t
0

2t
0
r
2
:c:0 dcd0dr

r
2
+ d
2
2dr cos 0
= 2

1
0

t
0
r
2
:c:0 d0dr

r
2
+ d
2
2dr cos 0
Para calcular
J =

t
0
r
2
:c:0 d0dr

r
2
+ d
2
2dr cos 0
podemos hacer
: = r
2
+ d
2
2dr cos 0
d: = 2dr:c:0d0
Adems, 0 = 0 == : = r
2
+ d
2
2dr = (d r)
2
0 = == : = r
2
+ d
2
+ 2dr = (d + r)
2
Por lo tanto
J =
r
2d

(J+:)
2
(J:)
2
:
1/2
d: =
r
2d
2:
1/2

(J+:)
2
(J:)
2
=
r
2d
[2 (d + r) 2 (d r)]
=
r
2d
[4r] =
2r
2
d
1 = 2

1
0
2r
2
d
dr
1 =
4
d
r
3
3

1
0
1 =
4
3d
1
3
21