Estruturas Algebricas Grupos e Aneis

MONOGRAF AS MAT E MT I CAS
U T F S M
ESTRUCTURAS ALGEBRAICAS
GRUPOS Y ANILLOS
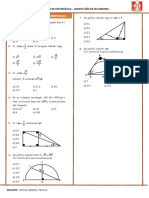
[ e a b c d f

e [ e a b c d f
a [ a b e f c d
b [ b e a d f c
c [ c d f e a b
d [ d f c b e a
f [ f c d a b e
Departamento de Matemtica
Universidad Tcnica Federico Santa Mara
Rubn A. Hidalgo
GRUPOS Y ANILLOS
PRIMERA EDICIN 2009
Rubn A. Hidalgo
Departamento de Matemtica, Universidad Tcnica Federico Santa Mara, Valparaso,
Chile.
E-mail : ruben.hidalgo@usm.cl
Url : http://docencia.mat.utfsm.cl/~rhidalgo
Este libro fu parcialmente patrocinado por los proyectos Fondecyt 1070271 y UTFSM 12.09.02.
GRUPOS Y ANILLOS
PRIMERA EDICIN 2009
Rubn A. Hidalgo
A Betty, Cata y Pucky
INTRODUCCIN
El propsito de este libro es presentar desde un punto de vista bsico (en lo posible) el
concepto de grupos y anillos que puedan ser utilizados por estudiantes de Licenciatura en
Matemticas e Ingeniera Civil Matemtica de nuestro Departamento de Matemtica de
la UTFSM.
Muchos de los fenmenos que encontramos en la naturaleza tienen ciertas simetras
con las cuales podemos sacar conclusiones que nos permitan entender tal situacin de
una manera simple. Muchos casos corresponden a problemas de la fsica y biologa. Por
ejemplo en fsica, conceptos como momentos angulares, tensores, etc., aparecen como
propiedades de la teora de grupos. En biologa podemos entender molculas y cristales
por sus grupos de simetras.
Muchos temas se han propuesto como ejercicios para que el estudiante pueda poner
en prctica los conceptos ya estudiados. Por supuesto, esto podra tener la desventaja de
producir una idea de aislamiento de los temarios tratados, lo cual no es nuestro propsito.
Es claro que en esta primera version existen muchos errores tipogrcos y de temarios.
Esperamos que durante el transcurso del curso los estudiantes puedan hacer las correc-
ciones al escrito y as poder tener en el futuro unas notas mejoradas, las cuales debern
crecer con el tiempo.
Mis primeros agradecimientos van dirigidos a Betty, Cata y Pucky, a quienes quite
tiempo de dedicacin para escribir esta monografa, por su comprensin durante ese
tiempo. Quiero tambin agradecer de manera especial a Sebastian Reyes, Vctor Gonzlez
y a todos aquellos quienes leyeron parte de estas notas y me indicaron algunos errores.
Valparaso, Chile 2009 Rubn A. Hidalgo
TABLA DE MATERIAS
Introduccin. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ix
Parte I. Teora Bsica de Grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1. Grupos de Permutaciones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.1. Grupos por medio de permutaciones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2. Orden de un grupo de permutaciones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3. Subgrupo de permutaciones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2. Grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1. Denicin de grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2. Grupos Abelianos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.3. Subgrupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.4. Generadores. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.5. El pequeo teorema de Fermat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.6. El teorema de Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.7. Grupo fundamental . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3. Homomorsmos de Grupos y Automorsmos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.1. Homomorsmos de grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.2. Grupo de automorsmos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.3. Teorema de Caeley. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.4. Automorsmos interiores y grupos Abelianos. . . . . . . . . . . . . . . . . . . . . . . . . . . 22
4. Grupos Cclicos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
5. Grupos Cocientes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6. Algunos Subgrupos Normales y Abelianizacin de Grupos. . . . . . . . . . . . . . . . . 37
7. Productos de Grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
7.1. Producto Directo de Grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
7.2. Producto Dbil de Grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
7.3. Producto Directo Interno. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
xii TABLA DE MATERIAS
7.4. Producto Semidirecto de Grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
8. Producto Libre de Grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
9. Producto Libre Amalgamado. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
10. HNN-Extensin. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
11. Grupos Libres. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
12. Grupos Abelianos Finitamente Generados. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
12.1. Grupos Abelianos Libres. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
12.2. Grupos Abelianos Finitamente Generados. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
13. Grupos Como Cociente de Grupos Libres. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
14. Grupos de Permutaciones Finitos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
Parte II. Accin de Grupos y Aplicaciones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
15. Accin de Grupos sobre Conjuntos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
16. Los Teoremas de Sylow. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
17. Aplicaciones de los Teoremas de Sylow. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
17.1. Aplicacin 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
17.2. Aplicacin 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
17.3. Aplicacin 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
17.4. Aplicacin 4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
Parte III. Anillos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
18. Denicin y Ejemplos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
19. Homomorsmos de Anillos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
20. Ideales y Anillos Cocientes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
21. Ideales Primos y Maximales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
22. Cuerpo Cociente de un Dominio Entero. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
23. Dominios Euclidianos, Principales y Factorizacin nica. . . . . . . . . . . . . . . . . . 119
23.1. Dominios Euclidianos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
23.2. Dominios de Ideales Principales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
23.3. Dominios de Factorizacin nica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
23.4. Relaciones entre Dominios. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
24. Anillo de Polinomios y Factorizacin Unica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
25. Anillos Noetherianos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
TABLA DE MATERIAS xiii
Parte IV. Representaciones Lineales de Grupos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
26. Representaciones Lineales. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
27. Algunos Ejemplos de Representaciones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
27.1. Representacin regular dada por la accin de un grupo. . . . . . . . . . . . . . . . . . 139
27.2. Representacin suma directa. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
27.3. representacin producto tensorial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
27.4. Representacin wedge. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
27.5. Representacin Hom. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
27.6. Representacin cociente. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141
28. Representaciones Irreducibles y Reducibles. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143
29. Homomorsmos de Representaciones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
30. Carcteres y Conteo de Representaciones Irreducibles. . . . . . . . . . . . . . . . . . . . 155
Referencias. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163
Indice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165
PARTE I
TEORA BSICA DE GRUPOS
En la naturaleza aparecen en diversas formas la idea de simetra, como es el caso de
cristales, molculas, movimiento de electrones por un campo simtrico, etc. Todos esos
fenmenos tienen un concepto comn el cual es la nocin de un grupo.
CAPTULO 1
GRUPOS DE PERMUTACIONES
En esta parte introduciremos el concepto de grupos desde un punto de vista clsico,
dado por biyecciones de algn conjunto no vaco. En el prximo captulo daremos la
nocin general de grupos.
1.1. Grupos por medio de permutaciones
Denicin 1.1.1. Consideremos primero algn conjunto no vaco X (por ejemplo, re-
presentando una molcula, cristales, etc). Una permutacin de X ser por denicin una
funcin biyectiva f : X X. Denotemos por Perm(X) al conjunto de las permuta-
ciones de X.
Observemos que todo conjunto X posee la permutacin trivial dada por la funcin
identidad I
X
. Tambin, dada una permutacin f : X X, siempre tenemos la permuta-
cin inversa f
1
: X X.
Ejercicio 1.1.2. Vericar que X es un conjunto nito s y slo si Perm(X) es nito.
En el caso que X es un conjunto nito de cardinalidad n, calcular la cardinalidad de
Perm(X).
Dadas dos permutaciones f, g Perm(X) del conjunto X, tenemos que al componer-
las obtenemos nuevamente una permutacin g f Perm(X). Esto como consecuencia
del hecho que la composicin de dos biyecciones es de nuevo una biyeccin. As, tenemos
en Perm(X) una operacin (binaria) dada por la composicin, que satisface las siguientes
propiedades :
(1) La operacin de composicin en Perm(X) es asociativa, es decir,
f (g h) = (f g) h,
para todos f, g, h Perm(X).
4 CAPTULO 1. GRUPOS DE PERMUTACIONES
(2) La funcin identidad I
X
es un elemento neutro para la composicin, es decir,
f I
X
= f = I
X
f
para todo f Perm(X).
(3) Toda permutacin f Perm(X) tiene un elemento inverso f
1
Perm(X).
Denicin 1.1.3. Decimos que el par (Perm(X), ) es el grupo de permutaciones del
conjunto X.
Desde ahora en adelante usaremos indistintamente la notacin Perm(X) para denotar
tanto al conjunto de permutaciones de X como al grupo de permutaciones de X ya que
esto no produce confusin alguna.
1.2. Orden de un grupo de permutaciones
Denicin 1.2.1. La cardinalidad de Perm(X) es llamado el orden del grupo de per-
mutaciones Perm(X).
Notacin : Sea k 0, 1, 2, 3, .... Si k > 0, entonces usaremos la notacin f
k
para denotar la composicin de f consigo misma k veces. La notacin f
k
indicar que
hacemos la composicin de f
1
consigo misma k veces. Por ltimo, f
0
indicar el neutro
I
X
.
Ejemplo 1.2.2. Consideremos X = a, b, c un conjunto de tres elementos. Entonces
Perm(X) = I
X
, A, A
2
, B, A B, A
2
B, donde
A : (a, b, c) = (b, c, a) y B(a, b, c) = (b, a, c)
Es decir, Perm(X) es un grupo de permutaciones de orden 6.
Ejercicio 1.2.3. Sea X un conjunto de n > 0 elementos. Determinar los elementos
de Perm(X). Vericar que el orden de Perm(X) es n!.
1.3. Subgrupo de permutaciones
Hay veces en que no estaremos interesados en todas las permutaciones de un conjunto,
pero slo de algunas de ellas, por ejemplo, de aquellas que preservan cierta propiedad.
Denicin 1.3.1. Supongamos que tenemos un conjunto X ,= y un subconjunto
G Perm(X) de algunas de las permutaciones de X. Si :
(1) Para todos. El conjunto G consiste f, g G vale que f g G;
1.3. SUBGRUPO DE PERMUTACIONES 5
(2) Para todo f G vale que f
1
G,
entonces diremos que G es un subgrupo de permutaciones de X y esto lo denotaremos
con el smbolo G < Perm(X). La cardinalidad de G es llamado el orden del subgrupo
de permutaciones G.
Observacin 1.3.2. Observar que las condiciones (1) y (2) obligan a tener I
X
G y
que G satisface las mismas propiedades antes vericadas para Perm(X).
Ejercicio 1.3.3. Calcular todos los subgrupos del grupo Perm(X) del ejemplo 1.2.2.
Ejemplo 1.3.4. Sea X un conjunto no vaco y p X un punto que hemos jamos.
Consideremos el conjunto Gformado por las permutaciones de X que tienen la propiedad
de dejar al punto p jo. Entonces claramente valen las dos propiedades anteriores y vemos
que G es un subgrupo de permutaciones de X. Por ejemplo, en el caso X = a, b, c y
p = a, entonces G = I
X
, A B.
Ejemplo 1.3.5. Generalicemos un poco ms el ejemplo anterior. Sea X un conjunto
no vaco y A X un subconjunto que hemos jamos. Consideremos el conjunto G
formado por las permutaciones de X que tienen la propiedad de dejar invariante al sub-
conjunto A, es decir, para cada g G y cada a A vale que g(a) A. Entonces
G es un subgrupo de permutaciones de X. Observemos que cada g G, al restrin-
girla a A, produce una permutacin (g) de A. Luego tenemos inducida una funcin
: G Perm(A), denida por tal restriccin. Puede ocurrir que tengamos g
1
, g
2
G
tales que g
1
,= g
2
pero que sus restricciones coincidan en A; luego, no es necesaria-
mente una funcin inyectiva. Por otro lado, cada permutacin h Perm(A) puede ser
extendida a una permutacin (h) Perm(X) por extensin como la funcin identidad
en X A. Tenemos entonces una funcin, ahora inyectiva, : Perm(A) Perm(X).
Observemos que (Perm(A)) es un subgrupo de permutaciones de X (Vericar).
Ejemplo 1.3.6. Si X = V es un espacio vectorial sobre un cuerpo K, entonces el
grupo Perm(V ) contiene como subgrupo a
GL(V ) = L : V V : L es un isomorsmo de V
es decir, los isomorsmos lineales de V es un subgrupo de permutaciones de V (las per-
mutaciones que preservan la estructura de espacio vectorial).
Por otro lado, si Q V , entonces
G = L GL(V ) : L(Q) = Q,
resulta tambin ser un subgrupo de Perm(V ).
6 CAPTULO 1. GRUPOS DE PERMUTACIONES
Tenemos las contenciones
G GL(V ) Perm(V )
Supongamos por ejemplo que Q es alguna gura geomtrica dentro de V , que podra
estar representando una molcula, una coleccin de electrones o un cristal. Entonces G
estara formado por aquellos isomorsmos que preservan tal conguracin. Veamos esto
de una manera un poco ms concreta. Supongamos V = R
2
, K = R y Q un polgono
regular de n 3 lados con centro en el orgen (0, 0) y uno de sus vrtices localizado en
(1, 0). Entonces todo elemento de G debe obligatoriamente ser una rotacin (de determi-
nante positivo o negativo). Ms an, si R es la rotacin positiva en ngulo /n, S es la
reexin S(x, y) = (x, y) y T = R S R
1
, entonces se puede vericar que todo
elemento de G se obtiene con todas las posibles composiciones entre T y S y que este
tiene orden 2n (mirar la gura de la tapa para n = 6).
Ahora, supongamos que en el espacio vectorial real V tenemos un producto interior
Euclidiano , ). Por ejemplo, en R
n
podemos usar el producto punto
(x
1
, ..., x
n
), (y
1
, ..., y
n
)) = x
1
y
1
+x
2
y
2
+ +x
n
y
n
Denotemos por O
,
al conjunto de todas los isomorsmos L GL(V ) tales que
preservan tal producto, es decir,
L(x), L(y)) = x, y), para todos x, y V
Si V es de dimensin nita, digamos n, entonces podemos considerar una base =
v
1
, ..., v
n
de V y formar la matriz simtrica A GL(n, R) cuyo coeciente a
ij
=<
v
i
, v
j
>=< v
j
, v
i
>. Entonces escribiendo x = x
1
v
1
+ +x
n
v
n
, y = y
1
v
1
+ +y
n
v
n
,
vale que
< x, y >= (x
1
x
n
)A
t
(y
1
y
n
)
De esta manera si M M(n, R) es la matriz que representa a la transformacin lineal
L : V V en la base , entonces tenemos que L O
,
s y slo si
MA
t
M = A
Llamamos a O
,
el grupo de isometras del espacio Euclidiano (V, , )). Se tiene que
O
,
es un subgrupo de permutaciones de Perm(V ). Este tipo de permutaciones (llamados
isometras de (V, , ))) son los que interesan para el estudio de algunos fenmenos de la
naturaleza.
Ejercicio 1.3.7. Vericar y completar los detalles del ejercicio anterior.
Ejercicio 1.3.8. Para cada entero n 3 considere el polgono regular P de n lados
centrado en el orgen en R
2
. Use el producto punto usual
(a, b), (c, d)) = ac +bd
y determine las isometras de P.
CAPTULO 2
GRUPOS
La pregunta natural es si existe en el fondo alguna diferencia entre un grupo de si-
metras Perm(X) y alguno de sus subgrupos. La verdad es que, excepto por la propiedad
que uno es subconjunto del otro, no hay diferencia conceptual entre ellos. En este captulo
veremos la denicin general de grupos, el cual responde a la interrogante anterior.
2.1. Denicin de grupos
Denicin 2.1.1. Un conjunto G ,= junto a una funcin
: GG G
llamada una operacin binaria en G es llamado un grupo si valen las siguientes propie-
dades :
(1) La operacin binaria es asociativa, es decir,
g
1
(g
2
g
3
) = (g
1
g
2
) g
3
,
para todos g
1
, g
2
, g
3
G.
(2) Existe un elemento neutro para la operacin binaria , denotado por I
G
, que satis-
face :
g I
G
= g = I
G
g
para todo g G.
(3) Todo elemento g G tiene un elemento inverso respecto a la operacin binaria ,
es decir que existe un elemento g
1
G tal que g g
1
= I
G
= g
1
g.
Ejercicio 2.1.2. Vericar que el elemento neutro y los inversos son nicos en un
grupo.
8 CAPTULO 2. GRUPOS
Denicin 2.1.3. El orden de un grupo (G, ), denotado por [G[, es denido como
la cardinalidad de conjunto G. De la misma manera, por cada elemento g G I
G
llamaremos el orden de g, denotado por o(g), al entero positivo k ms pequeo tal que
g
k
= I
G
en caso de existir, o o(g) = en caso contrario. Diremos que el orden del
neutro es 1.
Ejercicio 2.1.4. Ver que todo grupo de permutaciones es un grupo con la operacin
de composicin.
Ejercicio 2.1.5. Sea (G, ) un grupo y dos elementos x, y G de ordenes n > 1 y
m > 1 respectivamente. Supongamos que x y = y x. Vericar que el orden de x y
es el mnimo comn mltiplo M.C.M.(n, m) entre n y m.
Ejercicio 2.1.6. Supongamos que (G, ) es un grupo nito donde la ecuacin x
2
=
I
G
tiene como nica solucin a x = I
G
. Calcular el valor en G del producto de todos los
elementos de G.
Ejemplo 2.1.7. Para analizar conjuntos nitos muy pequeos con alguna operacin
binaria dada, uno puede utilizar tablas de multiplicacin para analizar si estamos en pre-
sencia de un grupo on no. Por ejemplo, consideremos el conjunto G = e, a, b, c, d, f y
denamos la operacin binaria dada por la siguiente tabla :
[ e a b c d f

e [ e a b c d f
a [ a b e f c d
b [ b e a d f c
c [ c d f e a b
d [ d f c b e a
f [ f c d a b e
Lo que esta tabla nos dice, por ejemplo, que el coeciente (2, 3), es decir, e es igual a
a b.
Ejercicio 2.1.8. Vericar que el grupo del Ejemplo 2.1.7 tiene orden 6.
2.3. SUBGRUPOS 9
2.2. Grupos Abelianos
Denicin 2.2.1. Un grupo (G, ) es llamado un un grupo Abeliano si se satisface la
siguiente propiedad de commutatividad
(*) para todo par de elementos x, y G vale que x y = y x.
Ejemplo 2.2.2. Es claro que no todo grupo puede ser Abeliano. Un ejemplo tpico
es el grupo Perm(X) cuando la cardinalidad de X es al menos 3. Otro ejemplo es el
siguiente. Sea GL(n, Z) el conjunto de las matrices cuadradas de tamao nn invertibles
con coecientes enteros (las inversas con coecientes enteros tambin). Usando como la
operacin binaria el producto usual de matrices, tenemos que para n 2 este da un grupo
no Abeliano.
Ejercicio 2.2.3. Vericar que el Ejemplo 2.1.7 dene un grupo que no es Abeliano.
Ejemplo 2.2.4. Supongamos que tenemos un grupo (G, ) con la propiedad que todos
sus elementos diferentes del neutro son de orden 2. Si x, y G, entonces x y x
1
y
1
= x y x y = (x y)
2
= I
G
, es decir, G es un grupo Abeliano.
2.3. Subgrupos
Denicin 2.3.1. Si (G, ) es un grupo y H Gsatisface ser un grupo con la misma
operacin , entonces H es llamado un subgrupo de G, denotado esto por H < G.
Ejercicio 2.3.2. Obtener todos los subgrupos del grupo del Ejemplo 2.1.7.
Ejercicio 2.3.3. Sea (G, ) un grupo y H ,= un subconjunto de G. Vericar que H
es un subgrupo de G s y slo si :
(1) Para cada h H se tiene que h
1
H ; y
(2) Si h
1
, h
2
G, entonces h
1
h
2
H.
Concluir que I
H
= I
G
y que todo inverso en H es inverso en G.
Es claro que todo grupo de permutaciones y todo subgrupo de permutaciones es un
grupo (donde = ) en la versin moderna. Antes de vericar que todo grupo, en la
notacin moderna, es un subgrupo de permutaciones de algn conjunto, necesitaremos un
concepto que permita comparar grupos, estos son los homomorsmos.
10 CAPTULO 2. GRUPOS
Ejercicio 2.3.4. Determinar que todos los subgrupos del grupo Abeliano Z son de la
forma nZ = nk : k Z.
Ejemplo 2.3.5. Consideremos el grupo R con la operacin binaria de la suma usual
de nmero reales. Recordemos del curso de anlisis 1 que R es un espacio normado,
la norma siendo el valor absoluto. Un subgrupo H de R tiene dos posibilidades : ser
un subconjunto discreto (es decir, no tiene puntos de acumulacin) o no serlo. En caso
que H no sea discreto entonces existe una sucesin x
n
H que converge hacia un
nmero real p. Entonces y
n
= x
n+1
x
n
H nos d una sucesin que converge hacia
0 H. Escojamos cualquier intervalo abierto (a, b) R. Entonces podemos escoger y
n
de manera que z = [y
n
[ < (b a). Es claro que z H y que kz = z + +z H para
todo k Z. Como existe k
0
Z tal que k
0
z (a, b), tenemos que si H no es discreto,
entonces debe ser un subconjunto denso de R. Ahora, si H es discreto, entonces lo anterior
tambin nos dice que w = mnimoh H : h > 0 > 0. Ahora, consideremos wZ =
kw : k Z. Se tiene que wZ es un subgrupo de R y tambin de H. Si wZ ,= H,
entonces es posible encontrar k Z y h H tales que (k 1)w < h < kw. Pero en
este caso, 0 < kw h < h. Como kw h H, obtenemos una contradiccin con la
minimalidad de w. En consecuencia, el hemos obtenido lo siguiente :
Teorema 2.3.6. Todo subgrupo aditivo de R es o bin denso o de la forma wZ para
cierto w > 0.
Ejemplo 2.3.7. Sea K un cuerpo (por ejemplo, Q, R, C) y denotemos por GL(n, K)
al conjunto de las matrices de tamao n n, con coecientes en K, que son invertibles.
Entonces, con la operacin de jultiplicacin de matrices, obtenemos que GL(n, K) es un
grupo. Este grupo es un modelo del grupo GL(V ) donde V es un espacio vectorial sobre
K y dimensin n. Denamos la relacin de equivalencia
A B s y slo si existe K 0 tal que B = A
Sea PGL(n, K) el conjunto de las clases de equivalencia y denotemos por
: GL(n, K) PGL(n, K)
la proyeccin natural que asocia a cada matriz A GL(n, K) su clase de equivalencia
(A) := [A] PGL(n, K). Si denimos la operacin
[A] [B] := [AB]
la cual est bin denida, entonces obtenemos en PGL(n, K) una estructura de grupo,
cual es llamado el grupo proyectivo lineal.
Observemos que el grupo especial lineal SL(n, K), formado de las matrices de
GL(n, K) de determinante 1, satisface que (SL(n, K)) = PSL(n, K) es un subgrupo
de PGL(n, K).
2.3. SUBGRUPOS 11
Ejercicio 2.3.8.
(1) Vericar que PSL(n, C) = PGL(n, C).
(2) Es verdad lo anterior con C reemplazado por R?
Ejemplo 2.3.9. Un grafo ( es una coleccin disjunta de objetos llamados "vrtices"
y objetos llamados "ejes" que conectan dos vrtices (puede ocurrir que los dos vrtices
conectados por un eje sean el mismo). Un automorsmo del grafo ( es una funcin bijec-
tiva al nivel de vrtices y al nivel de ejes, es decir, este enva vrtices en vrtices y enva
ejes en ejes. Denotamos por Aut(() al conjunto de los automorsmos del grafo (. Junto
con la operacin de composicin de funciones obtenemos una estructura de grupo para
Aut(().
Ejercicio 2.3.10. Completar los detalles del ejemplo anterior.
La operacin conjuntista dada por la interseccin nos permite construir subgrupos de
algn grupo a partir de otros.
Proposicin 2.3.11. Sea (G, ) un grupo y H
j
: j J una coleccin cualquiera
de subgrupos de G. Entonces
jJ
H
j
es de nuevo un subgrupo de G.
Demonstracin. Supongamos que x, y

jJ
H
j
. Entonces x, y H
j
, para cada
j J. Como H
j
es subgrupo, entonces x y, x
1
H
j
y, como consecuencia, x
y, x
1
jJ
H
j
.
Ejercicio 2.3.12. Vericar que la unin de subgrupos no es necesariamente un sub-
grupo. Dar un ejemplo.
Ejemplo 2.3.13. Un ejemplo de un grupo es dado por las rotaciones Euclidianas en
R
3
. Consideremos dos ngulos de rotacin , R y consideremos las rotaciones en R
3
dadas por
A =
_
_
cos() sin() 0
sin() cos() 0
0 0 1
_
_
B =
_
_
cos() sin() 0
sin() cos() 0
0 0 1
_
_
tenemos A B = B A, pero con las rotaciones
C =
_
_
cos() sin() 0
sin() cos() 0
0 0 1
_
_
D =
_
_
cos() 0 sin()
0 1 0
sin() 0 cos()
_
_
tenemos C D ,= D C.
Ejemplo 2.3.14. Consideremos un grupo (G, ) de orden par. Entonces GI
G
es
un conjunto de cardinalidad impar. Consideremos la funcin
: G G : x x
1
Observamos que es una bijeccin, es su propia inversa y que (I
G
) = I
G
. As,
tenemos una bijeccin : GI
G
GI
G
. Como es su propia funcin inversa,
tenemos que para cada x GI
G
vale que (x, x
1
) = x, x
1
. Esto nos obliga
a tener al menos un elemento x GI
G
con (x) = x, es decir, G tiene al menos un
elemento de orden 2.
Ejercicio 2.3.15. Sea (G, ) un grupo de orden par. Vericar que #x G : o(x) =
2 es impar (Ind. Use la funcin biyectiva dada por inversin, es decir, G G : x
x
1
).
Ejercicio 2.3.16. Consideremos el grupo de las matrices cuadradas de tamao 2 2
invertible reales, es decir G = GL(2, R) con la operacin binaria dada por multiplicacin
usual de matrices. Sean
x =
_
0 1
1 0
_
y =
_
0 1
1 1
_
Vericar que o(x) = 4, o(y) = 3 y o(x y) = . Comparar al ejercicio anterior.
2.4. Generadores
Consideremos un grupo (G, ) y un subconjunto A G. Lo ms probable es que A
no sea un subgrupo de G. Podemos preguntarnos por el subgrupo de G ms pequeo que
contenga A.
Lo que podemos intentar es considerar la interseccin de todos los subgrupos de Gque
contenga a A, es decir
A) =
H<G
AH
H
Esta interseccin es no vaca ya que G es uno de los subgrupos conteniendo A.
Como la interseccin de subgrupos de un grupo dado es nuevamente un subgrupo,
tenemos que en efecto A) es un subgrupo de G.
Denicin 2.4.1. El grupo A) es llamado el subgrupo de Ggenerado por A. En caso
que A) = G, decimos que A es un conjunto de generadores de G. En este caso decimos
tambin que los elementos de A son generadores de G.
Ejercicio 2.4.2. Buscar generadores para los grupos del ejemplo 1.3.6.
2.5. EL PEQUEO TEOREMA DE FERMAT 13
2.5. El pequeo teorema de Fermat
Denicin 2.5.1. Sea p un nmero primo y sea G = 1, 2, 3, ..., p 1. Considere la
operacin binaria de la siguiente manera : si a, b G entonces a b denota el resto de
dividir ab Z por p.
Ejercicio 2.5.2. (i) Vericar que (G, ) es un grupo conmutativo de orden p 1
(Ind. Si a G entonces (a, p) = 1, es decir, a no es divisible por p. Ms adelante
veremos que existen enteros n, m tales que na + mp = 1). Al grupo as construido
le denotaremos por (Z/pZ)
.
(ii) Vericar que si p no fuese un nmero primo, entonces la operacin denida no
determina una estructura de grupo en G.
Ejemplo 2.5.3. Consideremos un nmero primo p y formemos el grupo (Z/pZ)
.
Busquemos los elementos de orden 2, es decir a 1, 2, ..., p 1 tal que a a = 1, es
decir, a
2
1 sea divisible por p. Como a
2
1 = (a 1)(a +1) y (a 1) < p, debemos
tener que (a + 1) debe ser divisible por p, dando como nica solucin a = p 1. En
particular, como todo otro elemento de 2, 3, ..., p 2 tiene inverso diferente, tenemos
que 1 2 3 (p 1) = (p 1), es decir,
(p 1)! 1 mdulo p
Si n es un entero positivo tal que (n, p) = 1, es decir, p no divide n. Entonces n =
ap + r cierto r G. Ms adelante veremos que si G es un grupo nito de orden N
y x G, entonces vale que x
N
= 1, donde 1 G denota al elemento neutro. Luego
r
p1
= 1 en (G, ), es decir, vale la igualdad r
p1
= 1 + bp en Z para cierto entero b.
Luego, en Z tenemos que :
n
p
= nn
p1
= n(ap +r)
p1
= nr
p1
+pq, cierto entero q
es decir
n
p
= n(1 +bp) +pq = n +p(nb +q)
De donde concluimos el siguiente
Teorema 2.5.4 ( Pequeo teorema de Fermat). Sean p un primo y n un entero cual-
quiera, entonces
n
p
n mdulo p
2.6. El teorema de Euler
Denicin 2.6.1. Para cada nmero entero positivo q consideramos la funcin
e(q) = #k 1, 2, 3, ..., q 1 : (q, k) = 1
llamada la funcin de Euler.
Ejercicio 2.6.2. Vericar que
(i) si p es un nmero primo, t > 0 un entero, entonces
e(p
t
) = p
t
_
1
1
p
_
(ii) Si q, r son enteros positivos y (q, r) = 1, entonces e(qr) = e(q)e(r).
(iii) Sea G = k 1, 2, 3, ..., q 1 : (q, k) = 1 y considere la operacin binaria
dada por : si a, b G, entonces a b denota el resto al dividir ab por q. Vericar
que (G, ) es un grupo abeliano de orden e(q) (Ind. Ms adelante veremos que si
(k, q) = 1, entonces existen enteros n, m Z de manera que nq + mr = 1).
De (iii) del problema enterior, podemos concluir la siguiente generalizacin al pequeo
teorema de Fermat.
Teorema 2.6.3 ( Teorema de Euler). Si q, n Z, q > 0, son tales que (q, n) = 1,
entonces
n
e(q)
1 mdulo q
2.7. Grupo fundamental
Consideremos un espacio topolgico (X, ) y escojamos un punto p X. Sea A(p)
el conjunto de todas las funciones continuas : [0, 1] X tal que (0) = (1) = p.
Para
1
,
2
A(p), denamos la operacin binaria dada por
1

2
=
_

1
(2t), 0 t
1
2
2
(2t 1),
1
2
t 1
Desgraciadamente, esta operacin binaria no es asociativa, es decir, en general tenemos
que
1
(
2
3
) ,= (
1
2
)
3
. Para arreglar esto, denimos una relacin de equivalencia
sobre A(p) denida de la siguiente manera. Sean
1
,
2
A(p), entonces decimos que
ellas son homotpicamente equivalentes relativo al punto p, es decir,
1

2
si existe una funcin continua F : [0, 1] [0, 1] X tal que
(i) F(t, 0) =
1
(t), para todo t [0, 1] ;
(ii) F(t, 1) =
2
, para todo t [0, 1] ;
2.7. GRUPO FUNDAMENTAL 15
(iii) F(0, s) = F(1, s) = p, para todo s [0, 1].
Lo importante de esta relacin de equivalencia es que si tenemos
1
,
2
,
1
,
2
A(p)
tales que
1

1
y
2

2
, entonces
1

2

1

2
Denotemos por [] la clase de equivalencia de A(p) y por
1
(X, p) al conjunto
de las clases de equivalencia. Podemos hacer descender la operacin hasta
1
(X, p), es
decir,
[
1
] [
2
] := [
1

2
]
Ahora la operacin es asociativa. Si e
p
A(p) es el camino constante e
p
(t) = p,
entonces se tiene que [e
p
] [] = [] = [] [e
p
], es decir, [e
p
] es un neutro para tal
operacin.
Dado cualquier camino A(p), tenemos su camino de vuelta
1
(t) := (1 t)
A(p). En este caso, tenemos que [] [
1
] = [e
p
] = [
1
] [], es decir, [
1
] es inverso
de [] para esta operacin.
Hemos obtenido que (
(
X, p), ) dene un grupo, llamado grupo fundamental de X
basado en el punto p.
Ejercicio 2.7.1. Completar los detalles del ejemplo anterior.
CAPTULO 3
HOMOMORFISMOS DE GRUPOS Y AUTOMORFISMOS
3.1. Homomorsmos de grupos
Denicin 3.1.1. Sean (G
1
,
1
) y (G
2
,
2
) dos grupos y : G
1
G
2
una funcin.
Diremos que es un homomorsmos de grupos si vale que
(x
1
y) = (x)
2
(y), para todos x, y G
1
Observacin 3.1.2. Sea : (G
1
,
1
) (G
2
,
2
) un homomorsmo de grupos. En-
tonces para cada x G
1
tenemos que
(x) = (x
1
I
G1
) = (x)
2
(I
G1
)
luego, vale que
(I
G1
) = I
G2
Denicin 3.1.3. Sean (G
1
,
1
) y (G
2
,
2
) dos grupos y : G
1
G
2
un homomor-
smo de grupos. Entonces
Ker() =
1
(I
G1
) = g G
1
: (g) = I
G2
es llamado el ncleo de y
Im() = h G
2
: existe g G
1
tal que (g) = h
es llamado la mgen de .
Denicin 3.1.4. En caso que un homomorsmo de grupos sea inyectivo, diremos
que es un monomorsmo. Si este es sobreyectivo, entonces hablamos de un epimorsmo
o homomorsmo sobreyectivo. Un isomorsmo de grupos es un homomorsmo biyectivo.
En este caso diremos que los respectivos grupos son grupos isomorfos. Un isomorsmo
de un grupo en si mismo es llamado un automorsmo del grupo.
18 CAPTULO 3. HOMOMORFISMOS DE GRUPOS Y AUTOMORFISMOS
La idea es que grupos isomorfos son el mismo desde el punto de vista algebraico.
Ejercicio 3.1.5.
(i) Vericar que las funciones : G Perm(A) y : Perm(A) Perm(X) del
ejemplo 1.3.5 son homomorsmos de grupos.
(ii) Deducir del ejemplo 2.3.5 que todo subgrupo aditivo no denso de R es isomorfo a
Z.
(iii) Sea (G, ) un grupo, X un conjunto y F : G X una funcin biyectiva. Veri-
car que es posible dotar de una operacin binaria a X de manera que (X, ) es
un grupo y F : (G, ) (X, ) es un isomorsmo de grupos. Ver adems que tal
operacin binaria es nica.
(iv) Sean (G
1
,
1
) y (G
2
,
2
) dos grupos y : G
1
G
2
un homomorsmo de
grupos. Vericar que :
(iv.1) Ker() es un subgrupo de G
1
.
(iv.2) Im() es un subgrupo de G
2
.
(iv.3) es monomorsmo s y slo si Ker() = I
G1
. En este caso ver que
: G
1
Im() es un isomorsmo.
(iv.4) es epimorsmo s y slo si Im() = G
2
.
(iv.5) Si H es subgrupo de G
1
, entonces (H) es subgrupo de G
2
.
(iv.6) Si U es subgrupo de G
2
, entonces
1
(U) es un subgrupo de G
1
conte-
niendo a Ker().
(v) Vericar que la funcin logaritmo Log : (R, +) (R0, ) es un isomorsmo.
Determinar la inversa.
(vi) Sea S
1
= z C : [z[ = 1 junto a la operacin dada por la multiplicacin usual
de nmeros complejos, denotada por . Vericar que tenemos un grupo Abeliano.
Para cada nmero real a R dena la funcin
F
a
: (S
1
, ) (S
1
, ) : w = e
i
w
a
= e
ia
Vericar que F
a
es un homomorsmo de grupos. Calcular Ker(F
a
).
(vii) Sea (G, ) un grupo para el cual la funcin de inversin
J : (G, ) (G, ) : x x
1
es un homomorsmo de grupos. Vericar que (G, ) es un grupo Abeliano.
Ejercicio 3.1.6. Sea (X, ) un espacio topolgico y sean p, q X en la misma com-
ponente arcoconexa. Vericar que los grupos fundamentales
1
(X, p) y
1
(X, q) son
isomorfos. Qu pasa si p y q estn en componentes diferentes ?
Ejemplo 3.1.7. Sea (G, ) un grupo nito y supongamos que tenemos un automor-
smo involutivo sin puntos jos no triviales, es decir, un automorsmo T : (G, )
(G, ) de (G, ) tal que T T = I y T(x) = x slo vale para x = I
G
. Veamos que
3.2. GRUPO DE AUTOMORFISMOS 19
esto obliga a tener (G, ) Abeliano. En efecto, primero consideremos el subconjunto de
G siguiente
K = x
1
T(x) : x G G
La igualdad x
1
T(x) = y
1
T(y) es equivalente a tener T(y x
1
) = y x
1
,
la condicin sobre los puntos jos de T asegura x = y. En particular, K = G. De esta
manera, podemos escribir cada elemento de G como u = x
1
T(x). Ahora, T(u) =
T(x
1
T(x)) = T(x)
1
x = u
1
, es decir, T en la nueva representacin es dada
por inversin. Parte (vii) del Ejercicio 3.1.5 nos permite concluir que (G, ) es un grupo
Abeliano.
Ejemplo 3.1.8. Dado un grupo (G, ) denamos la siguiente operacin binaria
: GG G : (x, y) x y := y x
Sean x, y, z G. Entonces :
(i) (x y) z = Z (y x) = (z y) x = x (y z), es decir, es una operacin
asociativa.
(ii) x I
G
= I
G
x = x = x I
G
= I
G
x, es decir, tenemos un elemento neutro,
el cual coincide con el elemento neutro para la operacin binaria .
(iii) x x
1
= x
1
x = I
G
= x x
1
= x
1
x, es decir, cada elemento de G
tiene un inverso respecto a la operacin binaria el cual es el mismo como para la
operacin binaria .
Luego, (G, ) resulta ser un grupo. Si consideramos la funcin
: (G, ) (G, ) : x x
1
entonces obtenemos que
(x y) = (x y)
1
= y
1
x
1
= x
1
y
1
= (x) (y)
es decir, es homomorsmo de grupos. Como adems es una bijeccin, tenemos que
es un isomorsmo de grupos. Llamaremos al grupo (G, ) el grupo reejado del grupo
(G, ).
Ejercicio 3.1.9. Vericar que I : (G, ) (G, ) : x x no es un homomorsmo
si G no es un grupo Abeliano.
3.2. Grupo de automorsmos
Denicin 3.2.1. Dado un grupo (G, ), denimos el conjunto Aut(G), formado por
todos los automorsmos de (G, ). Un isomorsmo : (G, ) (G, ) ser llamado un
antiautomorsmo de (G, ). Denotaremos por Aut
(G) al conjunto de los antiautomor-

smos de (G, ).
Ejercicio 3.2.2. Vericar que Aut(G) es un grupo con la regla de composicin y de
hecho un subgrupo de Perm(G). Si (G, ) es un grupo Abeliano, entonces Aut(G) =
Aut
(G), es decir, todo antiautomorsmo es tambin un automorsmo. Qu pasa para

grupos no Abelianos ? Es Aut
(G) un grupo bajo la regla de composicin?

Denicin 3.2.3. Algunos automorsmos de (G, ) se pueden obtener por conjuga-
cin, es decir, para cada g G la funcin
(g) : G G : k g k g
1
resulta ser un automorsmo de (G, ), llamados automorsmos interiores. Denotaremos
por Int(G) al conjunto de los automorsmos interiores de G.
Ejercicio 3.2.4. Vericar que Int(G), con la operacin de composicin, es un sub-
grupo de Aut(G) y luego un subgrupo de Perm(G).
Ejercicio 3.2.5.
(1) Sea G
n
un grupo cclico de orden n. Vericar que existe un isomorsmo de grupos
entre Aut(G
n
) y (Z/nZ)
.
(2) Calcular Aut(Perm(X)) para un conjunto X de cardinalidad 2, 3, 4.
3.3. Teorema de Caeley
A continuacin veremos el clsico teorema de Caeley, el cual nos dice que todo grupo
se puede ver como un subgrupo de permutaciones de algn conjunto.
Sea (G, ) un grupo y consideremos al conjunto X = G. Entonces tenemos la funcin
: G Perm(G)
denida por
(g) : G G : k g k
Este es un ejemplo de lo que deniremos ms adelante como la accin de un grupo.
Ejercicio 3.3.1. Vericar que : G Perm(G) es un monomorsmo.
Teorema 3.3.2 (Teorema de Caeley). Todo grupo (G, ) es isomorfo a un subgrupo
del grupo Perm(G). De hecho, tal subgrupo est contenido en el subgrupo de Perm(G)
formado por los automorsmo interiores de G.
3.3. TEOREMA DE CAELEY 21
Ejemplo 3.3.3. Consideremos dos conjunto X e Y y supongamos que existe una fun-
cin biyectiva f : X Y . Entonces tenemos que para cada h Perm(X) vale que
f
(h) = f h f
1
Perm(Y ). La funcin
f
: Perm(X) Perm(Y ) es un iso-
morsmo de grupos. Como todo conjunto X de cardinalidad n > 0 es biyectivo con
el conjunto de los n primeros ndices 1, 2, ..., n, podemos identicar (mdulo isomor-
smos) el grupo Perm(X) con el grupo Perm(1, 2, ..., n) := o
n
, llamado el grupo
simtrico de n letras. Este grupo lo analizaremos en una seccin futura.
Ejercicio 3.3.4. Dar un ejemplo de un grupo de orden n para cada n 1, 2, 3, 4, ....
Ejemplo 3.3.5. Sea (G, ) un grupo nito de orden n. Por el teorema de Caeley, existe
un monomorsmo : (G, ) o
n
. Por otro lado, podemos construir un monomorsmo
: o
n
GL(n, Z)
denido por
((1, 2, ..., n)) =
_
_
_
_
_
_
_
_
0 0 0 0 1
1 0 0 0 0
0 1 0 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 1 0
_
_
_
_
_
_
_
_
((1, 2)) =
_
_
_
_
_
_
_
_
_
_
0 1 0 0 0
1 0 0 0 0
0 0 1 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 1 0
0 0 0 0 1
_
_
_
_
_
_
_
_
_
_
Luego, componiendo los dos monomorsmos anteriores permite obtener un monomor-
smo
: (G, ) GL(n, Z)
Ejercicio 3.3.6. Describir el monomorsmo : (G, ) GL(n, Z) construido
en el Ejemplo anterior.
3.4. Automorsmos interiores y grupos Abelianos
Ahora veremos que los automorsmos interiores de un grupo sirven para medir que
tan lejos esta un grupo de ser Abeliano.
Proposicin 3.4.1. Sea (G, ) un grupo. Entonces Int(G) = I, donde I : G G
denota al automorsmo identidad s y slo si G es Abeliano.
Demonstracin. Sea (G, ) un grupo Abeliano, g G y consideremos el automor-
smo interno
g
: G Gdenido por g. Entonces
g
(h) = ghg
1
= gg
1
h = h,
es decir,
g
= I. Recprocamente, si tenemos que Int(G) = I, entonces para g, h G
vale que
g
(h) = h, lo cual es equivalente a tener gh = hg. Como esto lo hemos hecho
para cualquier par de elementos de G, tenemos que G es Abeliano como queramos.
Ejemplo 3.4.2.
(1) Consideremos el grupo aditivo Z. Como este grupo es Abeliano, tenemos que
Int(Z) = I. Ahora, sea : Z Z un automorsmo. Sabemos que los ni-
cos generadores de Z son 1 y 1. As, (1) 1, 1. Si (1) = 1, entonces es
claro que (k) = k para cada k Z y luego obtenemos el automorsmo identidad
I. Si (1) = 1, entonces (k) = k para cada k Z obteniendo = I. De
esta manera obtenemos que Aut(Z) es un grupo cclico de orden 2.
(2) Consideremos un grupo G cclico de orden n y sea x un generador de G. Luego
G = I
G
, x, x
2
, x
3
, ..., x
n1
.
Sea e(n) la funcin de Euler evaluada en n. Ms adelante veremos que el n-
mero total de generadores de G es e(n). Al ser G Abeliano tenemos que Int(G)
es trivial. Sea Aut(G). Entonces (x) puede tomar como valor cualquiera de
los generadores de G. Adems, una vez indicado el valor de (x) tenemos deter-
minado completamente el automorsmo ya que (x
l
) = (x)
l
por ser este un
homomorsmo de grupo. De esta manera obtenemos que [Aut(G)[ = e(n).
CAPTULO 4
GRUPOS CCLICOS
Denicin 4.0.3. Aquellos grupos que se pueden generar con un slo elemento son
llamados grupos cclicos.
Tenemos dos tipos de casos ; grupos cclicos nitos y grupos cclicos innitos. Obser-
vemos que si (G, ) es un grupo cclico nito, con un generador x, entonces [G[ = o(x).
El primer resultado bsico es el siguiente.
Proposicin 4.0.4. Todo grupo cclico es Abeliano
Demonstracin. Sea x un generador del grupo cco G. Entonces todo elemento de G
es de la forma x
a
para algn a Z. Como
x
a
x
b
= x
a+b
= x
b+a
= x
b
x
a
tenemos lo deseado
Ejemplo 4.0.5.
(1) En ejercicio 1.2.2 tenemos que S y T son generadores de Perm(X). Ms an, este
no puede ser cclico. De hecho, el grupo Perm(X) no puede ser cclico cuando la
cardinalidad de X es al menos 3.
(2) El grupo aditivo Z tiene como generador a 1 (tambin lo es 1 y no hay otros) y,
en particular, es un grupo cclico.
(3) El conjunto aditivo R no puede ser generado con un nmero nito de generadores
(la razn de esto lo tendremos que ver mucho ms adelante). Este no puede ser un
grupo cclico como consecuencia del siguiente.
Ejemplo 4.0.6 (Grupos Cclicos innitos). Sea Gun grupo un grupo cclico innito,
digamos generado por x.
24 CAPTULO 4. GRUPOS CCLICOS
(i) Sea H un subgrupo de G diferente de I y consideremos la menor potencia po-
sitiva de x, digamos x
m
, contenida en H. Entonces el grupo cclico generado por
x
m
est contenido en H. Si esta contencin fuese estricta, entonces debe existir
x
n
H x
m
). Esto nos dice que existe s > 0 tal que (s 1)m < n < sm. Esto
nos segura que x
smn
H contradiciendo la minimalidad de m. En particular,
todo subgrupo de un grupo cclico innito es tambin un grupo cclico innito.
(ii) Si x
n
es otro generador de G, entonces debe existir un entero r Z de manera
que x
nr
= x, es decir, x
nr1
= I. Como x tiene orden innito, esto obliga a tener
nr = 1, es decir, n 1. En consecuencia, si x genera un grupo cclico innito,
entonces x
1
es el nico generador diferente de x.
(iii) La funcin : Z G, denida por (k) = x
k
, resulta ser un isomorsmo de
grupos.
Ejemplo 4.0.7 (Grupos Cclicos nitos). Sea G un grupo cclico de orden n, diga-
mos generado por x, luego o(x) = n.
(i) Sea H un subgrupo de G, diferente de I
G
. Si consideramos la menor potencia de
x contenido en H, digamos x
m
, entonces H es un grupo cclico generado por x
m
.
En efecto, si no fuese esto cierto, deberiamos tener alguna potencia x
k
H que no
estn x
m
) = I
G
, x
m
, x
2m
, ..., x
rm
. En tal caso, debemos tener que (s 1)m <
k < sm, para algn s 1, ..., r. Pero en tal caso, x
k(s1)m
H y obtenemos
una contradiccin de la minimalidad de m.
(ii) Si escogemos d > 0 un divisor de n, entonces existe un y nico subgrupo de G
de orden igual a d. En efecto, si tomamos y = x
n
d
, entonces el grupo generado por
y es de orden d. Esto no da la existencia. Para ver la unicidad, supongamos que H
es un subgrupo de G de orden d. Por (i), H = x
m
) donde m lo podemos escoger
dividiendo n y tal que
n
m
= d. Luego m =
n
d
.
(iii) Sea m 1, 2, 3, ..., n, y = x
m
y H el subgrupo generado por y. Por el teorema
de Lagrange, [H[ = o(y) = t divide n. En particular, podemos escribir n = tq para
cierto q 1, 2, 3, ..., n 1. Consideremos K el subgrupo generado por z = x
q
,
el cual tiene orden t. Por (ii) tenemos que H = K. En particular, existe un entero a
tal que x
am
= x
q
. Esto ltimo dice que existen enteros a, b tales que am+bn = q,
es decir M.C.D.(m, n) = q (mximo comn divisor entre m y n).
(iv) De (iii) vemos que x
m
genera G s y slo si M.C.D.(m, n) = 1, es decir
(m, n) = 1.
(v) La funcin : Z/nZ G, denida por ([k]) = x
k
, resulta ser un isomorsmo
de grupos.
Proposicin 4.0.8. Sea G un grupo cclico de orden n, digamos generado por x.
(a) Para k 1, 2, ..., n 1 tenemos que x
k
genera G s y slo si (k, n) = 1, es
decir, k y n son relativamente primos. En particular, la cantidad de generadores de
G es e(n).
CAPTULO 4. GRUPOS CCLICOS 25
(b) Todo subgrupo de G es cclico y est generado por una potencia x
d
, donde d
divide n, y tiene orden n/d. Adems hay exctamente un subgrupo de cada posible
orden.
(c) Sean k 1, 2, ..., n 1 y q = M.C.D.(k, n). Entonces x
k
y x
q
generan el
mismo subgrupo.
Proposicin 4.0.9. Sean n, menteros y q = M.C.D.(n, m). Entonces existen enteros
a, b Z tales que
q = an +bm
En particular, si (m, n) = 1, entonces existen enteros a, b Z tales que
1 = an +bm
Demonstracin.
(1) Usando grupos cclicos nitos. Es claro lo anterior cuando n = m. Supongamos
entonces que n > m. Consideremos el grupo cclico de orden n generado por un
elemento x. Ahora procedemos como en (iii) del ejemplo anterior.
(2) Usando grupos cclicos innitos. Podemos vericar la proposicin de la siguiente
manera. Consideremos el grupo cclico innito Z y sea H su subgrupo generado por
n y m. Sabemos que H debe ser cclico, digamos generado por r 0, 1, 2, ....
Como n, m H, tenemos que r divide a ambos n y m y como consecuencia, r
divide a d = M.C.D.(n, m). Esto ltimo nos dice que el grupo cclico generado
por d est contenido en H. Pero, como d divide a ambos n y m, tenemos que H est
contenido en el grupo cclico generado por d. Como consecuencia, H = d).
Ejercicio 4.0.10. Generalizar lo anterior, es decir, vericar que dados enteros
n
1
, ..., n
m
y d = M.C.D.(n
1
, ..., n
m
), entonces existen enteros r
1
, ..., r
n
tales que
d = r
1
n
1
+ +r
m
n
m
CAPTULO 5
GRUPOS COCIENTES
Partamos con un grupo (G, ) y un subgrupo H de este. Podemos denir la relacin
de equivalencia siguiente : Sean x, y G, diremos que ellos son equivalentes por H a
la derecha si existe h H tal que y = x h. La clase de equivalencia derecha de x la
denotaremos por xH. De manera similar, diremos que ellos son equivalentes por H a la
izquierda si existe h H tal que y = h x. La clase de equivalencia izquierda de x es
denotada por Hx.
Ejercicio 5.0.11. Vericar que las anteriores son relaciones de equivalencia
Consideremos la relacin de equivalencia derecha de H en G(lo que haremos es simi-
lar para la otra relacin de equivalencia). Denotemos por G/H al conjunto de las clases
de equivalencias derechas de los elementos de G y por
H
: G G/H a la proyeccin
natural, es decir,
H
(x) = xH. Observemos que H es la clase de equivalencia de I
G
.
Tomemos una clase cualquiera, digamos xH. Entonces la funcin f : H xH,
denida por f(h) = xh, es una funcin biyectiva. De esta manera, la cardinalidad de toda
clase de equivalencia es igual al orden de H, es decir a [H[.
Denicin 5.0.12. Denotemos por [G : H] la cardinalidad del conjunto de clases
G/H, tambin llamado el ndice de H en G.
Usando el hecho que dos clases de equivalencia coinciden o son disjuntos, obtenemos
el siguiente :
Teorema 5.0.13 (Teorema de Lagrange). Si G tiene orden nito, entonces
[G[ = [G : H][H[
Ejercicio 5.0.14. Usar el teorema de Lagrange para obtener lo siguiente. Sea G un
grupo nito y sean subgrupos K < H < G. Entonces [G : K] = [G : H][H : K]
28 CAPTULO 5. GRUPOS COCIENTES
Si tomamos un elemento g G, donde (G, ) es algn grupo, entonces el subgrupo
generado por l g) tienen orden igual a o(g). Una primera aplicacin de este resultado es
el siguiente :
Corolario 5.0.15. Sea (G, ) un grupo de orden nito, H un subgrupo de G y g G.
Entonces [H[ y o(g) dividen al orden de G como consecuencia del teorema de Lagrange.
Lo anterior, por ejemplo, nos permite ver que un grupo de orden 6 no puede tener ele-
mentos ni subgrupos de orden 4. Una segunda aplicacin es la siguiente caracterizacin.
Proposicin 5.0.16. Sea G un grupo nito de orden p, donde p es algn primo. En-
tonces G es necesariamente un grupo cclico.
Demonstracin. Tomemos cualquier elemento x G I
G
. Por la proposicin
anterior, o(x) divide al nmero primo p. Como o(x) > 1, necesariamente o(x) = p.
Consideremos el subgrupo cclico de G dado por x). Como el orden de x) coincide con
o(x) = p, tenemos que G = x).
Ejemplo 5.0.17. Consideremos un grupo (G, ) de orden 4. Si G contiene un ele-
mento de orden 4, digamos x, entonces G = x), es decir, G es un grupo cclico de orden
4. Supongamos ahora que G no contiene elementos de orden 4. Como el orden de cada
elemento no trivial (es decir diferente del neutro) debe dividir 4, debemos tener que todos
ellos tienen orden 2. Sea x G I
G
. Luego x) est formado por el neutro I
G
y x.
Como Gtiene orden 4, podemos escoger otro elemento y Gx). Tenemos que y tiene
orden 2. Como (xy)
2
= I
G
, x
2
= y
2
= I
G
, tenemos xy = yx. Consideremos el sub-
grupo H de Ggenerado por x e y. Tenemos que H = I
G
, x, y, xy (xy ,= x, y ya que
x, y ,= I
G
). Pero [H[ = 4, lo cual dice que G = H. Ahora, consideremos / = x) y)
con la operacin binaria denida componente a componente (en cada factor usamos la
operacin ). Este grupo es llamado el grupo de Klein. Consideremos la funcin
F : K G : (x
a
, y
b
) x
a
y
b
Tenemos que F es un isomorsmo de grupos. Adems, como / no es cclico, obtenemos
que mdulo isomorsmos slo hay dos grupos.
Ejercicio 5.0.18. Vericar que la operacin binaria para / dota de la estructura de un
grupo Abeliano a /, que F es en efecto un isomorsmo de grupos. Calcular y comparar
las tablas de multiplicacin de estos dos tipos de grupos de orden 4.
Ejercicio 5.0.19. Vericar que dos grupos cclicos nitos del mismo orden son
siempre isomorfos.
CAPTULO 5. GRUPOS COCIENTES 29
Ejercicio 5.0.20. Determinar, mdulo isomorsmos, los grupos de orden n
1, 2, ..., 7.
Volvamos a mirar la proyeccin
H
: G G/H : x xH
Una pregunta natural es la posibilidad de dotar a G/H de una estructura de grupo que sea
compatible con la de G por medio de
H
. Compatibilidad signica que haga
H
de un
homomorsmo de grupos. En la mayora de los casos esto no ser posible, pero existen
ciertos subgrupos que permiten esto. Tratemos de forzar una operacin binaria en G/H
para que haga de
H
un homomorsmo. Primero, debemos tener
H
(x y) =
H
(x)
H
(y)
lo que es equivalente a decir
(x y)H = x Hy H
para todos x, y G. Luego tenemos forzada nuestra operacin binaria a ser denida
como :
: G/H G/H G/H : (xH, yH) (x y)H
Para que esta funcin tenga sentido, debemos asegurarnos que lo anterior no dependa
de los representantes de las clases respectivas, es decir, si x
H = xH, y
H = yH,
entonces (x
)H = (x y)H. Pero x
= x h
1
e y
= y h
2
para ciertos h
1
, h
2
H.
Luego lo anterior es equivalente a tener
(x h
1
y h
2
)H = (x y)H
es decir
(h
1
y)H = yH
o de manera equivalente
y
1
h
1
y H
En resumen, para que lo anterior tenga sentido, debemos tener la propiedad
zH = Hz, para todo z G
Denicin 5.0.21. Un subgrupo H de G con la propiedad que
zH = Hz, para todo z G
es llamado un subgrupo normal de G.
Proposicin 5.0.22. Sea H un subgrupo normal de G. Entonces G/H resulta ser un
grupo con la operacin binaria con la cual
H
: G G/H es un homomorsmo de
grupos cuyo ncleo es exactamente H. Este grupo cociente es tambin llamado el grupo
de las clases laterales de H en G. Ms an, (i) si G es Abeliano, entonces G/H tambin
es Abeliano; y (ii) si G es cclico, entonces G/H tambin es cclico.
Demonstracin. La asociatividad de es heredada por la de . Por otro lado,
HH = H (H es la clase de I
G
), lo cual nos est forzando a tomar H como elemento
neutro I
G/H
. Hasta ahora todo camina bin. Sea xH G/H y tratemos de buscar un
candidato para el inverso. Por la condicin de hacer
H
de un homomorsmo, estamos
obligados a tener
H
(x
1
) =
H
(x)
1
lo cual es equivalente a pedir que
(xH)
1
= x
1
H
Esta denicin funciona correctamente y tenemos que G/H resulta ser un grupo con la
operacin binaria con la cual
H
: G G/H es un homomorsmo de grupos cuyo
ncleo es exactamente H.
La denicin de la operacin asegura que si es commutativa, entonces tambin lo
es . Por otro lado, si G es cclico generado por x, entonces xH es generador de G/H.
Ejemplo 5.0.23. Sea H un subgrupo de ndice dos en un grupo G (con operacin
binaria de grupo dada por ). Entonces podemos escribir
G = H xH = H Hx
para cualquier x G H, donde las uniones son disjuntas. Tomemos g G. entonces
(i) g H, en cuyo caso g h g
1
H, para todo h H, o (ii) g = x h
1
= h
2
x,
para ciertos h
1
, h2 H. Ahora, si h H, entonces g h g
1
= x h
1
h
1
3
x
1
=
xh
4
x
1
, donde h
4
H. Si tenemos xh
4
x
1
/ H, entonces xh
4
x
1
xH,
lo cual dice que h
4
x
1
H. Esto ltimo asegura que x H, una contradiccin. Hemos
vericado el siguiente.
Proposicin 5.0.24. Todo subgrupo de ndice dos es necesariamente un subgrupo
normal.
Ejemplo 5.0.25. Consideremos el grupo, con la regla de composicin, de todos los
difeomorsmos de R
n
. Sea H el subgrupo de los difeomorsmos con jacobiano positivo
(difeomorsmos que preservan la orientacin). Como el jacobiano de una composicin
es el producto de los respectivos jacobianos, tenemos entonces que H es un subgrupo de
ndice dos y luego un subgrupo normal.
Ejemplo 5.0.26.
(1) Si G es un grupo Abeliano, entonces todo subgrupo es necesariamente normal.
(2) Consideremos X = 1, 2, 3 y G = Perm(X). Tenemos que
A =
_
_
_
1 2
2 3
3 1
y B =
_
_
_
1 2
2 1
3 3
forman un conjunto de generadores de G (comparar con el ejemplo 1.2.2). Los
subgrupos de G son, aparte del trivial I
G
y del total G, los subgrupos de or-
den dos B), A B), A
2
B) y el grupo de orden tres A), todos ellos ccli-
cos. Como B A B = A
3
, tenemos que A) es subgrupo normal de G. Pero
ABA
1
= A
2
B , AABA
1
= AB y AA
2
BA
1
= B, tenemos
que ninguno de los tres subgrupos de orden dos es subgrupo normal. Observemos
tambin que [G : A)] = 2, luego G/A) es un grupo de orden dos (luego cclico).
Ejercicio 5.0.27. Considere el grupo multiplicativo de las matrices reales de tamao
n n y determinante no cero (es decir, la invertibles). Calcular todos su subgrupos nor-
males.
Ejemplo 5.0.28. Consideremos el grupo aditivo Z y sea n 2, 3, 4, 5, .... Entonces
se tiene que nZ = nk : k Z es un subgrupo de Z y, como este es Abeliano, es
tambin subgrupo normal. Se tiene que [Z : nZ] = n y, como consecuencia,
Z/nZ
es un grupo Abeliano de orden n, llamado el grupo de las clases residuales de orden n.
Este es un grupo cclico de orden n (luego todo grupo cclico de orden n es isomorfo
a Z/nZ. Como consecuencia, el grupo de Klein es isomorfo a Z/2Z Z/2Z, con la
operacin binaria componente a componente.
Ejemplo 5.0.29. Volvamos al grupo de automorsmos de un grupo G, Aut(G). Ya
habamos denido el subgrupo de Aut(G) dado por los automorsmos interiores, Int(G).
Para cada g G, tenemos el automorsmo interior
g
: G G, denido por
g
(h) =
g h g
1
. Sea T Aut(G). Entonces,
T
g
T
1
=
T(g)
obteniendo que Int(G) es un subgrupo normal de Aut(G). El grupo cociente
Out(G) = Aut(G)/Int(G)
es llamado el grupo de automorsmos exteriores de G. As, si G es un grupo Abeliano,
entonces Aut(G) = Out(G).
Ejercicio 5.0.30. Calcular Out(Perm(X)) para X como en el ejemplo 1.2.2.
Proposicin 5.0.31. Consideremos un homomorsmo de grupos : G K, donde
(G, ) y (K, ) son ciertos grupos. Entonces tenemos que Ker() es un subgrupo normal
de G. De hecho, si U es un subgrupo normal del grupo (G), entonces
1
(U) es sub-
grupo normal de G. Recprocamente, si H es un subgrupo normal de G, entonces (H)
es un subgrupo normal de (G).
Demonstracin. (i) Sea h Ker() y g G. Entonces
(g h g
1
) = (g) (h) (g)
1
= I
K
(ii) Sea U subgrupo normal de (G), entonces sabemos que
1
(U) es un subgrupo de G.
Por otro lado, si h
1
(U) y g G, entonces (ghg
1
) = (g)(h)(g)
1
U,
obteniendo la normalidad de
1
(U). (iii) Sea H un subgrupo normal de G. Ya sabemos
que (H) es un subgrupo de (G). Ahora, si tomamos t (G) y k (H), entonces
existen g G y h H tales que (g) = t y (h) = k. Luego t k t
1
= (g) (h)
(g)
1
= (g h g
1
) (H).
El resultado anterior nos permite considerar el grupo cociente G/Ker() para cada
homomorsmo de grupos : G K. Podemos entonces denir la nueva funcin

:
G/Ker() K como
(xKer()) = (x)
Proposicin 5.0.32 (Primer teorema del isomorsmo).
La funcin

: G/Ker() K est bin denida y es un monomorsmo.
Demonstracin. Para ver que est bin denida basta ver que si x G y h Ker()
entonces (x h) = (x). Ahora,
(xKer()xKer()) =

((x y)Ker()) = (x y) =
= (x) (y) =

(xKer())

(yKer())
Corolario 5.0.33. La funcin

: G/Ker() (G) es un isomorsmo. En particu-
lar ; si G tiene orden nito, entonces tenemos que [(G)[ = [G : Ker()].
Ejemplo 5.0.34. Sean : G K un homomorsmo de grupos y H un subgrupo de
G. Podemos restringir nuestro homomorsmo a H, [
H
: H K. Ahora, Ker([
H
) =
Ker() H. Luego tenemos un isomorsmo entre (H) y G/(H Ker()).
Como consecuencia de esto es que si H es adems un subgrupo normal de G, entonces
usando K = G/H, tenemos una biyeccin, dada por =
H
, entre los subgrupos
(normales) de G/H y los subgrupos (normales) de G que contienen a H.
Para nuestro siguiente ejemplo necesitaremos el subgrupo generado por la unin de dos
subgrupos, lo cual pasamos a mirar inmediatamente. Supongamos que tenemos un grupo
(G, ) y dos subgrupos de este, digamos H y K. Podemos entonces mirar el subgrupo de
G generado por H y K, es decir, H K). Es claro que
HK = h k : h H, k K H K)
Luego, la igualdad H K) = HK es cierta s y slo si HK es un subgrupo de G. El
siguiente resultado nos permite ver cuando ocurre esta situacin.
Proposicin 5.0.35. HK es subgrupo de G s y slo si HK = KH.
Demonstracin. Supongamos que HK es un subgrupo de G. En tal caso considere-
mos un elemento h k HK. Tenemos que su inverso (h k)
1
= k
1
h
1
pertenece
a KH. Como todo elemento de HK (por ser subgrupo) es inverso de alguno de sus otros
elementos, tenemos la contencin HK KH. Por otro lado, dado kh KH, entonces
h
1
k
1
HK. Al ser HK subgrupo tenemos que este debe contener al inverso, es decir
k h HK, obteniendo la contencin KH HK.
Veamos ahora el recproco y supongamos la igualdad HK = KH. Sean h
1
k
1
, h
2
k
2
HK. Luego (h
1
k
1
) (h
2
k
2
) = h
1
(k
1
h
2
) k
2
. Pero la igualdad HK = KH
asegura que k
1
h
2
= h
3
k
3
, as, (h
1
k
1
) (h
2
k
2
) = (h
1
h
3
) (k
3
k
2
) HK.
Tambin, si h k HK, entonces (h k)
1
= k
1
h
1
KH = HK. Como
consecuencia, HK es un subgrupo de G.
Observacin 5.0.36. Si tenemos H, K subgrupos de G y uno de ellos es un subgrupo
normal, entonces la condicin HK = KH vale trivialmente. Ms an, si ambos son
subgrupos normales, entonces HK tambin lo es.
Ejercicio 5.0.37. Vericar la observacin anterior.
Suponiendo que G es un grupo de orden nito, tenemos que HK (independiente de
ser o no un subgrupo) tiene una cardinalidad nita. Para ver que valor tiene esta, conside-
remos la funcin
F : H K HK : (h, k) h k
Por la denicin de HK, F es una funcin sobreyectiva. Tambin sabemos que [H
K[ = [H[[K[. Por otro lado, si HK, entonces
F
1
() = (h, k) H K : h k =
Ahora, si (h
1
, k
1
), (h
2
, k
2
) F
1
(), entonces h
1
k
1
= h
2
k
2
, lo cual asegura que
h
1
2
h
1
= k
2
k
1
1
= x H K. Entonces h
2
= h
1
x
1
, k
2
= x k
1
. En forma
recproca, si x H K y (h, k) F
1
(), entonces F(h x
1
, x k) = . Como
consecuencia, #F
1
() = [H K[. De esta manera, como preimgenes de valores
diferentes son disjuntos y la unin de todas la preimgenes es H K, obtenemos
#HK =
[H[[K[
[H K[
Ejemplo 5.0.38 (Segundo Teorema del isomorsmo). Sean (G, ) un grupo, H, K
subgrupos de G y supongamos que H es adems subgrupo normal de G. De esta manera
nos aseguramos que HK es subgrupo de G. Como H es tambin subgrupo de HK,
tenemos que H es subgrupo normal de HK. Consideremos la proyeccin : HK
HK/H : x xH. Consideremos las restriccin a K, es decir, [
K
: K HK/H.
Tenemos que Ker([
K
) = K H. Veamos ahora que [
K
es sobreyectiva. En efecto, si
z = (h k)H HK/H, entonces como HK = KH, tenemos que h k = k
1
h
1
y
luego [
K
(k
1
) = z. En consecuencia, tenemos un isomorsmo
K
K H
=
HK
H
Ejemplo 5.0.39 (Tercer Teorema del isomorsmo). Consideremos un grupo (G, )
y dos subgrupos normales de G, digamos K y H, tales que K < H. Consideremos la
funcin
: G/K G/H : gK gH
Entonces resulta ser un homomormos sobreyectivo. Por otro lado,
Ker() = gK : g H = H/K
es decir
G/H

= (G/K)/(H/K)
Ejemplo 5.0.40. Consideremos un grupo nito (G, ) y H un subgrupo normal de G
tal que ([G : H], [H[) = 1, es decir, [G : H] y [H[ son relativamente primos. Veamos
que no existe otro subgrupo de G del mismo orden que H. En efecto, supongamos que
existe K subgrupo (no necesariamente normal) de G tal que [K[ = [H[. Tomemos el
homomorsmo : K G/H : k kH. Entonces, Ker() = KH y K/(KH)
=
(K). En particular, [K : K H] divide [G : H], por el teorema de Lagrange, es decir,
[G : H] = [K : K H]M = [K[R
para ciertos enteros positivos M, R. Esto dice que [H[ = [K[ divide [G : H], una contra-
diccin a menos que K = H.
Ejercicio 5.0.41.
(i) Sea (G, ) un grupo y sean H, K dos subgrupos de G. Suponga que [G : H] <
y [G : K] < . Vericar que [G : H K] <
(ii) Sea S
1
el grupo multiplicativo de los nmeros complejos de valor absoluto 1 con
la operacin usual de producto. Consideremos el grupo aditivo (R, +) y su subgrupo
normal Z. Vericar que el siguiente es un isomorsmo de grupos
P : R/Z S
1
: xZ e
2xi
(iii) Sea (G, ) un grupo y sea H = x
2
: x G). Vericar que H es subgrupo
normal de G y que el grupo cociente G/H es un grupo Abeliano.
(iv) Sea (G, ) un grupo y sea n > 1 un entero positivo jo. Supongamos que para
todo x, y G vale la igualdad (x y)
n
= x
n
y
n
. Dena
G
n
= x : o(x) = n)
G
n
= x
n
: x G)
Vericar que ambos son grupos normales de G y que G/G
n

= G
n
(Ind. Utilizar el
homomorsmo : G G
n
: x x
n
).
CAPTULO 6
ALGUNOS SUBGRUPOS NORMALES Y ABELIANIZACIN DE
GRUPOS
Dado un grupo (G, ), existe la posibilidad que este sea Abeliano, pero en general no
es as. La condicin de ser Abeliano es equivalente a que la ecuacin
[x : y] = x y x
1
y
1
= I
G
sea siempre valida para cualquier x, y G.
Denicin 6.0.42. Cada expresin
[x : y] = x y x
1
y
1
es llamada un conmutador de x e y. Denotamos por [G, G] al subgrupo de G generado
por todos los conmutadores.
Ejercicio 6.0.43. Sea (G, ) un grupo. Vericar que
[G, G] = x
1
x
2
x
n
x
1
1
x
1
2
x
1
n
: x
j
G, n 2
y concluir que [G, G] es un subgrupo normal de G.
(Ind. (a b a
1
b
1
) (c d c
1
d
1
) =
a (b a
1
) b
1
c (d c
1
) d
1
a
1
(a b
1
) b c
1
(c d
1
) d)
Proposicin 6.0.44. La interseccin arbitraria de subgrupos normales de un grupo
(G, ) es un subgrupo normal.
Demonstracin. Sean H
j
: j J una coleccin de subgrupos normales de G. Ya
habamos vericado que la interseccin de estos subgrupos es un subgrupo de G. Ahora
slo necesitamos vericar la normalidad. Sea g G y h H =
jJ
H
j
. Entonces,
h H
j
, para cada j J. Como H
j
es subgrupo normal, tenemos que g h g
1
H
j
,
para cada j J y, como consecuencia, g h g
1
H.
38 CAPTULO 6. ALGUNOS SUBGRUPOS NORMALES Y ABELIANIZACIN DE GRUPOS
Observemos que si G es Abeliano, entonces [G, G] = I
G
. Recprocamente,
[G, G] = I
G
asegura que [x : y] = I
G
siempre vale para cualquier x, y G,
obteniendo que G es Abeliano. Es decir, tenemos que
Proposicin 6.0.45. Un grupo (G, ) es Abeliano s y slo si [G, G] = I
G
.
Luego, si (G, ) no es un grupo Abeliano, entonces [G, G] ,= I
G
nos d un subgrupo
normal no trivial de G. La normalidad de [G, G] nos permite mirar el grupo
G
abel
= G/[G, G]
el cual es llamado la abelianizacin de G.
Proposicin 6.0.46. El grupo cociente G
abel
es un grupo Abeliano.
Demonstracin. sean x[G, G], y[G, G] G
abel
. Luego,
[x[G, G] : y[G, G]] = x[G, G]y[G, G](x[G, G])
1
(y[G, G])
1
=
= x[G, G]y[G, G]x
1
[G, G]y
1
[G, G] = (x y x
1
y
1
)[G, G] =
= [G, G]
Denicin 6.0.47. Otro de los subgrupos de (G, ) que mide la cercana de G a ser
Abeliano es el siguiente :
Z(G) = g G : [g, x] = I
G
para todo x G
llamado el centralizador de G. Tambin podemos hablar del centralizador de un elemento
g del grupo G que est denido por
Z(G; g) = x G : g x = x g
Ejercicio 6.0.48. Vericar que Z(G; g) es un subgrupo de G y que Z(G; g) = G s y
slo si g Z(G).
Proposicin 6.0.49. Z(G) es siempre un subgrupo normal de G.
Demonstracin. Es claro que I
G
Z(G), luego Z(G) ,= . Sean x, y Z(G),
entonces [x, w] = [w, x] = [y, w] = [w, y] = I
G
, vale para cada w G. Pero, para
cada w G, tenemos que x [x
1
: w] X
1
= [w, x] = I
G
asegurando que [x
1
:
w] = I
G
y, como consecuencia, x
1
Z(G). Tambin, para cada w G, tenemos que
[x y, w] = [x, w] = I
G
y, como consecuencia, x y Z(G). Hemos vericado que
Z(G) es un subgrupo de G.
CAPTULO 6. ALGUNOS SUBGRUPOS NORMALES Y ABELIANIZACIN DE GRUPOS 39
Sea g G, x Z(G). entonces [g x g
1
, y] = g x g
1
y g x
1
g
1
y
1
.
Pero x Z(G) dice que x conmuta con cada elemento de G, luego [g x g
1
, y] = I
G
,
es decir, g x g
1
Z(G), con lo cual obtenemos la normalidad de Z(G) en G.
Observemos que si G es Abeliano, entonces Z(G) = G. Recprocamente, si Z(G) =
G, entonces [y, x] = I
G
es vlido para todo x, y G, es decir, G es Abeliano ; luego
tenemos el siguiente.
Proposicin 6.0.50. Un grupo (G, ) es Abeliano s y slo si
Z(G) = G.
Proposicin 6.0.51. Si (G, ) no es un grupo Abeliano, entonces G/Z(G) no puede
ser un grupo cclico. En particular, [G : Z(G)] no puede ser un primo.
Demonstracin. Sea (G, ) un grupo que no es Abeliano, es decir G ,= Z(G). Supon-
gamos por el contrario que G/Z(G) es un grupo cclico. Podemos escoger u GZ(G)
tal que uZ(G) genera G/Z(G). Tomemos un elemento x G Z(G). Existe a
1, 2, ..., p 1 tal que xZ(G) = u
a
Z(G). Para cada y Z(G) tenemos [x : y] = I
G
.
Para y GZ(G) tenemos que yZ(G) = u
b
Z(G), para cierto b 1, ..., p 1. Esto
nos dice que podemos encontrar z, w Z(G) tales que x = u
a
z, y = u
b
w. En
particular,
[x : y] = (u
a
z) (u
b
w) (u
a
z)
1
(u
b
w)
1
=
= u
a
z u
b
w z
1
u
a
w
1
u
b
= u
a+bab
= I
G
Como consecuencia, x Z(G), una contradiccin.
Proposicin 6.0.52. Sea G un grupo nito y x
1
, x
2
G elementos de orden 2 tales
que x
1
x
2
tiene orden n. Entonces Z(G; x
j
) tiene orden a lo ms 2[G[/n, para j = 1, 2.
Demonstracin. Sea H el subgrupo de G generado por x
1
y x
2
. Denotemos por D
n
el grupo dihedral de orden 2n generado por a y b, con las relaciones
a
n
= b
2
= (ab)
2
= 1
Entonces tenemos un homomorsmo sobreyectivo : D
n
H, denido por : (b) = x
1
y (a) = x
2
x
1
. Ahora, el ncleo de es un subgrupo normal de D
n
. Pero los nicos
subgrupo normales de D
n
son los subgrupos triviales 1, D
n
y los subgrupos cclicos
generados por una potencia no trivial de a. Los ltimos dos casos obligarn tener que el
cociente D
n
/Ker()
= H es trivial el elemento a se proyecta a un elemento de orden

menor a n, una contradiccin. Luego : D
n
H es un isomorsmo. Ahora, se puede
vericar que Z(H; x
j
) es isomorfo a Z/2Z si n es impar bin isomorfo a Z/2ZZ/2Z
si n es par. En cualquier caso, el orden de Z(H; x
j
) es a lo ms 4.
Consideremos una descomposicin en clases laterales izquierda de G por H, es decir
G = H z
1
H z
2
H z
3
H z
n
40 CAPTULO 6. ALGUNOS SUBGRUPOS NORMALES Y ABELIANIZACIN DE GRUPOS
donde n = [G : H] y z
1
= I
G
. Tenemos que Z(G; x
j
) H = Z(H; x
j
). Supongamos
que tenemos dos elementos de Z(G; x
j
) en la misma H z
l
, digamos g
1
= h
1
z
l
, g
2
=
h
2
z
l
Z(G; x
j
). Entonces h
1
h
1
2
= g
1
g
1
2
H Z(G; x
j
) = Z(H; x
j
).
Luego el orden de Z(G; x
j
) H z
l
es el mismo orden de Z(H; x
j
). Como tenemos la
descomposicin disjunta
Z(G; x
j
) = (Z(G; x
j
) H) (Z(G; x
j
) H z
2
) (Z(G; x
j
) H z
n
),
tenemos de lo anterior que el orden de Z(G; x
j
) es igual a [G : H] veces el orden de
Z(H; x
j
), es decir a lo ms 4[G[/[H[ = 2[G[/n.
Ejemplo 6.0.53. Consideremos un grupo (G, ) y denotemos por G
tor
el subgrupo
generado por todos los elementos de orden nito de G. Si h tiene orden nito y g G,
entonces g h g
1
tiene el mismo orden nito que h. Como los elementos de G
tor
son
de la forma x
1
x
2
x
n
, donde x
j
G tienen orden nito, obtenemos que G
tor
es un subgrupo normal de G. Es claro que si G es de orden nito, entonces G = G
tor
.
Podemos tener grupos G de orden innito con G = G
tor
, por ejemplo, considere G
el grupo generado por las reexiones de Mbius A(z) = z y B(z) = z + 1. Este
grupo contiene a la translacin B A(z) = z + 1 y luego G es innito. Por otro lado,
A, B G
tor
asegura que G = G
tor
. De manera ms general, si Gpuede ser generado por
elementos de ordenes nito, entonces G = G
tor
. Si G no contiene elementos de orden
nito diferentes del neutro, entonces G
tor
= I
G
. Un grupo que tiene la propiedad que
sus elementos diferentes de la identidad no tienen orden nito, es decir, G
tor
= I
G
son
llamados grupos sin torsin.
Dado un subgrupo H de un grupo dado (G, ), lo ms probable que ocurra es que H
no sea un subgrupo normal de G. Una de las cosas que podemos hacer es considerar el
subgrupo normal ms pequeo de G que contenga a H,
H))
el cual resulta ser la interseccin de todos los subgrupos normales de G que contienen
a H. Tal coleccin sobre la que hacemos la interseccin no es vaca ya que G pertenece
trivialmente a esta. Llamamos a tal subgrupo normal la cpsula normal del subgrupo H.
El siguiente es claro por la denicin.
Proposicin 6.0.54. H = H)) s y slo si H es subgrupo normal de G.
Otra cosa que podemos hacer es considerar el normalizador de H, denido por
N
G
(H) = g G : g H g
1
= H
Puede ocurrir que N
G
(H) no sea un subgrupo normal de G. Es claro que cada h
H debe pertenecer a N
G
(H), ya que si t H, entonces h
1
t h H y luego
h (h
1
t h) h
1
= t. De esta manera, H es un subgrupo de N
G
(H). Como cada
elemento de N
G
(H) tiene la propiedad de conjugar H en si mismo, obtenemos que :
CAPTULO 6. ALGUNOS SUBGRUPOS NORMALES Y ABELIANIZACIN DE GRUPOS 41
Proposicin 6.0.55. H es subgrupo normal de N
G
(H).
CAPTULO 7
PRODUCTOS DE GRUPOS
7.1. Producto Directo de Grupos
Una de las maneras de producir nuevos grupos a partir de algunos dados es por medio
del producto directo. Sea (G
j
,
j
) : j J una coleccin no vaca de grupos (nita o
innita). Formemos el producto cartesiano
jJ
G
j
= f : J
_
jJ
G
j
: f(j) G
j
La operacin binaria es dada por

f g(j) = f
j

j
g
j
Proposicin 7.1.1. La operacin binaria as denida dene en
jJ
G
j
una estruc-
tura de grupo, llamado el producto directo de los grupos G
j
, j J.
Demonstracin. La asociatividad es equivalente a la asociatividad coordenada a co-
ordenada. El neutro es dado por I, donde I(j) = I
Gj
. El inverso de cada f

jJ
G
j
es dado por f
1
(j) = f
1
j
.
Observacin 7.1.2. Cuando cada grupo G
j
es un grupo Abeliano, usualmente habla-
mos de la en vez del producto directo y se acostumbra a denotarlo por
jG
G
j
Ejercicio 7.1.3. Supongamos que G
k
, k = 1, 2, 3, ..., n son n grupos nitos. Vericar
que [
n
j=1
G
j
[ =
n
j=1
[G
j
[.
Por cada k J tenemos de manera natural la inclusin
i
k
: G
k

jJ
G
j
44 CAPTULO 7. PRODUCTOS DE GRUPOS
denido por
i
k
(x) : J
jJ
G
j
: j
_
I
Gj
j ,= k
x j = k
Ejercicio 7.1.4. Vericar que i
k
: G
k

jJ
G
j
es un monomorsmo, con lo cual
podemos mirar cada G
k
como subgrupo de su producto directo.
Proposicin 7.1.5. Consideremos dos grupos cclicos (H, ) y (K, ) de ordenes p
y q, respectivamente. Supongamos que p y q son relativamente primos, es decir el nico
factor positivo entero comn es 1. Entonces el producto directo HK es un grupo cclico
de orden pq.
Demonstracin. Consideremos dos nmeros enteros positivos p, q que sean relativa-
mente primos, es decir no hay factores positivos comunes diferentes de 1. Sea (Z, ) un
grupo cclico de orden pq. Sean x, y y w generadores de H, K y Z, respectivamente.
Consideremos la funcin
: H K Z : (x
a
, y
b
) w
aq+bp
Este es claramente un homomorsmo de grupos. Por otro lado, si (x
a
, y
b
) = I
Z
, en-
tonces aq + bp 0 mdulo pq. Luego, p/aq y q/bp y, como p y q son relativamente
primos, tenemos que p/a y q/b, es decir, x
a
= I
H
y tambin y
b
= I
K
. De esta manera
obtenemos que es un monomorsmo. Como la cardinalidad de HK y Z es la misma,
pq, tenemos gratis la sobreyectividad y luego el isomorsmo deseado.
7.2. Producto Dbil de Grupos
Al igual que en la seccin anterior, consideremos una coleccin de grupos (G
j
,
j
) :
j J y consideremos su producto directo
jJ
G
j
. El subconjunto
debil
jJ
G
j
de
jJ
G
j
denido por aquellas funciones f : J
jJ
G
j
tales que f(j) G
j
, para
cada j J y f(j) = I
Gj
con la posible excepcin de un nmero nito de valores de j,
resulta ser un subgrupo, llamado el producto dbil de los grupos G
j
, j J. Observemos
que si #J < , entonces el producto directo y el producto dbil coinciden.
debil
jJ
G
j
es en efecto un subgrupo de
jJ
G
j
.
7.4. PRODUCTO SEMIDIRECTO DE GRUPOS 45
Ejemplo 7.2.2. Los productos dbiles de grupos Abelianos tienen cierta propiedad
universal que pasamos a ver. Supongamos que tenemos una coleccin de grupos Abelia-
nos (G
j
,
j
) : j J y consideremos su producto dbil G =
jJ
G
j
. Es claro que G
(de hecho el producto directo) es un grupo Abeliano. Supongamos que tenemos un grupo
Abeliano K y una coleccin de homomorsmos
j
: G
j
A, para cada j J. Por cada
f
debil
jJ
G
j
podemos considerar el producto h(f) =
jG

j
(f(j)) (el producto en
la operacin binaria de K), el cual tiene sentido ya que, excepto por un nmero nito de
dices j J, vale que
j
(f(j)) = I
K
, y los grupos involucrados al ser Abelianos no im-
porta el orden para el producto. Se puede vericar que h : G K es un homomorsmo
que satisface h i
j
= j, para todo j J.
Ejercicio 7.2.3. Completar los detalles del ejemplo anterior y deducir que h : G K
es nico con la propiedad de ser homomorsmo y h i
j
= j, para todo j J.
7.3. Producto Directo Interno
Supongamos que tenemos un grupo (G, ) y una coleccin de subgrupos H
j
:
j = 1, 2, ..., n. Diremos que G es producto directo interno de los subgrupos H
j
,
j = 1, 2, ..., n, si
:
j{1,2,...,n}
H
j
G : f
n
j=1
f(j) = f(1) f(2) f(j)
resulta ser un isomorsmo. De esta denicin es claro que cada elemento g Gse puede
escribir de manera nica como g = h
1
h
2
h
n
, donde h
j
H
j
.
7.4. Producto Semidirecto de Grupos
Consideremos dos grupos (H, ), (K, ) y un homomorsmo de grupos : K
Aut(H). El conjunto K H junto con la operacin binaria
(k
1
, h
1
)
(k
2
, h
2
) = (k
1
k
2
, h
1
(k
1
)(h
2
))
resulta ser un grupo llamado el producto semidirecto de los grupos K y H el cual denota-
mos por G = K H. En este caso, el elemento neutro es dado por (1
K
, 1
H
), donde 1
K
y 1
H
denotan los elementos neutros de K y H, respectivamente. El elemento inverso de
(k, h) es dado por (k
1
, (k
1
)(h
1
)). Observemos tambin que 1
K
H y K1
H
resultan ser subgrupos de K H y se tiene que las inclusiones

j
H
: H 1
K
H : h (1
K
, h)
j
K
: K K 1
H
: k (k, 1
H
)
resultan ser isomorsmos. Ms an, el subgrupo j
H
(H) = 1
K
H resulta ser un
subgrupo normal de K H.
46 CAPTULO 7. PRODUCTOS DE GRUPOS
(i) la operacin binaria
dene una estructura de grupo ;

(ii) las funciones j
H
y j
K
son efectivamente isomorsmos ;
(iii) j
H
(H) es subgrupo normal de K H.
Ejemplo 7.4.2. Supongamos que tenemos un grupo (G, ) que contenga dos subgru-
pos H y K, donde H es normal en G, H K = 1
G
y G = HK. Consideremos el
homomorsmo de grupos : K Aut(H) donde (k)(h) = k h k
1
y formemos el
producto semidirecto K H. Tenemos que : K H G : (k, h) k h resulta ser
un isomorsmo de grupos. Diremos que G es el producto semidirecto interno de K y G.
Ejercicio 7.4.3.
(1) Completar los detalles del ejemplo anterior.
(2) Sean Gun grupo abeliano, H y K subgrupos de Gtales que G = HK y HK =
1
G
. Vericar que G
= H K.
(3) Sea G un grupo, H, K < G tales que H G y HK = G. Vericar que :
K H G : (k, h) kh dene un isomorsmo.
(4) Sean H, G, K grupos, i : H G, : G K, : K G homomorsmos de
grupos tales que :
(i) i es inyectivo ;
(ii) es sobreyectivo;
(iii) i(H) = Ker() ;
(iv) = I
K
.
Las condiciones (i), (ii) y (iii) dicen que la sucesin corta siguiente es exacta.
1 H
i
G

K 1
Vericar que : K H G : (k, h) (k)h dene un isomorsmo.
CAPTULO 8
PRODUCTO LIBRE DE GRUPOS
Ahora procederemos a generar un nuevo grupo a partir de unos ya dados, pero de
manera de no producir nuevas relaciones entre los elementos. En el caso de productos di-
rectos o dbiles, por ejemplo, cuando los grupos involucrados son Abelianos, el resultado
nos da un grupo Abeliano, es decir hay ms relaciones que las originales (slo valan en
cada grupo).
Nuevamente, consideremos una coleccin no vaca de grupos (G
j
,
j
) : j J.
Denimos una palabra reducida (en estos grupos) de longitud n > 0 a una sucesin nita
(x
1
, ..., x
n
), donde cada x
j
pertenece a alguno de nuestros grupos y tienen las siguientes
dos propiedades :
(i) ningn x
j
es el neutro del grupo a cual pertenece ; y
(ii) dos trminos consecutivos no pertenecen al mismo grupo.
Denotaremos por 1 la palabra de longitud 0 (usualmente llamada la palabra vaca). Sea
G la coleccin de tales palabras. Ahora procederemos a construir una operacin binaria
sobre este conjunto.
1 1 := 1
1 (x
1
, ..., x
n
) := (x
1
, ..., x
n
)
(x
1
, ..., x
n
) 1 := (x
1
, ..., x
n
)
Ahora supongamos que tenemos dos palabras de longitudes positivas, digamos
(x
1
, ..., x
n
) y (y
1
, ..., y
m
). Queremos denir
(x
1
, ..., x
n
) (y
1
, ..., y
m
)
Caso 1 : Si x
n
y y
1
no pertenecen al mismo grupo, entonces denimos
(x
1
, ..., x
n
) (y
1
, ..., y
m
) = (x
1
, ..., x
n
, y
1
, ..., y
m
)
Caso 2 : Si x
n
y y
1
pertenecen al mismo grupo G
j
, pero x
n

j
y
1
,= I
Gj
, entonces
denimos
(x
1
, ..., x
n
) (y
1
, ..., y
m
) = (x
1
, ..., x
n1
, x
n
j
y
1
, y
2
..., y
m
)
48 CAPTULO 8. PRODUCTO LIBRE DE GRUPOS
Caso 3 : Si x
n
y y
1
pertenecen al mismo grupo G
j
, x
n
j
y
1
= I
Gj
, entonces exigimos,
siguiendo las deniciones anteriores,
(x
1
, ..., x
n
) (y
1
, ..., y
m
) = (x
1
, ..., x
n1
) (y
2
, ..., y
m
)
La operacin binaria que hemos denido recibe tambin el nombre de yuxtaposicin.
Observemos que la,operacin binaria es asociativa por denicin, 1 es neutro y cada pa-
labra reducida (x
1
, ..., x
n
) tiene como inversa (respecto a esta operacin) a la palabra
reducida (x
1
n
, ..., x
1
1
).
Denicin 8.0.4. Al grupo obtenido de esta manera es llamado el producto libre de
los grupos (G
j
,
j
) : j J.
Notacin. Desde ahora en adelante identicaremos cada palabra reducida (x
1
, ..., x
n
), de
longitud n > 0, con x
1
x
2
x
n
(es decir, no haremos uso del smbolo ni de los
parntesis.
Observacin 8.0.5. Cuando tenemos un nmero nito de grupos, G
1
,..., G
n
, entonces
se estila usar la notacin
G
1
G
2
G
n
para denotar su producto libre. Observemos que la denicin del producto libre no de-
pende de ningn orden en los grupos factores, es decir, si o
n
, entonces
G
1
G
2
G
n
= G
(1)
G
(2)
G
(n)
De manera anloga, para el producto libre arbitrario denotamos este por
jJ
G
j
.
Ejemplo 8.0.6. Consideremos G
1
= I
1
, x (es decir, un grupo de orden 2, luego
x
2
= I
1
) y G
2
= I
2
, y, y
2
(es decir, un grupo de orden 3, luego y
3
= I
2
). Entonces
una lista de algunas de las palabras reducidas de G
1
G
2
son las siguientes :
Longitud 0 : 1
Longitud 1 : x, y, y
2
= y
1
Longitud 2 : xy, xy
2
, yx, y
2
x
Una propiedad universal del producto libre de grupos es el siguiente. Consideremos
una coleccin de grupos (G
j
,
j
) : j J y su producto libre de grupos
jJ
G
j
.
Entonces, por cada k J tenemos naturalmente un monomorsmo i
k
: G
k

jJ
G
j
(a cada x G
k
I
G
k
le asigna la palabra x de longitud 1, y a I
G
k
le asigna 1). Sea
(K, ) un grupo y supongamos que tenemos homomorsmos
j
: G
j
K, para cada
j J. Denamos la funcin h :
jJ
G
j
K de la siguiente manera. h(1) = I
K
,
y si x
1
x
2
x
n
es una palabra reducida de longitud n > 0, donde x
r
G
jr
, entonces
h(x
1
x
2
x
n
) =
j1
(x
1
)
j2
(x
2
)
jn
(x
n
). Resulta que h es un homomorsmo
que satisface que h i
j
=
j
, para cada j J.
CAPTULO 8. PRODUCTO LIBRE DE GRUPOS 49
Ejercicio 8.0.7. Vericar que h es en efecto un homomorsmo de grupos y que est
nicamente denido por la condicin h i
j
=
j
, para cada j J.
Ejemplo 8.0.8. Consideremos un espacio topolgico (X, ) arco-conexo y local-
mente arco-conexo. Sean A, B abiertos arconexos tales que A B = X y A B sea
arco-conexo y simplemente conexo. Entonces, si p A B, tenemos que
1
(X, p) =
1
(A, p)
1
(B, p)
CAPTULO 9
PRODUCTO LIBRE AMALGAMADO
Consideremos dos grupos (G
1
,
1
), (G
2
,
2
) y subgrupos H
j
< G
j
, para j = 1, 2.
Supongamos que tenemos un isomormo de grupos
: H
1
H
2
En el producto libre G
1
G
2
consideremos el subgrupo normal ms pequeo K que
contega todas las palabras de la forma
h
1
(h), donde h H
1
Denicin 9.0.9. El grupo cociente
G
1
G
2
= G
1
G
2
/K
es llamado el producto libre amalgamado por : H
1
H
2
.
Observemos que si H
1
= I
G1
, entonces G
1
G
2
= G
1
G
2
.
mente arco-conexo. Sean A, B abiertos arconexos tales que A B = X y A B sea
arco-conexo. Entonces, si p A B, tenemos que
1
(X, p) =
1
(A, p)

1
(B, p)
donde :
1
(A B, p) <
1
(A, p) <
1
(A B, p)
1
(A B, p) <
1
(B, p) <
1
(A B, p) es el isomorsmo de amalgacin.
CAPTULO 10
HNN-EXTENSIN
Sean (G, ) un grupo y H, K dos subgrupos de G. Supongamos que tenemos un iso-
morsmo : H K. Consideremos un grupo cclico innito t).
En el producto libre G t) consideremos el subgrupo normal ms pequeo K que
contega todas las palabras de la forma
tht
1
(h)
1
, donde h H
Denicin 10.0.11. El grupo cociente
G
= G t)/K
es llamado la HNN-extensin de G por : H K.
mente arco-conexo. Sean A, B abiertos arconexos tales que A B = . Supongamos
que tenemos un homeomorsmo F : A B y consideramos el espacio topolgico X
F
obtenido al identicar cada punto a A con cada punto F(a) B. Entonces, si p X
F
,
tenemos que
1
(X
F
, p) =
1
(X, p)
donde :
1
(A, p) <
1
(X, p)
1
(B, p) <
1
(X, p) es el isomorsmo de HNN-
extensin.
CAPTULO 11
GRUPOS LIBRES
La construccin anterior de productos libres podemos usarla para construir cierto grupo
a partir de un conjunto dado S. Este grupo tiene la propiedad de ser generado por S y ser
el ms grande con tal propiedad.
Supongamos que S = x
j
: j J ,= . Entonces por cada j J denimos el grupo
F
j
= 1
j
= x
0
j
, x
1
j
, x
2
j
, ..., x
n
j
, ....
con la operacin binaria
j
denida por
1
j
j
1
j
= 1
j
1
j

j
x
n
j
= x
n
j
= x
n
j

j
1
j
x
n
j

j
x
m
j
= x
n+m
j
Ejercicio 11.0.13. Vericar que (F
j
,
j
) es un grupo cclico innito generado por x
j
,
luego isomorfo al grupo aditivo Z. Establecer dicho isomorsmo.
Denicin 11.0.14. Consideremos un conjunto no vaco S = x
j
: j J , = y
(F
j
,
j
) : j J los grupos cclicos arriba construidos. El producto libre
F(S) =
jJ
F
j
es llamado el grupo libre generado por S. La cardinalidad de S es llamado el rango del
grupo libre generado por S.
Por la propiedad universal vista para los productos libres, vemos que si (K, %) es
cualquier grupo para el cual existe un monomorsmo desde cada F
j
hacia este, entonces
existe un homomorsmo desde

jJ
F
j
hacia K. Esto dice que el grupo libre es el
grupo ms grande posible respecto al conjunto de generadores S.
56 CAPTULO 11. GRUPOS LIBRES
Ejercicio 11.0.15. Vericar que todo grupo libre de rango 1 es isomorfo al grupo
aditivo Z.
CAPTULO 12
GRUPOS ABELIANOS FINITAMENTE GENERADOS
12.1. Grupos Abelianos Libres
Dado un conjunto S = x
j
: j J , = , consideremos el grupo libre generado
por S, es decir F(S). Este grupo no es Abeliano y de hecho no hay relaciones entre los
diferentes generadores x
j
.
Denicin 12.1.1. La abelianizacin de F(S), es decir
F(S)
abel
= F(S)/[F(S), F(S)]
es llamado el grupo libre abeliano generado por el conjunto S. El rango de F(S)
abel
es
el rango de F(S), es decir, la cardinalidad de S.
Ejercicio 12.1.2. Sea S = x
1
, ..., x
n
. Verique que
F(S)
abel

=
n
j=1
Z
Supongamos que tenemos un grupo Abeliano (G, ) que es generado por el conjunto
x
j
: j J G. Consideremos un conjunto S = y
j
: j J y formemos el grupo
libre F(S). Entonces tenemos un homomorsmo sobreyectivo natural dado por
: F(S) G
denido por la propiedad que (y
j
) = x
j
, j J. Entonces tenemos que el subgrupo
de conmutadores [F(S), F(S)] es subgrupo del ncleo de tal homomorsmo, es decir,
tenemos inducido un homomorsmo sobreyectivo
abel
: F(S)
abel
G
El ncleo K de
abel
es exactamente
[F(S),F(S)]
(Ker()), donde
[F(S),F(S)]
: F(S)
F(S)
abel
es la proyeccin natural. Tenemos ahora un isomorsmo
G
= F(S)
abel
/K
58 CAPTULO 12. GRUPOS ABELIANOS FINITAMENTE GENERADOS
12.2. Grupos Abelianos Finitamente Generados
En el caso particular que (G, ) es grupo Abeliano nitamente generado, digamos por
x
1
,...,x
n
, entonces de lo anterior tenemos que
G
=
_
_
n
j=1
Z
_
_
/K
es decir, G es la imgen homomorfa de un grupo Abeliano libre de rango nito. Ahora,
en este caso, tenemos el siguiente resultado que puede encontrarse en [3].
Proposicin 12.2.1. Sea F un grupo abeliano libre de rango nito n y K un subgrupo
no trivial de G. Entonces existen una base x
1
, ..., x
n
de F y enteros positivos d
1
,..., d
s
,
para cierto s n, de manera que d
j
divide d
j+1
y K tiene base dada por x
d1
1
, ..., x
ds
s
.
En particular,
F/K

=
_
_
ns
j=1
Z
_
_
_
s
k=1
Z/d
k
Z
_
Luego, como consecuencia de la proposicin 12.2.1, tenemos que
G
=
_
_
l
j=1
Z
_
_
_
s
k=1
Z/d
k
Z
_
,
donde d
1
,...., d
s
son enteros positivos tales que d
j
divide d
j+1
. Observemos que necesa-
riamente en este caso tenemos
G
tor
=
s
k=1
Z/d
k
Z.
CAPTULO 13
GRUPOS COMO COCIENTE DE GRUPOS LIBRES
Consideremos un conjunto S ,= y el grupo libre F(S) generado por S. En la seccin
anterior usamos el subgrupo normal dado por los conmutadores, es decir [F(S), F(S)]
para obtener un grupo Abeliano F(S)
abel
= F(S)/[F(S), F(S)]. De manera ms ge-
neral, supongamos que tenemos dado un subgrupo normal de F(S), digamos N, en-
tonces tenemos un grupo cociente G = F(S)/N y un homomorsmo sobreyectivo na-
tural
N
: F(S) G. Tenemos que
N
(S) G es un conjunto de generadores de G.
Cada palabra w N determina una relacin entre los generadores inducidos por S en G
y estas son todas. De hecho, no es necesario considerar todas las palabras de N para ver
todas las relaciones en G; basta considerar un conjunto R N de generadores de N. As,
todas las relaciones en G son consecuencia de las relaciones en R. Ms an, supongamos
que T R es tal que N es el subgrupo normal de F(S) ms pequeo que contiene T,
entonces todas las relaciones en G son consecuencias de las relaciones inducidas por T.
Ejemplo 13.0.2. Sea S = x, y y F(S)
= Z Z el grupo libre de rango 2 generado

por S. Tomemos un entero positivo n y consideremos T = x
2
, y
n
, (xy)
2
:= xyxy. En
este caso, el grupo cociente G = F(S)/N est generado por
n
(x) = X,
N
(y) = Y
y satisfacen las relaciones
X
2
= Y
n
= (XY )
2
= 1
La relacin (XY )
2
nos dice que todos los elementos de G pueden escribirse como
X
a
Y
b
, donde a = 0, 1 y b = 0, 1, ..., n 1. Esto nos dice que G tiene a lo ms 2n
elementos. Por otro lado, si dos elementos de esta forma coinciden, entonces debemos
tener en F(S) una relacin x
a
y
b
= 1, lo cual es slo posible para a = b = 0. En
particular, [G[ = 2n. El grupo que hemos construido es llamado el grupo dihedral de
orden 2n y usualmente denotado por D
n
.
Ejercicio 13.0.3.
60 CAPTULO 13. GRUPOS COMO COCIENTE DE GRUPOS LIBRES
(1) Sea n un entero positivo y sean las siguientes transformaciones de Mbius U(z) =
e
i/2n
z y V (z) = 1/z. Considere el subgrupo de Perm(C) H generado por U y V .
Verique que H

= D
n
.
(2) Considere un polgono regular P R
2
de n 3 lados. Considere el grupo de
isometras de P respecto al producto interior usual, digamos Isom(P). Vericar
que Isom(P) contiene un subgrupo de ndice dos (luego normal) que es isomorfo a
D
n
.
Ejemplo 13.0.4. Sea S = x y F(S)

= Z el grupo libre generado por S. Sea T =
x
n
, para algn n 1, 2, 3, .... Entonces G = F(S)/N resulta ser un grupo cclico
de orden n.
En forma recproca, partamos de un grupo (G, ) y tomemos un conjunto S de gene-
radores de G. Formemos el grupo libre F(S) generado por S y consideremos la funcin
Q : F(S) G
denida por la regla
Q(1) = I
G
Q(x
1
x
2
x
n
) = x
1
x
2
x
n
Ejercicio 13.0.5. Vericar que Q es un homomorsmo sobreyectivo.
Sea N = Ker(Q). Entonces tenemos que F(S)/Ker(Q)

= G, es decir, todo grupo
puede obtenerse por el procedimiento anterior. Lo ms importante de todo lo dicho en
esta seccin es que cada grupo puede ser representado por medio de
Generadores y Relaciones
es decir, de la forma
G = S, T)
Ejemplo 13.0.6.
D
n
= X, Y : X
2
, Y
n
, (XY )
n
)
el grupo dihedral de orden 2n, que resulta ser el grupo de isometras Euclidianas de un
polgono regular plano de n lados,
Z/nZ = A : A
n
) = U, V : U
n
, UV )
el grupo cclico nito de orden n, que resulta ser el grupo de isometras Euclidianas de
los rayos que unen (0, 0) con cada raz nsima de la unidad,
/
4
= A, B : A
3
, B
2
, (AB)
3
)
CAPTULO 13. GRUPOS COMO COCIENTE DE GRUPOS LIBRES 61
este grupo es llamado el grupo alternante en cuatro letras y resulta ser el grupo de isome-
tras Euclidianas de una pirmide regular centrada en (0, 0, 0) R
3
,
o
4
= A, B : A
4
, B
2
, (AB)
3
)
este grupo es el grupo simtrico en cuatro letras (isomorfo a Perm(1, 2, 3, 4)) y resulta
ser el grupo de isometras Euclidianas de un cubo regular centrado en (0, 0, 0) R
3
,
/
5
= A, B : A
5
, B
2
, (AB)
3
)
este grupo es llamado el grupo alternante en cinco letras y resulta ser el grupo de isome-
tras Euclidianas de un icosaedro regular centrado en (0, 0, 0) R
3
.
Ejercicio 13.0.7. Calcular las tablas de multiplicacin de cada uno de los grupos an-
teriores y determinar sus rdenes. Represente estos grupos por medio de transformaciones
(extendidas) de Mbius y tambin por rotaciones espaciales.
CAPTULO 14
GRUPOS DE PERMUTACIONES FINITOS
Como hemos visto al comienzo de estas notas, podemos mirar todo grupo como sub-
grupo de un grupo de permutaciones Perm(X) para cierto conjunto no vaco X. Esto
nos est diciendo que sera bueno el poder entender un poco ms tales grupos. Para sim-
plicar el trabajo, consideraremos slo conjuntos nitos. Como todo conjunto X nito
de cardinalidad n > 0 es biyectivo al conjunto 1, 2, 3, ..., n, y tenemos que en este
caso Perm(X) y Perm(1, 2, ..., n) son necesariamente isomorfos, bastar considerar
X = 1, 2, ..., n. Como habamos dicho antes, usaremos el smbolo o
n
para denotar
Perm(1, 2, ..., n). Este grupo recibe tambin el nombre de grupo simtrico de n letras.
Antes que nada, veamos algunas notaciones que nos simplicarn el trabajo.
Denicin 14.0.8. El smbolo (a
1
, a
2
, ..., a
k
), donde k 2, 3, ..., n, a
j

1, 2, ..., n y a
j
,= a
r
para j ,= r, denotar la permutacin que enva a
1
en a
2
, a
2
en a
3
,..., a
k1
en a
k
, a
k
en a
1
y ja todos los otros elementos. Este es llamado un cclo
de longitud k. Cuando k = 2 hablamos de transposiciones en vez de decir un cclo de
longitud dos.
La operacin de dos cclos corresponde a la composicin de las dos permutaciones
que denen, es decir de derecha hacia la izquierda, por ejemplo (1, 2)(2, 3) = (1, 2, 3),
(2, 3)(1, 2) = (1, 3, 2).
Ejercicio 14.0.9. Calcular la cantidad de cclos de logitud k 2, 3, ..., n que hay
en o
n
.
Ejemplo 14.0.10. Consideremos n = 3. En este caso tenemos que o
3
est formado
por el neutro I, las transposiciones a = (1, 2), b = (1, 3), c = (2, 3) y los cclos de
longitud tres d = (1, 2, 3) y e = (1, 3, 2). Observemos que e = d
1
, dad
1
= c y
d
1
ad = b. Es decir que o
3
est generado por a y d. Observemos que valen las relaciones
a
2
= I, d
3
= I y como ad = (2, 3), entonces (ad)
2
= I.
64 CAPTULO 14. GRUPOS DE PERMUTACIONES FINITOS
Ejercicio 14.0.11. Vericar que toda otra relacin o
3
es consecuencia de las tres re-
laciones dadas en ele ejemplo anterior. Verique que existe un isomorsmo entre o
3
y el
grupo dihedral D
3
.
Ahora, si consideramos una permutacin o
n
, entonces podemos escribirla como
producto de un nmero nito y disjunto de cclos. Para ver esto, primero consideramos
el subconjunto J 1, 2, ..., n que son los puntos jos de la permutacin . Entonces,
tomamos el menor elemento a
1
1, 2, ..., n J y formamos el cclo
C
1
= (a
1
, a
2
= (a
1
), a
3
=
2
(a
1
), ..., a
k1
=
k11
(a
1
))
donde
k1
(a
1
) = a
1
. Ahora, consideramos el menor elemento de 1, 2, ..., n (J
a
1
, a
2
, ..., a
k
), digamos b
1
. Entonces formamos el cclo
C
2
= (b
1
, b
2
= (b
1
), b
3
=
2
(b
1
), ..., b
k2
=
k21
(b
1
))
donde
k2
(b
1
) = b
1
. Como el conjunto 1, 2, ..., n es nito, obtenemos por este procedi-
miento una coleccin nita de cclos, digamos C
1
,..., C
r
, de respectivas longitudes k
1
,...,
k
r
. La inyectividad de asegura que dos cualquiera de tales cclos deben ser disjuntos.
Ahora no es difcil darse cuenta que
= C
1
C
2
C
r
y adems el orden de los cclos no afecta al producto. En particular, hemos obtenido el
siguiente resultado.
Proposicin 14.0.12. El grupo simtrico o
n
est generado por todos su cclos.
Por otro lado, cada cclo puede escribirse como producto de transposiciones. En efecto,
consideremos un cclo (a
1
, ..., a
k
), entonces tenemos que
(a
1
, ..., a
k
) = (a
1
, a
k
)(a
1
, a
k1
) (a
1
, a
3
)(a
1
, a
2
)
es decir, tenemos el siguiente.
Proposicin 14.0.13. El grupo simtrico o
n
est generado por todas sus transposi-
ciones.
Corolario 14.0.14. El grupo simtrico o
n
est generado por el cclo de longitud n
dado por a = (1, 2, 3, ..., n) y la transposicin b = (1, 2).
Demonstracin. Primero que nada, observemos que b
n
= a
1
ba = (n, 1), b
n1
=
a
2
ba
2
= (n 1, n), b
n2
= a
3
ba
3
= (n 2, n1),..., b
2
= aba
1
= (2, 3). Dena-
mos b
1
= b. Segundo, c
3
= bb
2
b = (1, 3), c
4
= c
3
b
3
c
3
= (1, 4), c
5
= c
4
b
4
c
4
= (1, 5),...,
c
n1
= c
n2
b
n2
c
n2
= (1, n 2). Hasta ahora hemos logrado obtener todas las trans-
posiciones de la forma (1, k), k = 2, 3, ..., n. Ahora, conjugando estas transposiciones
CAPTULO 14. GRUPOS DE PERMUTACIONES FINITOS 65
por a
t
, donde t = 1, 2, 3, ..., n 1, obtendremos todas las transposiciones posibles. El
resultado entonces sigue de la proposicin anterior.
Sea /
n
el subconjunto de o
n
formado por todos los productos de un nmero par de
transposiciones junto a la permutacin trivial I. Entonces como
((a
1
, a
2
)(a
3
, a
4
) (a
2k+1
, a
2k
))
1
= (a
2k+1
, a
2k
)(a
2k1
, a
2k2
) (a
1
, a
2
)
tenemos que /
n
contiene los inversos de sus elementos. Por otro lado, si hacemos el
producto de dos elementos de /
n
, entonces el resultado sigue siendo un producto de un
nmero par de transposiciones.
Proposicin 14.0.15. /
n
es un subgrupo de o
n
llamado el grupo alternante en n
letras.
Nuestra denicin del grupo alternante /
n
no deja afuera la posibilidad de que sea
todo el grupo o
n
. El siguiente resultado nos dice que esto no es cierto.
Proposicin 14.0.16. No es posible escribir una misma permutacin como el pro-
ducto de un nmero par de ciertas transposiciones y tambin como el producto de un
nmero impar de otras transposiciones.
Demonstracin. Supongamos que tenemos una permutacin o
n
que puede escri-
birse de dos maneras diferentes como :
=
1
2

2k1
=
1
2

2r
donde
j
,
l
son transposiciones. Entonces tenemos que la identidad I =
1
de poder
escribirse como un producto impar de transposiciones. Supongamos entonces que tene-
mos
I =
1
2

s
donde
j
son transposiciones. Queremos ver que obligatoriamente s debe ser par, dando
una contradiccin a lo anterior. Sea m 1, 2, ..., n tal que aparezca en alguna de las
transposiciones
j
y consideremos
jm
la primera transposicin (de derecha a izquierda)
que contenga m. Debemos tener j
m
> 1 ya que si j
m
= 1, entonces I no ja a m, una
contradiccin. Miremos las posibilidades para
jm1
jm
:
(m, x)(m, x) = I
(m, y)(m, x) = (m, x)(x, y)
(y, z)(m, x) = (m, x)(y, z)
(x, y)(m, x) = (m, y)(x, y)
Esto dice que podemos reemplazar
jm1
jm
por otro par de transposiciones de ma-
nera que ahora la primera transposicin (de derecha a izquierda) conteniendo m sea
jm1
, o bien la cantidad de transposiciones nuevas a decrecido en 2. Adems en las
nuevas transposiciones slo aparecen los enteros que ya aparecan en las transposiciones
originales. Como no podemos llevar m a la primera transposicin, debemos en algn
momento hacer decrecer en un nmero par de transposiciones antes de hacer desapare-
cer m de todas las nuevas transposiciones. Si procedemos de esta manera por cada valor
en las restantes transposiciones y lo eliminamos, entonces la cantidad de transposiciones
decrece en un nmero par positivo. Luego, s debe ser par.
Por ejemplo, la transposicin (1, 2) / /
n
. Pero como el producto de dos permu-
taciones, cada una de ellas siendo el producto de un nmero impar de transposiciones,
resulta ser un producto de un nmero par de ellas, obtenemos que [o : /
n
] = 2 y luego
/
n
es un subgrupo normal de ndice dos en el grupo simtrico o
n
. Las permutaciones en
/
n
son llamadas permutaciones pares y las que no son llamadas permutaciones impares.
Proposicin 14.0.17. El grupo alternante /
n
es un subgrupo normal de o
n
, de he-
cho, un subgrupo de ndice dos.
Demonstracin. Si tomamos dos permutaciones /
n
, o
n
, entonces
1
es
producto par de transposiciones. De esta manera, obtenemos la normalidad. Otra manera
de ver esto es que /
n
tiene ndice 2 y, como consecuencia de la proposicin 5.0.24, este
es un subgrupo normal.
Ya hemos visto que un cclo de longitud k 2 puede escribirse ccomo un producto
de (k 1) transposiciones. Luego, todo cclo de longitud impar pertenece a /
n
. Por otro
lado, el siguiente resultado dice que todo cclo de longitud par no puede pertenecer a /
n
ya que este es subgrupo normal diferente a o
n
y este ltimo es generado por todos sus
cclos.
Proposicin 14.0.18. Todo cclo de longitud k 2 es conjugado al cclo (1, 2, 3, ..., k).
Demonstracin. Sea el cclo x = (a
1
, ..., a
k
) y considere cualquier permutacin
que satisface (a
j
) = j. Entonces x
1
= (1, 2, ..., k).
Por lo anterior, todo cclo de longitud 3 pertenece a /
n
. El siguiente muestra que estos
le generan.
Proposicin 14.0.19. El subgrupo /
n
est generado por todos los cclos de longitud
3.
Demonstracin. Un cclo de longitud 3, digamos (a, b, c) = (a, c)(a, b), pertenece
a /
n
. Como las permutaciones de /
n
se escriben como producto de un nmero par de
transposiciones, bastar con vericar que el producto de dos transposiciones diferentes es
producto de cclos de longitud 3. Esto se ve como sigue :
(a, b)(a, c) = (a, c, b)
CAPTULO 14. GRUPOS DE PERMUTACIONES FINITOS 67
(a, b)(c, d) = (a, b)(a, c)(c, a)(c, d) = (a, c, b)(c, d, a)
Ejemplo 14.0.20. Por lo dicho anteriormente, cada permutacin puede escribirse
como producto disjunto de cclos. Como hay cclos de diferentes longitudes, podemos
preguntarnos cuantos cclos de una longitud dada hay. La permutacin identidad, el
neutro, diremos que es un cclo de longitud 0. Para cada k 1, 2, ..., n denotemos por
n
k
el nmero de diferentes cclos de longitud k que tenemos en el grupo simtrico o
n
.
Es claro que n
1
= n y que para k 2, 3, ..., n tenemos que
n
k
= (k 1)!
_
n
k
_
=
n!(k 1)!
k!(n k)!
ya que para formar un k-cclo, debemos escoger k ndices diferentes en 1, 2, 3, ..., n
y adems tener en cuenta que un cclo no cambia por una permutacin cclica de sus
componentes.
Ahora, tomemos una permutacin o
n
y escribamosla como producto de cclos
disjuntos. En esta descripcin aparecen una cantidad v
2
de transposiciones, una cantidad
v
3
de cclos de longitud 3,..., una cantidad v
n
de cclos de longitud n. Es claro que v
n

0, 1 y que si v
n
= 1, entonces es un cclo de longitud n. Denotemos por v
1
la cantidad
de puntos jos por en el conjunto 1, 2, ..., n. Debemos tener la igualdad
v
1
+ 2v
2
+ 3v
3
+ +nv
n
= n
ya que la permutacin acta sobre n puntos. Por ejemplo, tomemos n = 6 y considere-
mos la permutacin = (1, 2)(3, 4). Entonces tenemos v
1
= 2, v
2
= 2, v
3
= v
4
= v
5
=
v
6
= 0.
Dos permutaciones con el mismo tipo de descomposicin en ciclos, es decir, que cor-
responden a los mismos v
1
, v
2
,..., v
n
, son siempre conjugados en o
n
. En forma recproca,
dos permutaciones que son conjugadas tienen la misma descomposicin. Diremos que dos
permutaciones son de la misma clase si estos son conjugados. Esto dene una relacin de
equivalencia en o
n
. Podemos preguntarnos por la cantidad de clases de conjugacin dife-
rentes hay. Para resolver esto, nos conviene que escribamos el sistema lineal
_
_
v
1
+ v
2
+ v
n
=
1
+ v
2
+ v
n
=
2
.
.
. =
.
.
.
v
n
=
n
restricto a las condiciones
1
+
2
+ +
n
= n
1

2

n
0
De esta manera, primero buscamos todas las soluciones (
1
, ...,
n
) satisfaciendo las
dos ltimas propiedades y luego por cada solucin analizamos el sistema lineal por el
mtodo de Cramer. En otras palabras, la cantidad de diferentes clases de conjugacin en
o
n
es igual al nmero de soluciones (
1
, ...,
n
) de las dos ecuaciones anteriores.
Por ejemplo, consideremos n = 3, es decir, o
3
. En este caso, las soluciones son dadas
por (
1
,
2
,
3
) (1, 1, 1), (2, 1, 0), (3, 0, 0). Para el primer triple (1, 1, 1) tenemos
v
1
= v
2
= 0 y v
3
= 1, es decir los 3-cclos (forman una clase de conjugacin formada de
dos 3-cclos). Para el segundo triple (2, 1, 0) tenemos v
1
= v
2
= 1 y v
3
= 0, es decir los
2-cclos (forman una clase de conjugacin formada de tres 2-cclos). Para el tercer triple
(3, 0, 0) tenemos v
2
= v
3
= 0 y v
1
= 3, es decir la clase formada de slo la permutacin
trivial.
Observacin 14.0.21. La cantidad de clases de conjugacin en el grupo o
n
es impor-
tante en la teora de representaciones lineales (que veremos en un prximo captulo). Tal
nmero coincide con el nmero de representaciones irreducibles de tal grupo.
Tambin podemos ver cual es el nmero de permutaciones en o
n
que tienen una des-
composicin similar (mismos valores de v
k
), es decir, cuantas permutaciones pertenecen
a una clase de conjugacin dada. Para esto, primero hay que escoger v
1
puntos jos, es
decir,
_
n
v
1
_
=
n!
v
1
!(n v
1
)!
posibilidades. Ahora hay que escoger de los restantes puntos v
2
pares disjuntos y sin
importar su orden, es decir,
1
v
2
!
_
n v
1
2
__
n v
1
2
2
__
n v
1
4
2
_

_
n v
1
2(v
2
1)
2
_
=
=
(n v
1
)!
2
v2
v
2
!(n v
1
2v
2
)!
Ahora hay que escoger de los restantes puntos v
3
trios disjuntos y sin importar su
orden, es decir,
1
v
3
!
_
n v
1
2v
2
3
__
n v
1
2v
2
3
3
_

_
n v
1
2v
2
3(v
3
1)
3
_
=
=
(n v
1
2v
2
)!
3
v3
v
3
!(n v
1
2v
2
3v
3
)!
En forma similar para los restantes. Uno obtiene que el nmero total que buscamos es
el producto de todos los anteriores, es decir
n!
v
1
!2
v2
v
2
!3
v3
v
3
! n
vn
v
n
!
Ejercicio 14.0.22.
(i) Vericar que /
n
, n 5 es un grupo simple, es decir, no posee subgrupos normales
no triviales. Analizar los casos /
3
y /
4
.
(ii) Calcular Z(S
n
).
PARTE II
ACCIN DE GRUPOS Y APLICACIONES
En este captulo estudiaremos las propiedades de los grupos por medio de acciones
sobre conjuntos como grupo de permutaciones. Como aplicacin de estos conceptos ob-
tendremos los teoremas de Sylow, los cuales dan informacin sobre grupos nitos. Luego
miraremos un ejemplo particular que corresponde a las representaciones lineales.
CAPTULO 15
ACCIN DE GRUPOS SOBRE CONJUNTOS
Denicin 15.0.23. Una accin por la izquierda de un grupo (G, ) sobre un
conjunto X ,= es por denicin un homomorsmo
: (G, ) (Perm(X), )
Un homomorsmo
: (G, ) (Perm(X), )
donde (Perm(X), ) es el grupo reejado de (Perm(X), ), es llamada una accin por
la derecha de un grupo (G, ) sobre el conjunto X. Si el homomorsmo en cuestin es
adems inyectivo, entonces hablamos de una accin el.
Consideremos el isomorsmo natural
: (Perm(X), ) (Perm(X), ) :
1
y una representacin por la izquierda : (G, ) (Perm(X), ). Entonces tenemos
que : (G, ) (Perm(X), ) nos d una accin por la derecha, la cual es el s
y slo si es el. Recprocamente, si tenemos una accin por la derecha : (G, )
(Perm(X), ), entonces
1
: (G, ) (Perm(X), ) nos d una accin por la
izquierda, la cual es el s y slo si es el.
Lo anterior nos permite tener una biyeccin natural entre las acciones por la derecha y
acciones por la izquierda de un grupo dado (G, ) sobre un conjunto jo X.
Acciones por la izquierda Acciones por la derecha
=
Por lo tanto, desde ahora en adelante nos preocuparemos de acciones por la izquierda ;
los resultados equivalentes para acciones por la derecha se obtienen usando la relacin
anterior.
72 CAPTULO 15. ACCIN DE GRUPOS SOBRE CONJUNTOS
Observacin 15.0.24. Aveces una accin por la izquierda : (G, ) (Perm(X), )
se escribe como una funcin
: GX X : (g, x) (g, x) := (g)(x)
la cual satisface las siguientes propiedades :
(i) (I
G
, x) = x, para todo x X ;
(ii) (g h, x) = (g, (h, x)) ;
(iii) (g, ) : X X : x (g, x) dene una permutacin de X.
Ejercicio 15.0.25. Considere una funcin : GX X satisfaciendo
(i) (I
G
, x) = x, para todo x X ;
(ii) (g h, x) = (g, (h, x)) ;
(iii) (g, ) : X X : x (g, x) dene una permutacin de X.
Verique que existe un homomorsmo : (G, ) (Perm(X), ) de manera que
(g, x) := (g)(x). Ms an, verique que condicin (i) es consecuencia de las las
otras dos (Ind. Llame T = (I
G
, ) Perm(X). Si x X, entonces (ii) dice que
T(T(x)) = T(x) y (iii) dice que T es invertible.)
Ejemplo 15.0.26. Consideremos un espacio topolgico (X, ), su -lgebra de Borel
/ y una medida de probabilidad P : / [0, 1]. Supongamos que tenemos una accin
el : (G, ) Perm(X), donde (G, ) es un grupo nito o numerable, tal que (g) :
X X es un homomorsmo para cada g G. Consideremos la relacin de equivalencia
x
= y s y slo si existe g G tal que (g)(x) = y

y denotemos por X/Gal conjunto de las clases de equivalencia y por : X X/G a la
proyeccin natural. Podemos dotar a X/G de la topologa cociente ; entonces se torna
continua y abierta (ya que la accin es por homeomorsmos). Denotemos por /
X/G
el
-lgebra de Borel del espacio X/G. Entonces la propiedad que tiene nos asegura que
/
X/G
= (A) : A /
Podemos entonces construir la funcin P
: /
X/G
[0, 1] denida por
P
((A)) = P(
1
(A)) = P(
gG
(g)(A))
Por ejemplo, supongamos que escogemos A / de manera que A (g)(A) =
para todo g G y P(A) > 0. Entonces tendremos que
P
((A)) =
gG
P((g)(A))
En esta situacin tendremos que si G es innito, entonces para cada sucesin g
n
en
G vale que
lim
n+
P((g
n
)(A)) = 0
CAPTULO 15. ACCIN DE GRUPOS SOBRE CONJUNTOS 73
y, en particular, no podemos pedir a (G) estar contenido en el grupo de homeomorsmos
de X que preservan la medida P.
Ejemplo 15.0.27. Recordemos de las primeras secciones del captulo anterior el ho-
momorsmo de grupos
: (G, ) (Perm(G), ) : g (g)
donde
(g)(x) = g x g
1
En este caso tenemos una accin por la izquierda del grupo (G, ) sobre el conjunto G.
Ejemplo 15.0.28. Consideremos una funcin diferenciable
X : R
n
R
n
donde es una regin del espacio R
n
. Miremos el sistema dinmico
x
= X(x)
Por el teorema de existencia y unicidad de soluciones, tenemos que para cada p
existe una nica solucin x(, p) : R del sistema anterior con la condicin x(0, p) =
p. Ms an como x(t) = x(t + s, p) es tambin solucin del sistema para la condicin
x(0) = x(s, p), tenemos la relacin
x(t +s, p) = x(s, x(t, p))
Esta relacin nos permite construir la accin del grupo aditivo R sobre como
: (R, +) (Perm(), ) : t x(t, )
donde
x(t, ) : : p x(t, p).
Denicin 15.0.29. Supongamos que tenemos una accin : (G, ) (Perm(X), ).
(i) La rbita de un punto x X por la accin anterior es el conjunto de puntos que
recorre x por efecto de (G), es decir,
Orb(x) = (g)(x) : g G X
(ii) El estabilizador de un punto x X por la accin anterior es el conjunto de ele-
mentos de G que tienen a x como punto jo, es decir,
Stab(x) = g G : (g)(x) = x G
Proposicin 15.0.30. Para cada x X tenemos que el estabilizador Stab(x) es un
subgrupo de (G, ).
Demonstracin. Como (I
G
) = I, la permutacin identidad, tenemos que
I
G
Stab(x), luego, Stab(x) ,= . Si g Stab(x), entonces (g)(x) = x, luego
(g)
1
(x) = x. As, (g
1
)(x) = (g)
1
(x) = x, es decir, (g
1
) Stab(x).
Sean g, h Stab(x), es decir (g)(x) = x = (h)(x). Entonces, (g h)(x) =
(g)((h)(x)) = (g)(x) = x, es decir g h Stab(x).
Ejercicio 15.0.31. Vericar que dada una accin
: (G, ) (Perm(X), )
la relacin
x y s y slo si existe g G tal que (g)(x) = y
dene una relacin de equivalencia en X. Las clases de equivalencia son las rbitas. Al
conjunto de las clases de equivalencia la denotaremos por X/(G) o simplemente por
X/G en caso de no haber confusin de la accin.
Es claro que para cada x X, la representacin (G) acta como permutaciones del
conjunto Orb(x), por denicin de rbita. Luego tenemos una funcin inducida F : G
Orb(x) : g F(g) := (g)(x). Esta funcin es sobreyectiva. Observemos adems que
F(g) = F(h) es equivalente a tener t = g
1
h Stab(x). Recprocamente, para cada
t Stab(x) y cada g G vale que F(g t) = F(g). En otras palabras, tenemos el
siguiente :
Proposicin 15.0.32. Para cada x X tenemos una biyeccin natural entre el
conjunto de clases laterales G/Stab(x) y la rbita Orb(x). En particular,
#Orb(x) = [G : Stab(x)]
Ejemplo 15.0.33. Una accin (G, ) (Perm(X), ) es llamada una accin tran-
sitiva si existe un punto x
0
X tal que su rbita es todo X, es decir, Orb(x
0
) = X.
Como todo punto x X pertenece a Orb(x
0
), tenemos que Orb(x) = X. En este caso
la proposicin 15.0.32 nos dice que [G : Stab(x)] es independiente de x X. De hecho,
si tomamos g G tal que (g)(x
0
) = x, entonces
Stab(x) = g Stab(x
0
) g
1
Reemplazando X por la rbitas de los puntos de X, la ltima parte del ejemplo anterior
nos d el siguiente.
Proposicin 15.0.34. Sea (G, ) (Perm(X), ) una accin. Si dos puntos x, y
X pertenecen a la misma rbita, entonces sus estabilizadores son conjugados en G.
Ejemplo 15.0.35. Consideremos X como el conjunto de todos los subgrupos de G y
la accin
: (G, ) (Perm(X), ) : g (g)
denida por
(g) : X X : H g H g
1
En este ejemplo, H es subgrupo normal de G s y slo si Orb(H) = H.
Ejercicio 15.0.36. Sea (G, ) un grupo nito y H un subgrupo de G. Considere la
accin
: (H, ) (Perm(G), ) : h (h)
donde
(h) : G G : g h g
Verique que para todo g G vale que Stab(g) = I
G
y que #Orb(g) = [H[.
Utilice el hecho que G es la unin disjunta de sus rbitas para reobtener el teorema de
Lagrange.
Ejemplo 15.0.37. Consideremos un grupo de transformaciones de Mbius, con la re-
gla de la composicin, digamos G. Entonces tenemos una accin natural : (G, )
(Perm(
C), ) dada por biholomorsmos :

A :

C

C : z (A)(z) =
az +b
cz +d
a, b, c, d C, ad bc = 1. El estudio de este tipo de acciones es parte del estudio de
grupos Kleinianos que vern en el seminario de geometra compleja.
Consideremos un conjunto nito X ,= , un grupo nito (G, ), una accin :
(G, ) (Perm(X), ) y el conjunto U = (g, x) G X : g Stab(x). Por
cada g G denotemos por Fix(g) = x X : (g)(x) = x al conjunto de puntos
jos en X por g en la accin dada. Entonces, podemos ver que
#U =
gG
#Fix(g)
Por otro lado, por cada x X, podemos ver que existen tantos pares (x, g) U como
elementos en Stab(x) ; luego,
#U =
xX
[Stab(x)[
y como [G[/[Stab(x)[ = [G : Stab(x)] = #Orb(x), tenemos que
#U = [G[
xX
1/#Orb(x)
Escojamos una coleccin maximal, digamos x
1
, ..., x
r
X, de elementos no equiva-
lentes por G, es decir, cuyas rbitas son disjuntas y la unin de ellas es todo X. Entonces,
como la suma sobre cada rbita Orb(x) del valor 1/#Orb(x) d el valor 1, la igualdad
anterior pude escribirse como
#U = [G[r
obteniendo de esta manera la siguiente relacin entre los puntos jos de los elementos de
G, [G[ y #X/G.
Proposicin 15.0.38 (Igualdad de Burnside). Sea : (G, ) (Perm(X), ) una
accin de un grupo nito (G, ) sobre un conjunto nito. Denotemos por r la cardina-
lidad del conjunto cociente X/(G), es decir, el nmero de classes diferentes (rbitas
diferentes). Entonces
gG
#Fix(g) = r[G[
y en particular,
r = nmero de rbitas =
1
[G[
gG
#Fix(g)
Ejemplo 15.0.39. Veamos una aplicacin de la igualdad anterior. Supongamos que
tenemos un tetraedro T R
3
centrado en el orgen. Este tetraedro tiene 4 caras, las cuales
queremos pintar de cuatro clores diferentes, digamos de azul, verde, lila y rojo. Es claro
que hay 4! = 24 posibles maneras de hacer esto : (i) la eleccin de la cara que pintaremos
con azul nos da 4 posibilidades, (ii) la elecin dejada para la que pintaremos de verde es 3,
(iii) la elecin para la que pintaremos de lila es 2, (iV) queda luego slo una posible cara
que pintar de rojo. Si consideramos el grupo de isometras Euclidianas (rotaciones) que
dejan invariante T, vemos que cada elecin va a parar a otra eleccin que en la prctica no
es diferente de la anterior, slo la estaremos mirando desde otra posicin. Como el grupo
de tales isometras es /
4
, el grupo alternante de 4 letras, cuyo orden es 12, vemos que en
realidad hay slo dos maneras totalmente diferentes de pintarlo, 2 = [o
2
: /
4
]. Ahora,
miremos esto utilizando la igualdad de Burnside. En este caso consideremos
X = (C
i1
, C
i2
, C
i3
, C
i4
) : i
1
, i
2
, i
3
, i
4
1, 2, 3, 4, i
j
,= i
k
, j ,= k
donde cada cu
druple est formada por las cuatro caras de T, es decir #X = 24 y el

grupo G = /
4
. La accin de /
4
es dada por permutaciones de las 4 coordendas (en cada
cudruple). Lo que necesitamos encontrar es entonces r, es decir, la cantidad de rbitas
diferentes. Para cada g GI
G
se tiene Fix(g) = y #Fix(I
G
) = 24. As, en este
caso la cantidad de rbitas posibles es r = 24/12 = 2 como era lo esperado.
Denicin 15.0.40. Todo grupo de orden una potencia de un primo p es llamado un
p-grupo.
Ejemplo 15.0.41. Volvamos a la accin por conjugacin
: (G, ) (Perm(G), ) : g (g)
donde
(g)(x) = g x g
1
Supongamos que G tiene orden nito, entonces tenemos las siguientes propiedades
(i) dos rbitas coinciden o son disjuntas,
(ii) cada elemento x Z(G) tiene como rbita Orb(x) = x,
(iii) la unin de las rbitas es todo G.
Como consecuecia de todo esto tenemos la ecuacin de las clases
[G[ = [Z(G)[ + #Orb(x
1
) + #Orb(x
2
) + + #Orb(x
r
)
donde x
1
, ..., x
r
es una coleccin maximal de elementos no conjugados en GZ(G).
Supongamos que [G[ = p
n
, es decir, un p-grupo. Ya que
(i) #Orb(x
j
) > 1, pues x
j
/ Z(G), y
(ii) #Orb(x
j
) divide [G[ = p
n
por la proposicin 15.0.32,
tenemos que
#Orb(x
j
) = p
nj
para algn n
j
1, 2, ..., n
Como consecuencia p debe dividir [Z(G)[ y, en particular, tenemos el siguiente.
Proposicin 15.0.42. Sea p un nmero primo y (G, ) un p-grupo. Entonces Z(G)
tiene al menos p elementos.
Anteriormente habamos visto que todo grupo de orden un nmero primo es un grupo
cclico, luego Abeliano. Usando el resultado anterior podemos obtener el siguiente.
Corolario 15.0.43. Si (G, ) es un grupo de orden p
2
, donde p es un nmero primo,
entonces (G, ) es Abeliano.
Demonstracin. Por el teorema de Lagrange, [Z(G)[ divide p
2
. La proposicin an-
terior nos dice entonces que [Z(G)[ p, p
2
. En el caso que [Z(G)[ = p
2
tendremos
G = Z(G) y luego Ges Abeliano. Supongamos por el contrario que [Z(G)[ = p, es decir
(G, ) no es Abeliano. Entonces la proposicin 6.0.51 nos d una contradiccin.
Ejemplo 15.0.44. Generalizemos el ejemplo anterior como sigue. Sea (G, ) un grupo
nito y una accin : (G, ) (Perm(X), ) sobre un conjunto nito. Sea r = #X/G,
es decir, podemos escoger x
1
, ..., x
r
X puntos conrbitas diferentes y cuya unin es
todo X, es decir, tenemos
#X =
r
j=1
#Orb(x
j
)
Denotemos por
X
G
= x X : (g)(x) = x para todo g G
Entonces, podemos suponer que x
1
, .., x
s
X
G
y x
s+1
, ..., x
r
/ X
G
. De esta manera,
#Orb(x
j
) = 1 para j = 1, ..., s y #Orb(x
j
) > 1 para j = s + 1, ..., r. As, hemos
obtenido una frmula que generaliza la ecuacin de clases para la accin particular de
conjugacin cuando X = G.
Proposicin 15.0.45 (Generalizacin de la ecuacin de clases)
Sea (G, ) un grupo nito y una accin : (G, ) (Perm(X), ) sobre un conjunto
nito X. Sea x
1
, ..., x
r
puntos conrbitas diferentes y cuya unin es todo X. Supongamos
que x
1
, .., x
s
X
G
y x
s+1
, ..., x
r
/ X
G
. Entonces
#X = #X
G
+
r
j=s+1
#Orb(x
j
)
Proposicin 15.0.46. Sea p un nmero primo y (G, ) un p-grupo. Entonces
#X #X
G
mdulo p
Demonstracin. Tenemos la igualdad
#X = #X
G
+
r
j=s+1
#Orb(x
j
)
y sabemos que #Orb(x
j
) = [G : Stab(x
j
)]. Pero para j s + 1 tambin sabemos
que Stab(x
j
) ,= G y, por el teorema de Lagrange, [Stab(x
j
)[ es una potencia de p no
maximal. Luego,
r
j=s+1
#Orb(x
j
) es divisible por p como queremos.
Ejemplo 15.0.47. Consideremos un grupo nito (G, ) y p un nmero primo que di-
vida [G[. Denotemos por G
p
el producto cartesiano de p copias de G y consideremos el
conjunto
X = (g
1
, g
2
, ..., g
p
) G
p
: g
1
g
2
g
p
= I
G
Observemos que #X = [G[

p1
ya que cualquier eleccin de g
1
, ..., g
p1
G nos
permite elegir g
p
= g
1
p1
g
1
p2
g
1
2
g
1
1
. Consideremos el subgrupo cclico del
grupo simtrico o
p
generado por el cclo = (1, 2, 3, ..., p) y la accin natural : )
=
Z/pZ Perm(X) dada por la permutacin cclica de las coordenadas.
Usando la proposicin 15.0.46
#X #X
mdulo p
y el hecho que p divide #X, tenemos que #X
tambin es divisible por p. Como

(I
G
, I
G
, ..., I
G
) X
, tenemos necesariamente que #X
es un mltiplo positivo de
p, en particular, existen al menos p elementos de X
. Pero (g
1
, ..., g
p
) X
s y slo
si g
1
= g
2
= = g
p
= g y g
p
= I
G
. Este ejemplo nos muestra que existe g GI
G
de orden p.
Proposicin 15.0.48 (Teorema de Cauchy). Sea (G, ) un grupo nito y p un n-
mero primo que divide a [G[. Entonces existen elementos de G con orden p.
Este resultado nos da una denicin equivalente para un p-grupo como sigue.
Corolario 15.0.49. Sea p un nmero primo. Entonces un grupo nito (G, ) es un p-
grupo s y slo si todo elemento de G diferente del neutro tiene orden una potencia de
p.
Demonstracin. Es claro que si Ges un p-grupo, es decir [G[ = p
n
para cierto n > 0,
entonces, por el teorema de Lagrange, todo elemento diferente del neutro tiene orden una
potencia de p. Recprocamente, supongamos que todo elemento de G, diferente del neutro
tiene orden una potencia de p. Si G no es un p-grupo, entonces debe existir un nmero
primo q ,= p que divide [G[. Por el teorema de Cauchy, debe entonces existir un elemento
de orden q, una contradiccin.
Ejemplo 15.0.50. Consideremos un grupo nito (G, ), p un nmero primo que di-
vide [G[ y H us p-subgrupo de G. Consideremos la accin
: (H, ) (Perm(G/H), )
donde
(h)(gH) = (h g)H
En este caso tenemos de la proposicin 15.0.46 la equivalencia
#G/H #(G/H)
H
mdulo p
En este caso,
(G/H)
H
= gH : (h g)H = gH, h H =
= gH : (g
1
h g) H, h H
es decir, (G/H)
H
coincide con las clases laterales de los elementos del normalizador
N
G
(H), el cual es N
G
(H)/H. En particular, como #G/H = [G : H], obtenemos
[G : H] [N
G
(H) : H] mdulo p
Ejemplo 15.0.51. Sea (G, ) un grupo y H un subgrupo de ndice n. Formemos el
conjunto X = G/H de las clases de equivalencia laterales derechas de G por H. Como
#X = [G : H] = n, tenemos un isomorsmo natural entre (Perm(X), ) y o
n
. Tenemos
la accin
: (G, ) (Perm(X), )
= o
n
dada por
(g)(xH) = (g x)H
Escribamos X = x
1
H, x
2
H, ..., x
n
H. En este caso, podemos mirar Ker() que nos
d los elementos de G que hacen de tal accin no el.
Ker() =
n
j=1
Stab(x
j
H) =
n
j=1
g G : (g x
j
)H = x
j
H, j = 1, 2, ..., n =
=
n
j=1
g G : x
1
j
g x
j
H =
=
n
j=1
x
j
Hx
1
j
H
Este ejemplo tiene dos simples consecuencias.
Proposicin 15.0.52. Si (G, ) es un grupo, nito innito, que contiene un subgrupo
de ndice nito n > 1, entonces contiene tambin un subgrupo normal de ndice nito.
Demonstracin. Basta escoger K = Ker() del ejemplo ya que [G : K] = [G :
H][H : K], [G : H] es nito y [H : K] n!.
Proposicin 15.0.53. Sea (G, ) un grupo simple, es decir, no contiene subgrupos
normales diferente de los triviales. Supongamos que existe H subgrupo de G de ndice
n > 1. Entonces existe un monomorsmo : (G, ) o
n
.
Demonstracin. Del ejemplo tenemos que K = Ker(). Pero como (G, ) es simple,
tenemos dos posibilidades : (i) K = I
G
, en cuyo caso estamos en lo deseado, (ii)
K = G, en cuyo caso obliga a tener H = G, una contradiccin.
Ejemplo 15.0.54. Consideremos un grupo (G, ) y una accin el transitiva
: (G, ) (Perm(X), ) sobre algn conjunto X ,= de cardinalidad. nita
n > 1. Como n = #X = #Orb(x) = [G : Stab(x)], entonces H = Stab(x) es un
subgrupo de ndice n > 1. Por lo visto anteriormente, el grupo (G, ) debe contener un
subgrupo normal de ndice nito. Desgraciadamente, H no es normal. En efecto, si existe
h HI
G
tal que para todo g Gg h g
1
H, entonces (g h g
1
)(x) = x,
es decir, h Stab((g
1
)(x)), para cada g G. En particular,
h
xX
Stab(x) = Ker() = I
G
pus la accin es el, dando una contradiccin. Ms an, esto tambin asegura que
Stab(x) es un grupo simple.
Recprocamente, supongamos que tenemos un grupo (G, ) el cual contiene un sub-
grupo H de ndice nito n que no es normal en G y el cual es adems simple (como fu
el caso de Stab(x) en el caso anterior). Procedamos a mirar la accin vista en el ejemplo
anterior
: (G, ) (Perm(X), )
= o
n
dada por
(g)(xH) = (g x)H
Ya habamos visto que K = Ker() < H, y como H es simple, tenemos que (i)
K = I
G
, en cuyo caso la accin es el, (ii) K = H, en cuyo caso H es subgrupo
normal de G, lo cual no es imposible por nuestra eleccin de H. Luego, es accin el.
Por otro lado, como (g)(H) = gH, tenemos que la accin es transitiva.
Este ejercicio nos d el siguiente resultado.
Proposicin 15.0.55. Sea (G, ) un grupo y un entero n > 1. Entonces existe una
accin transitiva : (G, ) o
n
s y slo si existe un subgrupo H de ndice n que no es
normal y simple.
CAPTULO 16
LOS TEOREMAS DE SYLOW
En esta seccin veremos tres resultados muy importantes en la teora de grupos -
nito, los llamados teoremas de Sylow. Estos resultados son consecuencia de mirar ciertas
acciones y utilizar la proposicin 15.0.46 el cula nos permite contar mdulo un primo.
Teorema 16.0.56 (Teoremas de Sylow). Sea (G, ) un grupo nito, p un nmero
primo y [G[ = p
a
q, donde (p, q) = 1, es decir, p y q son relativamente primos. Entonces :
(i) Para cada k 1, 2, ..., a existe un subgrupo de orden p
k
. Un subgrupo de orden
maximal p
a
ser llamado un p-subgrupo de Sylow de G;
(ii) Todo subgrupo de orden p
k
, donde k 1, 2, ..., a 1, es subgrupo normal de
un subgrupo de orden p
k+1
;
(iii) Dos p-subgrupos de Sylow de G son conjugados ;
(iv) El nmero N
p
de p-subgrupos de sylow satisface
N
p
1 mdulo p, N
p
divide [G[
Adems, si H es cualquier p-subgrupo de Sylow de G, entonces
N
p
= [G : N
G
(H)]
Demonstracin.
Parte (i) y (ii). Por el teorema de Cauchy, tenemos listo el caso k = 1. Ahora, veremos
que la existencia de un p-subgrupo de orden p
k
, donde k 1, 2, ..., a 1, asegura la
existencia de un p-subgrupo de orden p
k
, obteniendo de esta forma parte (i) del teorema.
Para esto, consideremos un subgrupo H de orden p
k
, k < a. Luego [G : H] es divisible
por p. Consecuencia de la equivalencia del ejemplo 15.0.50 es que [N
G
(H) : H] tambin
es divisible por p. Ahora, como H es subgrupo normal de N
G
(H), tenemos el grupo
cociente N
G
(H)/H de orden divisible por p. El teorema de Cauchy asegura la existencia
de un elemento zH H
G
(H)/H de orden p, es decir z
p
H = H. Consideremos el
homomorsmo sobreyectivo natural : N
G
(H) N
G
(H)/H y sea K =
1
(zH)).
Es claro que H = Ker() es subgrupo normal de K (al serlo de N
G
(H)), obteniendo
tambin como consecuencia parte (ii), y tiene orden p
k+1
como queramos.
84 CAPTULO 16. LOS TEOREMAS DE SYLOW
Parte (iii). Consideremos dos p-subgrupos de Sylow, digamos H y K. Consideremos la
accin
: (K, ) (Perm(G/H), )
dada por
(k)(gH) = (k g)H
Como consecuencia de la proposicin 15.0.46 tenemos la equivalencia
#G/H = [G : H] = #(G/H)
K
mdulo p
Como [G : H] ya no es divisible por p, el conjunto
(G/H)
K
= gH : (k g)H = gH, k K
no puede ser vaco. Escojamos gH (G/H)
K
, luego para cada k K vales que (k
g)H = gH, es decir g
1
kg H. Como H y K tienen el mismo orden, g
1
Kg = H.
Parte (iv). Tomemos un p-subgrupo de SylowH y denotemos por X al conjunto de todos
los p-subgrupos de Sylow. Miremos la accin
: (H, ) (Perm(X), )
dada por
(h)(K) = hKh
1
La proposicin 15.0.46 nos dice que
N
p
= #X #X
H
mdulo p
Pero en este caso X
H
esta formado por todos los p-subgrupos de Sylow K tales que
H est contenido en N
G
(K), luego, H es p-subgrupo de Sylow de N
G
(K).
Sea K X
H
. Por lo anterior H es p-subgrupo de Sylow de N
G
(K). Como K tambin
es p-subgrupo de Sylow de N
G
(K), tenemos por (iii) que ellos son conjugados por un
elemento de N
G
(K). Pero todo elemento de N
G
(K) conjuga K en si mismo, obteniendo
que K = H. Como consecuencia
X
H
= H
es decir
N
p
1 mdulo p
Ahora, usemos la accin : (G, ) (Perm(X), ), tambin dada por conjugacin,
es decir (g)(K) = gKg
1
. Por (iii) slo existe una rbita. Adems, para cada K X
vale que Stab(K) = N
G
(K). En particular, tomando uno de los p-subgrupos de Sylow
de G, digamos H, obtenemos
N
p
= #X = #Orb(H) = [G : N
G
(H)]
y como [G : N
G
(H)] divide [G[, entonces N
p
divide [G[.
CAPTULO 17
APLICACIONES DE LOS TEOREMAS DE SYLOW
17.1. Aplicacin 1
Sea p un nmero primo dado. Hemos visto que todo grupo (G, ) de orden p es nece-
sariamente un grupo cclico, es decir, isomorfo a Z/pZ. Tambin hemos visto que todo
grupo (G, ) de orden p
2
es Abeliano. Analizemos esta situacin con mayor detalle. Si
existe un elemento de orden p
2
, entonces este elemento es un generador de (G, ) y tene-
mos que (G, ) es un grupo cclico, es decir, isomorfo a Z/p
2
Z. Supongamos ahora que no
hay elementos de orden p
2
. Luego, por el teorema de Lagrange, todo elemento, diferente
del neutro, tiene orden p. Podemos escoger x, y GI
G
, tales que x) y) = I
G
.
Denotemos por H = x) y por K = y). Como Ges Abeliano, HK = KH, es decir HK
es subgrupo de G. Adems como #(H K) = 1, tenemos que #HK = [H[[K[ = p
2
y
luego HK = G. Consideremos la funcin
: H K G = HK : (x
a
, y
b
) x
a
y
b
,
donde H K es producto directo de los dos grupos cclicos, la cual es claramente un
homomorsmo de grupos (gracias a que Ges Abeliano) sobreyectivo. Por otro lado, como
H K = I
G
, tenemos que es tambin inyectiva, es decir, G

= H K y, como
consecuencia, G es producto directo interno de sus subgrupos H y K. En este caso,
G
= Z/pZ Z/pZ. Podemos resumir estos resultados de la siguiente manera :

Proposicin 17.1.1. Sea p un nmero primo.
(i) Si (G, ) es un grupo de orden p, entonces G
= Z/pZ.
(ii) Si (G, ) es un grupo de orden p
2
, entonces G

= Z/p
2
Z bin G

= Z/pZ
Z/pZ.
Ahora, supongamos que tenemos un grupo (G, ) de orden pq, donde p < q son n-
mero primos. Si existe un elemento de orden pq, entonces G

= Z/pqZ. Supongamos
ahora que no existe tal elemento. Por el teorema de Lagrange, todo elemento de G, dife-
rente del neutro, tiene orden p q. Por el teorema de Cauchy, existe un elemento x G
de orden p y existe un elemento y Gde orden q. Sean H = x) y por K = y). Es claro
86 CAPTULO 17. APLICACIONES DE LOS TEOREMAS DE SYLOW
que H K = I
G
ya que todo elemento de H I
G
es de orden p y todo elemento
de K I
G
es de orden q. De esta manera, #HK = [H[[K[ = pq y luego
G = HK = x
a
y
b
: a 0, 1, ..., p 1, b 0, 1, ..., q 1
Tenemos que H es un p-subgrupo de Sylow y K es un q-subgrupo de Sylow. En este
caso, por el teorema de Sylow,
N
q
= 1 +rq, cierto r 0, 1, 2, ...
y adems
N
q
/pq
luego,
N
q
1, p, q, pq
Observemos que N
q
= 1+rq no puede ser q ni puede ser pq ya que en tal caso estaremos
diciendo que 1 es divisible por q. Por otro lado, si N
q
= p, entonces p = N
q
= 1 + rq
para algn r > 0, una contradiccin al hecho que p < q. De esta manera, tenemos que
N
q
= 1 y, como consecuencia del teorema de Sylow, K es un subgrupo normal de G.
Esto nos dice que existe un valor 1, 2, 3, ..., q 1 de manera que
x y x
1
= y
De esta manera, tenemos que

G = x, y : x
p
, y
q
, x y x
1
y
)
Si = 1, entonces tenemos que G es Abeliano ya que x y = y x. En este caso,
podemos proceder de la misma manera como lo hicimos en el caso p
2
para obtener que
G

= Z/pZ Z/qZ

= Z/pqZ (lo ltimo como consecuencia de la proposicin 7.1.5).
Esta es la situacin obligada si tenemos que q no es congruente a 1 mdulo p. En efecto,
si estamos bajo tal condicin, entonces
N
p
= 1 +sp, cierto s 0, 1, 2, ...
y
N
p
/pq
Pero N
p
no puede ser p ni pq ya que en tal caso 1 sera divisible por p. Luego, N
p
1, q.
Pero q = N
p
= 1 + sp dice que q es congruente a 1 mdulo p lo que contradice nuestro
supuesto, luego N
p
= 1 y, como consecuencia, H tambin es subgrupo normal de G.
Luego, debe existir 1, 2, ..., p 1 tal que
y x y
1
= x
y luego, si > 1, tenemos que

y x = x
y = x
1
x y = x
1
y
x
de lo cual
y = x
1
y
es decir, x
1
HK = I
G
, con lo cual obtenemos una contradiccin. En resumen :
17.2. APLICACIN 2 87
Proposicin 17.1.2. Sean p < q nmeros primos y (G, ) un grupo de orden pq.
Entonces
(i) G es Abeliano y
G
= Z/pqZ
(ii) G no es Abeliano y existe 2, 3, ..., q 1 tal que
G = x, y : x
p
, y
q
, x y x
1
y
)
(iii) Si q no es congruente a 1 mdulo p, entonces estamos en el caso (i).
Ejemplo 17.1.3. Sea (G, ) un grupo de orden 10. En este caso p = 2, q = 5 y q es
congruente a 1 mdulo p. Si (G, ) es Abeliano, entonces tenemos
G
= Z/10Z
En el caso que G no sea Abeliano, entonces las posibilidades para son = 2, 3, 4.
El caso = 4 nos da el grupo dihedral
G = x, y : x
2
, y
5
, (x y)
2
)
= D
5
En el caso = 2 tenemos
G = x, y : x
2
, y
5
, x y = y
2
x) =
= x, y : x
2
, y
5
, y
1
x = x y
2
)
si tomamos z = y
3
, entonces
G = x, z : x
2
, z
5
, z
3
x = x z)
que corresponde al caso = 3. Es decir, en el caso de orden 10 slo tenemos 3 grupos no
isomorfos.
Ejercicio 17.1.4. Determinar los grupos de orden 8 no isomorfos.
17.2. Aplicacin 2
Consideremos un grupo Abeliano nito (G, ) y un entero positivo n que divide al
orden de G. Si escribimos
[G[ = p
r1
1
p
r2
2
p
rm
m
la descomposicin en nmeros primos diferentes, entonces
n = p
s1
j1
p
s2
j2
p
s
b
j
b
donde
1 j
1
< j
2
< < j
b
m
y
s
i
1, 2, ..., r
ji

Por el teorema de Sylow, existen subgrupos H
1
,..., H
b
, donde
[H
i
[ = p
si
ji
, i = 1, ..., b
Consideremos H = H
1
H
2
H
b
= x
1
x
2
x
b
: x
j
H
j
. Al ser G un
grupo Abeliano, uno puede vericar que H es realmente un subgrupo de G y de orden n,
luego el subgrupo deseado. De esta manera, tenemos el siguiente recproco del teorema
de Lagrange para grupos Abelianos.
Proposicin 17.2.1. Sea (G, ) un grupo Abeliano nito y n un entero positivo que
divide al orden de G. Entonces existe un subgrupo de G de orden n.
Ejercicio 17.2.2. Vericar en la construccin dada anteriormente que existe un iso-
morsmo entre el producto directo H
1
H
2
H
b
y el grupo H. Deducir que todo
grupo Abeliano nito es siempre isomorfo a un grupo de la forma
(Z/n
1
Z)
a1
(Z/n
r
Z)
ar
Comparar esto con la descomposicin hecha en el captulo anterior, seccin Grupos Abe-
lianos libres.
17.3. Aplicacin 3
Denicin 17.3.1. Diremos que un grupo es simple si no tiene subgrupos no triviales
que sean normales.
Ejemplo 17.3.2. Ejemplos de grupos simples son los siguientes.
(i) todo grupo cclico de orden un nmero primo es un grupo simple, pero un grupo
cclico de orden un nmero que no sea primo no es simple.
(ii) El grupo dihedral
D
n
= x, y : x
2
, y
n
, (x y)
2
)
tiene al subgrupo normal y), luego no es simple.
(iii) Por la clasicacin de los grupos Abelianos nitos, vemos que todo grupo Abe-
liano de orden que no sea un nmero primo no puede ser simple.
(iv) Si tenemos un grupo de orden p
n
, donde p es un nmero primo y n 2, entonces
por el teorema de Sylow este grupo no es simple ya que posse un subgrupo de orden
p
n1
que es normal.
(v) Si tenemos un grupo de orden pq, donde p < q son nmeros primos, entonces ya
habamos visto que necesariamente N
q
= 1 y luego todo q-subgrupo de Sylow es
normal, luego el grupo no puede ser simple.
(vi) Si tenemos un grupo de orden p
n
q, donde p < q son nmeros primos tales que q
no es congruente a 1 mdulo p y n 2, entonces el grupo no es simple. En efecto,
tenemos que N
p
= 1 +rp para algn entero r 0, 1, 2, ... y adems debe dividir
p
n
q. Esto obliga a tener que los factores primos de N
q
estn contenidos en p, q.
Como 1 no es divisible por p, entonces N
p
1, q. Pero N
p
= q nos dice que q
es congruente a 1 modulo p, lo cual hemos descartado en nuestra hiptesis. Luego,
N
p
= 1 y, como consecuencia, un psubgrupo de Sylow es subgrupo normal.
(vii) Sea (G, ) un grupo de orden 2q
n
, donde q > 2 es un nmero primo y n
1, 2, 3, .... Entonces G no es simple. En efecto, consideremos N
q
= 1 + rq, r
0, 1, 2, ..., que debe dividir 2q
n
. Esto obliga a tener que los factores primos de
N
q
estn contenidos en 2, q. Como 1 no es divisible por q, debemos tener N
q

1, 2. Pero N
q
= 2 no es posible para ningn valor de r, luego N
q
= 1.
(viii) Consideremos un grupo de orden 6q, donde q > 5 es un nmero primo. Entonces
el grupo no puede ser simple. En efecto, en este caso, N
q
= 1 + qr, cierto r
0, 1, 2, 3, .., que divide 6q. Como 1 no es divisible por q, tenemos que N
q

1, 2, 3, 6. Es claro que no podemos lograr los valores 2, 3, 6 con ningn r, luego
N
q
= 1 y todo q-subgrupo de Sylow es normal.
(ix) Ningn grupo de orden 30 es simple. En efecto, en este caso como 30 = 235,
miremos N
5
= 1 + 5r, cierto r 0, 1, 2, 3, .., que divide 30. Como 1 no es
divisible por 5, tenemos que N
5
1, 6. Si N
5
= 1 tenemos que todo 5-subgrupo
de Sylow es normal. Supongamos por el contrario que N
5
= 6. Entonces tenemos
64 = 24 elementos diferentes de orden 5 en nuestro grupo (diferentes del neutro).
Por otro lado, N
3
= 1 +3t, cierto t 0, 1, 2, 3, .., divide 30, luego N
3
1, 10.
Si N
3
= 1, entonces todo 3-subgrupo de Sylow es normal. Si colocamos n
3
= 10,
tendremos 2 10 = 20 elementos diferentes de orden 3. En total ya tenedramos
1 + 24 + 20 > 30 elementos diferentes en el grupo, una contradiccin.
(x) Ningn grupo de orden 36 es simple. En efecto, como 36 = 2
2
3
2
, entonces N
3
=
1 + 3r, al gun r 0, 1, 2, ..., divide 36. Como 1 no es divisible por 3, N
3

1, 2, 4. Pero N
3
= 2 no puede lograrse con ninguna de las posibles r. As, N
3

1, 4. Si N
3
= 1, entonces todo 3-subgrupo de Sylow es normal. Supongamos
que N
3
= 4. Consideremos un 3-subgrupos de Sylow, digamos H. Tenemos que
[H[ = 9. Consideremos el conjunto X = g H g
1
: g G que tiene
cardinalidad N
3
= 4. Miremos la accin
: (G, ) (Perm(X), )
dada por conjugacin. Como [G[ = 36 > 24 = [Perm(X)[, tenemos que K =
Ker() es un subgrupo normal de orden mayor que 1. Pero tambin tenemos que
K es necesariamente un subgrupo de N
G
(H), y como [G : N
G
(H)] = N
3
= 4,
tenemos que K es subgrupo propio de G. Entonces K es subgrupo normal no trivial.
(xi) Ningn grupo de orden 48 es simple. Como 48 = 2
4
3, podemos mirar N
3
=
1 + 3r, algn r 0, 1, 2, ..., dividiendo 48. De esta manera obtenemos N
3

1, 3. Si N
3
= 1, entonces todo 3-subgrupo de Sylow es normal. Supongamos que
N
3
= 3 y tomemos dos 3-subgrupos de Sylow diferentes, digamso H
1
y H
2
. Luego,
[H
j
[ = 16. Como
48 #H
1
H
2
=
[H
1
H
2
[
[H
1
H
2
[
obtenemos que
[H
1
H
2
[
16
2
48
> 5
Por el teorema de Lagrange, [H
1
H
2
[ divide [H
1
[ = 16 y, como consecuencia,
[H
1
H
2
[ = 8 (ya que H
1
,= H
2
). De esta manera, H
1
H
2
es subgrupo de ndice
2 en H
j
, j = 1, 2, y como consecuencia, subgrupo normal. Esto nos dice que H
1
y
H
2
son subgrupos de N
G
(H
1
H
2
). Es decir, [N
G
(H
1
H
2
)[ debe dividir 48, y ser
divisible por 16 (al contener H
1
y H
2
) y por el orden del grupo H
1
, H
2
), generado
por H
1
y H
2
, que tiene la forma 16k, con cierto k 2 (ya que H
1
,= H
2
). De esto
vemos que N
G
(H
1
H
2
) = G y, en particular, H
1
H
2
es subgrupo normal no
trivial de G.
(xii) Sea (G, ) un grupo de orden 160. Entonces G no es simple. En efecto, como
160 = 2
5
5, miremos N
5
= 1 +5r, cierto r 0, 1, 2, .., que divide 160. Tenemos
que N
5
1, 5. Si N
5
= 1, entonces todo 5-subgrupo de Sylow es normal. Supon-
gamos que N
5
= 5 y escojamos un 5-subgrupo de Sylow H, luego [H[ = 2
5
= 32.
Adems, tenemos por el teorema de Sylow que [G : N
G
(H)] = N
5
= 5 > 1, con
lo cual vemos que N
G
(H) es subgrupo propio de G. Consideremos el conjunto X
formado por todos los 5-subgrupos de Sylow, luego #X = N
5
= 5, y la accin
por conjugacin : (G, ) (Perm(X), ). Sea K el subgrupo normal de G dado
por Ker(). Como todo g K debe jar H, tenemos que g N
G
(H), es decir,
K < N
G
(H) y luego K ,= G. Por otro lado, como 160 = [G[ > 120 = [Perm(X),
tenemos que no es monomorsmo, es decir, K ,= I
G
. Luego, K es subgrupo
normal no trivial de G.
Ejercicio 17.3.3. Encontrar todos los grupos simples de orden menor que 60. Vericar
que /
5
es grupo simple de orden 60.
17.4. Aplicacin 4
Denicin 17.4.1. Diremos que un grupo Ges orientable si existe un homomorsmo
sobreyectivo : G Z/2Z. En tal caso el par (G, ) es llamado un grupo orientado. El
ncleo Ker() := G
+
es llamado el subgrupo de elementos que preservan orientacin.
Es claro que G
+
es un subgrupo de ndice dos y luego un subgrupo normal de G. Los
elementos de GG
+
son llamados elementos que revierten orientacin.
Una consecuencia directa de los teoremas de Sylow es el siguiente :
Proposicin 17.4.2. Sea (G, ) un grupo orientado nito tal que 2 divide [G[. Si 2
n
es la mxima potencia de 2 que divide a G, entonces G tiene a los ms 2
n1
elementos
de orden 2 que revierten orientacin y que no son conjugados en G.
Demonstracin. Denotemos por H un 2-subgrupo de Sylow. Sabemos que cada ele-
mento de orden 2 en Gtiene un conjugado en H. Luego debemos contar cuantos elemen-
tos de H pueden revertir orientacin. Ya que el producto de dos elementos de H preserva
orientacin, tenemos que H
+
:= H G
+
es de ndice 2 en H, es decir, [H
+
[ = 2
n1
y como tenemos la unin disjunta H = H
+
T, donde T denota el subconjunto de los
elementos de H que revierten orientacin, tenemos que #T = 2
n1
.
Observacin 17.4.3. El resultado anterior ha sido utilizado por G. Gromadzki (On
ovals on Riemann surfaces, Revista Matemtica Iberoamericana 16 (2000), 515-527) para
obtener informacin sobre el nmero mximo de ovalos de reexiones en supercies de
Riemann cerradas.
PARTE III
ANILLOS
Hasta ahora hemos estudiado estructuras donde slo est involucrada una operacin
binaria. Ahora miraremos estructuras donde aparecen dos estructuras.
CAPTULO 18
DEFINICIN Y EJEMPLOS
Denicin 18.0.4. Un anillo es por denicin un triple (R, +, ) donde R es un
conjunto no vaco y +, : R R R son dos operaciones binarias sobre R, llamadas
suma y multiplicacin repectivamente, tales que :
(1) (R, +) es un grupo abeliano ;
(2) vale la propiedad asociativa para la operacin de multiplicacin, es decir, para
r, s, t R se tiene
r (s t) = (r s) t
(3) para r, s, t R vale la propiedad distributiva :
r (s +t) = r s +r t
(r +s) t = r t +s t
Observacin 18.0.5. Al neutro de la operacin de suma lo denotaremos por 0, al in-
verso de r R respecto a la suma lo denotaremos por r y rs denotar r s. Si r R
y n > 0 es un entero, entonces denotaremos por r
n
al proceso de multiplicar r consigo
mismo n veces.
Ejercicio 18.0.6. Sea (R, +, ) un anillo. Vericar las siguientes propiedades :
(i) r0 = 0r = 0, para todo r R; concluir que si #R > 1, entonces 0 no puede ser
neutro multiplicativo.
(ii) r(s) = (r)s = (rs), para todo r, s R; concluir que (r)(s) = rs.
Ejemplo 18.0.7. Los primeros ejemplos de anillos que tenemos son Z, el anillo de
los nmeros enteros ; Q, el anillo de los nmeros racionales ; R, el anillo de los nmeros
reales ; C, el anillo de los nmeros complejos.
96 CAPTULO 18. DEFINICIN Y EJEMPLOS
Ejemplo 18.0.8. Otro ejemplo es considerar un entero positivo m > 0 y considerar
mZ = mn : n Z, el conjunto de los enteros mltiplos de m. Usando las operaciones
usuales de suma y multiplicacin de nmeros entros, se tiene un anillo.
De este ltimo ejemplo observamos, tomando m > 1, que hay anillos que no poseen
un neutro para la multiplicacin.
Denicin 18.0.9. Diremos que un anillo tiene unidad si existe un neutro para la mul-
tiplicacin, el cual denotaremos por 1.
Ejercicio 18.0.10. Vericar que la unidad es nica.
Por otro lado, si miramos el anillo Z, entonces podemos observar que un anillo con
unidad puede que no tenga inversos multiplicativos de sus elementos diferentes de 0.
Denicin 18.0.11. Diremos que un anillo con unidad con la propiedad que todo sus
elementos diferentes de cero tienen inverso multiplicativo es un anillo de divisin.
El anillo Z es un dominio entero, el cual no es de divisin. Pero Q, R y Cson dominios
enteros que adems son de divisin.
Ejercicio 18.0.12. Sea (R, +, ) un anillo con unidad y sea r R un elemento que
posee un inverso multiplicativo en R. Vericar que tal inverso multiplicativo es nico.
Observacin 18.0.13. Si r R, entonces denotaremos por r
1
R a su inverso
multiplicativo, en caso de existir. As, si r R posee un inverso r
1
y n < 0 es un
entero, entonces denotaremos por r
n
al elemento (r
1
)
n
.
Ejemplo 18.0.14 (Anillo de un grupo). Sea (G, ) un grupo y (R, +, ) un anillo.
Formamos el conjunto R[G] cuyos elementos son combinaciones lineales nitas de ele-
mentos de G con coecientes en R, es decir, objetos de la forma
r
1
g
1
+ +r
n
g
n
donde r
j
R y g
j
G. Denimos la suma como,
(r
1
g
1
+ +r
n
g
n
) + (s
1
g
1
+ +s
n
g
n
) = (r
1
+s
1
)g
1
+ + (r
n
+s
n
)g
n
y el producto como
n
j=1
r
j
g
j
m
i=1
s
i
h
i
=
n
j=1
m
i=1
r
j
s
i
g
j
h
i
De esta manera obtenemos un anillo (R[G], +, ) llamado el anillo del grupo G res-
pecto al anillo R.
CAPTULO 18. DEFINICIN Y EJEMPLOS 97
Ejercicio 18.0.15. Si G = x : x
3
) y R = Z/5Z, describir los elementos de R[G] y
las tablas de suma y multiplicacin.
Ejemplo 18.0.16 (Anillo de polinomios). Consideremos un anillo (R, +, ) y una va-
riable desconocida x / R. Formemos el conjunto R[x] formado por todas las series
j=0
r
j
x
j
donde asumimos que slo un nmero nito de los coecientes r
j
pueden ser diferente de
cero. Llamamos a cada uno de esos objetos un polinomio con coecientes en R y variable
desconocida x. Al mayor valor n0, 1, 2, ... tal que r
n
,= 0 le llamamos el grado del
polinomio. Usualmente no escribimos los trminos donde r
j
= 0 ; por jemplo si r
1
= 2,
r
3
= 1 y todos los dems r
j
= 0, entonces escribimos este polinomio como 2x + x
3
.
Tambin acostumbramos a denotar r
0
x
0
como r
0
. Denimos la suma de polinomios como
_
_
j=0
r
j
x
j
_
_
+
_
_
j=0
s
j
x
j
_
_
=
_
_
j=0
(r
j
+s
j
)x
j
_
_
y denimos el producto de polinomios como
_
_
j=0
r
j
x
j
_
_
i=0
s
i
x
i
_
=
_
_
k=0
_
_
i+j=k
r
j
s
i
_
_
x
k
_
_
Obtenemos de esta manera un anillo, llamado el anillo de polinomios con coecientes
en el anillo R.
Ejercicio 18.0.17. Vericar que el anillo R[x] tiene unidad s y slo si R lo tiene.
Ejemplo 18.0.18. Siguiendo con el ejemplo anterior, podemos partir de un anillo R
y formar el nuevo anillo R[x]. Pero ahora podemos formar el anillo R[x][y], es decir, los
polinomios en la variable y y coecientes en R[x]. En forma inductiva, podemos formar
el anillo R[x
1
][x
2
] [x
n
] formado por los polinomios en la variable x
n
y coecientes
en el anillo R[x
1
][x
2
] [x
n1
]. Los elementos de R[x
1
][x
2
] [x
n
] son llamados poli-
nomios en varias variables y coecientes en R. Usualmente escribimos este anillo como
R[x
1
, ..., x
n
].
Ejemplo 18.0.19. Consideremos un anillo (R, +, ) y un entero n 1. Consideremos
el conjunto M(n, R) formado por todas las matrices de tamao n n y coecientes en
R. La suma y producto usual de matrices hacen de este un anillo. La matriz 0, es decir,
todos sus coecientes igual a 0 R, es el ) M(n, R). En este caso, si R tiene una
unidad 1 R, entonces la matriz identidad es unidad en M(n, R). Supongamos n 2,
entonces se puede ver que la operacin de multiplicacin no es conmutativa ; por ejemplo,
si n = 2, consideremos
A =
_
0 1
0 0
_
y B =
_
0 0
0 1
_
entonces tenemos que
AB =
_
0 1
0 0
_
y BA =
_
0 0
0 0
_
Este ltimo ejemplo nos muestra que existen anillos en los cuales la operacin de
multiplicacin no es conmutativa.
Denicin 18.0.20. Diremos que un anillo R es un anillo conmutativo si para todo
par x, y R vale que xy = yx.
El ejemplo anterior tambin nos muestra que es posible tener dos elementos diferentes
de 0 que al multiplicarlos obtenemos como resultado 0.
Denicin 18.0.21. Sea R un anillo. Dos elementos x, y R0 tales que xy = 0
son llamados divisores de cero del anillo.
Ejercicio 18.0.22. Ver que un anillo de divisin no puede contener divisores de cero.
Denicin 18.0.23. Un anillo con unidad, sin divisores de cero y conmutativo es lla-
mado un dominio entero.
Ejercicio 18.0.24. Todo anillo de divisin conmutativo es un dominio entero.
Denicin 18.0.25. Un anillo de divisin conmutativo es llamado un cuerpo.
As, Q, R y C son ejemplos de cuerpos.
Ejemplo 18.0.26. Consideremos el grupo abeliano R
4
con la suma usual dada com-
ponente a componente, es decir,
(x
1
, x
2
, x
3
, x
4
) + (y
1
, y
2
, y
3
, y
4
) = (x
1
+y
1
, x
2
+y
2
, x
3
+y
3
, x
4
+y
4
)
Si denotamos por
1 = (1, 0, 0, 0), i = (0, 1, 0, 0), j = (0, 0, 1, 0), k = (0, 0, 0, 1),
entonces podemos escribir
(a, b, c, d) = a1 + bi +cj +dk
Usaremos la identicacin a1 = a, luego
(a, b, c, d) = a +bi +cj +dk
En esta notacin la suma queda expresda como :
(x
1
+x
2
i +x
3
j +x
4
k) + (y
1
+y
2
i +y
3
j +y
4
k)
[[
(x
1
+y
1
) + (x
2
+y
2
)i + (x
3
+y
3
)j + (x
4
+ y
4
)k
Procedemos a denir una multiplicacin como sigue :
(x
1
+x
2
i +x
3
j +x
4
k) (y
1
+y
2
i + y
3
j +y
4
k)
[[
(x
1
y
1
x
2
y
2
x
3
y
3
x
4
y
4
) + (x
1
y
2
+x
2
y
1
+x
3
y
4
x
4
y
3
)i
+
(x
1
y
3
x
2
y
4
+x
3
y
1
+x
4
y
2
)j + (x
1
y
4
+x
2
y
3
x
3
y
2
+x
4
y
1
)k
Obtenemos de esta manera un anillo con unidad, siendo esta 1. Denotamos este anillo
por Q y le llamamos el anillo de los cuaternios. En este anillo tenemos las propiedades
i
2
= j
2
= k
2
= 1
ij = k, jk = i, ki = j, ji = k, kj = i, ik = j,
en particular, este anillo no es conmutativo. Por otro lado, si tomamos un elemento dife-
rente de 0, digamos a+bi +cj +dk Q, entonces este tiene inverso multiplicativo dado
por
1
a
2
+b
2
+c
2
+d
2
(a bi cj dk)
En este ejemplo tenemos un anillo que es casi un cuerpo, pero falla la conmutatividad
de la multiplicacin.
Denicin 18.0.27. Un anillo de divisin no conmutativo es llamado un cuerpo no
conmutativo semicuerpo.
Ejemplo 18.0.28. Consideremos una coleccin de anillos (R
1
, +, ),..., (R
n
, +, ) y
formemos el producto cartesiano R
1
R
n
. Consideremos la suma y multiplicacin
denidas componente a componente, es decir,
(r
1
, ..., r
n
) + (s
1
, ..., s
n
) = (r
1
+s
1
, ..., r
n
+s
n
)
(r
1
, ..., r
n
) (s
1
, ..., s
n
) = (r
1
s
1
, ..., r
n
s
n
)
donde r
j
, s
j
R
j
, para j = 1, 2, ..., n. As obtenemos un anillo llamado el producto
directo de los anillos. Observemos que este anillo tiene unidad s y slo si cada anillo
componente lo tiene. Por otro lado, si todos los anillos R
j
son dominios enteros, y n 2,
entonces el producto directo ya no es dominio entero ya que (1, 0, ..., 0) (0, 1, 0, ..., 0) =
(0, ..., 0).
Ejercicio 18.0.29. Consideremos un entero positivo d > 0 con la propiedad que
d /
Z. Consideremos los conjuntos
Z[
d] = a +b
d : a, b Z
Q[
d] = a +b
d : a, b Q
Consideramos la suma usual de nmeros complejos y el producto usual de nmeros
complejos. Vericar que los anteriores son dominios enteros, que Q[
d] es un cuerpo y
Z[
d] no lo es. Vericar que Q[
d] es el cuerpo ms pequeo dentro de R que contiene

al dominio entero Z[
d].
Ejercicio 18.0.30. Por cada entero positivo m > 0 consideremos el grupo cclico
Z/mZ. Denamos la multiplicacin a b, donde a, b 0, 1, ..., m 1, como el resto
mdulo m del entero ab Z. Vericar que de esta manera obtenemos un anillo con
unidad y conmutativo. Vericar que este anillo tiene divisores de cero s y slo si m no es
un nmero primo. En el caso que m es un nmero primo, vericar que este es de hecho
un cuerpo. Ms adelante daremos un argumento de este hecho.
La situacin del ejemplo anterior es caso particular del siguiente hecho.
Teorema 18.0.31. Todo dominio entero nito es un cuerpo.
Demonstracin. Sea R = 0, 1, r
1
, ..., r
n
. Basta vericar que todo elemento dife-
rente de 0 tiene un inverso multiplicativo. Para eso, sea r R, r ,= 0. Como la coleccin
r, rr
1
, ..., rr
n
son dos a dos diferentes y distintos de 0, alguno de ellos debe ser igual a 1.
En algunos de los ejemplos anteriores hemos visto que hay anillos que estn contenidos
en otros anillos (con las operaciones inducidas). Estos son llamados subanillos.
Ejercicio 18.0.32. Sea (R, +, ) un anillo y S R un subconjunto no vaco. Vericar
que S dene un subanillo de R s y slo si
(i) para todo s S, s S ;
(ii) si s, r S, entonces s r S ;
(iii) si r, s S, entonces sr S.
Ejercicio 18.0.33. Sea (R, +, ) un anillo y r R. Consideremos el subconjunto
I
r
= rx : x R
Vericar que I
r
es un subanillo de R. Vericar adems que el grupo abeliano (I
r
, +) est
generado por r
n
: n 1, 2, ...
Ejercicio 18.0.34. Vericar que la interseccin arbitraria de subanillos de un anillo
es un subanillo. Sea r R. Sea r) la interseccin de todos los subanillos de R que
contienen a r. Entonces r) es el subanillo ms pequeo de R que contiene a r.
Ejemplo 18.0.35. Sea R una anillo con la propiedad que x
2
= x es vlido para todo
x R. Si consideramos r, s R obtenemos que
r +s = (r +s)
2
= r
2
+ s
2
+rs +sr = r +s +rs +sr
r s = (r s)
2
= r
2
+ s
2
rs sr = r +s rs sr
de donde obtenemos
rs +sr = 0 y rs +sr = 2s
es decir, s+s = 0, de donde s = s y luego rs = sr, es decir, Res un anillo conmutativo.
Ejemplo 18.0.36. Sea (G, ) un grupo abeliano y consideremos el conjunto Hom(G)
formado por todos los homomorsmo de grupo h : G G (endomorsmos). Usando la
suma
(f +g)(x) := f(x) g(x)
y la regla de composicin de funciones como multiplicacin, tenemos el anillo de en-
domorsmos de G. En este caso, el neutro aditivo es dado por la funcion 0(x) = e,
donde e G denota el neutro del grupo G. El inverso aditivo de f es el homomorsmo
f(x) := f(x)
1
. Este anillo tiene unidad dada por el automorsmo identidad. En ge-
neral este anillo no es conmutativo, pero por ejemplo Hom(Z, +) si lo es ya que cada
homomorsmo de grupo para Z es de la forma f(x) = ax, para cierto a Z.
CAPTULO 19
HOMOMORFISMOS DE ANILLOS
Al igual que en el caso de grupos, existen funciones que nos permiten relacionar
anillos. Estas funciones deben preservar las dos operaciones binarias en juego. De ma-
nera ms precisa :
Denicin 19.0.37.
(1) Dados dos anillos (R, +, ) y (S, +, ), diremos que una funcin h : R S es un
homomorsmo de anillos si para todo par r
1
, r
2
R valen las siguientes :
(i) h(r
1
+r
2
) = h(r
1
) +h(r
2
)
(ii) h(r
1
r
2
) = h(r
1
)h(r
2
)
(2) Si el homomorsmo de anillos h : R S es biyectiva, entonces decimos que es
un isomorsmo de anillos, en cuyo caso decimos que los anillos son anillos isomor-
fos.
Ejercicio 19.0.38.
(i) Si h : R S es un homomorsmo de anillos, entonces h(0) = 0, h(r) =
h(r).
(ii) Si h : R S es un isomorsmo de anillos, entonces h
1
: S R tambin lo es.
(iii) La propiedad de ser isomorfos es una relacin de equivalencia en el conjunto de
todos los anillos.
(iv) Si h : R S es un homomorsmo de anillos, entonces
Ker(h) = r R : h(r) = 0
es un subanillo de R, llamado el ncleo de h y
Im(h) = s S : existe r R tal que h(r) = s
es un subanillo de S, llamado la imgen de h.
(v) Sea h : R S un homomorsmo de anillos. Vericar que la imgen de subanillos
de R son subanillos de S y, recprocamente, la preimgen de subanillos de S son
subanillos de R.
104 CAPTULO 19. HOMOMORFISMOS DE ANILLOS
(vi) Si h : R S es homomorsmo de anillos y R tiene unidad 1, entonces h(1) = x
debe satisfacer la ecuacin x
2
= x en S. Concluir que
(a) las funciones h : Z 2Z : n 2n, y h : Z Z : n 2n, no son
homomorsmo de anillos ; y
(b) determinar todos los homomorsmos de anillos h : Z Z.
(vii) Calcular Hom((Z Z, +)) y vericar que este anillo no es isomorfo al anillo
Z Z.
Ejemplo 19.0.39. Sea R un anillo y variables x, y para formar los anillos de polino-
mios R[x, y] y R[y, x]. Los polinomios en R[x, y] son de la forma
j=0
_

i=0
a
j
i
x
i
_
y
j
y los de R[y, x] son de la forma
i=0
_
_
j=0
b
j
i
y
j
_
_
x
i
Podemos considerar la funcin : R[x, y] R[y, x], denida como
_
_
j=0
_

i=0
a
j
i
x
i
_
y
j
_
_
=
i=0
_
_
j=0
a
j
i
y
j
_
_
x
i
la cual defne un isomorsmo de anillos. De esta manera, podemos hablar indistintamente
de uno u otro y usaremos cualquiera de las siguientes notaciones para representar un
polinomio en las varaibles x, y y coecientes en R :
i,j=0
a
j
i
x
i
y
j
=
i,j=0
a
j
i
y
j
x
i
Lo anterior se generaliza a ms variables.
Ejercicio 19.0.40. Vericar los detalles del ejemplo anterior.
Ejemplo 19.0.41. Consideremos un anillo conmutativo R y su anillo de polinomios
en una variable R[x]. Supongamos que S es un subanillo de R. Entonces tenemos que el
anillo de polinomios S[x] es un subanillo de R[x]. Para cada r R, denamos la funcin
E
r
: S[x] R :
j=0
a
j
x
j
j=0
a
j
r
j
Recordemos que los coecientes a
j
son igual a 0 con la posible excepcin de un n-
mero nito de ndices, luego la funcin anterior tiene sentido. Por la denicin de suma
y multiplicacin de polinomios podemos vericar que E
r
es de hecho un homomorsmo
de anillos, llamado el homomorsmo de evaluacin en r. Podemos adems ver que si S
CAPTULO 19. HOMOMORFISMOS DE ANILLOS 105
tiene unidad 1, entonces tenemos el polinomio x S[x], para el cual E
r
(x) = r. Si
identicamos S con los polinomios de grado cero, entonces E
r
: S R : s s es un
isomorsmo. El ncleo del homomorsmo E
r
est formado por todos aquellos polino-
mios p S[x] tales que E
r
(p) = 0. Diremos en tal caso que r es un cero del polinomio
p.
Si consideramos por ejemplo el polinomio 1 + x
2
R[x], entonces este no tiene
ceros en R, pero si tiene ceros en C. En forma similar, si tomamos S = Q, entonces el
polinomio 2 x
2
Q[x] no tiene ceros en Q, pero si los tiene en R. As, podemos ver
que es probable que un polinomio p S[x] no tenga ceros en S, pero que exista un anillo
R, conteniendo a S como subanillo, donde si tiene ceros. En un captulo posterior nos
preocuparemos de este problema para el caso en que nuestros anillos son cuerpos ya que
esto simplicar mucho las operaciones.
: C M(2, R) : x +iy
_
x y
y x
_
es un isomorsmo.
CAPTULO 20
IDEALES Y ANILLOS COCIENTES
En el captulo de grupos vimos que hay ciertos subgrupos muy especiales, estos son
los subgrupos normales. Estos subgrupos tienen la propiedad de que el cociente resulta
ser un grupo, el grupo cociente. A nivel de anillos podemos hacer lo mismo. Supongamos
que tenemos un anillo (R, +, ) y un subanillo S de R. Entonces, al ser (R, +) un grupo
abeliano y S subgrupo de (R, +), tenemos que este es subgrupo normal de manera tri-
vial. As, podemos formar el grupo cociente (R/S, +) que es tambin un grupo abeliano.
Tenemos la proyeccin natural
: R R/S : r r +S
que es un homomorsmo sobreyectivo de grupos. Hasta ahora no hemos involucrado la
operacin de multiplicacin. Nuestra pregunta natural es :
Es posible dotar a R/S de una multiplicacin que le transforme en un anillo de
manera que resulte un homomorsmo de anillos ?
Observemos que la condicin (r
1
r
2
) = (r
1
)(r
2
) es equivalente a tener la deni-
cin de multiplicacin siguiente :
r
1
r
2
+S = (r
1
+S)(r
2
+S) = r
1
r
2
+r
1
S +Sr
2
Tomando r
2
= 0 obtenemos que r
1
S S y tomando r
1
= 0 obtenemos que Sr
2
S.
As, condiciones necesarias para que tenga sentido la multiplicacin anterior es que
rS S, Sr S
valga para todo r S. En forma recproca, si valen las dos condiciones necesarias, en-
tonces tenemos que (r
1
r
2
) = (r
1
)(r
2
) es vlida para todos r
1
, r
2
R.
Por otro lado, una vez que tenemos la validz de lo anterior, entonces es fcil ver que
la propiedad distributiva es vlida.
Denicin 20.0.43. Diremos que un subanillo S de un anillo R es un ideal izquierdo
si para todo r R vale que rS S y es un ideal derecho si para todo r R vale que
Sr S. Un ideal es un subanillo que es ideal izquierdo y derecho.
108 CAPTULO 20. IDEALES Y ANILLOS COCIENTES
Luego, lo anterior nos est diciendo lo siguiente : El tipo de anillos en el cual estaremos
interesados es el siguiente.
Proposicin 20.0.44. R/S es un anillo (llamado anillo cociente), que hace de la
proyeccin : R R/S un homomorsmo de anillos, s y slo si S es un ideal de
R.
De lo anterior vemos que el equivalente, en la teora de anillos, de los subgrupos nor-
males son los ideales. Tambin nos dimos cuenta que podemos ver cada subgrupo normal
de un grupo como el ncleo de algn homomorsmo y que todo ncleo de un homomor-
smo de grupos es subgrupo normal. Para los anillos tenemos la situacin similar. Lo
anterior nos permite ver cada ideal como el ncleo de algn homomorsmo de anillos.
Por otro lado, si h : R S es un homomorsmo de anillos, entonces Ker(h) es un
ideal de R. En efecto, si r
1
, r
2
Ker(h), entonces h(r
1
r
2
) = h(r
1
)h
(
r
2
) = 0, luego
r
1
r
2
Ker(h), obteniendo que h es subanillo. Por otro lado, si r R y s Ker(h),
entonces h(rs) = h(r)h(s) = 0, h(sr) = h(s)h(r) = 0 diciendo que rs, sr Ker(h),
es decir, Ker(h) es ideal.
Supongamos que tenemos un homomorsmo de anillos
h : R S.
Consideremos el ideal K = Ker(h) y la proyeccin : R R/K. Entonces podemos
denir la nueva funcin
t : R/K S : r +K h(r)
la cual est s bin denida y resulta ser un homomorsmo de anillos inyectivo ; luego los
anillos h(R) y R/K son isomorfos.
Ejercicio 20.0.45. Completar los detalles de lo anterior.
Proposicin 20.0.46. Sea R una anillo con unidad 1 y sea I un ideal de R. Si 1 I,
entonces I = R. En particular, los nicos ideales de un cuerpo R son 0 y R.
Demonstracin. Si 1 I, entonces para todo r R debemos tener r = r 1 I.
Supongamos ahora que R es un cuerpo y que I ,= 0. Sea s I, s ,= 0. Como R es
cuerpo, existe s
1
R y luego 1 = s
1
s I.
Ejercicio 20.0.47.
(i) Determinar todos los ideales de Z, Z Z.
(ii) Vericar que si R es un anillo con unidad y S es un ideal de R, S ,= R, entonces
el anillo cociente R/S tiene unidad.
Ejercicio 20.0.48. Vericar que la interseccin arbitraria de ideales es un ideal.
CAPTULO 20. IDEALES Y ANILLOS COCIENTES 109
Ejemplo 20.0.49. Sea R un anillo conmutativo y consideremos el homomorsmo de
evaluacin E
0
: R[x] R. Su ncleo es el ideal formado por todos los polinomios
en R[x] cuyo coeciente constante es igual a 0. Luego R/Ker(E
0
) es un anillo conmu-
tativo isomorfo a R. Cada clase de equivalencia en R/Ker(E
0
) es representado por un
polinomio con trmino constante jo.
Denicin 20.0.50. Sea M R un subconjunto de un anillo R. Denimos el ideal
generado por M al ideal ms pequeo que contiene a M, donotado por M).
Una consecuencia del ejercicio anterior es el siguiente
Proposicin 20.0.51. Sea M R, donde R es un anillo. Entonces
M) =
I Ideal de R
M I
I
Ejercicio 20.0.52. Si un anillo R tiene unidad 1 y r R es invertible, entonces r) =
R.
Denicin 20.0.53. Un ideal que se pueda generar con un elemento es llamado un
ideal principal. As, en un cuerpo tenemos tenemos que todo ideal es principal. Por su-
puesto, si R es cualquier anillo con unidad, entonces R es ideal principal.
Ejercicio 20.0.54. Sean r
1
, ..., r
n
Z tales que el ideal I = r
1
, ..., r
n
) sea principal.
Vericar que si d es el mximo comn divisor de r
1
, ..., r
n
, entonces I = d). Ind.
Recordar que existen enteros a
1
, ..., a
n
tales que a
1
r
1
+ a
n
r
n
= d.
Ejemplo 20.0.55. Consideremos el anillo de polinomios Z[x], el cual es un dominio
entero. Sea I =
j=1
a
j
x
j
Z[x] : a
0
= 0. Entonces vemos que la propiedad de
tener trmino constante igual a cero se preserva bajo suma y multiplicacin, de lo cual
obtenemos que I es un ideal de Z. Consideremos el ideal principal x) el cual est conte-
nido en I. Como todo elemento de I es suma de productos de polinomios monomiales
con el polinomio x, observamos que I = x). Por otro lado, si consideramos el ideal J
generado por los polinomios 2 y x, entonces este no puede ser principal. Esto por que si lo
fuese, digamos generado por el polinomio q, entonces tener qp = 2 para algn polinomio
p obliga a tener q de grado cero, es decir que q Z. Adems, als nicas posibilidades
para q, mdulo signo, son q = 1 q = 2. En el caso q = 1 diriamos que J = Z[x], pero
el ideal J slo contiene polinomios con coeciente par. Si q = 2, entonces debe existir
un polinomio f tal que 2f = x, pero 2f tiene coecientes pares. Luego, en cualquier
110 CAPTULO 20. IDEALES Y ANILLOS COCIENTES
caso obtenemos una contradiccin y, en particular, obtenemos que J no es principal. En
resumen, en el dominio entero Z[x] hay ideales que no son principales.
Ejercicio 20.0.56. Sea R un anillo conmutativo y r R.
(i) Vericar que
I
r
= x : rx = 0
es un ideal de R.
(ii) Vericar que si S es un ideal de R, entonces
S = x R : x
n
S para algn n > 0
es un ideal de R; llamado el radical de S.
Ejercicio 20.0.57. Sea R un anillo y dos ideales U y V de R. Dena
U +V = u +v : u U, v V
UV =
n
i=1
u
i
v
i
: u
i
U, v
i
V, n 1, 2, 3, ...
Vericar que U +V y UV son ideales de R, tales que U, V U +V y UV U V .
CAPTULO 21
IDEALES PRIMOS Y MAXIMALES
Ahora que sabemos que para construir anillos cocientes necesitamos cocientar anillos
por ideales, podemos preguntarnos que tipo de ideal es necesario para que el cociente
sea un dominio entero an mejor un cuerpo. Consideremos un anillo R y un ideal I
de R. Miremos el anillo cociente R/I. Si I = R, entonces R/I es el anillo 0, el
cual no tiene unidad. Supongamos entonces que I es ideal propio de R. Es claro que si
R es conmutativo y tiene unidad, entonces R/I tambin es conmutativo y tiene unidad.
Supongamos entonces que R es de tal tipo. Para obtener que R/I sea un dominio entero
debemos asegurarnos que no tiene divisores de cero. La existencia de divisores de cero
en R/I implica la existencia de dos elementos x + I, y + I, donde x, y / I, tales que
(x+I)(y +I) = I, es decir, xy I. Luego, la no existencia de divisores de cero en R/I
es equivalente a la propiedad siguiente :
si x, y R son tales que xy I, entonces x I y I.
Denicin 21.0.58. Un ideal propio de R con tal propiedad que si x, y R son tales
que xy I, entonces x I y I, es llamado un ideal primo.
Ahora, para que adems R/I sea un cuerpo, debemos tener que todo elemento x + I,
donde x / I, posee un inverso, es decir, debe existir y / I tal que (x+I)(y +I) = 1+I,
lo cual es equivalente a tener xy 1 +I. Luego, tenemos que R/I es un cuerpo s y slo
si
I es ideal primo y adems para cada x RI, existe y RI tal que xy 1 I.
Denicin 21.0.59. Un ideal primo I con tal que para cada x R I, existe y
R I tal que xy 1 I, es llamado un ideal maximal.
La razn de este nombre es la siguiente. Primero, si tenemos un ideal maximal I conte-
nido estrictamente en otro ideal J de R, entonces existe j J I. luego debe existir
112 CAPTULO 21. IDEALES PRIMOS Y MAXIMALES
h R I tal que hj 1 I. Esto dice que existe i I tal que hj 1 = i, con lo cual
obtenemos 1 = hj i J, es decir J = R. En otras palabras, un ideal maximal no puede
estar contenido propiamente en otro ideal propio de R. En forma recproca, si tenemos
un ideal propio I de R con la propiedad que no existe ideal propio de R conteniendolo,
entonces tenemos
(i) Si x R I es tal que x / I, entonces consideremos el ideal generado por I y
x. Como x / I, este ideal contiene estrictamente a I, luego debe ser R, es decir,
1 x, I). Como 1 / I, tenemos que 1 = xy + i, para cierto i I y cierto
y R I.
(ii) Si x, y R son tales que xy I. Supongamos que x, y / I. Por (i) tenemos que
existen u, v / I tales que xu 1, yv 1 I. En este caso, xyuv xu yv +1 =
(xu1)(yv1) I y como xy I, tenemos que xu(yv1) = xuyv+1 I
y, en particular, xu I. Est ltimo junto a tener xu1 I nos obliga atener 1 I,
una contradiccin. Luego I debe ser primo.
De esta manera obtenemos la denicin equivalente de un ideal maximal :
Teorema 21.0.60. Un ideal maximal es un ideal propio de R que no est contenido
estrictamente en otro ideal propio de R.
Resumiendo todo lo anterior, tenemos :
Proposicin 21.0.61. Sea R un anillo conmutativo con unidad e I un ideal propio de
R. Entonces :
(1) R/I es un dominio entero s y slo si I es un ideal primo.
(2) R/I es un cuerpo s y slo si I es un ideal maximal.
(3) Todo ideal maximal es primo.
Ejemplo 21.0.62. En un cuerpo K tenemos slo dos ideales : 0 y K. En este caso
0 es el nico ideal propio y adems es maximal y K/0 es isomorfo a K. Supongamos
ahora que R es un anillo conmutativo con unidad de manera que sus nicos ideales son
0 y R. Entonces 0 es ideal maximal y como R/0 es isomorfo a R, tenemos que R
debe ser un cuerpo.
Proposicin 21.0.63. Sea R una anillo conmutativo con unidad. Entonces R es un
cuerpo s y slo si sus nicos ideales son 0 y R.
Ejemplo 21.0.64. Consideremos el domnio entero Z. Sus subgrupos aditivos son de
la forma mZ, donde m 0, 1, 2, .... Estos son cerrados bajo la operacin de multipli-
cacin, luego son sus subanillos. Si multiplicamos cualquier entero por un mltiplo de
m volvemos a tener un mltiplo de m, es decir, todos sus subanillos son ideales. Esto se
CAPTULO 21. IDEALES PRIMOS Y MAXIMALES 113
parece mucho al hecho que en un grupo abeliano todos sus subgrupos son normales. Es-
tos ideales son principales, generado por m. Como sabemos que 0 es siempre un ideal
primo, consideremos m > 1 (el caso m = 1 nos d todo el anillo Z). En este caso, si
tenemos dos enteros a, b Z tales que ab mZ, entonces debe ocurrir que los factores
primos de m se distribuyen en a y b. As, m es un nmero primo s y slo si mZ es un
ideal primo. Como todo ideal mZ, donde m = pq, siempre est contenido en el ideal
pZ, tambin obsevamos que los ideales primos son maximales. Como consecuencia, para
todo nmero primo p tenemos que el anillo cociente Z/pZ es un cuerpo.
Denicin 21.0.65. Los cuerpos Z/pZ, donde p es primo, y Q reciben el nombre de
cuerpos primos.
Denicin 21.0.66. Supongamos que tenemos un anillo R con unidad. Si existe un
entero n > 0 tal que n 1 = 1 + 1 + + 1
. .
n veces
= 0, diremos que el menor de tales enteros
es la caracterstica de R. En caso de no existir tal valor, decimos que la caracterstica de
R es 0.
Por ejemplo, Z, Q, R, C, Q[
d], donde d > 0 no es el cuadrado de un entero, tienen

caraterstica 0, mientras que los anillos Z/mZ tienen caracterstica m. Consideremos el
homomorsmo
: Z R : n n 1
cuyo ncleo es mZ, si m es la caracterstica de R. En particular, si m = 0, entonces es
un homomorsmo inyectivo. Esto nos d la siguiente in formacin :
Proposicin 21.0.67. Sea R un anillo con caracterstica m.
(1) Si m = 0, entonces R contiene un subanillo isomorfo a Z.
(2) Si m > 0, entonces R contiene un subanillo isomorfo a Z/mZ.
(3) Si R es un cuerpo de caracterstica 0, entonces este contiene un subcuerpo iso-
morfo a Q.
(4) Si R es un cuerpo de caracterstica m, entonces m debe ser primo y R contiene
un subcuerpo isomorfo a Z/mZ.
Demonstracin. Lo nico que falta por vericar es que la caracterstica de un cuerpo
R es cero un nmero primo. En efecto, supongamos que la caracterstica es diferente de
cero e igual a un valor m > 0. Usando el homomorsmo obtenemos que R contiene un
subanillo isomorfo a Z/mZ, el cual contiene divisores de cero para m no primo ; luego,
m est obligado ser un nmero primo.
114 CAPTULO 21. IDEALES PRIMOS Y MAXIMALES
Ejemplo 21.0.68. Otro ejemplo importante de ideal maximal es el siguiente. Sea
(X, ) un espacio topolgico y sea p X algn punto que jaremos. Denotemos por

(
p
al conjunto de todas las funciones a valores reales denidas en algn entorno abierto de
p. Denimos en

(
p
la siguiente relacin de equivalencia. Si
f : U
f
R, g : U
g
R

(
p
,
entonces decimos que ellas son equivalentes si es posible encontrar un abierto V U
f

U
g
, p V , de manera que f = g en V . Denotemos por [f] la clase de equivalencia
de f : U
f
R

(
p
y por (
p
al conjunto de classes de equivalencia. Cada clase [f]
es llamada un germen de funcin real continua en p y (
p
el anillo de funciones reales
continuas en p. Para ver que (
p
es en efecto un anillo, de hecho un dominio de intero,
denimos las operaciones :
[f] + [g] = [f +g]; [f][g] = [fg],
donde las operaciones f + g, fg estn denidas en un abierto comn de denicin. El
elemento unidad es dada por el germen de la funcin constante 1 y la denotamos por
[1]. La denicin de la relacin de equivalencia nos asegura que si [f] = [g], entonces
f(p) = 0 s y slo si g(p) = 0. La continuidad nos asegura que si [f] es tal que f(p) ,= 0,
entonces existe [1/f], en particular, [f] es invertible. Ms an, los elementos invertibles
de (
p
son exctamente las clases [f] tales que f(p) ,= 0.
El conjunto
m
p
= [f] (
p
: f(p) = 0,
es un ideal maximal de (
p
. Esto es dado por :
(i) si [f], [g] m
p
, es decir f(p) = g(p) = 0, entonces (f + g)(p) = 0 de donde
[f +g] m
p
;
(ii) si [f] m
p
, entonces f(p) = 0, es decir, [f] = [f] m
p
;
(iii) si [f] m
p
y [g] (
p
, entonces f(p)g(p) = 0, luego, [f][g] m
p
.
Como cada [f] con f(p) ,= 0 es invertible, esto nos dice que m
p
es de hecho el nico
ideal maximal de (
p
.
Ejercicio 21.0.69. Vea que si reemplazamos (X, ) por un abierto de R
n
y en vez de
considerar funciones continuas consideramos funciones de clase C
k
, entonces obtenemos
el mismo resultado. Analice tambin el caso cuando reeplazamos X por un abierto del
plano complejo y reemplazamos la continuidad por analiticidad.
CAPTULO 22
CUERPO COCIENTE DE UN DOMINIO ENTERO
Hemos visto que todo cuerpo es en particular un dominio entero y que todo dominio
entero nito es necesariamente un cuerpo. El anillo Z es un ejemplo de un dominio entero
innito que no es un cuerpo. Nos podemos preguntar si es posible encontrar un cuerpo,
lo ms pequeo posible, que contenga al dominio como subanillo. Veamos por ejemplo
el dominio anterior Z. Podemos ver que si el cuerpo Q le contiene como un subanillo.
Por otro lado, si tenemos un cuerpo K conteniendo a Z y n Z, entonces debe existir
n
1
K y, en particular, los elementos nm
1
=
n
m
K. De esta manera vemos que Q
es el cuerpo ms pequeo conteniendo a Z. La construccin de Q puede realizarse de la
siguiente manera. Consideremos el conjunto
Q = (r, s) Z
2
: s ,= 0
y la funcin
L : Q Q : (r, s)
r
s
Vemos que L es sobreyectiva pero no es inyectiva ya que es fcil ver que L(r, s) =
L(u, v) s y slo si rv = su. Consideremos la relacin de equivalencia
(r, s)
= (u, v) rv = su
y denotemos por Q
Z
al conjunto de las clases de equivalencia. As, podemos considerar
la funcin inducida
L : Q
Z
Q : [(r, s)]
r
s
,
la cual es ahora una biyeccin. Podemos usar L para escribir las operaciones de suma
y multiplicacin de nmeros racionales, obteniendo en Q
Z
las correspondientes opera-
ciones :
[(r, s)] + [(u, v)] = [(rv +su, sv)]
[(r, s)] [(u, v)] = [(ru, sv)]
De esta manera obtenemos en Q
Z
una estructura de cuerpo el cual es isomorfo a Q por
el isomomorsmo L. La funcin
J : Z Q
Z
: n [(n, 1)]
116 CAPTULO 22. CUERPO COCIENTE DE UN DOMINIO ENTERO
resulta ser un homomorsmo inyectivo de anillos.
Lo anterior nos permite generalizar la construccin para cualquier dominio entero R.
Consideramos el conjunto
Q = (r, s) R
2
: s ,= 0
y la relacin de equivalencia
(r, s)
= (u, v) rv = su
Denotemos por Q
R
al conjunto de las clases de equivalencia y denimos las corres-
pondientes operaciones :
[(r, s)] + [(u, v)] = [(rv +su, sv)]
[(r, s)] [(u, v)] = [(ru, sv)]
Ejercicio 22.0.70. Vericar que las operaciones anteriores hacen de Q
R
un cuerpo y
que la funcin
J : R Q
R
: r [(r, 1)]
resulta ser un homomorsmo inyectivo de anillos.
Por otro lado, supongamos que tenemos un cuerpo K y un homomorsmo inyectivo
: R K. Entonces podemos denir la funcin
: Q
R
K : [(r, s)] (r)(s)
1
Para ver que esta funcin est bin denida, observemos que si (r, s)

= (u, v), en-
tonces rv = su. Luego (rv) = (su), es decir, (r)(v) = (s)(u) equivalente-
mente (r)(s)
1
= (u)(v)
1
.
La funcin es inyectiva ya que si ([(r, s)]) = ([(u, v)]), entonces (r)(s)
1
=
(u)(v)
1
equivalentemente (rv) = (us). Com es inyectiva, esto nos dice que
rv = us, es decir, [(r, s)] = [(u, v)].
Veamos que es de hecho un homomorsmo de anillos. Como todo cuerpo es conmu-
tativo y es homomorsmo, tenemos
([(r, s)] + [(u, v)]) = ([rv +su, sv)] = (rv +su)(sv)
1
=
= ((r)(v) + (s)(u))(v)
1
(s)
1
= (r)(s)
1
+ (u)(v)
1
=
= ([(r, s)]) + ([(u, v)])
([(r, s)] [(u, v)]) = ([(ru, sv)] = (ru)(sv)
1
=
= (r)(s)
1
(u)(v)
1
= ([(r, s)])([(u, v)])
Podemos resumir todo lo anterior en el siguiente :
CAPTULO 22. CUERPO COCIENTE DE UN DOMINIO ENTERO 117
Teorema 22.0.71. Sea R un dominio entero. Entonces existe un cuerpo Q
R
y un
homomorsmo inyectivo J : R Q
R
de manera que si si K es cualquier cuerpo y
: R K es un homomorsmo inyectivo, entonces existe un homomorsmo inyectivo
: Q
R
K tal que J = .
Lo anterior nos est diciendo que el cuerpo Q
R
es el cuerpo ms pequeo conteniendo
una copia isomorfa de R.
Denicin 22.0.72. Sea R un dominio entero. El cuerpo Q
R
es llamado el cuerpo de
fracciones del dominio R. Es costumbre denotar cada clase [(r, s)] como la fraccin
r
s
.
Ejercicio 22.0.73. Sea d > 0 un entero que no es cuadrado de otro entero y conside-
remos el dominio Z[
d]. Vericar que su cuerpo de fracciones es isomorfo a Q[
d].
CAPTULO 23
DOMINIOS EUCLIDIANOS, PRINCIPALES Y
FACTORIZACIN NICA
23.1. Dominios Euclidianos
Denicin 23.1.1. Diremos que un dominio entero D es un Dominio Euclidiano si
existe una funcin
v : D0 0, 1, 2, ...
llamada una valuacin en D que satisface las siguientes dos propiedades :
(v1) Para cada par a, b D, b ,= 0, existen s, r D tales que
a = sb +r
donde r = 0 bin v(r) < v(b). El valor r es llamado el resto de dividir a por b ;
(v2) Para cada par a, b D0, se tiene que v(a) v(ab).
Ejemplo 23.1.2.
(i) El dominio D = Z con la valuacion usual v(n) = [n[ es un dominio Euclidiano.
En efecto, si tomamos dos enteros a, b Z, donde b ,= 0, entonces se puede ver
que existen enteros r, s tales que a [sb, s(b + 1)). Si a = sb, entonces r = 0. Si
a ,= sb, entonces r = a sb y es claro en este caso que [r[ < [b[. Tambin es claro
que si a, b Z 0, entonces [a[ [ab[.
(ii) Si F es un cuerpo, entonces usando la valuacin trivial v(r) = 0, obtenemos que
F es dominio Euclidiano. En este caso, siempre ocurre que el resto r = 0.
(iii) Sea D = F[x], donde F es un cuerpo y la valuacin v(p(x)) siendo el grado del
polinomio p(x). Es claro que la funcin grado satisface ser una valuacin usando la
divisin usual de polinomios. Vericar los detalles.
(iv) El dominio entero Z[x] no es un dominio Euclidiano. Esto lo veremos ms tarde.
Ejercicio 23.1.3.
120 CAPTULO 23. DOMINIOS EUCLIDIANOS, PRINCIPALES Y FACTORIZACIN NICA
(1) Vericar que el dominio entero Z + Zi = a + bi : a, b Z, llamado el anillo
de los enteros Gausianos, resulta ser un dominio Euclidiano con la valuacin v(a +
bi) = a
2
+b
2
.
(2) Sea d 2, 3, 5, 6, ... un entero que no es cuadrado de otro entero y consideremos
el dominio entero Z[
d]. Utilize v(a+b
d) = adb
2
y verique si este es dominio
Euclidiano.
(3) Sea d 2, 3, 5, 6, ... un entero que no es cuadrado de otro entero y consideremos
el dominio entero Z[
d]. Utilize v(a + b
d) = a + db
2
y verique si este es
dominio Euclidiano.
Ahora procedemos a enunciar el algoritmo de divisin que tenemos en todo dominio
entero. De manera ms precisa :
Proposicin 23.1.4 (Algoritmo de Divisin). Sea D un dominio Euclidiano respecto
a la valuacin v : D0 0, 1, 2, ... Entonces para todo par p, q D0 existen
a, b D tales que MCD(p, q) = ap + bq. En particular, si p y q son relativamente
primos, entonces existen a, b D tales que ap +bq = 1.
Demonstracin. Sean p, q D0 y d = MCD(p, q). Por la propiedad de divisin
existen r
1
, t
1
D tales que p = qt
1
+ r
1
, donde r
1
= 0 v(r
1
) < v(q).
Si tenemos que r
1
= 0, entonces MCD(p, q) = q y estamos listos tomando a = 0,
b = 1.
Si tenemos que r
1
,= 0, entonces podemos proceder como antes usando q en lugar de p
y r
1
en lugar de q para obtener valores r
2
, t
2
D tales que q = r
1
t
2
+r
2
, donde r
2
= 0
v(r
2
) < v(r
1
).
Si r
2
= 0, entonces tenemos que MCD(p, q) = r
1
y estaremos listos tomando a = 1
y b = t
1
t
2
.
Si tenemos que r
2
,= 0, entonces seguimos con este proceso inductivo. Como v(q) >
v(r
1
) > v(r
2
) > 0 y la valuacin v toma valores enteros, este proceso terminar
despus de un nmero nito de pasos.
23.2. Dominios de Ideales Principales
Denicin 23.2.1. Un dominio entero para el cual todo ideal es principal es llamado
un dominio de ideales principales.
Ejemplo 23.2.2.
(i) Todo cuerpo F es un dominio de ideales principales. Este hecho se debe a que los
nicos ideales de un cuerpo son 0 y F =< 1 >.
(ii) Sea D un dominio de idelaes principales. Entonces si a
1
, ..., a
n
D0, existe
un mximo comn divisor MCD(a
1
, ..., a
n
) D para ellos. Ms an, el ideal ge-
nerado por a
1
, ..., a
n
es igual al ideal generado por MCD(a
1
, ..., a
n
). En particular,
23.3. DOMINIOS DE FACTORIZACIN NICA 121
esto nos asegura que dos mximos comn divisores de tales elementos son uno el
mltiplo del otro por un elemento invertible en D. En efecto, sea I el ideal generado
por los elementos a
1
,..., a
n
. Como estamos en un ideal principal, existe d D tal
que I =< d >. En particular, todo divisor comn a los elementos a
1
,..., a
n
debe
dividir d ya que d = r
1
x
1
+ +r
n
x
n
al pertenecer al ideal I generado por los ele-
mentos a
j
. Por otro lado, como cada a
j
I =< d >, tenemos que x
j
= s
j
d, con
lo cual vemos que d divide a cada a
j
, obteniendo en resumen que d es un mximo
comn divisor de a
1
,..., a
n
. Si tenemos d
1
D otro mximo comn divisor de estos
elementos, entonces I es subanillo del ideal < d
1
>. Esto asegura que d
1
divide
d, es decir d = ad
1
. Como d
1
es mximo comn divisor y d divide a los elemen-
tos a
1
,..., a
n
, debemos tener que d divide d
1
, es decir d
1
= bd. Esto nos dice que
d
1
= bd = bad
1
, de donde d
1
(1 ba) = 0. Pero d
1
,= 0 y estamos en un dominio
entero, es decir, no hay divisores de cero, luego ab = 1, es decir, a es invertible en
D.
(iii) El dominio entero Z[x] no es dominio de ideales principales. En efecto, conside-
remos el ideal I generado por 2 y x. Es claro que I consiste de polinomios cuyo
coeciente constante es par. Por otro lado, si Z[x] fuese un dominio de idelaes prin-
cipales, parte (ii) anterior nos dice que I seria generado por el MCD(2, x) = 1, es
decir, I = Z[x], una contradiccin.
23.3. Dominios de Factorizacin nica
Denicin 23.3.1. Sea D un dominio entero y a D 0. Diremos que que a es
un elemento irreducible si no es invertible y no puede escribirse como producto de dos
elementos ambos no invertibles.
Ejemplo 23.3.2. Consideremos un dominio Euclidiano D con valuacin v : D
0 0, 1, 2, .... Se puede vericar que los elementos invertibles de D es exactamente
el conjuto
a D : a invertible =
a D : v(a) = v(1) =
a D0 : v(b) = v(ab) para todos b D 0
En efecto, si a D es invertible, entonces v(b) v(ab) v(a
1
ab) = v(b), es
decir, v(b) = v(ab). En particular, para b = 1 lo anterior asegura que v(a) = v(1).
Recprocamente, si a es tal que v(b) = v(ab) para algn b D0, entonces al dividir
b por ab obtenemos que
b = s(ab) +r
donde r = 0 v(r) < v(ab) = v(b). Ahora, r = b s(ab) = (1 sa)b de donde
v(b) v(r) < v(b), una contradiccin si r ,= 0. As, r = 0 y b = s(ab), es decir,
(1 sa)b = 0. Como D es dominio entero y b ,= 0, debemos tener sa = 1, es decir, a
invertible.
Denicin 23.3.3. Un dominio entero D es llamado un dominio de factorizacin
nica si todo elemento a D 0 que no es invertible puede escribirse de manera
nica como producto de elementos irreducibles, es decir, si a D 0 no es inver-
tible, entonces existen irreducibles p
1
, ..., p
n
D tales que a = p
1
p
n
. Ms an, si
existe otra descomposicin en irreducibles, digamos a = q
1
q
m
, entonces n = m y
q
j
= t
j
p
j
, donde t
j
D es invertible.
Ejemplo 23.3.4. Si D es dominio de factorizacin nica, entonces es posible calcular
el mximo comn mltiplo en D. En efecto, tomemos a, b en D 0. Escribimos las
descomposiciones en factores irreducibles de ambos elementos. Podemos escribir
a = p
1
p
n
p
n+1
p
l
b = p
1
p
n
q
1
q
s
donde ningun q
j
es producto de un elemento p
i
por un invertible. As, tenemos que
MCD(a, b) = p
1
p
n
.
Proposicin 23.3.5 (Gauss). Si D es un dominio de factorizacin nica, entonces
D[x] tambin lo es.
Este resultado lo vericaremos en una seccin posterior.
23.4. Relaciones entre Dominios
Ahora procedemos a mostrar el resultado ms importante de esta seccin.
Teorema 23.4.1. Todo dominio Euclidiano es un dominio de ideales principales y
todo dominio de ideales principales es un dominio de factorizacin nica.
Ejemplo 23.4.2. Como consecuencia del resultado anterior es que si F es un cuerpo,
entonces al ser F[x] un dominio Euclidiano (usando como valuacin el grado de po-
linomios) se tiene que todo polinomio puede escribirse como producto (nico mdulo
constantes) de polinomios irreducibles. Tambin, todo ideal es principal y el ideal gene-
rado por polinomios (no ceros) p
1
(x),..., p
n
(x) es generado por un polinomio q(x) que es
mximo comn divisor de ellos. En particular, si son relativamente primos, ellos generan
todo F[x].
23.4. RELACIONES ENTRE DOMINIOS 123
Para vericar la proposicin anterior, primero veremos que todo dominio Euclidiano es
principal y luego que todo dominio de ideales principales es necesariamente un dominio
de factorizacin nica.
Proposicin 23.4.3. Todo dominio Euclidiano es de ideales principales
Demonstracin. Consideremos un ideal I ,= 0 de D. Queremos ver que este es
principal. Consideremos el conjunto
v(I) = v(x) : x I 0 0, 1, 2, 3, ...
Consideremos a I tal que v(a) = Mnimo(v(I), el cual existe al ser 0, 1, 2, 3, ..
discreto y bin ordenado. Podemos considerar el ideal principal generado por a, es decir,
< a >, el cual es esta contenido en I. Supongamos que podemos escoger x I < a >.
Sabemos que existen valores r, t D tales que x = ta +r, donde r = 0 v(r) < v(a).
Pero como x / < a >, r ,= 0. As, tenemos que r D 0 es tal que v(r) < v(a).
pero, r = x ta I, lo cual contradice la minimalidad de v(a). Luego, I =< a >.
Proposicin 23.4.4. Todo dominio de ideales principales es dominio de factorizacin
nica
Antes de proceder a dar una demostracin de este hecho, recordemos que en un ideal
principal tenemos los siguientes :
(1) Existencia de MCD(x
1
, ..., x
n
) ;
(2) < x
1
, ..., x
n
>=< MCD(x
1
, ..., x
n
) >, en particular, existen a
1
, ..., a
n
D
tales que
MCD(x
1
, ..., x
n
) = a
1
x
1
+ +a
n
x
n
;
(3) Dos mximos comn divisores de los mismos elementos son el mltiplo de un
invertible por el otro.
Primeros necesitamos vericar que todo elemento no invertible x D 0, donde
D es un dominio de ideales principales, puede descomponerse como un producto nito
de elementos irreducibles. Esto es consecuencia del siguiente.
Lema 23.4.5. Sea D un dominio de ideales principales y x D 0, un elemento
no invertible. Entonces x es producto nito de elementos irreducibles de D.
Demonstracin. Sea x D0 no invertible. Si este es irreducible, entonces esta-
mos listos. Supongamos por el contrario que no lo es, es decir, x = ab, donde a, b D
no son invertibles. Es claro que
< x >< a > y < x >< b >
Supongamos que a o b no es irreducible, digamos a no es irreducible. Entonces pode-
mos escribir a = a
1
a
2
, donde a
j
no es invertible. Ahora tenemos
< x >< a >< a
1
> y < x >< a >< a
2
>
Si el lema que estamos vericando es falso, procediendo de esta manera obtendremos
una sucesin innita de ideales
I
1
I
2

lo cual ser contradiccin al siguiente lema.
Lema 23.4.6. Sea D un dominio de ideales principales. Entonces no es posible en-
contrar una sucesin innita de ideales
I
1
I
2

Demonstracin. Supongamos que tenemos una coleccin de ideales
I
1
I
2

Entonces
I =
j=1
I
j
resulta ser un ideal. Por otro lado, como D es principal, tenemos la existencia de un
elemento a D tal que < a >= I. As, como a I, debe ocurrir que a I
n
para algn
n, en cuyo caso tendremos que I = I
n
Ahora necesitamos vericar que la descomposicin es nica mdulo factores irredu-
cibles y permutacin de factores. Esto es consecuencia del siguiente.
Lema 23.4.7. La descomposicin en factores irreducibles en un dominio de ideales
principales es nica mdulo multiplicacin por invertibles y permutacin de factores.
Demonstracin. Supongamos que tenemos la igualdad
p
1
p
2
p
n
= q
1
q
2
q
m
donde p
j
, q
i
D son elementos irreducibles. Supongamos que n m. Por el lema de
Euclides ms abajo, tenemos que p
1
divide algn q
j
, digamos q
1
. Entonces q
1
= r
1
p
1
,
donde r
1
D es algn invertible. Factorizando en D el elemento p
1
en la igualdad
anterior (ya que no hay divisores de cero), obtenemos la igualdad
p
2
p
n
= r
1
q
2
q
m
Ahora procedemos con p
2
de la misma manera que con p
1
para ver que, mdulo per-
mutacin de ndices q
2
= r
2
p
2
, donde r
2
D es invertible y, en particular, tener la
igualdad
p
3
p
n
= r
1
r
2
q
3
q
m
Procediendo de esta manera, mdulo permutacin de ndices, obtendremos que
q
j
= r
j
p
j
, j = 1, ..., n
23.4. RELACIONES ENTRE DOMINIOS 125
donde r
j
D es invertible, y la igualdad
1 = r
1
r
2
r
n
q
n+1
q
m
Si m > n, entonces esta ltima igualdad dira que q
m
es invertible, una contradiccin.
Luego m = n y obtenemos lo deseado.
Lema 23.4.8 (Euclides). Sea D un dominio de ideales principales, p D un ele-
mento irreducible y a, b D tales que p divide ab. Entonces p divide a o divide b. En
otras palabras, todo ideal generado por un elemento irreducible es un ideal primo.
Demonstracin. Podemos asumir que a, b D 0. Podemos calcular un mximo
comn divisor d = MCD(a, b) en el dominio de ideales principales D. Supongamos que
p no divide a, en cuyo caso MCD(p, a) = 1. Sabemos que es posible encontrar valores
r, s D tales que 1 = rp + sa. Luego, al multiplicar por b ontenemos b = brp + sab y
como p divide ambos sumandos del lado derecho, p debe dividir b.
CAPTULO 24
ANILLO DE POLINOMIOS Y FACTORIZACIN UNICA
En esta seccin nos preocuparemos de manera particular de los anillos de polinomios
de dominios enteros y estudiaremos algunas propiedades que tienen estos.
Ejercicio 24.0.9. Sea D un dominio entero y considere el anillo de polinomios en una
variable D[x]. Sean P(x) D[x] y Q(x) = a
0
+a
1
x+ +a
n
x
n
D[x] tal que a
n
D
es un invertible. Verique que es posible encontrar polinomios T(x), R(x) D[x] tales
que
P(x) = Q(x)T(x) +R(x)
donde R(x) = 0 bin grad(R) < grad(Q).
Ejemplo 24.0.10. Consideremos un cuerpo k y el anillo de polinomios en una variable
k[x]. Sabemos que k[x] es un dominio Euclidiano usando como valuacin el grado de
polinomios. En particular, k[x] es tambin un dominio de ideales principales y un dominio
de factorizacin nica. Ahora, si R(x), S(x) k[x] son relativamente primos, tenemos
que
1 = R(x)A(x) +S(x)B(x)
para ciertos polinomios A(x), B(x) k[x]. As, si T(x) k[x], entonces
T(x) = R(x)C(x) +S(x)D(x)
para ciertos polinomios C(x), D(x) k[x]. En este caso C(x) = T(x)A(x) y D(x) =
T(x)B(x). El algoritmo de la divisin nos permite calcular efectivamente los polinomios
A(x), B(x) y luego C(x), D(x). Una consecuencia de esta pequea observacin es la
descomposicin en fracciones parciales : Sean P(x), Q(x) k[x] y supongamos que
Q(x) = Q
1
(x)
d1
Q
n
(x)
dn
es descomposicin en polinomios irreducibles. Entonces
es posible calcular de manera explcita polinomios P
1
(x), ..., P
n
(x) k[x] tales que
P(x)
Q(x)
=
n
j=1
P
j
(x)
Q
j
(x)
dj
128 CAPTULO 24. ANILLO DE POLINOMIOS Y FACTORIZACIN UNICA
Ejercicio 24.0.11. Verique la descomposicin en fracciones parciales del ejemplo
anterior. Utilize la observacin hecha en el mismo ejemplo con
R(x) =
Q(x)
Q
n
(x)
dn
= Q
1
(x)
d1
Q
n1
(x)
dn1
S(x) = Q
n
(x)
dn
y T(x) = P(x)
El ejemplo anterior nos dice que los dominio k[x], donde k es un cuerpo, son dominios
Euclidianos y, en particular, dominios de idelaes principales y de factorizacin nica.
Hemos visto que Z[x] no es un dominio Euclidiano ni dominio de ideales principales,
pero an queda la pregunta si este es un dominio de factorizacin nica.
Teorema 24.0.12 (Gauss). Si D es un dominio de factorizacin nica, entonces D[x]
tambin lo es.
Este resultado al ser usado de manera iterativa permite obtener el siguiente.
Corolario 24.0.13. Si D es un dominio de factorizacin nica, entonces D[x
1
, ..., x
n
]
tambin lo es.
Demostracin del teorema de Gauss. Sea D un dominio entero y k su cuerpo de frac-
ciones. Entonces tenemos de manera natural la incrustacin D[x] k[x]. Sea P(x)
D[x] ; podemos escribir
P(x) = dP
1
(x)
donde P
1
(x) D[x] tiene la propiedad que la coleccin de sus coecientes son relativa-
mente primos y d D es el mximo comn divisor de los coecientes de P(x). Como D
es dominio de factorizacin nica, tenemos una descomposicin "nica"
d = p
1
p
2
p
r
donde p
j
D son elementos irreducibles. Tambin tenemos una descomposicin "nica"
en polinomios irreducibles de k[x], digamos
P
1
(x) = Q
1
(x)Q
2
(x) Q
n
(x)
Q
1
(x), ..., Q
n
(x) k[x], polinomios irreducibles.
Ahora, cada polinomio Q
j
(x) puede escribirse como
Q
j
(x) =
a
j
b
j
T
j
(x)
donde T
j
(x) D[x] y de manera que los coecientes de T
j
(x) son relativamente primos.
Es claro que T
j
(x) k[x] es irreducible (es un mltiplo de Q
j
(x) por un invertible de
k[x]). Luego, T
j
(x) D[x] debe tambin ser irreducible en D[x]. Tenemos la igualdad
P
1
(x) =
a
1
a
n
b
1
b
n
T
1
(x) T
n
(x)
CAPTULO 24. ANILLO DE POLINOMIOS Y FACTORIZACIN UNICA 129
de manera equivalente
H(x) = b
1
b
n
P
1
(x) = a
1
a
n
T
1
(x) T
n
(x) = L(x)
Luego, un mximo comn divisor de los coecientes del polinomio H(x) D[x], es
b
1
b
n
D, y un mximo comn divisor del polinomio L(x) D[x], es a
1
a
n
D.
De esta manera tenemos la igualdad
a
1
a
n
= b
1
b
n
s
para cierto elemento invertible s D ya que D es dominio de factorizacin nica. As,
a
1
a
n
b
1
b
n
= s D
y, en particular,
P
1
(x) = sT
1
(x) T
n
(x)
con lo cual nalmente tenemos la descomposicin en factores irreducibles en D[x]
P(x) = p
1
p
2
p
r
sT
1
(x) T
n
(x)
Esto nos ha permitido vericar al menos la existencia de una factorizacin en irredu-
cibles en D[x]. Ahora debemos vericar su unicidad mdulo invertibles y permutacin de
factores.
Ejercicio 24.0.14. Vericar la unicidad del teorema anterior. Indicacin : considere
una igualdad
p
1
p
n
P
1
(x) P
m
(x) = q
1
q
r
Q
1
(x) Q
s
(x)
donde p
j
, q
j
D son irreducibles y P
j
(x), Q
j
(x) D[x] son polinomios irreducibles.
Vea que se puede suponer que cada polinomio P
j
(x), Q
j
(x) tiene sus coecientes re-
lativamente primos. De esta manera, vea que existe a D invertible tal p
1
p
n
=
q
1
q
r
a y que r = n, al ser D dominio de factorizacin nica. Ahora, analize la igual-
dad P
1
p
m
= aQ
1
Q
s
en k[x], utilize que k[x] es dominio de factorizacin nica y
el mismo tipo de ideas como en la demostracin para completar el argumento.
CAPTULO 25
ANILLOS NOETHERIANOS
En esta seccin veremos que todo ideal del anillo de polinomios k[x
1
, ..., x
n
]. donde
k es un cuerpo es nitamente generado. Este resultado es de mucha importancia en el
estudio de soluciones de sistemas innitos polinomiales y, en particular, en geometra
algebraica.
Denicin 25.0.15. Un anillo A conmutativo con unidad es llamado Noetheriano si
todo ideal de A es nitamente generado.
Ejemplo 25.0.16. Cuerpos y Z son ejemplos de anillos Noetherianos.
Teorema 25.0.17 (Teorema Fundamental de Hilbert). Si A es un anillo Noethe-
riano, entonces A[x
1
, ..., x
n
] tambin es Noetheriano.
Corolario 25.0.18. Si k es un cuerpo, entonces k[x
1
, ..., x
n
] es Noetheriano.
Demostracin del teorema fundamental de Hilbert. Slo es necesario vericar que
A[x] es anillo Noetheriano. Supongamos que tenemos un ideal I en A[x]. Deseamos
encontrar un nmero nito de generadores de I.
Dado un polinomio p(x) = a
0
+a
1
x + +a
n
x
n
A[x], con a
n
,= 0, es decir p(x)
es de grado n, llamaremos al coeciente a
n
el coeciente principal de p(x). Denimos el
coeciente principal del polinomio cero como el 0 A.
Sea J Ael conjunto formado de los coecientes principales de todos los polinomios
en I.
Hecho 1. J es un ideal de A.
La razn de esto es :
(1) El coeciente principal de la suma de dos polinomios es la suma de los coecientes
principales ;
132 CAPTULO 25. ANILLOS NOETHERIANOS
(2) El coeciente principal del polinomio p(x) es el opuesto aditivo del coeciente
principal de p(x) ;
(3) El coeciente principal del producto de dos polinomios es el producto de los coe-
cientes principales ;
(4) Si p(x) I y r A, entonces el coeciente principal de rp(x) es r veces el
coeciente principal de p(x).
Ahora que tenemos que J es un ideal de A, como A es Noetheriano, tenemos la exis-
tencia de un nmero nito de polinomios
p
1
(x), ..., p
m
(x) I
tal que J est generado por los coecientes principales de ellos. Sea N el mximo de los
grados de los polinomios p
1
(x),..., p
m
(x).
Para cada entero k < N denimos como J
k
al subconjunto de A formado de los
coecientes principales de todos aquellos polinomios en I de grado a lo ms k.
Hecho 2. J
k
es un ideal de A.
La razn de esto es muy similar a como vimos que J es un ideal. Se puede ver que J
k
es cerrado bajo la suma y la resta. Veamos que J
k
es cerrado bajo la multiplicacin y que
es ideal. Para esto, sea a J
k
y r A. Veremos que ra J
k
y tendremos ambos hechos
vlidos. Sea p(x) I cuyo coeciente principal es a y considere el polinomio de grado
cero q(x) = r A[x]. Como I es un ideal de A[x], tenemos que p(x)q(x) = rp(x) I.
Ya que el coeciente principal de rp(x) es ra, estamos listos.
Ahora, al ser J
k
un ideal en A, la condicin de A ser Noetheriano nos asegura que
podemos encontrar un nmero nito de polinomios
q
k,1
(x), ..., q
k,n
k
(x) I
de manera que sus coecientes principales generan J
k
.
Denotemos por

I al ideal de A[x] generado por todos los polinomios anteriores :
p
1
(x), ..., p
m
(x), q
0,1
(x), ..., q
0,n0
(x), ..., q
N,1
(x), ..., q
N,nN
(x).
Por construccin, el ideal

I I es nitamente generado.
Hecho 3. I =

I.
Como sabemos que
I I, necesitamos ver que I
I = . Supongamos por el contrario

que existe t(x) I

I. Podemos escoger t(x) de grado menor con tal propiedad. Sea
s A el coeciente principal de t(x).
(1) Supongamos que el grado de t(x) es al menos N. Como s J, existen polinomios
(monomios) r
1
(x), ..., r
m
(x) A[x] tal que u(x) =
m
j=1
r
j
(x)p
j
(x)

I tiene
coeciente principal s y cuyo grado sea igual al de t(x). Ahora, como q(x) = t(x)
u(x) I tiene grado menor que t(x), debe ocurrir (por la minimalidad de la eleccin
de t(x)) que q(x)

I. Esto nos dice que t(x) = q(x)+u(x)

I, una contradiccin.
CAPTULO 25. ANILLOS NOETHERIANOS 133
(2) Si el grado de t(x) es k < N, entonces s J
k
para cierto k. Ahora pode-
mos encontrar polinomios (monomios) r
k,j
(x) A[x] de manera que v(x) =
n
k
j=1
r
k,j
(x)q
k,j
(x)

I tenga coeciente principal igual s y cuyo grado coin-
cida con el grado de t(x). Ahora procedemos como en el caso (1) para obtener
nuevamente una contradiccin.
Ejemplo 25.0.19. Sea k un cuerpo y supongamos que tenemos un sistema innito
() p
j
(x
1
, ..., x
n
) = 0; j /,
donde p
j
(x
1
, ..., x
n
) k[x
1
, ..., x
n
].
Denotemos por V k
n
al conjunto de soluciones de tal sistema innito. Sea I(V )
k[x
1
, ..., x
n
] formado de aquellos polinomios q(x
1
, ..., x
n
) tales que q(a
1
, ..., a
n
) = 0
para todo (a
1
, ..., a
n
) V.
Se tiene que I(V ) es un ideal de k[x
1
, ..., x
n
]. Luego, al ser k[x
1
, ..., x
n
] un anillo
Noetheriano, existen un nmero nito de polinomios
q
1
(x
1
, ..., x
n
), ..., q
d
(x
1
, ..., x
n
) I(V )
tales que generan I(V ).
Denotemos por W k
n
al conjunto de soluciones del sistema nito de polinomios
_
_
q
1
(x
1
, ..., x
n
) = 0
.
.
.
.
.
.
q
d
(x
1
, ..., x
n
) = 0
Ya que
q
1
(x
1
, ..., x
n
), ...., q
d
(x
1
, ..., x
n
) I(V ),
tenemos que V W.
Por otro lado, como cada p
j
(x
1
, ..., x
n
) puede escribirse de la forma
p
j
=
d
i=1
r
j
q
i
,
tenemos W V . En consecuencia,
W = V.
Ejercicio 25.0.20.
1.- Considere en C[x] el ideal I generado por todos los polinomios
p
k
(x) = k + x
k
, k = 1, 2, 3, .....
Ya que C[x] es dominio de ideales principales, I es generado por un polinomio.
Encuentre tal generador.
134 CAPTULO 25. ANILLOS NOETHERIANOS
2.- Considere en Z[x] el ideal I generado por los polinomios
p
n,m
(x) = 2nx + 3m, n, m = 0, 1, 2, ....
Vericar que I est generado por 3 y 2x.
PARTE IV
REPRESENTACIONES LINEALES DE
GRUPOS
Para estudiar algunos grupos es til usar algunas acciones especiales, con ciertas pro-
piedades lineales. No pretenderemos escribir un captulo demasiado preciso sobre repre-
sentaciones lineales, slo presentaremos algunos temas bsicos que se relacionan con lo
expuesto en los captulos anteriores.
CAPTULO 26
REPRESENTACIONES LINEALES
Denicin 26.0.21. Una representacin lineal de un grupo (G, ) en un espacio vec-
torial V (sobre algn cuerpo /, que para nuestro inters puede ser Q, R C) es por
denicin una accin
: G GL(V )
La dimensin del espacio vectorial V es llamada el grado de la representacin. Cuando el
homomorsmo : G GL(V ) es adems inyectivo, es decir una accin el, entonces
hablamos de una representacin el.
Ejemplo 26.0.22. Sea (G, ) un grupo simple. Entonces cualquier representacin li-
neal de G es el o es la representacin trivial ((g) = I, para todo g G). En efecto,
dada una representacin lineal : G GL(V ) tenemos que Ker() es un subgrupo
normal de G. Como G es simple, tenemos que Ker() = 0, en cuyo caso es el, o
Ker() = G, en cuyo caso (g) = I para g G.
Ejemplo 26.0.23. Dado un grupo (G, ) y un cuerpo /, siempre tenemos la represen-
tacin de grado uno
1 : G GL(/) = /
: g 1
De manera ms general, si V es un espacio vectorial sobre /, entonces siempre tene-
mos la representacin trivial
I : G GL(V ) : g I
Ejemplo 26.0.24. Sea G = x : x
2
)

= Z/2Z. Entonces tenemos tambin la repre-
sentacin de grado uno
(1) : G GL(Q)
denida por
(1)(I
G
) = 1 (1)(x) = 1
138 CAPTULO 26. REPRESENTACIONES LINEALES
Ejemplo 26.0.25. Consideremos un grupo (G, ) y una representacin de grado 1,
digamos : G GL(V ), es decir V es un espacio vectorial de dimensin uno sobre
el cuerpo /. Escojamos un vector no cero v ,= 0 en V ; entonces v es base de V .
Para cada g G tenemos que (g)(v) =
g
v para algn valor /
= / 0.
Como es un homomorsmo de grupos, tenemos que (g
1
g
2
) = (g
1
)(g
2
), es decir
g1g2
=
g1
g2
, para todos g
1
, g
2
G. Por ejemplo,
IG
= 1. Tenemos adems un
isomorsmo natural, dado por la base anterior, L : GL(V ) /
: v . Luego,
podemos mirar la representacin L : G /
: g
g
.
Observemos que si escogemos otro vector no cero de V , digamos v, entonces tenemos
que v = av para cierto a /
. Luego, no es dicil ver que (g)( v) =

g
v. En otras
palabras, el valor
g
/
est nicamente determinado por g G y , es decir, no

depende del vector v V 0 escogido.
Suponiendo que g G es de orden o(g) nito, se tiene que
o(g)
g
= 1, es decir,
g
es
una raiz o(g)-sima de la unidad.
Ejercicio 26.0.26. Sea (G, ) un grupo cclico nito. Determinar las representaciones
de grado 1 en (i) Q, (ii) R y en (iii) C.
Observacin 26.0.27. Dados un grupo (G, ), una representacin lineal : G
GL(V ), donde V en un espacio vectorial V sobre un cuerpo /, y un subanillo R de /,
podemos dotar de manera natural a V de una estructura de RG-mdulo. La idea es la
siguiente, primero consideramos un anillo R[G] del grupo G respecto al anillo R. Ahora
denimos la operacin binaria
n
j=1
r
j
g
j
v =
n
j=1
r
j
(g
j
)(v)
la cual realiza a V como un R[G]-mdulo.
CAPTULO 27
ALGUNOS EJEMPLOS DE REPRESENTACIONES
27.1. Representacin regular dada por la accin de un grupo
Consideremos una accin de un grupo nito (G, ) sobre un conjunto nito X =
x
1
, ..., x
n
, digamos : G Perm(X). Consideremos un espacio vectorial V de
dimensin n y una base v
1
, ..., v
n
. Entonces, podemos construir una representacin
lineal inducida por la accin anterior de la siguiente manera :
: G GL(V ) : g (g)
denida por
(g)(
n
j=1
a
j
v
j
) =
n
j=1
a
j
v
g(j)
donde g(j) 1, 2, ..., n es tal que (g)(x
j
) = x
g(j)
. Lo que estamos haciendo es
permutar los elementos de la base de la misma manera como se permutan los elementos
de X.
Ejercicio 27.1.1. En el ejemplo anterior considere X = G y la accin : G
Perm(G) denida por (g) : G G : h g h. La representacin obtenida es llamada
la representacin regular del grupo G.
27.2. Representacin suma directa
Sea (G, ) un grupo y V, W espacios vectoriales sobre un cuerpo /. Consideremos
dos representaciones lineales
: G GL(V ) y : G GL(W)
Entonces podemos formar el espacio producto V W y construir la representacin
producto suma directa
(, ) := : G GL(V W)
140 CAPTULO 27. ALGUNOS EJEMPLOS DE REPRESENTACIONES
denida como
(, )(g) : V W V W : (v, w) ((g)(v), (g)(w))
27.3. representacin producto tensorial
Tambim podemos hacer el producto tensorial de estos espacios vectoriales V V y
construir la representacin producto tensorial
: G GL(V W)
denida como
(g) : V W V W : v w (g)(v) (g)(w)
27.4. Representacin wedge
Podemos considerar es el espacio vectorial wedge V V y la representacin cua
: G GL(V V ) : g
donde
(g) : V V : v (g)(v) (g)(v)
27.5. Representacin Hom
Otro espacio vectorial que podemos formar es Hom(V, W), el espacio vectorial de
todas las funciones lineales de V en W. Dada una funcin lineal L : V W y g G,
podemos considerar la nueva funcin lineal
Hom(, )(g)(L) = (g) L (g
1
) : V W
de donde obtenemos una nueva representacin lineal
Hom(, ) : G GL(Hom(V, W)) : g Hom(, )(g)
llamada la representacin homomorsmo.
Ejemplo 27.5.1. Sea (G, ) un grupo y V un espacio vectorial sobre un cuerpo /.
Consideremos una representacin lineal : G GL(V ). Entonces podemos construir
su representacin dual
: G GL(V
) denida como sigue : Si L : V / es una

funcin lineal, entonces para cada g Gtenemos que L(g)
1
= L(g
1
) : V /
es de nuevo una funcin lineal. Denimos
(g) : V
: L L (g
1
). Esta
representacin es la representacin homomorsmo para W = /.
27.6. REPRESENTACIN COCIENTE 141
27.6. Representacin cociente
Supongamos que tenemos una representacin lineal de un grupo (G, ), digamos :
G GL(V ). Si H es un subgrupo de G, entonces tenemos gratis una representacin
lineal de H dada por restriccin de a H, llamada la representacin restriccin a H. Si
adems H es subgrupo normal, entonces tenemos el grupo cociente G/H. Desgraciada-
mente no podemos hacer descender la representacin lineal para obtener una represen-
tacin lineal del cociente. Pero si tenemos que (h) = I para todo h H, entonces si lo
podemos hacer como
G/H
: G/H GL(V ) : gH (g)
llamada la representacin cociente.
CAPTULO 28
REPRESENTACIONES IRREDUCIBLES Y REDUCIBLES
Denicin 28.0.1. Consideremos una representacin : G GL(V ), donde V es
un subespacio vectorial sobre un cuerpo /. Si existe un subespacio propio W ,= 0 de
V que resulta invariante por cada una de las transformaciones (g), g G, entonces uno
dice que la representacin es una representacin reducible ; en caso contrario, decimos
que esta es una representacin irreducible. En el caso de existir W ,= 0 invariante por
(G), tenemos una representacin natural [
W
: G GL(W) denida por [
W
(g) =
(g), la cual es llamada la subrepresentacin inducida de .
Ejercicio 28.0.2. Si tenemos una representacin : G GL(V ), donde V es un
espacio vectorial sobre Q, entonces tenemos gratis representaciones reales y complejas
(cada (g) es una matriz con coecientes en Q, luego con coecientes en R y en C).
Puede ocurrir que sea una representacin irreducible (sobre Q) pero que no lo sea sobre
R en C. Dar un ejemplo de esta situacin.
El siguiente resultado para representaciones lineales de grupos nitos es de gran ayuda
en el estudio de estos.
Proposicin 28.0.3. Sea G un grupo nito y consideremos una representacin :
G GL(V ) de grado nito. Entonces podemos escoger en V un producto interior
Euclidiano (Hermitiano positivo denido en el caso complejo) , )
G
, de manera que (G)
es subgrupo del grupo se isometras O
,
.
Demonstracin. Sea , ) cualquier producto Euclidiano (Hermitiano positivo en el
caso complejo) para V . Entonces basta considerar el producto promediado
x, y)
G
=
gG
(g)(x), (g)(y))
144 CAPTULO 28. REPRESENTACIONES IRREDUCIBLES Y REDUCIBLES
Observacin 28.0.4. En la hiptesis de la proposicin anterior la condicin de ser
grado nito fu para asegurar la existencia de un producto interior para partir nuestro
argumento. La nitud de G fu para estar seguros de que la suma usada fuese nita.
Ejercicio 28.0.5. Vericar que en caso que la representacin es irreducible, entonces
el producto interior construido en la demostracin del teorema es nico mdulo producto
por un escalar.
Corolario 28.0.6. Sea G un grupo nito y consideremos una representacin : G
GL(V ) de grado nito. Si W es un subespacio vectorial de V que es invariante por cada
transformacin (g), con g G, entonces existe un subespacio complementario a W
que tambin es invariante.
Demonstracin. Usando la proposicin anterior, podemos asumir que (g) preserva
un producto interior Euclidiano (Hermitiano positivo en el caso complejo) , ) para cada
g G. Basta entonces escoger
W
= v V : v, w) = 0, para todo w W
CAPTULO 29
HOMOMORFISMOS DE REPRESENTACIONES
Podemos relacionar diferentes representaciones lineales del mismo grupo G sobre es-
pacios vectoriales sobre el mismo cuerpo de la siguiente manera.
Denicin 29.0.7. Sean : G GL(V ) y : G GL(W) dos representaciones
lineales de G, donde V y W son espacios vectoriales sobre el mismo cuerpo /. Un ho-
momorsmo entre estas representaciones es una funcin lineal L : V W tal que
L((g)(v)) = (g)(L(v)), para todo v V y todo g G. Cuando L : V W es un
isomorsmo lineal, entonces diremos que las representaciones son equivalentes, en cuyo
caso tenemos (g) = L (g) L
1
para todo g G. Denotamos por Hom
G
(, )
al conjunto de todos lo homomorsmos de representaciones entre : G GL(V ) y
: G GL(W).
Observacin 29.0.8. No confundir las notaciones Hom(, ) y Hom
G
(, ). La pri-
mera es una representacin mientras la segunda es un conjunto, de hecho un espacio
vectorial.
Ejercicio 29.0.9. Vericar que Hom
G
(, ) es un subespacio vectorial del espacio
vectorial Hom(V, W), formado por todas las funciones lineales de V en W.
Observacin 29.0.10. Consideremos una representacin lineal : G GL(V ),
donde V es un espacio vectorial sobre un cuerpo /.
(1) Habamos visto que para cada anillo R en /, podamos construir el anillo R[G] y
hacer que V tuviese una estructura de R[G]-mdulo. Un homomorsmo de V como
R[G]-mdulo es una funcin lineal L : V V que respecta la multiplicacin
por elementos de R[G], es decir L(
n
j=1
r
j
g
j
v) =
n
j=1
r
j
g
j
L(v). Esto es
equivalente a que valga la igualdad L(gv) = gL(v), es decir, L(g) = L. Esto
ltimo decie que L Hom
G
(, ). Es claro que vale el recproco. De esta manera
146 CAPTULO 29. HOMOMORFISMOS DE REPRESENTACIONES
Hom
G
(, ) corresponde exactamente a los homorsmos de V como R[G]-mdulo.
En forma similar, Hom
G
(, ) corresponde exactamente a los homorsmos de V
en W como R[G]-mdulos.
(2) Para g G, el isomorsmo de espacio vectorial (g) : V V no tiene por que
pertenecer a Hom
G
(, ). La condicin para que (g) Hom
G
(, ) es que para
todo h G valga la igualdad (g)(h v) = h (g)(v), es decir (g h) =
(hg). Por ejemplo, si la representacin es el, entonces lo anterior es equivalente
a tener g Z(G). En todo caso, si (G, ) es nito consideramos la funcin lineal
promediada
L =
1
[G[
gG
(g) : V V
la cual satisface L Hom
G
(, ).
Ejercicio 29.0.11. Vericar que la funcin lineal
L :=
1
[G[
gG
(g) : V V
satisface las siguientes propiedades :
(i) Im(L) = v V : (g)(v) = v para todo g G
(ii) L L = L
(iii) Concluir que L es una proyeccin.
Ejemplo 29.0.12. Consideremos un grupo (G, ) y dos representacin : G
GL(V ), : G W, donde V y W son espacios vectoriales sobre un cuerpo /. Su-
pongamos que tenemos un homomorsmo de representaciones L : V W. Asociado a
la funcin lineal L tenemos los dos subespacios siguientes :
Ker(L) = v V : L(v) = 0
Im(L) = w W : L(v) = w, para algn v V
De la igualdad L((g)(v)) = (g)(L(v)), para todo v V y todo g G, es claro
que Ker(L) es un subespacio invariante de (G) y Im(L) es un subespacio invariante
por (G). En particular, si la representacin : G GL(V ) es irreducible, entonces
Ker(L) 0, V , es decir la funcin lineal L es inyectiva o es trivial L 0. De
manera similar, si la representacin : G GL(W) es irreducible, entonces tenemos
que Im(L) 0, W, es decir la funcin lineal L es sobreyectiva o es trivial L 0.
Esto nos permite concluir el siguiente resultado.
Proposicin 29.0.13 (Lema de Schur). Sea (G, ) un grupo y dos representaciones
irreducibles : G GL(V ), : G GL(W), donde V, W son espacios vectoriales
sobre el mismo cuerpo. Si L : V W es un homomorsmo entre esas representaciones,
entonces L 0 o L es un isomorsmo.
CAPTULO 29. HOMOMORFISMOS DE REPRESENTACIONES 147
Corolario 29.0.14. Sea (G, ) un grupo y dos representaciones irreducibles : G
GL(V ), : G GL(V ), donde V es un espacio vectorial sobre el cuerpo de los
nmeros complejos C. Si L : V V es un homomorsmo entre esas representaciones,
entonces existe C tal que para cada v V vale que L(v) = v.
Demonstracin. Como todo polinomio de coecientes complejos de grado mayor o
igual a uno tiene ceros complejos, tenemos que L tiene al menos un valor propio C.
La funcin lineal N = LI : V V sigue siendo un homomorsmo de las represen-
taciones anteriores. Por el lema de Schur, tenemos que N 0 o N es isomorsmo. Pero
al ser valor propio de L, entonces N tiene ncleo no trivial, luego N 0.
Ejemplo 29.0.15. Consideremos un grupo (G, ) y representaciones
j
: G
GL(V
j
), donde V
j
son espacios vectoriales sobre el mismo cuerpo, j = 1, 2, ..., N.
Entonces tenemos de manera natural el espacio vectorial producto V
1
V
2
V
N
.
Existe un monomorsmo natural
J : GL(V
1
) GL(V
2
) GL(V
N
) GL(V
1
V
2
V
N
)
dado por
J(L
1
, L
2
, ..., L
N
)(v
1
, v
2
, ..., v
N
) = (L
1
(v
1
), L
2
(v
2
), ..., L
N
(v
N
))
Esto nos permite construir la representacin producto
(
1
, ...,
N
) : G GL(V
1
V
2
V
N
)
denido por
(
1
, ...,
N
)(g) = J(
1
(g), ...,
N
(g))
Observemos que cada subespacio

V
j
= (0, ..., 0, v, 0, ..., 0) V
1
V
N
es
invariante por (
1
, ...,
N
). Luego esta representacin es reducible. Matricialmente ha-
blando, lo que estamos haciendo es formar una gran matriz a partir de matrices pequeas
colocandolas en manera diagonal.
El siguiente resultado nos dice que para entender las representaciones lineales de un
grupo nito basta con entender las representaciones irreducibles.
Proposicin 29.0.16. Sean (G, ) un grupo nito y V un espacio vectorial de dimen-
sin nita. Entonces, toda representacin : G GL(V ) es equivalente a una nica
representacin producto, mdulo isomorsmo de representaciones, donde cada represen-
tacin involucrada es irreducible.
Demonstracin. Como V tiene dimensin nita y G es de orden nito, podemos in-
troducir un producto interior Euclidiano (Hermitiano positivo denido en el caso com-
plejo) , ) de manera que (G) < O
,
. Si la representacin es irreducible, entonces no
hay nada que vericar. Supongamos que existen subespacios invariantes no triviales. To-
memos uno de la menor dimensin posible, digamos V
1
. Entonces sabemos que W = V
1
(espacio ortogonal a V
1
respecto a nuestro producto interior) tambin es invariante por
(G) por el corolario anterior. Tenemos que la representacin inducida por , digamos
1
: G GL(V
1
) es irreducible por la minimalidad de la dimensin. Ahora mira-
mos la representacin : G GL(W) y procedemos de la misma manera como lo
hemos hecho para V . Este proceso termina despues de un nmero nito de pasos de-
bido a que V tiene dimensin nita y nos entrega una descomposicin ortogonal V =
V
1
V
2
V
N
y representaciones irreducibles
j
= : G GL(V
j
). Ahora es
claro por la construccin que : G GL(V ) es equivalente al producto de las represen-
taciones
j
: G GL(V
j
). Ahora necesitamos ver la unicidad mdulo isomorsmos de
representaciones. Para esto, supongamos que tenemos otra representacin equivalente a
la representacin = (
1
, ...,
N
) : G GL(V
1
) GL(V
N
), digamos la represen-
tacin = (
1
, ...,
M
) : G GL(W
1
) GL(W
M
), donde cada representacin
j
: G GL(W
j
) es irreducible. Sea L : V
1
V
N
W
1
W
M
el iso-
morsmo de tales representaciones. Entonces, L(V
j
) es un subespacio invariante por la
representacin , luego debe coincidir por la irreducibilidad a una de los subespacios W
r
.
As, L establece una biyeccin entre los espacios V
1
,..., V
N
y los espacios W
1
,..., W
M
,
enparticular, N = M.
Observacin 29.0.17. En el resultado anterior, tenemos que en la representacin pro-
ducto = (
1
, ...,
N
) : G GL(V
1
) GL(V
N
) en representaciones factores
irreducibles, puede occurrir que dos de ellas, digamos
i
: G GL(V
i
) y
j
: G
GL(V
j
), sean isomorfas. En ese caso, podemos reordenar los factores de manera que los
factores
1
: G GL(V
1
),...,
k
: G GL(V
k
) son los factores no equivalentes y
escribir como
= (
n1
1
, ...,
n
k
k
) : G GL(V
n1
1
) GL(V
n
k
k
),
donde n
j
denota la cantidad de factores equivalentes a la representacin
j
.
Ejemplo 29.0.18. Consideremos el espacio vectorial real (podemos usar otros cuer-
pos) V = R
n
. Tenemos de manera natural una representacin de grado n del grupo
simtrico o
n
actuando por permutaciones en las coordenadas de los vectores de V . De
manera ms precisa, consideremos los generadores a = (1, 2, 3, ..., n), b = (1, 2). En-
tonces denimos
n
(a) =
_
_
_
_
_
_
_
_
0 0 0 0 1
1 0 0 0 0
0 1 0 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 1 0
_
_
_
_
_
_
_
_
n
(b) =
_
_
_
_
_
_
_
_
_
_
0 1 0 0 0
1 0 0 0 0
0 0 1 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 1 0
0 0 0 0 1
_
_
_
_
_
_
_
_
_
_
La representacin
n
: o
n
O
n
< GL(R
n
)

= GL(n, R) resulta ser reducible,
donde O
n
denota el subgrupo de las rotaciones. En efecto, si consideramos el subespacio
vectorial de dimensin uno W generado por el vector (1, 1, ..., 1, 1), entonces obtenemos
que
n
(g)(W) = W, para cada g o
n
. Como
n
(o
n
) < O
n
, tenemos que cada (g),
g o
n
es una simetra para el producto Euclidiano estandard (dado por el producto
punto). En particular, W
, el subespacio ortogonal a W, tambin resulta invariante, donde

W
= (x
1
, ..., x
n
) R
n
: x
1
+x
2
+ +x
n
= 0
= R
n1
Consideremos el isomorsmo
: R
n1
W
denido por
(e
j
) = E
j
E
n
donde e
j
R
n1
(respectivamente, E
j
R
n
) es el vector cannico con todas sus coor-
denadas igual a cero excepto la coordenada j-sima que es igual a 1. Usando este isomor-
smo, podemos mirar la representacin inducida
n
(o
n
) sobre W como una representa-
cin en R
n1
, digamos
n1
: o
n
GL(R
n1
),
denida por
n1
(g) =
1
(g). Se puede ver que
n1
(a) =
_
_
_
_
_
_
_
_
0 1 0 0 0
0 0 1 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 0 1
1 1 1 1 1
_
_
_
_
_
_
_
_
n1
(b) =
_
_
_
_
_
_
_
_
_
_
0 1 0 0 0
1 0 0 0 0
0 0 1 0 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 1 0
0 0 0 0 1
_
_
_
_
_
_
_
_
_
_
Esta representacin de grado (n1) es llamada la representacin estandard del grupo
o
n
. Se sabe que esta representacin es irreducible. La idea es que si tomamos un vector
v ,= 0 R
n1
, entonces v,
n1
(a)(v),
n1
(a
2
)(v),...,
n1
(a
n2
)(v) resulta ser una
base de R
n1
. Por ejemplo, si n = 3 y v = (u, v) ,= (0, 0), entonces la condicin para
que v y
2
(a)(v) = (v, uv) sean linealmente dependientes es equivalente a que exista
R tal que el sistema lineal
_
u + v = 0
u + (1 +)v = 0
tenga como solucin a (u, v). Esto obliga a que el determinante de la matriz asociada al
sistema sea cero. Pero el determinante de tal matriz es
2
++1, el cual no tiene solucin
real, una contradiccin.
De lo anterior tenemos la descomposicin en factores irreducibles
n
= (
n1
, (1)),
donde (1) es la representacin uno-dimensional que enva a las permutacions pares en
1 y a las impares en 1.
Ejercicio 29.0.19. Vericar la irreducibilidad de la representacin
n1
(o
n
) del
ejemplo anterior.
Ejemplo 29.0.20. El ejemplo anterior, para el caso n = 3, nos da una representacin
irreducible de o
3
en el espacio vectorial real R
2
, ms an, en el espacio vectorial Q
2
.
Miremos otras representaciones de este grupo. Podemos hacer actuar el grupo en si mismo
como sigue
: o
3
Perm(o
3
) : ()
donde
() : o
3
o
3
:
Por ejemplo, ((1, 2, 3)) acta de la siguiente manera :
x
1
= I (1, 2, 3) = x
2
x
2
= (1, 2, 3) (1, 3, 2) = x
3
x
3
= (1, 3, 2) I = x
1
x
4
= (1, 2) (1, 3) = x
5
x
5
= (1, 3) (2, 3) = x
6
x
6
= (2, 3) (1, 2) = x
4
Luego podemos mirar en las coordenadas
_
_
x
1
x
2
x
3
x
4
x
5
x
6
_
_
Q
6
que ((1, 2, 3) puede ser representada por la matriz
A =
_
_
0 1 0 0 0 0
0 0 1 0 0 0
1 0 0 0 0 0
0 0 0 0 1 0
0 0 0 0 0 1
0 0 0 1 0 0
_
_
En forma similar, ((1, 2)) es dada por
x
1
= I (1, 2) = x
4
x
2
= (1, 2, 3) (2, 3) = x
6
x
3
= (1, 3, 2) (1, 3) = x
5
x
4
= (1, 2) I = x
1
x
5
= (1, 3) (1, 3, 2) = x
3
x
6
= (2, 3) (1, 2, 3) = x
2
puede ser representada por la matriz
B =
_
_
0 0 0 1 0 0
0 0 0 0 0 1
0 0 0 0 1 0
1 0 0 0 0 0
0 0 1 0 0 0
0 1 0 0 0 0
_
_
La funcin dada por
: o
3
GL(Q
6
)
denida por ((1, 2, 3)) = A y ((1, 2)) = B, dene una representacin racional de
grado 6. Consideremos el subespacio W < Q
6
de dimensin 3 correspondiente a tomar
w
1
= x
1
+ x
4
= (1, 0, 0, 1, 0, 0), w
2
= x
2
+ x
5
= (0, 1, 0, 0, 1, 0), w
3
= x
3
+ x
6
=
(0, 0, 1, 0, 0, 1). Entonces W es invariante, es decir, la representacin es reducible. Ms
an, la representacin en W es dada por
A =
_
_
0 1 0
0 0 1
1 0 0
_
_
B =
_
_
1 0 0
0 0 1
0 1 0
_
_
es decir, obtenemos la representacin reducible
3
del ejemplo anterior.
Ejemplo 29.0.21. Consideremos el grupo ms simple que tenemos, es decir, el grupo
cclico de orden dos
G = x : x
2
)
= Z/2Z
Consideremos cualquier representacin
: G GL(V )
donde V es algn espacio vectorial sobre un cuerpo /. Entonces si consideramos los
espacios propios
V
+
= v V : (x)(v) = v
V
= v V : (x)(v) = v
entonces tenemos la descomposicin
V = V
+
V
Escogiendo una base para V

+
y una base de V
, obtenemos al juntarlas una base de V .

En esta base, la representacin es entonces equivalente a la representacin
: G GL(V
+
V
) < GL(V
+
) GL(V
)
donde
(x) =
_
I 0
0 I
_
De aqu observamos que las nicas representaciones irreducibles de G son las siguientes
dos de grado 1 :
+
: G GL(/) = /
: x 1
: G GL(/) = /
: x 1
Ejemplo 29.0.22. Consideremos ahora el grupo Abeliano ms simple que no sea c-
clico, es decir,
G = x, y : x
2
, y
2
, (xy)
2
)
= Z/2Z Z/2Z
Consideremos cualquier representacin
: G GL(V )
donde V es algn espacio vectorial sobre un cuerpo /. Entonces si consideramos los
espacios propios
V
+
= v V : (x)(v) = v
V
= v V : (x)(v) = v
El hecho que (x) y (y) conmutan asegura que (y) deja a los subespacios V
+
y V
invariantes. Entonces podemos escoger los subespacios siguientes :

V
+
+
= v V
+
: (y)(v) = v
V
+
= v V
+
: (y)(v) = v
V
+
= v V
: (y)(v) = v
V
= v V
: (y)(v) = v
Tenemos entoces que
V = V
+
+
V
+
+
V

Podemos escoger una base de V adjuntando primero una bse de V
+
+
, luego una base de
V
+
, luego una base de V
+
y nalmente una base de V
. En esta base, la representacin

es entonces equivalente a la representacin
: G GL(V
+
+
V
+
+
V
) < GL(V
+
+
) GL(V
+
) GL(V
+
) GL(V
)
donde
(x) =
_
_
I 0 0 0
0 I 0 0
0 0 I 0
0 0 0 I
_
_
(y) =
_
_
I 0 0 0
0 I 0 0
0 0 I 0
0 0 0 I
_
_
Luego las representaciones irreducibles de G son las siguientes cuatro de grado 1 :
++
: G GL(/) = /
: x 1, y 1
+
: G GL(/) = /
: x 1, y 1
+
: G GL(/) = /
: x 1 y 1
: G GL(/) = /
: x 1 y 1
CAPTULO 30
CARCTERES Y CONTEO DE REPRESENTACIONES
IRREDUCIBLES
En esta seccin veremos como determinar cuantas representaciones irreducibles no
equivalentes sobre el cuerpo de los nmeros complejos existen para cada grupo nito
(G, ). De manera ms precisa.
Teorema 30.0.23. Sea (G, ) un grupo nito. Entonces el nmero de representaciones
irreducibles complejas no equivalentes es igual al nmero de clases de conjugacin en
G.
Ejemplo 30.0.24. Para el grupo simtrico o
n
habamos visto en la seccin 14 que el
nmero de clases de conjugacin es igual al nmero de soluciones del sistema
1
+
2
+ +
n
= n
1

2

n
0
luego, ese nmero es exactamente la cantidad de representaciones irreducibles complejas
no equivalentes de o
n
.
Necesitaremos algunos conceptos que iremos deniendo a continuacin.
Denicin 30.0.25. Cada representacin compleja : G GL(V ), de un grupo
(G, ) (nito o innito) de grado nito tiene asociada la funcin
: G C : g Tr((g))
donde Tr((g)) denota la traza del automorsmo lineal (g) : V V . A esta funcin
la llamaremos el carcter de . Observemos que
(I
G
) = dim(V )
156 CAPTULO 30. CARCTERES Y CONTEO DE REPRESENTACIONES IRREDUCIBLES
Como conjugacin preserva las trazas, vemos que el carcter de representaciones equi-
valentes es el mismo. Ms an, si g, h G, entonces vale que
(g) =
(h g h
1
) ;
luego el carcter es constante en cada clase de conjugacin en G.
Ejercicio 30.0.26. Ya que hemos hablado de producto de representaciones, digamos
en este punto que si : G GL(V ) y : G GL(W) son dos representaciones del
grupo nito (G, ), ambas de grado nito, entonces
(,)
=
Vericar que el conjunto de los carcteres de todas las representaciones lineales de grado
nito de un grupo nito (G, ) no es necesariamente un espacio vectorial.
tenemos que el conjunto de los carcteres no dene un espacio vectorial.
Denicin 30.0.27. El conjunto de las funciones de clase es
F(G) = f : G C : f es constante en las clases de conjugacin de G
Denicin 30.0.28. Denotemos por Car(G) F(G) al conjunto de los carcteres
de las representaciones de grado nito de G.
Ejercicio 30.0.29. Vericar que F(G) es el espacio vectorial ms pequeo que
contiene Car(G).
Ejercicio 30.0.30. Calcular los carcteres asociados a las representaciones de grado
nito de las secciones anteriores. En particular,
(i) para la representacin lineal asociado a una accin : G Perm(X), del grupo
nito (G, ) sobre un conjunto nito X, vericar que el carcter evaluado en g G
coincide con la cardinalidad de Fix((g)) ;
(ii)
(g) =
(g)
(g)
(iii)
(g) =
(g)
(iv)
(g) =
1
2
_
(g)
2
(g
2
)
_
Ejercicio 30.0.31. Sea : G GL(V ) una representacin compleja de grado nito
del grupo nito (G, ) y
: G C su carcter asociado. Vericar que
permite
conocer los valores propios de (g) para cada g G (observe que si los valores propios
de g son
j
, entonces los valores propios de g
k
son
k
j
).
CAPTULO 30. CARCTERES Y CONTEO DE REPRESENTACIONES IRREDUCIBLES 157
Supongamos que tenemos una representacin compleja de grado nito de un grupo
nito (G, ), digamos
: G GL(V )
Como
(I
G
) = dim(V ), tenemos que el carcter determina el grado de la representa-
cin. Para esta accin tenemos que
V
G
= v V : (g)(v) = v para cada g G
Ejercicio 30.0.32. Vericar que V
G
es un subespacio vectorial de V y que la repre-
sentacin es irreducible s y slo si V
G
= 0.
Una manera de calcular explcitamente el subespacio vectorial V
G
es la siguiente.
Consideremos la funcin lineal dada por el promedio
L =
1
[G[
gG
(g) : V V Hom
G
(, )
Tenemos que
(i) L(v) V
G
, para cada v V ;
(ii) L(v) = v, para cada v V
G
.
De esta manera, L : V V
G
es una proyeccin sobre V
G
y adems
V
G
= Fix(L)
en particular,
dim(V
G
) = Tr(L) =
1
[G[
gG
Tr((g)) =
=
1
[G[
gG
(g)
En particular, si es una representacin irreducible, entonces necesariamente debemos
tener
gG
(g) = 0
Consideremos ahora dos representaciones irreducibles
: G GL(V ) y : G GL(W)
podemos considerar el espacio vectorial Hom
G
(, ) formado por todos los homomor-
smos M : V W de las dos representaciones. Como consecuencia del lema de Schur
y su corolario, tenemos que
dim(Hom
G
(, )) =
_
1 si y son equivalentes
0 en caso contrario
Consideremos la representacin homomorsmo
= Hom(, ) : G GL(Hom(V, W))
cuyo carcter asociado es dado por

En este caso, tenemos que Hom(V, W)
G
= Hom
G
(, ).
As, por lo anterior tenemos que
1
[G[
gG
(g)
(g) =
1
[G[
gG
(g) = dim(Hom
G
(, )) =
= dim(Hom(V, W))
G
=
_
1 si las representaciones son equivalentes
0 en caso contrario
Esta frmula nos permite denir un producto interior Hermitiano
(f
1
, f
2
) =
1
[G[
gG
f
1
(g)f
2
(g)
sobre el espacio vectorial F(G) de las funciones de clases de G de manera que los carc-
teres de representaciones irreducibles no equivalentes forman un conjunto ortonormal.
Una consecuencia de esta situacin es la siguiente.
Proposicin 30.0.33. Toda representacin compleja de grado nito de un grupo nito
(G, ), digamos : G GL(V ), est nicamente determinada, mdulo equivalencia,
por su carcter. Ms an, la representacin es irreducible s y slo si (
) = 1.
Demonstracin.
Situacin Irreducible. Consideremos dos representaciones irreducibles : G GL(V )
y : G GL(W), ambas de grado nito con el mismo carcter . Supongamos pri-
mero que ambas representaciones son irreducibles, entonces podemos utilizar lo hecho
anteriormente para obtener nuestro resultado.
Situacin General. Supongamos que la representacin no es irreducible. Entonces, po-
demos encontrar representaciones irreducibles no equivalentes
j
: G GL(V
j
), para
j = 1, ..., r, de manera que = (
a1
1
, ...,
ar
r
) : G GL(V
a1
1
V
ar
r
) es equivalente
a . En este caso tenemos que
=
r
j=1
a
j
j
Como cada representacin irreducible est determinada por su carcter, tenemos que
la representacin queda determinada por su carcter. Observemos que en este caso
(
) =
r
j=1
a
2
j
.
De lo anterior, vemos que las representaciones lineales de grado nito de un grupo
nito (G, ) quedan determinados, mdulo equivalencia, por sus ccteres.
Supongamos que A
1
,..., A
n
son las diferentes clases de conjugacin del grupo G,
donde A
1
= I
G
. Escojamos un representante de cada clase, digamos g
j
A
j
, j =
2, 3, ..., n. Sea a
j
= #A
j
. Si f : G C es una funcin de clase del grupo nito de G,
entonces consideremos el vector
(f(I
G
), f(g
2
), ..., f(g
n
)) C
n
Esto nos permite construir una funcin lineal inyectiva
M : F(G) C
n
y as considerar F(G) como un subespacio de C
n
y, en particular, considerar Car(G)
como un conjunto de vectores.
En el espacio vectorial C
n
podemos considerar el producto interior Hermitiano
(x
1
, ..., x
n
), (y
1
, ..., y
n
)) =
1
[G[
n
j=1
a
j
x
j
y
j
Ejercicio 30.0.34. Vericar que este producto Hermitiano hace que M sea una iso-
metra respecto al producto Hermitiano considerado anteriormente para F(G).
Ahora, los vectores en C
n
que corresponden a los carcteres de representaciones irre-
ducibles forman un conjunto ortonormal respecto al producto Hermitiano, en particular,
se tiene la segunda consecuencia, una aproximacin del teorema 30.0.23.
Proposicin 30.0.35. El nmero de representaciones irreducibles no equivalente de
grado nito de un grupo nito (G, ) es a lo ms el nmero de clases de conjugacin en
G.
Ejemplo 30.0.36. Consideremos (G, ) un grupo nito y la accin : G
Perm(G) : h g h. Consideremos la representacin lineal que esta dene, es decir la
representacin regular de G, denotemosla por
G
: G GL(V ), donde dim(V ) = [G[.
En este caso
G
(g) =
_
0 si g ,= I
G
[G[ si g = I
G
En particular
G
,
G
) = [G[
2
, con lo cual obtenemos que esta representacin lineal
no es irreducible para [G[ > 1. En este caso, tenemos que
G
es equivalente a la repre-
sentacin = (
a1
1
, ...,
ar
r
), donde
1
,...,
r
son todas las repersentaciones irreducibles
de G de grado nito y a
j
0, 1, 2, ... Habamos observado que
a
j
=
j
, ) =
j
,
G
) =
1
[G[
gG
j
(g)
G
(g) =
1
[G[
j
(I
G
)
G
(I
G
) =
=
j
(I
G
) = grado de la representacin
j
> 0
Como consecuencia de esto vemos que en la representacin regular
G
del grupo G
aparecen todas las representaciones irreducibles de G, cada una apareciendo exactamente
tantas veces como su grado. Una consecuencia simple de esto es que el nmero de repre-
sentaciones irreducibles no equivalentes es nita (lo que ya sabamos por la proposicin
anterior). Adems, tenemos que
[G[ =
G
,
G
) =
r
j=1
a
2
j
Proposicin 30.0.37. La suma de los cuadrados de los grados de todas las represen-
taciones irreducibles no equivalentes de un grupo nito es igual al orden de este.
Ejemplo 30.0.38. Para el grupo o
3
tenemos a lo ms tres representaciones irredu-
cibles no equivalentes. Por la proposicin anterior se puede ver que no hay slo una re-
presentacin irreducible ya que 6 no es un cuadrado de un entero. Si hubiesen slo dos
representaciones irreducibles, entonces estaramos diciendo que 6 es suma de dos cuadra-
dos, lo cual no es posible. De esta manera, obtenemos que deben haber exactamente tres
representaciones irreducibles no equivalentes. Si denotamos por a
1
, a
2
, a
3
1, 2, .. los
grados de estas, entonces debemos tener a
2
1
+ a
2
2
+ a
2
3
= 6. De aqu vemos que la nica
posibilidad es dada por el siguiente tro, mdulo permutacin, (1, 1, 2).
Ahora procedemos a vericar que el conjunto ortonormal de vectores que correspon-
den a las representaciones irreducibles de G es de hecho una base, obteniendo de esta
manera la demostracin del teorema 30.0.23.
Para esto supongamos que tenemos la posibilidad de escoger una funcin de clases de
G, digamos f F(G), que sea ortogonal a cada carcter de una representacin irredu-
cible de G. Bastar con vericar que f = 0.
Consideremos una representacin lineal : G GL(V ) de grado nito d. Denamos
la funcin lineal L : V V por
L(v) =
gG
f(g)(g)(v)
Para cada h G y cada v V , tenemos que
(h) L (h
1
)(v) =
gG
f(g)(h g h
1
)(v) =
=
gG
f(h g h
1
)(h g h
1
)(v) =
kG
f(k)(k)(v) = L(v)
en particular, L Hom
G
(, ). Como consecuencia del corolario al lema de Schur vale
que L(v) = v para cierto valor C, luego
d = Tr(L) =
gG
f(g)Tr((g)) =
gG
f(g)
(g) =
= [G[f,
) = [G[f,
) = [G[f,
)
y como
es una combinacin lineal de los carcteres de las representaciones irredu-

cibles que descomponen la representacin , obtenemos nalmente
d = 0
y, en particular, = 0 como deseabamos para completar la demostracin del teorema
30.0.23.
En resumen. Dado un grupo nito (G, ), procedemos como sigue :
(1) determinamos la cantidad n de clases de conjugacin y las respectivas cardinali-
dades a
1
= 1, a
2
,..., a
n
.
(2) consideramos el producto interior Hermitiano en C
n
dado por
(x
1
, ..., x
n
), (y
1
, ..., y
n
)) =
1
[G[
n
j=1
a
j
x
j
y
j
(3) buscamos bases ortonormales de C
n
con la propiedad de que la primera coorde-
nada de cada vector involucrado sea un entero positivo y tal que la suma de los
cuadrados de las primeras coordenadas sea igual al orden del grupo. Uno de los
vectores involucrados siempre es (1, 1, ..., 1) que corresponde a la representacin
trivial
1 : G C
: g 1
Ejemplo 30.0.39. Consideremos el grupo simtrico o
3
. En este caso tenemos 3 clases
de conjugacin A
1
= I, A
2
= (1, 2), (1, 3), (2, 3) y A
3
= (1, 2, 3), (1, 3, 2).
De esto sabemos que hay exactamente tres representaciones irreducibles de o
3
. En C
3
entonces consideramos el producto Hermitiano
(x
1
, x
2
, x
3
), (y
1
, y
2
, y
3
)) =
1
6
(x
1
y
1
+ 3x
2
y
2
+ 2x
3
y
3
)
Si consideramos tres vectores (a
j
, b
j
, c
j
) C
3
, donde a
j
1, 2, ..., formando una
base ortonormal, entonces debemos tener las ecuaciones (i ,= j 1, 2, 3)
a
2
j
+ 3[b
j
[
2
+ 2[c
j
[
2
= 6
a
i
a
j
+ 3b
i
b
j
+ 2c
i
c
j
= 0
La igualdad aj
2
+ 3[b
j
[
2
+ 2[c
j
[
2
= 6 de donde podemos observar que a
j
1, 2.
De esta informacin obtenemos que las tres representaciones irreducibles son de grado
1 y/o 2. Por un lado, siempre est la representacin irreducible de grado 1 trivial
1 : o
3
C
: g 1
cuyo carcter corresponde al vector (1, 1, 1). Otra representacin irreducible de grado 1
es
1 : o C
: g
_
1 si g tiene orden par
1 en caso contrario
cuyo carcter corresponde al vector (1, 1, 1). La tercera representacin irreducible tiene
carcter correspondiente a un vector (a, b, c), donde a 1, 2 y valen las igualdades :
a
2
+ 3[b[
2
+ 2[c[
2
= 6
a + 3b + 2c = 0
a 3b + 2c = 0
De las dos ltimas igualdades obtenemos al sumarlas a = 2c, de donde estamos
obligados a tomar a = 2, c = 1 y luego b = 0. En particular, la tercera representacin
irreducible es dada por el vector (2, 0, 1) que es de grado 2. Esta representacin es dada
por : G GL(C
2
) tal que
(1, 2, 3) =
_
e
i/3
0
0 e
i/3
_
(1, 2) =
_
0 1
1 0
_
REFERENCIAS
[1] Burnside, W. Theory of Groups of Finite Order, Dover, 1955.
[2] Coxeter, H.S. and Moser, W.O. Generators and Relations for Discrete Groups,
Springer-Verlag, 1965.
[3] Fraleigh, J.B. A First Course in Abstract Algebra, Addison-Wesley,1982.
[4] Fulton, W. and Harris, J.H. Representation Theory, Springer-Verlag, 1991.
[5] Jacobson, N. Lecture in Abstract Algebra, Princeton, vol.1, 1951, vol.2, 1953, vol.3,
1964.
[6] Herstein, I.N. Topics in Algebra, Blaisdell, 1964.
[7] Van der Waerden, B.L. Modrn Algebra, Ungar, vol.1, 1949, vol2, 1940.
INDICE
p-Grupo, 76
Abelianizacin de un grupo, 38
Accin el, 71
Accin por la derecha de un grupo, 71
Accin por la izquierda de un grupo, 71
Accin transitiva, 74
Anillo, 95
Anillo cociente, 108
Anillo con unidad, 96
Anillo conmutativo, 98
Anillo de divisin, 96
Anillo de polinomios, 97
Anillo de un grupo, 96
Anillo Noetheriano, 131
Anillos isomorfos, 103
Antiautomorsmo de grupos, 19
Asociatividad, 7
Automorsmo interior, 20
Automorsmos de grupo, 17
Cpsula normal, 40
Cclo, 63
Carcter de una representacin, 155
Caracterstica, 113
Centralizador de un elemento, 38
Centralizador de un grupo, 38
Cero de un polinomio, 105
Commutatividad, 9
Conmutador, 37
Cuaternios, 99
Cuerpo, 98
Cuerpo de fracciones, 117
Cuerpo no conmutativo, 99
Cuerpos primos, 113
Descomposicin en Fracciones Parciales, 127
Divisores de cero, 98
Dominio de factorizacin Unica, 122
Dominio de Ideales Principales, 120
Dominio entero, 98
Dominio Euclidiano, 119
Ecuacin de las clases, 77
Elemento inverso, 7
Elemento Irreducible, 121
Elemento Neutro, 7
Enteros Gausianos, 120
Estabilizador de un punto, 73
Funcin de clase, 156
Funcin de Euler, 14
Grado de un polinomio, 97
Grado de una representacin, 137
Grafo, 11
Grupo Abeliano, 9
Grupo alternante, 65
Grupo de automorsmos exteriores, 31
Grupo de clases laterales, 29
Grupo de isometras, 6
Grupo de Klein, 28
Grupo de las clases residuales, 31
Grupo dihedral, 59
Grupo Especial Lineal, 10
Grupo fundamental, 15
Grupo libre, 55
Grupo libre abeliano, 57
Grupo orientable, 90
Grupo orientado, 90
Grupo Proyectivo Lineal, 10
Grupo reejado, 19
166 INDICE
Grupo Simtrico, 21
Grupo simtrico, 63
Grupo simple, 88
Grupos cclicos, 23
Grupos de permutaciones, 4
Grupos isomorfos, 17
Grupos sin torsin, 40
HNN-extensin, 53
Homomorsmo de anillos, 103
Homomorsmo de evaluacin, 104
Homomorsmo de grupos, 17
Ideal, 107
Ideal derecho, 107
Ideal generado, 109
Ideal izquierdo, 107
Ideal maximal, 111
Ideal primo, 111
Ideal principal, 109
Imgen de un homomorsmo, 17
Indice de un subgrupo, 27
Isomorsmo de anillos, 103
Isomorsmo de grupos, 17
Longitud de una palabra reducida, 47
Ncleo de un homomorsmo, 17
Normalizador, 40
Orbita por una accin, 73
Orden de un grupo, 8
Orden del grupo de permutaciones, 4
Orden del subgrupo de permutaciones, 5
Palabra reducida, 47
Permutacin, 3
Permutaciones impares, 66
Permutaciones pares, 66
Polinomios, 97
Primer teorema del isomorsmo, 32
Producto dbil, 44
Producto directo, 43
Producto directo de anillos, 99
Producto directo interno, 45
Producto libre, 48
Producto libre amalgamado, 51
Producto semidirecto, 45
Producto semidirecto interno, 46
Radical, 110
Rango de un grupo libre, 55
Representacin cociente, 141
Representacin cua, 140
Representacin estandard del grupo simtrico, 149
Representacin el, 137
Representacin homomorsmo, 140
Representacin irreducible, 143
Representacin Lineal, 137
Representacin producto, 139
Representacin producto tensorial, 140
Representacin reducible, 143
Representacin regular, 139
Representacin restriccin, 141
Representacin suma directa, 139
Segundo teorema del isomorsmo, 34
Semicuerpo, 99
Subanillos, 100
Subgrupo, 9
Subgrupo de conmutadores, 37
Subgrupo de permutaciones, 5
Subgrupo normal, 29
Subrepresentacin inducida, 143
Sucesin corta exacta, 46
Suma directa, 43
Teorema de Euler, 14
Teorema de Fermat, 13
Teorema de Lagrange, 27
Teoremas de Sylow, 83
Tercer teorema del isomorsmo, 34
Transposiciones, 63
Valuacin, 119
Yuxtaposicin de palabras, 48

Estruturas Algebricas Grupos e Aneis

Cargado por

Información del documento

Título original

Derechos de autor

Formatos disponibles

Compartir este documento

Compartir o incrustar documentos

Opciones para compartir

¿Le pareció útil este documento?

¿Este contenido es inapropiado?

Copyright:

Formatos disponibles

Estruturas Algebricas Grupos e Aneis

Cargado por

Copyright:

Formatos disponibles

MONOGRAF AS MAT E MT I CAS

(G) al conjunto de los antiautomor-

(G), es decir, todo antiautomorsmo es tambin un automorsmo. Qu pasa para

(G) un grupo bajo la regla de composicin?

= H es trivial el elemento a se proyecta a un elemento de orden

La operacin binaria es dada por

resultan ser subgrupos de K H y se tiene que las inclusiones

dene una estructura de grupo ;

= Z Z el grupo libre de rango 2 generado

= y s y slo si existe g G tal que (g)(x) = y

C), ) dada por biholomorsmos :

druple est formada por las cuatro caras de T, es decir #X = 24 y el

Observemos que #X = [G[

tambin es divisible por p. Como

, tenemos necesariamente que #X

= Z/pZ Z/pZ. Podemos resumir estos resultados de la siguiente manera :

De esta manera, tenemos que

y luego, si > 1, tenemos que

88 CAPTULO 17. APLICACIONES DE LOS TEOREMAS DE SYLOW

d] no lo es. Vericar que Q[

d] es el cuerpo ms pequeo dentro de R que contiene

d], donde d > 0 no es el cuadrado de un entero, tienen

d]. Vericar que su cuerpo de fracciones es isomorfo a Q[

d]. Utilize v(a+b

d]. Utilize v(a + b

I I, necesitamos ver que I

I = . Supongamos por el contrario

. Luego, no es dicil ver que (g)( v) =

est nicamente determinado por g G y , es decir, no

) denida como sigue : Si L : V / es una

, el subespacio ortogonal a W, tambin resulta invariante, donde

Escogiendo una base para V

, obtenemos al juntarlas una base de V .

invariantes. Entonces podemos escoger los subespacios siguientes :

CAPTULO 29. HOMOMORFISMOS DE REPRESENTACIONES 153

, luego una base de V

. En esta base, la representacin

: G C su carcter asociado. Vericar que

158 CAPTULO 30. CARCTERES Y CONTEO DE REPRESENTACIONES IRREDUCIBLES

es una combinacin lineal de los carcteres de las representaciones irredu-

También podría gustarte