UCV - EECA Matemática II 1° Parcial

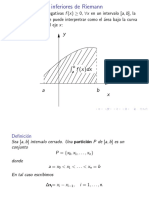
Integrales de Riemann Partición

es Riemann Integrable en el Dado un Intervalo [a,b] se denomina Partición de [a,b] y se denota " P " a:
f ( x) Intervalo [a,b]
P= { X 0 , X 1 , X 2 ,... , X n −1 , X n } donde a = X 0 < X1 < X 2 < ... < X n−1 < X n = b
f ( x) es R[ a ,b ]
Ejemplo : Intervalo [-1,3] Partición [-1,3] → P = {-1,1,3} ( P = {X 0, X1, Xn} )
Refinamiento " P' " (Nota: Los Intervalos poseen Infinitas Particiones)
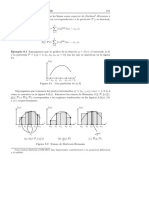
Sean Dos Particiones Pa y Pb Norma de una Partición
Pa = {-1,0,1,2} Se denomina Norma de una Partición del Intervalo [a,b] y se denota " │ P│" a:
Pb = {-1,-½,0,½,1,2}
P = Max{Δ xi ; ∀ i = 1,2,..., n} donde Δ xi = X i − X i −1
Como Pa ⊂ Pb entonces
Ejemplo : P = {-1,-½,0,3} →│P│= Max {(-½+1),(-½-0),(3-0)} →│P│= Max {½,-½,3}
P'a es Refinamiento de Pb entonces si [(-½ < ½ < 3) → Max = 3] → │P│= 3
Suma Riemann Integral Inferior y Superior

∀ x ∈ [a , b]
Sea P = { una Partición de [a,b]} ; S = {S(f ,P) : P ∈ [a,b]} ; I = {I(f ,P) : P ∈ [a,b]}
m ≤ f ( x) ≤ M Integral Inferior
m = Mínimo o Cota Inferior b
M = Máximo o Cota Superior
∫ f ( x ) = Sup{ I ( f , P): P ∈ [a , b ]} = A A∈R
Suma Inferior I(f , P)
a
n
I ( f , P) = ∑ m ( f )⋅ Δx
i i
Integral Superior
i =1 b

∫ f ( x ) = Inf { S ( f , P): P ∈ [ a, b]} = B B∈R

mi ( f ) = Inf { f ( x ): x ∈ [ X i−1 , X i ]} a

Suma Superior S(f,P) Se Cumple

n m ⋅ (b − a ) ≤ I ( f , P) ≤ S ( f , P ) ≤ M ⋅ (b − a )
S ( f , P) = ∑ M ( f )⋅ Δx
i =1
i i m ⋅ (b − a ) ≤ I ( f , P ) ≤
b

∫ f ( x) ≤
b

∫ f ( x ) ≤ S ( f , P ) ≤ M ⋅ (b − a )
a a

Mi ( f ) = Sup{ f ( x ): x ∈ [ X i −1 , X i ]} Cota Inferior de la Integral Cota Superior de la Integral

Función Integrable
Se Cumple
m ⋅ (b − a ) ≤ I ( f , P ) ≤ S ( f , P ) ≤ M ⋅ (b − a)
b b b

m ≤ mi ( f ) ≤ M i ( f ) ≤ M
∫ f ( x) = ∫ f ( x) = ∫ f ( x)
a a a

b
← (El Resultado es un Número)
∫ f ( x )dx = F ( x ) + C = [ F (b) − F ( a )] + C
b
Integral Definida
Integral

a
a Para Ambos Casos
Integral Indefinida, a ^ b = Extremos de Integración

∫ f ( x )dx =
← (El Resultado una
Antiderivada ó F ( x) + C Función)
f(x) = Función Integrado
Integral Primitiva F'(x) = f(x)

①
Si f(x) esta acotada en [a,b] , entonces se
cumple →
m ≤ f ( x) ≤ M ; ∀ x ∈ [a , b ] m = Cota Inferior
M = Cota Superior
②
Si P' es un Refinamiento de P y f(x) esta
acotada en [a,b] , entonces se cumple →
① I ( f , P ) ≤ I ( f , P' ) ② S ( f , P ) ≥ S ( f , P ')
TEOREMAS DE LA INTEGRAL

Si f(x) es R[a,b] y P es una Partición de

b b

③ m ⋅ (b − a ) ≤ I ( f , P ) ≤ ∫ f ( x) ≤ ∫ f ( x ) ≤ S ( f , P ) ≤ M ⋅ (b − a )
[a,b] entonces se cumple → a a

④
(Condición Necesaria y Suficiente) Una f(x)
acotada en [a,b] , es R[a,b] si y solo si →
∀ε ( > 0)(∃ p ∈ P), S ( f , P) = I ( f , P) < ε (Si Reciproco)

⑤ (Condición Suficiente) Si f(x) es continua y acotada en [a,b] , entonces f(x) es R[a,b] (No Reciproco)

⑥ (Condición Suficiente) Si f(x) es Monótona y acotada en [a,b] , entonces f(x) es R[a,b] (No Reciproco)

⑦ (Condición Suficiente) Si f(x) y f'(x) están acotadas en [a,b] , entonces f(x) es R[a,b] (No Reciproco)
Una Aproximación al Valor de Integral entre Una Cota de Error " e "cometido al tomar la Aproximación del
[a,b] viene dado por : Valor de la Integral es:
⑧ b
I ( f , P) + S ( f , P) b
I ( f , P) + S ( f , P) S ( f , P) − I ( f , P )
∫ f ( x) ≈
2
e= ∫ f ( x) −
a
2
≤
2
a

Si f(x) esta acotada en [a,b] y P es una Partición Genérica de [a,b] y si →

Lim I ( f , P) = Lim S ( f , P ) = L
L = Es una Aproximación
⑨ b

x→ ∞ x→ ∞
entonces → ∫ a
f ( x) ≈ L del Valor de la Integral

Elaborado por: Eder Nunes

UCV - EECA Matemática II 1° Parcial

PROPIEDADES Y OPERACIONES BÁSICAS

S a b i e n d o q u e ↓: (C1 ^ C2) = Constantes

f ( x ) acotada en [ a , b] → f ( x ) ∈ R[ a ,b ] y g ( x ) acotada en [a , b ] → g ( x ) ∈ R[ a ,b ] y C1 ∧ C2 ∈ R
① ②

f ( x ) ∈ R[ a ,b] ∧ c ∈ [ a, b] ⎯ entonces
Si los Extremos de Integración son iguales, entonces →
a
⎯ ⎯ → f ( x ) ∈ R[ a,c ] ∧ f ( x ) ∈ R[ c ,b]
∫ f (x) = 0 b c b

a y se cumple → ∫ f ( x) = ∫ f ( x) + ∫ f ( x)
③ a a c

b ④
∫C = C1 ⋅ (b − a )
a
1
f ( x) ∈ R[ a ,c ] ∧ f ( x) ∈ R[ c ,b ] ⎯ entonces
⎯ ⎯ → f ( x ) ∈ R[ a ,b ]
⑤ c b b

b b y se cumple → ∫ f ( x) + ∫ f ( x) = ∫ f ( x)
∫C⋅ f ( x) = C ⋅ ∫ f ( x) a c a

a a ⑥
⑦ (No se Cumple el Reciproco)
(No se Cumple el Reciproco) b b b

f ( x ) ≤ g ( x); ∀ x ∈ [ a , b] →
b b
∫ (C 1 ⋅ f ( x ) ± C2 ⋅ g ( x) ) = C1 ⋅ ∫ f ( x ) ± C2 ⋅ ∫ g ( x )
∫ f ( x) ≤ ∫ g( x ) a a a
a a ⑧
⑨ (No se Cumple el Reciproco)
(No se Cumple el Reciproco)
Si f ( x ) ∈ R[ a ,b ] ⎯ entonces
⎯ ⎯ → f ( x ) ∈ R[ a ,b ]
Si f ( x) ∈ R[ a ,b ] ∧ [c, d ] ⊂ [a ,b] ⎯ entonces
⎯ ⎯ → f ( x) ∈ R[ c ,d ] b b

∫ f ( x) ≤ ∫ f ( x)
⑪ a a

b b
⑩

b < a ⎯ ⎯ ⎯→ ∫ f ( x) = − ∫ f ( x)
entonces b
Si f ( x) ≥ 0; ∀ x ∈ [a , b ] ⎯ entonces
a a
Si ⎯ ⎯→ ∫
a
f ( x) ≥ 0

x y f(t) es continua en un Intervalo cerrado y

∫ g '( x ) = f ( t )
Sea g(x)
g ( x) =
Fundamentales del

①
→
f (t ) dt acotado " I"; y si " a ∈ I", entonces g(x) es
Diferenciable en " I" y se verifica →
Teoremas

a
Calculo

(Viene dado por el Teorema Anterior) Si f(t) es continua en un Intervalo cerrado y acotado " [a,b] "; y si F(x)
es Diferenciable en " [a,b] " entonces:

F '( x ) = f (t ) ∀ t ∈ [a, b]
② b

∫ f (t ) = F ( x ) a = F (a ) − F (b )
b
y se verifica →
a

(Íntimamente relacionado con el Teorema del Valor Medio para Derivadas) Valor Medio o
Teorema del Valor Promedio
Medio para b
Si f ( x) es continua en [ a, b] → ∃ c ∈ ( a, b): ⎯ tal
⎯⎯ que
→ ∫ f ( x) = f ( c) ⋅ (b − a )
Integrales a

Métodos de Integración
① Método por Parte ② Método por Sustitución ó Método de Cambio de Variable
b b b β

∫ f ( x ) dx = ∫( g )( x ) ⋅ ( g ( x ) )'
∫ f ⋅ g' = f ⋅ g − ∫ g⋅
b f o

a
f' a α
a a Ejemplo: Asumimos (f o g )(x) = u y ( g (x))' = u'
en textos aparece como:
x ⋅ dx 2 x ⋅ dx
1 1 2
1 ⎛ Aplicamos ⎞ 1 du
b b ∫ x2 + 1
⇒
2 ∫
⋅
x2 + 1
⇒ ⎜
⎝ Metodo ⎠
⎟ ⇒
2
⋅ ∫ u
∫ u ⋅ dv = u⋅ v − ∫ v ⋅ du
b 0 0 1
a
(Aplicamos u = x 2 +1 x=1 →u=2
a a → Extremos →
Método) du = 2xdx x=0 →u=1

Elaborado por: Eder Nunes

UCV - EECA Matemática II 1° Parcial

③ Método por Sustitución Trigonometrica

a x = a ⋅ Sen(t ) t= arcSen( x a)
( )

Cambios:
x
Caso

∫ a 2 − x 2 dx
①
f
dx = a ⋅ Cos( t ) ⋅ dt
a2 − x 2
x = a ⋅ Tg (t ) arcTg ( x a )
( )
a2 + x2 t =

Cambios:
x
∫
Caso

f a + x dx
2 2
②

a dx = a ⋅ Sec 2 (t ) ⋅ dt
x = a ⋅ Sec(t ) t = arcSec( x a )
( )dx
x

Cambios:
∫
Caso

f x −a2 2 x −a 2 2
③

a dx = a ⋅ Sec( t ) ⋅ Tg (t ) ⋅ dt
④ Integrales Racionales (Polinómicas)
Caso ①
Esta Formula se aplica si n≥2
dx 2 ax + b 2 a( 2n − 3) dx
∫ = +
(n − 1)(4ac − b
⋅∫
) (ax
(ax ) (n − 1)(4ac − b )(ax ) )
n n −1 2 n −1
2
+ bx + c 2 2
+ bx + c 2
+ bx + c
Caso ②
Lo que queremos es P ( x) En el supuesto caso de que el grado P ( x) R ( x)
∫ ⎯⎯ → P ( x) ≥ Q ( x ) = C( x ) +
si
que el Grado de dx de Q(x) < P(x) , entonces Dividimos
Q(x) > P(x) → Q( x) → Q( x ) Q( x )
ENTONCES
P( x) R( x )
∫ Q( x )
= ∫ C( x ) + ∫ Q( x )
y una vez hecho esto, vamos a Factorizar Q(x) dividimos en Casos ↓

Factorizar Q(x)

Q( x ) = ( x − x A ) + ( x − xB ) + ( x − xC )+ ...+ ( x − x N ) El denominador tiene solamente factores lineales, ninguno

de los cuales se repite , en este caso la función racional es la
Caso ① P( x ) A B C N suma de fracciones parciales, cada una de las cuales es igual a
= + + + ...+
Q( x) ( x − x A ) ( x − xB ) ( x − xC ) (x − xN ) una constante dividida por el denominador.

El denominador tiene solamente factores

P( x ) A1 A2 A3 Ak
= + + + ...+ lineales, algunos de los cuales se repite , en
( xn )
Caso ②
Q( x ) ( x − x1 )k ( x − x2 ) k − 1 ( x − x3 ) k − 2 x − este caso correspondiéndose por un factor " k "
veces; hay " k " factores parciales de la forma:

P( x ) Ax + B El denominador tiene uno o más factores cuadráticos, ninguno de los cuales se

Caso ③ =
Q( x) ax 2 + bx + c repite , en este caso por cada factor cuadrático, hay una fracción parcial de la forma:

P( x ) A1 x + B1 A2 x + B2 A3 x + B3 Ak x + Bk
= + + + ...+
Caso ④
Q( x ) (
ax + bx + c
2
)
k
(ax 2
+ bx + c )
k −1
(ax 2
+ bx + c )
k −2
( ax 2 + bx + c )
El denominador tiene uno o más factores cuadráticos, alguno de los cuales se repite , en este caso por cada factor
cuadrático repetido " k " veces, vamos atener " k " términos de la forma: ↑

⑤ Integrales Trigonometricas (Racionales)

∫ R(Senx, Cosx)dx (
∫ R Sen x ,Cos x, Senx ⋅ Cosx dx ) ∫ R( Senx, Cos x )Cosx ⋅ dx ④ ∫ R(Cosx, Sen 2 x )Senx ⋅ dx
2 2 2
① ② ③

u = Sen( x ) u = Cos( x)
u = Tg ( x ) ← Cambio
Universal
u = Tg ( x ) x = arcTg(u)
2
du u2 x= arcSen(u) x= arcCos(u)
x = 2arcTg (u ) dx =
2du
dx = Sen2 ( x ) =
1 + u2 1 + u2 1+ u2 du du du du
dx = = dx = − = −
Cos( x) 1 − u2 Sen( x ) 1− u2
1− u 1 u
Cos 2 ( x) = Sen( x) ⋅ Cos( x) =
2
2u
Sen ( x) = Cos( x ) =
1 + u2 1+ u2 1 + u 2
1 + u2 Cos 2 ( x ) = 1 − u2 Sen 2 ( x ) = 1 − u 2

Elaborado por: Eder Nunes

UCV - EECA Matemática II 1° Parcial

Integrales Irracionales
Caso ① Caso ②

∫ x m ⋅ a + bx n ( ) p
dx
∫
( Ax + B )dx
ax 2 + bx + c
1.) p ∈ Z → x = t D[ m,n ] D[m,n] = Mínimo Denominador Común
entre m y n 1.) Factorizar → ax 2 + bx + c , x1 = α ^ x2 = β
m+ 1
a + bx n = t [ ]
y si tiene Raíces entonces, tenemos que:
p ∉ Z→ ∈ Z→
D p
2.) Si
n
D[p] = Denominador de p
ax + bx + c = t ⋅ ( x − α ) o t ⋅ ( x − β )
2

m+ 1 m+ 1 a + bx n a > 0→ ax 2 + bx + c = x a + t
3.) Si ∉ Z→ + p ∈ Z→ = t D [ p] 2.) Si No
n n n tiene
x
D[p] = Denominador de p
Raíces → c > 0→ ax 2 + bx + c = t ⋅ x + c

Método de Sumas Superiores e Inferiores

Una Aproximación al Valor de Integral entre Una Cota de Error " e "cometido al tomar la Aproximación del
[a,b] viene dado por : Valor de la Integral es:
b
I ( f , P) + S ( f , P ) b
I ( f , P) + S ( f , P) S ( f , P) − I ( f , P )
∫ f ( x) ≈
2
e= ∫ f ( x) −
a
2
≤
2
a
(Proporcionan Aproximaciones para Integrales que no poseen Primitiva)

②
(Método Deficiente)
n = Número de Particiones
b n

∫ f ( x) ≈ ∑ f ( X i ) ⋅ ( X i − X i −1 ) donde X = Numero cualquiera del Sub − Intervalo X i ∈ [ X i −1 , X i ]

i
Métodos Numéricos de Integración

a i=1

Regla del Trapezoide

(Método Muy Exacto)
n = Número de Particiones

[( 12) ⋅ f (a) + ( 2) ⋅ f (b)]

a

∫ f ( x) ≈ h ⋅ f ( a + h) + f (a + 2 ⋅ h) + ...+ f ( a + ( n − 1) ⋅ h) ) + 1
b

b− a M ⋅ h2
h=
n
, Si ∃ f ' ' ( x ) en [a , b ] ∧ f ' ' ( x ) ≤ M ; ∀ x ∈ [a , b ] →entonces→ ( Error) = e ≤ ⋅ (b − a )
12
M = Una Cota (Máximo); es decir f''(x) estará acotada por un máximo " M "
Regla de Simpson
(Método Bueno)
n = Número de Particiones (el cual en este caso debe ser un Número PAR )
a
h ⎡
∫ f (x ) ≈ ⋅ f ( a ) + 4 ⋅ f ( a + h) + 2 ⋅ f ( a + 2 ⋅ h) + 4 ⋅ f ( a + 3 ⋅ h ) + ... + 2 ⋅ f (a + ( n − 2) ⋅ h )) + 4 ⋅ f ( a + ( n − 1) ⋅ h) + f (b) ⎤
b
3 ⎣⎢ alternado ⎦⎥
NOTA (Alternando) : El 4 y el 2 se alternan de tal forma que, el 4 ocupará los lugares Pares y el 2 los Impares.
b− a M ⋅ h4
h=
n
, Si ∃ f IV ( x) en [a , b] ∧ f IV ( x) ≤ M ; ∀ x ∈ [a , b] →entonces→ ( Error ) = e ≤
180
⋅ (b − a )
IV
M = Una Cota (Máximo); es decir f (x) estará acotada por un máximo " M "

Elaborado por: Eder Nunes