Teorema de Taylor

Ir a la navegaciónIr a la búsqueda

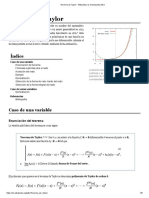
La función exponencial {\displaystyle y={\text{e}}^{x}}{\displaystyle

y={\text{e}}^{x}} (línea roja continua) y su aproximación mediante un polinomio de
Taylor alrededor del origen de coordenadas (línea verde discontinua)
En cálculo diferencial, el teorema de Taylor, recibe su nombre del matemático
británico, Brook Taylor, quien lo enunció con mayor generalidad en 1712, aunque
previamente James Gregory lo había descubierto en 1671.1 Este teorema permite
obtener aproximaciones polinómicas de una función en un entorno de cierto punto en
el que la función sea diferenciable. Además el teorema permite acotar el error
obtenido mediante dicha estimación.

Índice
1 Caso de una variable
1.1 Enunciado del teorema
1.2 Fórmulas explícitas para el resto
1.3 Acotación del resto
1.4 Ejemplo
1.5 Demostración
1.6 Obtención de la forma de valor medio del resto
1.7 Obtención de la forma integral del resto
2 Caso de varias variables
2.1 Demostración
3 Referencias
4 Bibliografía
Caso de una variable
Enunciado del teorema
La versión más básica del teorema es como sigue:

Teorema de Taylor.234 Sea k ≥ 1 un entero y sea f : R → R una función diferenciable

k veces en el punto a ∈ R. Entonces existe una función hk : R → R tal que

(1){\displaystyle f(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac

{f^{(k)}(a)}{k!}}(x-a)^{k}+h_{k}(x)(x-a)^{k},}{\displaystyle f(x)=f(a)+f'(a)(x-a)+
{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+h_{k}(x)(x-
a)^{k},}

con {\displaystyle \quad \lim _{x\to a}h_{k}(x)=0}{\displaystyle \quad \lim _{x\to

a}h_{k}(x)=0}. Esta es la llamada forma de Peano del resto.

El polinomio que aparece en el teorema de Taylor,

{\displaystyle P_{k}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +

{\frac {f^{(k)}(a)}{k!}}(x-a)^{k},}{\displaystyle P_{k}(x)=f(a)+f'(a)(x-a)+{\frac
{f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k},}
se denomina polinomio de Taylor de orden k de la función f en el punto a. El
polinomio de Taylor es el único polinomio que «mejor aproxima la función en forma
asintótica», en el sentido de que si existe una función hk : R → R y un polinomio p
de orden k tal que

{\displaystyle f(x)=p(x)+h_{k}(x)(x-a)^{k},\quad \lim _{x\to a}h_{k}(x)=0,}

{\displaystyle f(x)=p(x)+h_{k}(x)(x-a)^{k},\quad \lim _{x\to a}h_{k}(x)=0,}
entonces p = Pk. El teorema de Taylor describe el comportamiento asintótico del
término del resto

{\displaystyle \ R_{k}(x)=f(x)-P_{k}(x),}{\displaystyle \ R_{k}(x)=f(x)-P_{k}(x),}

el cual es el error de aproximación cuando se aproxima f con su polinomio de
Taylor. Utilizando la notación o el teorema de Taylor se puede expresar de la
siguiente forma:

{\displaystyle R_{k}(x)=o(|x-a|^{k}),\quad x\to a.}{\displaystyle R_{k}(x)=o(|x-a|

^{k}),\quad x\to a.}
Fórmulas explícitas para el resto
Existen diferentes formas de expresar {\displaystyle R_{k}(x)}{\displaystyle R_{k}
(x)} que se mencionan a continuación:

Forma de valor medio del resto. Sea f : R → R, diferenciable k + 1 veces en el

intervalo abierto con f (k) continua en el intervalo cerrado entre a y x. Entonces

(2a){\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi _{L})}{(k+1)!}}(x-a)^{k+1}}

{\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi _{L})}{(k+1)!}}(x-a)^{k+1}}

para algún número real ξL entre a y x. Esta es la forma de Lagrange5 del resto.
Similarmente,

(2b){\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi _{C})}{k!}}(x-\xi _{C})^{k}(x-a)}

{\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi _{C})}{k!}}(x-\xi _{C})^{k}(x-a)}

para algún número real ξC entre a y x. Esta es la forma de Cauchy6 del resto.

Usualmente, esta refinación del teorema de Taylor, se demuestra con el teorema del
valor medio, de ahí su nombre. También se pueden hallar expresiones similares. Por
ejemplo, si G(t) es continua en el intervalo cerrado y diferenciable con derivadas
no nulas en el intervalo abierto entre a y x, entonces

{\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi )}{k!}}(x-\xi )^{k}{\frac {G(x)-G(a)}

{G'(\xi )}}}{\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi )}{k!}}(x-\xi )^{k}{\frac
{G(x)-G(a)}{G'(\xi )}}}
para algún número ξ entre a y x. Esta versión generaliza las formas de Lagrange y
Cauchy del resto, que son tomadas como casos especiales, y se demuestran usando el
teorema del valor medio de Cauchy.

En el caso de la forma integral del resto, se requieren conceptos de la teoría

integral de Lebesgue para una generalidad completa. Sin embargo, se mantiene el
concepto que provee la integral de Riemann donde la derivada (k + 1)-ésima de f es
continua en el intervalo cerrado [a,x].

Forma integral del resto.7 Sea f (k), continua absolutamente en el intervalo

cerrado entre a y x. Entonces

(3){\displaystyle R_{k}(x)=\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt.}

{\displaystyle R_{k}(x)=\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt.}

Debido a la continuidad absoluta de f (k) en el intervalo cerrado entre a y x su

derivada f (k+1) existe como una función L1, y el resultado puede probarse con un
cálculo formal usando el teorema fundamental del cálculo e integración por partes.

Para algunas funciones {\displaystyle f(x)}f(x), se puede probar que el resto,

{\displaystyle R_{n}(f)}{\displaystyle R_{n}(f)}, se aproxima a cero cuando
{\displaystyle n}n se acerca al infinito; dichas funciones pueden ser expresadas
como series de Taylor en un entorno reducido alrededor de un punto {\displaystyle
a}a y son denominadas funciones analíticas.

El teorema de Taylor con {\displaystyle R_{n}(f)}{\displaystyle R_{n}(f)} expresado

de la segunda forma es también válido si la función {\displaystyle f}f tiene
números complejos o valores vectoriales. Además existe una variación del teorema de
Taylor para funciones con múltiples variables.

Acotación del resto

Suele ser muy útil en la práctica acotar el término del resto de la aproximación de
Taylor, en lugar de tener la fórmula exacta de este. Suponiendo que f es
continuamente diferenciable {\displaystyle k+1}{\displaystyle k+1} veces en un
intervalo {\displaystyle I}I que contiene a {\displaystyle a}a. Suponemos que hay
constantes {\displaystyle q}q y {\displaystyle Q}Q tal que

{\displaystyle q\leq f^{(k+1)}(x)\leq Q}{\displaystyle q\leq f^{(k+1)}(x)\leq Q}

en el intervalo {\displaystyle I}I. Entonces el término del resto satisface la
desigualdad8

{\displaystyle q{\frac {(x-a)^{k+1}}{(k+1)!}}\leq R_{k}(x)\leq Q{\frac {(x-

a)^{k+1}}{(k+1)!}}.}{\displaystyle q{\frac {(x-a)^{k+1}}{(k+1)!}}\leq R_{k}(x)\leq
Q{\frac {(x-a)^{k+1}}{(k+1)!}}.}
Si {\displaystyle x>a}{\displaystyle x>a}, y similarmente si {\displaystyle x<a}
{\displaystyle x<a}. Esta es una consecuencia simple de la forma de Lagrange del
resto. En particular, si

{\displaystyle |f^{(k+1)}(x)|\leq M}{\displaystyle |f^{(k+1)}(x)|\leq M}

sobre un intervalo {\displaystyle I=(a-r,a+r)}{\displaystyle I=(a-r,a+r)} con algún
{\displaystyle r>0}{\displaystyle r>0} , entonces

{\displaystyle |R_{k}(x)|\leq M{\frac {|x-a|^{k+1}}{(k+1)!}}\leq M{\frac {r^{k+1}}

{(k+1)!}}}{\displaystyle |R_{k}(x)|\leq M{\frac {|x-a|^{k+1}}{(k+1)!}}\leq M{\frac
{r^{k+1}}{(k+1)!}}}
para todo {\displaystyle x\in (a-r,a+r)}{\displaystyle x\in (a-r,a+r)}. A la
segunda desigualdad se la llama acotación uniforme, porque permanece uniformemente
para todo x sobre el intervalo {\displaystyle (a-r,a+r)}{\displaystyle (a-r,a+r)}.

Ejemplo

Aproximación de ex (azul) por su polinomio de Taylor Pk de orden k = 1, …, 7

centrado en x = 0 (rojo)
Suponiendo que se desea aproximar la función f (x) = ex en el intervalo [−1,1] con
un error no mayor a 10−5. Este ejemplo necesita que se conozcan las siguientes
propiedades de la función exponencial:

(*){\displaystyle \qquad e^{0}=1,\qquad {\frac {d}{dx}}e^{x}=e^{x},\qquad

e^{x}>0,\qquad x\in \mathbb {R} .}{\displaystyle \qquad e^{0}=1,\qquad {\frac {d}
{dx}}e^{x}=e^{x},\qquad e^{x}>0,\qquad x\in \mathbb {R} .}

De estas propiedades se tiene que f (k)(x) = ex para todo k, y en particular, f (k)

(0) = 1. Entonces el polinomio de Taylor de orden k de f en 0 y su resto bajo la
forma de Lagrange son:

{\displaystyle P_{k}(x)=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{k}}{k!}},\qquad

R_{k}(x)={\frac {e^{\xi }}{(k+1)!}}x^{k+1},}{\displaystyle P_{k}(x)=1+x+{\frac
{x^{2}}{2!}}+\cdots +{\frac {x^{k}}{k!}},\qquad R_{k}(x)={\frac {e^{\xi }}
{(k+1)!}}x^{k+1},}
donde ξ es algún número entre 0 y x. Ya que ex es creciente (*), podemos usar
simplemente que ex ≤ 1 para x ∈ [−1, 0] para acotar el resto sobre el subintervalo
[−1, 0]. Para obtener una cota superior para el resto en [0,1], usamos la propiedad
eξ < ex para 0<ξ<x para acotar

{\displaystyle e^{x}=1+x+{\frac {e^{\xi }}{2}}x^{2}<1+x+{\frac {e^{x}}

{2}}x^{2},\qquad 0<x\leq 1}{\displaystyle e^{x}=1+x+{\frac {e^{\xi }}{2}}x^{2}<1+x+
{\frac {e^{x}}{2}}x^{2},\qquad 0<x\leq 1}
usando la expansión de Taylor de segundo orden. Entonces resolvemos ex para deducir
que

{\displaystyle e^{x}\leq {\frac {1+x}{1-{\frac {x^{2}}{2}}}}=2{\frac {1+x}{2-

x^{2}}}\leq 4,\qquad 0\leq x\leq 1}{\displaystyle e^{x}\leq {\frac {1+x}{1-{\frac
{x^{2}}{2}}}}=2{\frac {1+x}{2-x^{2}}}\leq 4,\qquad 0\leq x\leq 1}
simplemente maximizando el numerador y minimizando el denominador. Combinando estas
acotaciones para ex vemos que

{\displaystyle |R_{k}(x)|\leq {\frac {4|x|^{k+1}}{(k+1)!}}\leq {\frac {4}

{(k+1)!}},\qquad -1\leq x\leq 1,}{\displaystyle |R_{k}(x)|\leq {\frac {4|x|^{k+1}}
{(k+1)!}}\leq {\frac {4}{(k+1)!}},\qquad -1\leq x\leq 1,}
así se alcanza la precisión requerida, donde

{\displaystyle {\frac {4}{(k+1)!}}<10^{-5}\quad \Longleftrightarrow \quad 4\cdot

10^{5}<(k+1)!\quad \Longleftrightarrow \quad k\geq 9.}{\displaystyle {\frac {4}
{(k+1)!}}<10^{-5}\quad \Longleftrightarrow \quad 4\cdot 10^{5}<(k+1)!\quad
\Longleftrightarrow \quad k\geq 9.}
(ver factorial o calcular manualmente los valores 9!=362 880 y 10!=3 628 800). Como
conclusión, el teorema de Taylor permite la aproximación

{\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{9}}{9!}}+R_{9}

(x),\qquad |R_{9}(x)|<10^{-5},\qquad -1\leq x\leq 1.}{\displaystyle e^{x}=1+x+
{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{9}}{9!}}+R_{9}(x),\qquad |R_{9}(x)|<10^{-
5},\qquad -1\leq x\leq 1.}
Luego, esta aproximación nos da la expresión decimal e ≈ 2,71828, correcta hasta
cinco dígitos decimales.

Demostración
Sea9

{\displaystyle h_{k}(x)={\begin{cases}{\frac {f(x)-P(x)}{(x-a)^{k}}}&x\not

=a\\0&x=a\end{cases}}}{\displaystyle h_{k}(x)={\begin{cases}{\frac {f(x)-P(x)}{(x-
a)^{k}}}&x\not =a\\0&x=a\end{cases}}}
donde, como dice en el enunciado del teorema de Taylor,

{\displaystyle P(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac

{f^{(k)}(a)}{k!}}(x-a)^{k}.}{\displaystyle P(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}
{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}.}
Es suficiente mostrar que

{\displaystyle \lim _{x\to a}h_{k}(x)=0.}{\displaystyle \lim _{x\to a}h_{k}(x)=0.}