TEOREMA DE VALOR MEDIO

El teorema de valor medio (de Lagrange), teorema de los incrementos finitos, teorema de
Bonnet-Lagrange o teoría del punto medio es una propiedad de las funciones derivables
en un intervalo. Algunos matemáticos consideran que este teorema es el más importante
del cálculo (véase también el teorema fundamental del cálculo integral). El teorema de
valor medio puede usarse para demostrar el teorema de Taylor y el teorema de Rolle, ya
que ambos son un caso especial.
Empezamos por recordar el Teorema del Valor Medio en el caso de funciones reales de una
variable:
Sea f : [a,b] −→ R una función continua, derivable en (a,b); existe un punto c ∈ (a,b) tal que

f(b) − f(a) = f0(c)(b – a) o

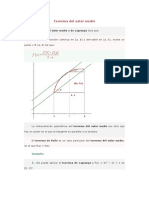
Geométricamente esto significa:
Que hay un punto del intervalo en el que la recta tangente a la gráfica de f tiene la misma
pendiente que la recta secante que pasa por los puntos (a,f (a)) y (b,f (b))

f (b)

α
f (a)
α

a c b

Otro ejemplo: Si f(t) representa la longitud que hemos recorrido hasta el instante t , la
velocidad media entre , y la velocidad en un instante t es f’(t).
Según el teorema del valor medio, si la velocidad media es de 60 km/h, en algún instante
entre a y b hemos circulado exactamente a 60 km/h.

En el caso de funciones vectoriales, F: [a, b] −→ Rm, (m > 1) parece fácil generalizar el

teorema de teorema: podríamos estudiar si existe un punto c en (a, b) en el que la recta
tangente a la imagen de F sea paralelo a la recta que pasa por F(a) y por F(b).
El dibujo parece convincente, sin embargo el resultado no es cierto:
Consideremos la función F(x) = (x2,x3) definida en el intervalo [0,1]. Buscamos un punto x
∈ [0,1] que verifique

F (1) − F(0) = F 0(x)(1 − 0)

Donde F(1) = (1,1), F(0) = (0,0), y F 0(x) = (2x,3x2). La ecuación anterior es realmente un
sistema de dos ecuaciones, una por cada coordenada

1−0=2 x
{1−0=3 x 2

Que no tiene solución, ya que tendría que ser x = 1/2 y x = 1/√3 a l vez.
En cambio, el teorema si se puede generalizar al caso de funciones reales de varias
variables, y es lo que vamos a demostrar en este capítulo. Utilizaremos en el teorema el
segmento entre dos puntos: dados x e y en Rn, el segmento
[x,y] de x a y es el conjunto de puntos
[x,y] = {x + t(y − x); t ∈ [0,1]} = {ty + (1 − t)x; t ∈ [0,1]}

Teorema (Teorema del Valor Medio en Rn).

Sea U un conjunto abierto de Rn, y f : U :−→ R una función diferenciable en todo U. Sean
x e y dos puntos de U tales que el segmento [x,y] este totalmente contenido en U.
entonces existe un punto z ∈ [x,y] tal que
f(y) − f(x) = df(z)(y − x) =< ∇ f(z),y − x >
Escribimos el segmento [x, y] como imagen de una función:

Sea Φ : [0, 1] → Rm, definida por Φ(t) = x + t(y − x). Φ es continua,

su imagen es el segmento [x, y], y es diferenciable,

Con dΦ(t) = (y − x) en cualquier punto t ∈ [0, 1].
Demostración

Para estudiar el comportamiento de f sobre el segmento, consideramos la composición de

las dos funciones, g(t) = f ◦ Φ(t). Esta función g es ahora una función de [0, 1] en R ,
continua y derivable, por lo que podemos aplicar el teorema del Valor Medio para ese tipo
de funciones, y tenemos
g(1) − g(0) = g 0 (c)(1 − 0) = g 0 (c)
donde c es algún punto en [0, 1].
Ahora bien, g(1) = f(Φ(1)) = f(y), g(0) = f(Φ(0)) = f(x), y aplicando la regla de la cadena

dg(c) = df(Φ(c)) ◦ dΦ(c)

es decir, escribiendo la igualdad entre las matrices correspondientes
g 0 (c) =< ∇f(Φ(c)), y − x >
Sustituyendo en la ecuación anterior queda
f(y) − f(x) =< ∇f(Φ(c)), y − x > donde Φ(c) = z es un punto de [x, y], lo que prueba el
resultado.
Como hemos visto por el ejemplo antes del teorema, no se puede generalizar al caso de
funciones vectoriales, con valores en Rm . En este caso, solo se puede aplicar a cada
componente por separado: si F: U: → en Rm es diferenciable, F (f1,. . ., fm), y [x, y] ⊆ U,
entonces para cada componente fj existirá un punto zj ∈ [x, y] tal que
fj (y) − fj (x) = dfj (zj )(y − x) =< ∇fj (zj ), y − x >
pero no se puede asegurar que sea el mismo punto zj para todas las componentes de f.
Aun así, esto es suficiente para demostrar otra generalización a funciones de varias
variables de un resultado bien conocido de las funciones reales de una variable real: si
una función derivable tiene derivada cero en un intervalo, entonces es constante en él.