Documentos de Académico
Documentos de Profesional
Documentos de Cultura
Derivación Bajo El Signo de Integral
Derivación Bajo El Signo de Integral
Cargado por
Andres FernandezDerechos de autor
Formatos disponibles
Compartir este documento
Compartir o incrustar documentos
¿Le pareció útil este documento?
¿Este contenido es inapropiado?
Denunciar este documentoCopyright:
Formatos disponibles
Derivación Bajo El Signo de Integral
Derivación Bajo El Signo de Integral
Cargado por
Andres FernandezCopyright:
Formatos disponibles
Derivaci on bajo la integral
Jose Alfredo Ca nizo Rinc on
1 de julio, 2004
1. Introducci on
Estas notas contienen una presentaci on de los teoremas usuales de derivaci on ba-
jo la integral y la regla de Leibniz. El objetivo es enunciar con precisi on y demostrar
un resultado que se suele dar por supuesto aunque no aparezca tan com unmente en
los libros de an alisis, y que lo hace rara vez enunciado con precisi on.
Pueden consultarse versiones mas generales que incluyen condiciones necesarias
y sucientes para intercambiar integral y derivada en [2]. Un curioso error causado
por el uso injusticado de dicho intercambio por parte de Cauchy esta recogido en
[1].
La regla de derivacion bajo la integral es la siguiente igualdad:
d
d
f(x, ) dx =
(x, ) dx , (1)
que dice esencialmente que cuando se deriva una integral respecto de un par ametro
distinto a la variable en la que se integra, derivada e integral pueden intercambiarse.
Seg un el sentido que se quiera dar a la integral y a la derivada, este resultado requiere
distintas condiciones sobre la funcion f. A veces esta regla se llama tambien regla de
Leibniz, pero es m as com un reservar el nombre de regla de Leibniz para la siguiente:
d
d
g()
t
0
f(x, ) dx = f(g(), ) g
() +
g()
t
0
f
(x, ) dx, (2)
que tambien se demuestra en estos apuntes.
2. Resultado clasico
Desde un punto de vista cl asico se puede intentar entender lo anterior en terminos
de la integral de Riemann y la derivada cl asica. Las condiciones naturales para
plantearlo parecen ser las siguientes a primera vista: si f es una funcion real que
depende de dos variables x, , necesitamos que sea Riemann integrable en x para
cualquier jo para que el miembro de la izquierda tenga sentido, y tambien que
1
la derivada con respecto a exista para todo x jo para dar sentido al miembro
derecho. Necesitamos tambien que dicha derivada sea integrable. Que se obtiene al
intentar derivar
f(x, ) d?. Para h peque no,
1
h
f(x, + h) dx
f(x, ) dx
1
h
(f(x, + h) f(x, )) dx , (3)
y necesitamos pasar al lmite en esta ultima integral. Esto puede hacerse cuando,
jado , el lmite cuando h 0 dentro de dicha integral (que es, puntualmente,
df
d
(x, )) sea uniforme en x. Podemos escribir, gracias al teorema del valor medio,
para cierto
x
en el intervalo [, + h]:
1
h
(f(x, + h) f(x, )) =
f
(x,
x
), (4)
as que bastara si
(x,
x
)
f
(x, )
(la diferencia entre este valor y el lmite
puntual) fuese peque no independientemente de x. Una condicion que asegura esto y
que es f acil de enunciar es que
f
sea uniformemente continua en sus dos variables. En
un dominio compacto, es suciente que sea continua. Esta ultima condici on incluye
a la de que la parcial de f sea integrable en , as que esto nos da el siguiente
resultado, que aparece tambien en [3]:
Teorema 2.1 (Version cl asica). Sean I, J intervalos reales no triviales, con I com-
pacto y J abierto. Sea f : I J R una funcion tal que
f(, ) es integrable en I para todo J
f(x, ) es derivable en J para todo x I.
Supongamos ademas que
f
es continua en I J. Entonces,
f
(, ) es integrable para todo J
I
f(x, ) dx es derivable con derivada continua en J para todo x I
y se cumple la regla de derivacion bajo la integral,
d
d
I
f(x, ) dx =
I
f
(x, ) dx J (5)
Observacion 2.2. Todas las integrales que aparecen en este teorema son integrales
en el sentido de Riemann.
Observacion 2.3. Las condiciones sobre los intervalos I, J son tecnicas: se exige I
compacto porque la integral de Riemann est a denida s olo sobre intervalos compac-
tos (aunque es posible extender el teorema para la integral de Riemann impropia);
y se exige J abierto para evitar preocuparse de la derivada en los extremos, aunque
el resultado es v alido para cualquier intervalo J.
2
Demostracion. Fijemos J, y demostremos que existe el lmite de la derivada en
y es el que se pide. Sea > 0. Tomemos d > 0 sucientemente peque no para que
[d, +d] J. Como
f
es uniformemente continua en I [d, +d], podemos
elegir 0 < d tal que
(x,
1
)
f
(x,
2
)
|I|
x I,
1
,
2
[ d, + d]
tales que |
1
2
| (6)
Tomemos cualquier h R con |h| , h = 0. El teorema del valor medio asegura
que para cada x I hay un cierto
x
en el intervalo delimitado por y + h tal
que
1
h
(f(x, + h) f(x, )) =
f
(x,
x
)
y esto nos permite probar que el lmite que dene la derivada de f con respecto a
es uniforme:
1
h
(f(x, + h) f(x, ))
f
(x, )
(x,
x
)
f
(x, )
(6)
|I|
.
Entonces, como
f
es tambien integrable en I (ya que es continua), estamos en
condici on de probar que el lmite de la derivada existe y es el esperado:
1
h
I
f(x, + h) dx
I
f(x, ) dx
I
f
(x, ) dx
1
h
(f(x, + h) dx f(x, ))
f
(x, )
dx
1
h
(f(x, + h) dx f(x, ))
f
(x, )
dx
|I|
dx = .
Por denici on de derivada se cumple (7).
Falta comprobar que la derivada es continua. Sea J cualquiera, y dado > 0
elijamos d, > 0 igual que en (6). Entonces para h R, |h| < ,
I
f
(x, ) dx
I
f
(x, + h) dx
(x, )
f
(x, + h)
dx
|I|
dx = ,
luego la derivada es efectivamente continua.
3
2.1. Regla de derivaci on de Leibniz
Lema 2.4. Sean I, J intervalos reales no triviales, con I compacto y J abierto. Sea
f : I J R una funcion continua tal que f(x, ) es derivable en J para todo x I.
Supongamos ademas que
f
es continua en I J.
Fijemos t
0
I. Entonces, la funcion
G : I J R
(t, )
t
t
0
f(x, ) dx
es derivable en el sentido de Frechet en cualquier punto del interior de I J.
Demostracion. Calculemos las derivadas parciales de G y veamos que son conti-
nuas; entonces, resultados usuales prueban que G es Frechet derivable en los puntos
interiores. El teorema fundamental del c alculo dice que para (t, ) I J,
d
dt
t
t
0
f(x, ) dx = f(t, ),
una funci on continua. Por otro lado, la funci on f est a en las hip otesis del teorema
2.1 en cualquier conjunto [t
0
, t] J con t I, luego G tiene derivada parcial con
respecto a y
d
d
t
t
0
f(x, ) dx =
t
t
0
f
(x, ) dx
(observar que se cumple sin importar si t es mayor o menor que t
0
). Veamos que
esta funcion es continua en I J. Sea (t, ) I J, y > 0. Elijamos > 0 tal que
[ , + ] J y para todo h con |h| < ,
(x, ) dx
f
(x, + h)
dx <
2
(sabemos que esto puede hacerse; ver nal de la demostraci on de 2.1). Elijamos
tambien una cota M > 0 de f en el compacto I [ , + ]. Entonces, para
h
1
, h
2
R tales que |h
1
|
2M
, |h
2
| ,
t
t
0
f
(x, ) dx
t+h
1
t
0
f
(x, + h
2
) dx
t
t
0
(x, ) dx
f
(x, + h
2
)
dx +
t
t+h
1
f
(x, + h
2
) dx
(x, ) dx
f
(x, + h
2
)
dx +|h
1
| M
2
+
2
=
4
Corolario 2.5 (Regla de derivaci on de Leibniz). Sean I, J intervalos reales no
triviales, con I compacto y J abierto. Sea f : I J R una funcion continua en
I J tal que f(x, ) es derivable en J para todo x I. Supongamos ademas que
f
es continua en I J.
Sea t
0
I y g : J I una funcion derivable. Entonces,
f
(, ) es integrable para todo J
g()
t
0
f(x, ) dx es derivable en J para todo x I
y se cumple la regla de derivacion de Leibniz,
d
d
g()
t
0
f(x, ) dx = f(g(), ) g
() +
g()
t
0
f
(x, ) dx J (7)
Demostracion. La funcion
g()
t
0
f(x, ) dx no es mas que la composici on de la
funci on G del lema anterior con la funcion
F : J I J
(g(), ).
La regla de la cadena usual demuestra entonces el resultado.
3. Version para la integral de Lebesgue
3.1. Primera versi on
La principal dicultad en la demostraci on anterior es justicar el paso al lmite
de la integral. La funci on es derivable, y el lmite usual converge puntualmente a su
derivada, pero justica eso la convergencia de las integrales?. No en general, desde
luego. Una de las ventajas que siempre se mencionan de la integral de Lebesgue
sobre la de Riemann es que los teoremas de convergencia son mas generales. Si
consideramos las integrales anteriores como integrales de Lebesgue podemos intentar
aplicar el teorema de la convergencia dominada en lugar de buscar una convergencia
uniforme. De hecho, teniendo en cuenta la convergencia puntual dentro de la integral
en (3) y la igualdad (4), bastara con exigir que
(x, )
m(x) para todo (x, ) y
cierta funcion m integrable.
Esta es la idea fundamental; el enunciado del resultado
y su demostraci on son consecuencias de ella. Ni siquiera hace falta usar el teorema
del valor medio, con lo que la diferenciabilidad que se requiere es ligeramente mas
debil: en su lugar, podemos escribir
1
h
(f(x, + h) f(x, )) =
1
h
+h
(x, s) ds,
lo que nos permitir a probar que la convergencia es dominada de forma muy parecida.
5
Dado que la integral de Lebesgue se dene en circunstancias m as generales es
natural enunciar el teorema integrando sobre un espacio de medida cualquiera en
lugar de un intervalo. El resultado es el siguiente:
Teorema 3.1. Sea J un intervalo real y (, A, ) un espacio de medida. Sea f :
J R tal que
1. f(x, ) es absolutamente continua en J para casi todo x
2. Para todo J, existe
f
(x, ) para casi todo x
3. f(, ) es integrable en para todo J.
En particular, estas condiciones implican que
f
x
(x, ) esta denida en casi todo
(x, ) J. Supongamos que existe una funcion m, integrable en , tal que
(x, )
m(x) (x, ) J donde
f
x
(x, ) este denida. (8)
Entonces
f
(, ) es integrable en para todo J,
f(x, ) dx es derivable en J
y se cumple
d
d
f(x, ) dx =
(x, ) dx J.
Observacion 3.2. Si vemos f como una funci on distinta para cada valor del parame-
tro , la derivabilidad que se le pide a f signica que esta funci on cambia de forma
derivable con en casi todos sus puntos. Las dos primeras condiciones sobre f se
cumplen en particular si, para todo x , f(x, ) es derivable con derivada integra-
ble en J. Observese tambien que la condici on 1 del teorema implica que para casi
todo , existe
f
para casi todo x, lo cual es ligeramente mas debil que la condici on
2.
Demostracion. Fijemos J cualquiera. La condici on 2 sobre f asegura que
f
(x, ) existe en casi todo x , y dado que
f
(x, ) = lm
h0
1
h
(f(x, + h) f(x, )) para casi todo x ,
dicha parcial es lmite puntual c.p.d. de funciones medibles en y es por tanto
medible en . Su cota m asegura que es ademas integrable en . Podemos usar el
6
teorema fundamental del calculo para la integral de Lebesgue para cualquier x para
el que f(x, ) sea absolutamente continua (por la condicion 1, para casi todo x):
1
h
(f(x, + h) f(x, ))
=
1
h
+h
(x, s) ds
1
h
+h
(x, s)
ds
1
h
+h
m(x) ds
= m(x),
y vemos que la convergencia puntual esta dominada por m. Por el teorema de la
convergencia dominada,
d
d
f(x, ) dx
= lm
h0
1
h
(f(x, + h) f(x, )) dx
TCD
=
(x, ) dx J.
3.2. Segunda versi on
Si en lugar de buscar la derivada en todo punto usamos el concepto de derivada
que va asociado de forma natural a la integral de Lebesgue por medio del teorema
fundamental del c alculo, el enunciado de derivacion bajo la integral se convierte
en un enunciado sobre el intercambio del orden de las integrales. En este caso el
resultado es ligeramente mas debil, como lo son tambien las condiciones. En esencia,
podemos quitar la condici on 2 del teorema anterior si estamos dispuestos a aceptar
derivabilidad s olo en casi todo punto:
Teorema 3.3. Sea J un intervalo real (en el que usaremos siempre la medida usual
de Lebesgue) y (, A, ) un espacio de medida. Sea f : J R tal que
f(x, ) es absolutamente continua en J para casi todo x
f(, ) es medible en para casi todo J, y es integrable para al menos un
cierto
0
J.
Estas condiciones implican que
f
x
(x, ) esta denida en casi todo (x, ) J.
Supongamos que existe una funcion m, integrable en , tal que
(x, )
m(x) (x, ) J donde
f
x
(x, ) este denida. (9)
Entonces
f(, ) es integrable para todo J,
7
f
es integrable en
J para cualquier
J J compacto (en particular, es
integrable en x para casi todo ),
f(x, ) dx es absolutamente continua en J
y se cumple
d
d
f(x, ) dx =
(x, ) dx p.c.t. J.
Observacion 3.4. Las integrales del teorema anterior se entienden en el sentido de
Lebesgue. Notemos que en este caso la ultima igualdad se tiene s olo en casi todo
punto, a diferencia de los teoremas anteriores.
Observacion 3.5. La condici on (11) puede sustituirse por la siguiente condicion m as
debil:
f
(x, ) es integrable en cualquier
J con
J J compacto.
La demostraci on puede hacerse de la misma forma, ya que (11) s olo se usa para de-
ducir precisamente esto. No he incluido esta condicion en el enunciado simplemente
porque es menos com un encontrarla en los libros de an alisis.
Lema 3.6. Sea J un intervalo real y (, A, ) un espacio de medida. Sea f : J
R tal que
f(, ) es medible para casi todo J jo
f(x, ) es continua para casi todo x jo
Entonces f es medible en J.
Demostracion. Para hacer la demostraci on podemos suponer que J = [a, b], ya que
el que f sea medible en J equivale a que lo sea en en todo
J con
J J un
subintervalo compacto.
Dado n natural, dividimos el intervalo J = [a, b] en n intervalos iguales
J
i
n
= [a +
i 1
n
(b a), a +
i
n
(b a)[ para i = 1, . . . , n 1
J
n
n
= [a +
n 1
n
(b a), b]
y elegimos puntos
i
n
J
i
n
tales que f(,
i
n
) es medible. Denimos la funcion f
n
:
J R como
f
n
(x, ) = f(x,
i
n
) J
i
n
que es medible en J porque lo es en cada J
i
n
. La sucesi on de funciones f
n
converge puntualmente a f en casi todo punto de J (de hecho, converge en todo
punto (x, ) tal que f(x, ) es continua), luego f es medible.
8
Demostracion del teorema. Donde
f
est a denida,
f
(x, ) = lm
h0
1
h
(f(x, + h) f(x, )) ,
un lmite puntual de funciones medibles en J (por el lema anterior), as que
f
es medible en J. La cota (11) nos permite asegurar que
f
es integrable en
J para cualquier
J compacto contenido en J. Sea J. Por el teorema de
Fubini podemos calcular sus integrales iteradas en cualquier orden en el conjunto
[,
0
] y obtener que
(x, s) dx ds =
0
f
(x, s) ds dx. (10)
Para cualquier x para el que f(x, ) es absolutamente continua (en particular,
para casi todo x ) el teorema fundamental del calculo nos dice que
0
f
(x, s) ds = f(x, ) f(x,
0
).
Tanto el miembro izquierdo como f(x,
0
) son integrables en , luego f(x, ) es
integrable en para todo J y deducimos de (10) que
(x, s) dx ds =
f(x, ) dx
f(x,
0
) dx J
De nuevo por el teorema fundamental del c alculo, esto es equivalente a que
(x, s) dx
sea absolutamente continua y que se cumpla
d
d
f(x, ) dx =
(x, ) dx para casi todo J
3.3. Regla de derivaci on de Leibniz, segunda versi on
Aqu incluyo una versi on un tanto incompleta de la regla de Leibniz que exige
condiciones m as debiles sobre la funci on (de hecho, las mismas que las del teorema
anterior). Es incompleta porque no incluye una funci on cualquiera en los lmites de
la integral. Sin embargo, la he incluido porque me resultaba util en otro contexto.
La demostraci on es directa: no usa la derivaci on bajo la integral como en el caso
cl asico, sino que m as bien generaliza la forma de la prueba anterior. No se si es
posible obtener un resultado del tipo del lema 2.4 ni que tipo de regularidad tiene
la funcion G denida en dicho lema en este caso.
Teorema 3.7 (Regla de derivacion de Leibniz, segunda versi on). Sea J un intervalo
real no trivial. Sea f : J J R una funcion tal que
9
f(, ) es medible en J para casi todo J, y es integrable para al menos un
cierto
0
J.
f(x, ) es absolutamente continua en J para casi todo x J.
Estas condiciones implican que
f
x
(x, ) esta denida en casi todo (x, ) J J.
Supongamos que existe una funcion m, integrable en J, tal que
(x, )
m(x) (x, ) J J donde
f
x
(x, ) este denida. (11)
Sea t
0
J. Entonces,
f(, ) es integrable para todo J,
f
es integrable en J
J para cualquier
J J compacto (en particular, es
integrable en x para casi todo ),
t
0
f(x, ) dx es absolutamente continua en J,
y se cumple la regla de derivacion bajo la integral,
d
d
t
0
f(x, ) dx = f(, ) +
t
0
f
(x, ) dx p.c.t. J. (12)
Demostracion del teorema. Todas las armaciones salvo la ultima son parte del teo-
rema 3.3. Probar que
t
0
f(x, ) dx es absolutamente continua y que su derivada
es la que se dice es equivalente, por el teorema fundamental del c alculo, a probar
la correspondiente igualdad integral. Para cualquier t
1
I, integremos el segun-
do termino de la suma en (12) (que es integrable gracias al segundo punto de la
conclusi on y al teorema de Fubini) entre t
0
y t
1
:
t
1
t
0
t
0
f
(s, ) ds d =
t
1
t
0
t
1
s
f
(s, ) dds =
t
1
t
0
(f(s, t
1
) f(s, s)) ds,
donde en el primer paso hemos cambiado el orden de integraci on teniendo en cuenta
el conjunto en el que se integra. Esta aplicaci on del teorema de Fubini prueba que
t
1
s
f
(s, ) d es integrable en s, y como f(s, t
1
) es integrable en s, la igualdad
t
1
s
f
(s, ) d = f(s, t
1
) f(s, s)
prueba que f(s, s) es integrable en s. Podemos entonces integrar el miembro derecho
de (12) y obtener
t
1
t
0
f(, ) d +
t
1
t
0
t
0
f
(s, ) ds d
=
t
1
t
0
f(, ) d +
t
1
t
0
(f(s, t
1
) f(s, s)) ds =
t
1
t
0
f(s, t
1
) ds.
Esta es la forma integral de la armaci on (12), que se obtiene derivando respecto a
t
1
los miembros primero y ultimo de esta igualdad.
10
4. Sobre este texto
Para comentarios escribe a Jose Alfredo Ca nizo <canizo@mat.uab.cat>. Son
utiles, en particular, correcciones de errores o sugerencias sobre ampliaciones de los
resultados. Puedes encontrar la ultima version de este documento en
http://www.mat.uab.cat/~canizo/tex/
Este trabajo puede distribuirse en las condiciones de la licencia AttributionNon-
CommercialShareAlike de Creative Commons. Para ver una copia de esta licencia
ve a
http://creativecommons.org/licenses/by-nc-sa/1.0/
Esencialmente, esto signica que puedes usar este trabajo como quieras siempre
que menciones a su autor, no recibas dinero por el resultado y permitas la copia y
distribuci on de la misma forma en que se hace aqu. Para detalles sobre las condi-
ciones puedes leer la licencia antes mencionada.
Referencias
[1] Talvila, Erik, Some divergent trigonometric integrals. Amer. Math. Monthly
108 (2001), no. 5, 432436. [arXiv:math.CA/0101011]
[2] Talvila, Erik, Necessary and sucient conditions for dierentiating under
the integral sign. Amer. Math. Monthly 108 (2001), no. 6, 544548. [ar-
Xiv:math.CA/0101012]
[3] Richard Courant y Fritz John, Introduction to Calculus and Analysis, Volume
II/2. Springer, 2000
11
También podría gustarte
- Normas de Vectores y MatricesDocumento24 páginasNormas de Vectores y MatricesAmIn20122Aún no hay calificaciones
- TP2 - DerivadasDocumento2 páginasTP2 - DerivadasLuz alarcón100% (1)
- Informe de Laboratorio PH y Soluciones AmortiguadorasDocumento7 páginasInforme de Laboratorio PH y Soluciones AmortiguadorasJuan FernandezAún no hay calificaciones
- Tabla Integrales PDFDocumento1 páginaTabla Integrales PDFRichard Rosario Rodriguez0% (1)
- Variable Compleja ResiduosDocumento10 páginasVariable Compleja ResiduosAlejandro GafAún no hay calificaciones
- Teorema Cayley Hamilton 2Documento4 páginasTeorema Cayley Hamilton 2Dagoberto de la FuenteAún no hay calificaciones
- Libro Variable RosalesDocumento87 páginasLibro Variable RosalesRosa Janette Perez ChimalAún no hay calificaciones
- Integrales de Norma.Documento27 páginasIntegrales de Norma.Fatima PetillaAún no hay calificaciones
- Apuntes Análisis de Varias VariablesDocumento16 páginasApuntes Análisis de Varias Variablesmr_wopsAún no hay calificaciones
- Capítulo 8 - Teoremas de Convergencia y Derivación Bajo El Signo de La Integral PDFDocumento6 páginasCapítulo 8 - Teoremas de Convergencia y Derivación Bajo El Signo de La Integral PDFFabian Dos SantosAún no hay calificaciones
- Examen de Admision Resuelto Espol Fisica 2016 PDFDocumento14 páginasExamen de Admision Resuelto Espol Fisica 2016 PDFTábata VillegasAún no hay calificaciones
- Ejercicios de Teoria de GruposDocumento7 páginasEjercicios de Teoria de GruposFlorencia BasualdoAún no hay calificaciones
- Vectores en r3Documento10 páginasVectores en r3miguel_giraldo_10Aún no hay calificaciones
- Clasificacion Topologica de Los Sistemas Lineales BidimensionalesDocumento9 páginasClasificacion Topologica de Los Sistemas Lineales BidimensionalesLuchoAún no hay calificaciones
- Clases de Álgebra Lineal para IngenieríaDocumento284 páginasClases de Álgebra Lineal para IngenieríaJoaquin Melgarejo100% (4)
- Teorema de LiouvilleDocumento6 páginasTeorema de Liouvillegemunu271Aún no hay calificaciones
- Guia8 Usm Mat023 2015Documento4 páginasGuia8 Usm Mat023 2015Alonso CarrilloAún no hay calificaciones
- Cap1 (Compacidad)Documento12 páginasCap1 (Compacidad)Dyna CuelloAún no hay calificaciones
- Teorema Cantor BernsteinDocumento8 páginasTeorema Cantor BernsteinvicentAún no hay calificaciones
- Derivadas Discrecionales y GradientesDocumento8 páginasDerivadas Discrecionales y GradientesVictor Manuel Oliva MelendezAún no hay calificaciones
- Resumen de Continuidad en Los Espacios Métricos PDFDocumento8 páginasResumen de Continuidad en Los Espacios Métricos PDFDilcia PittiAún no hay calificaciones
- Algebra LinealDocumento92 páginasAlgebra LinealWedbleisAún no hay calificaciones
- Capitulo 2 FuncionesDocumento41 páginasCapitulo 2 FuncionesNartleb Cruz100% (1)
- Espacios MetricosDocumento21 páginasEspacios Metricossandra galvanlopezAún no hay calificaciones
- Funciones VectorialesDocumento87 páginasFunciones VectorialesLuis Enrique HpAún no hay calificaciones
- PRUEBA #1 (3) Calculo 3Documento1 páginaPRUEBA #1 (3) Calculo 3Aracelly CortesAún no hay calificaciones
- Funcion Logistica Atractor Smale 1Documento47 páginasFuncion Logistica Atractor Smale 1José Santiago García Cremades100% (1)
- Contrastes de HipotesisDocumento30 páginasContrastes de HipotesiscarlosAún no hay calificaciones
- Espacios MetricosDocumento14 páginasEspacios MetricosJose Miguel100% (1)
- Teoremas de Rolle, Lagrange y Cauchy, de Deriv-Cont y F InversasDocumento4 páginasTeoremas de Rolle, Lagrange y Cauchy, de Deriv-Cont y F InversasdiegogiusAún no hay calificaciones
- Convergencia MonotonaDocumento12 páginasConvergencia Monotonacharles marcelAún no hay calificaciones
- Prob V Compleja 00Documento15 páginasProb V Compleja 00Antonio OsorioAún no hay calificaciones
- El Grupo Fundamental y El Teorema de Seifert-Van KampenDocumento7 páginasEl Grupo Fundamental y El Teorema de Seifert-Van KampenLuis Mario Gamarra CamposAún no hay calificaciones
- YoyoDocumento8 páginasYoyoOscar Alfonso Sandoval SaenzAún no hay calificaciones
- El Espacio Proyectivo. José Luis Tábara PDFDocumento29 páginasEl Espacio Proyectivo. José Luis Tábara PDFMenelao ZubiriAún no hay calificaciones
- Conjuntos de BorelDocumento10 páginasConjuntos de BorelAndres GuevaraAún no hay calificaciones
- Medida e Integración. Ejercicios (v1)Documento10 páginasMedida e Integración. Ejercicios (v1)Ivan TavarezAún no hay calificaciones
- 02 Aritmetica ModularDocumento79 páginas02 Aritmetica Modularluis50% (2)
- Analisis MatematicoDocumento110 páginasAnalisis MatematicoJuanPastorAún no hay calificaciones
- Problemas TopologiaDocumento28 páginasProblemas TopologiaSamantha' Dextre EspinozaAún no hay calificaciones
- Teoría Elemental de CamposDocumento9 páginasTeoría Elemental de CamposVictor Martin SantamariaAún no hay calificaciones
- Fascículo Cálculo en Una Variable Límites y Continuidad EPNDocumento48 páginasFascículo Cálculo en Una Variable Límites y Continuidad EPNKAGGHGAún no hay calificaciones
- Tarea de Limites y Continuidad-2Documento8 páginasTarea de Limites y Continuidad-2Jorge Sánchez0% (1)
- Teorema de SardDocumento7 páginasTeorema de SardfffffffAún no hay calificaciones
- Analisis Matematico - Demostraciones y DefinicionesDocumento18 páginasAnalisis Matematico - Demostraciones y DefinicionesJorge RivadeneiraAún no hay calificaciones
- Unidad 2. Las Ecuaciones Diferenciales de Primer Orden y Sus SolucionesDocumento18 páginasUnidad 2. Las Ecuaciones Diferenciales de Primer Orden y Sus SolucionesGil Sandro GómezAún no hay calificaciones
- Funciones ComplejasDocumento21 páginasFunciones ComplejasEsteban MandirolaAún no hay calificaciones
- Análisis MatemáticoDocumento81 páginasAnálisis MatemáticoSekioz de NiafreAún no hay calificaciones
- Vectores en r3Documento25 páginasVectores en r3rominaslAún no hay calificaciones
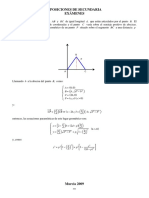
- Examenes MatesDocumento2 páginasExamenes MatesLuciia Méndez GutiérrezAún no hay calificaciones
- Actividad2 - Calculo DiferencialeintegralDocumento9 páginasActividad2 - Calculo DiferencialeintegralLuis GarciaAún no hay calificaciones
- ED Relacion 4 MATEMATICAS II UJAENDocumento4 páginasED Relacion 4 MATEMATICAS II UJAENAndrés C BriceñoAún no hay calificaciones
- Topologia 1Documento58 páginasTopologia 1wallaceAún no hay calificaciones
- Resumen Capítulos 12, 13 y 14 - IntegralMultiple - ResumenForoDocumento23 páginasResumen Capítulos 12, 13 y 14 - IntegralMultiple - ResumenForoscrjonAún no hay calificaciones
- Apuntes EDP PDFDocumento86 páginasApuntes EDP PDFCristianAún no hay calificaciones
- Análisis Matemático I - Parametrización de Curvas PlanasDocumento23 páginasAnálisis Matemático I - Parametrización de Curvas PlanasJhonatan Melqui Alcántara VegaAún no hay calificaciones
- DISTRIBUCIONESDocumento6 páginasDISTRIBUCIONESSharon NatividadAún no hay calificaciones
- Tema 7Documento12 páginasTema 7jaime Peinado LopezAún no hay calificaciones
- PracimDocumento21 páginasPracimEDU CIPANAAún no hay calificaciones
- LIMITEDocumento15 páginasLIMITELucas VenavidesAún no hay calificaciones
- Límites v1.7Documento26 páginasLímites v1.7Nick WilhelmAún no hay calificaciones
- 4.1 Variables y ConstantesDocumento2 páginas4.1 Variables y ConstantesgiancaruAún no hay calificaciones
- Previo Teorema 4.2.4Documento2 páginasPrevio Teorema 4.2.4Manuel Muñoz BlázquezAún no hay calificaciones
- Programa Analítico de BioestadisticaDocumento1 páginaPrograma Analítico de BioestadisticaAmira TalaAún no hay calificaciones
- Area Entre Dos Curvas Con Matlab PDFDocumento7 páginasArea Entre Dos Curvas Con Matlab PDFMiller Palacio NuñezAún no hay calificaciones
- Regresion BIVARIADADocumento9 páginasRegresion BIVARIADAValentinaAún no hay calificaciones
- Diferencial Total - Rcadena.optimización - calculo3.WA - MoralesDocumento12 páginasDiferencial Total - Rcadena.optimización - calculo3.WA - MoraleseduardoAún no hay calificaciones
- IV Sucesiones MonotonasDocumento9 páginasIV Sucesiones MonotonasBrandi FryAún no hay calificaciones
- Desarrollo de Las PreguntasDocumento4 páginasDesarrollo de Las PreguntasJohn James JohnflootpAún no hay calificaciones
- Método Simplex SEM 07Documento22 páginasMétodo Simplex SEM 07maximo jhoel rafael mendozaAún no hay calificaciones
- C3 - Cap2 - Indeterminación CinemáticaDocumento11 páginasC3 - Cap2 - Indeterminación CinemáticaRoberto Sotomayor MurilloAún no hay calificaciones
- Matemáticas Byn 2021-IIDocumento10 páginasMatemáticas Byn 2021-IIetwetAún no hay calificaciones
- Ejercicios Numeros ComplejosDocumento36 páginasEjercicios Numeros ComplejosbelcedubAún no hay calificaciones
- Descenso de Cargas Ejercicio 1Documento9 páginasDescenso de Cargas Ejercicio 1Eddy Herbas Guizada100% (1)
- Interpolacion SegmentariaDocumento12 páginasInterpolacion SegmentariaJonathan CronqueAún no hay calificaciones
- tallerTecnicasOptimizacion C1 2024-IDocumento6 páginastallerTecnicasOptimizacion C1 2024-IKaren NonzoqueAún no hay calificaciones
- Modelos de Estrategias - Gestiòn de Mantenimiento Alineado A Los ActivosDocumento4 páginasModelos de Estrategias - Gestiòn de Mantenimiento Alineado A Los ActivosWilliam DiazAún no hay calificaciones
- Tarea 28JULDocumento21 páginasTarea 28JULKATHERINE DEL CARMEN BARRENECHEA PORRASAún no hay calificaciones
- Deber 9 Transf. de Laplace (PUCE)Documento3 páginasDeber 9 Transf. de Laplace (PUCE)Joffre YapúAún no hay calificaciones
- Clase de Funciones Parte IiDocumento25 páginasClase de Funciones Parte IiMalenaVelasquezAún no hay calificaciones
- Mapa ConceptuaL LaplaceDocumento1 páginaMapa ConceptuaL LaplaceJessy Rivaz Herrera33% (3)
- Variable Compleja EJEMPLOSDocumento104 páginasVariable Compleja EJEMPLOSΦερ ΜοράλεςAún no hay calificaciones
- MM-412/IC-303 Análisis Numérico Fórmulas I Parcial: Polinomio de Taylor y Término Del ResiduoDocumento2 páginasMM-412/IC-303 Análisis Numérico Fórmulas I Parcial: Polinomio de Taylor y Término Del ResiduoAndrea RiveraAún no hay calificaciones
- Metodos Numericos Enfoque en CompetenciasDocumento162 páginasMetodos Numericos Enfoque en CompetenciasSergio Gonzales RodriguezAún no hay calificaciones
- Camara Aquietamiento DefinitivoDocumento10 páginasCamara Aquietamiento DefinitivoJose Miguel Caldera PrascaAún no hay calificaciones
- Practica I Actualizada de Analisis Real IIDocumento8 páginasPractica I Actualizada de Analisis Real IIEstarliAún no hay calificaciones
- Practica 06 SIMULINKDocumento10 páginasPractica 06 SIMULINKJean Carlos QvisPeAún no hay calificaciones
- Serie Algebra Lineal TEMA 1Documento7 páginasSerie Algebra Lineal TEMA 1Darío Fernando Núñez HernándezAún no hay calificaciones