LA CLASIFICACI

ON DE LAS C

ONICAS
Gabriel Chicas Reyes
21 de febrero de 2013
Resumen: Esta es una exposici on detallada de la clasicacion de las conicas reales en los casos afn y proyectivo, basada
en dos charlas impartidas por el autor en las Facultades Multidisciplinarias de Occidente (26 de diciembre de 2012) y
Oriente (3 de enero de 2013) de la Universidad de El Salvador. A excepci on de un mnimo de algebra lineal, no se asumen
conocimientos de matem atica universitaria. El autor agradece a los estudiantes y profesores que asistieron a las charlas
y contribuyeron a mejorar este documento con sus preguntas y comentarios.
I. LAS C

ONICAS EN EL PLANO EUCLIDIANO

La geometra analtica es un enfoque de la geometra euclidiana en el cual las guras geometricas
son estudiadas a traves de coordenadas; de este modo el razonamiento sintetico es completamente
reemplazado por manipulaciones algebraicas. Como cualquier estudiante de bachillerato sabe, el uso
de coordenadas cartesianas es sencillo, mas tiende a ser monotono y a opacar la intuicion geometrica.
El objetivo del presente documento es cambiar esta impresion, y a traves del estudio de ejemplos
concretos (las conicas) mostrar la efectividad del algebra en la resolucion de problemas geometricos,
especialmente en aquellos casos en los que no es posible visualizar los objetos en cuestion. Por este
motivo se han omitido intencionalmente guras de cualquier tipo.
En este apartado emprenderemos la clasicacion de las conicas apoyandonos en el algebra lineal, tal y
como en [4]; aparte de ser eciente, este metodo puede ser generalizado al caso proyectivo.
a. Repaso de c onicas
Antes que nada, que es una conica? Un buen alumno probablemente recuerde que, usando coorde-
nadas cartesianas, estamos hablando de alguna de las siguientes guras.
Parabola: y
2
= mx. Elipse:
x
2
a
2
+
y
2
b
2
= 1. Hiperbola:
x
2
a
2

y
2
b
2
= 1.
Por supuesto, hay muchas otras expresiones que denen conicas; sin embargo, todas ellas satisfacen
ser ecuaciones cuadraticas. Esta va a ser nuestra denicion general.
Denicion 1.1 Una conica real es la graca (es decir el conjunto de ceros reales) de un polinomio
cuadratico real en dos variables ax
2
+bxy +cy
2
+dx +ey +f.
Un inconveniente de esta denicion es que ya no es aparente a simple vista que tipo de gura representa
una ecuacion. Mas a un, hay gracas de ecuaciones cuadraticas que normalmente no consideraramos
conicas. Teniendo en cuenta estas complicaciones, como saber si una ecuacion cuadratica arbitraria
representa a una parabola, una elipse, una hiperbola u otro tipo de gura? Este es el problema de la
clasicacion de las conicas.
Ejemplo 1.2 La ecuacion 81x
2
+529y
2
1134x+1058y 38351 = 0 representa a una elipse, mientras
que x
2
y
2
68x 122y 2565 = 0 representa a un par de rectas. Incluso hay ecuaciones que no
representan a ninguna gura; por ejemplo x
2
+ 2xy +y
2
+ 1 = 0 no tiene soluciones reales.
Si nos referimos a cualquier texto de geometra analtica, nos daremos cuenta de que el procedimiento
general para clasicar una conica ax
2
+bxy +cy
2
+dx +ey +f = 0 es el siguiente:
1. Rotar el plano de modo que los ejes de simetra de la curva sean paralelos a los ejes.
2. Efectuar una traslacion del plano de tal forma que el centro (en el caso de la hiperbola y la
elipse) o el vertice (en el caso de la parabola) coincidan con el origen.
Usando coordenadas, las transformaciones utilizadas corresponden a ciertos cambios de variable. El
procedimiento algebraico correspondiente es el siguiente:
1. Eliminar el termino en xy mediante un cambio de variables; es decir, llevar la ecuacion a la forma
a

x
2
+c

y
2
+d

x +e

y +f

= 0.
2. Completar cuadrados y hacer otro cambio de variables para obtener una de las formas canonicas
descritas arriba.
1
Ejemplo 1.3 La ecuacion 81x
2
+ 529y
2
1134x + 1058y 38351 = 0 no tiene termino en xy, y por
tanto basta con completar cuadrados. Teniendo en cuenta que 81 = 9
2
y 529 = 23
2
podemos escribir
(x 7)
2
/23
2
+(y +1)
2
/9
2
= 1, y haciendo x

= x 7, y

= y +1 obtenemos una ecuacion simplicada

x
2
/23
2
+y
2
/9
2
= 1. Luego la conica en cuestion es una elipse, tal y como habamos dicho.
b. La clasificaci on de las c onicas reales
Geometricamente, el procedimiento anterior consiste en aplicar ciertas transformaciones (rotaciones
y traslaciones) para reducir una conica cualquiera a una de las guras que ya conocemos. Ya que
algebraicamente esto se traduce en cambios de coordenadas, el uso del algebra lineal es natural.
Denicion 1.4 Una transformacion euclidiana es una aplicacion R
2
R
2
de la forma x Ax+v,
donde A es una matriz ortogonal real de 2 2 y v R
2
es un vector jo.
2
Aqu la multiplicacion por una matriz ortogonal denota una rotacion y la suma de un vector jo re-
presenta una traslacion.
Denicion 1.5 Dos curvas en el plano euclidiano son equivalentes si existe una transformacion eu-
clidiana que transforme la ecuacion de la una en la otra.
Denicion 1.6 La matriz de la conica ax
2
+bxy +cy
2
+dx +ey +f = 0 se dene como

a b/2 d/2
b/2 c e/2
d/2 e/2 f

.
Observemos que esta matriz es simetrica y que es posible expresar la ecuacion de la conica como
(x y 1)

a b/2 d/2
b/2 c e/2
d/2 e/2 f

x
y
1

= 0.
Ejemplo 1.7 La matriz de la conica x
2
+ 2xy +y
2
+ 1 = 0 es

1 1 0
1 1 0
0 0 1

.
1
El adjetivo can onico se reere a que las ecuaciones en cuestion son particularmente simples.
2
Las transformaciones euclidianas reciben su nombre porque preservan la forma de las guras geometricas. Formal-
mente, se dice que son las isometras del plano euclidiano.
2
Emprendamos el primer paso. El cambio de coordenadas que elimina el termino en xy es una rotacion
de los ejes; para encontrarla es conveniente enfocarnos en los terminos cuadraticos de la ecuacion.
Denicion 1.8 Una forma cuadratica en dos variables x e y es un polinomio de la forma ax
2
+
bxy +cy
2
. La matriz de la forma cuadratica ax
2
+bxy +cy
2
se dene como

a b/2
b/2 c

.
Esta matriz es simetrica y usandola podemos escribir
ax
2
+bxy +cy
2
= (x y)

a b/2
b/2 c

x
y

.
Ejemplo 1.9 La representacion matricial de c
1
x
2
+c
2
y
2
es

c
1
0
0 c
2

, una matriz diagonal.

El ejemplo anterior sugiere que una forma cuadratica puede ser puesta en una forma canonica sin
el termino en xy diagonalizando la matriz correspondiente. Ese es el contenido del siguiente teorema:
Teorema 1.10 Para toda forma cuadratica p(x, y) = ax
2
+ bxy + cy
2
existe un cambio lineal de
coordenadas tal que p(x, y) puede escribirse en la forma canonica
1
x
2
+
2
y
2
. Mas a un,
1
,
2
R
son los autovalores de la matriz de p(x, y).
Demostracion. Recordemos que que una matriz simetrica real de n n tiene n autovalores reales
distintos (este es el llamado teorema espectral). Mas a un, los autovectores correspondientes son
ortogonales y pueden escogerse de modo que tengan norma 1; por tanto toda matriz simetrica real
puede ser diagonalizada mediante una matriz ortogonal.
En nuestro caso particular, si N es la matriz de p(x, y) tendramos que existe una matriz ortogonal Q
de 2 2 tal que
Q
1
NQ =

1
0
0
2

,
donde
1
y
2
son los autovalores de N. Este no es sino el resultado buscado.
Regresando al problema, observemos que la ecuacion general de una conica puede expresarse como
(x y)

a b/2
b/2 c

x
y

+dx +ey +f = 0.
Sea N la matriz de 2 2 que aparece en la ecuacion anterior. El teorema que acabamos de probar
garantiza que existe cierto cambio de variables de la forma

x
y
1

Q
0
0 1

que diagonaliza a N y por tanto transforma la ecuacion de la conica en

1
x
2
+
2
y
2
+x

+y

+f = 0,
o bien escribiendo en forma matricial
(x

1)

1
0 /2
0
2
/2
/2 /2 f

= 0.
Aqu
1
y
2
son los autovalores de N y , son constantes.
3
Observemos que la nueva matriz M

que acabamos de obtener es similar a la matriz original M.

El segundo paso consiste en eliminar los terminos lineales mediante una traslacion.
3
Hay dos posibles
casos a considerar:
Si los autovalores
1
y
2
son ambos distintos de 0, podemos efectuar la traslacion x

= x

/2
1
, y

= y

/2
2
, o bien en forma matricial

1 0 /2
1
0 1 /2
2
0 0 1

.
Al aplicar esta transformacion la ecuacion de la conica queda
1
x
2
+
2
y
2
+ = 0, donde
= f
2
/2
1

2
/2
2
. Consecuentemente, la ecuacion en forma matricial es
(x

1)

1
0 0
0
2
0
0 0

= 0.
Si al menos uno de los
1
y
2
es 0, lo mejor que podemos hacer es eliminar el termino lineal
en una de las variables. Suponiendo que
2
= 0, la traslacion x

= x

/2
1
, y

= y

lleva la
ecuacion de la conica a la forma
1
x
2
+y

+ = 0, donde = f
2
/2
1
. En otras palabras
(x

1)

1
0 0
0 0 /2
0 /2

= 0.
De nuevo, la matriz M

obtenida en este paso es similar a M

y por tanto a M.
En consecuencia, para estudiar una conica arbitraria basta enfocarnos en una de las formas anteriores.
Sigamos denotando por
1
y
2
a los autovalores del menor N. Tenemos los siguientes casos:
Los autovalores
1
y
2
son ambos distintos de cero. Aqu hay dos posibilidades.
Los autovalores tienen el mismo signo. Si tiene distinto signo al de los autovalores, obte-
nemos una elipse. Si = 0, la ecuacion
1
x
2
+
2
y
2
= 0 tiene una sola solucion (x

, y

) =
(0, 0); luego la conica se reduce a un punto. Finalmente, si tiene signo distinto al de los
autovalores, la ecuacion
1
x
2
+
2
y
2
+ = 0 no tiene soluciones reales; ya que ciertamente
existen soluciones imaginarias, este caso se denomina elipse imaginaria.
Los autovalores tienen signos opuestos. Si = 0, la expresion
1
x
2
+
2
y
2
= 0 factoriza
en dos terminos lineales y representa a dos rectas que se cortan. Por otro lado, si = 0 la
ecuacion dada representa a una hiperbola.
Uno de los autovalores es cero, digamos
2
= 0. Hay nuevamente dos casos:
La constante es diferente de cero. Entonces la ecuacion
1
x
2
+y

+ = 0 claramente
representa a una parabola.
La constante es igual a cero. Si y
1
tienen signos opuestos, la ecuacion x
2
+/
1
= 0
representa a dos rectas paralelas. Si y
1
tienen el mismo signo no existen soluciones
reales, pero hablamos de un par de rectas paralelas imaginarias. Y si = 0 entonces

1
x
2
= 0 representa dos veces a una misma recta.
3
Al nivel de manipulaciones algebraicas, lo que vamos a hacer es simplemente completar cuadrados.
4
Resumiendo, hemos establecido el siguiente resultado:
Teorema 1.11 (Clasicacion de las conicas reales) Toda conica real es equivalente a una de las
siguientes guras: elipse real, elipse imaginaria, par abola, hiperbola, punto, par de rectas que se cortan,
par de paralelas reales, par de paralelas imaginarias y par de rectas coincidentes.
Ejemplo 1.12 Retomando la conica x
2
+2xy +y
2
+1 = 0 del ejemplo anterior, el menor a considerar
es N =

1 1
1 1

. Al diagonalizar esta matriz resulta que Q

1
NQ =

2 0
0 0

, donde Q =

1 1
1 1

.
Se sigue que el cambio de variables x

= x + y, y

= x y transforma la ecuacion de la conica en

2x
2
+ 1 = 0.
c. El rango y el discriminante
La demostracion del teorema anterior nos permite averiguar que tipo de conica representa una ecuacion
cualquiera; sin embargo, sera posible hacer esto sin necesidad de encontrar la forma canonica? La res-
puesta es armativa; este metodo alternativo de clasicacion se basa en ciertas cantidades que son
invariantes durante el calculo de la forma canonica, y por tanto pueden usarse para identicar cada
uno de los nueve casos. Una de ellas es el rango.
Denicion 1.13 El rango de una conica es el rango de su matriz asociada.
Ahora necesitamos denir formalmente que entendemos por degeneracion.
Denicion 1.14 Una conica es degenerada si el determinante de su matriz asociada es 0. De lo
contrario decimos que la conica es no degenerada.
Es un ejercicio sencillo comprobar que, usando esta denicion, las conicas no degeneradas son precisa-
mente la parabola, la elipse (real o imaginaria) y la hiperbola. Tal y como nuestra intuicion lo dicta,
las conicas que se reducen a puntos o pares de rectas son degeneradas.
Lema 1.15 Las conicas reales degeneradas son las siguientes: punto real, par de rectas que se cortan,
par de paralelas reales, par de paralelas imaginarias y par de rectas coincidentes.
Demostracion. Basta con ver la matriz de la forma canonica de cada una de estas guras.
Proposicion 1.16 Dos conicas equivalentes tienen el mismo rango.
Demostracion. En efecto, en el transcurso de la clasicacion hemos observado que al cambiar coorde-
nadas siempre obtenemos una matriz similar a la matriz de la conica. De aqu que el rango de la conica
permanece invariante.
Corolario 1.17 Las propiedad de no degeneracion es invariante ante cambios de coordenadas.
Proposicion 1.18 Una conica es degenerada si y solo si tiene rango menor que 3.
Demostracion. Una conica tiene rango menor que 3 si y solo si su matriz no es invertible, o sea si y
solo si el determinante de esta matriz es cero.
Ahora necesitamos introducir una segunda invariante que seguramente es familiar para algunos estu-
diantes: el discriminante. En los libros de texto de geometra analtica, esta cantidad aparece durante
el estudio de la ecuacion general de segundo grado.
5
Denicion 1.19 El discriminante de una conica se dene como = b
2
4ac.
Proposicion 1.20 Dos conicas equivalentes tienen el mismo discriminante.
Demostracion. Ya hemos visto que el calculo de la forma canonica consiste en rotaciones y traslaciones.
Al rotar estamos cambiando N por una matriz similar, que tiene la misma ecuacion caracterstica. Por
otro lado, N es invariante ante traslaciones del plano ya que estas no afectan a los coecientes de segun-
do grado a, b, c. Se sigue que la ecuacion caracterstica de N es invariante ante cambios de coordenadas.
Ya que esta ecuacion esta dada por
2
(a +c) +
4ac b
2
4
= 0, concluimos que det N = 4ac b
2
y
tr N = a +c son invariantes.
Finalmente tenemos el famoso criterio del discriminante:
Corolario 1.21 Una conica es una elipse, parabola o hiperbola (posiblemente degenerada) dependien-
do de si el discriminante = b
2
4ac es negativo, cero o positivo, respectivamente.
Demostracion. Nuevamente usamos la forma canonica y consideramos dos casos. Si alguno de los au-
tovalores del menor N es cero, sabemos que la conica es una parabola. Pero esta condicion implica que
N es singular y por tanto su determinante es cero. Luego = 0 para una parabola.
En cambio, si ambos autovalores son distintos de cero, inspeccionando la clasicacion en este caso
vemos que una elipse (real o imaginaria) corresponde al caso en que
1
y
2
tienen el mismo signo;
pero det N =
1

2
, as que < 0. Si en cambio consideramos una hiperbola,
1
y
2
tienen signos
opuestos, de donde > 0 en este caso.
Un criterio para distinguir las conicas degeneradas entre s se deja como ejercicio para el lector.
Ejemplo 1.22 La conica x
2
y
2
68x122y2565 = 0 es degenerada, pues

1 0 34
0 1 61
34 61 2565

= 0.
Ademas, = 4(1) = 4 > 0, de donde la conica corresponde al caso degenerado de la hiperbola, es
decir un par de rectas que se cortan.
Ejercicios
1. Encuentre los cambios de variable que diagonalizan las siguientes formas cuadraticas:
(i) x
2
xy +y
2
. (ii) x
2
+ 4xy +y
2
. (iii) 3x
2
+ 4

2xy + 3y
2
.
2. Clasique las siguientes conicas, comparando los metodos expuestos en este apartado:
(i) 2x
2
+ 5xy +y
2
1 = 0. (ii) x
2
4xy + 4y
2
4 = 0. (iii) 5x
2
+ 6xy + 5y
2
4x + 4y 4 = 0.
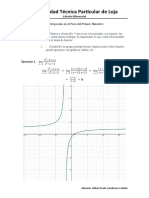
3. Calcule la integral

e
x
2
+xyy
2
dxdy.
Sugerencia: Use un cambio de variables para reducir el problema a una integral famosa.
4. Enuncie un criterio para clasicar una conica dada usando los autovalores
1
y
2
del menor N.
5. Enuncie un criterio para distinguir los 6 casos de conicas degeneradas usando el discriminante.
6. Enuncie un criterio para averiguar si una conica dada representa a una circunferencia.
7. Una conica central es tal que posee un centro de simetra, como la elipse y la hiperbola.
Demuestre que en este caso los ejes de la conica son paralelos a los autovectores del menor N.
6
8. Muestre que el centro de una conica central satisface el sistema de ecuaciones:
ax +
b
2
y +
d
2
= 0
b
2
x +cy +
e
2
= 0
Que sucede si la conica es una parabola?
9. Pruebe el angulo de rotacion en el paso 1 viene dado por la formula
=
1
2
arctan
2b
c a
.
Sugerencia: Recuerde que las entradas de una matriz ortogonal real de 2 2 pueden ser escritas
en terminos de los senos y cosenos del angulo de rotacion.
10. Una cuadrica en R
3
es una supercie denida por un polinomio cuadratico en 3 variables.
Investigue la clasicacion de las cuadricas. Sugerencia: Utilice la ley de inercia de Sylvester.
4
II. EL PLANO PROYECTIVO REAL
En la geometra euclidiana existen rectas (las paralelas) que no se cortan. Sin embargo, a veces es con-
veniente considerar que dos rectas paralelas se cortan en el innito. Si bien esta idea puede parecer
extra na, en realidad estamos acostumbrados a verla a diario: dos rectas paralelas (las aceras de una
calle, las lneas de tren, etc.) se juntan en el horizonte.
El plano proyectivo es un objeto idealizado obtenido al a nadir puntos al innito al plano euclidiano,
de modo que dos rectas cualesquiera se corten. En esta nueva geometra solamente tiene sentido consi-
derar propiedades invariantes ante el cambio de perspectiva (por ejemplo concurrencia y colinealidad),
mas otras como longitud, angulo, etc. son descartadas. Este es el mundo de la geometra proyectiva.
5
Es posible estudiar el plano proyectivo a traves de coordenadas, de forma similar a la geometra
analtica del plano euclidiano. Estas coordenadas (homogeneas) son mas simetricas que las coordenadas
cartesianas, y permiten dar un tratamiento unicado y sencillo de varios resultados de la geometra
euclidiana, entre ellos la clasicacion de las conicas.
6
a. Definici on de P
2
R
Denicion 2.1 El plano proyectivo real P
2
R es un espacio donde cada punto es representado por
una tripleta de n umeros reales [X : Y : Z], llamados coordenadas homogeneas, que satisfacen las
siguientes reglas: (i) [0 : 0 : 0] no esta denido; es decir, al menos uno de los X, Y , Z tiene que ser
distinto de cero. (ii) Para todo R, [X : Y : Z] = [X : Y : Z]. Para evitar confusiones con el
plano proyectivo, a veces nos referiremos al plano euclidiano R
2
como el plano afn.
7
Ejemplo 2.2 El punto [1 : 2 : 3] P
2
R admite numerosas representaciones:
[1 : 2 : 3] = [5 : 10 : 15] = [2013 : 4026 : 6039] =

1
2
: 1 :
3
2

= [ : 2 : 3] =
4
La ley de inercia de Sylvester es un resultado de algebra lineal que permite clasicar formas cuadraticas reales en
cualquier n umero de variables.
5
La geometra proyectiva es una geometra no euclidiana; concretamente es una geometra elptica ya que dados una
recta y un punto fuera de ella, no existe ninguna paralela a la recta que pase por dicho punto
6
Tambien es posible dar un tratamiento puramente sintetico (axiomatico) de la geometra proyectiva, de manera
analoga a los Elementos de Euclides. El lector interesado puede consultar un texto como [2].
7
Es posible denir espacios proyectivos P
n
R para cualquier n > 0 exactamente de la misma manera, incluso reem-
plazando R por C o cualquier otro cuerpo.
7
Como podemos ver, las coordenadas homogeneas no son unicas: podemos multiplicarlas por cualquier
n umero distinto de cero. El lector que tenga dicultades con esta denicion debera tener en mente que
es la razon de las coordenadas la que importa.
A continuacion explicaremos a que nos referimos al decir que el plano afn R
2
esta contenido en P
2
R.
Proposicion 2.3 Sea S = {[X : Y : Z] P
2
:Z = 0} P
2
. Entonces existe una biyeccion entre los
puntos de R
2
y los puntos de S tal que (x, y) R
2
es enviado a [x : y : 1] S.
Demostracion. Denamos una aplicaci on S R
2
enviando [X : Y : Z] S a (X/Z, Y/Z), el cual
pertenece a R
2
puesto que Z = 0. Veamos que esta es la aplicacion inversa de la aplicacion de la
proposicion.
Si (x, y) R
2
, entonces trivialmente (x, y) [x : y : 1] (x, y). Ademas si [X : Y : Z] S, entonces
[X : Y : Z] (X/Z, Y/Z) [X/Z : Y/Z : 1]. Pero [X/Z : Y/Z : 1] = [X : Y : Z] ya que Z = 0.
El conjunto S es llamado a veces una carta afn. Observemos que hay otras dos cartas anes, respecto
a X e Y , y la union de las tres cartas es igual a P
2
. Por simplicidad siempre trabajaremos en la carta S.
El resultado anterior nos dice que podemos intercambiar entre coordenadas anes (cartesianas) y ho-
mogeneas seg un nos convenga.
Ejemplo 2.4 Una recta en el plano proyectivo es el conjunto de ceros de un polinomio homogeneo
lineal aX +bY +cZ = 0. Supongamos que tenemos una recta ax +by +c = 0 en el plano euclidiano.
Pasando a coordenadas homogeneas, es decir haciendo x = X/Z, y = Y/Z y reordenando obtenemos
aX +bY +cZ = 0, que es una recta tal y como lo acabamos de denir.
Supongamos que [x
0
: y
0
: 0] P
2
R es la interseccion de las dos rectas aX + bY + cZ = 0 y Z = 0,
esto es, se cumple que ax
0
+ by
0
= 0. Ahora bien, en geometra analtica aprendimos que una recta
paralela a ax+by +c = 0 debe tener la misma pendiente, y por tanto su ecuacion a

x+b

y +c

= 0 es
tal que b/a = b

/a

(o bien b = b

si a = 0). Pasando a coordenadas homogeneas obtenemos otra recta

a

X + b

Y + c

Z = 0, cuya interseccion con Z = 0 tambien es [x

0
: y
0
: 0]. Luego las rectas paralelas
ax +by +c = 0 y a

x +b

y +c

= 0 se cortan en P
2
R!
Sea T = {[X : Y : Z] P
2
R : Z = 0} P
2
R. Entonces P
2
R = S T. Por el ejemplo anterior cada
punto de T corresponde a una direccion diferente de rectas paralelas; por eso suelen llamarse puntos
al innito. Estos puntos estan todos sobre la recta Z = 0, que por ende se denomina la recta al
innito. Luego P
2
es igual al plano euclidiano mas un conjunto de puntos al innito, tal y como
indicamos al principio de este apartado.
b. Las c onicas en P
2
R
Recordemos que una curva en el plano euclidiano es el conjunto de soluciones de una ecuacion polino-
mial. Esta denicion no es aplicable al plano proyectivo, ya que las coordenadas homogeneas pueden
multiplicarse por escalares sin alterar su valor, pero puede rescatarse con un ajuste menor.
Denicion 2.5 Un polinomio homogeneo en tres variables consta solamente de monomios de igual
grado. El grado de dicho polinomio es el grado de los monomios.
Denicion 2.6 Una curva en el plano proyectivo es el conjunto de ceros de un polinomio homogeneo
de tres variables. Una conica en el plano proyectivo es el conjunto de ceros de un polinomio cuadratico
homogeneo aX
2
+bXY +cY
2
+dXZ +eY Z +fZ
2
(tambien llamado forma cuadratica).
8
8
Observemos que s tiene sentido decir que un punto [X
0
: Y
0
: Z
0
] es un cero de un polinomio homogeneo P de grado
d: Si P(X
0
, Y
0
, Z
0
) = 0 y = 0 es cualquier constante, entonces P(X
0
, Y
0
, Z
0
) =
d
P(X
0
, Y
0
, Z
0
) = 0.
8
Ejemplo 2.7 Los polinomios homogeneos de grado 1 son de la forma aX +bY +cZ; luego las rectas
en el plano proyectivo tienen ecuaciones de la forma aX + bY + cZ = 0, tal y como dijimos arriba.
Algunas c onicas en P
2
R son X
2
Y Z = 0 y X
2
+Y
2
Z
2
= 0.
Al igual que en el caso afn, la clasicacion de las conicas en P
2
R se basa en llevar la curva a una forma
estandar mediante un cambio de coordenadas. Aqu debemos detenernos un momento para pregun-
tarnos: como son los cambios de coordenadas en P
2
R? Intuitivamente estos deben corresponder a un
cambio de perspectiva en el plano. Ya que cambiando el punto de vista podemos convertir, por ejemplo,
un cuadrado en un paralelogramo, una circunferencia en una elipse, dos paralelas en dos rectas que se
cortan, etc., esperaramos que mucha informacion preservada en el caso euclidiano sea descartada.
Denicion 2.8 Una proyectividad de P
2
R es una aplicacion de la forma v Mv, donde M es una
matriz real invertible de 3 3; es decir, es una transformacion lineal invertible de P
2
R en P
2
R.
9
Denicion 2.9 Dos curvas en P
2
R son equivalentes si existe una proyectividad que convierta la una
en la otra.
A continuacion presentamos la clasicacion de las conicas en el plano proyectivo. Por lo recien dis-
cutido arriba, es de esperarse que el uso de proyectividades ofrezca una simplicacion drastica de la
clasicacion en el caso euclidiano.
Denicion 2.10 La matriz de la conica aX
2
+bXY +cY
2
+dXZ +eY Z +fZ
2
= 0 se dene como

a b/2 d/2
b/2 c e/2
d/2 e/2 f

.
Esta matriz es simetrica y podemos expresar la ecuacion de la conica como
(X Y Z)

a b/2 d/2
b/2 c e/2
d/2 e/2 f

X
Y
Z

.
Proposicion 2.11 Para toda forma cuadratica P(X, Y, Z) en R
3
existe un cambio lineal de coorde-
nadas tal que P puede escribirse en la forma canonica
1
X
2
+
2
Y
2
+
3
Z
2
, donde
1
,
2
y
3
son
constantes que dependen de P (de hecho, son los autovalores de la matriz asociada a P).
Demostracion. Esto es una consecuencia del teorema espectral, tal y como en en el Teorema 1.10.
Esto nos dice que, mediante un cambio de coordenadas adecuado, cualquier conica en P
2
R puede ser
llevada a la forma canonica de la proposicion. Obtenemos por tanto:
Teorema 2.12 (Clasicacion de las conicas en P
2
R) Usando un cambio de coordenadas adecuado,
toda conica en el plano proyectivo real puede ser puesta en alguna de las siguientes formas:
Conica no degenerada: X
2
+Y
2
Z
2
= 0.
Punto: X
2
+Y
2
= 0.
Par de rectas: X
2
Y
2
= 0.
Par de rectas coincidentes: X
2
= 0.
Conjunto vaco: X
2
+Y
2
+Z
2
= 0.
9
Notemos que los coecientes de M pueden ser multiplicados por cualquier constante = 0, sin cambiar el valor de
Mv. El conjunto de todas las proyectividades se conoce como el grupo lineal general proyectivo PGL(2, R).
9
Usando las mismas deniciones de degeneracion y rango, podemos enunciar una consecuencia notable
de la clasicacion.
Corolario 2.13 Existe una unica conica no degenerada en P
2
R, salvo proyectividades.
Ejemplo 2.14 En el plano euclidiano, una parabola y una circunferencia tienen ecuaciones y = x
2
y x
2
+ y
2
= 1 respectivamente. Pasando a coordenadas homogeneas obtenemos sendas ecuaciones
Y Z = X
2
y X
2
+Y
2
= Z
2
. Es sencillo comprobar que el cambio de coordenadas X

= X, Y

= Y Z,
Z

= Y +Z convierte la ecuacion de la parabola en la ecuacion de la circunferencia.

Ejercicios
1. Encuentre los cambios de variable que diagonalizan las siguientes formas cuadraticas:
(i) x
2
2xy + 2yz +z
2
. (ii) 7x
2
+y
2
+z
2
+ 8xy + 8yz 16yz. (iii) x
2
+y
2
+z
2
+xy +yz +zx.
2. De una clasicacion de las conicas en el plano proyectivo complejo P
2
C.
3. Verique que la imagen de una recta bajo una proyectividad es otra recta, y que rectas concu-
rrentes son enviadas a rectas concurrentes (en otras palabras, una proyectividad preserva coli-
nealidades y concurrencias).
4. Un punto singular [X
0
: Y
0
: Z
0
] de la curva P(X, Y, Z) = 0 es tal que anula las derivadas
parciales de P, esto es P
x
(X
0
, Y
0
, Z
0
) = P
y
(X
0
, Y
0
, Z
0
) = P
z
(X
0
, Y
0
, Z
0
) = 0. Una curva
P(X, Y, Z) = 0 es no singular si carece de puntos no singulares. Cuales de las cinco conicas
de la clasicacion de este apartado son no singulares?
5. Una curva P(X, Y, Z) = 0 es irreducible si el polinomio P(X, Y, Z) es irreducible. Demuestre
que toda curva no singular es irreducible. Concluya que la conica no degenerada en el plano
proyectivo es irreducible.
6. Sean f R[x, y] un polinomio y F R[X, Y, Z] su homogeneizacion
10
, que denen sendas curvas
c y C. Pruebe que si (a, b) R
2
es un punto singular de c, entonces [a : b : 1] P
2
R es un punto
singular de C.
7. (Clasicacion de las conicas, version geometrico-algebraica) Dada una conica real cualquiera C,
encajela en el plano proyectivo (cf. Proposicion 2.3) y considere su interseccion con la recta al
innito L. Demuestre que:
C es una elipse si C L = .
C es una hiperbola si C L consta de dos puntos diferentes.
C es una parabola si C L consta de un solo punto doble.
8. Es posible que una conica no degenerada en el plano euclidiano sea equivalente a una conica
degenerada en el plano proyectivo?
9. De una clasicacion de las cuadricas
11
en P
2
R y P
2
C. Cuantas cuadricas no degeneradas hay
en cada caso?
10. Discuta la veracidad del converso de la Proposicion 1.16: Si dos conicas en P
2
R tienen el mismo
rango, entonces son equivalentes. Que sucede si trabajamos en P
2
C?
10
El termino homogeneizaci on se reere a que obtendremos un polinomio homogeneo al pasar de coordenadas carte-
sianas a homogeneas. Cf. Proposici on 2.3.
11
Una cuadrica en el plano proyectivo se dene como el conjunto de ceros de una forma cuadratica en cuatro variables.
10
III. CONCLUSI

ON
El estudio de las conicas y de la geometra proyectiva en general es, en opinion del autor, benecioso
para cualquier estudiante de matematica, ya que esta relacionado con otras teoras mas profundas. En
este apartado seran sugeridas algunas alternativas para los lectores interesados.
Las conicas son ejemplos importantes de curvas algebraicas, es decir el conjunto de ceros de un poli-
nomio. Resolver un sistema de dos ecuaciones polinomiales es equivalente a intersecar dos curvas, y el
estudio de dichas intersecciones revela muchos detalles sobre la geometra de las curvas
12
(un resultado
fundamental en esta direccion es el teorema de Bezout). Asimismo, las curvas denidas sobre los
n umeros complejos poseen una rica teora que relaciona el algebra con el analisis complejo, debido a
la presencia de una estructura compleja adicional, la de supercies de Riemann. En general, los
conjuntos de soluciones de sistemas de ecuaciones polinomiales son el objeto de estudio tradicional de
la geometra algebraica. Dos buenos textos introductorios sobre estos temas son [3] y [5].
Por otra parte, la clasicacion de las formas cuadraticas es un problema fundamental. Los casos real y
complejo pueden ser resueltos facilmente usando algebra lineal, mediante la ley de inercia de Sylvester.
La cuesti on se vuelve mas interesante al considerar coecientes en otros conjuntos: el caso de las formas
cuadraticas con coecientes en un cuerpo numerico es un problema famoso de la teora de n umeros
algebraica (el teorema de Hasse-Minkowski), tal y como se discute en [6].
Finalmente, vale la pena resaltar que el paradigma de la clasicacion en los tipos elptico, parabolico e
hiperbolico es recurrente en diversas ramas de la matematica. Un ejemplo notable es el de las ecuaciones
diferenciales parciales de segundo orden, en la cual los miembros de cada tipo tienen propiedades muy
diferentes entre s: elptico (v.g. las ecuaciones de Laplace y Poisson), parabolico (v.g. la ecuacion
del calor) e hiperbolico (v.g. la ecuacion de onda). El lector interesado en ecuaciones diferenciales
parciales en general tendra a bien consultar un texto exhaustivo como [1].
REFERENCIAS
[1] Chester, C.R., Techniques in Partial Dierential Equations, International Series in Pure and Ap-
plied Mathematics, McGraw-Hill, 1971.
[2] Coxeter, H.S.M., Projective Geometry, 2nd ed., Springer-Verlag, 1987.
[3] Kirwan, F., Complex Algebraic Curves, London Mathematical Society Student Texts 23, Cambridge
University Press, 1992.
[4] Pettofrezzo, A.J., Matrices and Transformations, Dover Publications, 1978.
[5] Reid. M., Undergraduate Algebraic Geometry, London Mathematical Society Student Texts 12,
Cambridge University Press, 1988.
[6] Serre, J.-P., A Course in Arithmetic, Graduate Texts in Mathematics 7, Springer-Verlag, 1973.
Gabriel Chicas Reyes (University of Tokyo)
E-mail address: gachr.ebc253@gmail.com
Website: http://salvamate.wordpress.com/
12
Un ejemplo de esta armaci on puede encontrarse en el ejercicio 7 del apartado II.
11