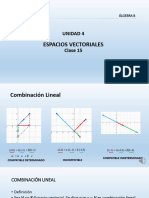
DIAGRAMAS DE FASE DE SISTEMAS LINEALES

DE ECUACIONES DIFERENCIALES DE PRIMER

ORDEN
Alejandro Lugon
26 de mayo de 2010

1.

Ecuaciones planares: dos dimensiones

Las soluciones del sistema homogeneo:
x = ax + by
y = cx + dy

se agrupan en tres categoras de acuerdo a las races de la ecuacion (o polinomio) caracterstica(o) de A:

Det(A I) = 0
esta ecuacion es un polinomio de segundo grado y por lo tanto tiene 2 races. Estas races
pueden ser:
1. Reales y diferentes
2. Reales e iguales
3. Complejos conjugados
Cada posibilidad es una categora. En lo que sigue consideramos det(A) 6= 0:

1.1.

Races reales diferentes

Sean 1 y 2 dichas races, estas son los valores propios de A. Consideremos a v y w los
respectivos vectores propios asociados.

Luego la solucion sera:

"

x(t)
y(t)

"

#
= K1 e1 t v + K2 e2 t w = K1 e1 t

v1
v2

"

#
+ K 2 e 2 t

w1
w2

es decir
x(t) = K1 v1 e1 t + K2 w1 e2 t
y(t) = K1 v2 e1 t + K2 w2 e2 t
donde las constantes K1 y K2 se determinan con las condiciones iniciales:
x0 = x(0) = K1 v1 + K2 w1
y0 = y(0) = K1 v2 + K2 w2
resolviendo estas ecuaciones encontramos1
w2 x0 w1 y0
w2 v1 w1 v2
v1 y0 v2 x0
=
w2 v1 w1 v2

K1 =
K2

Para cada vector propio tenemos un subespacio invariante (una recta que pasa por el origen):
Tv = {rv|r R} = {(x, y)|yv1 xv2 = 0}
Tw = {rw|r R} = {(x, y)|yw1 xw2 = 0}
de manera que si la condicion inicial pertenece a uno de estos subespacios toda la solucion
tambien pertenecera.
Por ejemplo si (x0 , y0 ) Tv entonces v1 y0 v2 x0 = 0, esto implica que K2 = 0 y que la
solucion particular es:

x(t) = K1 v1 e1 t
y(t) = K1 v2 e1 t
de donde podemos calcular:
v1 y(t) v2 x(t) = 0
1

El denominador no es nulo porque v y w son linealmente independientes (no paralelos).

y verificar que para todo t:

(x(t), y(t)) Tv
De igual manera se puede proceder con Tw .
Los subespacios invariantes seran convergentes o divergentes seg
un el valor propio asociado sea negativo o positivo.
Si los dos valores propios son negativos tendremos dos subespacios invariantes convergentes, el equilibrio sera un nodo (asintoticamente) estable como en 1a2 .
Si un valor propio es positivo y el otro negativo tendremos un subespacio invariante
divergente y otro convergente, el equilibrio sera tipo silla como en 1b. Algunas veces se
refiere a este tipo de equilibrio como condicionalmente estable.
Si los dos valores propios son positivos tendremos dos subespacios invariantes divergentes,
el equilibrio sera un nodo inestable como en 1c.

1.2.

Races reales iguales

Sea 6= 0 el valor de dicha raz y v el vector propio asociado3 . Podemos conseguir otro
vector propio generalizadow resolviendo el sistema (A I)w = v (v y W son linelamente
independientes)
2

En este y todos los diagramas siguientes, el punto central corresponde al equilibrio (0, 0) y los ejes
coordenados X Y no se dibujan para dar claridad al esquema.
3
No consideramos el caso especial en el cual podemos encontrar dos vectores propios linealmente independientes asociados a .

Con estos dos vectores la solucion buscada es:

"
#
x(t)
= K1 et v + K2 et (w + tv)
y(t)
= (K1 v + K2 w)et + (K2 v)tet
"
#
"
#
K1 v1 + K2 w1
K2 v1
t
=
e +
tet
K1 v2 + K2 w2
K2 v2
es decir
x(t) = (K1 v1 + K2 w1 )et + K2 v1 tet
y(t) = (K1 v2 + K2 w2 )et + K2 v2 tet
donde las constantes K1 y K2 se determinan con las condiciones iniciales:
x0 = x(0) = K1 v1 + K2 w1
y0 = y(0) = K1 v2 + K2 w2
resolviendo estas ecuaciones encontramos
w2 x0 w1 y0
w2 v1 w1 v2
v1 y0 v2 x0
=
w2 v1 w1 v2

K1 =
K2
Dados (x0 , y0 ) la solucion particular es:

v1 y0 v2 x0
v1 tet
w2 v1 w1 v2
v1 y0 v2 x0
y(t) = y0 et +
v2 tet
w2 v1 w1 v2

x(t) = x0 et +

Para este caso solo hay un subespacio invariante determinado por el vector v:
Tv = {(x, y)|yv1 xv2 = 0}
Nuevamente si (x0 , y0 ) Tv : v1 y0 v2 x0 = 0, K2 = 0 y la solucion particular es:

x(t) = K1 v1 e1 t
y(t) = K1 v2 e1 t

de donde podemos calcular:

v1 y(t) v2 x(t) = 0
y verificar que para todo t:
(x(t), y(t)) Tv
El subespacio invariante sera convergente o divergente seg
un el valor propio doble sea
negativo o positivo.
Si el valor propio es positivo tendremos un subespacio invariante divergente, el equilibrio
sera un nodo inestable como en 2a o 2c.
Si el valor propio es negativo tendremos un subespacio invariante convergente, el equilibrio
sera un nodo (asintoticamente) estable como en 2b o 2d.

1.3.

Races complejas conjugadas

Sean + i y i las races del polinomio caracterstico. En general estos no tienen

vectores propios reales asociados a ellos, pero si podemos encontrar v y w vectores linealmente

independientes, tales que:

Av = v w
Aw = v + w
La solucion es
x(t) = K1 et Cos(t) + K2 et Sen(t)
y(t) = L1 et Cos(t) + L2 et Sen(t)
para ciertas constantes K1 , K2 , L1 y L2 .
En este caso no se tienen subespacios invariantes. Las trayectorias de las soluciones son
oscilantes alrededor del equilibrio. Si 6= 0 las soluciones seran espirales elpticas, la estabilidad esta determinada por el signo de , si es negativo tendremos un equilibrio asintoticamente estable, como en 3c, si es positivo tendremos un equilibrio inestable, como en 3b.
Si = 0 las soluciones seran ciclos cerrados elpticos y el equilibrio sera estable pero no
asintoticamente estable, como en 3a. En todos los casos el sentido del giro se puede determinar con el signo de x evaluado en el punto (0, 1): x|
(0,1) = b, si b > 0 entonces x|
(0,1) > 0
y el sentido es horario, como en 3a, 3b y 3c, si b < 0 entonces x|
(0,1) < 0 y el sentido es
antihorario4 .

En 3a las lneas punteadas corresponden a los ejes de la elipse.

Si b = 0 no se tienen races complejas.