UAB - Introducción A Las Ecuaciones Diferenciales Estocásticas

Aureli Alabert
Departament de Matem` atiques

Universitat Aut` onoma de Barcelona
Introducci
on a las
ecuaciones diferenciales
estoc
asticas
Cali, Enero de 2004
Draft Version: 2004/1/16. A. Alabert
Indice i
Indice
Indice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . i
1. Motivaci on y ejemplos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
2. Conceptos basicos de probabilidad y procesos estocasticos. . . . . . . . . . . . . 5
3. El proceso de Wiener. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4. Los modelos de Einstein-Smoluchowski y de
Ornstein-Uhlenbeck para el movimiento browniano . . . . . . . . . . . . . . . . . . . 15
4.1 El modelo de Einstein-Smoluchowski . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
4.2 El modelo de Ornstein-Uhlenbeck . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
5. Integraci on estocastica (I) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
5.1 El problema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
5.2 Integrales estoc asticas elementales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
6. Integraci on estocastica (II) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
6.1 La integral estoc astica de It o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
7. Calculo estocastico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
8. Ecuaciones diferenciales estocasticas. Existencia y unicidad . . . . . . . . . . 37
9. Referencias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
Motivaci on y ejemplos 1
1. Motivaci on y ejemplos
Desde que en el siglo XVII Newton y Leibniz pusieron las bases del que ahora llamamos C alculo
Diferencial, las ecuaciones diferenciales han sido una herramienta matem atica fundamental para
modelizar sistemas fsicos. Las leyes fsicas que gobiernan un sistema determinan las ecuaciones
correspondientes, que despues intentamos resolver, es decir, de las cuales intentamos obtener una
expresi on del estado del sistema en el instante de tiempo t como funci on explcita de t.
A veces el sistema fsico que queremos modelizar es demasiado complejo no s olo para resolver
efectivamente las ecuaciones asociadas sino incluso para llegar a formular un conjunto de ecuaciones
diferenciales que sea sucientemente representativo de sus caractersticas. Resulta que en muchas
de estas situaciones desesperadas es posible usar cierta informaci on parcial al alcance sobre
las fuerzas que interact uan y a cambio obtener determinados resultados parciales del problema.
Concretamente, veremos c omo el uso de hip otesis estadsticas en la formulaci on nos permite llegar
a conclusiones probabilsticas como resultado. Esto signica: si el estado de un sistema en el
instante t est a representado por un vector n-dimensional x(t), renunciamos a asignar un valor
a este vector, pero hacemos uso de nuestro conocimiento del comportamiento estadstico de los
elementos que afectan x(t) para contestar preguntas tales como: Cu al es la probabilidad de que
x(t) se encuentre en una cierta regi on A de R
n
?, y otras parecidas.
1.1 El ejemplo fundamental: El movimiento browniano
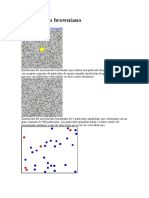
Considerese una peque na partcula (de di ametro, digamos, una micra) inmersa en un uido. A
traves de un microscopio se puede observar que la partcula se mueve de manera muy r apida e
irregular en todas direcciones, y que este movimiento no cesa nunca. Cuando el fen omeno fue
descrito por primera vez a principios del siglo XIX, diversas teoras (equivocadas) surgieron para
explicar sus causas. Actualmente, con la existencia de los atomos rmemente establecida, sabemos
que estos movimientos ca oticos son debidos al bombardeo intensivo de la partcula por parte
de las moleculas del uido que la rodea. Bajo condiciones normales de presi on y temperatura, la
partcula soporta del orden de 10
21
colisiones moleculares por segundo, cada una con su propia
direcci on y energa. A pesar de que cada colisi on individual tienen un efecto inapreciable (les
moleculas son todava mucho m as peque nas que la partcula) la superposici on de un n umero tan
enorme de choques s produce un efecto observable.
Es obvio que el c alculo diferencial cl asico puede ayudar muy poco al estudio de esta situaci on.
Que puede hacerse entonces para resolver (al menos parcialmente) el problema?
Por simplicidad, supongamos que ning un otro campo de fuerzas, como podra ser la gravedad,
interact ua con el sistema que acabamos de describir, y normalicemos a 1 la masa de la partcula.
S olo hay entonces dos orgenes de fuerzas a considerar: Por un lado, la fricci on din amica sistem atica
sufrida por la partcula en sus traslaciones, y por otro, las colisiones moleculares irregulares,
negligibles individualmente pero con efecto macrosc opico apreciable.
2 Motivaci on y ejemplos
Si olvidamos por un momento esta ultima fuente de movimiento, y denotamos por v(t) la velocidad
en el instante t, la segunda ley de Newton nos lleva inmediatamente a la ecuaci on diferencial de
primer orden
dv(t)
dt
= v(t)
v(0) = v
0
_
, (1.1)
donde la constante se determina para partculas esfericas mediante la ley de Stokes: = 6r,
siendo r el radio de la partcula y el coeciente din amico de viscosidad del uido (para partculas
no esfericas hay que cambiar el factor 6 por otro adecuado).
Consideremos la versi on integral de la ecuaci on (1.1):
v(t + t) v(t) =
_
t+t
t
v(s) ds
v(0) = v
0
_
_
_
. (1.2)
Denotemos por M(t) el incremento de momento neto ganado por la partcula debido a la segunda
fuente de fuerzas citada durante el intervalo temporal [0, t]. Teniendo en cuenta esta funci on,
v(t + t) v(t) =
_
t+t
t
v(s) ds +M(t + t) M(t)
v(0) = v
0
_
_
_
. (1.3)
M(t) es una funci on desconocida, pero si aceptamos ciertas hip otesis fsicas sobre las fuerzas que re-
presenta, estas se traducir an en propiedades matem aticas (probabilsticas) de M. Concretamente,
supongamos:
1) Las condiciones del entorno (tales como presi on, temperatura, . . . ) son constantes en el
tiempo.
2) El bombardeo sufrido por la partcula durante un intervalo de tiempo dado es independiente
de (esto es, no tiene relaci on fsica con) el sufrido en intervalos de tiempo anteriores.
3) La aceleraci on total hasta el instante t cambia continuamente respecto de t.
4) El medio es is otropo.
Veremos m as tarde c omo puede construirse un modelo matem atico que represente estas condicio-
nes. Dejando de lado la cuesti on de si 1), 2), 3) y 4) son lo bastante adecuadas al sistema que
hemos descrito (esto puede ser tema de mucha discusi on, especialmente 2)), se nalemos s olo que
el modelo que se deducir a produce resultados que se ajustan bastante bien a las observaciones
empricas.
Este ejemplo es muy cl asico (vease, por ejemplo, Nelson [22]) y continuaremos su discusi on en
captulo sucesivos. Citemos dos ejemplos m as de situaciones similares, sin especicar detalles.
1.2 Ejemplo: Verhulst
El conocido modelo de Verhulst para a la evoluci on del volumen de individuos de una especie viene
dado por la ecuaci on diferencial
dx(t)
dt
= x(t)
_
a bx(t)
_
(1.4)
(la ecuaci on logstica), que se deduce de suponer una tasa de natalidad constante a y una tasa
de mortalidad proporcional a la poblaci on bx(t). (1.4) se puede pensar como la aproximaci on
continua del planteo discreto
x(n + 1) x(n) = x(n)
_
a bx(n)
_
(1.5)
Tpicamente, las constantes a y b son idealizaciones de cantidades sometidas a uctuaciones im-
previsibles a priori. Supongamos, por ejemplo, que cambiamos a por una funci on a +(n), donde
Motivaci on y ejemplos 3
(n) representa una peque na perturbaci on de la tasa de natalidad, que es desconocida y que es
independiente (i.e., no hay relaci on de causaefecto) de las perturbaciones (m), m ,= n. Si deno-
tamos por M(n) la acumulaci on de estas perturbaciones des del instante 0 hasta el n 1, o sea
M(n) =

n1
k=0
(k), obtendremos la ecuaci on modicada
x(n + 1) x(n) = x(n)
_
a +M(n + 1) M(n) bx(n)
_
. (1.6)
Construimos ahora la aproximaci on continua de (1.6). El an alogo de los incrementos x(n+1)x(n)
en modo continuo es
x(t + t) x(t)
t
, y an alogamente para M(n+1) M(n). Escribiremos pues
x(t + t) x(t) = x(t)
_
a bx(t)
_
t +x(t)
_
M(t + t) M(t)
_
. (1.7)
Si suponemos constante el entorno en el sentido de que las causas de las perturbaciones son
invariables en el tiempo, mantenemos la independencia del valor de las perturbaciones que afectan
al sistema en intervalos disjuntos, y nalmente hacemos la hip otesis razonable de que la funci on
M(t) ha de ser continua en el tiempo, volvemos a encontrar exactamente las condiciones 1), 2)
y 3) propuestas en el ejemplo anterior como propiedades de la funci on desconocida M. Resulta
pues formalmente la misma situaci on del Ejemplo 1.1.
1.3 Ejemplo: Filtraje
Consideremos ahora el problema de llevar un satelite articial a su orbita geoestacionaria, a partir
de la orbita elptica de transferencia, que es el estadio intermedio entre la fase de lanzamiento y
el posicionamiento denitivo.
Para controlar esta delicada maniobra hay que tener una informaci on lo m as precisa posible de la
posici on del satelite en cada instante. En primera aproximaci on, teniendo en cuenta s olo la acci on
del campo gravitatorio terrestre, las ecuaciones del movimiento pueden escribirse en la forma
dx(t)
dt
= f(x(t)) (1.8)
con x(t) R
6
(tres par ametros de posici on, tres par ametros de velocidad).
Otros elementos que inuyen en la trayectoria del sate l.lit, como por ejemplo la no-esfericidad y
no-homogeneidad de la Tierra, la inuencia de otros cuerpos celestes, la presi on de radiaci on solar,
etc., pueden ser incorporados al modelo si se tiene un buen conocimiento de como act uan. Sin
embargo, intervendr an tambien perturbaciones con direcci on e intensidad no conocida a priori.
Una heurstica similar a la de los ejemplos anteriores nos lleva a escribir
x(t + t) x(t) =
_
t+t
t
f(x(s)) ds +M(t + t) M(t)
donde M es una funci on con las caractersticas 1), 2), 3) listadas en el Ejemplo 1.1.
Adem as, contamos con la informaci on adicional aportada por las estaciones de seguimiento, que
reciben una se nal
y(t) = g(t, x(t)) ,
a su vez contaminada tambien por perturbaciones en la medici on:
y(t + t) y(t) =
_
t+t
t
g(s, x(s)) ds +N(t + t) N(t) ,
siendo N(t) desconocida e independiente (en el sentido de que las causas lo son) de M(t). El
problema, que se llama ltraje, consiste en obtener la mejor informaci on posible sobre el valor de
x(t), teniendo en cuenta las observaciones y(t).
Nuestro prop osito en los captulos siguientes es presentar las herramientas matem aticas que per-
miten tratar los problemas de este tipo.
Conceptos b asicos de probabilidad y procesos estoc asticos 5
2. Conceptos b asicos de probabilidad y procesos estoc asticos
De costumbre, se dice que un experimento es aleatorio cuando su resultado no se puede conocer a
priori, a pesar de que no sea la primera vez que se realiza. El experimento puede esta gobernado
por claras leyes deterministas, pero renunciamos a efectuar los c alculos, o simplemente no sabe-
mos c omo hacerlos. A menudo, sin embargo, es posible decir algo sobre cada posible resultado.
Por ejemplo, al tirar repetidamente una moneda equilibrada, es de esperar que el cociente entre
el n umero de cruces obtenidas y el n umero de lanzamientos (la llamada frecuencia relativa) se
aproxime a 1/2 a la larga. Esto nos invita a enunciar: 1/2 es la probabilidad de obtener cruz
en cada lanzamiento de una moneda equilibrada.
Denir el concepto de probabilidad apelando a los lmites de frecuencias relativas es bastante
problem atico. La formalizaci on habitual es axiom atica y el hecho de que las frecuencias relativas
converjan en un cierto sentido a la probabilidad de un suceso se obtiene como teorema (leyes de
los grandes n umeros).
La formalizaci on habitual es la siguiente:
Sea un conjunto y T T() una - algebra de partes de . Una probabilidad es una medida
positiva y nita sobre (, T) con masa total igual a 1.

Es decir, una probabilidad sobre (, T)
es una aplicaci on P: T [0, 1] tal que P() = 0, P() = 1, y para cada familia numerable
A
i
iI
de conjuntos de T tal que A
i
A
j
= , i, j I, se tiene P(
iI
A
i
) =

iI
P(A
i
). El
espacio de medida (, T, P) recibe el nombre de espacio de probabilidad. En este contexto,
cada conjunto medible A T se llama suceso. El n umero P(A) es la probabilidad del suceso
A. Al modelizar un experimento real, cada representa un posible resultado y P(A) es la
probabilidad de que el resultado pertenezca a A.
Sea (E, c) un otro espacio medible. Una variable aleatoria E-valuada sobre (, T, P) es una
aplicaci on medible X: (, T, P) (E, c). Cuando (E, c) es el conjunto de los n umeros reales
equipado con su - algebra de Borel natural, y que denotaremos (R, B(R)), decimos simplemente
que tenemos una variable aleatoria (real). Las variables aleatorias representan el mecanismo
mediante el cual se observa el experimento. Si observamos un conjunto B c, deducimos que el
resultado del experimento pertenece a X
1
(B) T.
Dada una variable aleatoria real sobre (, T, P), podemos denir una nueva probabilidad en
(R, B(R)) como (B) := P(X
1
(B)), B B(R)). Esta nueva probabilidad asociada a P y X se
llama la ley de X bajo P. Si es una probabilidad sobre (R, B(R)), la funci on F: R R denida
por F(x) := (] , x]) recibe el nombre de funci on de distribuci on de . F es una funci on
no-decreciente y continua por la derecha vericando lim
x
F(x) = 0 y lim
x+
F(x) = 1.
Recprocamente, toda funci on con estas propiedades determina unvocamente una probabilidad
. Si F es expresable como F(x) =
_
x
f(z) dz, para alguna funci on f: R R

+
, entonces f
es la funci on de densidad de respecto la medida de Lebesgue. En tal caso, tendremos que
6 Conceptos b asicos de probabilidad y procesos estoc asticos
B B(R), (B) =
_
B
f(z) dz. Estos conceptos se extienden f acilmente a variables aleatorias R
n
-
valuadas. A menudo estas variables son llamadas vectores aleatorios, y su ley de probabilidad
la ley conjunta de las componentes del vector.
Dos sucesos A
1
, A
2
T se llaman independientes si P(A
1
A
2
) = P(A
1
) P(A
2
). Dos variables
aleatorias reales X, Y denidas sobre el mismo espacio de probabilidad son independientes si
B
1
, B
2
B(R), los sucesos X
1
(B
1
) y Y
1
(B
2
) son sucesos independientes. Intuitivamente, esto
signica que la observaci on de un suceso A a traves de la variable aleatoria X no cambia la ley de
probabilidad de Y . La denici on es an aloga para variables valuadas en cualquier espacio y para
familias de variables aleatorias.
Dada una variable aleatoria X, denimos el p-esimo momento de X como
_
X()
p
P(d),
siempre que la integral exista y sea nita. Argumentos sencillos de teora de la medida muestran
que si es la ley de X bajo P y F es la funci on de distribuci on asociada, el p-esimo momento de
X se puede calcular como la integral de Stieljes
_
R
x
p
dF(x). Si, adem as, F tiene una funci on de
densidad f, la ultima integral coincide con la integral ordinaria
_
R
x
p
f(x) dx. El primer momento
de X se llama esperanza o media de X. Lo denotamos por E[X]. Si para dos variables aleatorias
X, Y se tiene la igualdad P( : X() = Y ()) = 1, decimos que X = Y casi seguro (c.s.).
Esta no es m as que la conocida equivalencia casi por todo de la teora de la integraci on de Lebesgue.
Mediante esta relaci on, se denen los habituales espacios de Lebesgue L
p
(, T, P) de (clases de)
variables aleatorias que poseen p-esimo momento, para 0 < p < . L
(, T, P) ser a el espacio de
las variables aleatorias acotadas, mientras que L
0
(, T, p) representa el espacio vectorial de todas
las variables aleatorias, sin ninguna condici on de integrabilidad. En cualquier espacio de medida
nita se tiene 0 q p L
p
L
q
.
Sea T un conjunto ordenado. Un proceso estocastico indexado por T es una familia de variables
aleatorias (reales, si no se especica otra cosa) X
t
, t T, todas ellas denidas sobre el mismo
espacio de probabilidad. Normalmente, T es R
+
= [0, [ o N = 0, 1, 2, . . . , y se interpreta como
el tiempo, en modo continuo o discreto, de forma que un proceso estoc astico es la herramienta
apropiada para modelizar sistemas din amicos cuando el estado del sistema en cada instante t est a
gobernado por una ley de probabilidad, la ley de X
t
. Supondremos a partir de ahora T = [0, [.
Para cada jado, la funci on
X(): T R
t X
t
(w)
se llama una trayectoria del proceso. Este punto de vista nos permite pensar en un proceso
estoc astico como una variable aleatoria valuada en alg un espacio E de funciones:
X: E
X(w)
Cada posible resultado aleatorio w determina un elemento del espacio funcional, que puede ser
el espacio de todas las funciones R
T
o uno m as peque no. Se puede denir la ley de un proceso
siguiendo la misma pauta que para las variables aleatorias reales o R
n
-valuadas. Se puede de-
mostrar, por otro lado, que la ley del proceso est a completamente determinada por las leyes en
dimensi on nita, i.e. las leyes de las proyecciones de rango nito
X: R
n
(X
t1
(), . . . , X
tn
())
n N, t
1
, . . . , t
n
T.
Se caracterizan diversas clases particulares de procesos seg un propiedades de sus trayectorias o bien
propiedades relacionadas con la ley del proceso. Por ejemplo, decimos que un proceso estoc astico
es continuo si, para cada , la trayectoria X() es una funci on continua.
Conceptos b asicos de probabilidad y procesos estoc asticos 7
La continuidad es una propiedad de las trayectorias. Son ropiedades relacionadas con la ley las
siguientes: Un proceso tiene incrementos estacionarios si la ley de la variable aleatoria X
t
X
s
depende s olo de la diferencia t s, para todos t y s en T. Decimos que un proceso estoc astico tiene
incrementos independientes (del pasado) si para todos t, s T, s < t, la variable X
t
X
s
es independiente de la familia X
r
, r T, r s.
Por su importancia en aplicaciones, la ley gaussiana (o normal) merece especial atenci on. Una
variable aleatoria real X es gaussiana si su ley de probabilidad tiene funci on de densidad
f(x) =
1
2
2
exp
_
(x m)
2
2
2
_
(2.1)
para ciertos m R y
2
> 0. Lo escribimos X N(m,
2
). Se comprueba f acilmente que
las cantidades E[X] y Var[X] := E[(X E[X])
2
], llamadas media y varianza de X valen m
y
2
respectivamente. Por tanto, la media y la varianza de una variable aleatoria gaussiana
determinan completamente su ley. Es conveniente considerar tambien el caso degenerado
2
= 0
como gaussiano. Si hacemos tender
2
a cero en (2.1), observamos que f(x) converge a una de
Dirac, de forma que para
2
= 0 no hay una verdadera densidad. La ley representada por esta
densidad generalitzada concentra toda su masa en el punto m.
El an alogo de las variables gaussianas en R
n
son los vectores aleatorios con densidad
f(x) = ((2)
n
det D)
1/2
exp
_
1
2
(x m)D
1
(x m)
_
, x R
n
, (2.2)
donde m R
n
es el vector de medias y D es la matriz de covarianzas, que ha de ser denida-
positiva (o s olo semidenida-positiva en los casos degenerados en que la ley se concentra en una
variedad afn de R
n
). Cualquier proyecci on de un vector aleatorio gaussiano es de nuevo gaussiano.
La ley gaussiana n-dimensional juega un papel central en el estudio de las probabilidades en
R
n
. El an alogo en dimensi on innita a los vectores aleatorios gaussianos son los procesos es-
tocasticos gaussianos. Decimos que X
t
, t R
+
es gaussiano si sus leyes en dimensi on nita
son gaussianas.
Los siguientes teoremas, que relacionan algunos de los conceptos introducidos, nos ser an utiles
despues. (Vease Yeh [27, p` ag. 202 y 255] para una demostraci on detallada).
2.1 Teorema
Sea X X
t
, t R
+
un proceso real tal que
(H.1) es continuo y con incrementos independientes del pasado.
Entonces, existen una funci on continua m: R
+
R y una funci on continua no-decreciente
v: R
+
R tales que s, t R
+
, s < t, la variable aleatoria X
t
X
s
es gaussiana con
E[X
t
X
s
] = m(t) m(s), Var[X
t
X
s
] = v(t) v(s) . (2.3)
Si, adem as,
(H.2) X tiene incrementos estacionarios
entonces m y v satisfacen
m(t) m(s) = (t s)
v(t) v(s) =
2
(t s)
para ciertas constantes R y
2
R
+
.
y
2
se llaman coeciente de deriva y coeciente de difusi on respectivamente.
8 Conceptos b asicos de probabilidad y procesos estoc asticos
El recproco del Teorema es cierto, en el sentido de que dadas las funciones m continua y v
continua no-decreciente, existe un proceso continuo con incrementos independientes X vericando
las igualdades (2.3).
2.2 Teorema
Bajo la hip otesis (H.1), si X
0
es una variable gaussiana, entonces X
t
, t R
+
es un proceso
gaussiano.
En particular, un proceso continuo con incrementos independientes tal que X
0
x R, ha de ser
forzosamente gaussiano.
2.3 Denici on
Un proceso estoc astico real W W
t
, t R
+
es un proceso de Wiener (o movimiento
browniano) si
i) es continuo,
ii) tiene incrementos independientes del pasado,
iii) t, s, s < t, W
t
W
s
es una variable aleatoria gaussiana con esperanza cero y varianza
2
(t s), para alg un
2
R
+
.
Un proceso de Wiener comienza en x R si W
0
= x c.s.
Si, adem as,
2
= 1, W se llama proceso de Wiener estandar comenzando en x R.
Observese que un proceso de Wiener est andar es un proceso gaussiano con incrementos estaciona-
rios, y por otro lado, si X X
t
, t R
+
es un proceso continuo con incrementos estacionarios
e independientes del pasado, con X
0
= 0 c.s. y coeciente de deriva = 0, entonces X = W,
donde W es un proceso de Wiener est andar comenzando en 0.
2.4 Ejemplo (el movimiento browniano, 2)
Usando los conceptos introducidos a el captulo anterior, podemos ahora dar una versi on ma-
tem atica precisa de las hip otesis fsicas sobre la funci on M(t) del Ejemplo 1.1. Imaginaremos,
para simplicar, que el problema es unidimensional (la partcula se mueve sobre una recta). De
hecho, ser a evidente en seguida que el problema real se puede estudiar coordenada por coordenada.
Primeramente, nos hemos referido a M(t) como una funci on desconocida. Por tanto, se puede
pensar de manera natural como un proceso estoc astico M
t
(), t R
+
denido en alg un espacio
de probabilidad (, T, P). El hecho de que las causas de las fuerzas resumidas en M
t
son invarian-
tes en el tiempo (condici on 1) se modeliza imponiendo que la ley de M
t
M
s
dependa s olo de la
diferencia ts. En otras palabras, el proceso M
t
, t R
+
ha de tener incrementos estacionarios.
La incorrelaci on fsica entre las fuerzas que act uan en un intervalo dado y las que han actuado
previamente (condici on 2) signica que el proceso ha de tener incrementos independientes del pa-
sado. Finalmente, la condici on 3 de continuidad simplemente se traduce en que M
t
, t R
+
es
un proceso continuo. Podemos adem as imponer arbitrariamente M
0
= 0 en el origen del tiempo.
Seg un los Teoremas 2.1 y 2.2, en esta situaci on el proceso ha de ser gaussiano con E[M
t
] = t y
Var[M
t
] =
2
t. La isotropa del medio en que se mueve la partcula (no hay ninguna direcci on
privilegiada para las fuerzas provenientes de los choques moleculares) la representamos poniendo
coeciente de deriva = 0.
Ahora s olo hay que usar las observaciones que siguen a la denici on de proceso de Wiener para
concluir que M
t
= W
t
, siendo W un proceso de Wiener est andar comenzando en 0. Sobre el
valor concreto de volveremos m as adelante.
La ecuaci on (1.3) puede escribirse pues
v(t + t) v(t) =
_
t+t
t
v(s) ds +
_
W(t + t) W(t)
_
v(0) = v
0
_
_
_
. (2.4)
El proceso de Wiener 9
3. El proceso de Wiener
Hay ciertas propiedades de las trayectorias del proceso de Wiener denido en el Captulo 2 que es
importante remarcar. Estas s on:
- Las trayectorias W
t
(), t R
+
del proceso de Wiener son no-derivables en ning un punto,
casi seguro. Esto es consecuencia esencialmente de la propiedad de incrementos independien-
tes.
- Las trayectorias del proceso de Wiener tienen variaci on total innita en todo intervalo [a, b], a <
b, casi seguro. Es una consecuencia inmediata de la anterior.
- La variaci on cuadr atica de las trayectorias del proceso de Wiener es no nula y nita. El
sentido preciso de esta armaci on se ver a cuando especiquemos que entendemos por variaci on
cuadr atica en este contexto. Intuitivamente, dado que E[[W
t
W
s
[
2
] = t s, la variaci on
[W
t
W
s
[ ser a posiblemente del orden de

t s, lo que hace que, dada una partici on t
0
<
< t
n
de un intervalo [a, b], sea l ogico esperar que
n
k=1
[W
t
k
W
t
k1
[
2
b a .
En este captulo se enuncian y demuestran rigurosamente estas propiedades, que por otra parte
pueden encontrarse en multitud de libros.
3.1 Proposici on
Casi seguro, las trayectorias de un proceso de Wiener W son no-diferenciables en ning un punto.
Demostraci on: Supongamos para simplicar que estamos hablando de un proceso de Wiener
est andar. (Si no, algunas de las cantidades que aparecer an vendr an afectadas por una constante,
pero los argumentos no cambian.) Para k, n N, sean
X
nk
:= max
_
[W
k2
n W
(k1)2
n[, [W
(k+1)2
n W
k2
n[, [W
(k+2)2
n W
(k+1)2
n[
_
y
Y
n
:= min
k
n
2
n
X
nk
.
Las tres variables dentro de los valores absolutos son independientes y tienen la misma ley que
2
n/2
W
1
, de donde
PX
nk
=
_
P[W
1
[ 2
n/2
_
3
(22
n/2
)
3
,
10 El proceso de Wiener
y obtenemos
PY
n

n2
n
k=0
PX
nk
n2
n
(2
n/2+1
)
3
.
Denotemos
A := : W() tiene derivada en alg un punto .
Si W() es derivable en el punto t y D es su derivada, entonces existir a = (t, ) tal que
[s t[ [W
s
() W
t
()[ ([D[ + 1)[s t[.
Existe un n
0
= n
0
(t, ) tal que
n n
0

_
_
n > t ,
n > 2([D[ + 1) ,
2
n
< /2 .
Para cada n n
0
, escogemos k tal que k2
n
t <
k+1
2
n
. Entonces [t i2
n
[ < para i =
k 1, k, k + 1, k + 2. Por tanto,
X
nk
([D[ + 1)2 2
n
n2
n
,
y en consecuencia, como k 2
n
t < 2
n
n,
Y
n
n2
n
.
Hemos probado que A A
n
:= Y
n
n2
n
, para todo n a partir de un cierto n
0
. Es
decir,
A lim
n
A
n
.
Finalmente,
P(A) P(lim
n
A
n
) = P(
n
kn
A
k
) = lim
n
P(
kn
A
k
)
lim
n
P(A
n
) lim
n
n2
n
(2 2
n/2
n2
n
)
3
= 0 .
3.2 Deniciones
Dados una funci on f: [a, b] R y una partici on = a = t
0
< t
1
< < t
n
= b de [a, b], se
llama variaci on de f en [a, b] respecto la partici on a la cantidad
V
[a,b],
(f) :=
ti,ti+1
[f(t
i+1
) f(t
i
)[ .
Se llama variaci on de f en [a, b] a la cantidad
V
[a,b]
(f) := sup
ti,ti+1
[f(t
i+1
) f(t
i
)[ ,
donde vara en el conjunto de todas las particiones de [a, b].
Una funci on tal que V
[a,b]
(f) < se dice que es de variaci on acotada (o nita) en [a, b].
Toda funci on real de variable real con variaci on acotada en un intervalo [a, b] es derivable en
[a, b] excepto en un conjunto de medida de Lebesgue cero. Por tanto, como consecuencia de
la Proposici on 3.1, las trayectorias del proceso de Wiener son de variaci on no-acotada en todo
intervalo no degenerado [a, b], casi seguro. Veremos que esto se deduce tambien del hecho de que
las trayectorias tienen casi seguro variaci on cuadr atica no nula (vease la Proposici on 3.7).
La denici on de variaci on cuadr atica que se usa en An alisis es la que parece natural: La variaci on
cuadr atica de f en un intervalo [a, b] es
V
2
[a,b]
(f) := sup
ti,ti+1
[f(t
i+1
) f(t
i
)[
2
,
y en general se puede denir la variaci on de orden k de manera similar. No obstante, cuando
hablamos de variaci on cuadr atica en la teora de procesos estoc asticos no nos referimos exactamente
a esto, sino al concepto que denimos seguidamente.
Denotaremos por [[[[ := max
ti,ti+1
[t
i+1
t
i
[ la norma de una partici on . Una sucesi on
n
n
de
particiones de [a, b] decimos que es renante si
n

n+1
, n.
3.3 Denici on
Sea
n
n
una sucesi on renante de particiones de [a, b] tal que lim
n
[[
n
[[ = 0.
Se llama variaci on cuadratica de f: [a, b] R al lmite, si existe y no depende de la sucesi on
n
escogida,
V
2
[a,b]
(f) := lim
n
V
2
[a,b],
(f) := lim
n
ti,ti+1n
[f(t
i+1
) f(t
i
)[
2
.
Para funciones continuas, se tiene que
V
[a,b]
(f) := lim
n
ti,ti+1n
[f(t
i+1
) f(t
i
)[ ,
si
n
es cualquier sucesi on renante con lim
n
[[
n
[[ = 0. Pero esto no es cierto para la variaci on
cuadr atica.
3.4 Proposici on
Las trayectorias de un proceso de Wiener est andar W tienen casi seguro variaci on cuadr atica igual
a la constante b a en todo intervalo [a, b].
Idea de la demostraci on: Este resultado se puede demostrar de la manera siguiente:
1) Tomar una sucesi on renante
n
n
de [a, b] con lim
n
[[
n
[[ = 0 y ver que
L
2
()- lim
n
V
2
[a,b],n
(W) = b a .
2) Demostrar que
c.s.- lim
n
V
2
[a,b],n
(W)
existe.
3) De 1) y 2) se obtiene que el lmite casi seguro de V
2
[a,b],n
(W) ha de ser b a.
La manera eciente de demostrar la parte 2) de la proposici on anterior requiere profundizar pre-
viamente en la teora de martingalas, y no lo haremos aqu. Nos limitaremos a demostrar la parte
1), con una peque na ampliaci on: Como es habitual cuando se tiene convergencia en L
2
(o sim-
plemente en probabilidad), si podemos asegurar que la convergencia es sucientemente r apida, se
obtiene tambien convergencia casi segura, va el fundamental Lema de BorelCantelli, que puede
encontrarse en cualquier referencia b` asica de probablidades.
3.5 Proposici on
Sea W un proceso de Wiener est andar. Sea
n
n
una sucesi on renante de particiones de [a, b]
tal que lim
n
[[
n
[[ = 0.
12 El proceso de Wiener
Entonces
L
2
- lim
n
V
2
[a,b],n
(W) = b a .
Si, adem as, se cumple

n
[[
n
[[ < , entonces
c.s.- lim
n
V
2
[a,b],n
(W) = b a .
Demostraci on: Simplicaremos la notaci on poniendo
i
:= t
i+1
t
i
W(
i
) := W
ti+1
W
ti
V
2
n
:= V
2
[a,b],n
(W) =
ti,ti+1
W(
i
)
2
.
Usando la independencia de incrementos del proceso de Wiener y las propiedades de la ley normal,
tenemos que
E[(V
2
n
(b a))
2
] =
i,j
E
_

W(
i
)
2

W(
j
)
2
2(b a)
i
E
_

W(
i
)
2
+ (b a)
2
=
i=j
j
+ 3
2
i
2(b a)
i
+ (b a)
2
= 3
2
i
+
i=j
j

_
i
_
2
+
_
i
(b a)
_
2
= 3
2
i

2
i
2[[
n
[[
i
= 2[[
n
[[(b a)
n
0 .
Supongamos ahora que [[[[
n
0. Denotemos X
n
= V
2
n
(b a). Acabamos de ver que
E[X
2
n
] 2[[
n
[[(ba), para todo n. Por la desigualdad de Chebishef, si ponemos A
n
:= [X
n
[ > ,
P(A
n
)
E[X
2
n
]
2

2[[
n
[[(b a)
2
,
n=1
P(A
n
) < .
Por el Lema de BorelCantelli, P
_
n=1
m=n
A
c
n
_
= 1. Es decir, para todo en este conjunto de
probabilidad 1, existe n tal que si m n, se tiene [X
n
()[ , y obtenemos la convergencia casi
segura.
3.6 Observaci on
Si el proceso de Wiener tiene varianza
2
, entonces la variaci on cuadr atica en [a, b] es
2
(b a).
Ya hemos razonado que las trayectorias del proceso de Wiener han de ser casi seguro de variaci on
no-acotada. Veamos como se puede deducir esto de la Proposici on 3.5.
3.7 Proposici on
Las trayectorias de un proceso de Wiener est andar W tienen casi seguro variaci on no-acotada en
todo intervalo no degenerado [a, b].
Demostraci on: En el conjunto V
[a,b]
(W) < , tendremos
b a = lim
n
ti,ti+1n
[W
ti+1
W
ti
[
2
lim
n
sup
ti,ti+1n
[W
ti+1
W
ti
[
ti,ti+1n
[W
ti+1
W
ti
[
V
[a,b]
(W) lim
n
sup
ti,ti+1n
[W
ti+1
W
ti
[
= 0 , c.s.,
puesto que las trayectorias de W son uniformemente continuas en [a, b], y la desigualdad es absurda.
Por tanto, el conjunto V
[a,b]
(W) < tiene probabilidad cero.
Adem as, el conjunto de probabilidad cero donde la variaci on s es acotada, no depende del intervalo
[a, b] escogido. En efecto, esto es obviamente cierto si nos restringimos a intervalos con extremos
racionales. Pero cualquier intervalo abierto es uni on numerable de intervalos de este tipo.
3.8 Ejemplo (movimiento browniano, 3)
Sabemos que las trayectorias del proceso de Wiener son no-derivables en ning un punto. Por tanto,
esta claro que en la ecuaci on (2.4) no podemos dividir por t y tomar lim
t0
para llegar a una
ecuaci on diferencial ordinaria, parametrizada por . Hemos de quedarnos con la forma integral
v
t
= v
0

_
t
0
v
s
ds +W
t
. (3.1)
La ecuaci on (3.1), a pesar de todo, se puede resolver deriv andola formalmente y aplicando tecnicas
elementales de ecuaciones diferenciales ordinarias. La soluci on que se obtiene,
v
t
= e
t
_
v
0
+
_
t
0
W
s
e
s
ds
_
,
puede expresarse, despues de integrar por partes, como
v
t
= e
t
_
v
0
+W
t
e
t
_
t
0
W
s
e
s
ds
_
, (3.2)
que vuelve a tener sentido riguroso y se puede comprobar directamente que satisface (3.1). A
partir de la velocidad encontramos, simplemente integrando, la funci on que nos da la posici on de
la partcula browniana en cada instante:
x
t
= x
0
+
_
t
0
_
e
s
_
v
0
+ W
s
e
s
_
s
0
W
r
e
r
dr
_
_
ds . (3.3)
Los procesos x
t
, t R
+
y v
t
, t R
+
reciben el nombre de proceso de posici on y pro-
ceso de velocidad de Ornstein-Uhlenbeck, respectivamente. Las f ormulas (3.2) y (3.3) dan
explcitamente las trayectorias de x y v en funci on de las de W, y a partir de ellas podemos calcular
la ley de estos procesos, que es en realidad la informaci on util que buscamos. x y v resultan ser
procesos gaussianos con
E[v
t
] = v
0
e
t
Cov[v
t
, v
s
] =

2
2
_
e
2(ts)
1
_
e
(t+s)
E[x
t
] = x
0
+
v
0
(1 e
t
)
Cov[x
t
, x
s
] =

2
2
(s t) +

2
2
3
_
e
(t+s)
e
|ts|
+ 2(e
s
+e
t
1)
_
donde Cov[X, Y ] := E[(X E[X])(Y E[Y ])] se llama covarianza de las variables X e Y . La
ley de un proceso gaussiano queda determinada por las medias y las covarianzas entre las variables
del proceso. Los c alculos anteriores est an detallados, por ejemplo, en Arnold [1].
Los modelos de Einstein-Smoluchowski y de Ornstein-Uhlenbeck para el movimiento browniano 15
4. Los modelos de Einstein-Smoluchowski y de
Ornstein-Uhlenbeck para el movimiento browniano
Los movimientos err aticos de partculas peque nas en un uido del Ejemplo 1.1 fueron estudiados
por primera vez por el bot anico ingles Robert Brown alrededor de 1827 ([5], [6]). (Parece ser que
hay tambien un trabajo anterior del neerlandes Jan Ingenhousz, hacia el 1785.) Desde entonces,
este fen omeno ha sido conocido con el nombre de movimiento browniano. La primera des-
cripci on matem atica del movimiento browniano fue presentada por Albert Einstein [10] en 1905
(vease Nelson [22] para un breve resumen de la historia del tema), quien propuso el proceso de
Wiener como modelo matem atico para las trayectorias de las partculas. Por cierto, Einstein dice
que no conoca el trabajo de Brown; su deducci on de la existencia de movimientos observables
de las peque nas partculas es puramente te orica, y se obtiene como consecuencia de la teora
at omica. Actualmente, movimiento browniano y proceso de Wiener se usan frecuentemente
como sin onimos.
M as tarde el modelo de Einstein fue mejorado por Ornstein y Uhlenbeck (vease Uhlenbeck-Ornstein
[26], Chandrasekar [7], Wang-Uhlenbeck [28], y especialmente Doob [9]) los cuales hicieron inter-
venir el proceso de Wiener en su modelo pero no directamente como versi on matem atica del mo-
vimiento browniano. Para evitar confusiones, parece mejor usar el nombre de proceso de Wiener
para el objeto matem atico, y el de movimiento browniano para el fen omeno fsico.
4.1 El modelo de Einstein-Smoluchowski
La primera explicaci on mnimamente satisfactoria del movimiento browniano fue dada por Einstein
(1905) y tambien independientemente por Marian von Smoluchowski (1906), quien trabaj o m as en
el tema tanto desde el punto de vista te orico como experimental. La modelizaci on del movimiento
browniano como proceso de Wiener se conoce como el modelo de EinsteinSmoluchowski.
El razonamiento que hizo Einstein es como sigue (no hay mucho rigor matem atico, pero las ideas
son buenas):
Se supone que cada partcula individual ejecuta un movimiento que es independiente de los mo-
vimientos de las dem as partculas. Se supone tambien que los movimientos de una determinada
partcula en intervalos disjuntos de tiempo son procesos fsicos independientes, siempre que estos
intervalos no se tomen demasiado peque nos.
Introducimos un intervalo temporal de longitud , muy peque no comparado con los intervalos
temporales observables, pero todava lo bastante grande para que en dos intervalos sucesivos, los
movimientos ejecutados puedan pensarse como independientes uno del otro.
16 Los modelos de Einstein-Smoluchowski y de Ornstein-Uhlenbeck para el movimiento browniano
Sea N el n umero total de partculas en suspensi on en un lquido. En un intervalo temporal ,
las coordenadas de las partculas individuales se incrementar an en una cantidad , donde, para
cada partcula, tendr a un valor diferente (positivo o negativo). seguir a una cierta ley de
frecuencias; la cantidad dN de partculas que experimentaran un desplazamiento que est a entre
y +d ser a expresable como
dN = N() d ,
donde
_
+
() d = 1 ,
y es diferente de cero s olo para valores muy peque nos de , y satisface
() = () .
Nos restringiremos al caso en que la concentraci on (cantidad de partculas por unidad de volumen)
depende s olo de la coordenada x y el tiempo t. Denotemosla por f(x, t).
Calcularemos la distribuci on de las partculas en el instante t + a partir de la distribuci on en el
instante t. La cantidad de partculas que en el instante t + se encontrar an entre los puntos x y
x +dx ser a
f(x, t +) dx = dx
_
+
f(x + , t)() d . (4.1)

Como es muy peque no, podemos poner
f(x, t +) = f(x, t) +
f
t
(x, t) .
Por otra parte, desarrollemos f(x + , t) en potencias de :
f(x + , t) = f(x, t) +
f(x, t)
x
+

2
2!
2
f(x, t)
x
2
+
Podemos usar esta serie para hacer la integral de (4.1), porque s olo nos interesan valores peque nos
de . Obtenemos
f +
f
t
= f
_

() d +
f
x
_

() d +

2
f
x
2
_

2
2
() d + (4.2)
Por la simetra de , los terminos segundo, cuarto, etc, de la derecha se anulan. Entre los otros,
cada termino es muy peque no comparado con el anterior. Nos quedaremos s olo con el primero y
el tercero. Introducimos la constante
D :=
1
_
+
2
2
() d
y nos queda
f
t
= D
2
f
x
2
, (4.3)
la ecuaci on de la difusi on, ya conocida en tiempos de Einstein. La difusi on es un fen omeno
fsico que consiste en el hecho de que un conjunto de partculas disueltas en un uido tienden
a desplazarse de las zonas de m as concentraci on a las zonas de menos concentraci on, como por
ejemplo una gota de tinta en un cubo de agua, que se va esparciendo y perdiendo color, hasta
desaparecer. D es una constante dependiente del medio que se llama coeciente de difusi on.
La soluci on es, suponiendo que hacemos difusi on de N partculas a partir del origen, y despreciando
la interacci on entre ellas,
f(x, t) =
N
4Dt
expx
2
/4Dt . (4.4)
Los modelos de Einstein-Smoluchowski y de Ornstein-Uhlenbeck para el movimiento browniano 17
En R
3
, obtendramos la ecuaci on
df
dt
= D
3
i=1
2
f
x
2
i
, (4.5)
y el resultado sera
f(t, x) =
N
(4Dt)
3/2
exp
_
[x[
2
4Dt
_
. (4.6)
Para una sola partcula (N = 1), (4.6) puede interpretarse como la densidad de probabilidad de
encontrar la partcula en una regi on del espacio determinada al cabo de un tiempo t. Es decir, la
probabilidad de encontrar la partcula en la regi on A viene dada por
_
A
(4Dt)
3/2
exp[x[
2
/4Dt dx . (4.7)
Esta densidad esencialmente caracteriza al proceso de Wiener (el proceso de Wiener en R
3
tiene
por coordenadas procesos de Wiener reales independientes). M as precisamente, es la densidad
de X
t
=

2DW
t
, donde W es un proceso de Wiener est andar (tridimensional). Esto justica
el nombre de coeciente de difusi on para la constante
2
en el Teorema 2.1. (En realidad, sale
2
= 2D. Si es quiere que el 2 no aparezca, hay que cambiar D por D/2 en las ecuaciones (4.3) y
(4.5).
Los diversos artculos de Einstein sobre el movimiento browniano est an recogidos en el libro de
Furth [12]. Los artculos cl asicos posteriores de Uhlenbeck y Ornstein, Chandrasekar, Wang y
Uhlenbeck, y Doob, se encuentran reunidos tambien en forma de libro (Wax [29]).
El proceso de Wiener fue estudiado por primera vez con rigor por Norbert Wiener, en una serie
de trabajos entre 1923 y 1934, y de ah su nombre. Wiener se beneci o de los recientes avances en
teora de la medida llevados a cabo por

Emile Borel, Henri Lebesgue y J. P. Daniell, para hacer
una construcci on del proceso a partir del espacio de trayectorias. Einstein no dispona todava de
estas herramientas y su construcci on se limita a la ley; no a las trayectorias.
4.2 El modelo de Ornstein-Uhlenbeck
Modelizar el movimiento browniano como un proceso de Wiener (modelo de Einstein-Smoluchowski)
tiene el inconveniente de que la propiedad de variaci on total innita de las trayectorias implica
que la partcula browniana recorre caminos de longitud innita en tiempo nito. Esto estimul o el
abandono de este modelo.
En cambio, el modelo que estamos desarrollando (conocido como modelo de Ornstein-Uhlenbeck)
da lugar a velocidades nitas. Son las aceleraciones las que pasan a tener valores innitos.
Hemos empezado formulando unas ciertas hip otesis fsicas de tipo microsc opico (de comporta-
miento mec anico molecular) con la idea que a partir de ellas se puedan predecir de forma te orica
los comportamientos macrosc opicos observables. Esto nos ha llevado a la ecuaci on fsica (1.3).
Posteriormente, hemos visto las herramientas que posibilitan formular un modelo con pleno sentido
matem atico, (2.4) o (3.1). Un ultimo paso, puramente notacional en este momento, es expresar la
ecuaci on (3.1) en forma diferencial
dv
t
= v
t
dt + dW
t
, (4.8)
o
v
t
= v
t
+

W
t
. (4.9)
A pesar de que dW
t
no existe, podemos tomar (4.8) y (4.9) simplemente como smbolos que
abrevian la formulaci on integral (3.1). En todo caso, constituyen un primer ejemplo (muy sencillo!)
de lo que llamamos una ecuaci on diferencial estoc astica.
18 Los modelos de Einstein-Smoluchowski y de Ornstein-Uhlenbeck para el movimiento browniano
Vamos a completar la formulaci on del modelo de Ornstein-Uhlenbeck para el movimiento brow-
niano, determinando el unico elemento de la ecuaci on que las hip otesis iniciales no nos han per-
mitido determinar: el coeciente .
De la f ormula para Cov[v
t
, v
s
] del Captulo 3, deducimos que
Var[v
t
] =

2
2
_
1 e
2t
_
,
y por tanto, haciendo t , obtenemos una varianza lmite de
2
/2, sea cual sea la velocidad
inicial v
0
. An alogamente, se observa que lim
t
E[v
t
] = 0. La ley de equirepartici on de la energa
en mec anica estadstica arma que la energa cinetica media de un sistema de partculas (las
moleculas del uido) en estado de equilibrio termodin amico ha de valer
1
2
kT por grado de libertad
del sistema, siendo k la constante de Boltzmann y T la temperatura absoluta. La partcula
sumergida en el uido ha de compartir esta misma energa media. La esperanza de la energa
cinetica de la partcula se puede calcular pues como
E[
1
2
v
2
] =

2
4
(donde v representa la velocidad lmite y seguimos haciendo el convenio de que la masa de la
partcula vale 1), y obtenemos por tanto la igualdad
2
4
=
kT
2
. (4.10)
Por otro lado, hay una relaci on sencilla entre el coeciente de difusi on D y el de fricci on ,
demostrada por Einstein:
D =
kT
. (4.11)
Deducimos de (4.10) y (4.11) que, en el caso de dimensi on 1,
2
se expresa en terminos de los
coecientes de fricci on y de difusi on como
2
= 2
2
D .
Nuestra ecuaci on diferencial estoc astica (4.8) para la velocidad de la partcula browniana es pues
dv
t
= v
t
dt +
2DdW
t
,
y queda completo el modelo. La nueva hip otesis que hemos introducido para poder determinar
es que el sistema de moleculas verica la ecuaci on termica de los gases ideales
pV = nkT ,
que es de donde se deduce la ley de equirepartici on. Aqu p es la presi on, V el volumen y n el
n umero total de moleculas.
Integraci on estoc astica (I) 19
5. Integraci on estoc astica (I)
5.1 El problema
Hemos podido resolver la ecuaci on (3.1) sin usar nada m as que los trucos habituales del c alculo,
pero se trata de hecho de un caso muy particular. El punto clave es que, aunque no tenga sentido
hablar del diferencial dW
t
para ninguna trayectoria, en cambio s se puede dar un sentido evidente
a la expresi on
_
t
0
dW
s
. Tan solo hay que denir este smbolo como W
t
W
0
, que no es m as que el
valor que se obtiene mediante sumas de Riemann. En general, si X
t
es una funci on (o un proceso)
de variaci on acotada, y teniendo en cuenta que W es un proceso continuo, se puede denir
_
t
0
X
s
dW
s
mediante sumas de Riemann para cada valor del par ametro . El resultado coincide con el que se
obtendra integrando formalmente por partes:
X
t
W
t
X
0
W
0

_
t
0
W
s
dX
s
,
donde la ultima integral tiene sentido como integral de RiemannStieljes cl asica. (Recuerdese que,
m as en general, para toda funci on de variaci on acotada , se puede denir la integral de Lebesgue
respecto d
_
b
a
f(t) d(t)
de cualquier funci on f que sea Lebesgue-integrable en [a, b] respecto la variaci on total de .)
5.1 Ejemplo (Verhulst, 2)
Retomando el Ejemplo 1.2 del Captulo 1 (modelo de Verhulst con tasa de natalidad perturbada),
apliquemos a la ecuaci on discretizada (1.7) el mismo razonamiento que hemos usado en el movi-
miento browniano. Obtenemos, en forma integral, (tal vez con alguna constante multiplicando
a W)
x
t
= x
0
+
_
t
0
x
s
(a bx
s
) ds +
_
t
0
x
s
dW
s
,
i en forma diferencial,
dx
t
= x
t
(a bx
t
) dt +x
t
dW
t
, (5.1)
con la condici on inicial x
0
.
20 Integraci on estoc astica (I)
Como se ha visto en los ejemplos, hay situaciones en las cuales no funciona la integraci on por
partes para denir la integral respecto de un proceso estoc astico con trayectorias irregulares. En
efecto, observese en (5.1) si el proceso soluci on x
t
fuera de variaci on acotada, tambien lo sera
integral respecto dt y en consecuencia la integral respecto dW
t
tambien debera serlo; por otra
parte, integrando por partes esta integral el resultado es claramente de variaci on no acotada. Por
tanto no es en absoluto obvio el sentido que hay que dar al smbolo
_
t
0
x
t
dW
t
en estos casos. La ecuaci on (5.1) es una genuina ecuaci on diferencial estoc astica, en el sentido
que no es una pura aleatorizaci on de una ecuaci on diferencial ordinaria.
En general, si la inuencia de una perturbaci on externa a un sistema depende del tiempo y del
estado del sistema en cada instante, frecuentemente se puede modelizar el sistema resultante
mediante una ecuaci on diferencial del tipo
dx(t) = f(t, x(t)) dt +g(t, x(t)) dM(t) , (5.2)
donde dx(t) = f(t, x(t))dt es la ecuaci on correspondiente al sistema sin perturbar y g es una
funci on que representa la sensitividad del sistema a la perturbaci on M.
Cuando M es aleatoria e irregular, es frecuente que pueda modelizarse mediante un proceso de
Wiener, y se obtiene una ecuaci on que no s olo no tiene sentido cl asico en forma diferencial, sino
que tampoco lo tiene en forma integral
x
t
= x
0
+
_
t
0
f(s, x
s
) ds +
_
t
0
g(s, x
s
) dW
s
, (5.3)
a menos que g sea tan regular que suavice las irregularidades que x
t
hereda de W
t
, como suceda
en nuestro primer ejemplo (g constante).
Hay que dar un sentido pues al smbolo
_
t
0
g(s, x
s
) dW
s
(5.4)
de forma que se pueda interpretar como la aportaci on total de la perturbaci on aleatoria al estado
del sistema en el intervalo [0, t].
El resultado de integrar un proceso en un intervalo jado [0, t] ser a naturalmente una variable
aleatoria. Por tanto lo que buscamos es un operador con dominio un cierto espacio de procesos, a
valores en L
0
(, T, P) y que para merecer el nombre de integral, debera ser
1) lineal,
2) continuo en alg un sentido (lo que equivale a tener alg un teorema de convergencia).
Queremos, adem as, que
3) si X
s
() es de variaci on acotada para todo , se tenga
_
_
t
0
X
s
dW
s
_
() =
_
t
0
X
s
() dW
s
() ,
extendiendo de este modo el concepto de integral de Stieljes usual.
Un objetivo modesto es intentar que el operador act ue al menos sobre procesos continuos. Las
condiciones 2) y 3) sugieren entonces denir la integral de un proceso continuo f
t
() respecto el
proceso de Wiener como el lmite de las sumas
_
_
t
0
X
s
dW
s
_
() := lim
n
ti,ti+1n
X
i
()
_
W
ti+1
() W
ti
()
_
,
si el lmite de la derecha existe y es independiente de la sucesi on de particiones renante
n
nN
con [[
n
[[ 0 y los puntos
i
[t
i
, t
i+1
] escogidos. Y esto para cada jado o, m as debilmente,
tomando el lmite en la topologa natural de L
0
(, T, P), i.e. la topologa de la convergencia en
medida. Esto correspondera a denir un operador continuo entre el espacio de procesos continuos
con la topologa inducida por la convergencia uniforme (en (t, )) y el espacio de variables aleatorias
L
0
(, T, p) con la convergencia en medida.
Pero desgraciadamente esto es imposible. En efecto:
5.2 Teorema
Sea (t) una funci on continua en [0, 1].
Sea
n
nN
una sucesi on renante de particiones de [0, 1] tal que la sucesi on de normas tiende a
cero.
Entonces,
ti,ti+1n
f(t
i
) ((t
i+1
) (t
i
))
converge a un lmite nito cuando n para toda funci on continua f si y s olo si (t) es de
variaci on acotada.
Reproducimos aqu una demostraci on simple de este Teorema, sugerida por Meyer [20] y que
contiene la clave para evitar estas dicultades. La demostraci on usa el conocido Teorema de
BanachSteinhauss, que recordamos:
5.3 Lema (Teorema de BanachSteinhauss).
Sean B
1
un espacio de Banach y B
2
un espacio normado. Sea T
i
iI
una familia de operadores
lineales acotados T
i
: B
1
B
2
.
Si para cada x B
1
, sup
iI
[[T
i
x[[ < , entonces sup
iI
[[T
i
[[ < .
Demostraci on del Teorema:
) Es conocido. Converge a la integral de RiemannStieljes
_
1
0
f(t) d(t).
) Sean B
1
el espacio de funciones continuas en [0, 1] con la norma del supremo, B
2
= R con el
valor absoluto.
Para a cada n N, sea T
n
: B
1
B
2
el operador denido por
T
n
f :=
ti,ti+1n
f(t
i
) ((t
i+1
) (t
i
)) .
Por hip otesis, lim
n
T
n
f existe, y por tanto sup
n
[T
n
f[ < . Gracias al Lema, sup
n
[[T
n
[[ < .
Vamos a ver que la variaci on de ,
V
(1)
() := sup
P
ti,ti+1
[(t
i+1
) (t
i
)[ ,
es m as peque na que sup
n
[[T
n
[[, con lo que habremos acabado. Efectivamente, para cada n N
jado, sea f una funci on continua tal que f(t
i
) = signo(t
i+1
) (t
i
) y [[f[[
= 1. Entonces:
T
n
f =
ti,ti+1n
f(t
i
)((t
i+1
) (t
i
)) =
ti,ti+1n
[(t
i+1
) (t
i
)[
[[T
n
[[

ti,ti+1n
[(t
i+1
) (t
i
)[
sup
n
[[T
n
[[ sup
n
ti,ti+1n
[(t
i+1
) (t
i
)[ = V
(1)
() ,
la ultima igualdad gracias a que el sup
n
es sustituible por lim
n
, y la caracterizaci on de la variaci on
de una funci on en terminos de sucesiones de particiones mencionada en el Captulo 3.
Se puede pensar que, al ser el operador que buscamos valuado en L
0
(, T, p) en vez de R, tal vez
s que se puede obtener la convergencia en medida de las sumas
ti,ti+1n
f
ti
() (
ti+1
()
ti
()) (5.5)
en vez de la convergencia casi segura en . Pero la situaci on no es mejor, ya que en el conjunto
A = :
t
() no es de variaci on acotada podramos construir una sucesi on parcial de (5.5)
convergente casi seguro, y repetir la demostraci on del Teorema para esta parcial. Por tanto, si
P(A) > 0, llegamos a la misma dicultad que en el caso determinista, en que no est` a.
5.2 Integrales estocasticas elementales
Llamamos integrales estocasticas a las expresiones del tipo
_
b
a
X
t
dZ
t
, (5.6)
en que Z es un proceso estoc astico, y X es una funci on determinista o, tal vez, otro proceso
estoc astico. Hay tres tipos de integrales estoc asticas que podemos llamar elementales:
Hemos visto que si X y Z tienen trayectorias de variaci on acotada, podemos denir de manera
natural la variable aleatoria (5.6) como
_
_
b
a
X
t
dZ
t
_
() :=
_
b
a
X
t
() dZ
t
() . (5.7)
y en general podemos usar esta denici on siempre que tenga sentido el termino de la derecha con
probabilidad 1.
Si Z no tiene trayectorias de variaci on acotada pero X s, entonces podemos usar la integraci on
por partes (estamos suponiendo que ahora X y Z son continuos para simplicar):
_
b
a
X
t
dZ
t
:= X
t
Z
t
X
0
Z
0
_
b
a
Z
t
dX
t
,
donde la ultima integral se dene por como en (5.7).
El tercer tipo de integral que podramos todava llamar elemental, pero que empieza a mostrar
algunos elementos caractersticos de la integraci on estoc astica no trivial, es la que puede construirse
cuando el integrando es determinista, y el integrador es de cuadrado integrable (Z
t
L
2
(), t) y
con incrementos independientes. Esta integral tiene interes por s misma aparte de las ecuaciones
diferenciales estoc asticas, pues se usa en la teora de procesos estacionarios y en el estudio de series
temporales.
Queremos denir la integral de f respecto W en [a, b] para toda funci on f del espacio L
2
([a, b], dt).
Sea o L
2
([a, b], dt) el conjunto de todas las funciones f de la forma
f(t) :=
n
i=1
c
i
1
]ti1,ti]
(t) ,
a = t
0
< t
1
< < t
n
= b (funciones escalonadas).
Para f o denimos
_
b
a
f(t) dW
t
:=
n
i=1
c
i
(W
ti
W
ti1
) .
Esta denici on es independiente de la representaci on particular de la funci on f.
5.4 Proposici on
La aplicaci on
I: o L
2
([a, b], dt) L
2
(, T, P)
f
_
b
a
f(t) dW
t
tiene las propiedades siguientes:
1) I(c
1
f
1
+c
2
f
2
) = c
1
I(f
1
) +c
2
I(f
2
).
2) E[I(f)] = 0.
3) E
_
I(f)I(g)
=
_
b
a
f(t)g(t) dt, y, en particular, preserva la norma: [[I(f)[[
L
2
()
= [[f[[
L
2
([a,b],dt)
.
Demostraci on:
(1) Inmediato.
(2) Sale del hecho de que W es un proceso centrado (E[W
t
] = 0, t).
(3) Representamos f y g respecto la misma partici on:
f(t) =
n
i=1
c
i
1
]ti1,ti]
,
g(t) =
n
i=1
d
i
1
]ti1,ti]
.
Entonces,
E
_
I(f)I(g)
= E
_
n
i,j=1
c
i
d
j
(W
ti
W
ti1
)(W
tj
W
tj1
)
_
=
n
i=1
c
i
d
i
E
_
(W
ti
W
ti1
)
2
=
n
i=1
c
i
d
i
(t
i
t
i1
)
=
_
b
a
f(t)g(t) dt .
5.5 Proposici on
El conjunto o es un subespacio denso de L
2
([a, b], dt).
Sea f L
2
([a, b], dt), y sea f
n
n
o una sucesi on convergente a f en L
2
([a, b], dt). Esta sucesi on
ser a de Cauchy en L
2
([a, b], dt) y, por la propiedad de isometra (Proposici on 5.4, 3), su imagen
I(f
n
)
n
ser a de Cauchy en L
2
(), y por tanto convergente.
5.6 Denici on
En la situaci on anterior, se dene la integral estoc astica de f respecto W en [a, b] como
_
b
a
f(t) dW
t
:= lim
n
_
b
a
f
n
(t) dW
t
.
Para que la denici on tenga sentido, tiene que ser independiente de la sucesi on f
n
n
escogida.
Se puede comprobar que lo es.
Hemos denido pues un operador
I: L
2
([a, b], dt) L
2
()
f
_
b
a
f(t) dW
t
5.7 Proposici on
El operador integral estoc astica I tiene las propiedades 1), 2) y 3) de la Proposici on 5.4.
Demostraci on: S olo hay que ver que las citadas propiedades se conserven por paso al lmite
en L
2
([a, b], dt): La linealidad es obvia; la convergencia en L
2
implica la convergencia de las
esperanzas; por ultimo, en todo espacio de Hilbert, si x
n
x y y
n
y, entonces x
n
, y
n
) x, y).
Se puede considerar la integral estoc astica como un proceso: Dada f
tR
+
L
2
([0, t]), podemos
considerar el proceso integral estocastica
_
_
t
0
f(s) dW
s
, t R
+
_
.
5.8 Proposici on
El proceso integral estoc astica tiene incrementos independientes.
Esta construcci on de la integral estoc astica es v alida usando cualquier proceso Z con incrementos
independientes y continuo por la derecha en L
2
(es decir, tal que E[[Z
t
Z
s
[
2
] 0 cuando
t s) como integrador. En tal caso, existe una funci on de distribuci on (i.e., una funci on creciente
continua por la derecha) F tal que
F(b) F(a) = E[[Z
b
Z
a
[
2
] , 0 a b . (5.8)
Las funciones f que podemos usar como integrandos son las del espacio L
2
([a, b], dF), y la integral
estoc astica es una isometra
I: L
2
([a, b], dF) L
2
()
f
_
b
a
f(t) dZ
t
No tiene dicultad repetir todo lo anterior en esta situaci on m as general. Adem as, se tiene el
siguiente resultado de tipo Radon-Nikod ym:
5.9 Proposici on
Sea F la funci on de distribuci on asociada al proceso con incrementos independientes Z. Sean
f L
2
([0, t], dF) y Y
t
:=
_
t
0
f(t) dZ
t
.
Entonces, el proceso con incrementos independientes Y tiene funci on de distribuci on asociada
G(t) =
_
t
0
f
2
(t) dF(t), y si g L
2
([0, t], dG) se tiene
_
t
0
g(s) dY
s
=
_
t
0
g(s)f(s) dZ
s
, c.s .
Integraci on estoc astica (II) 25
6. Integraci on estoc astica (II)
6.1 La integral estocastica de It o
Para construir la integral estoc astica con integrandos aleatorios, la construcci on anterior no es
suciente. La demostraci on del Teorema 5.2 nos dar a una pista de c omo proceder ahora. En prin-
cipio, este teorema parece que nos previene de poder hacer una denici on de la integral mediante
sumas de Riemann; no obstante, eso es precisamente lo que vamos a hacer.
Est a claro que tendremos que imponer alguna restricci on al integrando, pero no queremos pedir
m as regularidad a sus trayectorias, porque no obtendramos nada util de cara a las ecuaciones
diferenciales estoc asticas. Buscaremos restricciones de otro tipo.
Repasemos un momento la demostraci on del ultimo Teorema. Para ver la necesidad de que el
integrador sea de variaci on acotada hemos usado funciones que tomaban unos valores determinados
sobre los puntos de cada partici on:
f(t
i
) := signo(t
i+1
) (t
i
)
Observemos que, para asignar estos valores, f mira hacia adelante la funci on ; es decir, el valor
de f en t
i
depende del valor de en t
i+1
. Si prohibimos esta dependencia, la demostraci on queda
invalidada.
Nuestro objetivo es pues poner esta restricci on en terminos matem aticos, y observar despues que
no impide modelizar problemas reales con el formalismo de (5.4). Hay que introducir primero unos
cuantos conceptos adicionales.
Dado un espacio de probabilidad (, T, P) , cualquier familia creciente T
t
, t R
+
de sub--
algebras de T se llama una ltraci on, y la estructura (, T, P, T
t
, t R
+
) es un espacio de
probabilidad ltrado. Una ltraci on toma nota de la evoluci on en el tiempo de la informaci on
disponible en cada instante. Expliquemos esta frase. Una variable aleatoria X denida en (, T, P)
induce una sub-- algebra de T, llamada - algebra generada por X), que es la m as peque na que
hace medible la aplicaci on X, y que se denota habitualmente por <X>. Esta - algebra est a
formada por los unicos conjuntos que son observables a traves de X; dicho de otro modo, de
los unicos sucesos que podemos decidir si se han vericado o no (i.e., si pertenece a el o no)
con la sola informaci on del resultado concreto X(). En este sentido <X> es la informaci on
suministrada por X. Ahora, si X X
t
, t R
+
es un proceso estoc astico, la informaci on total
suministrada por el proceso hasta en el instante t es la m as peque na - algebra que hace medibles
todas las aplicaciones de la familia X
s
, s t. Lo escribimos <X
s
, s t>. Los conjuntos
26 Integraci on estoc astica (II)
de esta - algebra son los observables a traves del proceso una vez este ha llegado al instante t.
<X
s
, s t>, t R
+
es la ltraci on generada por el proceso X.
Dado un espacio de probabilidad ltrado (, T, P, T
t
, t R
+
), un proceso estoc astico X sobre
(, T, P) se dice que es adaptado a T
t
, t R
+
si X
t
es T
t
-medible (medible respecto T
t
)
para cada t R
+
. Si T
t
, t R
+
es la ltraci on generada por un otro proceso Y decimos que
X es adaptado a Y .
Sea W W
t
, t R
+
un proceso de Wiener. Una ltraci on T
t
, t R
+
se dice que no
anticipa W si se satisfacen las condiciones siguientes:
1) W es adaptado a T
t
, t R
+
.
2) s R, T
s
y <W
t
W
s
, t s> son - algebras independientes (esto es, todo suceso de
una de ellas es independiente de todo suceso de la otra).
Tales ltraciones efectivamente existen. T omese por ejemplo la inducida por el propio W, o sea
<W
s
, s t>, t R
+
, gracias a la propiedad de incrementos independientes de W.
Un proceso estoc astico X se dice que es medible si, como aplicaci on X: R
+
R, es medible
respecto la - algebra producto de los borelianos de R
+
con T.
Diremos que un proceso estoc astico X es no-anticipativo respecto un proceso de Wiener W si:
1) X es un proceso medible.
2) X es adaptado a alguna ltraci on no-anticipativa de W.
A veces los llamaremos simplemente procesos medibles y adaptados.
Ahora tenemos a la nuestra disposici on los ingredientes necesarios para modelizar la condici on
no vale mirar hacia adelante de la que habl abamos. Como veremos en seguida, la condici on
de noanticipaci on del integrando permite desarrollar una teora satisfactoria de la integraci on
respecto al proceso de Wiener.
6.1 Notaci on
Denotaremos por T[a, b] la colecci on de procesos no-anticipativos X tales que P : X()
L
2
([a, b]) = 1.
Normalmente, identicaremos en T[a, b] dos procesos que sean indistinguibles (es decir, con las
mismas trayectorias excepto un conjunto de probabilidad cero). De esta manera estamos haciendo
un paso al cociente, pero seguiremos usando la notaci on T[a, b] para este conjunto cociente.
6.2 Proposici on
El conjunto T[a, b] es un espacio vectorial con las operaciones usuales de suma y producto por
escalares.
Demostraci on: Si X
1
, . . . , X
n
son procesos no-anticipativos y H: R
n
R es una funci on medible,
est a claro que H(X
1
, . . . , X
n
) es un proceso no-anticipativo. En particular, es cierto si H es una
funci on lineal.
Vamos a introducir una convergencia a el espacio vectorial T[a, b], y veremos que le dota de
estructura de espacio metrico.
6.3 Denici on
Sea X
n
n
T[a, b].
Diremos que X
n
n
converge a X T[a, b] si la sucesi on de variables aleatorias
_

_
b
a
[X
n
t
() X
t
()[
2
dt
_
n
converge a cero en probabilidad. Dicho de otra manera, si
[[X
n
X[[
L
2
([a,b])
P
0 .
6.4 Proposici on
La aplicaci on
d: T[a, b] T[a, b] R
+
(X, Y ) E
_
[[X Y [[
L
2
([a,b])
1 +[[X Y [[
L
2
([a,b])
_
es una distancia y metriza la convergencia de la Denici on 6.3.
Demostraci on: Sabemos que d(X, Y ) := [[X Y [[ es una distancia en L
2
([a, b]). Por otra parte,
siempre que d es una distancia en un espacio metrico, se tiene que d
(x, y) =
d(x,y)
1+d(x,y)
es tambien
una distancia en el mismo espacio (equivalente al anterior). Esto nos da la desigualdad triangular
[[X Y [[
L
2
([a,b])
1 +[[X Y [[
L
2
([a,b])
[[X Z[[
L
2
([a,b])
1 +[[X Z[[
L
2
([a,b])
+
[[Z Y [[
L
2
([a,b])
1 +[[Z Y [[
L
2
([a,b])
.
Tomando esperanzas, resulta la desigualdad triangular de la aplicaci on d, que es la unica dicultad
por comprobar que es una distancia.
Veamos ahora que metriza la convergencia que hemos denido en T[a, b]: Supongamos primer que
> 0, P[[X
n
X[[
L
2
([a,b])
>
n
0 .
Entonces,
E
_
[[X
n
X[[
L
2
([a,b])
1 +[[X
n
X[[
L
2
([a,b])
_
=
_
{||X
n
X||
L
2
([a,b])
}
[[X
n
X[[
L
2
([a,b])
1 +[[X
n
X[[
L
2
([a,b])
dP +
_
{||X
n
X||
L
2
([a,b])
<}
[[X
n
X[[
L
2
([a,b])
1 +[[X
n
X[[
L
2
([a,b])
dP
P[[X
n
X[[
L
2
([a,b])
+P[[X
n
X[[
L
2
([a,b])
<
P[[X
n
X[[
L
2
([a,b])
+
n
.
Siendo esto v alido para todo > 0, resulta que d(X
n
, X)
n
0, como queramos ver.
Recprocamente, suponemos que d(X
n
, X)
n
0. Fijemos > 0.
P[[X
n
X[[
L
2
([a,b])
= P
_
[[X
n
X[[
L
2
([a,b])
1 +[[X
n
X[[
L
2
([a,b])

1 +
_
1 +
E
_
[[X
n
X[[
L
2
([a,b])
1 +[[X
n
X[[
L
2
([a,b])
_

n
0 .
6.5 Notaci on
Denotaremos por L
2
a
([a, b] ) el conjunto de procesos de L
2
([a, b] ) adaptados a la ltraci on
no-anticipativa T
t
, t R
+
:
L
2
a
([a, b] ) :=
_
X : X es no-anticipativo y E
_
_
b
a
X
2
t
dt
_
<
_
.
Est a claro que el conjunto L
2
a
([a, b] ) es un subespacio de el espacio de Hilbert L
2
([a, b] ) y
que est a contenido en T[a, b].
6.6 Denici on
Un proceso estoc astico no-anticipativo X diremos que es simple (o escalonado) en [a, b] si existe
una partici on a = t
0
< t
1
< < t
n
= b tal que
X
t
() = X
t
k
() , , t [t
k
, t
k+1
[ .
Equivalentemente, si X se puede escribir en [a, b] como
X
t
() =
n1
k=0
c
k
()1
[t
k
,t
k+1
[
(t) ,
con c
k
variables aleatorias T
t
k
-medibles.
Denotaremos por o[a, b] el conjunto de procesos simples, que es claramente un subespacio vectorial
de T[a, b]
6.7 Denici on
Sea X o[a, b].
Denimos la integral de X respecto el proceso de Wiener W como la variable aleatoria sobre
(, T, P)
_
_
b
a
X
t
dW
t
_
() :=
n1
k=0
c
k
()
_
W
t
k+1
W
t
k
() .
6.8 Proposici on
La aplicaci on entre espacios vectoriales
o[a, b] P[a, b] L
0
()
X
_
b
a
X
t
dW
t
est a bien denida y es lineal.
6.9 Proposici on
Sea X o[a, b]. Entonces:
1) Si [a
, b
] [a, b], entonces X o[a
, b
], X 1
[a
[
o[a, b], y
_
b
X
t
dW
t
=
_
b
a
X
t
1
[a
,b
[
(t) dW
t
.
2) Si c ]a, b[, entonces X o[a, c], X o[c, b], y
_
b
a
X
t
dW
t
=
_
c
a
X
t
dW
t
+
_
b
c
X
t
dW
t
.
3)
_
E[X
t
] < , t [a, b]
_
= E
_
_
b
a
X
t
dW
t
_
= 0 .
4)
_
E[X
2
t
] < , t [a, b]
_
=E
_
_
b
a
X
t
dW
t
2
_
=
_
b
a
E[X
2
t
] dt .
6.10 Proposici on
Sea X o[a, b].
Entonces, > 0, N > 0,
P
_
_
b
a
X
t
dW
t
> N
_
P
_
_
b
a
X
2
t
dW
t
>
_
+

N
2
.
6.11 Proposici on
o[a, b] es denso en T[a, b].
Demostraci on: Se demuestra siguiendo estos tres pasos:
1) o es denso en los procesos continuos.
2) Los procesos continuos son densos en los acotados.
3) Los procesos acotados son densos en T[a, b].
6.12 Proposici on
La aplicaci on entre espacios metricos
o[a, b] T[a, b] L
0
()
X
_
b
a
X
t
dW
t
es continua y transforma sucesiones de Cauchy en sucesiones de Cauchy.
6.13 Lema (Teorema de extensi on de funciones continuas.)
Sean E un espacio metrico y F un espacio metrico completo.
Sean A

A = E, y f: A F una funci on continua.
Entonces: Existe una extensi on continua de f a E si y s olo si f transforma sucesiones de Cauchy
en sucesiones de Cauchy.
En caso armativo, la extensi on es unica y viene dada por
f: EF
x

f(x) := lim
n
f(x
n
)
donde x
n
n
A es una sucesi on cualquiera que converge a x.
6.14 Denici on
Sea X T[a, b].
Sea X
n
n
o[a, b] una sucesi on cualquiera que converja a X en el espacio metrico T[a, b].
Entonces denimos la integral estoc astica de X respecto el proceso de Wiener W como la variable
aleatoria sobre (, T, P)
_
b
a
X
t
dW
t
:= P- lim
n
_
b
a
X
n
t
dW
t
.
6.15 Proposici on
La aplicaci on entre espacios vectoriales
T[a, b] L
0
()
X
_
b
a
X
t
dW
t
obtenida en la Denici on 6.14 es lineal.
6.16 Proposici on
Sea X T[a, b].
Entonces, > 0, N > 0,
P
_
_
b
a
X
t
dW
t
> N
_
P
_
_
b
a
X
2
t
dW
t
>
_
+

N
2
.
6.17 Proposici on
Sea X L
2
a
([a, b] ).
Entonces, existe X
n
n
o[a, b] L
2
a
([a, b] ) tal que
1) [[X
n
t
X
t
[[
L
2
([a,b])

n
0 .
2) [[
_
b
a
X
n
t
dW
t

_
b
a
X
t
dW
t
[[
L
2
()

n
0 .
6.18 Observaci on
La Proposici on 6.17 sugiere que si nos restringimos a procesos de L
2
a
, podemos denir la integral
estoc astica como un operador continuo entre espacios de Hilbert
L
2
a
([a, b] ) L
2
() .
Efectivamente, podemos repetir todo el que hemos hecho en esta situaci on m as agradable, pero
menos general.
6.19 Proposici on
Sea X T[a, b]. Entonces:
1) Si [a
, b
] [a, b], entonces X o[a
, b
], X 1
[a
[
o[a, b], y
_
b
X
t
dW
t
=
_
b
a
X
t
1
[a
,b
[
(t) dW
t
.
2) Si c ]a, b[, entonces X o[a, c], X o[c, b], y
_
b
a
X
t
dW
t
=
_
c
a
X
t
dW
t
+
_
b
c
X
t
dW
t
.
Si, adem as, X L
2
a
([a, b] ), entonces
3) E
_
_
b
a
X
t
dW
t
_
= 0 .
4) E
_
_
b
a
X
t
dW
t
2
_
=
_
b
a
E[X
2
t
] dt .
6.20 Proposici on (Aproximaci on por sumas de Riemann.)
Sea X T[a, b] un proceso continuo c.s.
Entonces, para cualquier sucesi on de particiones
n
= a = t
(n)
0
< t
(n)
1
< < t
(n)
mn
= b de [a, b]
tal que [[
n
[[ 0, se cumple
mn1
k=0
X
t
(n)
k
_
W
t
(n)
k+1
W
t
(n)
k
n
_
b
a
X
t
dW
t
.
6.21 Observaci on
Si, en la situaci on de la Proposici on 6.20, consideramos
S
n
=
mn1
k=0
W
u
(n)
k
_
W
t
(n)
k+1
W
t
(n)
k
,
donde cada u
(n)
k
es un punto arbitrario de [t
(n)
k
, t
(n)
k+1
], entonces la existencia y el valor concreto de
P- lim
n
S
n
depende de la elecci on de los u
(n)
k
.
Por ejemplo, si ponemos
u
(n)
k
= t
(n)
k+1
+ (1 )t
(n)
k
, para un cierto [0, 1], n, k,
se obtiene
S
n
L
2
n
1
2
(W
2
b
W
2
a
) + (
1
2
)(b a) .
En particular, usando la Proposici on 6.20, esto nos dice que
_
b
a
W
t
dW
t
=
1
2
(W
2
b
W
2
a
)
1
2
(b a) ,
y concluimos que la integral de It o no sigue las regles del c alculo newtoniano.
Se puede denir una integral estoc astica que respete las regles del c alculo newtoniano? El ejemplo
que hemos visto sugiere que podramos hacerlo, al menos para procesos continuos, deniendo
_
b
a
X
t
dW
t
:= P- lim
n
mn1
k=0
X
1
2
(t
(n)
k
+t
(n)
k+1
)
_
W
t
(n)
k+1
W
t
(n)
k
.
Esto se puede hacer, en efecto, y obtendramos, para X
t
= W
t
_
b
a
W
t
dW
t
=
1
2
(W
2
b
W
2
a
) .
Pero esta integral (llamada integral de Stratonovich) tiene otros inconvenientes.
C alculo estoc astico 33
7. C alculo estoc astico
En el c alculo diferencial e integral cl asico, los teoremas fuertes como por ejemplo los de Cambio
de Variable, Integraci on por Partes, Teorema Fundamental del C alculo, etc. nos permiten calcular
integrales sin recurrir a los complicados pasos al lmite que se desprenden de las deniciones.
Es razonable esperar que resultados an alogos puedan ser demostrados para el c alculo asociado a
las integrales estoc asticas, al que llamamos C alculo Estoc astico. Esto es as, efectivamente, pero
las f ormulas que resulten no son formalmente iguales a las correspondientes del c alculo cl asico.
Empezaremos enunciando la f ormula de Cambio de Variable, de la cual pueden deducirse las
dem as.
Denotemos T
2
:=
t
T[0, t], con t R
+
o t [0, T].
7.1 Teorema (Cambio de Variable).
Sea g T
2
.
Sea X
t
el proceso denido por X
t
:=
_
t
0
g
s
dW
s
.
Sea : R R una funci on dos veces derivable con continuidad.
Entonces:
(X
t
) = (X
0
) +
_
t
0
(X
s
) g
s
dW
s
+
1
2
_
t
0
(X
s
) g
2
s
ds . (7.1)
Si comparamos esta f ormula con la an aloga del c alculo integral habitual observamos que aparece
un termino adicional.
7.2 Ejemplo
Sean X
t
= W
t
y (x) = x
n
. Obtendremos:
W
n
t
=
_
t
0
nW
n1
s
dW
s
+
1
2
_
t
0
n(n 1)W
n2
s
ds
_
t
0
W
n1
s
dW
s
=
W
n
t
n

n 1
2
_
t
0
W
n2
s
ds .
En particular:
_
t
0
W
s
dW
s
=
W
2
t
2

t
2
,
resultado diferente al que se obtiene con el c alculo diferencial tradicional.
Una consecuencia inmediata del Teorema 7.1 es que el conjunto de procesos que son integrales
estoc asticas no es cerrado por transformaciones tan regulares como x x
2
del ejemplo anterior.
34 C alculo estoc astico
Una dW
s
-integral es convierte en un proceso suma de una dW
s
-integral y una ds-integral. (Una ds-
integral es claramente de variaci on acotada mientras que la dW
s
-integral tiene variaci on cuadr atica
no nula; de ah que ninguna de ellas se puede convertir en la otra).
La raz on intuitiva por la que aparece el termino adicional es la siguiente: Usando la f ormula de
Taylor para en el punto W
t
, evaluada en W
t+t
, y dividiendo por t, se tiene:
(W
t+t
) (W
t
)
t
=
(W
t
)
W
t+t
W
t
t
+
1
2
(W
t
)
(W
t+t
W
t
)
2
t
+
Si W
t
fuese una funci on derivable, el termino cuadr atico y todos los de orden superior convergeran
claramente a cero cuando t 0 y obtendramos la conocida regla de la cadena para la compo-
sici on W. En el nuestro caso, deniendo
dW
t
dt
= lim
t0
W
t+t
W
t
t
(esto es precisamente
lo que estamos haciendo cuando ponemos W
t
W
s
:=
_
t
s
dW
r
), y observando que (W
t+t
W
t
)
2
es del orden de t cuando t 0 (variaci on cuadr atica de W), obtenemos justamente (7.1) para
el caso X
t
= W
t
. Lo mismo sucede cuando X
t
es un proceso integral estoc astica.
Denotemos por T
1
el conjunto de procesos no-anticipativos con trayectorias integrables en el
intervalo que se este considerando.
7.3 Denici on
Sean g T
2
y f T
1
.
Sea X
0
una variable aleatoria T
0
-medible.
Un proceso X de la forma
X
t
= X
0
+
_
t
0
f
s
ds +
_
t
0
g
s
dW
s
se llama proceso de It o.
Es inmediato de la denici on que un proceso de It o es siempre continuo y adaptado. La clase de
los procesos de It o es cerrada por Cambio de Variable. Formularemos una versi on m as general del
Teorema 7.1, dejando que act ue sobre n procesos de It o al mismo tiempo (en lugar de una sola
integral estoc astica) y que dependa tambien de t. Esta versi on se conoce como a F ormula de
It o y es la herramienta b asica del C alculo Estoc astico.
7.4 Teorema (F ormula de It o).
Sean X
(i)
n
i=1
, n procesos de It o con representaci on
X
(i)
t
= X
(i)
0
+
_
t
0
f
(i)
s
ds +
_
t
0
g
(i)
s
dW
s
, i = 1, . . . , n .
Denotemos

X
t
= (X
(1)
t
, . . . , X
(n)
t
).
Sea
: R R
n
R
(t, x) (t, x)
una funci on tal que

t
,

x
i
,

2
x
i
x
j
existen y son continuas.
Entonces, Y
t
:= (t,

X
t
) es de nuevo un proceso de It o, y se puede escribir como
Y
t
= Y
0
+
_
t
0
_
s
(s,

X
s
) +

x
i
(s,

X
s
)f
(i)
s
+
1
2
x
i
x
j
(s,

X
s
)g
(i)
s
g
(j)
s
_
ds
+
_
t
0
x
i
(s,

X
s
)g
(i)
s
dW
s
C alculo estoc astico 35
(sumando de 1 a n sobre los ndices repetidos).
7.5 Denici on
Si X
t
= X
0
+
_
t
0
f
s
ds+
_
t
0
g
s
dW
s
es un proceso de It o, decimos que tiene diferencial estocastica
dX
t
= f
t
dt +g
t
dW
t
.
Por ejemplo, hemos visto que dW
2
t
= 2W
t
dW
t
+ dt. La notaci on de diferenciales estoc asticas
permite una economa en la escritura. La F ormula de It o puesta en forma diferencial,
dY
t
=
_
t
(t,

X
t
) +

x
i
(t,

X
t
)f
(i)
t
+
1
2
x
i
x
j
(t,

X
t
) g
(i)
t
g
(j)
t
_
dt +

x
i
(t,

X
t
)g
(i)
t
dW
t
(7.2)
sugiere el nombreRegla de la cadena, con el que tambien se la conoce. Si hacemos el convenio
dW
t
dW
t
= dt, dW
t
dt = dt dW
t
= 0, dt dt = 0, y dX
1
dX
2
es la multiplicaci on de los respectivos
binomios, podemos escribir (7.2) en la forma m as compacta
dY
t
=

t
(t,

X
t
) dt +

x
i
(t,

X
t
) dX
(i)
t
+
1
2
x
i
x
j
(t,

X
t
) dX
(i)
t
dX
(j)
t
.
Aplicando la regla de la cadena a las diferenciales estoc asticas
dX
(1)
t
= f
(1)
t
dt +g
(1)
t
dW
t
dX
(2)
t
= f
(2)
t
dt +g
(2)
t
dW
t
con (t, x
1
, x
2
) = x
1
x
2
obtenemos la F ormula de Integraci on por Partes
d(X
(1)
t
X
(2)
t
) = X
(1)
t
dX
(2)
t
+X
(1)
t
dX
(2)
t
+dX
(1)
t
dX
(2)
t
.
Por ejemplo, podemos calcular otra vez
_
t
0
W
s
dW
s
integrando por partes:
_
t
0
W
s
dW
s
= W
2
t

_
t
0
W
s
dW
s

_
t
0
ds
_
t
0
W
s
dW
s
=
W
2
t
2

t
2
.
Aplicando el Teorema 7.1 a X
t
=
_
t
0
dW
s
= W
t
, obtenemos, para de clase C
2
,
(W
t
) = (W
0
) +
_
t
0
(W
s
) dW
s
+
1
2
_
t
0
(W
s
) ds ,
que sera un Teorema Fundamental del Calculo, o bien
_
t
0
(W
s
) dW
s
= (W
t
) (W
0
)
1
2
_
t
0
(W
s
) ds ,
en forma de Regla de Barrow.
7.6 Ejemplo
Veamos ahora como se resuelve una ecuaci on diferencial estoc astica muy sencilla usando el c alculo
estoc astico. Se trata de la ecuaci on del modelo de Verhulst sin mortalidad:
dX
t
= aX
t
dt +X
t
dW
t
con condici on inicial X
0
dada.
36 C alculo estoc astico
Si W fuera derivable, escribiramos
dX
t
X
t
= (a +

W
t
) dt ,
y la soluci on se encuentra en seguida integrando y tomando exponenciales. Siguiendo la misma
idea, calculamos d(log X
t
) usando la f ormula de It o:
d(log X
t
) =
1
X
t
dX
t
+
1
2

1
X
2
t
(dX
t
)
2
=
1
X
t
(aX
t
dt +X
t
dW
t
)
1
2

1
X
2
t
2
X
2
t
dt
= (a
2
/2) dt + dW
t
,
de donde
log X
t
= log X
0
+
_
t
0
(a
2
/2) ds +
_
t
0
dW
s
= log X
0
+ (a
2
/2)t +W
t
,
y nalmente
X
t
= X
0
exp(a
2
/2)t +W
t
.
7.7 Ejemplo
An alogamente al ejemplo anterior, se resuelve la ecuaci on diferencial
dX
t
= X
t
dW
t
X
0
= 1
_
.
d(log X
t
) =
1
X
t
dX
t
+
1
2

1
X
2
t
(dX
t
)
2
dt = dW
t

1
2
dt .
Integrando y usando X
0
= 1, obtenemos
log X
t
= W
t

1
2
t ,
y tomando exponenciales
X
t
= expW
t

1
2
t .
Por analoga con el c alculo cl asico, llamamos a X
t
la funci on exponencial estocastica, que
diere de la usual en el factor exp
1
2
t.
Ecuaciones diferenciales estoc asticas. Existencia y unicidad 37
8. Ecuaciones diferenciales estoc asticas. Existencia y unicidad
Hemos desarrollado un concepto de integral y unas reglas de c alculo que pretenden ser bien adap-
tados al estudio de sistemas con incertidumbre. Para acabar de justicar esta armaci on s olo
hay que comprobar si situaciones como las de los ejemplos vistos pueden ser modelizadas con el
formalismo de las ecuaciones diferenciales estoc asticas del tipo de (4.8) o (5.1). Esto ser a cierto
siempre que tengamos la seguridad que las integrales que hay implcitas en la ecuaci on diferencial
estoc astica tienen sentido. La cuesti on crtica es sin duda si el integrando de la integral estoc astica
es o no adaptado a una ltraci on noanticipativa del proceso de Wiener.
Una forma bastante general de ecuaci on diferencial estoc astica de primer orden en dimensi on 1 es
dX
t
= f(t, X
t
) dt +g(t, X
t
) dW
t
, t R
+
, (8.1)
donde X
t
es el proceso inc ognita, W
t
es el proceso de Wiener, y f(t, x) y g(t, x) son funciones
reales denidas y medibles en R
+
R, que llamamos coecientes de la ecuaci on.
Supongamos que combinamos esta ecuaci on con una condici on inicial x
0
R (es decir, una variable
aleatoria constante) y que la evoluci on de X
t
no tiene otra causa de aleatoriedad que la inducida
por la evoluci on del proceso W W
t
, t R
+
. En tal caso, no tiene sentido pensar que la
soluci on hasta el instante t vaya a depender de lo que el azar deparar a despues del instante t. Por
lo tanto, es razonable buscar soluciones sin esta dependencia, y el formalismo funciona.
M as generalmente, supongamos que la condici on inicial es una variable aleatoria X
0
independiente
de todas las variables del proceso W. Entonces esperaremos soluciones que hasta el instante t
dependan de la condici on inicial y del proceso W hasta t, pero no m as all a.
En este captulo precisaremos el concepto de soluci on de (8.1) y enunciaremos dos resultados
cl asicos (de existencia y unicidad, y de dependencia de condiciones iniciales) para este tipo de
ecuaciones. No se trata de los mejores enunciados posibles; s olo pretenden ilustrar algunas ana-
logas y diferencias con los resultados hom ologos de la teora de ecuaciones diferenciales ordinarias.
Comencemos con la denici on de soluci on de (8.1), lo que equivale a precisar exactamente que
entendemos por la expresi on (8.1).
8.1 Denici on
Un proceso X
t
, t R
+
T es soluci on de (8.1) con condici on inicial X
0
= si y s olo si:
1) X
t
, t R
+
es adaptado a alguna ltraci on T
t
, t T noanticipativa de W.
2) g
t
:= g(t, X
t
) T
2
i

f
t
:= f(t, X
t
) T
1
.
3) X
t
tiene diferencial estoc astica
dx
t
=

f
t
dt + g
t
dW
t
.
38 Ecuaciones diferenciales estoc asticas. Existencia y unicidad
Equivalentmente, X
t
satisface
X
t
= +
_
t
0
f(s, X
s
) ds +
_
t
0
g(s, X
s
) dW
s
, t R
+
. (8.2)
Las condiciones 1) y 2) de la denici on garantizan que las expresiones de 3) tienen sentido. En
particular, observese que
dX
t
= f(t, X
t
) dt +g(t, X
t
) dW
t
X
0
=
_
(8.3)
s olo podr a tener soluci on si es una variable aleatoria independiente de todo el proceso W.
Para el problema de Cauchy (8.3) con g 0 (ecuaci on diferencial ordinaria), el resultado cl asico
de existencia y unicidad de soluci on requiere que f cumpla alguna condici on de Lipschitz. Esto
permite demostrar mediante iteraciones de Picard la existencia y unicidad. Es natural intentar el
mismo tipo de planteo en el caso g , 0.
8.2 Teorema
Supongamos que:
1) existe K > 0 tal que
[f(t, x) f(t, y)[ +[g(t, x) g(t, y)[ K [x y[ , t [0, T] , x, y R .
2) existe L > 0 tal que
[f(t, x)[
2
+[g(t, x)[
2
L (1 +[x[
2
) , t [0, T] , x, y R .
3) es una variable aleatoria independiente de W
t
, t T.
Entonces:
a) Existe una soluci on de (8.3) que es un proceso continuo.
b) Si X
1
y X
2
son procesos continuos soluci on de (8.3), entonces sup
t[0,T]
[X
1
t
X
2
t
[ = 0, c.s.
S olo se asegura la unicidad de soluci on continua debido a la ambig uedad en la denici on del proceso
integral estoc astica. De hecho, la exigencia de continuidad puede incorporarse a la denici on de
soluci on, y entonces es puede armar que dos soluciones s olo dieren en un conjunto de trayectorias
de probabilidad nula.
La dependencia de la soluci on respecto de la condici on inicial es similar a la que se encuentra en
el caso determinista. En particular, se tiene el siguiente resultado de diferenciabilidad de primer
orden respecto una condici on inicial constante.
8.3 Teorema
Supongamos:
1) Las funciones f(t, x) y g(t, x) satisfacen las hip otesis 1) y 2) del Teorema 8.1.
2) Las derivadas parciales

x
f(t, x) y

x
g(t, x) existen y son continuas y acotadas.
Ecuaciones diferenciales estoc asticas. Existencia y unicidad 39
Entonces, la soluci on X
t
(c), t R
+
del problema de Cauchy
dx
t
= f(t, x
t
) dt +g(t, x
t
) dW
t
x
0
= c
_
,
con R, es derivable en L
2
() respecto c (esto es, existe L
2
() lim
h0
X
t
(c +h) X
t
(c)
h
) y
el proceso derivada y
t
(c) :=
d
dc
x
t
(c), t R
+
satisface la ecuaci on variacional
dy
t
(c) =

x
f(t, x
t
(c)) y
t
(c) dt +

x
g(t, x
t
(c)) y
t
(c) dW
t
y
0
(c) = 1
_
. (8.4)
N otese que (8.4) es una ecuaci on lineal (en el sentido que los coecientes son lineales respecto
el proceso inc ognita) en Y
t
(c), pero con coecientes aleatorios. Es por tanto, en realidad, una
ecuaci on de primer orden de un tipo m as general que (8.1).
I.V. Girsanov encontr o, en 1962, un ejemplo muy sencillo de ecuaci on diferencial estoc astica que
tiene un comportamiento diferente que su an aloga determinista por lo que respecta a la unicidad
de soluciones. La mayora de libros sobre ecuaciones diferenciales estoc asticas la mencionan:
La ecuaci on diferencial ordinaria
dx
t
= [x
t
[
dt
x
0
= 0
_
, t [0, T] , (8.5)
con 0 < < 1, tiene una innidad de soluciones. En efecto, para todo s [0, T], la funci on
x
t
=
_
0 , si 0 t s
[(1 )(t s)]
(1)
1
, si t s
es soluci on de (8.5).
En cambio, la ecuaci on estoc astica
dX
t
= [X
t
[
dW
t
X
0
= 0
_
, t [0, T] , (8.6)
resulta tener innitas soluciones si 0 < < 1/2, pero s olo una unica soluci on (la trivial) para
1/2, aunque no cumple las condiciones del Teorema 8.1.
M as detalles sobre los resultados apuntados en este captulo y en general sobre la teora de las
ecuaciones diferenciales estoc asticas se pueden encontrar en Gihhman-Skorohod [14], Arnold [1] o
Gard [13].
Uno puede preguntarse si podemos aproximar la soluci on de una ecuaci on diferencial estoc astica
por soluciones de ecuaciones diferenciales con una perturbaci on aleatoria m as regular, que per-
mita ser tratada con los medios del c alculo cl asico, y obtener la soluci on de la ecuaci on estoc astica
por paso al lmite.
Supongamos que W
(n)
n
es una sucesi on de procesos estoc asticos, con trayectorias de clase C
1
,
tal que para todo (con probabilidad 1), converge al proceso de Wiener
W
(n)
t
() W
t
()
uniformemente en t sobre intervalos acotados. Para cada , sea X
(n)
t
() la soluci on de la corres-
pondiente ecuaci on determinista
dX
t
= f(t, X
t
) dt +g(t, X
t
) dW
(n)
t
.
40 Ecuaciones diferenciales estoc asticas. Existencia y unicidad
Se demuestra que la sucesi on de procesos X
(n)
n
converge tambien uniformemente sobre interva-
los acotados a un cierto proceso X. Este proceso resulta ser la soluci on de una ecuaci on diferencial
estoc astica con los mismos coecientes, siempre y cuando la integral estoc astica se interprete en
el sentido de Stratonovich (vease el Captulo 6):
X
t
= X
0
+
_
t
0
f(s, X
s
) ds +
_
t
0
g(s, X
s
) dW
t
. (8.7)
Esto es un argumento a favor de la interpretaci on de Stratonovich al formular una ecuaci on
diferencial estoc astica. Sin embargo, la caracterstica de no mirar hacia adelante de la integral
de It o puede hacerla adecuada en muchos casos. Adem as, desde el punto de vista probabilstico,
la integral de It o es m as f acil de tratar.
Afortunadamente, hay una relaci on relativamente simple entre las soluciones de una ecuaci on de
Stratonovich y una ecuaci on de It o, por lo que el desarrollo de la teora para uno de los dos tipos
produce tambien muchos resultados para el otro. En efecto, bajo hip otesis apropiadas, se tiene que
la soluci on de la ecuaci on de Stratonovich (8.7) coincide con la de la ecuaci on de It o modicada
X
t
= X
0
+
_
t
0
_
f(s, X
s
) +
1
2
g
(s, X
s
)g(s, X
s
)
ds +
_
t
0
g(s, X
s
) dW
t
,
donde g
denota la derivada de g respecto al segundo argumento.

Finalmente, hablaremos de un concepto de soluci on que no tiene an alogo en el caso determinista.
En primer lugar, notemos que en el teorema de existencia y unicidad 8.2 no se especica la ltraci on
noanticipativa respecto la que existe una soluci on. En realidad, bajo las hip otesis dadas, se puede
demostrar que tal ltraci on puede tomarse como la generada por la variable condici on inicial y el
proceso W. Cuando esto sucede, hablamos de una soluci on fuerte de la ecuaci on.
En cambio, cuando s olo los datos X
0
, f, g vienen dados, la pregunta m as natural, desde el punto
de vista de la modelizaci on, es si existen un espacio de probabilidad, un proceso de Wiener W,
una ltraci on noanticipativa, y un proceso X tales que se cumple (8.2). En tal caso se habla de
soluci on debil.
El concepto de unicidad del Teorema 8.2 se llama unicidad fuerte o trayectorial; mientras que la
unicidad en el sentido de las soluciones debiles signica que dos soluciones cualesquiera tienen la
misma ley.
Evidentemente, toda soluci on fuerte es una soluci on debil. El recproco no es cierto, y de hecho el
siguiente ejemplo muestra una ecuaci on sin soluci on fuerte, pero con una unica soluci on debil:
dX
t
= signo(X
t
) dW
t
x
0
= 0
_
,
donde
signo(x) =
_
+1, si x 0
1, si x < 0
.
Referencias 41
9. Referencias
[1] L. Arnold: Stochastic Dierential Equations: Theory and Applications, John Wiley & Sons, 1974.
[5] R. Brown: A brief Account of Microscopical Observations made in the Months of June, July and
August, 1827, on the Particles contained in the Pollen of Plants; and on the general Existence of
active Molecules in Organic and Inorganic Bodies, Philosophical Magazine N.S., 4 (1828).
[6] R. Brown: Additional Remarks on Active Molecules, Philosophical Magazine N.S., 6 (1829).
[7] S. Chandrasekar: Stochastic Problems in Physics and Astronomy, Reviews of Modern Physics, 15
(1943).
[9] J.L. Doob: The Brownian Movement and Stochastic Equations, Annals of Mathematics, 43 (1942).
[10] A. Einstein: On the Movement of Small Particles Suspended in a Stationary Liquid Demanded by
the MolecularKinetic Theory of Heat, Annalen der Physik, 17 (1905).
[12] R. F urth (ed.): Albert Einstein: Investigations on the Theory of the Brownian Movement, Dover,
1956.
[13] T.C. Gard: Introduction to Stochastic Dierential Equations, Marcel Dekker, 1988.
[14] I.I. Gihman, A.V. Skorohod: Stochastic Dierential Equations, SpringerVerlag, 1972.
[20] P.A. Meyer: Geometrie Dierentielle Stochastique, Colloque en lHonneur de Laurent Schwartz,
Asterisque 131, 1985.
[22] E. Nelson: Dynamical Theories of Brownian Motion, Princeton University Press, 1967.
[24] B. ksendal: Stochastic Dierential Equations, fth edition, SpringerVerlag, 1998.
[26] G.E. Uhlenbeck, L.S. Ornstein: On the Theory of Brownian Motion, Physical Review, 36 (1930).
[27] J. Yeh: Stochastic Processes and the Wiener Integral, Marcel Dekker, 1973.
[28] M.C. Wang, G.E. Uhlenbeck: On the Theory of Brownian Motion II, Reviews of Modern Physics,
17 (1945).
[29] N. Wax (ed.): Selected Papers on Noise and Stochastic Processes, Dover, 1954.

UAB - Introducción A Las Ecuaciones Diferenciales Estocásticas

Cargado por

Información del documento

Título original

Derechos de autor

Formatos disponibles

Compartir este documento

Compartir o incrustar documentos

Opciones para compartir

¿Le pareció útil este documento?

¿Este contenido es inapropiado?

Copyright:

Formatos disponibles

UAB - Introducción A Las Ecuaciones Diferenciales Estocásticas

Cargado por

Copyright:

Formatos disponibles

Aureli Alabert

Departament de Matem` atiques

f(z) dz, para alguna funci on f: R R

f(x + , t)() d . (4.1)

] [a, b], entonces X o[a

] [a, b], entonces X o[a

denota la derivada de g respecto al segundo argumento.

También podría gustarte