CALCULO DIFERENCIAL E INTEGRAL

Concepto de diferencial : La forma en que hemos abordado el concepto de

derivada, aunque existen varios conceptos, fue el encontrar la relacin de la
pendiente de la lnea recta y =f (x) que era tangente a la funcin. Para un
punto en particular podemos llegar a la definicin de la derivada f '(x) y vimos
que f '(x
1
) es la pendiente de la recta tangente a la curva en x=x
1
.
Analizando el sistema funcin y lnea recta tangente a dicha funcin entonces
podemos analizar que existen dos puntos importantes a analizar, los de la
funcin y los de la recta tangente:
(1) Para referirnos al cambio que ocurre en el valor de f designaremos la
notacin dx.
(2) Para referirnos al cambio que ocurre en el valor de y para la recta
tangente utilizaremos la notacin dy.
Sea y = f(x) la funcin dada y su diferencial (derivada) f

(x) , que se identifica

como el valor de la derivada en P; si el incremento de la variable
independiente x
= dx =PB, con base en la definicin de diferencial resulta: y= f(x),
dy =
f

(x) dx.

Recordando que el valor de la derivada en cualquier punto de una curva es
igual a la pendiente de la tangente a la curva en dicho punto, tenemos:
dy =
f

(x) dx; = tg


= PB
Y=f(x)
Tg.
y
dx=
p
P

C
De acuerdo a la grafica tenemos que:
BC dy ) ( dy PB
PB
BC
PB
BC
tg
que
representa el incremento de la ordenada de la tg. Correspondiente a dx; si dx
representa un incremento cualquiera de la variable independiente x para un punto P
(x, y) de la curva y= f(x), tiene por derivada
tg x f
dx
dy
) (
.
Si el incremento dx = PB es muy pequeo, dy = BC =
y
= BP

Es decir que dy y
y
son aproximadamente iguales.
Ms precisa se encuentra la siguiente definicin:
Definicin de diferencial (informal)
Sea y=f(x) una funcin derivable en un intervalo abierto que contiene al
nmero x.
Se define a la diferencial de x como dx, cualquier nmero real diferente de
cero.
Se define a la diferencial de y como dy, dado por dy=f '(x) dx.
C a l c u l a r u n v a l o r a p r o x i m a d o p a r a 27

2 . 5 27
5.2 0.2 5 27 5 25 x y Si
0.2
10
2

25 2
2
dy
2
dy ; x y si
2 x dx 25 x x y

+


x
dx
sea
Realmente la 27 =5.196152, el valor determinado es mayor que el real por
0.003848 unidades.
C a l c u l a r u n v a l o r a p r o x i m a d o d e t g 4 7
0
.
S e a y = t g x ; x = 4 5
0
d x = x = 2
0
= 0.034906 radianes.
S i Y = t g x e n t o n c e s d y = s e c
2
x d x d e d o n d e d y = ( s e c 4 5
0
)
2
( 0 . 0 3 4 9 0 6 )
D y = 0 . 0 6 9 8 1 2 .
S i y = t g 4 5
0
= 1 . T e n e m o s :
T g 4 7
0
= y + d y = 1 + 0 . 0 6 9 8 1 2 = 1 . 0 6 9 8 1 2 r a d i a n e s .
R e a l m e n t e t g 4 7
0
= 1 . 0 7 2 2 3 6 8 r a d i a n e s , e l v a l o r d e t e r m i n a d o e s m e n o r q u e e l r e a l e n
0 . 0 0 2 5 5 6 r a d i a n e s .
D e t e r m i n a r e l v o l u m e n a p r o x i m a d o d e u n a c o n c h a e s f r i c a c u y o r a d i o i n t e r i o r
e s d e 1 0 c m y c u y o g r o s o r e s d e 0 . 1 5 6 2 6 c m .
( ) ( )

62.5 dv
0.15625 10 4 dv dr; r 4 dv
3
4
V Si
v dv
esferica concha la de grosor cm 0.15625 r dr
esferica. concha la de interior radio 10

3
4
V
2 2 3
3

r
cm r
r Sea
E l v o l u m e n a p r o x i m a d o d e l a c o n c h a e s f r i c a e s d e 6 2 . 5 c m
2
.
E l r a d i o d e u n g l o b o e s f r i c o m i d e 3 0 c m y e l e r r o r m x i m o e n l a m e d i c i n e s d e
0 . 1 5 c m e s t i m a r c a l c u l a r e l e r r o r m x i m o q u e s e c o m e t e a l c a l c u l a r e l v o l u m e n .
S i X e s e l v a l o r m e d i o d e l r a d i o y x dx = al error mximo en X:
x x exacto radio x - x +
( )
( ) ( ) ( )
2 2
2 2
1696 540 15 . 0 30 4 dV
0.15 dv v y 30 x para r 4 v DxV dv v si y
3
4
V
cm
dx r Si
t t t



E l e r r o r m x i m o p o s i b l e e n e l v o l u m e n d e b i d o a l e r r o r d e m e d i c i n d e l r a d i o e s
2
1696 cm t .
La medida efectuada a un lado de un cubo es de 30 cm con un error posible
de cm 02 . 0 t Cul es el error mximo posible aproximado en el volumen del cubo

( )
00066 . 0
1500
1
30
0.02
relativo o medio error El
54 02 . 0 30 3 dV 3 x V
3 2 2 3
t t
t t cm dx x V Si
D e t e r m i n a r e l i n c r e m e n t o d e l r e a d e u n c u a d r a d o d e 6 p u l g a d a s p o r l a d o , a l
a u m e n t a r e l l a d o
32
1
de pulgada.
375 . 0
8
3
dA ;
32
1
2(6) dA dx 2x dA ; x A Si
A dA lg
32
1
x dx y pulgadas 6 x ; x A
2
2

,
_

ada pu Sea
El incremento del rea de cuadrado es de 0.375 pulgadas cuadradas.
Sea y = x
3
y x un incremento de x
Determinar:
a)
y
b) dy
c)
y
- dy
d) El valor de
y
- dy para X = 1 y x = 0.02
( ) ( ) ( ) ( ) ( )
( ) ( ) [ ] ( ) ( )
( ) 001 . 0 02 . 0 )(0.02) 1 3( dy - y )
. 3 x 3x 3 3 dy - y c)
x. 3x dx 3x dy )
3 3 3 3 ) ( x x y )
3 2
3 2 2 3 2 2
2 2
3 2 2 3 2 2 3 3
+
+ + +

+ + + + + +
d
x x x x x x x x
b
x x x x x x x x x x x x f a
Se concluye que si dy se usa para estimar
y
cuando x cambia de 1 a 1.02 el error
que se comete es de 0.001
El error medio o relativo = x / x= 0.02/1= 0.02.
Use diferenciales para estima el cambio de f(x) cuando x varia de a a b.
f(x) y w 7 2 3 z f(z) c)
3.96 b 4; a para 7 8 -3x f(x) )
1.03 b 1; a para 5 3 6 4x f(x) )
2 3
3
2 4 5
+
+
+
z z
x b
x x a
Encuentre dw y estime el de w cuando z vara de 4 a 3.95
- EJERCICIOS: Aplicando diferenciales, hallar aproximadamente los valores para las
siguientes expresiones.
36.4 ln - 10.
63
1
. 5
46 tg - 9. 84 . 4
59 sec - 8.
50
1
- 3.
61 sen - 7. 37 . 2
81
17
- 6. 65 . 1
3
0 4
0
0
4
3

EJERCICIOS: Calcular la diferencial de las siguientes funciones para el valor dado

de la variable independiente y su incremento
0.0083 dx y 5 x cuando lnx y - 7.
0.045 dx y 3 x cuando 2x sen arc y - 6.
0.03528 dx y 5 4 x cuando x tg y - 5.
0.001 dx y 75 . 0 x cuando 1 y - 4.
0.1 dx y 2 x cuando ,
1
y - 3.
0.02 dx y 4 x cuando ,
x
1
x y - 2.
0.02139 - dx y 0 3 x cuando x cos y - 8.
0.0083 dx y 5 x cuando lnx y - 7.
0.045 dx y 3 x cuando 2x sen arc y - 6.
radianes 0.03528 dx y 5 4 x cuando x tg y - 5.
0.001 dx y 75 . 0 x cuando 1 y - 4.
0.1 dx y 2 x cuando ,
1
y - 3.
0.02 dx y 4 x cuando ,
x
1
x y - 2.
0.1 dx y 1 x cuando 5, 8x - 3x y . 1
2
0
2
3
0
2
0
2
3
2





+






+
+
x x
x
x x
x
( )
( )
( )
( ) ( )
1 25
dx
- dy ;
1 25 5
5
dx
dy

x - 1
2x
- dy ;
1
2
5x csc arc y 1 ln
x sec 2ax dy
) 2 ( sec
dx
dy

xdx
- dy ;
2
2
ax tgx y
3x cos 6 dy ; 3x cos 6
dx
dy
3 dy ; 3
3x sen y
2 2
2 2
2
2 2 2 2
2 2 2
2 2 2 2
2 2 2
2 2 2 2
2 3

+
+

x x x
x
x
dx
dy
x y
dx atgx
a tgx x x ax
x a x a
x
dx
dy
x a y
dx x x dx bx a bx a
dx
dy
bx ax y
EJERCICIOS: Halle las diferenciales:
( )
mx
2
2 2
2
3 2
2 3 4
5 y
2
x
sen arc y 10
x csc x y 1 1
4
4
y 4 3
2x 2cos y 2 4
2x sen ln y
2
2
3x) - ln(4 y 2 5 2
2


+
+


+
x
x
e y
y
x x y
x tg
x x y
x y
x
x
y
x x x x y
CLCULO INTEGRAL APLICACIONES DE LA INTEGRAL DEFINIDA
INTRODUCCIN.
Uno de los primeros logros del clculo, fue predecir la posicin futura de un objeto, a
partir de una ubicacin conocida y la funcin que representa su velocidad. Adems
hemos podido, en muchas ocasiones encontrado una funcin a partir de valores
conocidos y una frmula para su razn de cambio. En nuestros das, calcular la
rapidez que necesita un cohete en cierto punto para poder salir del campo
gravitacional de la Tierra o predecir el tiempo de vida til de un objeto a partir de su
nivel de actividad y su razn de decrecimiento, son procesos rutinarios, gracias al
clculo, mediante el uso de las derivadas. De aqu, podemos concluir que el
problema de esta es, que si conocemos el recorrido de un punto mvil, podemos
calcular su velocidad y adicionalmente si tenemos una curva podemos hallar la
pendiente de la recta tangente en cada uno de sus puntos.
Esto, es lo que hemos estudiado en la parte del clculo infinitesimal que denominan
como Clculo Diferencial. Ahora nos centraremos en otra parte de este, que
denominan Clculo Integral.
Encontrar una funcin f a partir de su derivada, involucra el hecho de encontrar toda
una familia de funciones cuya derivada puede ser f; estas funciones reciben el
nombre de antiderivadas, puesto que para encontrarlas es necesario llevar el
proceso contrario al de la derivacin y este proceso se llama integracin. En forma
anloga podemos concluir que el problema de esta es, que si tenemos la velocidad
de un punto mvil, podemos hallar su trayectoria o si tenemos la pendiente de una
curva, en cada uno se sus puntos, podemos calcular dicha curva. Esto es a groso
modo la una pequea definicin de integracin, pero esta es indefinida, es decir, que
mediante este proceso, podemos encontrar toda la familia de funciones cuya
derivada es nuestra funcin dada; ahora, veremos de que se trata la integracin
definida y sus aplicaciones, que es el motivo real de este trabajo.
LA INTEGRAL DEFINIDA
Como se ver ms adelante, para definir el rea de una regin en el plano
cartesiano, acotada por una curva, el eje x y las rectas x = a y x = b, se requiere
hallar la suma de muchos trminos; para simplificar estas sumas se utiliza el
concepto de sumatoria.

Sumatoria:
Propiedades de la sumatoria:
( ) ( )
6
7 3 10
4) - K(5k
2 2
6
5 15 10
2
) 1 (
4
6
1) 1)(2n n(n
5
4 5 4 5 4k) - (5k
4) - K(5k ).
2 3 n
1 k
2
2 3
1 1
2
1 1
2
n
1 k
2
n
1 k
n n n
n n
n n n n n
k k k k
a
n
k
n
k
n
k
n
k
+

+ +

1
]
1

1
]
1

+ +

[ ]
15150
2
) 1 100 ( 100 3
2
) 1 (
3 j 3
3 ).
100
1 j
100
1

1
]
1

n n
j b
j
1 2 2 2
2 2 ).
n 0 n
1
1

n
i
i i
c







La integral definida
Particin de un intervalo cerrado:
Suma de Riemann:

La integral definida:
Teorema:
Por lo anterior:
Si en cualquier figura delimitada por rectas y por una curva; se inscriben y circunscriben
rectngulos en nmero arbitrario, y si la anchura de tales rectngulos se va disminuyendo a
la par que se aumenta su nmero hasta el infinito, afirmo que las razones entre las figuras
inscrita y circunscrita y la figura curvilnea acabarn siendo razones de igualdadIsaac
Newton.
El rea, es un concepto familiar para todos nosotros, por el estudio de figuras geomtricas
sencillas como el tringulo, el cuadrado, el crculo y el rectngulo. La idea o el concepto que
manejamos de rea, es la magnitud que mide de algn modo el tamao de una regin
acotada, es decir, cuanto mide una superficie. Ciertamente, para hallar el rea de las figuras
geomtricas sencillas que ya conocemos, disponemos de formulas matemticas que
facilitan este clculo.
Ahora, nuestro problema consiste en encontrar un mtodo, que nos permita calcular el rea
de cualquier regin, sin importar la forma que esta tenga. Para lograr esto, es necesario
primero introducir el smbolo o la notacin de Sumatoria. Para representar esto, se una la
letra griega mayscula _ sigma, para abreviar la sumatoria, y se usa de este modo: y sus
partes son:
a: Representa los trminos de la sumatoria
ak: Representa el termino ksimo de la sumatoria
an: Representa el termino nsimo y ltimo de la sumatoria
k: Es el ndice de la sumatoria
1: Es el lmite inferior de la sumatoria
n: Es el lmite superior de la sumatoria
Grfica 1.
Como habamos mencionado anteriormente, nuestra preocupacin ahora, es encontrar el
rea de cualquier superficie sin importar su forma. Supongamos que queremos hallar el rea
de la regin comprendida entre el eje x, la recta x=a, la recta x=b y la grfica de la funcin
f(x) (Grfica 1).
Grfica 2.
Ahora, supongamos que tomamos la regin y la dividimos en una serie de rectngulos de
base _x (Grfica 2.). Si logrramos calcular el rea de cada uno de esos rectngulos, y las
sumramos todas, obtendramos una aproximacin del rea total de la regin que
deseamos.
Pero como ya vimos que esa sumatoria se puede reducir a una sola expresin, podramos
hacerlo de modo que, tomemos un valor xi, dentro del intervalo [a,b], tal que exista _xi y un
f(xi), de tal manera que se cumpla que: de esta manera se puede calcular el rea de ese
rectngulo as:
Puesto que el rea de un rectngulo, como todos sabemos, es base por altura. Debido a
que este rectngulo puede ser cualquier rectngulo dentro de la regin, puesto que xi puede
ser cualquier valor, ya podemos sumar sus reas para lograr la aproximacin: Donde esta
sumatoria nos representa el rea aproximada de la regin que deseamos. Como ya
habamos visto que _xi, representa cada una de las particiones de nuestra regin, ahora
definamos a P como la particin ms
grande de todas, es decir la base de rectngulo ms grande de dotas las de la regin y n el
nmero de particiones. As, si hacemos que P se haga tan pequeo como pueda o que el
nmero de particiones n, se haga lo ms grande que pueda, hallamos una mejor
aproximacin del rea que buscamos (Grfica 3).
Grfica 3.
De aqu podemos deducir que si hallamos el Lmite cuando el nmero de rectngulos sea
muy grande o cuando las longitudes de las bases de esos rectngulos sean muy pequeas,
lograremos la mejor y ms exacta aproximacin del rea que tanto hemos buscado. Y esto
se representa as: que es equivalente a, con esto ya encontramos la mejor aproximacin del
rea. Ahora si, podemos definir la integral definida ya que,
Por lo tanto podemos deducir que la integral definida es una suma y as la hemos definido. Y
de esta manera, tambin hemos mostrado la primera aplicacin de la integracin definida,
hallar el rea bajo una curva.
Ya que definimos la integral definida, identifiquemos cual es su notacin y las partes que la
componen.
Toda la expresin se lee, integradle f(x), desde a hasta b; a y b, son los lmites de
integracin, donde a es el lmite inferior y b es el lmite superior. El smbolo", es una s
mayscula alargada, que significa suma y se llama smbolo de integracin. La funcin f(x),
es el integrando y el dx, se llama diferencial y es el que lleva la variable de integracin que
en este caso es x.
PROPIEDADES DE LA INTEGRAL DEFINIDA













FUNCIN PRIMITIVA
En el clculo diferencial se determin la derivada f

(x) o la diferencial f

(x) dx de
una funcin dada f (x); en el calculo integral se realiza la operacin inversa, es
decir, se encuentra una funcin f (x) cuya derivada o diferencial es conocida.

+
+
c
x Sea
2
2
x dx 2x
dx 2x dy o 2
dx
dy
9 x f(x)
De la expresin

+ c
2
x dx 2x
, no sabemos cul es el valor de C (constante de
integracin); es un valor indefinido, por lo cual se denomina a este operacin
INTEGRAL INDEFINIDA.
En caso inverso y para efectos de verificar el calculo:

+ C a Sea
3 2
y dy 3ay
ALGUNAS FORMULAS PARA INTEGRALES INMEDIATAS
( )
lnC) (C ln ln ln ln
v
dv
. 5
1
u . 4
C w - u v dw du dw - du dv . 3
a adv . 2
. 1
1
n
+ +
+
+

+ + + +
+
+

+
Cv C v C v
C
n
u
du
dv
C av dv
C v dv
n
( )
( )
( ) ( )
( )
( )
c
t t
C t
t
c t C
t
C
t
dt t
dt t dt t
C my C
y
m dy y m dy my
+ +
+ +
1
]
1

+
1
1
]
1

+ +
+

+
+
+
+

3
3 2
3
9
3 2
3
9
2
2 3
3
3
1 3
3
1
3
3
dv
dt ; 3dt dv 3t; v 3 3 . 2
3
5
1 2
5 5 5 . 1
3
2 3
1
2
1
1
2
1
1
2
1
2
1
3
1 2
2 2

( )
c x x
x
dx dx x dx x dx dx
x
x
c x c
x
C
x
dx x
x
dx
+ + +
+ +

,
_

+ +
+ + +
+

5 14
5
6
5
x

5 7 3 x 5
7
3 x . 4
3
3
1
1
3
2
. 3
2
5
5
2
1
2
3
4
2
3
4
3
3
1
1
3
2
3
2
3
2

( )
( ) ( )
( )
( ) ( )
c x x
x
dx
dx dx dx
x
dx
x
x
c
a
b
c
b
a
dx ax dv b xdx b dx b
c
x
x a
ax
dx x dx x a dx x a
dx x ax ax dx x ax a dx a
c
x
x
c x
x
dx x dx x dx x x dx x x
+ + +

,
_

+
+

+
1
1
]
1

+ + +

,
_

+ +
+

,
_

+
,
_

ln 3 4
3
x
3 4 x
3
4 x
3 4 x
. 8
3
ax
2
3
ax
2
1
2 ax v Si ax ax x . 7
5
2
3
2
2
2 2 x x x - 6.
1
5
2
2
5
2
3 3 3 . 5
3
2 2
3
2
3
2
2
3
2
2
2
1
2 2
2
5
2
2
3
2
3
2
1
2
3
2
1 2
2
3
2
3
2
5
2
1
2
3
2
1
2
3

TEOREMAS FUNDAMENTALES DEL CLCULO
Primer teorema fundamental del clculo:
Segundo teorema fundamental del clculo:
CALCULO DE INTEGRALES DEFINIDAS














22.-

( ) ( )
5326 . 0 3
4
) 1 ( 3 0
8
2
cos 3
2
2 3 2 sen x 3 2x
2
2
0
2 2
0
2
0
2
0

1
]
1

x
x
dx x sen dx x dx
23.-
( ) ( )
79 . 2 4142 . 1 85505 . 1 3561 . 2 0
4
cos 2
4
3
4
3
cos 2 3 3
cos 2 3 3 2 6 3 sen x 2 6 3
2
4
0
2
4
0
2
4
0
4
0
4
0
4
0
+
1
1
]
1

,
_

+ +
+ + + + + +

x x x
x x x dx x sen xdx dx dx x
24.-
3
5
3
2
3
2
1
3
2

) 1 (
3
2
) 1 (
3
2
3
2
2 2
2
3
2
2
3
2
2
3
2
2
3
2
1
1
2
3
2
2
1
1 1
2
1
+ + + + +
1
]
1

+
1
]
1

+ + +

,
_

x x x x
x x t t dt t dt t dt t t
x
x x x

INTEGRALES IMPROPIAS: Las denominadas integrales impropias son una clase
especial de integrales definidas (integrales de Riemann) en las que el intervalo de
integracin o la funcin en el integrando o ambos presentan ciertas particularidades.
si los lmites existen.
Cuando los lmites, en las definiciones anteriores, existen, se dice que la integral es
convergente, en caso contrario, se dice que la integral es divergente.



3

6.
CONVERGE 1 1 0 1
1
lim
1 1
lim
1
lim lim
1
lim
1
1
1 1
2
1
2
1
2
2
+
1
]
1

1
]
1

,
_

1
]
1

1
]
1

t t t
x
dx x dx
x
dx
x
dx
x
y
t t
t t
t t
t
t
1 t
7.

] [ [ ]
[ [ ]

+ +

,
_

+ +
+

2
2
2 2 2 2
0 lim lim 0 0 lim 0 lim
lim lim
1
lim
1
lim
1
1 1 1 1 1 1
0
1 1
0
2
0
2 2
b tg a tg tg b tg a tg tg
x tg x tg
x
dx
x
dx
x
dx
b a b a
b
b a
b
b
a
a
a
8.-

[ ] [ ]
diverge
e b x
x
dx
x
dx
e
b
b
b
b
b

ln log ln 1 ln ln lim ln lim lim
0
1
1 1
1
9.-

[ ] [ ]
converge
e e e dx e dx e dx e
b
b
b
x
b
b
x
b
x
1 1 0 1 lim lim lim
0
0
0 0
+ + +

1
10.-

dx
x

+
0
2
1
1
[ ] [ ]
converge
2
0 0
0 lim lim
1
1
lim
1
1
1 1 1
1 1
0
1
0
2
0
2

tg tg tg
tg b tg x tg dx
x
dx
x
b
b
b
b
b

vale
2
cuando y tg tg 0 y sen si
y cos
y sen
y tg como
1 - 1

y y tg y tg
11.-
( )
( )
e e
e e
e
b
pero
e
b
e e
b
e
x
c
e
x
c e xe e dx e
e v
dx e x
b
b
b b
b
x
x
x x x x
x
x
1 1
0
0
1 1
lim lim : tiene se derivando
lim
1
lim lim dx -e x) - (1
-e x) - (1
e dv
-dx du x; - 1 u 1
b

b
b b
1 1
b
x -
x -
x -
1

1
]
1

1
]
1

+ + +

11.1.-
diverge
8
1
0
1
8
1
2
1
8
1
lim
2
1
lim
2
0
2
2
0
2
0
3
+ +
1
]
1

+
1
]
1

+ +

b x x
dx
b
b
b
12.-
converge
2
1
2
0 - 1
2
e - 1
2
e

2
lim lim
- 2 0
0
2
0
2
0
2

1
]
1

1
]
1

+
+

M
M
x
M
M
x
M
x
e e
dx e dx e
0 M
13.-
1 0 1
1
1 lim
1
lim lim
1 1
2
1
2

,
_

1
]
1

+ +
+
+

M x x
dx
x
dx
M
M
M
M
M
1 M
14.-
[ ] ( ) ( ) +
+ +
+
+

2 ln 2 ln ln lim ln lim lim
1
2 2
M x
x
dx
x
dx
M
M
M
M
M
2 M
15.-
( ) ( ) + +
+
+
+

3 ) ( 2 9 2 lim lim
9 9
M
x
dx
x
dx
M
M
M
16.-
( )
( ) ( ) ( )
( )
0
1 1
lim ) (derivando
1
lim
, 0 ) 1 ( lim el
). 1 ( lim 1 1 ( 1 lim 1 - x e lim
1 - x e e - xe v es e e dv si dx; du x; u si
lim
0
x
x x x x x
0 0
0

N
N
N
N
n
N
n
N
n
N
N
N
x
N
x
N
x
x
e e
N
N e pero
N e N e
dx dx xe
dx xe dx xe
dx xe
N a
17: fig = al 16
( ) ( ) ( )
( ) ( ) ( )
( ) 0
2
1
cos ( e 1
2
1
lim
) cos ( e
2
1
) 0 cos 0 ( e
2
1
lim cos e
2
1
lim
cos e
2
1
cos e cos e e e cos e
e e e dv y -sen x du x cos u : como cos e e
e v es e e dv si dx; x cos du sen x; u si sen x e
dx sen x e lim x
N
N 0
0
x
x x x x x x
x x x x x
x x x x
0
N
x
0
+

+

n
N
N N N
N
x
e porque N N sen
N N sen sen x senx
x senx x x senx dx senx x senx
dx v dx x senx
dx dx
dx sen e
18.- se denomina oscilante
[ ]
unidad. la es cos el porque 3 cos cos lim
cos lim dx sen x lim dx sen x
3
3 3






N
x
N
N
N
N
N
19.-
( ) ( )
converge
4
3
2 4
N tg arc - 1 tg arc lim x tg arc lim
1
lim
1
1
1
2
1
2

,
_

+



N
N
N
N
N
x
dx
x
dx
20.-
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( )

+ +

,
_

+ + +
+ + +
+ + + + +
+ + +
+ +
+
+ +

+ +

+ + +

+ +
+ +

+ +

2
2
2 2 4 2 2 4
4
lim ) 1 ( lim ) 1 ( lim
4
lim
1 lim ) 1 ( lim ) 1 ( lim 1 lim
) 1 0 ( ) 1 ( lim ) 1 ( ) 1 0 ( lim
) 1 ( lim ) 1 ( lim
1 1
lim
1 1
lim
1 1 1 1 2 2 2
1 1
1 1 1 1
0
1
0
1
0
2
0
2
2 2 2
b b a a
b b a a
b a
b
b
a
a
b
b
a
a
b a
tg b a tg
tg b tg a tg tg
x tg x tg
x
dx
x
dx
x
dx
x x
dx
x x
dx
SEGUNDA UNIDAD
INTEGRALES INDEFINIDAS y MTODOS DE INTEGRACIN.
INTEGRACIN DIRECTA
De cada regla de derivacin se puede deducir una regla correspondiente de
integracin. La integracin directa es aplicable cuando identificamos la funcin
primitiva de forma inmediata; esto es, cuando conocemos la regla de derivacin que
al aplicarla nos permite hallar el integrando a partir de la funcin primitiva.
Ejemplo:
Propiedades fundamentales de la antidiferenciacin

Esta propiedad indica que podemos sacar un factor constante de la
integral.



















INTEGRACION DIRECTA
1.
2.
3.
4.
5.-

6.
7.



11.-
Podemos transformar el integrando como sigue:
El primero de los sumandos nos da:
El segundo de los sumandos nos da:
Por lo que, finalmente:
12.-
Sabemos que sec x = 1/cos x; por lo tanto, podemos poner:
13.-
( )

+ + + + c x x dx x 3
2
7
3dx dx 7x 3 7
2
14.-
( )
( )
c x 5cos sen x 2
x cos - 5 - sen x 2
dx 5 dx cos 2 5 cos 2
+ +
+


c
x sen x dx x sen x
15.-
c
2x
5
- 3x - x
8
9

2
5
3
2
9
)
2
5
3
2
9
(
2
5 6 9
4
2 3 2 3
2
2 5
+
+ +
+


dx x dx dx x dx x x dx
x
x x
INTEGRACIN POR SUSTITUCIN
En muchas ocasiones, cuando la integracin directa no es tan obvia, es posible
resolver la integral simplemente con hacer un cambio de variable adecuado; este
procedimiento se conoce como integracin por sustitucin.
S o l u c i o n e s
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
21.-

23.-
24.







COMPLETAR CUADRADO:
c e tg
e
arctg c
a
u
arctg
a u a
du
e
dx e
dx e e u e a
e
dx
e
e
dx
e e
dx
x
x
x
x
x x x
x
x
x
x x
+
1
]
1

1
]
1

+
+

+

+

2 1
2
2 2 4
2
2 2 4 2 2
4
2
2
2 2
2
1
1 1
1
2
1 1
2
1
1
) 2 (
) 2 ( du , ; u : 1 ; 1 a
1
1
c x x x x x u u
dx du x u x u a
x
dx
x x x x x
x x
dx
+ + +

,
_

+ + +

,
_

,
_

,
_

+ + +
+

2 5
2
5
ln
4
17
2
5
2
5
ln a ln
;
2
5
;
2
5
; ;
4
17
;
4
17
a
4
17
2
5
4
17
2
5
2
4
25
4
25
5 2 5
2 5
2
2
2 2
2
2 2
2
2
2 2
2
c
x
sen c
a
u
ar csen
x
d x
x
x x
d x
+ +

5
4
4
1
4
1
1 6 2 5

4 d x du 4 x u ; ) 4 ( u ; 5 a ; 5 a
) 4 ( (5 )
d x
1 6 2 5
1
2
2 2 2
2 2 2
c
x
c
a
u
a
x x
dx
x x
dx
+ +

5
sec
5
1
sec
1

5 a : dx du x; u
) 5 ( ) ( 5
1 1
2 2 2
( ) ( ) ( )
( )
( ) ( )
( ) c x sen x x
x
c
x
sen x x
x
c
a
u
sen
a
u a
u
dx x x x
dx du x
x x x x x x x
+ +

,
_

+ + +

3 2
8
1
2 3
4
3 2

2
1
2
3
2
2
1
2 3
2
2
3

2 2
2
2
3
2
1
2 3
;
2
3
u
4
1
2
3
4
9
2
4
9
3 2 3 - 2 3
1 2
1
2
2
1
2
2 2
2
2
2
2
2 2 2
INTEGRACIN POR PARTES La frmula para la "integracin por partes"

vdu uv udv
ILATE
1.
2.
3.
4.
5.
6.
7.
8.




POTENCIAS DE LAS FUNCIONES TRIGONOMTRICAS
En este apartado aprenderemos a integrar funciones que presentan potencias
trigonomtricas, es decir, funciones con alguna de las siguientes formas:
Para tal efecto es conveniente tener frescas en la memoria las siguientes
identidades trigonomtricas:
Identidades trigonomtricas
Por lo regular, se concluye con las transformaciones trigonomtricas adecuadas,
el integrando queda expedito para aplicar la integracin por sustitucin. En otros
casos debemos recurrir a la integracin por partes.
1.
2.
3.
4.
5.

6.
7.
8.
9.
10.
11.
12.
13.
14.
16.-
( ) ( )
( ) ( ) c
x
c
u u
u du u u du
sen x
+ + + + +




5
sen
3
x 2sen
sen x
5 3
2
2 1 u - 1
dx x cos du sen x; u Si
dx x cos x 1 dx x cos cos dx x cos
5 3 5 3
4 2
2
2
2
2
2 5
1
17.-
( )
c x
x
c u
u
en os
s x en sen
+ +

cos
3
cos
3

dx x s du x; c u Si
dx en x s dx x
3 3
2 3
SUSTITUCIN TRIGONOMTRICA
A menudo es posible hallar la antiderivada de una funcin cuando el integrando
presenta expresiones de la forma:
Se elimina el radical haciendo la sustitucin trigonomtrica pertinente; el resultado es
un integrando que contiene funciones trigonomtricas cuya integracin nos es
familiar. En la siguiente tabla se muestra cul debe ser la sustitucin:
Expresin en el
integrando
Sustitucin
trigonomtrica

Sustituyendo estos valores en (1), se obtiene:

(Fig.1)
Sustituyendo estos valores en (1), se obtiene:



8.-
( )
( )
c u u
u
du
c tg
tg c v dv v
v
dv
d tg
tg d
tg
tg
d
tg
tg d
tg u tg
u
u
u
pero
u
du
dx e du dx
e
e
dx
e
e
x
x
x
x
x
+ + +
+
+ +
+ +
+ +
+
+
+ +

+
+


+
+
+

+

+

2
2
1
2
2
2
2
2 2
2
2
2
x
2 2
1 ln
1
sec ln d sec
sec ln ln
sec sec dv
sec v Si ;
sec
sec sec
sec
sec sec
sec
sec
sec
sec du
1
u

sec 1
;
cos
1
1
1
1
cos
1
; e u si
1

1

1
2
dx
e
e
x
x

+
=
x x
e e + +
2
1 ln
+ c
9.-

( )
[ ] [ ] [ ]
( ) [ ] ( ) [ ]
( )
. cos cos
1 1 1 dz. z cos dx z; sen 1 - x
z ec ;
z g ;
z ; :
1 1 1 1 - x
1 1 2 x 2 x x - 2x
1 1 2
2
2 2
2 2 2
2 2 2
2 2 2
2 2
2 2 2
2
2
2
2
z z
z sen x
s
b
a
u a u b
t
b
a
u u b a
sen
b
a
u u b a Pero
x
x x
dx
x
x
dx
x x
x



+


+

1
2
1 u +
u
( )
( )
( )
( )
( ) ( )
( )
( )
( )
( )
( )
( )
c x x
x x
sen arc
arc z c z
s
z Pero
x x b x x b
x b x x b x c a
c
z sen z
c
k k z sen z
dz z Pero
dz dz
x
x
x
dx
x
x
dx
x x
x
z
z
+

+
+ +
+
+

+ +
+
+
+ + + + +

+ +

+
2
2 2 2 2
2 2 2
3 2 1 2
2
2 2 2
cos
cos 1 z sen
2
2
2 2
2
2
2
2
2 2
2
2 1 - x
1 - x
2
3
1 - x sen
2
3
cos 2
4
2z en
2
3
:
2 ; 1 1 2
1 1 2 ; 1 , 1 1 x z sen Si
cos 2
4
2
2
3

k
z cos 2
4
2
2
2 cos 1
2
1
dz z sen :
z z 2cos dz z sen
dz dz z sen 2 dz z sen 1 z sen 2 z sen 1 z sen
1 1
1 z sen 1 z sen x z; sen 1 - x
1 1 2
2

sen z= x-1; arc sen (x-1) =z
sen 2z=2sen z cos z; Si sen z = x-1 entonces cos z = b/2= x x 2 /1

( )
c x x
x x x sen
+

2
2
2 -2 z 2cos ;
2
2 1
4
2z
1 x-1
2
2 x x
FUNCIONES RACIONALES, FRACCIONES PARCIALES, CUANDO EL
DENOMINADOR SLO TIENE FACTORES LINEALES

1.1.-

( )( )
( ) ( )
( ) ( ) 1 ln 2 2 ln 3
1
2
2
3
2
7
3 A -2 b 6; 3B 7 2
1
2 2 1 7
1 2 1 2
7
2
7
2
2
+

+
+

+
+
+ + + +

+
+

x x
x x x x
x
B A
B A
B A Bx Ax x B x A x
x
B
x
A
dx
x x
x
dx
x x
x
1.2.-

( )( )
( ) ( ) ( )

+

+
+

+ +
+

+ + +
+
+ + + + + + + + + +

+
+
+

+ +
+

+ +
+


1 2 ;
1
3
1
4
3
16
4 5
4 5
3
16
3
1
5 ; ;
3
1
- b -1 3B 4 4 4 4
5 - (-1) 5
4 4 4 1 4 5
1 4 1 4
4 5
4 5
4 5
2 2 2 4
2
2 2 2 2 2 2
2 2 2 2
2
2 4
2
a a x u Si
x x x x
x
A B A B A
B A B A
B A x B A B Bx A Ax x B x A x
x
B
x
A
x x
x
dx
x x
x
c arc arc arc arc + x tg
3
1
2
x
tg
3
8
1
x
tg
1
1
3
1
2
x
tg
2
1
3
16
1.3.-
( )
( ) ( ) ( )
( )
( ) 0 B - C
(1) 0 A - B C
2
1
C B 0 1
2
1
C 1 de 1; A 0 x Para
1 1 1 A 1

1 1 1
3
2
3 2 3 2 2 2 2 2
2 2 2

+
+
+ + + + + +

+
+
+

x
x
Cx Cx Bx Bx Ax A x Cx x Bx x
x
C
x
B
x
A
x x
dx

( )
( ) ( )
c
x
x
x
c x x
x
dx
x
dx
x
dx
x x
C
x
B
x
A
x x
dx
+

+
+
+ + + +

+
+
+

+
+
+

1
1
ln
3

1 ln
2
1
1 ln
2
1 3
-
1
2
1
1
2
1
1

1 1 1
3
3
2 2 2 2
1.4.-






FUNCIONES RACIONALES, POR FRACCIONES PARCIALES, CUANDO EL
DENOMINADOR CONTIENE FACTORES CUADRTICOS




5.--

Integrales en las que aparecen expresiones cuadrticas
De la descomposicin de fracciones parciales a veces resultan integrandos con
expresiones cuadrticas ireductibles. De la integracin de este tipo de funciones nos
ocuparemos en los siguientes ejercicios resueltos.

Integrales que producen funciones trigonomtricas inversas
Como ya se ha dicho antes, de cada frmula de derivacin se deduce una frmula
correspondiente de integracin. De las frmulas para las derivadas de las funciones
trigonomtricas inversas, obtenemos el siguiente teorema que da algunas frmulas
de integrales indefinidas:





6.-
Esta integral puede resolverse haciendo el cambio :
con lo que nos queda :
7.-
Esta integral puede resolverse haciendo el cambio :
y a partir de ah :
3.
4.
5.
6.
7.
8.
MISCELNEA DE EJERCICIOS
9.1








Tarea : EJERCICIOS RESUELTOS DE INTEGRALES
;




=
Igualamos los coeficientes de los dos miembros.
La primera integral es de tipo logartmico y la segunda la tenemos que descomponer
en dos, que sern de tipo logartmico y tipo arcotangente.
Multiplicamos por 2 en la segunda integral para ir preparndola.
El 2 del numerador de segunda integral lo transformamos en 1 + 1.
Descomponemos la segunda integral en otras dos.
Las dos primeras integrales son de tipo logartmico.
La integral que nos queda es de tipo arcotangente.
Vamos a transformar el denominador de modo que podamos aplicar la frmula de la
integral del arco tangente.
Transformamos el denominador en un binomio al cuadrado.
Multiplicamos numerador y denominador por 4/3, para obtener uno en el
denominador.
Dentro del binomio al cuadrado multiplicaremos por la raz cuadrada de 4/3.
Sumamos y restamos 3 en el numerador, descomponemos en dos fracciones y en la
primera sacamos factor comn 3.
Multiplicamos y dividimos en la primera fraccin por 2.
Vamos a transformar el denominador de modo que podamos aplicar la frmula de la
integral del arcotangente.
Transformamos el denominador en un binomio al cuadrado.
Realizamos un cambio de variable.




INTEGRA NDO POR PARTES .

Se realiza la integral racional.


Aplicamos las propiedades de los logaritmos.










;

Para calcular A, B y C, sustituimos x por 3:
Derivamos y volvemos a sustituir por 3:

Volvemos a derivar:
Tambin podemos hallar los coeficientes realizando las operaciones e igualando
coeficientes:










TERCERA UNIDAD
REA BAJO UNA CURVA:
Los antiguos griegos dieron una regla para calcular la medida del rea de un
rectngulo (producto de la base por la altura), de aqu se deduce que el rea de un
tringulo rectngulo es igual a "un medio del producto de los catetos". La
trigonometra facilita una frmula para hallar la medida de cualquier clase de
tringulo: "el rea de un tringulo cualquiera es igual a un medio del producto de dos
de sus lados por el seno del ngulo que forman dichos lados". Debido a que un
polgono se puede descomponer en tringulos, la obtencin de su rea se consigue
mediante la suma de las reas de los tringulos en que se ha dividido. Este
procedimiento de medir reas slo es aplicable a figuras planas limitadas por
segmentos de rectas. Para medir el rea de una figura limitada por curvas se debe
recurrir a otro mtodo, que es el que vamos a estudiar a continuacin.
(fig.1)
(fig.2)
(fig.3)
Definicin:
Ejercicios resueltos
8 a 11 evale el rea de la regin dada; emplee
rectngulos inscritos o circunscritos segn se indique. Para cada
ejercicio trace una figura que muestre la regin y el i-simo
rectngulo.
8. Solucin: f(x) = x
2

9. Solucin: f(x) = 2x
10. Solucin: f(x) = 4-x
2
REA ENTRE CURVAS
Como ya hemos definido la integral definida como una suma y adems hemos visto
como se halla el rea de una regin comprendida entre una curva y un eje, ahora
veremos como se hace este mismo clculo para hallar el rea de una regin que
este comprendida entre dos curvas, es decir, entre las grficas de dos funciones.
El concepto para calcular el rea entre dos curvas, es el mismo que ya habamos
estudiado. La regin a trabajar, se divide en rectngulos, y se determinan los
mismos parmetros para calcular el rea de este, es decir su base y su altura. La
diferencia en esta aplicacin es que la altura del rectngulo se define de una
manera algo distinta, debido a que hay dos funciones involucradas.
Grfica 4.
Como podemos ver en la Grfica 4, el intervalo de la regin esta definido por los
puntos de corte de las dos funciones, esto es en el caso de las los tengan dichos
puntos, por otro lado, si las funciones no se cortan, para hallar el rea entre ellas, es
necesario definir un intervalo mediante tapas, que son rectas constantes en funcin
de y, de igual manera que definimos el intervalo en la aplicacin anterior.
Ahora que ya sabemos todo el proceso para hallar el rea, slo resta, mostrar como
es que cambia el asunto de la altura del rectngulo. Y eso lo podemos representar
as: Donde f(x)g(x), representa la altura del rectngulo diferencial. Con esto ya
hemos mostrado y definido otra aplicacin de la integral definida.
En los ejercicios 1 a 7, encuentre el rea de la regin limitada
por las curvas dadas. En cada problema haga lo siguiente: (a)
trace una figura que muestre la regin, as como un elemento
rectangular de rea; (b) exprese el rea de la regin como el
lmite de una suma de Riemann; (c) determine el lmite de la
parte (b) evaluando una integral definida por el segundo teorema
fundamental del clculo



F(x) = -x
2


3
2
1
) ( x x f


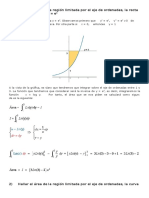
8.- Grafique y seale la regin acotada de -2 a 1 en donde a = 6.75
( )
75 . 6
3
26
12
23
) ( ) (
3
26
10
3
8
4 ) 2 (
12
23
2
5
3
1
4
1
) 1 (
2
5
3 4
5 ) (
1
2
2 3 4 1
2
2 3
+

+
+ +

a f b F
f
f
x x x
dx x x x x f

Sea:

[ ]
2558 . 8 12 7441 . 3 ) 3 ( 4 ) 3 (
5
3
4
5
3
4
3
5
4
3
4
3
3 2, - 4
3
3
5
3
2
3
5
3
2
3
5
3
2 -
3
2
3
2
3
2
3
2
3
2

,
_

x x
x
x
dx dx
x
dx
x x
y
Y = x
3
-3 x
2
x +3
[ ]
( )
( )
4
21
0 6
2
1
1
4
1
6 2 8 4 3
2 3
3
4
1
3 3 3 3
2 1, - 3 3
2
1
2
3 4
2
1
2
1
2
1
2
1
2 3
2
1
2 3
2 3
+

,
_

+ +
1
]
1

+
+ +
+

x
x
x x
dx xdx dx x dx x dx x x x
x x x y
(TAREA) Y = x
4
; y=2x-x
2
:
( )
( ) 1 X 0 2 x y 0, x
2 x x 0; 2x x ; x - 2x ones Intersecci )
3
3 2 4 4 2
+
+ +
x
x x x a
Tarea: Encuentre en cada caso el rea de la regin comprendida entre las
curvas:
a) y = x2 -1 , y - 2x +1 = 0. b) y = 5 x2 , y = x - 1
b) x = y2 , x - 3y - 4 = 0. x = y2 , 4y2 = x + 2.
c) y2 = 5-x , y2 = x + 6 x = y2 , x + 2y - 3 = 0
d) x = y2-9 , x - y - 3 = 0.
C L C U L O D E V O L M E N E S
A l i n t r o d u c i r l a i n t e g r a c i n , v i m o s q u e e l r e a e s s o l a m e n t e u n a d e l a s m u c h a s a p l i c a c i o n e s
d e l a i n t e g r a l d e f i n i d a . O t r a a p l i c a c i n i m p o r t a n t e l a t e n e m o s e n s u u s o p a r a c a l c u l a r e l
v o l u m e n d e u n s l i d o t r i d i m e n s i o n a l .
S i u n a r e g i n d e u n p l a n o s e g i r a a l r e d e d o r d e u n e j e E d e e s e m i s m o p l a n o , s e o b t i e n e u n a
r e g i n t r i d i m e n s i o n a l l l a m a d a s l i d o d e r e v o l u c i n g e n e r a d o p o r l a r e g i n p l a n a a l r e d e d o r
d e l o q u e s e c o n o c e c o m o e j e d e r e v o l u c i n . E s t e t i p o d e s l i d o s s u e l e a p a r e c e r
f r e c u e n t e m e n t e e n i n g e n i e r a y e n p r o c e s o s d e p r o d u c c i n . S o n e j e m p l o s d e s l i d o s d e
r e v o l u c i n : e j e s , e m b u d o s , p i l a r e s , b o t e l l a s y m b o l o s .
E x i s t e n d i s t i n t a s f r m u l a s p a r a e l v o l u m e n d e r e v o l u c i n , s e g n s e t o m e u n e j e d e g i r o
p a r a l e l o a l e j e O X o a l e j e O Y . I n c l u s o a v e c e s , e s p o s i b l e h a l l a r e l v o l u m e n d e c u e r p o s q u e
n o s o n d e r e v o l u c i n .
1 . V o l m e n e s d e r e v o l u c i n : E l M t o d o d e l o s d i s c o s
S i g i r a m o s u n a r e g i n d e l p l a n o a l r e d e d o r d e u n e j e o b t e n e m o s u n s l i d o d e r e v o l u c i n . E l
m s s i m p l e d e e l l o s e s e l c i l i n d r o c i r c u l a r r e c t o o d i s c o, q u e s e f o r m a a l g i r a r u n r e c t n g u l o
a l r e d e d o r d e u n e j e a d y a c e n t e a u n o d e l o s l a d o s d e l r e c t n g u l o . E l v o l u m e n d e e s t e d i s c o d e
r a d i o R y d e a n c h u r a e s :
V o l u m e n d e l d i s c o =
P a r a v e r c m o u s a r e l v o l u m e n d e l d i s c o p a r a c a l c u l a r e l v o l u m e n d e u n s l i d o d e r e v o l u c i n
g e n e r a l , c o n s i d e r e m o s u n a f u n c i n c o n t i n u a f ( x ) d e f i n i d a e n e l i n t e r v a l o [ a , b ] , c u y a g r f i c a
d e t e r m i n a c o n l a s r e c t a s x = a , x = b , y = 0 , e l r e c i n t o R . S i g i r a m o s e s t e r e c i n t o a l r e d e d o r
d e l e j e O X , o b t e n e m o s u n s l i d o d e r e v o l u c i n .
S e t r a t a d e h a l l a r e l v o l u m e n d e e s t e c u e r p o e n g e n d r a d o p o r R . P a r a e l l o h a y q u e s e g u i r u n
p r o c e s o s i m i l a r a l r e a l i z a d o e n l a d e f i n i c i n d e i n t e g r a l d e f i n i d a .
E l e g i m o s u n a p a r t i c i n r e g u l a r d e [ a , b ] :
E s t a s d i v i s i o n e s d e t e r m i n a n e n e l s l i d o n d i s c o s c u y a s u m a s e a p r o x i m a a l v o l u m e n d e l
m i s m o . T e n i e n d o e n c u e n t a q u e e l v o l u m e n d e u n d i s c o e s , l a s u m a d e R i e m a n n a s o c i a d a a
l a p a r t i c i n , y q u e d a u n v o l u m e n a p r o x i m a d o d e l s l i d o e s : s i e n d o :
, l a a l t u r a ( a n c h u r a ) d e l o s c i l i n d r o s p a r c i a l e s
e l r a d i o d e l o s c i l i n d r o s p a r c i a l e s
S i e l n m e r o d e c i l i n d r o s p a r c i a l e s a u m e n t a , s u s u m a s e a p r o x i m a c a d a v e z m s a l v o l u m e n
d e l s l i d o ; e s d e c i r :
P o r t a n t o , r e c o r d a n d o l a d e f i n i c i n d e i n t e g r a l d e f i n i d a d e R i e m a n n s e o b t i e n e q u e :
A d e m s , s i s e t o m a e l e j e d e r e v o l u c i n v e r t i c a l m e n t e , s e o b t i e n e u n a f r m u l a s i m i l a r :
2 . V o l m e n e s d e r e v o l u c i n : E l M t o d o d e l a s a r a n d e l a s
E l m t o d o d e l o s d i s c o s p u e d e e x t e n d e r s e f c i l m e n t e p a r a i n c l u i r s l i d o s d e r e v o l u c i n c o n
u n a g u j e r o , r e e m p l a z a n d o e l d i s c o r e p r e s e n t a t i v o p o r u n a a r a n d e l a r e p r e s e n t a t i v a . L a
a r a n d e l a s e o b t i e n e g i r a n d o u n r e c t n g u l o a l r e d e d o r d e u n e j e . S i R y r s o n l o s r a d i o s
e x t e r n o s e i n t e r n o s d e l a a r a n d e l a , y e s l a a n c h u r a d e l a a r a n d e l a , e n t o n c e s e l v o l u m e n
v i e n e d a d o p o r :
V o l u m e n d e l a a r a n d e l a =
E n t o n c e s , g e n e r a l i z a n d o d e f o r m a a n l o g a c o m o s e h i z o e n e l m t o d o d e l o s d i s c o s , s i
t e n e m o s d o s f u n c i o n e s c o n t i n u a s f ( x )y g ( x )d e f i n i d a s e n u n i n t e r v a l o c e r r a d o [ a , b ] c o n 0 "
g ( x )" f ( x ) , y l a s r e c t a s x = a ,y x = b, e l v o l u m e n e n g e n d r a d o s e c a l c u l a r e s t a n d o l o s s l i d o s
d e r e v o l u c i n e n g e n d r a d o s p o r l o s r e c i n t o s d e a m b a s f u n c i o n e s , e s d e c i r :
S i l a s f u n c i o n e s s e c o r t a n , h a b r q u e c a l c u l a r l o s v o l m e n e s d e l o s s l i d o s e n g e n d r a d o s e n
c a d a u n o d e l o s s u b i n t e r v a l o s d o n d e s e p u e d e a p l i c a r e l m t o d o a n t e r i o r .
3 . M t o d o d e s e c c i o n e s c o n o c i d a s
E n e s t e a p a r t a d o v e r e m o s c m o s e c a l c u l a e l v o l u m e n d e a l g u n o s c u e r p o s g e o m t r i c o s
c u a n d o c o n o c e m o s e l r e a d e l a s b a s e s d e l o s c i l i n d r o s p a r c i a l e s e n q u e h e m o s d i v i d i d o e l
s l i d o . C o n e l m t o d o d e d i s c o s , p o d e m o s h a l l a r e l v o l u m e n d e u n s l i d o q u e t e n g a u n a
s e c c i n c i r c u l a r c u y a r e a s e a A = R 2 . P o d e m o s g e n e r a l i z a r e s t e m t o d o a s l i d o s d e
c u a l q u i e r f o r m a s i e m p r e y c u a n d o s e p a m o s l a f r m u l a d e l r e a d e u n a s e c c i n a r b i t r a r i a ,
c o m o c u a d r a d o s , r e c t n g u l o s , t r i n g u l o s , s e m i c r c u l o s y t r a p e c i o s .
C o n s i d e r e m o s u n s l i d o q u e t i e n e l a p r o p i e d a d d e q u e l a s e c c i n t r a n s v e r s a l a u n a r e c t a
d a d a t i e n e r e a c o n o c i d a . E s t o e q u i v a l e a d e c i r i n t u i t i v a m e n t e q u e e n c a d a c o r t e q u e
h a c e m o s , c o n o c e m o s e l r e a d e l a s e c c i n c o r r e s p o n d i e n t e .
E n p a r t i c u l a r , s u p o n g a m o s q u e l a r e c t a e s e l e j e O X y q u e e l r e a d e l a s e c c i n t r a n s v e r s a l
e s t d a d a p o r l a f u n c i n A( x ) , d e f i n i d a y c o n t i n u a e n [ a , b ] . L a s e c c i n A( x ) e s t p r o d u c i d a p o r
e l p l a n o a p e r p e n d i c u l a r a O X .
S i g u i e n d o u n p r o c e s o s i m i l a r a l r e a l i z a d o e n l a d e f i n i c i n d e l a i n t e g r a l d e R i e m a n n :
E l e g i m o s u n a p a r t i c i n r e g u l a r d e [ a , b ] :
E s t a s d i v i s i o n e s d e t e r m i n a n e n e l s l i d o n s e c c i o n e s o r o d a j a s c u y a s u m a s e a p r o x i m a a l
v o l u m e n d e l m i s m o . T e n i e n d o e n c u e n t a q u e e l v o l u m e n d e u n c i l i n d r o e s R 2 , l a s u m a d e
R i e m a n n a s o c i a d a a l a p a r t i c i n , y q u e d a u n v o l u m e n a p r o x i m a d o d e l s l i d o e s : s i e n d o :
S i e n d o c i u n p u n t o i n t e r m e d i o d e l i n t e r v a l o [ x i - 1 , x i ]
= x i - x i - 1 , l a a l t u r a d e l o s c i l i n d r o s p a r c i a l e s
R 2 = A ( c i ) e l r e a d e l a b a s e d e l o s c i l i n d r o s p a r c i a l e s
S i e l n m e r o d e c i l i n d r o s p a r c i a l e s a u m e n t a , s u s u m a s e a p r o x i m a c a d a v e z m s a l v o l u m e n
d e l s l i d o ; e s d e c i r :
P o r t a n t o , r e c o r d a n d o l a d e f i n i c i n d e i n t e g r a l d e f i n i d a d e R i e m a n n s e o b t i e n e q u e :
P a r a h a l l a r e l v o l u m e n d e u n s l i d o p o r e l m t o d o d e l a s s e c c i o n e s , s e p r o c e d e c o m o s e
i n d i c a a c o n t i n u a c i n :
1 . E s b o z a r l a f i g u r a , i n c l u y e n d o u n e j e p e r p e n d i c u l a r a l a s s e c c i o n e s d e r e a c o n o c i d a ( e s
d e c i r , u n e j e O X )
2 . E s c o g e r u n a s e c c i n p e r p e n d i c u l a r a l e j e O X.
3 . E x p r e s a r e l r e a A ( x ) d e l a b a s e d e l a s e c c i n e n t r m i n o s d e s u p o s i c i n x s o b r e e l e j e
O X .
4 . I n t e g r a r e n t r e l o s l m i t e s a p r o p i a d o s .
4 . V o l m e n e s d e r e v o l u c i n : M t o d o d e c a p a s
E n e s t a s e c c i n e s t u d i a m o s u n m t o d o a l t e r n a t i v o p a r a e l c l c u l o d e u n v o l u m e n d e u n s l i d o
d e r e v o l u c i n ,
u n m t o d o q u e e m p l e a c a p a s c i l n d r i c a s .
P a r a i n t r o d u c i r e l m t o d o d e c a p a s , c o n s i d e r a m o s u n r e c t n g u l o r e p r e s e n t a t i v o , d o n d e :
= a n c h u r a d e l r e c t n g u l o ( e s p e s o r ) .
h = a l t u r a d e l r e c t n g u l o .
p = d i s t a n c i a d e l c e n t r o d e l r e c t n g u l o a l e j e d e l g i r o ( r a d i o m e d i o ) .
C u a n d o e s t e r e c t n g u l o g i r a e n t o r n o a l e j e d e r e v o l u c i n , e n g e n d r a u n a c a p a c i l n d r i c a ( o
t u b o ) d e a n c h u r a . P a r a c a l c u l a r e l v o l u m e n d e e s t a c a p a c o n s i d e r a m o s d o s c i l i n d r o s . E l
r a d i o d e l m a y o r c o r r e s p o n d e a l r a d i o e x t e r n o d e l a c a p a , y e l r a d i o d e l m e n o r a l r a d i o i n t e r n o
d e l a c a p a . P u e s t o q u e p e s e l r a d i o m e d i o d e l a c a p a , s a b e m o s q u e e l r a d i o e x t e r n o e s p +
( / 2 ) , y e l r a d i o i n t e r n o e s p -( / 2 ) . P o r t a n t o , e l v o l u m e n d e
l a c a p a , v i e n e d a d o p o r l a d i f e r e n c i a :
V o l u m e n d e l a c a p a = v o l u m e n d e l c i l i n d r o - v o l u m e n d e l a g u j e r o =
= 2 p h = 2 ( r a d i o m e d i o ) ( a l t u r a ) ( e s p e s o r )
U s a m o s e s t a f r m u l a p a r a c a l c u l a r e l v o l u m e n d e u n s l i d o d e r e v o l u c i n c o m o s i g u e .
S u p o n e m o s q u e l a r e g i n p l a n a g i r a s o b r e u n a r e c t a y e n g e n d r a a s d i c h o s l i d o . S i
c o l o c a m o s u n r e c t n g u l o d e a n c h u r a y p a r a l e l a m e n t e a l e j e d e r e v o l u c i n , e n t o n c e s a l h a c e r
g i r a r l a r e g i n p l a n a e n t o r n o a l e j e d e r e v o l u c i n , e l r e c t n g u l o g e n e r a u n a c a p a d e
v o l u m e n :
V = 2 [ p ( y ) h ( y ) ] y
S i a p r o x i m a m o s e l v o l u m e n d e l s l i d o p o r n d e t a l e s c a p a s d e a n c h u r a y, a l t u r a h ( y i ) , y r a d i o
m e d i o p ( y i ) , t e n e m o s :
v o l u m e n d e l s l i d o =
T o m a n d o e l l m i t e c u a n d o n ! ", t e n e m o s q u e :
V o l u m e n d e l s l i d o =
P o r t a n t o , p o d e m o s e n u n c i a r e l m t o d o d e c a p a s d e l a s i g u i e n t e f o r m a :
P a r a c a l c u l a r e l v o l u m e n d e u n s l i d o d e r e v o l u c i n c o n e l m t o d o d e c a p a s , s e u s a u n a d e
l a s d o s s i g u i e n t e s o p c i o n e s :
E j e h o r i z o n t a l d e r e v o l u c i n :
E j e v e r t i c a l d e r e v o l u c i n :
P a r a h a l l a r e l v o l u m e n d e u n s l i d o p o r e l m t o d o d e c a p a s , s e p r o c e d e c o m o s e i n d i c a a
c o n t i n u a c i n .
1 . E s b o z a r l a r e g i n p l a n a q u e v a a s e r g i r a d a , h a l l a n d o l o s p u n t o s d e i n t e r s e c c i n d e l a s
c u r v a s q u e l a l i m i t a n .
2 . S o b r e e l d i b u j o h a l l a r u n r e c t n g u l o p a r a l e l o a l e j e d e r e v o l u c i n .
3 . T e n i e n d o c o m o b a s e e l b o c e t o , e s c r i b i r e l v o l u m e n d e l a c a p a .
4 . I n t e g r a r e n t r e l o s l m i t e s a p r o p i a d o s .
O b s e r v a c i n : L o s m t o d o d e d i s c o s y d e c a p a s s e d i s t i n g u e n p o r q u e e n e l d e d i s c o s e l
r e c t n g u l o r e p r e s e n t a t i v o e s s i e m p r e p e r p e n d i c u l a r a l e j e d e g i r o , m i e n t r a s q u e e n e l d e
c a p a s e s p a r a l e l o .
C o n f r e c u e n c i a u n o d e l o s d o s m t o d o s e s p r e f e r i b l e a l o t r o .
C l c u l o d e l o n g i t u d e s :
l o n g i t u d d e r e v o l u c i n =
l o n g i t u d d e r e v o l u c i n e n t r e f u n c i o n e s =
SLIDOS DE REVOLUCIN
Ya est visto que la integral definida es aplicable, cuando se trata de hallar reas,
pero ser aplicable para hallar volmenes formados por rotacin de una funcin?,
la respuesta a esta pregunta es si, si es posible calcular estos volmenes, llamados
volmenes de revolucin, mediante integracin definida. Ms adelante y en el
transcurso de este tema, veremos que el clculo del volumen de un slido, es como
una expansin del clculo del rea, a una tercera dimensin.
Igual que para hallar el rea, tomemos una figura sencilla, para hallar su volumen,
por ejemplo un cilindro.
Dado que el cilindro es un prisma, igual que un paraleleppedo, su volumen puede
ser calculado como tal, rea de su base por su altura.
Mtodo de los discos
Grfica 5.
Como ya vimos, el volumen de un cilindro, ahora nos queda ms fcil comprender el
concepto de volumen por el mtodo de los discos. Como sabemos las dimensiones
del disco diferencial (Grfica 5.), son muy parecidas a las de un cilindro, de hecho el
disco es prcticamente un cilindro cuya altura es mucho menor al radio de su base.
De esto podemos deducir que si queremos hallar el volumen del slido de la grfica,
es necesario sumar los volmenes de los discos que quepan dentro del slido y si
llevamos esa cantidad, hacia el infinito, igual que con el rea, obtendremos la mejor
aproximacin del volumen y para esto ya vimos como funciona la integral definida,
es por eso que para este caso el clculo del volumen del slido, es una expansin
del clculo del rea de una superficie plana. Calculemos el volumen del disco si, el
radio es f(x) y su espesor es _x.
, de aqu, deducimos que, dado que el volumen esta entre a y b,
De esta manera, podemos calcular el volumen de un slido, mediante el mtodo de
los discos.
MTODO de las arandelas
Este mtodo, es sin duda una expansin del anterior, debido a que tambin se basa
en discos, pero esta vez con un agujero, es por eso que se les llama arandelas. El
hecho que se presente el agujero, se debe a que el volumen de revolucin lo forma
la rotacin de dos funciones, a un mismo sentido y a un mismo ritmo, de donde
generalmente se forma un slido hueco.
Grfica 6.
Ahora, si miramos la Grfica 6; nos damos cuenta que el proceso para hallar el
volumen es muy similar al del mtodo anterior, pero aqu es necesario hacer una
resta de volmenes para la arandela, si el radio mayor es f(x) y el radio menor es
g(x), y Va es el volumen de la arandela, de aqu ya podemos hallar fcilmente el
volumen del slido, desarrollando la integral definida en el intervalo [a,b].
MTODO DE LOS CASQUILLOS CILNDRICOS
Cuando necesitamos hallar el volumen de un slido de revolucin, a veces los
casquillos cilndricos nos pueden dar una solucin ms fcil, que el mtodo de las
arandelas. En parte, la razn es que la formula a la que nos llevan no requiere que
se eleve al cuadrado. Los mtodos de discos y arandelas usaban como elemento
representativo de volumen un disco circular, generado al girar un rectngulo
orientado perpendicularmente al eje de rotacin o revolucin. El mtodo de los
casquillos usa como elemento representativo de volumen un cilindro que es
generado al girar un rectngulo, orientado de forma paralela al eje de revolucin. En
primer lugar es necesario que desarrollemos la formula para el volumen del cilindro
diferencial.
Anteriormente ya habamos calculado el volumen de un cilindro, as que aqu,
miraremos una formula
geomtrica que nos dice que el volumen de un casquillo barrido por un rectngulo
es: V=2_(radio promedio del casquillo)(altura del casquillo)(grosor)
en nuestro caso es: Supongamos que hacemos girar la regin sombreada de la
Grfica 8, alrededor del eje y para generar un slido. Para hallar una aproximacin
del volumen del slido, as:
Como podemos ver en la rotacin resultan casquillos cilndricos diferenciales. Si
hacemos la sumatoria de volmenes de los casquillos diferenciales, obtendremos el
volumen del slido de revolucin.
Anteriormente, habamos definido el volumen de uno de los casquillos diferenciales
en trminos de la funcin, as que ya podemos afirmar que:
Esto es el resultado de hacer la sumatoria de los volmenes de los casquillos
diferenciales y es el mtodo de los casquillos para calcular volmenes de revolucin.
VOLMENES POR REBANADAS
Cuando analizamos el mtodo de los discos para hallar el volumen de un slido,
llegamos a la formula: donde , era el rea de la seccin circular y _x el espesor del
disco.
Ahora podemos generalizar este mtodo, para calcular el volumen de slidos con
forma arbitraria, si conocemos el rea de una de sus secciones. Por ejemplo si A(x),
representa el rea de una seccin en x, perpendicular al eje x, entonces el volumen
del slido se obtendr integrando A(x) con respecto a x.
Por ejemplo, si encontramos un slido cuyas secciones transversales son tringulos,
de manera que si calculamos el rea de uno de esos tringulos diferenciales y la
integramos con respecto a x, encontramos el volumen total del slido, es decir: y de
esta manera podemos encontrar, el volumen de cualquier slido, siempre que
conozcamos un elemento diferencial y la formula para hallar su rea.
SUPERFICIES DE REVOLUCIN
Ya hemos usado la integral definida para hallar volmenes de revolucin, longitudes
de arco y reas de regiones planas. Ahora vamos a aprovechar su utilidad para
calcular reas pero esta vez no de regiones planas sino de superficies de revolucin,
estas no son ms que la superficie exterior de cualquier slido de revolucin.
Para poder calcular el rea de una superficie de este tipo, es necesario primero
saber como calcular el rea superficial de un cono circular truncado o tronco de
cono.
Consideremos la figura de una Grfica, donde:
L: es la longitud del segmento
r: es la distancia de un extremo al eje de rotacin
R: es la distancia del otro extremo al eje de rotacin
Con los datos anteriores, podemos afirmar que el rea del tronco de cono es:
Supongamos que la funcin f(x), , tiene derivada constante y gira alrededor del eje x.
Sea una particin de [a,b] en subintervalos de anchuras _xi. Entonces el segmento
rectilneo de longitud: genera un tronco de rea lateral, _Si y la podemos definir
como: y por aplicacin del teorema del valor medio y del teorema del valor
intermedio, podemos asegurar que se cumple que:por lo tanto concluimos que:
Del mismo modo podramos demostrar que, si la grfica de f(x), gira alrededor del
eje y, el rea S, viene dada por: y de esta manera, con cualquiera de las dos
formulas, dependiendo el eje de rotacin podemos calcular el rea
de revolucin.
UNIDAD IV
Series y sucesiones
Sucesin es una secuencia ordenada de nmeros u otras cantidades, y serie es la
suma de todos los trminos de
dicha secuencia.
Una sucesin se representa como a1, a2 , an Las a son nmeros o cantidades,
distintas entre s o no; a1 es el
primer trmino, a2el segundo, y as sucesivamente. Si el ltimo trmino aparece en
la expresin, es una
sucesin finita; si no aparece es infinita. Una sucesin es definida o establecida si y
slo si existe una regla
dada que determina el trmino nsimo correspondiente a un n entero positivo; esta
regla puede estar dada por
la frmula del trmino nsimo. Por ejemplo, todos los nmeros enteros positivos, en
su orden natural,
forman una secuencia infinita definida por la frmula an=n. La frmula an = n2 define
la sucesin 1, 4, 9, 16
La regla de empezar con 0 y 1 y calcular cada trmino como la suma de los dos
trminos anteriores define la
sucesin 0, 1, 1, 2, 3, 5, 8, 13 ; que se conoce como sucesin de Fibonacci.
Entre los tipos ms importantes de sucesiones se encuentran las sucesiones
aritmticas (tambin conocidas
como progresiones aritmticas), en las que la diferencia entre dos trminos
sucesivos es constante; y las
sucesiones geomtricas (tambin conocidas como progresiones geomtricas), en las
que la razn entre dos
trminos sucesivos es constante. Un ejemplo de sucesiones se encuentra al intentar
calcular los intereses de un
cierto capital. Si el dinero se invierte al inters simple del 8%, entonces en n aos la
cantidad de dinero inicial
P se ha convertido en an = P + n (0,08)P. El mismo producto (0,08)P se aade
cada ao, por lo que las
cantidades an forman una progresin aritmtica. Si el inters es compuesto, las
cantidades ahorradas forman
una progresin geomtrica, gn = P (0,08)n. En ambos casos, est claro que an y
gn llegarn a ser mayores
que cualquier nmero entero imaginable.
Sin embargo, los trminos de una sucesin no tienen por qu crecer siempre. Por
ejemplo, a medida que n
crece, la sucesin an = 1/n se acerca a 0, que es su lmite; y bn = A + B/n tiende
hacia A. En este tipo de
sucesiones, existe un nmero finito L tal que, dada una tolerancia e, los valores de la
sucesin difieren de L en
una cantidad menor que e cuando n es lo suficientemente grande. Por ejemplo, en el
caso de la sucesin 2 +
(1)n/2n, el lmite es L = 2. Incluso si se toma una e tan pequea como 1/10.000, se
puede comprobar que
para n mayores que 5.000 la diferencia entre an y L es menor que e. El nmero L se
denomina lmite de la
sucesin, y aunque algunos de los trminos de la sucesin son mayores y otros
menores que L, los trminos
finalmente se agrupan alrededor de L cada vez ms cerca. Cuando una sucesin
tiene un lmite L, se dice que
converge hacia L. Para la sucesin an, por ejemplo, esto se escribe como lim an = L,
que se lee el lmite de an
cuando n tiende hacia infinito es L.
El trmino serie designa la siguiente suma, a1 + a2 + + an, o a1 + a2 + + an + , que
es la suma de los
trminos de una sucesin. Una serie es finita o infinita dependiendo de si la
correspondiente secuencia de
trminos es finita o infinita.
La sucesin s1 = a1, s2 = a1 + a2, s3 = a1 +a2 + a3, ,sn = a1 + a2 + + an, , se
denomina sucesin de sumas
parciales de la serie a1 + a2 + + an + La serie es convergente (divergente) si la
sucesin de sumas parciales
converge (diverge). Una serie de trminos constantes es aquella en la que los
trminos son nmeros; una serie
funcional es aquella en la que los trminos son funciones de una o ms variables.
Un caso especial es la serie
de potencias, que es la serie a0 + a1(x c) + a2(x c)2 + + an(x c)n + , en la que
la c y la a son constantes.
Para la serie de potencias, el problema es encontrar los valores de x para los que la
serie es convergente. Si la
serie converge para una cierta x, entonces el conjunto de todas las x para las que la
serie converge es un punto
o un intervalo. La teora bsica de la convergencia fue estudiada alrededor de 1820
por el matemtico francs
Augustin Louis Cauchy.
La teora y el uso de las series infinitas son importantes en prcticamente todas las
ramas de las matemticas
1
tanto, puras como aplicadas.
Progresin aritmtica
Secuencia de nmeros que crecen o decrecen en una cantidad fija llamada razn,
de manera que cualquier
nmero de la sucesin es la media aritmtica o trmino medio del nmero anterior y
el siguiente. Los nmeros
naturales 1, 2, 3, 4 forman una progresin aritmtica de razn 1. Los nmeros 22,
19, 16, 13, 10, 7 estn en
progresin aritmtica de razn 3. Para calcular la suma de los trminos de una
progresin aritmtica, se
multiplica la suma del primer y el ltimo trmino por la mitad del nmero de trminos.
De este modo, la suma
de los diez primeros nmeros naturales es (1 + 10) (10 : 2) = 55.
Usando el lenguaje algebraico, una progresin aritmtica se escribe como a0, a0 +
d, a0 + 2d, a0 + 3d, donde
tanto el trmino a0conocido como el trmino cero como la razn d son nmeros
arbitrarios. El trmino
ensimo de esta progresingeneralmente escrito como an est dado por la siguiente
frmula: an = a0 + n d. La
suma de los trminos de a0 a an es: 1 (n + 1) (a0 + an).
Progresin geomtrica
Sucesin de nmeros tales que la proporcin entre cualquier trmino (que no sea el
primero) y el trmino que
le precede es una cantidad fija llamada razn. Por ejemplo, la secuencia de nmeros
2, 4, 8, 16, 32, 64, 128 es
una progresin geomtrica con razn 2; y 1, 1, 3, 7, 9, >, (1)i, es una progresin
geomtrica con razn 1. La
primera es una progresin geomtrica finita con siete trminos; la segunda es una
progresin geomtrica
infinita. En general, una progresin geomtrica se puede describir utilizando la
siguiente notacin: a es el
primer trmino, la razn es r y, en una progresin finita, n es el nmero de trminos.
Una progresin
geomtrica finita se escribe formalmente como
y una progresin geomtrica infinita como
En general, si el trmino ensimo de una progresin geomtrica es an, se deduce de
la definicin que
Si el smbolo Sn representa la suma de los n primeros trminos de una progresin
geomtrica, se puede
comprobar que
Los trminos de una progresin geomtrica entre ai, y aj, con i < j, se denominan
medias geomtricas. La
media geomtrica de dos nmeros positivos x e y es la media proporcional de dichos
nmeros . En cualquier
progresin geomtrica, an es la media geomtrica o proporcional de an1 y an+ 1.
La suma formal de los trminos de una progresin geomtrica, escrita como
se denomina serie geomtrica. Al estudiar esta serie, se comprueba que converge si
y slo si el valor absoluto
de la razn es menor que 1; si esto no ocurre, la serie diverge. Si la serie converge,
el lmite S es igual a
2
El smbolo
se lee como "lmite de Sn cuando n tiende hacia infinito".
Las series y progresiones geomtricas tienen muchas aplicaciones en las ciencias
fsicas, biolgicas y sociales,
y tambin en clculos bancarios y financieros. Muchos problemas de inters
compuesto y anualidades se
resuelven utilizando estos conceptos.
Cauchy, Augustin Louis (17891857), matemtico francs, considerado uno de los
impulsores del anlisis
en el siglo XIX. Naci en Pars y estudi en la Escuela Politcnica de esta ciudad.
Fue profesor
simultneamente en el Colegio de Francia, en la Escuela Politcnica y en la
Universidad de Pars. En 1848 fue
nombrado profesor de astronoma matemtica de esa universidad.
Cauchy verific la existencia de funciones elpticas recurrentes, dio el primer impulso
a la teora general de
funciones y sent las bases para el tratamiento moderno de la convergencia de
series infinitas. Tambin
perfeccion el mtodo de integracin de las ecuaciones diferenciales de primer
grado. En el campo de la fsica
se interes por la propagacin de la luz y la teora de la elasticidad.
Gauss, Carl Friedrich (17771855), matemtico alemn conocido por sus muy
diversas contribuciones al
campo de la fsica, especialmente por sus estudios del electromagnetismo.
Naci en Braunschweig el 30 de abril de 1777 y estudi lenguas antiguas, pero a los
17 aos comenz a
interesarse por las matemticas e intent dar una solucin al problema clsico de la
construccin de un
heptgono regular, o figura de siete lados, con una regla y un comps. No solamente
consigui probar que
esto era imposible, sino que sigui aportando mtodos para construir figuras de 17,
257 y 65.537 lados.
Durante estos estudios, prob que la construccin, con regla y comps, de un
polgono regular con un nmero
de lados impar slo era posible cuando el nmero de lados era un nmero primo de
la serie 3, 5, 17, 257 y
65.537 o un producto de dos o ms de estos nmeros. A raz de este descubrimiento
abandon sus estudios de
lenguas y se dedic a las matemticas. Estudi en la Universidad de Gotinga desde
1795 hasta 1798; para su
tesis doctoral present una prueba de que cada ecuacin algebraica tiene al menos
una raz o solucin. Este
teorema, que ha sido un desafo para los matemticos durante siglos, se sigue
denominando teorema
fundamental de lgebra. Su tratado sobre la teora de nmeros, Disquisitiones
arithmeticae (1801), es una obra
clsica en el campo de las matemticas.
Ms tarde, Gauss dirigi su atencin hacia la astronoma. El asteroide Ceres haba
sido descubierto en 1801, y
puesto que los astrnomos pensaban que era un planeta, lo observaron con mucho
inters hasta que lo
perdieron de vista. Desde sus primeras observaciones, Gauss calcul su posicin
exacta, de forma que fue
fcil su redescubrimiento. Tambin plane un nuevo mtodo para calcular las rbitas
de los cuerpos celestes.
En 1807 fue nombrado profesor de matemticas y director del observatorio de
Gotinga, ocupando los dos
cargos hasta el 23 de febrero de 1855, fecha de su muerte.
Aunque Gauss hizo valiosas contribuciones tanto a la astronoma terica como
prctica, trabaj sobre todo en
matemticas y en fsica matemtica, abarcando prcticamente todas sus ramas. En
la teora de nmeros
desarroll el importante teorema de los nmeros primos. Gauss fue el primero en
desarrollar una geometra no
eucldia, pero no public estos importantes descubrimientos ya que deseaba evitar
todo tipo de publicidad. En
la teora de la probabilidad, desarroll el importante mtodo de los mnimos
cuadrados y las leyes
fundamentales de la distribucin de la probabilidad. El diagrama normal de la
probabilidad se sigue llamando
curva de Gauss. Realiz estudios geodsicos y aplic las matemticas a la
geodesiagt. Junto con el fsico
alemn Wilhelm Eduard Weber, Gauss realiz una intensa investigacin sobre el
magnetismo. Entre sus ms
importantes trabajos estn los de la aplicacin de las matemticas al magnetismo y
a la electricidad; una
3
unidad de induccin magntica recibe su nombre. Tambin llev a cabo
investigaciones en el campo de la
ptica, especialmente en los sistemas de lentes.
4
Sucesiones:
En el campo de las matemticas una sucesin es definida como una funcin cuyo
dominio es el conjunto de
enteros positivos. Aunque esta sea una funcin ,usualmente es representada con
una notacin de subindices en
vez de una notacin funcional.Por ejemplo:
1, 2, 3, 4, 5, .....n, ...........
a1, a2, a3, a4, a5, an, ...........
1 se aplica en a1, 2 en a2, etc. Llamamos a an el nsimo trmino de la sucesin y
esta s denotada por {an}.
Dominio general de una Sucesin:
Viene dado por el siguiente mtodo:
1) Para la sucesin {an}= {3+(1)n}, los cuatro trminos primeros son:
3 + (1)1, 3 + (1)2 , 3 + (1)3, 3 + (1)4, ....... R= 2, 4, 2, 4, ......
2) Para la sucesin {bn}= {2n/(1 + n), los cuatro trminos primeros son:
2*1 /(1 + 1), 2*2 /(1 + 2), 2.3/(1 + 3), 2*4 /(1 + 4),.....R= 2/2, 2/3, 6/4, 8/5,.....
Definicin del Lmite de una Sucesin:
Se define de la siguiente manera; Si para > 0 existe M >0 tal que [an L] <
siempre que n > M ,entonces
decimos que el lmite de la sucesin {an} es L y escribimos :
Limn an= L
Las sucesiones que tienen lmite (finito) se llaman covergentes y las dems
divergentes.
Lmite de una Sucesin:
Sea f funcin de una variable real tal que :
Lmxoo f (x) = L
Si {an}es una sucesin tal que f (n) = an para todo entero positivo n, entonces :
Lmnoo an = L
Propiedades de los Lmites de las sucesiones:
Si: Lmnoo an= L y Lmnoo bn = K
Las siguientes propiedades son vlidas:
1) Lmnoo(an+ bn) = L + K 2) Lm noo can = cL, c es cualquier nmero real.
1
3) Lmnoo (an bn) = LK 4) Lmnoo an/bn = L/K, solo si bn es diferente de 0
Determinando la Convergencia o Divergencia de una sucesin:
Determinar la convergencia en las siguientes sucesiones:
1) an = 3 + (1)n 2) bn = n / 12n
1) an = 3 + (1)n solucin: como an = 3 + (1)n tiene trminos 2, 4, 2, 4,..... que
oscilan entre 2 y 4 , no hay
lmite y la sucesin diverge.
2) Para {bn}, podemos dividir por n numerador el denominador para obtener:
Lmnoo n /(1 2n) = Lmnoo [1/(1/oo) 2] = 1/2 ,por lo tanto la sucesin
converge a 1/2.
Sucesiones Montonas:
Una sucesin es montona si sus trminos son no decrecientes:
1, 2, 3, 4, 5, 6, ........
o si sus trminos son no crecientes:
1, 4, 3, 8, 5, ...........
Determinando si una sucesin es montona,se toman las siguientes sucesiones
como ejemplos:
{an}= {3+(1)n} Esta sucesin alterna entre 2, y 4 por lo tanto no es montona. Y
{bn}= {2n/(1 + n) Montona , por que cada trmino es mayor que su predecesor.
Sucesiones Acotadas:
Una sucesin {an} es acotada si existe un nmero real positivo M tal que [an] sea
menor o igual que
M para todo n.
Llamamos a M una cota superior de la sucesin por ejemplo las tres sucesiones
siguientes son acotadas
debido a :
[3+(1)n] es <o = a 4, [2n / 1+n] es < o = a 2 y [n2/2n1] es < o = 4/3
Debido a que los nmeros reales son completos lo cual significa geomtricamente
que no hay agujeros ni
huecos en la recta real,este axioma de completitud de los reales puede ser utilizado
para concluir que si una
sucesin tiene cota superior, entonces ha de existir una mnima cota superior. As, la
cota superior mnima de
la sucesin {an} = {n /n + 1},
1/2, 2/3, 3/4, 4/5, ..., n/(n+1), .......
es 1, ya que la sucesin es montona y converge hacia 1 y [n/(n+1)] es menor o
igual a 1 lo que nos dice
entonces que si una sucesin {an}es montona y acotada entonces es
convergente.Por ejemplo:
2
1/2, 4/3, 9/4 , 16/5, ..........., n2/n+1........ es montona pero no acotada,pues:
Lmnoo an= oo
Por su parte ,la sucesin divergente:
2, 4, 2, 4, ........... [3 + (1)n] es acotada pero montona.
Series y Convergencias:
Definicin de Series infinitas:
Si {an}es una sucesin infinita,entoces:
oo=1 an= a1 + a2 + a3 + +an +
se llama una serie infinita o simplemente una serie. Los nmeros a1, a2 ,a3, ........ se
llaman los trminos de la
serie.
Para hallar las sumas de una serie infinita consideremos la siguiente sucesin de
sumas parciales:
S1= a1
S2= a1 + a2
S3= a1 + a2 + a3
Sn= a1 + a2 + a3 + an +.
Si esta sucesin converge y su suma es la que se indica en la siguiente definiciones:
Para la serie infinita an , la nsima suma parcial viene dada por :
Sn= a1 + a2 + a3 +.+ an
Si la sucesin de sumas parciales {Sn}converge a S,diremos que la serie an
converge . Llamaremos a S suma
de la serie y escribiremos
S= a1 + a2 + a3 ++ an +..
Si {Sn} diverge, diremos que la serie es divergente.
Por lo tanto esta definicin implica que una serie puede ser identificada con su
sucesin de sumas parciales
de manera que las siguientes propiedades son consecuencias directa de sus
anlogos en sucesiones.
Propiedades de las Series Infinitas :
Si an = A , bn = B y c es un nmero real, las siguientes series convergen las
sumas que se indican.
1. oon=1 can = cA 2. . oon=1 (an + bn) = A + B
3
3. oon=1 (an + bn)= A B
Si se suprimen los N trminos de una serie ,ello no destruye su convergencia ( o
divergencia)
Supresin de los N primeros trminos de una serie:
Para cualquier entero porsitivo N, las series
oon=1 an= a1 + a2 + a3 + y oon= N+1 an= aN+1 + aN+2 + aN+3 +..
Son ambas convergentes o ambas divergentes.Si ambas convergen sus sumas
difieren por la suma parcial Sn.
Criterio del trmino nsimo para la divergencia:
Si la sucesin {an} no converge a 0, entonces la serie an diverge.
Demostracin si la serie an converge, {an} converge a 0.supongamos que la serie
dada converge y que :
oon=1 an= lm noo Sn = L
Entonces como: Sn= Sn1 + an y lm noo Sn = lm noo Sn1 = L
Se sigue que: L= lmnoo Sn= lmnoo (Sn1 +an) = lmnoo an = L + lmnoo an
Lo cual exige que {an} converja a 0.
Usando el criterio del nsimo trmino :
Determinar , mediante el criterio precedente ,cuales de estas series divergen:
A) oon=0 2n B) oon=1 n!/(2n! +1)
Lmnoo 2n = oo y lmnoo n!/2n! +1 = lmnoo 1/ 2+(1/n!) =
Que por el criterio nsimo implica que ambas son divergentes.
Definicin de serie geomtrica:
La serie dada por : oon=0 arn= a + ar + ar2 + ......... +arn +...., a diferente de 0, es
llamada serie geomtrica
de razn r, el siguiente teorema da las condiciones para que sea convergente o
divergente:
Convergencia de una serie geomtrica : Una serie geomtrica de razn r diverge si
[r] mayor o igual a 1 . Si 0
es menor que [r] y menor que 1,entonces la serie converge con la suma:
oon=0 arn = a/ (1r) , 0 menor que [r] menor que 1
Ejemplos de Series Geomtricas:
La serie Geomtrica:
oon=0 3/2n = oon=0 3(1/2)2 = 3(1) + 3(1/2) + 3(1/2)2 +.
4
Tiene razn r = con a= 3 como 0 es menor que [r]y es menor que 1 la serie
converge a :
a/1r = 3/1(1/2) = 6
La serie geomtrica :
oon=0 (3/2)n = 1 +3/2 + 9/4 + 27/8 +..
Tiene razn r = 3/2, como [r] es mayor que 1 , la serie diverge
SUCESIONES
Diremos que {an} es convergente si lim an = L (finito)
n
Si {an}y {bn}son convergentes tales que
lim an = L lim bn = M ; Entonces:
n n
{an} (,*,/){bn}= L(,*,/) M
Si lim |
an| = 0 lim an=
0
n n
Dada {an} diremos que C R es una cota superior de {an} si C an; B R es una cota
inferior si B an . Toda
sucesin acotada, montona (creciente o decreciente) y continua es convergente, ya
que tiende a su cota.
SERIES NUMRICAS
Diremos que una serie an es convergente si lim an = L (finito)
n
Series Geomtricas (Krn1; K,r R)
n=1
La serie geomtrica converge si |
r|<
1 y converge a
k
Sn=
1r
Si an y bn son convergentes a A y B respectivamente entonces:
an bn= A
Si C*an ; C=cte. C*an = C*A
El carcter de convergencia de una serie no cambia si se le suprimen los n primeros
trminos.
Si dos series coinciden a partir de un trmino n, las dos tienen el mismo carcter.
Dada an convergente lim an = 0
1
n

np es convergente para p>1.

n=1
CRITERIO DE LA INTEGRAL
Sea y(x) una funcin continua, positiva y decreciente en [1, +) y tal que (n)= an
entonces:
+ +
(x)dx y an tienen el mismo carcter.
1 n=1
CRITERIO DE COMPARACIN
an y
bn de trminos positivos.
Si an bn si bn converge se tendr que an converge. Y si an diverge
entonces bn diverge.
COMPARACIN AL LMITE (para series de trminos positivos)
Si lim an/bn = L (finito, positivo) an L*bn
n
Entonces si an converge bn converge y viceversa.
Si lim an/bn = 0 si bn converge an converge.
n
Si lim an/bn = + si bn diverge an diverge.
n

SERIES ALTERNAS ((n+1 an (n an )
n=1 n=1
Criterio Para Series Alternas.
Si lim an =0 y { an } es decreciente, entonces la serie es convergente.
2
n
CONVERGENCIA ABSOLUTA
Dada an de trminos de cualquier signo.
|
an|
converge an es convergente y diremos que an converge absolutamente.
Si |
an|
diverge y an
converge, diremos que an converge condicionalmente.
CRITERIO DE LA RAZN
Si lim |an+1|/|an|= L; L<1 la serie converge absolutamente.
n
Si L=1 no se puede concluir. Si L>1 la serie diverge.
CRITERIO DE LA RAZ
Si lim (|an|n=L; L<1 la serie converge absolutamente.
n
Si L=1 no se puede concluir; si L>1 la serie diverge.
ESTIMACIN DEL RESTO
Criterio de la Integral.
Resto(Rn)=SSn=an+1 + an+2+ an+3+...
+ +
(x)dx Rn (x)dx
n+1 n
Para Series Alternas
|Rn
|
|an+1
|<error

SERIES DE POTENCIA (Cn(xa)n; serie de potencia centrada en a)
3
n=0

xn =1/(1x) |x|<1
n=0

xn/n!= ex
n=0
Si una serie de potencia es convergente para x=x1 converge absolutamente para
cualquier valor de x tal que
|x|<|x1|.
Si una serie de potencia es divergente para x=x2 tambin es divergente para
cualquier valor de x tal que
|x|>|x2|.
SERIE DE TAYLOR
Cn=n(a)/n! De lo que se obtiene:

(x)= n(a)(xa)n/n!; si a=0 entonces se habla de serie de Mc. Laurin.

n=0