Documentos de Académico
Documentos de Profesional
Documentos de Cultura
Vcoordenados
Cargado por
Andres SanchezTítulo original
Derechos de autor
Formatos disponibles
Compartir este documento
Compartir o incrustar documentos
¿Le pareció útil este documento?
¿Este contenido es inapropiado?
Denunciar este documentoCopyright:
Formatos disponibles
Vcoordenados
Cargado por
Andres SanchezCopyright:
Formatos disponibles
VECTORES COORDENADOS
Conceptos previos:
1. Vector unitario es todo vector de magnitud igual a la unidad. Por ejemplo:
r 1 r
dado v diferente del vector nulo, r v es un vector unitario o normalizado
|v|
r
en la dirección de v . La expresión “normalizar un vector”, en este contexto,
significa determinar un vector de magnitud igual a uno, pero con la dirección
y el sentido del vector especificado.
Con esta correspondencia, se puede pensar en un punto en el espacio
r r con coordenadas (a , b , c) como un vector que comienza en el origen de
2. Los vectores no nulos v y w son ortogonales si al aplicarlos en un mismo
r coordenadas y termina en el punto ( a , b , c ). A estos vectores se les
punto forman un ángulo de 90°, se denota v es ortogonal (perpendicular) a
r r r denomina Vectores coordenados o algebraicos.
w así: v ⊥ w .
r r r r r r 7. En ℝ
3. Si v ⊥ w y | v | = | w | = 1, entonces decimos que v y w son ortonormales.
0
4. Un vector geométrico de posición o localizado es un vector con un origen a. El vector 0 se conoce como el vector nulo o vector cero. El vector
fijo. Generalmente se designa con la letra O el origen de los vectores de 0
posición. nulo tiene magnitud cero. Como los puntos inicial y terminal
Notación: como se asume el punto O como el inicio de los vectores de coinciden, se dice que el vector nulo no tiene dirección ni sentido
posición, entonces, para nombrarlos sólo se usa el punto final, por ejemplo: definidos.
el vector sería el mismo . r
b. Sea el vector v de componentes ( a , b , c), se define la magnitud de
r r r
5. El conjunto de todos los vectores de posición de origen en el punto O lo v , denotada por | v |, como: | v | = a 2 + b 2 + c 2
designaremos como . x1 x2
c. Igualdad de vectores: y1 = y 2 si y sólo si x1 = x2, y1 = y2
6. Correspondencia biunívoca entre los conjuntos yℝ z z
Teniendo en cuenta la correspondencia existente entre puntos del espacio y 1 2
tripletas ordenadas de números reales podemos afirmar que a cada vector y z1 = z2
de posición del espacio le corresponde una y sólo una tripleta ordenada de x1 x2 x1 + x2
números reales y, recíprocamente a cada tripleta ordenada le corresponde d. Suma: si ↔ y1 y ↔ y 2 , entonces, + ↔ y1 + y 2 . La
uno y sólo un vector de posición. La tripleta estaría asociada a las z z z + z
coordenadas del punto final del vector. 1 2 1 2
suma en ℝ tiene las mismas propiedades que la suma en E2 vistas
= ↔ , , en clases anteriores.
e. Multiplicación por un escalar:
x1 λx
Si ↔ y1 y ∈ ℝ, entonces λ ↔ λy
z λz
1
Igual que en la suma se cumplen las mismas propiedades vistas para
E3.
r
8. En ℝ punto (1,0) lo denotaremos por i y al vector de posición del punto (0,1) lo
r r r
= ↔ , denotaremos por j , es decir, i ↔ (1,0) y j ↔ (0,1).
0
a. El vector se conoce como el vector nulo o vector cero. El vector r r
0 Los vectores i , j son vectores no nulos y no paralelos. Esto significa, de
nulo tiene magnitud cero. Como los puntos inicial y terminal acuerdo con el teorema de la base para el plano, que cualquier vector de
coinciden, se dice que el vector nulo no tiene dirección ni sentido r r
ℝ puede escribirse como combinación lineal de los vectores i , j de forma
definidos.
r r única. La base que forman estos vectores se denomina base ortonormal
b. Sea el vector v de componentes ( a , b ), se define la magnitud de v
r r por ser vectores unitarios y ortogonales (perpendiculares) entre sí.
, denotada por | v |, como: | v | = a + b
2 2
r
x1 x 2 Ejemplo: dado a ↔ ( 9 , 4 ) lo expresaremos como combinación lineal de
c. Igualdad de vectores: = si y sólo si x1= x2 y y1 = y2 r r
los vectores i , j .
y1 y 2 r r r
a = 9i + 4 j
x1 x x + x2
d. Suma: si ↔ y ↔ 2 , entonces, + ↔ 1 . La
y
1 y
2 y1 + y 2 11. Base ortonormal para ℝ
suma en ℝ tiene las mismas propiedades que la suma en E2 vistas
en clases anteriores. r r v
e. Multiplicación por un escalar: En R3 se define i ↔ (1,0,0), j ↔ (0,1,0) y k ↔ (0,0,1), es decir,
x λx
Si ↔ y ∈ ℝ, entonces λ ↔
y λy
Igual que en la suma se cumplen las mismas propiedades vistas para
E2.
9. Correspondencia entre vectores libres y coordenados
Todo vector libre puede aplicarse en el origen de coordenadas de algún
sistema de referencia, entonces podemos decir que a todo vector libre
r
le corresponde un único vector de posición, por ejemplo: si a ∈ E3 Cualquier vector en ℝ se puede escribir de manera única en términos de
r r r r v
entonces a ↔ ↔ (x , y , z ), es decir, al vector libre a le los vectores i , j , k .
corresponde la tripleta ordenada o vector coordenado (x , y , z ).
10. Base ortonormal para ℝ
Existen dos vectores especiales en ℝ que nos permiten representar otros
vectores en el plano de manera conveniente. Al vector de posición del
LUGARES GEOMÉTRICOS (conjunto de puntos) x − x1 y − y1 z − z1
= = con (x2-x1) (y2-y1) (z2-z1) ≠ 0
( x 2 − x1 ) ( y 2 − y1 ) ( z 2 − z1 )
LA RECTA Estas ecuaciones reciben el nombre de ecuaciones simétricas de una
recta.
• En el espacio:
r
2. L(A, v ): Recta determinada por un punto y un vector paralelo. Se aplica lo
1. L(P, Q): Recta determinada por dos puntos. Si se conocen dos puntos de mismo del punto anterior con la ventaja de no tener que encontrar un vector
una recta es posible encontrar su ecuación. paralelo a la recta porque ya está dado.
• En el plano:
Ecuación vectorial de la recta L
→ →
r
OR = OP + λv
Ecuaciones paramétricas
x = x1 + λ (x2-x1)
y = y1 + λ (y2-y1)
Ecuaciones simétricas
r x − x1 y − y1
r =
Sean P y Q puntos sobre la recta L. Sea P ↔ (x1, y1, z1) y Q ↔ (x2, y2, z2), ( x 2 − x1 ) ( y 2 − y1 )
→
r r r r
entonces: PQ = v = Q - P = (x2-x1 , y2-y1 , z2-z1). v || L. Sea R otro punto
→ →
Ecuación cartesiana
r r
sobre L con R=(x, y, z), entonces, PR || v y PR = λv para algún ∈ ℝ. ( y 2 − y1 )
→ → → y − y1 = ( x − x1 )
Para cualquier punto R sobre la recta se tiene que OR = OP + PR , entonces, ( x2 − x1 )
→ →
r
OR = OP + λv ecuación vectorial de la recta L. EL PLANO
Extendiendo por componentes la expresión anterior:
1. π (A, B, C): Plano determinado por tres puntos no colineales. Si se conocen tres
puntos de un plano es posible encontrar su ecuación.
(x , y , z) = (x1 , y1 , z1) + λ (x2-x1 , y2-y1 , z2-z1)
Por igualdad de vectores tenemos que:
x = x1 + λ (x2-x1)
y = y1 + λ (y2-y1)
z = z1 + λ (z2-z1)
Estas ecuaciones se conocen como las ecuaciones paramétricas de la
recta.
Despejando λ en las ecuaciones paramétricas e igualando las expresiones
resultantes obtenemos:
r
→ o La expresión “el vector libre v está en el plano π ” se entiende en el sentido
Sean A, B y C puntos no colineales sobre el plano π . Sea A ↔ (x1 , y1 , z1 ) , r
→ →
de que si se escoge en π un punto O y en éste se aplica el vector libre v de
B ↔ (x2 , y2 , z2 ) y C ↔ (x3 , y3 , z3 ), sea, → r
→
modo que OP = v (siendo P otro punto sobre π ), entonces el segmento
r → → →
AB = v = B - A = (x2-x1 , y2-y1 , z2-z1).
→ → → → →
orientado OP tiene todos sus puntos en el plano π .
r
sea AC = w = C - A =(x3-x1 , y3-y1 , z3-z1). v no es paralelo a w pero ambos
vectores son paralelos a π .
Sea P otro punto sobre el plano π con P=(x, y, z), entonces, POSICIONES RELATIVAS E INTERSECCIONES DE LUGARES
→ r → GEOMÉTRICOS
AP = ( λv + β w ) por el teorema de la base
→ → → → r →
P = A + AP = A + ( λv + β w ) para algún λ y β ∈ ℝ.
Rectas en ℝ 2: sean L1 y L2 dos rectas del plano.
→ → r →
P = A + ( λv + β w ) Ecuación vectorial del plano π .
L1 I L2 S.E.L Posición relativa
Extendiendo por componentes la expresión anterior y aplicando el concepto de ∅ Inconsistente paralelas no coincidentes
igualdad de vectores: {P} Solución única se cortan en un punto
L1 = L2 Infinitas soluciones rectas coincidentes
x = x1 + λ (x2-x1) + β (x3-x1)
y = y1 + λ (y2-y1) + β (y3-y1)
Rectas en ℝ 3: sean L1 y L2 dos rectas en el espacio.
z = z1 + λ (z2-z1) + β (z3-z1)
L1 I L2 S.E.L Posición relativa
Estas ecuaciones se conocen como las ecuaciones paramétricas del plano.
• Son paralelas no coincidentes
Si de las ecuaciones paramétricas eliminamos los parámetros λ y β obtendremos ∅ Inconsistente • No son paralelas y se cruzan
en el espacio
una ecuación lineal para las variables x, y y z de la forma:
{P} Solución única se cortan en un punto
L1 = L2 Infinitas soluciones rectas coincidentes
ax + by + cz = d
que llamaremos la ecuación cartesiana del plano
Recta y Plano en ℝ 3: sean la recta L y el plano π .
r →
2. π (A, v , w ): Plano determinado por un punto y dos vectores paralelos al plano no L1 I π S.E.L Posición relativa
paralelos entre sí. Se aplica lo mismo del punto anterior con la ventaja de no tener ∅ Inconsistente paralelos no coincidentes
que encontrar los vectores paralelos al plano porque ya están dados. {P} Solución única se cortan en un punto
L Infinitas soluciones El plano contiene a la recta
Notas:
Planos en ℝ 3: sean π 1 , π 2 dos planos.
• Un plano no tiene ecuaciones simétricas.
• En el espacio no hay ecuación cartesiana para la recta. π1 I π2 S.E.L Posición relativa
• Estrictamente hablando, el vector libre carece de puntos. No obstante, podemos ∅ Inconsistente paralelos no coincidentes
decir lo siguiente:
r π1= π2 Infinitas soluciones (con 2 paralelos coincidentes
o Un vector libre v está en un plano π , si dicho vector es paralelo al plano. parámetros)
o Dos o más vectores son coplanarios si existe un plano π paralelo a cada uno L Infinitas soluciones (con 1 parámetro) El plano contiene a la recta
de ellos.
También podría gustarte
- Diagrama de Facilidades de SuperficieDocumento14 páginasDiagrama de Facilidades de SuperficieAlejandro VillalbaAún no hay calificaciones
- Euler MascheroniDocumento8 páginasEuler MascheronijuanAún no hay calificaciones
- Examen Segundo Período Técnicas de Programación II Parte PrácticaDocumento1 páginaExamen Segundo Período Técnicas de Programación II Parte PrácticaDouglas GilAún no hay calificaciones
- Elgoibar - Gipuzkoa - Spain: Etxe-Tar S.ADocumento160 páginasElgoibar - Gipuzkoa - Spain: Etxe-Tar S.AgalvangrrAún no hay calificaciones
- Guia Configuraciones Basicas Router Observa Aw4062Documento30 páginasGuia Configuraciones Basicas Router Observa Aw4062Cesar DiazAún no hay calificaciones
- Trabajo TecnologiaDocumento15 páginasTrabajo TecnologiaFlorian IlieAún no hay calificaciones
- Tema 05 GenericidadDocumento12 páginasTema 05 GenericidadMauricio Jorge Cordeiro GarridoAún no hay calificaciones
- Taller 1Documento5 páginasTaller 1Hwver MuñozAún no hay calificaciones
- Tarea Semana 3 Luis ValdezDocumento3 páginasTarea Semana 3 Luis ValdezLuis valdezAún no hay calificaciones
- Planificador de MinaDocumento1 páginaPlanificador de MinaManuel NicAún no hay calificaciones
- TVV - 20 SetiembreDocumento5 páginasTVV - 20 SetiembrePaola carol huayhuaAún no hay calificaciones
- Apuntes de AlgoritmosDocumento100 páginasApuntes de AlgoritmosHalver de lacruzAún no hay calificaciones
- ListaDocumento10 páginasListaAlejandro KingAún no hay calificaciones
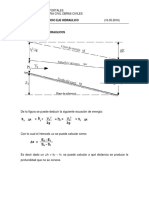
- Tarea Eje Hidraulico (16!05!2016)Documento3 páginasTarea Eje Hidraulico (16!05!2016)Jorge AlexisAún no hay calificaciones
- Aplicacion de Instrumentos de MedicionDocumento84 páginasAplicacion de Instrumentos de MedicionDavidAún no hay calificaciones
- El Desarrollo Del CelularDocumento2 páginasEl Desarrollo Del CelularOctavio Mondragon ArzateAún no hay calificaciones
- AUDITORIA INTERNA 2020 I XXXDocumento8 páginasAUDITORIA INTERNA 2020 I XXXKatty MallquiAún no hay calificaciones
- Cuestionario Scrum JCMMDocumento19 páginasCuestionario Scrum JCMMRuth Cujilan AriasAún no hay calificaciones
- TSP - Programación I - Pseudocódigo - UTN FRVTDocumento6 páginasTSP - Programación I - Pseudocódigo - UTN FRVTapi-3749301100% (1)
- Ejercicios Resueltos Ana - EstructuralDocumento11 páginasEjercicios Resueltos Ana - Estructuralalejo gutierrez condoriAún no hay calificaciones
- Polinomio de LagrangeDocumento14 páginasPolinomio de LagrangeDidier Gamaliel Buendia OrtizAún no hay calificaciones
- Componentes Del Sistema de InformacionDocumento28 páginasComponentes Del Sistema de InformacionAngelini S. IllanesAún no hay calificaciones
- Redes Informáticas - Tarea3Documento7 páginasRedes Informáticas - Tarea3KarenAún no hay calificaciones
- Mec40092evidencia088 Jessica Zapata - Liberar VBSDocumento4 páginasMec40092evidencia088 Jessica Zapata - Liberar VBSJessicaZapataCamargoAún no hay calificaciones
- Indicadores de Desempeño Programa Mantenimiento Por Condición-29Ago21Documento5 páginasIndicadores de Desempeño Programa Mantenimiento Por Condición-29Ago21Wilson GarciaAún no hay calificaciones
- Ejercicio 5 (Ficheros y Directorios)Documento3 páginasEjercicio 5 (Ficheros y Directorios)Neko BlackAún no hay calificaciones
- Formato Pat Pip 2024Documento6 páginasFormato Pat Pip 2024Milagros Velasque PichihuaAún no hay calificaciones
- Sesión 2 Control FULLDocumento27 páginasSesión 2 Control FULLStivent Alfonso Santiago MontañoAún no hay calificaciones
- Analisis de La Operaciones Los Diez Enfoques PrimariosDocumento10 páginasAnalisis de La Operaciones Los Diez Enfoques PrimariosSTALTHAM99Aún no hay calificaciones
- Ud 1 - Introducción A Los Sistemas de Información GeográficaDocumento23 páginasUd 1 - Introducción A Los Sistemas de Información GeográficaRosa LatiegueAún no hay calificaciones