REPASO DE LA DERIVADA bernardsanz

REPASO DERIVADAS
Incrementos
El incremento de una variable que pasa de un valor numérico a otro, es la diferencia que se
obtiene al restar el valor inicial del valor final.

x  x2  x1
y  y2  y1

Un incremento de x se representa por el símbolo x , que se lee “delta x ” o

“incremento de x ”. Este incremento puede ser positivo o negativo, según la variable en
cuestión aumente o disminuya al cambiar el valor.

y  significa el incremento de y
  significa el incremento de 
f (x)  significa el incremento de f (x)

Si en y  f (x) la variable independiente x toma un incremento x , entonces y indicara el

incremento correspondiente de la función f (x) .

El incremento y siempre ha de contarse desde el valor inicial definido de y , que corresponde

al valor inicial arbitrariamente fijado de x desde el cual se cuenta el incremento de x .

Definición de derivada
La derivada de una función es el límite de la razón del incremento de la función al incremento
de la variable independiente cuando este tiende a cero.

dy y f (x)
 lim  lim
dx x0 x x0 x

Cuando este límite existe, se dice que la función es derivable o que tiene derivada.

Ya que y  f (x  x)  f (x) , la derivada se queda como:

dy lim f (x  x)  f (x)

dx x0 x

Elaboro: Ing. Bernardino Sánchez Díaz 1

REPASO DE LA DERIVADA bernardsanz

Notación de la derivada


 y '  f '(x)  Dx y  Dx f (x)
dy df (x)

dx dx

d ()
Por lo tanto es el operador derivada.
dx

Interpretación Geométrica de la Derivada

Una de las principales motivaciones para el desarrollo de la derivada fue el problema de
encontrar la pendiente de una recta tangente a un punto de una gráfica. A continuación
explicamos dicho problema.

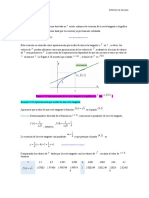
Supongamos que trazamos una recta secante en la curva de y  f (x) , que además pasa por
los puntos P y Q de la función (recta azul).

Para obtener la pendiente de esta secante utilizamos la conocida ecuación de geometría

y2  y1 y
analítica: m  tan  
x2  x1 x

Si empezamos a trazar rectas secantes haciendo que el punto Q se mueva sobre curva de
y  f (x) , aproximándose cada vez más al punto P el cual permanece fijo.

Elaboro: Ing. Bernardino Sánchez Díaz 2

REPASO DE LA DERIVADA bernardsanz

Al hacer esto vemos que los valores de x y y disminuyen. Cuando el punto Q casi llega al
punto P, la recta secante alcanza su posición “límite”, en este punto x es casi cero, por lo
tanto se dice que x  0 , y por definición la recta secante PQ se transforma en la recta
tangente a la curva en el punto P.
y
lim  lim tan  tan  lim f (x  x)  f (x) dy

x0 x x0 x0 x dx

Por lo tanto la interpretación geométrica de la derivada nos dice que la pendiente de una recta
tangente a un punto de una función, no es otra cosa que la derivada de la función evaluada en
dicho punto P.

dy df (x)
mt  
dx dx

Cálculo de la derivada a partir de la definición

En algunas bibliografías se le nombra el método de los cuatro pasos:
1 2

dy  lim f (x  x)  f (x)

4
 x
dx x0
3

En el paso 1 se incrementa la función, en el paso 2 se resta la función original, en el paso 3 se

divide por él x y en el paso 4 se evalúa el límite.

Ejemplo: calcular la derivada de la función y  f (x)  3x  5

2

y  y  3  x  x   5
2
paso 1
y  y  3  x2  2xx  x2   5
y  y  3x2  6xx  3x2  5
paso 2 y  y  3x2  6xx  3x2  5
y  3x2 5
y  6xx  3x2
y  6xx  3x x  6x  3x 6x  3x
2
paso 3  
x x x
y d  3x 2  5 
paso 4 lim
x0 x x0

 lim 6x  3x  6x  dx
 6x

Elaboro: Ing. Bernardino Sánchez Díaz 3

 REPASO DE LA DERIVADA bernardsanz

Regla de la Cadena (Derivada de una función compuesta)

Recordemos que la función compuesta f  g se define como:  f  g   x  f  g(x) 



A g(x) se le llama la función interna y a f (x) la función externa.

“la derivada de  f  g  es el producto de la derivada de la función externa f evaluada en g(x) y la

derivada de la función interna evaluada en x ”. Se asume que g es diferenciable en x y que f es

diferenciable en g(x) .

d  f  g(x)    f ' g(x)   g '(x)

dx 

Formulación alternativa de la regla de la cadena

Sea u  g(x) y y  f (u) , entonces la función compuesta de g y de f es y  f (u)  f  g(x)  , y

se tiene la fórmula:

dy dy du
  Regla de la cadena
dx du dx

En la formulación alternativa de la regla de la cadena, la y de la izquierda denota la función

compuesta de x , mientras que la y de la derecha señala la función original.
Es de gran importancia esta regla debido a que casi todas las fórmulas de derivación están

d  u n  nun1  du , el factor

basadas en la regla de la cadena, por ejemplo en la fórmula nun1 de la
dx dx
dy
fórmula representa a de la regla de la cadena.
du

Ejemplo: Sea y  u3  f (x) y u  4x2  2x  5  g(x) .

 f  g   x  f  g(x)   g 3   4x 2  2x  5 
3
Entonces
dy d  u 3  d  4x 2  2x  5 
 3u2 8x  2  3 4x 2  2x  5  8x  2 
2
 
dx du dx

Elaboro: Ing. Bernardino Sánchez Díaz 4

 REPASO DE LA DERIVADA bernardsanz


Para fines prácticos calcularemos derivadas por medio de fórmulas, se deja al estudiante que
así lo desee la consulta de la obtención de dichas fórmulas1. A continuación se presenta un
procedimiento para el cálculo de derivadas:

1.) Identificar a la función

Si surge otra derivada dentro

de la sustitución, y esta nueva
derivada es complicada, se
2.) Seleccionar la fórmula de
sugiere calcularla por separado
derivación
y después regresar con el
resultado parcial a la derivada
original y continuar con la
3.) Identificar componentes simplificación.

4.) Sustituir en fórmula y

simplificar

En el paso 1 la identificación de la función es crucial, ya que si identificamos mal el tipo de

función, seleccionaremos erróneamente la fórmula de derivación y todo lo que hagamos en los
pasos 3 y 4 será infructuoso. En muchas ocasiones, a fin de identificar la función a derivar es
necesario realizar una manipulación algebraica para poder aplicar alguna fórmula de derivación
como en el ejemplo 1.

2 6  2 4
Ejemplo 1. Derivar la función y    
3
x x
x3 4 x3
Paso 1. A fin de identificar la función se emplearán las leyes de los radicales y de los
exponentes para ver que se trata de una suma de funciones potenciales:
2 6
y   2 2 4  2x 2  6x 3 2x  
1 1 3 3
4 2 6 2 4x
 =    4

x 3
x x1 x1 x3 x3
x3 4
2 3 2 4
x3
Paso 2. Al seleccionar la fórmula empleamos la fórmula de potencia de una variable:

 x  nxn1
d n
dx
Paso 3. Los componentes los identificamos en el paréntesis, y para este ejemplo son las
potencias n de cada suma.

1
Podemos encontrar esta información en la referencia 2. Stewart.

Elaboro: Ing. Bernardino Sánchez Díaz 5

REPASO DE LA DERIVADA bernardsanz

 
d x
1
2
 
d x
1
3
d x  
3
2
 
d x
3
4

dy
2 6 2 4
dx dx dx dx dx
n1 n1 n3 n  3
2 3 2 4
Paso 4. Al sustituir en la fórmula tenemos:
dy  1
    1 1   3
    3
 2  x  212  6  x  314  2  x  1  4  x  1
1 3 3

 

 
 2
dx   3   2   4 
dy
dx

2
   
2 3 6 4
x 2  x 3


3
 
2  3  5


2
x 2
4  3  7
4
 
x 4  
1 2 3 3
dy 1 2 3 3      1  2  3  3
 3  4  5  7
x x x 3 x x2 x x 4 x3
dx x2 x3 x2 x4 x3 3 x4 x5 4 x7

Ejemplo 2. Derivar la función y  (x  1) x 2  2x  2

Paso 1. Esta es una función compuesta, en principio es un producto de funciones y uno de los
factores es una función potencial (el radical):
1
y  (x 1) x2  2x  2  (x 1)  x 2  2x  2  2
Paso 2. Emplearemos la fórmula del producto de dos funciones:
d du dv
 uv   v u
dx dx dx
Paso 3. Los componentes los identificamos en el paréntesis, y para este ejemplo son las
potencias n de cada suma.

dy d    2   21      2   12
 (x 1) x 2x 2  , u (x 1) v x 2x 2
dx dx  
Paso 4. Al sustituir en la fórmula tenemos:
dy 1
1 d   1

 x  2x  2   x 1  (x 1)  x  2x  2  2 
2 2 d 2

dx dx dx  
Al momento de sustituir apreciamos que surgen dos derivadas, de las cuales la primera es
bastante sencilla, la derivada de x es uno y la derivada de 1 es cero por ser una constante.
Pero para la segunda derivada no es el mismo caso, es más complicada por lo que optamos
por calcularla por separado y una vez que tengamos el resultado, volvemos con este a la
derivada original.

d  2  2x  2 12 , es una función compuesta del tipo potencial, por lo que emplearemos la
x 
dx 
fórmula  u   nu n1  du , resultando los componentes u  x2  2x  2 y n  1 .
d n
dx dx 2

Elaboro: Ing. Bernardino Sánchez Díaz 6

REPASO DE LA DERIVADA bernardsanz

d  x  d  x 
1
d 2
0
d  2 1 
2

x  2x  2    x2  2x  2  
2
d
2 
dx   dx dx dx dx

 x 2  2x  2 2  x2  2x  2

1
1 1 d
 2x21  2
2 dx

 1 x 2  2x  2 2 2x  2 
1

Nuevamente surge otra derivada  2x  2
2
2 (x 1) x 1
 
2 x2  2x  22
1
x  2x  2
2

Ya con este resultado parcial regresamos a la derivada original:

dy  (x 1)  x2  2x  2 (x 1)2
 x 2  2x  2  (x  1)   
dx  x 2
 2x  2  1 x2  2x  2
 x  2x  2   (x 1)
2
2 2
x 2  2x  2  x2  2x 1 
  
x2  2x  2 x2  2x  2
dy 2x 2  4x  3

dx x2  2x  2
Las funciones trigonométricas son más sencillas que las algebraicas compuestas.

Ejemplo 3. Derivar la función y  sen 3x  cos 2x .

Paso 1. La función es una suma de funciones trigonométricas, y son de fácil identificación.
d du d du
Paso 2. Las fórmulas a emplear son: sen u   cos u  y cos u   sen u  .
dxdx dx dx
Paso 3. Los componentes son u  3x para el seno y u  2x para el coseno .
Paso 4. Sustituyendo tenemos:

 cos 3x  d 3x   sen 2x  d 2x

3 2
dy
3cos 3x  2 sen 2x
dx dx dx
En este último ejercicio debemos tener cuidado de no multiplicar los números resultantes de las
dos derivadas por el argumento de la funciones trigonométricas, nunca hacer 33x  9x , ni
2  2x   4x ya que el cos 3x son una misma expresión al igual que él sen 2x .
Ejemplo 4. Derivar la función y  tan (e ) .
2 3x

Paso 1. La función es una compuesta de una potencia y el argumento de la tangente es una


y  f (x)  tan  e3x  
2
función exponencial:
Paso 2. La fórmula a emplear es: 
Paso 3. Los componentes son u  tan e   y n  2 .
3x

Elaboro: Ing. Bernardino Sánchez Díaz 7

REPASO DE LA DERIVADA bernardsanz

Paso 4. Sustituyendo tenemos:

21 d tan  e 1 d tan  e3x  3x 2
  sec 2  e3x   d  e 
3x
dy
dx

 2 tan  e 
3x

dx
Se calcula aparte
dx dx
dy
dx

 2 tan  e3x   3e3x sec 2  e3x    sec 2  e3x   3e3x

 6e3x tan  e3x   sec 2  e3x   3e3x  sec 2  e3x 

dy
dx
d  e3x  3x d 3x 3
3

 e 
dx dx
 3e3x

d du
Al surgir la primera derivada (1), la fórmula utilizada es  tan u   sec2 u  y el
dx dx
componente es u  e .
3x

Para la segunda derivada (2), se empleó la fórmula

d
 e   e  du
u u
y el componente es u  3x
dx dx
y la tercera derivada (3), es de fácil solución.

Para las funciones logarítmicas y exponenciales, todavía es más sencillo el cálculo de estas
derivadas.
Ejemplo 5. Derivar la función y  ln(3x  5) .
2

Paso 1. La función es del tipo logarítmica.

d 1 du
Paso 2. La fórmula a emplear es: ln u   
dx u dx
Paso 3. El componente es u  3x  5 . 2

Paso 4. Sustituyendo tenemos:

d  3x 2  5 
6x
dy 1  6x
 2  
dx 3x  5 dx 3x2  5
x4
Ejemplo 6. Derivar la función y  ln .
(3x  4)2
Paso 1. La función es del tipo logarítmica, pero aplicar la fórmula así como la tenemos sería
trabar de más. Para evitar esta dura labor, emplearemos las leyes de los logaritmos para
a
simplificar la función: 1) ln(ab)  ln a  ln b, 2) ln a r  r ln a, 3) ln  ln a  ln b
 b 

y  ln x4  ln x4  ln  3x  4  2  4 ln x  2 ln 3x  4
(3x  4)2

Elaboro: Ing. Bernardino Sánchez Díaz 8

 REPASO DE LA DERIVADA bernardsanz


De esta forma hemos cambiado una derivada con ciertas dificultades algebraicas, por dos
bastante sencillas.
d 1 du
Paso 2. La fórmula a emplear es: ln u   
dx u dx
Paso 3. Los componentes son2: u  x para la primera y u  3x  4 para la segunda.
Paso 4. Sustituyendo tenemos:

 1 dx 1  d  3x  4   4
3
dy 1 6 4  3x  4  6x
 4   2     
 x dx   3x  4  x 3x  4 x  3x  4
 
  

dx dx
   
dy 12x 16  6x  6x 16
 
dx x  3x  4 x  3x  4

Ejemplo 7. Derivar la función y  esen3x .

Paso 1. La función es exponencial, y el argumento es una función trigonométrica.
Paso 2. La fórmula a emplear es:
d
 e   e  du
u u

dx dx
Paso 3. El componente es: u  sen 3x .
Paso 4. Sustituyendo tenemos:
dy d (sen 3x) d (sen u) du
 esen3x   cos u 
dx dx dx dx
3
dy  esen3x  3cos 3x d (sen 3x) d (3x)
 cos 3x 
dx dx dx
dy
 3cos 3x  esen3x  3cos 3x
dx

Derivación implícita
Función Implícita: Una ecuación f (x, y)  0 , define a y como una función implícita de x . El
dominio de esa función implícitamente definida consta de tales x para las cuales existe una
única " y " tal que f (x, y)  0 .
dy
Si y en una función definida implícitamente por una ecuación f (x, y)  0 , la derivada y ' 
dx
puede hallarse de dos formas distintas:

du
2
Es importante hacer notar que siempre que u  x entonces  1.
dx

Elaboro: Ing. Bernardino Sánchez Díaz 9

REPASO DE LA DERIVADA bernardsanz

1. Despejar y , y calcular a y ' directamente. Salvo para ecuaciones muy sencillas, este
método es generalmente imposible o no práctico.
2. Considerar a y como una función de x  y  f (x)  , derivar ambos miembros de la
ecuación original f (x, y)  0 y despejar y ' en la ecuación resultante.
Ejemplo 8. Calcular la derivada de xy  x  2 y 1  0 .
1 y' 0 0
d  xy  d  x  d  y

d 1

d 0
 2
dx dx dx dx dx
La primera derivada corresponde a un producto de funciones, recordemos que x es la función
identidad y y  f (x) , con lo que:
1 y'
d  x d  y
y x 1 2 y '  0
dx dx
y  xy ' 2 y '  1
 y 1
y ' x  2    y 1 y'
x 2

Ejemplo 9. Calcular la derivada de x3  3x2 y  6xy2  2 y3  0 .

d  x3  d  x y  d  xy  d  y  d 0
2 2 3

3 6 2 

dx dx dx dx dx
La primera y la cuarta derivada corresponden a una potencia, con la diferencia que la cuarta
nos produce a y ' , la segunda y la tercera derivada son productos de funciones, por lo que:

y'  y' 

    d  x  1
 
2   0
d x 2
d  y   d y 
 2 3y 31
d  y   
d  0 
3x31  3  y  x2   6  y2 x
 dx dx   dx dx    dx  dx
     
 y' 
d  y   6 y 2 y '  0
3x 2  3y  2x 21   3x 2 y ' 6 y 2  6x  2 y 21 dx 
 
 
6xy  3x y '12xyy ' 6 y y '  6 y  3x
2 2 2 2

y '  3x 2 12xy  6 y 2   6 y 2  6xy  3x 2

6 y2  6xy  3x2 3  2 y 2  2xy  x2 

y '  2 
3x 12xy  6 y 2 3  x2  4xy  2 y 2 
2 2
2 y  2xy  x
y '  x2  4xy  2 y2

Elaboro: Ing. Bernardino Sánchez Díaz 10

REPASO DE LA DERIVADA bernardsanz

BIBLIOGRAFÍA

1) Swokowski E., Cálculo con geometría analítica, Editorial iberoamericana, México, 2002.
2) Stewart J., Cálculo Trascendentes Tempranas, 6 edición, Thomson Brooks/Cole,
México, 2008.
3) Leithold L., El Cálculo, Oxford University Press, 7 Edición, México, 1988.
4) Purcell E. J., Varberg D., Rigdon S. E., Cálculo, 9 Edición, Pearson Educación, México,
2007.
5) Swokowski E. y Cole J., Algebra y Trigonometría con Geometría Analítica, 11ª edición,
International Thomson Editores, México, 2006.
6) Stewart J., Redlin L., Watson S., Precalculus, 5th edition, Brooks/Cole, CENGAGE
Learning, USA, 2009.

Elaboro: Ing. Bernardino Sánchez Díaz 11