MATEMÁTICAI Amerinsa

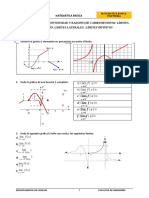
MATEMATICAS
PRIMER ANO
AMERINSA
1 PC
Année scolaire 2011 - 2012
Curso
Ejercicio
Auteur de la Ressource Pédagogique

Guy Athanaze
Matemáticas Primer año
AMERINSA
Versión en español
2011-2012
© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 2

PREFACIO
Este fascículo:
No es un curso exhaustivo que cubra el programa de primer año del programa
AMERINSA. N o se han incluido todas las demostraciones de las propiedades y teoremas.
Este fascículo no remplaza los cursos ni justifica faltar a las clases ni a las cesiones de
Ejercicios Dirigidos (ED).
Este fascículo:
Está destinado a a yudarles en la comprensión del curso de Matemáticas. Sigue de
cerca el plan de los capítulos con todas las definiciones y la mayoría de los teoremas. Se
detallan algunas de las demostraciones que no se hicieron durante las clases. Encontrarán
también ejemplos y ejercicios corregidos
Al final de cada capítulo, ejercicios de nivel 1 son propuestos (a veces con sus
correcciones). Se trata de aplicaciones directas del curso. Estos ejercicios deber ser resueltos
por los estudiandes luego de la presentación del curso correspondiente y antes de los TD. No
serán presentados por los profesores. Estos ejercicios han sido elaborados con la participación
de M.C. Douineau, A. Aymes, H. Ricard, J.B. Dill, A. Lachal, S. Balac.
Agradezco a C. Jaloux por su cooperación y participación en la parte de « ejercicios
corregidos ».
El último capítulo « A propósito de la redacción » contiene un cierto número de
ejercicios y problemas de evaluación del INSA. Los enunciados se presentan de manera
similar a la presentación de los alumnos. La resolución de los ejercicios es una copia fiel a la
original. Atención porque no se trata de las respuestas sino simplemente de un ejemplo de
redacción. Agradezco a los estudiantes que acepataron la publicación de sus ejercicios.
Post Scriptum.: S i detectan errores de mecanografiado o si tienen observaciones,

transmítanlos al autor... Gracias por adelantado.

Índice

PREFACIO 3
ÍNDICE 5
Cap. 0 : ALGUNOS CONCEPTOS FUNDAMENTALES 7
Cap. I : TEORÍA DE CONJUNTOS 13
Cap. II : LA LÓGICA MATEMÁTICA 22
Cap. III : LA DEMOSTRACIÓN MATEMÁTICA 43
Cap. IV : FUNCIÓN, APLICACIÓN, BIYECCIÓN 52
Cap. V : COMPLEMENTOS SOBRE LOS NÚMEROS COMPLEJOS 65
Cap. VI: COMPLEMENTOS EN TRIGONOMETRÍA 81
Cap. VII: LOS POLINOMIOS 88
Cap.VII: LAS FRACCIONES RACIONALES 107
Cap. IX: COMPLEMENTOS SOBRE LOS REALES 117
Cap. X: FUNCION DE UNA VARIABLE REAL 130
Cap. XI: FUNCIONES ELEMENTALES 157
Cap. XII: COMPARACIÓN DE FUNCIONES 181
Cap. XIII: CÁLCULO DIFERENCIAL 191
Cap. XIV: DESARROLLOS LÍMITES 211
Cap. XV: SUCESIONES DE REALES 231
Cap. XVI: INTEGRAL DE RIEMANN 250
Cap. XVII: CÁLCULO PRÁCTICO DE PRIMITIVAS Y DE INTEGRALES 266
Cap. XVIII: INTEGRALES GENERALIZADAS 285
Cap. XIX: ESPACIO VECTORIAL 304
Cap. XX: APLICACIONES LINEALES 327
Cap. XXI: MATRICES 346

Cap. XXII: MATRICES Y APLICACIONES LINEALES 356
Cap. XXIII: DETERMINANTES 371
Cap. XXIV: SISTEMA DE ECUACIONES LINEALES 385
Cap. XXV: REDUCCIÓN DE MATRICES CUADRÁTICAS 394
Cap. XXVI: A PROPOSITO DE LA REDACCION 411

ALGUNOS CONCEPTOS FUNDAMENTALES
En este capítulo preliminar, encontrarán una serie de las definiciones que se estu-
diarán en este fascículo. Algunas ya se conocen, otras no. Se les agrupó aquí con el fin de
tener una vista más sintética.
Encontrarán también una pequeña nota de fórmulas clásicas (trigonometría, identida-
des notables...).
APLICACIONES
Inyección o correspondencia inyectiva de E en F

Una aplicación f: E → F es inyectiva si y solamente si se cumple alguna de las propiedades
equivalentes:
• ∀ (x, x’)∈E2, x ≠ x’ ⇒ f(x) ≠ f(x’).
• ∀ (x, x’)∈E2, f(x)=f(x’) ⇒ x=x’.
• Todo elemento de F admite a lo sumo un antecedente en E.
Suprayección o correspondencia suprayectiva de E sobre F

Una aplicación f: E → F es suprayectiva si y solamente si se cumple alguna de las propieda-
des equivalentes:
• f(E)=F.
• Todo elemento de F admite al menos un antecedente en E.
Biyección o correspondencia biyectiva de E sobre F

Una aplicación f: E → F es biyectiva si y solamente si se cumple con alguna de las propie-
dades equivalentes:
• f es inyectiva y suprayectiva.
• Todo elemento de F admite un antecedente único en E.
Composición de las aplicaciones

1. La composición asociativa de las aplicaciones significa que cualesquiera que sean las apli-
caciones f, g, h tales que:
f g h
E →F→G→H
(h  g)  f = h  (g  f).
2. El compuesto de dos inyecciones es una inyección.

El compuesto de dos suprayecciones es una suprayección.
El compuesto de dos biyecciones es una biyección.

Involución o aplicación involutiva
Una aplicación f: E → E es una involución si y solamente si se cumple alguna de las propie-

dades equivalentes:
• f es biyectiva y f=f-1.
• f  f=id E .
Restricción de una aplicación. Prolongación

Sea una aplicación f: E → F y A ⊂ E. La restricción de f en la parte A es la aplicación
g :A → F tal que :
∀ x∈A, g(x)=f(x)
Se dice también que f es una prolongación de g en E.
ESTRUCTURAS
Grupo
(G,*) es un grupo si y solamente si:
• G tiene una ley de composición interna * (aplicación de G × G en G);
• la ley * es asociativa (cualquiera que sean a, b, c de G: (a*b)*c=a*(b*c));
• admite un elemento neutro ( existe e de G tal que cualquiera que sea a de G, a*e = e*a = a);
• todo elemento "a" de G admite un elemento simétrico a' en G para la ley * (a*a’=a’*a=e).
Grupo conmutativo
El grupo (G, *) es conmutativo si y solamente si la ley * es conmutativa (cualesquiera que

sean "a" y "b" de G: a*b=b*a).
Subgrupo
Sea un grupo (G, *). Una parte H de G es un subgrupo de G para la ley * si y solamente si
(H, *) es un grupo.
Cuerpo conmutativo
(K, +, × ) es un cuerpo conmutativo si y solamente si:
• (K, +) es un grupo conmutativo.
• K se tiene una ley interna × , asociativa, conmutativa, distributiva, con relación a la ley +
(cualesquiera que sean a, b, c de K: a(b+c)=ab+ac , (b+c)a=ba+ca), que admite un elemento
neutro y todo elemento no nulo de K admite un simétrico para la ley × .
Subcuerpo conmutativo
Sean (K, +, × ) un cuerpo conmutativo. Una parte L de K es un subcuerpo conmutativo de
(K, +, × ) si y solamente si (L, +, × ) es un cuerpo conmutativo.

Homomorfismo. Isomorfismo
Sean (E, *) y (F, o) dos conjuntos que tienen leyes de composición internas * y "o", una apli-
cación f: E  F es un homomorfismo (se dice también morfismo) si y solamente si
∀ (x, y)∈ E2, f(x*y)=f(x)of(y)
Un homomorfismo biyectivo se llama isomorfismo.
- Espacio vectorial o espacio vectorial en 

(V +, •) es un -espacio vectorial o un espacio vectorial en  si y solamente si:
• (V, +) es un grupo conmutativo;
• la ley de composición externa (aplicación de  × V en V) posee las propiedades siguien-
→ →
tes: cualesquiera que sean los elementos u y v de V y los reales λ y µ,
→ →
1• v = v
→ →
λ•(µ• v )=(λµ)• v
→ → →
(λ+µ)• v =λ• v + µ• v
→ → → →
λ•( u + v )= λ• u + λ• v
Subespacio vectorial
• Definición
Una parte V’ de V es un subespacio vectorial del espacio vectorial si V’ es un espacio
vectorial para las dos leyes + y • de V.
• Caracterización
V’ es un subespacio vectorial de V si y solamente si posee una de las dos propiedades
equivalentes siguientes :
1- - V’ es una parte de V que no está vacía
→ → → →
- ∀ ( u , v )∈V’², u + v ∈V’² (estabilidad para la ley +)
→ →
- ∀ v ∈V’, ∀ λ∈, λ• v ∈V’ (estabilidad para la ley •)
2- V’ es una parte de V que no está vacía
→ → → →
- ∀ ( u , v )∈V’², ∀ (λ,µ)∈², λ u + µ v ∈V’² (estabilidad para combinaciones
lineales).

COORDENADAS
→→
El plano P está dado con respecto a una referencia (O, i , j )
→
() ()→
• u xy , v xy'' son colinéales (se dice también que son linealmente dependientes o que la fami-
→→ → → →
lia ( u, v ) está conectada) si y solamente si λ u +µ v = 0 con (λ,µ) ≠ (0,0)
si y solamente si el determinante xyxy'' = xy’ - yx’ es nulo.
• Sea la recta D cuya ecuación es ax+by+c=0, (a, b) ≠ (0,0). La dirección de D es la recta vec-
→
torial D cuya ecuación es ax + by = 0.
→
• Un vector director de D es w −ab ( )
→→
P se da con respecto a una referencia con norma ortogonal (O, i , j )
→
()
• u xy
→
() →→
y v xy'' son ortogonales si y solamente si u.v =0 es decir xx’ + yy’ =0.
→
Un vector normal a D es n ab . ()
ax 0 +by0 +c
• La distancia de M(x 0 , y0 ) a D es: .
a²+b²
→→→
El espacio E está dado con respecto a una referencia (O, i , j,k )
• Sea el plano P cuya ecuación es ax+by+cz+d=O, (a, b, c) ≠ (0, 0,0).

→
La dirección de P es el plano vectorial P cuya ecuación es ax + by + cz = 0.
→
• Los vectores de P son los vectores con coordenadas:
 0   −c   −b 
 −c , 0 , a 
 b  a  0 

→→→
E se da con respecto a una referencia con norma ortogonal (O, i , j,k )
→ a 
• Un vector normal en P es n b  .
c
ax 0 +by0 +cz0 +d
• La distancia de M 0 (x0 , y0 , z 0 ) a P es
a²+b²+c²
CÁLCULOS ALGEBRAICOS
Identidades notables
(a +b)2 = a2+2ab+b2
(a - b)2 = a2 - 2ab + b2
(a +b+c)2=a2+b2 + c2+2ab+2bc+2ca
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a - b)3 = a3 - 3a2b + 3ab2 - b3
n
(a + b)n = ∑C a b
k =0
k k n −k
n Formula del binomio de Newton
a2 - b2 = (a - b)(a + b)
a3 + b3 = (a + b)(a2 - ab + b2)
a3 - b3 = (a - b)(a2 + ab + b2)
an - bn =(a - b)(an-1 + an-2b + ... + an-pbp + ... + bn-1)
FORMULAS DE TRIGONOMETRÍA
El plano P está orientado y dado con respecto a una referencia directa con norma ortogonal
→→ → →
() ()
(O, i , j ), sean u xy y v xy'' dos vectores que no son nulos:
→→
→→ xx'+yy'
cos( u, v )= →u.v→ =
u×v x²+ y² x'²+ y'²
→→
det → → (u, v) xx'
→→
( i , j) yy' xy'−yx'
sen( u, v )= → →
= =
u×v x²+ y² x'²+ y'² x²+ y² x'²+ y'²

Formulas de adición
En el formulario siguiente, todas las fórmulas son verdaderas a reserva de la existencia de los
términos.
cos(a + b) = cos a cos b - sen a sen b
cos(a-b) = cos a cos b + sen a senb
sen(a+b) = sen a cos b + cos a sen b
sen(a-b) = sen a cos b - cos a sen b
tan(a+b) = tan a + tan b
1 - tan a tan b
tan(a-b) = tan a − tan b
1 + tan a tan b
Formulas de multiplicación por dos

cos 2a=cos² a – sen² a=2cos2 a - 1=1 - 2 sen² a
sen 2a =2 sen a cos a
tan 2a= 2tan a
1 - tan²a
Si tan =t, cos x = 1−t² , sen x = 2t , tan x = 2t
x
2 1+ t² 1+ t² 1−t²
Transformación de productos en sumas

cos a cos b= 1 [cos(a+b)+cos(a-b)]
2
sen a sen b=- 1 [cos(a+b)-cos(a-b)]
2
sen a cos b= 1 [sen(a+b)+sen(a-b)]
2
cos²x= 1+ cos 2x
2
sen²x= 1−cos 2x
2
Transformación de sumas en productos

p+q p−q
cos p + cos q = 2 cos cos
2 2
p+q p−q
cos p – cos q = -2sen sen
2 2
p+q p−q
sen p + sen q = 2sen cos
2 2
p−q p+q
sen p - sen q = 2sen cos
2 2
1+ cos x = 2 cos² x
2
1-cos x = 2 sen² x
2

Capítulo 1
TEORÍA DE CONJUNTOS
Presentación histórica:
Peano Giuseppe (1858-1932) es un matemático italiano, así

como lingüista (intentó ratificar una lengua internacional cercana al
latín), procesó el cálculo infinitesimal (cálculo diferencial y cálculo
integral) en la academia militar de Turín pero sus trabajos están dedi-
cados esencialmente a la lógica matemática, la teoría de los conjuntos la
axiomatización del conjunto de los números enteros naturales.
A él debemos la creación de un sistema de anotaciones suscep-
tibles de enunciar y de demonstrar las proposiciones matemáticas utili-
zando un mínimo de signos compatibles con el razonamiento deductivo
basado sobre nociones de principios aceptados (axiomas). Fue el primero en usar anotaciones
sobre los conjuntos  para los números enteros naturales (naturale),  para los números ra-
cionales –las fracciones- o cociente (quoziente). También le debemos (1888) la noción de es-
pacio vectorial (real) abstracto generalizando los trabajos de Grassmann sobre el cálculo
vectorial (llamado en la época cálculo geométrico).
A él debemos:
• los símbolos de los conjuntos ∈ , ⊂ , ,  (pero el signo ⊂ es más seguramente fruto

del trabajo de Schröder).
• Siguiendo los trabajos de Dedekind, una construcción del conjunto de los números
enteros naturales y la noción moderna de la serie numérica en tanto que aplicación de 
en  y la noción rigurosa de razonamiento « por recurrencia » .
Conjunto
1. Definiciones:
Un conjunto es una colección de objetos llamados elementos del conjunto. Decimos que estos
elementos pertenecen al conjunto. La notación « x ∈ E »significa « x pertenece al conjunto E ».
La notación « x ∉ E » significa « x no pertenece al conjunto E ».
Un conjunto puede ser definido en dos maneras: en extensión o en comprensión.

2. representación de un conjunto con un diagrama de Venn
B A
1
3 4
5 2
3. El conjunto vacío es un conjunto que no contiene ningún elemento. Se representa con la

letra griega: ∅ .
4. Un conjunto unitario es un conjunto que posee un único elemento.
Subconjunto – inclusión
Sean A y B dos conjuntos. Se dice que A está incluido en B si todo elemento de A es

elemento de B. Entonces escribimos: A ⊂ B.
Se dice también que A es un subconjunto de B, o una parte de B.
Atención: No confundir entre “pertenece” e “incluido”.
Sea A un conjunto. El conjunto de sus sub-conjuntos (de sus partes) es el conjunto de

partes de A notado P(A).
Observación: Si el cardinal (número de elementos) de A es finito e igual al entero n, entonces el

cardinal (el número de elementos) de P(A) es 2n.
Igualdad de dos conjuntos
1- 1 Dos conjuntos son iguales si tienen los mismos elementos.
2- Teorema: Sean A y B dos conjuntos A=B equivale a A ⊂ B y B ⊂ A.
Complemento
1- Se llama complemento de A en E al conjunto formado por los elementos de E que
no pertenecen a A. Se escribe E A o para que no haya ambigüedad se pone Ac o A .
2- Propiedad: A =A
∅ =E y E = ∅ si E es el referencial.

Unión de dos conjuntos
1- Sean A y B dos conjuntos. La reunión de A y B, escrito como A  B (y se lee A

unión B) es el conjunto formado por elementos pertenecientes a A o (inclusivo) a B.
2- Propiedad:
AB=BA Conmutatividad
A⊂ AB
∅A=A
AA =A
Si A ⊂ B, AB=B
A(BC)=(AB)C Asociatividad
Observación: 1- La unión corresponde a un «o inclusivo», veremos en un ejercicio la diferencia

simétrica que corresponde a «o exclusivo».
2- Para escribir A ⊂ B, podemos escribir B ⊃ A.
Intersección
1- Sean A y B dos conjuntos. La intersección de A y B, escrita como A  B (y se lee A

intersección B) es el conjunto formado por elementos pertenecientes a A y a B.
2- Propiedad:
AB=BA Conmutatividad
AB⊂A
∅A=∅
AA =A
Si A ⊂ B, AB=A
A(BC)=(AB)C Asociatividad
3- Dos conjuntos A y B tales que AB=∅ se les llama disjuntos.
Relaciones entre reunión y intersección
1- Distributiva de la intersección en la unión: A(BC)=(AB)(AC) .

2- Distributiva de la unión en la intersección: A(BC)=(AB)(AC) .
3- Leyes de De Morgan: A  B = A  B y A  B = A  B .
Demostración de las leyes de De Morgan:

1- Sea x tal que x ∈ A  B lo que significa que x pertenece a A o B .
Si x∈ A , x ∉ A ⇒ x ∉ A  B ⇒ x ∈ A  B
Si x∈ B , x ∉ B ⇒ x ∉ A  B ⇒ x ∈ A  B
Esto es pues verdadero para todo x de A  B , se deduce que:

AB ⊂ AB
Sea x tal que x ∈ A  B , lo que significa que x no es un elemento común a A y B.

Si x ∈ A, x ∉ B ⇒ x ∈ B ⇒ x∈ A  B
Si x ∈ B, x ∉ A ⇒ x ∈ A ⇒ x∈ A  B
Si x∉A y x ∉B ⇒ x ∈ A y x ∈ B ⇒ x∈ A  B
Esto es pues verdadero para todo x de A  B , se deduce que:
AB ⊂ AB
De ahí:
A  B= A  B
2- Sobre un diagrama de Venn, la demostración es análoga a la anterior.
A
E
La parte sombrada representa A  B , donde se comprueba que:

AB= AB
Observación : La intersección es prioritaria sobre la reunión, es decir A  B  C = ( A  B )  C

et non A  ( B  C ) .
Ilustraciones
Lenguaje probabilista Lenguaje de los conjuntos Diagrama de Venn

A y B dos eventos de Ω A y B dos partes de E
AyB A∩B
A y B son incompatibles A ∩ B= ∅

AoB A∪B
A evento contrario a A E A =AC
A\B diferencia de dos A/B={x/x ∈ A y x ∉B}

eventos
Producto cartesiano
Sean A y B dos conjuntos. Llamamos producto cartesiano de A y B el conjunto de pares de
elementos de A y de B, tomados en este orden. Se escribe A × B y se lee «A cruz B».
Se generaliza esta definición para n conjuntos.
Observaciones: - A × A se escribe A²
- No confundir "pareja" con "par".
Propiedad: Si A y B son dos elementos finitos, el número de elementos de A × B es el

producto de los números de elementos de A y de B.

EJERCICIOS DE NIVEL 1
Ejercicio 1. Sean A, B y C tres partes de un conjunto E.

1. Si A ∪ B = A ∪ C , podemos decir que B = C ?
2. Si A ∪ B = A ∩ B , podemos decir que A = B ?
Ejercicio 2. Sean A, B y C tres sub-conjuntos del conjunto E. Dar una escritura más simple de
los siguientes conjuntos:
1- (A  (A  B))  B.
2- (A  B)  (A  B ).
3- ( A  B)  (C  A ).
4- ((A  B)  (B  C))  (A  C).

ELEMENTOS DE CORRECCION DE LOS EJERCICIOS DE NIVEL 1
Ejercicio 1. 1- no, 2- sí.
Ejercicio 2. 1- A ∩ B ; 2- A ; 3- A ∩ B ; 4- A ∪ C .

EJERCICIOS
Ejercicio 1. Sea un conjunto E de 32 personas de lengua francesa de los que 18 conocen el

alemán y 24 el inglés. Todas las personas hablan por lo menos una de las dos lenguas, alemán o
inglés.
1. ¿Cuántas personas de E conocen a la vez el alemán y e l inglés?
2. Se desea tomar en E para servir de intérprete:
- sea una persona que habla a la vez el alemán y el inglés,
- o un par de personas que conocen una el inglés solamente, otro el alemán solamente. ¿De
cuántas maneras se puede hacer esta elección?
Ejercicio 2. Sean A y B dos partes de un conjunto de E. Si A ⊂ B, qué podemos decir de B con

relación a A ?
Ejercicio 3. Sean A, B, C, tres partes de un conjunto E no vacío:

Poner de manifiesto que si A  B=A  C y A  B=A  C entonces B=C.
Ejercicio 4. Sean a y b dos reales. Establecemos A={a, b}. Las relaciones siguientes estan o no
verificadas por esta relación?
(i) a ∈ A.
(ii){a}∈A.
(iii) Ø∈A.
(iv) {a}∈P(A).
(v) Ø∈ P(A).
Ejercicio 5. Sean a, b, c tres números reales. Encontrar x para que se compruebe la relación
x∈{a, b, c}. Misma pregunta con {x} ∈ {a, {b}}, y luego con {x}∈{a, b, c}.
Ejercicio 6. Sean A y B dos sub-conjuntos de E. Llamamos la diferencia A\B el conjunto

A B.
Realizar un diagrama de Venn representando A\B y caracterizar este conjunto con una frase
francés.
Esta operación es conmutativa?
Demostrar que:
(i) (A\B)\C = A\(B  C).
(ii) (A\B)  (C\D) = (A  C)\(B  D).
Ejercicio 10. Sean A y B dos sub-conjuntos de E. Llamamos diferencia simétrica Α∆Β el

conjunto (A\B)  (B\A).
Realizar un a diagrama de Venn representando A∆B y caracterizar este conjunto con una frase
en francés.
Esta operación tiene alguna relación con el operador lógico “o exclusivo”? Ella es conmutativa?
Demostrar que A ∆ B = (A ∪ B) \ (A ∩ B).
Simplificar (A∆B)  (A∆ B ).
Demostrar que la operación ∆ es conmutativa.

¿Qué valen A∆Ø, A∆A, A∆B cuando A ⊂ B?
Ejercicio 7. Encontrar el conjunto de los subconjuntos de A=P (P (Ø)).
Ejercicio 8. Sean A, B y C tres conjuntos. Simplificar las expresiones siguientes:
1)  A ∩ ( A ∩ B )  ∩ B (
2) ( A ∩ B ) ∪ A ∪ B )
3) ( A ∩ C ) ∩ ( B ∩ C )  ∩ A 4) (( A ∩ C ) ∩ ( A ∩ B) ) ∪ ( C ∪ B)
Ejercicio 9. Sea A={1, 2, 3} y B={3,π}. Describir los conjuntos A\B, B\A, A × B, P ( A  B ) y
P(A)  P(B).
Hacer lo mismo para A=[-2, 5[ y B={1}  [ 4, +∞[ salvo para el conjunto de las partes.
Ejercicio 10. En el plano orthonormal, definimos los conjuntos C 1 et C 2 como sigue :

1} y C 2 = {M(x, y) / ∃θ ∈ [ 0, 2π[ , x=cosθ et y=sinθ} .
C 1 = {M(x, y) / x² + y² =
Demostrar por inclusión doble que C 1 =C 2 .

Capítulo 2
LÓGICA MATEMÁTICA
Presentación histórica :
Georg Ferdinand Cantor (1845-1918), de origen danès,

nació en San-Petersburgo. Se interesó al análisis y a la teoria de los
números, el núcleo de su búsqueda siendo las dificultades encontra-
das en los conceptos de límite y de continuidad de funciones y de
curvas, indisociables del de los numeros reales y del de un lenguaje
matemático preciso.
Las consecuencias de sus trabajos iban a r evolucionar los
fundamentos de las matemáticas, considerados hasta entonces como
incontestables, hasta 1963 con los trabajos de Gödel y de Cohen, y el
« descubrimiento » de proposiciones indecidibles (de las que no se
pueden probar, en el seno de la teoria misma y de los axiomas que la
definen, si son verdaderas o falsas).
Gödel Kurt (1906-1978), americano, es un filósofo y

lógico de origen austriaco. Formuló teoremas fundamentales rela-
tivos a la teoría de los conjuntos y sobre las relaciones indecidibles
y las teorías contradictorias, llamadas también no consistentes : de
las cuales el sistema de axiomas lleva a una contradicción, es decir
a la existencia de un teorema que sería, en la teoría misma, a la vez
verdadero y falso.
Le debemos el teorema de la incompletud : toda teoría
formal T (fundada sobre un axiomatismo) consistente y susceptible
de formalizar, en sus principios, la aritmética (teoría de los
números) es incompleta :existe al menos una proposición aritmé-
tica indemostrable dentro de T (no podremos probar ni si es ver-
dadera ni si es falsa). Este resultado arruina las esperanzas de Hilbert en cuanto al formalismo,
que supuestamente hacía frente a las contradicciones encontradas desde la creación de la teoría
de los conjuntos de Cantor, y muestra los límites del razonamiento lógico y de la imposibilidad
de construir la aritmética sobre el único soporte lógico como lo querían los partidarios de la
lógica que fueron Frege y Russell.
La lógica usual se dice "insuficiente" para los matemáticos en general ; nos establecemos
entonces en un nivel superior : hablamos de meta lógica y de metamatemática. En fin, había que
redefinir el concepto de demonstración. En 1940, Ackermann demostró gracias a esto la con-
sistencia de la aritmética, sin por en cambio despertar un gran entusiasmo.

1. Declaración (Propuesta o aserción)
Consideramos una afirmación que es verdadera (V) o falsa (F) pero nunca las dos a la
vez. Es lo que se llama el principio del tercer excluido (en lógica matemática binaria).
2. Los tres principales operadores
1- La negación
La negación de P se escribe ¬ P (se lee «no P»).

P ¬P
2- La conjunción
Sean P y Q dos propuestas. La conjunción de P y Q se escribe P ∧ Q (se lee «P y Q»).
P Q P∧Q
3- La disyunción
Sean P y Q dos propuestas. La disyunción de P y Q se escribe P ∨ Q (se lee «P o Q»).
P Q P∨Q
Observación : Existen relaciones entre la teoría de conjuntos y la lógica matemática.

En teoría de conjuntos, existe tres operaciones principales : la unión, la intersección y el com-
plementario.
En lógica matemática, existe tres conectadores : o, y, no.
Sea E un conjunto y A,B dos partes de E. Consideremos P la propiedad « x ∈ A » y Q la pro-
piedad « x ∈ B ».Entonces ,
- P ∨ Q es la propiedad « x ∈ A  B »
- P ∧ Q es la propiedad « x ∈ A  B »
- ¬ P es la propiedad « x ∉ A » lo que quiere decir « x ∈ Ac ».
Usualmente, decimos que ∨ corresponde a  , ∧ corresponde a  , ¬ corresponde al com-
plementario.

4- Leyes de De Morgan
¬(P ∨ Q) y (¬P) ∧ (¬Q) tienen las mismas tablas de verdad.

¬(P ∧ Q) y (¬P) ∨ (¬Q) tienen las mismas tablas de verdad.
3. Otros operadores
1- La equivalencia
Sean P y Q dos propuestas. La equivalencia de P y Q se escribe P ⇔ Q (se lee «P equivalente a

Q»).
P Q P⇔Q
2- La implicación
Sean P y Q dos propuestas. La implicación de P a Q se escribe P ⇒ Q (se lee «P implica a Q»).
P Q P⇒Q
Propiedad: 1- Las propuestas P ⇒ Q y ¬P ∨ Q tienen las mismas tablas de verdad.

2- Las propuestas P ⇔ Q y (P ⇒ Q) ∧ (Q ⇒ P) tienen las mismas tablas de verdad.
Observación : 1- La negación de una implicación (P ⇒ Q) no es una implicación sino una

conjunción ( P ∧ ( ¬Q ) ) .
2- La recíproca de la implicación P ⇒ Q es la implicación Q ⇒ P.
3- A qué propiedad de la teoría de conjuntos corresponde la implicación ?
Observaciones encuanto la definicion de implicacion:

1- Para los estudiantes que encuentren « extraño» la definición que hemos escogido de
implicación, o sea la equivalencia entre P ⇒ Q y ¬P ∨ Q , estudiar la equivalencia entre
¬ (P ⇒ Q) y P ∧ ¬Q es más fácil de interpretar…
2- Lewis Caroll y las paradojas de la implicación
Si la definición de operadores lógicos tales como la conjunción, la disjunción o l a
equivalencia no causan ningún problema a l "hombre honesto", no ocurre lo mismo con la
implicación. El autor de Alicia en el país de las maravillas, que se pasionaba por la lógica, se
sumergió en este problema en un tratado de lógica que el redactó (Symbolic Logic, 1896). Al
mismo modo, en sus Principios de Matemáticas (1980, ed. Blanchard), Louis Couturat nota lo
que el llama "las paradojas de la implicación material".

Todas las proposiciones verdaderas son equivalentes. Todas las proposiciones falsas son
equivalentes. Cada proposición falsa implica todas las proposiciones (verdaderas o falsas) ;
cada proposición verdadera está implicada por todas las proposiciones (falsas o verdaderas).
Estas paradojas inevitables (porque son consecuencias necesarias al cálculo, y esto en cualquier
sistema de Lógica) se explican por el hecho que la implicación acá considerada es la implica-
ción material, y no la implicación formal [...en la cual todo el mundo piensa cuando hablamos
de implicación (en la vida corriente)]. La implicación material (P ⇒ Q) no significa nada más
que esto: "O P es falso, o Q es verdadero". Poco importa que las proposiciones P y Q tengan
entre ellas una relación lógica o empírica alguna: la implicación es verificada de que P es falso
(cualquiera que sea Q) o de que Q es verdadero (cualquiera que sea P. He ahí el por qué lle-
gamos a este resultado paradójico, que lo falso implica lo verdadero.
Estas verdades paradójicas sirven entre otras para resolver correctamente algunos pa-
ralogismos o algunas paradojas en donde el buen sentido vulgar se pondría en un aprieto. Tal es
por ejemplo el problema de Lewis Caroll :
[Supongamos que] "Q implica R; pero [también que] P implica que Q implique no-R; Qué hay
que deducir? [...] Lewis Caroll [adoptando el punto de vista del sentido común] razona por lo
tanto: si Q implica R, es imposible que Q implique no-R; entonces P implica lo imposible, y por
consiguiente es falso.
1 – Utilizando el método de las tablas de verdad, demuestre que la conclusión, y en-
tonces el razonamiento, de Lewis Caroll son erróneos.
2 – Cuál es el "eslabón" de la demonstración de Caroll que causa problemas?. Por qué?
3 – Finalmente, qué conclusión podemos dar de las dos hipótesis iniciales?
4. Los cuantificadores
1- El cuantificador universal: ∀
∀x ∈ A se lee << sea cualquier elemento x de A >> o << para todo x que pertenece a A >>
Observación: La notación ∀ es una A invertida. A es la inicial del alemán Alle.
2- El cuantificador existencial : ∃
∃x ∈A se lee << existe un elemento x de A>>
Observación : La notación ∃ es una E volteada.. E es la inicial del alemán Existieren.
Observación: Decimos que un elemento teniendo una propiedad P en un conjunto E es único si

dos de E teniendo la propiedad P son forzosamente iguales, dicho de otro modo:
∃(x1 , x 2 ) ∈ E 2 (P(x1 ) ∧ P(x 2 )) ⇒ x1 =
x2
El hecho que sea único no implica la existencia : cuando hay unicidad, ya sea existe un único
elemento teniendo la propiedad P, ya sea no lo hay.
El hecho que haya conjuntamente existencia y unicidad del elemento x teniendo la propiedad P
se simboliza por: ∃! x ∈ E, P(x).
3- Orden de los cuantificadores:

a- Se pueden permutar dos cuantificadores de la misma naturaleza
b- No se pueden permutar dos cuantificadores de diferente naturaleza

4- Negación de fórmula con cuantificadores
La negación de ( ∀x ∈ A, P(x)) es ( ∃x ∈A, ¬ P(x)).

La negación de ( ∃x ∈A, P(x)) es ( ∀x ∈ A, ¬ P(x)).
Ejemplo: Traducir en lenguaje matemático, con cuantificadores, el hecho que una función f de
 es creciente. Luego, negar esta proposición.
Respuesta: El hecho que f sea creciente se traduce de la siguiente manera:
∀ ( x, y ) ∈ ², x ≤ y ⇒ f (x) ≤ f (y)
La negación de esta propiedad se escribe:
∃ ( x, y ) ∈ ², ( x < y ) ∧ ( f (x) > f (y) )
Recordamos que hemos visto que: ¬ (P ⇒ Q) ⇔ P ∧ ¬Q.
5. Tautología y contradicción
Una tautología es una proposición que, sea lo que sean los valores de verdad de estos
« átomos » es verdadera.
Una contradicción es una proposición que, sea lo que sean los valores de verdad de
estos « átomos » es falsa.
Una proposición es satisfactoria si existen valores de verdad de esos « átomos » que la
vuelven verdadera.
Ejemplos : ( P ⇒ Q ) ⇔ ( ¬P ∨ Q ) es una tautología.
P ⇔ ¬P es una contradicción
( P ⇒ Q ) ⇒ P es una proposición satisfactoria.

De nuevo al tema de la implicación…
La implicación lógica « P ⇒ Q » es verdadera si y solamente si P es falso o Q es ver-

dadero. Esta noción es la más difícil a dominar, contrariamente a aquello que podemos pensar al
primer contacto.
Tomemos un ejemplo para demostrar este hecho. Consideremos un circuito eléctrico en serie
constituido de un generador de corriente, un interruptor y una lámpara.
interruptor
generador
lámpara
El interruptor puede estar abierto o cerrado ; la lámpara puede estar prendida o apagada.
Sea P la proposición : la lámpara esta prendida.
Sea Q la proposición : el interruptor está cerrado.
Cuál es la relación de implicación lógica entre P y Q ? Tenemos P ⇒ Q ? Q ⇒ P ?
Tenemos la equivalencia P ⇔ Q ? Precisamos que no buscamos una relación causal, tal como la
concibe un físico. Buscamos una relación lógica que permita hacer una deducción.
Hay tres situaciones posibles:�
interruptor abierto interruptor cerrado interruptor cerrado

lámpara apagada lámpara prendida lámpara apagada
situaciones las más comunes situación inhabitual
Una sola situación es imposible :

interruptor abierto
lámpara prendida
La sola implicación lógica es la siguiente:

P ⇒ Q : si la lámpara está prendida, entonces el interruptor está cerrado.
La implicación Q ⇒ P (si el interruptor está cerrado, entonces la lámpara está prendida)

corresponde a una explicación causal del alumbramiento de la lámpara, pero sólo es posible en
un mundo ideal y perfecto donde las lámparas no se averían jamás, y no constituye en nada una
consecuencia lógica.
Reflexionaremos al hecho que todas las frases que siguen tienen la misma significación :
P⇒Q Lámpara prendida ⇒ interruptor cerrado

no Q ⇒ no P (contrapuesto) Interruptor abierto ⇒ lámpara apagada
si P entonces Q Si la lámpara esta prendida, entonces dedu-
cimos que el interruptor está cerrado.
P es suficiente para Q Basta con que la lámpara este prendida para
basta P para tener Q concluir que el interruptor está cerrado.
P solamente si Q La lámpara esta prendida solamente si el in-
terruptor está cerrado.
Q es necesario para P El interruptor tiene que está cerrado para que
Hay que tener Q para tener P la lámpara este prendida.
no P o Q La lámpara esta prendida o el interruptor esta
cerrado.
Resulta de esto que la implicación es verificada en los tres casos siguientes (corres-
pondiendo a nuestros tres dibujos):
P es verdadero y Q es verdadero
P es falso y Q es verdadero
P es falso y Q es falso
Asi, si P es falso, Q es cualquiera y no hay nada a demostrar. La sola cosa a demostrar es que si
P es verdadero entonces Q es verdadero.
La implicación es falsa solo en el caso siguiente:

P es verdadero y Q es falso
No puede haber implicación ya que la hipótesis esta verificada, pero no la conclusión.
La recíproca de la implicación P ⇒ Q es Q ⇒ P. Ella puede ser verdadera o falsa, indepen-
dientemente del valor de verdad de P ⇒ Q. En nuestro ejemplo, la recíproca es falsa. Todas las
frases que siguen son equivalentes a Q ⇒ P. Ellas son entonces falsas, el contra-ejemplo está
ilustrado en el tercer dibujo :

Q⇒P Interruptor cerrado ⇒ lámpara prendida
no P ⇒ no Q (contrapuesto) Lámpara apagada ⇒ interruptor abierto
si Q entonces P Si el interruptor esta cerrado, entonces la
lámpara esta prendida.
Q es suficiente para P Basta con que el interruptor esté cerrado para
basta con Q para tener P concluir que la lámpara esta prendida.
Q solamente si P El interruptor esta cerrado solamente si la
lámpara esta prendida.
P es necesario para Q La lámpara tiene que estar prendida para
Hay que tener P para tener Q concluir que el interruptor esta cerrado.
no Q o P El interruptor esta abierto, o la lámpara esta
prendida.
En fin, decir que P ⇒ Q y Q ⇒ P, es decir que P ⇔ Q.

Teoremas fundamentales de lógica matemática
Teoremas fundamentales de cálculo de propuestas
(1) A ∨ ¬A Principio del tercer excluido

(2) ¬(A∧¬A) Ley de no contradicción
(3) ¬(¬A)⇔ A Ley de la doble negación
(4) ¬(A∧B)⇔¬A∨¬B Leyes de De Morgan
(5) ¬(A∨ B)⇔¬A∧¬B Leyes de De Morgan
(6) A ⇒B⇔¬B⇒¬A Regla de contraposición
(7) (A ⇒B)∧A⇒B Regla del modus ponens
(8) (A⇒B)∧¬B⇒¬A Regla del modus tollens
(9) (A⇒B)∧(B⇒C)⇒(A⇒C) Regla del modus barbara
(10) A∧(B∨C)⇔(A∧B)∨(A∧C) Regla distributiva
(11) A∨(B∧C)⇔(A∨ B)∧(A∨C) Regla distributiva
Teoremas fundamentales del cálculo de predicados
(1) ¬∀x A(x) ⇔∃x ¬A(x) Reglas de negación

(2) ¬∀x ¬A(x) ⇔∃x A(x) Reglas de negación
(3) ¬∃x A(x) ⇔∀x ¬A(x) Reglas de negación
(4) ¬∃x ¬A(x) ⇔∀x A(x) Reglas de negación
(5) ∀x ∀y A(x,y)⇔∀y ∀x A(x,y) Reglas de intercambio
(6) ∃x ∃y A(x,y)⇔∃y ∃x A(x,y) Reglas de intercambio
(7) ∃x ∀y A(x,y)⇒∀y ∃x A(x,y) Reglas de intercambio
(8) ∀x A(x) ⇒A(x)
(9) A(x) ⇒∃x A(x)

Ejercicio 1. Traducir en lenguaje matemático, con los cuantificadores, las siguientes frases, y
escribir sus negaciones:
1. todo nombre real inferior a 1 verifica la desigualdad x 2 ≤ x ;
2. el producto de 2 enteros impares es un entero par ;
3. todo número complejo igual a su conjugada es un número real.
Ejercicio 2. Traducir en lenguaje natural las siguientes aserciones , estudiar su lógica y escribir
sus negaciones :
1. ∀x ∈ , ∃y ∈ , x ≥ y ;
2. ∀x ∈ , (x =−1) ∨ (x ≠ 4) ;
3. ∀x ∈, (x =3) ⇒ (x 2 =9) ;
4. ∀x ∈ , (x 2 = 9) ⇒ (x = 3) ;
Ejercicio 3. Sean P, Q y R tres aserciones.

1. Mostrar que P ∧ (P ∨ Q) y P tienen la misma tabla de verdad.
2. Dar la tabla de verdad de P ∧ (Q ∧ R) y de (P ∧ Q) ∧ R .

Ejercicio 1. 1- ∀x ∈ , (x ≤ 1) ⇒ (x 2 ≤ x)
Negación : ∃x ∈, (x 2 > x) ∧ (x ≤ 1)
2- ∀(p, q) ∈ ², ∃k ∈, (2p + 1)(2q + 1) =
2k
Negación : ∃(p, q) ∈², ∀k ∈, (2p + 1)(2q + 1) ≠ 2k
3- ∀z ∈ , (z
= z) ⇒ (z ∈ )
Negación : ∃z ∈ , (z ∈ ) ∧(z ≠ z) .
Ejercicio 2. 1- « Para todo real x, existe un real y que es inferior o igual a x. »

Esta aserción es verdadera, para todo real x basta con tomar el real x-1, que
verifica la aserción.
La negación es : ∃x ∈, ∀y ∈ , x < y .
2- « Todo real x es sea igual a -1, sea diferente de 4. »
Esta aserción es evidentemente falsa, el real 4 es un contra-ejemplo para esta
aserción.
La negación es: ∃x ∈, (x ≠ −1) ∧ (x =4) .
3- « Todo real x verifica, si x es igual a 3, entonces x² es igual 9. »
Esta aserción es verdadera. Su negación es: ∃x ∈, (x 2 ≠ 9) ∧ (x =. 3)
4- « Todo real x del cual su cuadrado es 9 es igual a 3. »
Esta aserción es falsa, -3 es un contra-ejemplo.
La negación es: ∃x ∈, (x ≠ 3) ∧ (x 2 =. 9)
Ejercicio 3. 1- P Q P ∨ Q P ∧ (P ∨ Q)
V V V V
V F V V
F V V F
F F F F
2- P Q R Q∧R P∧ (Q ∧ R) P ∧ Q (P ∧ Q) ∧ R
V V V V V V V
V V F F F V F
V F V F F F F
V F F F F F F
F V V V F F F
F V F F F F F
F F V F F F F
F F F F F F F

EJERCICIOS
Ejercicio 1. ¿Los enunciados o las fórmulas siguientes son verdaderas o falsas?

(i) La función t  e-t es decreciente en .
(ii) La función t  sen t es creciente.
(iii) Cualquier función limitada en  admite un límite en ± ∞ .
(iv) Toda sucesión o secuencia geométrica converge.
(v) Una sucesión geométrica converge si su razón r confirma que |r| ≤ 1.
(vi) Todo real es límite de una sucesión de reales.
Ejercicio 2. Se consideran las fórmulas matemáticas siguientes:

(i) P 1 (x) : «todo número real superior a x es positivo».
(ii) P 2 (x) : «x real y ln x ≥ 0 ».
(iii) P 3 (x, y) : «la función t  cos t es creciente en el intervalo [x, y]»
(iv) P 4 (x, y): «x e y son reales y confirma que x² ≤ y ≤ x ."
¿Por qué constantes se pueden sustituir a las variables "x" e "y" para obtener enunciados ver-
daderos?
Ejercicio 3. Con ayuda de las tablas de verdad, poner de manifiesto que:

(i) p∧¬p es una contradicción.
(ii) p⇔((q⇒p )∧(¬q⇒p )) .
(iii) p∧(p∨q)⇔ p .
Ejercicio 4. Elaborar las tablas de verdad de ¬(p⇒q) y p∧¬q . ¿Qué confirma usted?
Ejercicio 5. Escribir la negación de las frases siguientes:

1- Adrian va a la playa o al terreno de tenis.
2- Paul tiene un pantalón rojo y un sombrero azul.
3- Si nieve, entonces voy a esquiar.
4- John es feliz si y solamente si hace ejercicios de lógica.
Ejercicio 6. Sean f y g dos aplicación de  en .Traducir en términos de cuantificadores las

expresiones siguientes :
1) f esta mayorado. 2) f jamás se anula. 3) f no es una función nula.
4) f es par. 5) f es inferior a g. 6) f no es inferior a g.
Ejercicio 7. Dar las interpretaciones de las propiedades P, Q y R (por ejemplo P = Verdad; Q =

Falso; R = Falso) que hacen falsas las fórmulas siguientes :
1- R ∧ ¬P ⇒ ( Q ∨ (R ⇒ P) )
2- ( Q ⇒ (R ⇒ P) ) ∨ ¬R ∨ P

Ejercicio 8. 1 - Precisar, utilizando el método de las tablas de verdad, si las fórmulas siguientes
son tautologías, contradicciones, o de proposiciones simplemente satisfactorias. Buscaremos a
limitar al máximo los cálculos.
1- (P ∧ Q) ∧ (¬P ∨ Q)
2- P ∨ ¬(P ∧ Q)
3- ¬P ⇒ (P ∧ Q)
4- (P ⇒ Q) ⇒ (Q ⇒ P)
5- (P ⇒ Q) ∧ (Q ⇒ R) ⇒ (P ⇒ R)
Ejercicio 9. Precisar, utilizando el método de tablas de verdad, cuáles son las expresiones,
entre las siguientes fórmulas, que son de tautologías. Buscaremos a limitar al máximo los
cálculos.
1- (P ⇒ Q) ⇒ P
2- P ∧ Q ∧ R ⇒ P ∨ Q
3- ( P ⇔ (Q ∨ R) ) ⇒ ( ¬Q ⇒ P ∨ R )
Ejercicio 10. El conector NAND (y negado) está definido por : pNANDq ⇔ ¬(p∧q) . Dar su
tabla de verdad. ¿Corresponde éste a un conjunto?
Qué se puede decir de pNANDp? ¿Es posible definir los 3 operadores principales solamente en
función de NAND?
El operador NOR (no-o) se define por ¬(p∨q) . Dar su tabla de verdad. ¿Corresponde éste a un
conjunto?
¿Es que se puede definir los 3 operadores principales solamente en función de NOR?
Observación : El conector NAND es también notado ↑ . Este operador tiene gran importancia
en informática y en electrónica, ya que le permite de representar los conjuntos de funciones
lógicas necesarias para poner en marcha los circuitos de las computadoras.
Ejercicio 11. Traducir en lenguaje matemático, utilizando los cuantificadores existenciales y

universales, las siguientes frases:
(i) Todo número real positivo inferior a 1 confirma que x2 ≤ x.
(ii) Para todo x real, existe "n", un entero natural estrictamente superior a x.
(iii) Entre dos números reales distintos, se puede encontrar un número racional.
Ejercicio 12. Decir que una sucesión (u n) n de reales está limitada significa intuitivamente que
se puede encontrar un número M tal que todos los elementos de la sucesión le siguen siendo
inferiores en valor absoluto. Matemáticamente, eso se escribe : ∃ M > 0, ∀ n ∈ N, |u n | ≤ M.
Negar la propuesta anterior.
Ejercicio 13. Sea x  f(x) una función de la variable real x. Intuitivamente, esta función ad-
mite un límite real l en un punto x o de D f si cuando x se aproxima lo más cerca posible de x 0
(pero sin alcanzarlo), f(x) se aproxima a l y se puede hacer f(x) tan cercano como se quiera a l
con la única condición de hacer x cercano de x0 . Si además l = f(x o ), se dice que f es continuo en
x0 . Matemáticamente, la continuidad en x0 se traduce por:
∀ε > 0, ∃δ > 0 , ∀x ∈ D f, | x-x o |<δ ⇒ |f(x)-f(x o)| <ε
Negar esta propuesta lo que significará que f es discontinuo en x 0 .

Ejercicio 14. Decir que una sucesión (u n ) n admite un límite real l significa matemáticamente:
∀ε > 0, ∃N 0 ∈, ∀n ∈ , n>N 0 ⇒ |u n -l| <ε
Negar esta propuesta.
Ejercicio 15. Sea x  f(x) una función de la variable real x. Se dice que f es una función cre-
ciente si para todo x y x’ pertenecientes a D f, si x > x’ entonces f(x) ≥ f(x’).
Escribir matemáticamente que f es una función creciente. Negar esta propuesta.
Ejercicio 16. Una aplicación f de E en F se dice sobreyectiva si todo elemento de F es la

imagen por f de al menos de un elemento de E.
Escribir matemáticamente que la aplicación f es una sobreyección. Negar esta propuesta.
Ejercicio 17. Traducir al español:

(i) ∀ x ∈ , ∃ y ∈  tal que x ≥ y.
(ii) ∀ x ∈ , ∀ y ∈ , ∃ z ∈  tal que xy=z.
(iii) ∃ n ∈  tal que ∀ x ∈  |x| ≤ n.
(iv) ∀ x ∈ +, ∃ y ∈+ tal que ∀ z ∈ , xy> z.
Ejercicio 18. Sea f una función de  en . Escribir las negaciones de las proposiciones si-
guientes:
1- Para todo x>2, f(x)<1.
2- Existe x real positivo tal que f(x)<0.
3- Si x es elemento de [3, 4], entonces f(x)<4x².
Ejercicio 19. Decir si las afirmaciones siguientes son verdaderas y escribir sus negaciones.
a- ∃x ∈, ∃y ∈ , x+y>0
b- ∀x ∈ , ∀y ∈ , x+y>0
c- ∀x ∈ , ∃y ∈ , x+y>0
d- ∃x ∈, ∀y ∈ , x+y>0

Solución del ejercicio 5:
Comencemos por introducir las notaciones.
Llamamos R la propiedad el objeto es raro y C la propiedad el objeto es caro.
Las dos afirmaciones anteriores se escriben entonces bajo la forma:
1. R ⇒ C ( ⇔ ¬R ∨ C )
2. C ⇒ ¬R ( ⇔ ¬C ∨ ¬R )
Escribamos ahora la tabla de verdad de estas dos proposiciones :
R C ¬R R⇒C C ⇒ ¬R
0 0 1 1 1
0 1 1 1 1
1 0 0 0 1
1 1 0 1 0
Vemos así que las dos afirmaciones anteriores pueden ser verdaderas simultáneamente, en-
tonces este conjunto es satisfactorio.

Los dos anexos que siguen a continuación estan destinados a los es-
tudíantes que se interesen a los fundamentos de las matemáticas.
Anexo 1 :
Conjuntos denominados y no denominados
1- Podríamos pensar que sólo hay dos tipos de conjuntos, los conjuntos finitos y los
conjuntos infinitos, estos últimos tienen todos la misma naturaleza. Esta visión fue puesta en en
error por Georg Cantor (1845 -1918). Sus trabajos fueron la base de la Teoría de conjuntos en el
siglo XX. El define varios tipos de infinitos.
Un conjunto infinito esta en bijección con una de sus partes estrictas. Por ejemplo, 
esta en bijección con *, mediante la bijección siguiente:  → *, n  n+l.
Ya sean varios conjuntos infinitos, por ejemplo , ,  ,y . Están ellos en bijección
los unos con los otros ? Demostraremos que ,  y  están efectivamente en bijección, pero no
es el caso de . Los primeros son dichos denominados.
Galileo se da cuenta que los términos "tanto de elementos", "menos de elementos"

o"más de elementos" no pueden aplicarse sin paradoja a los conjuntos infinitos. El término
bijección no existia aún, pero Galileo puso en evidencia una bijección entre  y una parte es-
tricta de  :
1 2 3 4 .. . n ...
1 4 9 16 ... n2 ...
2- Dos conjuntos en bijección son llamados equipotentes. Si ellos son finitos, esto sig-
nifica que ellos tienen el mismo número de elementos. Sea E un conjunto cualquiera, y P(E) el
conjunto de sus partes. Entonces E y P(E) no son equipotentnes. Esto es evidente si E es finito,
con n e lementos, ya que entonces P(E) posee 2n elementos, y para todo n, 2n> n. Pero esta
propiedad queda verdadera si E es finito. Queda por demostrar que no puede exisitr bijección f
entre E y P(E). Razonemos por lo absurdo y supongamos la existencia de tal bijección f :
f : E → P(E), x  f(x)
Para todo elemento x de E, f asocia f(x), elemento de P(E), dicho de otro modo, f(x) es
una parte de E. Consideremos ahora la parte A de E definida de la manera siguiente :
A = {x ∈ E / x ∉ f(x)}
Por definición de A, tenemos la equivalencia: x ∈ A ⇔ x ∉ f(x). Ya que f es una bi-
jección de E sobre P(E), y siendo A una parte de E es un elemento de P(E), A posee un ante-
cedente único por f, a. Tenemos entonces f(a) = A. Nos planteamos entonces la pregunta si-
guiente :Tenemos a ∈ f(a) ? Como a ∈ f(a) ⇔ a ∈ A porque f(a) = A
⇔ a ∉ f(a) por definición de la pertenencia hacia A
Asi, la proposición a ∈ f(a) es equivalente a s u negación. La contradicción p uede ser
eliminada rechazando la hipótesis de la existencia de f.

Esta demostración asegura la existencia de conjuntos no denominados, lo que quiere
decir que no están en bijección con , por ejemplo P(). Recalcamos incluso una jerarquía
infinita de espacios , P(), P(P()), …
3-  es el conjunto infinito más pequeño. Si E es un conjunto cualquiera, entonces ya sea

E es finito , o sino él es denominado (en bijección con ), o sino existe una injeccion de  en E
pero no una bijección (ejemplos: E = P() o E = ). Un conjunto denominado, siendo una
bijección con , puede escribirse bajo la forma {x n /n ∈ } ; la bijección es la aplicación f :
 → E, n  x n . Un conjunto denominado se reconoce a aquello que podemos enumerar sus
elementos.
Toda parte de un conjunto denominado es finita o de nominada, toda imagen de un

conjunto denominado es finita o denominada.
La reunión de dos conjuntos denominados es denominada. Asi  es denominada. He

aqui un bijección entre  y  :
n n +1
f :  → , n  si n es par y - si n es impar.
2 2
El producto de dos conjuntos denominados es denominado. Asi 2 es denomidado.

Basta con enumerar sus elementos en el orden siguiente :
1
(0,0)
2 3
(1,0) (0,1)
4 5 6
(2,0) (1,1) (0,2)
7 8 9 10
(3,0) (2,1) (1,2) (0,3)
11 12 13 14 15
(4,0) (3,1) (2,2) (1,3) (0,4)
n(n − 1) n(n + 1)
+1 ... ...
2 2
(n-1,0) (n-2,1) (n-3,2) ... (0,n-1)
En particular  es denominado. En efecto + puede injectarse en 2 mediante una

p
aplicación de tipo  (p,q).
q

4-  no es denominado. Si lo fuera, sería lo mismo de [0,1[. Consideremos entonces una
enumeración ( x n )n∈* de [0,1 [, obtenida mediante la bijección f : * → [0,1 [, n  x n , y con-
sideremos el desarrollo decimal de x n .
x1 = 0,a 11 a 12 a 13 ...a 1p ...
x2 = 0,a 21 a 22 a 23 ...a 2p ...
...
x n = 0,a n1 a n2 a n3 ...a np ...
…
a np es la psima cifra de la descomposición decimal de x n . Es un elemento de {0,1,...,9}. Consi-

deremos ahora el elemento y de ]0,1[ definido de la siguiente manera :
y = 0,b 1 b2 b 3 ...b p...
en donde b p= 0 si a pp ≠ 0 y bp=1 si a pp =0.
Obtenemos el desarrollo decimal de un real distinto de todos los x n . En efecto, la nsima
cifra x n e y son diferentes ( ∀ n, b n ≠ a nn ). De otra parte, es evidente que y pertenezca a [0,1[.
Esto es contradictorio con el hecho de que f sea bijectiva, ya que entonces, todo elemento de
[0,1[ sería de la forma de uno de x n. Esta demostración es conocida con el nombre de díago-
nalización de Canton.
Podemos demostrar que  es equipotente a P(), y que los tres conjuntos siguientes son
equipotentes : P(), P(P()) y C 0() conjunto de funciones continuas sobre .
5- Señalemos igualmente una pregunta sorprendente. Podemos encontrar un conjunto E com-

prendido entre  y , pero que no sea equipotente ni a , ni a  ? Tendriíamos solamente
injecciones de  en E y de E en . Recordemos que  ,no responde a la pregunta ya que es una
bijección con . Hemos demostrado que era imposible responder a esta pregunta. Esto no
significa que no hemos aún encontrado si esta propiedad es verdadera o falsa, sino que no po-
demos ni demostrar que ella es verdadera, ni demostrar que ella es falsa.. Se dice que es inde-
cidida. Ella no proviene de axiomas de la Teoría de conjuntos, tampoco su negación. Esto sig-
nifica igualmente que podemos tomar como axioma la no existencia de un tal conjunto E sin
aportar contradicción al edificio de las Matemáticas, o al contrario, de tomar como axioma la
no-existencia de E. En este último caso, adoptamos aquello que llamamos la hipótesis de lo
continuo. Una u otra opción conduce entonces a dos Teorías matemáticas diferentes.
Estas consideraciones no tienen ninguna importancia para lo que nos concierne, ya que
nunca utilisaremos esta propiedad, ni su negación.
6- Demos una consecuencia curiosa de lo que precede en informáticas. Podemos mostrar que el
conjunto de todos los algoritmos posibles es denominado, mientras que el conjunto de funciones
de  en  es equipotente a . Existe entonces funciones de  en  que no son calculables por
ninguna computadora. Ningun algortimo permite calcularlos. Tales funciones han sido expli-
citamente definidas.

Anexo II :
Axiomas
Qué es un axioma ?
D'Alembert escribe, en su Enciclopedía (1788) :
Axioma : En Matemáticas, llamamos axiomas a las proposiciónes evidentes por ellas
mismás, y que no tienen necesidad de demostración. Tales son las proposiciones siguientes : el
todo es más grande que la parte ; si a dos magnitudes iguales agregamos magnitudes iguales, las
adiciones seran iguales ; si dos figuras aplicadas la una sobre la otra se cubren perfectamete,
esas dos figuras son iguales en todo.
Teorema: Es una proposición que enuncia y que demuestra una verdad.
Nuestra concepción moderna de axiomas no corresponde a nociones evidentes por ellas

mismas o a principios muy claros. Actualmente, apoyamos una Teoría matemática sobre no-
ciones primitivas (no definidas) y los axiomas sólo sirven para describir las reglas de utilisación
de esas nociones primitivas. He aquí ejemplos modernos de axiomas y de nociones de primi-
tivas :
i) La noción de conjunto y de pertenencia es una noción primitiva. No buscaremos a
definir ni la una ni la otra.
ii) Frege, en 1893, propuso como axioma lo siguiente : φ siendo un predicado cual-
quiera, existe un conjunto A tal que, para todo x, x pertenece a A si y solamente si φ(x) es
verdadero. Russel, en 1902, propone tomar como predicado: φ(x) ⇔ x∉x. De acuerdo a Frege,
existe entonces un conjunto A tal que :
∀x, x ∈ A ⇔ x ∉ x
Esta equivalencia es verdadera en particular mientras x = A, lo que dona:
A∈A ⇔ A∉A
Que es contradictorio. Este ejemplo prueba que no podemos tomar lo que sea como
axioma, particularmente aquello que concerne la construcción de conjuntos. He aquí algunos
axiomas actualmente en vigor.
- La reunión de una familia de conjuntos (teniendo como índice un conjunto) es un
conjunto.
- La familia constituída de partes de un conjunto es un conjunto.
- Existe un conjunto infinito.
- El 5to postulado de Euclide : para un punto dado, pasa por allí una paralela a una
recta dada y una sola.
- La existencia del límite superior en 
Un axioma criticado, el axioma de la opción

Consideremos la siguiente proposición :
Sea f una aplicación injectiva de E en F. Entonces existe una aplicación surjectiva g de F en E al
que g  f = Id.
Demostración:
Sea a un elemento cualquiera de E. Tomamos :
i) si y pertenece a f(E), g(y) = x en donde x es el único elemento tal que y=f (x).
ii) si y no pertenence a f(E), tomamos g(y) = a.
Entonces g surjectiva y g  f = Id.

Consideremos ahora la siguiente proposición :
Sea f una aplicación surjectiva de E en F. Entonces, existe una aplicación injectiva g de F en E
tal que f  g = Id.
Demostración
Para todo y de F, f-1({ y}) no vacío. Sea g(y) un elemento de esta parte. Entonces g es injectiva y
f  g=Id.
Hay una diferencia fundamental entre estas dos demostraciones. La primera sólo llama a
la opción arbitraria de un único elemento a, mientras que el segundo llama a la opción si-
multánea y arbitraria de un número cualquiera y eventualmente infinito de elementos g(y). La
posibilidad de tal opción a sido vivamente contestada al comienzo de este siglo y necesita un
axioma : el axioma de la opción . Este último esta igualmente ligado a la cuestion de dar un
conjunto de un « buen orden » ; un conjunto es dicho ordenado si toda parte no vacía admite al
elemento más pequeño. Un ejemplo típico de conjunto bien ordenado es . Por el contrario, 
no está bien ordenado con el orden usual. Cantor pensaba que todo conjunto podía proveerse de
un buen orden, y la necesidad de una demostración se impuso. Nos preguntamos, en efecto,
cómo dotar por ejemplo  de un buen orden. Al principio del siglo, un matemático piensa haber
demostrado la imposibilidad de dotar  de un buen orden.. Pero Zermelo prueba lo contrario
utilisando por primera vez aquello que se convertiría en el axioma de la opción :
Sea ( A i )i∈I una familia de conjuntos no vacíos, con índice un conjunto I cualquiera y sea
A la reunión des Ai . Existe entonces una applicación f de I en A tal que :
∀i ∈ I, f(i) ∈ A i
La función f permite de elegir un elemento con notación f(i) en cada Ai . Otras formu-
laciones equivalentes son posibles. Por ejemplo, el producto ∏ A i no esta vacío.
i∈I
Mostramos que este axioma permite dotar  de un buen orden, sin que podemos ex-
plicarlo, y esto choca a un gran número de matemáticos que la rechazan.. Sin embargo, otros
teoremas, en que los enunciados parecen ser verdaderos a la comunidad matemática, necesitan
el axioma de la opción. E aqui algunos :
- Sea E y F dos conjuntos. Entonces ya sea existe una injección de E en F o sino existe
una injección de F en E (Teorema de Cantor, equivalente al axioma de la opción)
- Sea E un espacio vectorial. Existe entonces una base en E.
- Todo conjunto inductivo admite un elemento máximo. (Un conjunto es inductivo si
toda parte totalmente ordenada es mayorada). (Teorema de Zorn, equivalente al axioma de la
opción).
Sin embargo, algunos resultados son probados por medio de la axioma de la opción y
fuertemente contrarios a la intuición :
- Lebesgue desarrollo una Teoría de la integración muy poderosa. Todas las funciones
usuales son comparadas al sentido de Lebesgue. Los solos ejemplos no comparados que han
sido descubiertos necesitan el axioma de la opción.

- La esfera unidad puede ser decompuesta en cuatro partes isométricas A,B,C,D siendo
D igualmente isométrica a A  B. (D es entonces al mismo tiempo el cuarto y el tercio dde la
esfera). (Teorema de Hausdorf, extremadamente chocante).
- En el mismo orden de idea, dos conjuntos limitados cualquiera de 3 de interior no
vacío pueden ser separados en dos familias finitas respectivas (A i ) y (B i ) de manera que A i sea
isométrico a B i . (Teorema de Banach-Tarski).
- Existen funciones de  sobre  tal que f(x+y) = f(x)+f(y), siendo f diferente de las
funciones linearias x  ax. Sin embargo ninguna de esas funciones no puede ser explícita
Entonces, a favor o en contra del axioma de la opción ?

Capítulo 3
LA DEMOSTRACIÓN EN MATEMÁTICAS
Un poco de vocabulario
Recordemos que llamamos conjetura, toda aserción (proposición) que consideramos
como verdadera pero que no sabemos demostrar en el estado actual del conocimiento. Del latín
cum = con, conjunto y jacere = tirar : emitir, avanzar ideas formando una totalidad. No lo
tenemos que confundir con conjetura proveniente de jungere = unir : conjunción de diversos
acontecimientos que llevan a u na situación presente. Pero nos podemos perder en conjeturas
relativas a la conjetura…
Si un conjetura es demostrada, se convierte en un teorema, del griego theôrein = exa-
minar y theôrêma = objeto de contemplación, objeto de estudio y, por extensión : proposición
de la que podemos aportar su demostración. Por proposición, entendemos a menudo un teorema
de menor importancia. Enfin, un lemma (del griego lêmma = argumento, y tambien lo que
cogemos ) es un resultado (teorema) preliminar que facilita la demostración de un teorema
difícil de establecer.
1. La teoría matemática
Enfoque hipotético-deductivo.
2. Los principales métodos de demostración

a) Razonamiento directo (o por hipótesis auxiliar o por deducción) :
Utiliza la regla de Modus-Ponens, o syllogisme :
Si H es verdadero y (H ⇒ C) es verdadero, entonces C es verdadero.
Se trata del método mas utilizado. Ha sido popularizado por:
Todo hombre es mortal, como Sócrates es un hombre, entonces Sócrates es mortal.
Observación : Un sofisme es un razonamiento falso teniendo una apariencia de verdad.

Ejemplo clásico: Todos los gatos son mortales, como Sócrates es un mortal, entonces Sócrates
es un gato.
b) Razonamiente por contrapuesto

Utiliza la regla del modus-tollens : (A ⇒ B) ⇔ (¬B ⇒ ¬A )
Ejemplos: Demostrar que siendo n un entero dado, si n² es impar, entonces n es impar.

Demostrar que siendo n un entero dado, si n² es par, entonces n es par.

c) Razonamiento por lo absurdo
Para demostrar que una proposición es verdadera, se supone su contrario verdadero y se
demuestra que esto viene a contradecir una proposición verdadera.
Ejemplo: demostrar que:

- La suma de un racional y de un irracional es un irracional.
- 2 es un irracional.
d) Razonamiento por recurrencia

Para probar que P(n) es verdadero para todo entero n superior a n0 , basta con estable-
cer :
1- P(n0 ) verdadero (decimos que la propiedad esta fundada)
2- Sea i un entero natural superior a n0 . P(i) verdadero implica P(i+1) verdadero (de-
cimos que la propiedad es hereditaria)
La recurrencia así presentada es la recurrencia simple.
Veremos en la continuación del curso la recurrencia fuerte donde razonaremos sobre
varios rangos. En este caso, modificaremos la fundación y la herencia. Por ejemplo, para una
recurrencia doble, el razonamiento es el siguiente :
Mostramos las propiedades :
1- P(n0 ) y P(n 0 +1) verdaderas
2- Sea i un entero natural superior a n 0 . P(i) y P(i+1) verdaderas implica P(i+2) verda-
dero
Deducimos que P(n) es verdadero para todo entero superior a n 0 .
Ver en los ejercicios un ejemplo de la recurrencia fuerte.
Ejemplo: Demostrar por recurrencia que para todo entero natural n ≥ 4, tenemos:
1 3 + 2 3 + … + n 3 = (1 + 2 + … + n) 2
Respuesta: Sea n ≥ 4 .
Anotemos P ( n ) la propiedad 1 3 + 2 3 + … + n 3 = (1 + 2 + … + n) 2.
Inicialización :
Para n=4, tenemos a 1 3 + 2 3 + … + n 3 = 1 + 8 + 27 + 64 = 100
Por otro lado, (1 + 2 + … + n) 2 = (1 + 2 + 3 + 4 ) ²= 10²= 100
Por lo cual P ( 4 ) verdad.
Herencia:
P ( n ) ⇒ P ( n + 1)
Supongamos P ( n ) entonces:
13 + 23 + ... + n 3 + ( n + 1) = (1 + 2 + ... + n ) + ( n + 1)
3 2 3
n
n ( n + 1)
Como sabemos que ∑ k =1 + 2 + ... + n =
k =1 2
Tenemos entonces:

2
 n ( n + 1)  n² ( n + 1)
2
1 + 2 + ... + n + ( n=
+ 1)   + ( n=
+ 1) + ( n + 1)
3 3 3 3 3 3
 2  4
2  n²  2  n² + 4n + 4 
= ( n + 1)  + n + 1 = ( n + 1)  
 4   4 
 ( n + 2 )2   ( n + 1)( n + 2 )  2
( n + 1) 
2
= =
4   2


 
= (1 + 2 + ... + n + ( n + 1) )
2
Por lo cual P ( n + 1) verdad.

Concluímos por recurrencia que para todo entero natural n ≥ 4, tenemos:
1 3 + 2 3 + … + n 3 = (1 + 2 + … + n ) 2.
e) Razonamiento del contra-ejemplo

Para mostrar que la propiedad ∀x P(x) es falsa, basta con dar un ejemplo en donde P(x)
es falsa.
f) Razonamiento del análisis de síntesis

Ejemplo: Mostrar que toda función definida sobre  es la suma de una función par y de una
función impar.
Análisis: Suponemos el problema resuelto. Entonces existe una función p par y una función i
impar tales que: ∀x ∈ , f(x) = p(x) + i(x),
entonces ∀x ∈ , f(−x) = p(−x) + i(−x) = p(x) − i(x).
f(x) + f(-x) f(x) - f(-x)
Entonces obtenemos necesariamente : p(x) = 2 et i(x) = 2 .
Síntesis: Verificamos que los resultados obtenidos son convenientes. Si proponemos

f(x) + f(-x) f(x) - f(-x)
∀x ∈ , p(x) = 2 et i(x) = 2 , entonces i y p poseen la propiedades ade-
cuadas.
3. Condición necesaria, suficiente, necesaria y suficiente
a) Condición necesaria (CN), suficiente (CS)

Sean P y Q dos propuestas tales que la implicación P ⇒ Q sea verdadera.
P es una condición suficiente de Q.
Q es una condición necesaria de P.
b) Condición necesaria y suficiente (CNS)

Sean P y Q dos propuestas.
Decir que P es una condición necesaria y suficiente de Q significa que tenemos que P ⇒ Q y
Q ⇒ P; entonces tenemos que P ⇔ Q.

Observación: Las nociones definidas en este párrafo son con frecuencia una fuente de confu-
sión. Esta confusión es debida, entre otras, a u n mal empleo de la expresión « hay que» en
lenguaje natural.
De hecho, muy frecuente, utilisamos la expresión « hay que» en lugar de la expresión « basta
con».
Por ejemplo : para cenar esta noche, hay que hacer las compras alimentarias. Siendo la buena
expresion: para cenar esta noche, basta con hacer las compras alimetarias. Podemos muy bien
cenar sin tener que hacer las compras, por ejemplo, yendo a un restaurante… El contexto en la
vida corriente permite quitar este error. En matemáticas, no sera tal el caso. Hay que, en un
razonamiento, de una redacción, se refiere a la expresión utilisada (« Hay que» o « Basta con»)
sino existirá una confusión entre hipótesis y conclusión…
Espero que con esta advertencia basta…

Ejercicio 1. Mostrar encontrando un contra-ejemplo que las aserciones siguientes son falsas:
1. Si un entero n es divisible por 2, es divisible por 4.
2. Todos los polinomios de grado 2 tienen dos raíces reales.

Ejercicio 1. 1- 6 es un contra-ejemplo.
2- X²+1 es un contra-ejemplo.

EJERCICIOS
Ejercicio 1. Mostrar, utilizando un raciocinio por lo absurdo, la propiedad:

No existen reales a, b, c tales que : ∀x ∈ , ex=ax²+bx+c
Ejercicio 2. Sean ‘x’ y ‘y’ dos reales positivos. Mostrar que: sí x ≠ y, entonces
x− y ≠ y− x .
Ejercicio 3. Mostrar el teorema: si x es un número real y ∀ ε>0, |x| < ε entonces x=0.
Ejercicio 4. Poner de manifiesto que la aplicación f de  hacia  definida por: x  3x - 1 es

inyectiva.
Ejercicio 5. Poner de manifiesto que 3 es un número irracional.
Ejercicio 6. Poner de manifiesto que para toda n ≥ 1, 2n ≥ n.
Ejercicio 7. Consideramos un número real x tal que x > −1 .
Demostrar por recurrencia que : ∀n ∈ , (1 + x ) ≥ 1 + nx (inigualdad de Bernoulli)

n
Ejercicio 8. Poner de manifiesto que para toda n ≥ 2:

• 1+3+5+….+(2n-1)=n²
• 2+4+6+...+2n=n2+n
Ejercicio 9. Sean n, m dos enteros naturales, m ≠ 0. Se llama división euclidiana de n por m a

toda pareja (q, r) de enteros naturales tales que n = mq + r, con r∈{0,1,...,m-1}.
(i) Sea P(n) la propiedad que para todo m ≥ 1 existen (q, r) enteros naturales tales que n=mq
+ r, con r∈{0,1,... , m-1}. Poner de manifiesto que P(n) para todo n ∈ I.
(ii) Poner de manifiesto que la pareja (p, q) es única.
Ejercicio 10. Criticar el razonamiente siguiente :

Demostremos que n puntos distintos dados del plano están siempre alineados sobre la misma
recta.
Esto es verdadero para n = 1, y lo mismo para n = 2.
Supongamos que n puntos distintos dados del plan son siempre alineados sobre la misma recta
(hipótesis de recurrencia) y consideremos n + 1 puntos del plan A 1 , A2 ,…, A n , A n+1 .
De acuerdo a la hipótesis de recurrencia, los n puntos A1 , A2 ,…, An están alineados sobre una
recta D y los n puntos A2 ,…, An , A n+1 están alineados sobre una recta D’ ; pero como los puntos
A 2 y A 3 son comunes a D y D’, D = D’ y los n + 1 puntos A1 , A2 ,…, A n , A n+1 están alineados
sobre D = D’, lo que termina la recurrencia.

Ejercicio 11. Sea (P n ) n la familia de polinomios definida por :
P 0 =1, P 1 =X, ∀n ∈ *, P n+1 =XP n -nP n-1
Demostrar que: para toda n ≥ 1, P n’= nP n-1 .
Ejercicio 12. La condición de continuidad de una función f en x 0 es una condición necesaria,

una condición suficiente o las dos, para que f se pueda derivar en x0 ?
n
Ejercicio 13. Sea (u n ) una sucesión o secuencia real. Para todo n ≥ 0, tenemos S n = ∑ u i .
i =0
Poner de manifiesto que una condición necesaria para que la sucesión (S n ) admita un límite que
es lim u n =0. ¿Es una condición suficiente?

Algunos ejercicios corregidos
Ejercicio 14. Poner de manifiesto que si una función "f" admite un límite λ cuando x tiende
hacia x0 , este límite es único.
Corrección : Comencemos por dar la definición de un límite:

∀ε > 0 ∃δ > 0 ∀x ∈ Df x − x 0 ≤ δ ⇒ f ( x ) − λ ≤ ε
Razonamos por el absurdo.
Para ello, suponemos que existe λ diferente de λ tal que f tiende también hacia λ en x 0 .
Por definición, tenemos entonces:
∀ε > 0 ∃δ > 0 ∀x ∈ Df x − x 0 ≤ δ ⇒ f ( x ) − λ ≤ ε
Sea entonces ε > 0 cualquiera.
Escogamos δ et δ como precedentemente, y anotemos
= β min δ, δ . ( )
Tenemos, de acuerdo con la desigualdad triangular:
λ − λ ≤ λ − f ( x ) + f ( x ) − λ
Pero escogiendo x tal que x − x 0 ≤ β , obtenemos:
λ − λ ≤ ε + ε ≤ 2ε
Venemos de demostrar que : ∀ε > 0 λ − λ ≤ ε
Pero , de acuerdo a un ejercicio del capítulo anterior, hemos visto que aquello implica que
λ − λ = 0 sea λ = λ
Esto contredice nuestra hipótesis, de donde entonces tenemos el resultado.
Ejercicio 15 Sean (u n) y (v n ) dos sucesiones reales. ¿La convergencia de cada una de estas
sucesiones es una condición necesaria (suficiente o las dos) para que la sucesión (w n ) definida
por w n =u n +v n sea también convergente?
Corrección : 1- Es una CS : (u n ) n y (v n ) n convergen ⇒ (w n ) n converge

En efecto, supongamos que (u n) n y (v n ) n convergen hacia respectivamente lu et l v entonces:
∀ε > 0, ∃ ( N u , N v ) ∈ ×  ( n ≥ N u ) ⇒ u n − lu < ε et ( n ≥ N v ) ⇒ v n − l v < ε
Sea entonces ε > 0 y anotemos N = max ( N u , N v ) .
Entonces w n − ( lu + l v =
) u n + v n − ( lu + l v =
) u n − lu + v n − lv ≤ u n − lu + v n − l v ≤ ε + ε
Entonces, (w n ) n converge hacia lu + l v .
2- Por el contrario, no es una CN : ¬ ( (w n ) n converge ⇒ (u n ) n et (v n ) n convergent ) .
Consideremos por ejemplo u n = −vn = sin(n) .
Resulta que (u n) n y (v n ) n no convergen.
Por el contrario, (w n) n (que es la sucesión nula) converge evidentement hacia 0.
En particular, no es una CNS.

Capítulo 4
FUNCIONES - APLICACIONES - BIYECCIONES
0. Presentación
El concepto de relación es la base de toda la matemática donde el objetivo es el de es-
tudiar - por observación & deducción (razonamiento), cálculo & comparación - de configura-
tiones abstractas o concretas de sus objetos (números, formas, sombras, estructuras) buscando
a establecer vínculos lógicos, númericos o conceptuales entre estos objetos.
Consideremos dos conjuntos no vacios E y F. Si a algunos elementos de E podemos
asociar por una regla precisa denominada R (no ambigua) un elemento y de F, definimos en-
tonces una relación de E hacia F llamada binaria porquehace intervenir dos elementos. Escri-
bimos :
R:E F et x R y
• Cuando E = F, Hablamos de relación binaria en E.
• Si x R y, Decimos que y es una imagen de x por la relación R y que x es un anteceden-
te de y por esta misma relación
• El conjunto de las parejas (x,y) tal que x R y sea una asserción verdadera se denomina
gráfico de la relación R. Es una parte del producto cartesiano E x F. Podemos repre-
sentar estas parejas en un referencial (O,Ox,Oy) : Hablamos entonces de representa-
ción gráfica de la relación R.
• Cuando esto se puede realizar, la relación R', de F hacia E, definída por xR'y es solo y
solamente si yRx, es dicha recíproca de R. La notamos a menudo R-1 por analogia con
la noción elementaria de potencia.
• El conjunto D de elementos de E que tienen al menos una imagen por R se denomina
conjunto de definición de R.
• Cuando cada elemento de E possede como mucho

una imagen (ninguna o una sola), decimos que R es
una función.
Cuando una relación R es una función, notamos

y= R(x), más que xRy, la única imagen de x por R si esta
imagen existe.
Esta notación funcional se debe a Leibniz (Alemán,
1646-1716).

1. Funciones, aplicaciones
a) Función
Sean A y B dos conjuntos. Llamamos función de A hacia B todo modo de correspon-
dencia para el que a todo elemento de A asocia como máximo un elemento de B.
Noción de imagen y antecedente.
El conjunto de elementos de A que tienen una imagen por la aplicación de la función f

constituye el conjunto de definición de f (a veces escrito como D f).
Sea D un parte de A. El conjunto de las imágenes de los elementos de D por aplicación

de la función f se escribe f(D).
f(D)={y ∈ B / ∃ x ∈ D, y=f(x)}
f(D) es la imagen (directa) de D por f.
Sea E una parte de B. El conjunto de los antecedentes de los elementos de E por la

función f es notado f -1(E).
f -1(E)={x ∈ A / ∃ y ∈ E, y=f(x)}
-1
f (E) es la imagen recíproca de E por f.
Precaución: Para toda función f de A hacia B, podemos definir f -1(E) para E subconjunto de
B, sin importar que f sea biyectiva o no. No hemos utilizado f -1, en la definición de f -1(E).
Noción de restricción y de prolongación.
b) Aplicación
Sean A y B dos conjuntos. Llamamos aplicación de A hacia B a u na función de A
hacia B que a todo elemento de A asocia un (único) elemento de B.
Una aplicación de A hacia B es pues una función de A hacia B cuyo dominio de defi-
nición es A.
2. Composición de funciones
1- Sean A, B, C tres conjuntos. Sea f una función de A hacia B y g una función de B
hacia C. Se define la función h=g  f de A hacia C por:
h(x)=(g  f)(x)=g[f(x)]
2- La composición es asociativa y no conmutativa.
3. Inyección, Suprayección, biyección

Sea f una aplicación de A hacia B.
1- Inyección
f es inyectiva de A hacia B cuando todo elemento de B admite como muxo un antecedente
por f.
Matemáticamente, este fenómeno se traduce por :

∀ ( x1 , x 2 ) ∈ A 2 , f(x1=
) f (x 2 ) ⇒ x=
1 x2
2- Suryección
f es suryectiva de A hacia B cuando todo elemento de B admite al menos un antecedente por
f.
Matemáticamente, ésta se traduce mediante una de las propiedades equivalentes :
1- ∀y ∈ B, ∃x ∈ A, y=f(x)
2- f(A)=B
3- Biyección
f es biyectiva de A hacia B cuando es a la vez inyectiva y suryectiva. Esto significa que todo
elemento de B admite un único antecedente por f.
Matemáticamente, se traduce por :
∀y ∈ B, ∃!x ∈ A, y=f(x)
4- Biyección recíproca
Sea f una bijección de A hacia B. Existe entonces una bijección recíproca de B hacia A nota-
da f -1.
-1
Observación : la notación f ha sido escogida por analogía con el inverso de los reales.
1
Atención a no confundir bijección recíproca f -1 (mientras ella existe) y función inversa
f
(mientras ella existe).
De las notaciones anteriores, tenemos :

f -1  f = Id A et f  f -1 = Id B
lo que quiere decir:
∀x ∈ A, f -1 (f (x)) =x et ∀x ∈ B, f (f -1 (x)) =x
Atención: en las fórmulas precedentes, x representa una vez un elemento de B, una vez un
elemento de A…
Ejemplos :
+
1- Con la función ln bijección de * en 
+
2- Con la función f :  →  definida por f(x)=x².
Observación general sobre las definiciones de este capítulo : Desde el momento en que
empleamos las nociones de funciones, aplicaciones, inyecciones, es indispensable precisar los
conjuntos de partida y de llegada.
Ejemplo: Sea f definida por f(x)=x². Tomar como conjunto de partida y de llegada , +, -
…

Ejemplos de representaciones gráficas, con funciones de  en , de nociones de inyec-
ción, suryección y de bijección:
1- Con la función x  x²
a- de [-3,3] en [0,9], f es una suryección no inyectiva.

b- de [-3,3] en , f no es ni suryección ni inyección.
c- de [0,3] en , f es una inyección no suryectiva.
d- de [0,3] en [0,9], f es una biyección.
 x² + 6x + 1 si x<2
2- Con la función definida por : 
 5x²+5 si x ≥ 2
a- de [-1,3] en [-4,50], f es una inyección no suryectiva.

b- de [-1,3] en [-4,17[  [25,50], f es una biyección

Ejemplos de representaciones gráficas, con funciones diagramas de Venn, nociones de
inyección, suryección y biyección:
1- f : A → B, con A={a,b,c} y B={1,2,3,4}
a 1
2
b
3
c
4
f es inyectiva no suryectiva de A hacia B
2- f : A → B, con A={a,b,c,d} y B={1,2,3}
a 1
2
b
3
c
f es suryectiva no inyectiva de A hacia B.

3- f : A → B, con A={a,b,c,d} y B={1,2,3,4}
a 1
2
b
3
c
4
d
f es biyectiva de A hacia B.

Ejercicio 1. 1- Decir si las siguientes funciones de  en  son aplicaciones, sino, definir la

aplicación naturalmente inducida, precisar entonces si ésta es inyectiva, suryectiva o biyectiva
1 ln ( x − 1 ) si x ≠ 1
x  , x  cos(x), x  tan ²(x) + 1, x  
x 1 s i x =1
2- Dar para cada uno de los casos que preceden, un conjunto I tal que f restringida a I
sea inyectiva.
3- Dar para cada uno de los casos que preceden, un conjunto J tal que f sea suryectiva
de su dominio de definición hacia J.
Ejercicio 2 . Sean E, F y G tres conjuntos. Consideremos dos aplicaciones f : E → F y

g : F → G . Demostrar que si f y g son inyectivas (respectivamente suryectivas, respectiva-
mente biyectivas) entonces g  f es inyectiva (respectivamente suryectivas, respectivamente
biyectivas).
Ejercicio 3. Consideramos aplicaciones definidas de  hacia .

Demostrar las siguientes proposiciones o dar un contra-ejemplo.
1. La suma de dos aplicaciones inyectivas es inyectiva.
2. El producto de dos aplicaciones inyectivas es inyectivo.
3. La suma de dos aplicaciones suryectivas es suryectiva.
4. El producto de dos aplicaciones suryectivas es suryectivo.
5. Si f es biyectiva y n es un entero, entonces f n es biyectiva.
Ejercicio 4. Determinar los conjuntos más grandes A y B de  tales que la función f definida
ex + 2
por f (x) = constituya una biyección de A hacia B y determinar su biyección recíproca.
ex − 1

Ejercicio 1. 1- a- f no es una aplicación, debemos restringirla a *, en ese caso, es inyectiva

pero no suryectiva.
b- f es una aplicación, no es ni inyectiva ni suryectiva.
 π π 
c- f no es una aplicación, D=f   − + kπ; + kπ  , no es ni inyectiva ni suryec-
k∈Z  2 2 
tiva.
d- f es una aplicación, no es inyectiva ni suryectiva.
2 y 3- Cuidado, hay varias respuestas posibles.
a- J=*
b- =
I [0; π] , J= [ −1;1]
 π 
c-=I   kπ; + kπ  , = J [1; +∞[
k∈Z  2 
d-=I [1;e + 1[ ∪ ]e + 1; +∞[
Ejercicio 3. Todas estas afirmaciones son falsas (encontrar contra-ejemplos). Sin embargo, la
afirmación 5 es falsa enunciada tal cual, pero es verdadera si n es impar (ver ejercicio 2).
Ejercicio 4. Estudiamos f ( derivada, tabla de variaciones) y obtenemos: A=* y

 2+ y
B= ]−∞; −2[ ∪ ]1; +∞[ . Para y ∈ B, f −1 (y) =
ln  .
 y −1 

EJERCICIOS
Ejercicio 1. Trazar el gráfico de una función:

a- ni ni inyectiva ni suryectiva
b- inyectiva y no suryectiva
c- suryectiva y no biyectiva
d- inyectiva y suryectiva
Ejercicio 2. Sean A ,B y C tres conjuntos, f una aplicación de A hacia B y g una aplicación

de B hacia C. Mostrar que:
a- Si f y g son inyectivas, entonces g ° f es inyectiva. La recíproca es verdad?
b- Si f y g son suryectivas, entonces g ° f es suryectiva. La recíproca es verdad?
c- Si f y g son biyectivas, entonces g ° f es biyectiva. La recíproca es verdad ?
Ejercicio 3. Sean E y F dos conjuntos y "f" una aplicación de E en F. Sean A y B dos subcon-
juntos de E.
(i) Poner de manifiesto que f(A  B)=f(A)  f(B).
(ii) ¿Tendríamos f(A  B)=f(A)  f(B)?
(iii) ¿Tendríamos f(A\B) = f(A)\f(B)?
(iv) Se supone además que f es suprayectiva de E en F. ¿Se obtendría f (A) =f( A )?
Ejercicio 4. Sea una aplicación f : E → F y sean A y B dos subconjuntos de E.

Mostrar que f ( A  B ) ⊂ f ( A )  f ( B ) y que tenemos la igualdad si f es inyectiva.
 π 
Ejercicio 5. 1- Sea f definida sobre  por f(x)= sin(x). Dar f(A) para A=  − , 0  , para
 2 
 π 2π  π 
A=  ,  , para A=  + kπ, k ∈   .
2 3  3 
 1 3
Dar f-1(B) para B= [ 2, +∞[ , para B=  − ,  , para B=*.
 2 2 
Ejercicio 6. Sean E y F dos conjuntos y f una aplicación de E en F. sean G y H dos subcon-

juntos de F.
Dado f -1(G) = {x ∈ E/f(x) ∈ G}.
Mostrar que:
(i) f -1(G  H) = f -1(G)  f –1(H)
(ii) f -1(G  H)=f -1(G)  f -1(H)
(iii) f -1(G\H)= f -1(G)\f -1(H)
(iv) f -1( G )= f −1 (G)
(v) ¿Se tendría f -1(f(A))=A, para todo A subconjunto de E?
(vi) ¿Se tendría f(f -1(G))=G?
Ejercicio 7. Sea f una aplicación de E en F.

(i) Mostrar que la aplicación f es inyectiva si y solamente si, para todo C ⊂ E, C=f -1(f(C)).

(ii) Mostrar que f es suprayectiva si y solamente si, para todo A ⊂ F, f(f -1(A))=A.
Ejercicio 8. Mostrar que la aplicación f definida en \{2} con valores en \{1} por:
f: x  x +2
x −2
es una biyección. Determinar la aplicación recíproca f –1.
Ejercicio 9. Sean P y D dos partes de  definidas por :

P={z ∈  / Im(z)>0} y D={z ∈  / |z|<1}
z −i
Demostremos que la aplicación f definida por : z  es una biyección de P sobre D. De-
z+i
terminar la aplicación recíproca f –1.
Ejercicio 10. Sean E un conjunto y A y B dos elementos de P(E). Sea f la aplicación definida
en P (E) con valores en P (E) × P (E) por:
f: X  (X  A,X  B)
¿Podemos encontrar una condición necesaria y suficiente en A y B para que f sea inyectiva
(suryectiva,luego biyectiva)?
Ejercicio 11. Sean E un conjunto y A y B dos elementos de P (E). Sea f la aplicación defini-
da en P (E) con valores en P (E) × P (E) por:
f: X  (X  A,X  B)
¿Podemos encontrar una condición necesaria y suficiente en A y B para que f sea inyectiva
(suryectiva,luego biyectiva)?
Ejercicio 12. Sean E, F, G tres conjuntos, f : E → F, g : F → G dos aplicaciones.

(i) Demostrar que si g  f es inyectiva de E en G, entonces f es inyectiva de E en F y que si
encima f es suryectiva de E en F, entonces g es inyectiva de F en G.
(ii) Demostrar que si g  f es suryectiva de E en G, entonces g es suryectiva de F en G y
que si encima g es inyectiva de F en G, entonces f es suryectiva de E en F.
(iii) Suponemos E=G y g  f=I E . Que podemos decir sobre f y sobre g?
(iv) Suponemos E=G, g  f=I E y f  g=I F . Que podemos decir de f y g?

Elementos de soluciones de algunos ejercicios.
Ejercicio 2.
a- Sean f y g dos aplicaciones inyectivas.
Sean x e y tales que g  f ( x ) = g  f ( y ) , ie : g ( f ( x )) = g ( f ( y ) ) .
g inyectiva implica que : f ( x ) = f ( y ) .
f inyectiva implica que : x = y .
Deducimos que g ° f es inyectiva.
La recíproca es falsa.
En efecto, anotemos f : + →  definida por f(x)= x y g :  → + definida por g(x)=x².
Es fácil verificar que : g  f : + → + y es definida por: g  f(x)=x.
Esta aplicación es biyectiva.
Además, es claro que g no es inyectiva.
b- Sea f y g dos aplicaciones suryectivas.

Sea z ∈ C .
Como g es suryectiva, ∃y ∈ B, g ( y ) =z .
Comme f est suryectiva, ∃x ∈ A, f ( x ) =y .
Entonces ∃x ∈ A, g  f ( x ) =z y así g ° f es suryectiva.
La recíproca es falsa.
Retomamos el ejemplo anterior.
Es claro que f no es suryectiva.
Ejercicio 3.
(iii) Sea "y" elemento de f(A)\f(B). Entonces existe "a" como elemento de A tal que y=f(a)
y no existe ninguna "b" de B tal que y=f(b). Entonces, "a" no es elemento de B. De ahí que "y"
es elemento de f(A\B).
Se obtiene pues la inclusión : f(A)\f(B) ⊂ f(A\B).
La inclusión recíproca es falsa.
Basta con considerar f:x  x², A=[-1,2] y B=[-1,0].
(iv) Sea "y" un elemento de f (A) . Entonces "y" no es un elemento de f(A). Entonces para
todo "a" de A, y ≠ f(a). Entonces, "y" es un elemento de f( A ) (con f suprayectiva de E en F).
Se obtiene entonces la inclusión : f (A) ⊂ f( A ).
La inclusión recíproca es falsa. Basta con considerar: f:x  x², A=[-1,2].
Ejercicio 4.
Sea y ∈ f ( A  B ) .
Por definición , ∃x ∈ A  B, y =f ( x ) .
Particularmente, como A  B ⊂ A , ∃x ∈ A, y =f ( x ) y entonces y ∈ f ( A ) .
Del mismo modo, vemos claramente que y ∈ f ( B ) .
Deducimos entonces que y ∈ f ( A )  f ( B ) y así que f ( A  B ) ⊂ f ( A )  f ( B ) .

La inclusión: f ( A  B ) ⊃ f ( A )  f ( B ) es falsa en el caso general ( Buscar un ejemplo).
Ahora supongamos que f es inyectiva.
Por definición, esto significa que f ( x= ) f ( y ) ⇒ x= y .
De acuerdo con lo precedido, para demostrar la igualdad, basta con demostrar la inclusión
f ( A  B) ⊃ f ( A )  f ( B) .
Sea entonces y ∈ f ( A )  f ( B ) .
Esto significa que y ∈ f ( A ) et y ∈ f ( B ) .
A, y f ( a ) et ∃b ∈=
Entonces ∃a ∈= B, y f ( b ) .
PEro en ese caso, tenemos f ( a ) = f ( b ) y por inyectividad de f, esto implica a=b.
Así a ∈ A  B y como y = f ( a ) , deducimos que y ∈ f ( A  B ) .
Ejercicio 5.
(vi) Demostremos que f(f -1(G)) ⊂ G. Sea y ∈ f(f -1(G)). Existe x ∈ f -1(G) tal que y=f(x) ;
como x ∈ f -1(G), tenemos entonces f(x) ∈ G. De lo cual: y ∈ G.
Hemos demostrado así que : f(f -1(G)) ⊂ G.
La inclusión recíproca es falsa. Para demostrarlo, basta con proponer un ejemplo contrario.
Tomemos la aplicación E :  →  con E(x)=Parte entera de x y G =[0,2].
Obtenemos : f-1(G)=[0,3[ y f(f -1(G))={0,1,2} ≠ G.
Ejercicio 6.
A continuación f es una aplicación de E en F.
(i) Sea C ⊂ E y sea x un elemento de C. Entonces y=f(x) es elemento de f(C) con x=f -1(y)
que es elemento de f -1(f(C)). Entonces C ⊂ f-1(f(C)). (Observemos que aún no hemos utilizado
la inyectividad de f).
Para la inclusión recíproca, vamos a utilizar la inyectividad de f.
Sea x elemento de f -1(f(C)).
Entonces, f(x) es elemento de f(C), entonces existe x’ elemento de C que comprueba que
f(x)=f(x’), de ahí x=x’.
(cf. inyectividad de f). Entonces x es un elemento de C.
Hemos ya mostrado que (f inyectiva) ⇒ ( para todo C ⊂ E, C=f -1(f(C))).
Mostramos la implicación recíproca.
Se supone para todo C ⊂ E que C=f -1(f(C)). (En realidad solamente tendremos necesidad de
f -1(f(C)) ⊂ C). Mostremos que f es inyectiva.
Sean tanto x como x’ tales que f(x)=f(x’). Tomando C={x}, f -1(f({x})) contiene sólo a x. Sin
embargo x’ es elemento de f-1(f({x})). Por lo tanto x=x’ también f es inyectiva.
(ii) Como anteriormente una inclusión se comprueba siempre f(f -1(A)) ⊂ A. En efecto, sea x
elemento de f(f -1(A)).
∃z ∈ f −1 (A) /x=f(z).
Así pues z es elemento de f -1(A), de ahí x=f(z) es elemento de f -1(A).
Se mostró así que f(f -1(A)) ⊂ A.
Supongamos que f es suprayectiva. Sea A un parte de F y sea "a" elemento de A. Existe x,
elemento de E tal que a=f(x). Pues "a" es elemento de f(f -1(A)) porque x es elemento de
f -1({a}).
Si A ⊂ f(f -1(A)) para toda A, sea "y" elemento de F con A={y}. Como {y} ⊂ f(f -1({y}), existe
x elemento de E tal que y=f(x). Así f es bien suprayectiva.

Ejercicio 9.
1- La Condición Necesaria y Suficiente (CNS) para que f sea inyectiva es A  B=E. En
efecto,
a) Supongamos f inyectiva. Entonces,
f(A  B)=((A  B)  A,(A  B)  B)=(A,B)=f(E). Pues, A  B=E.
b) Supongamos A  B=E y sea (X,Y) ∈ P(E)²/f(X)=f(Y). Entonces
X=X  E=X  (A  B)=(X  A)  (X  B)=(Y  A)  (Y  B)=Y  (A  B)=Y  E=Y. Enton-
ces, f es una inyección de P(E) en P(E) × P(E).
2- La CNS para que f sea suprayectiva es A  B= ∅ . En efecto,

a) Supongamos f como suprayectiva. ∃X ∈ P(E) / f (X) = (∅, B) . Así X ⊂ Ac y X ⊂ B,
entonces A  B= ∅ .
b) Supongamos A  B= ∅ y sea (X,Y) ∈ P(E)². Tenemos:
f(X  Y)=((X  A)  (Y  A),(X  B)  (Y  B))=(X,Y) ya que X  B=Y  A= ∅ .
Ejercicio 10.
1- La CNS para que f sea inyectiva es A  B= ∅ . En efecto :
a- Supongamos f inyectiva. Entonces, f(A  B)=(A,B)=f( ∅ ). Por lo cual, A  B= ∅ .
b- Supongamos A  B= ∅ y sea (X,Y) ∈ P(E)²/f(X)=f(Y). Entonces :
X ⊂ (X  A) = Y  A (porque f(X)=f(Y)) y X ⊂ ( X  B ) = Y  B . Por lo cual,
X ⊂ (( Y  A )  ( Y  B)) =
Y.
La inclusión recíproca (Y ⊂ X) se obtiene de la misma manera. Por lo cual : X=Y.
2- La aplicación f jamás es suryectica. Si fuera el caso, ( ∅, ∅ ) admite un antecedente,

entonces A=B= ∅ .
Por lo tanto, para todo X de P(E), tenemos f(X)=(X,X) pero entonces (E, ∅ ) no tiene antece-
dente.

Capítulo 5
COMPLEMENTOS SOBRE NÚMEROS COMPLEJOS
0- Presentación Histórica :
La ingeniosa invención del número i se debe a Bombelli en su obra « Algebra » en

1572. El reconocimiento de estos números imaginarios sigue siendo muy controvertido para
los matemáticos hasta su representación geométrica por Gauss descrita en su carta a Bessel en
1811 : « …de la misma manera que podemos representar todo el dominio de las cantidades
reales por el medio de una linea recta indefinida, pode-
mos representar el dominio completo de todas las canti-
dades, las reales y las imaginarias, por el medio de un
plano indefinido; donde cada punto determinado por su
abscisa a y por su ordenada b representa al mismo tiem-
po la cantidad a+ib ». La invención de Bombelli accede
al estatuto de « número ».
El símbolo « i » fue introducido por Euler por la
primera vez en 1777 suplantando la notación más que
ambigüa de « −1 »,utilizada desde mediados del siglo
XVI por los algebristas y geómetras.
En efecto, las raices cuadradas de –1 fueron a
Euler menudo señaladas −1 y - −1 .
Euler
Desgraciadamente, esta notación conduce a
enormes contradicciones.
Efectuar el producto ( −1 )x( −1 ) :
- por una parte aplicando la definición de la raiz cuadrada ;
- y por otra parte aplicando la regla : a × b = ab ;
La presencia del símbolo incita a ap licar una regla unicamente valida para reales
positivos. Para no sucumbir a esta tentation, y para evitar sus fastidiosas consecuencias, Euler
propuso de remplazar los símbolos −1 y - −1 por i y -i. Entonces i² = -1 y ( -i)²=-1. Esta
notación, retomada por Gauss, todavia se utiliza.
En el siguiente extracto, Gauss situa la invención de los numeros complejos en el cuadro de las
extensiones succesivas de los conjuntos numéricos.
« Nuestra arithmética general, que sobresa ampliamente la geometria antigua, es en su totali-
dad la creación de la época moderna. Nacida del concepto de los números enteros, a ensancha-
do progresivamente su dominio. A los números enteros han venido a añadirse los números
fractionarios, a los números rationales los irrationales, a los números positivos los negativos, y
a los números reales, los imaginarios. Sin embargo, esta progresión se ha efectuado a p asos
inseguros y dubitativos. Los primeros algebristas todavia llamaban raices falsas a l as raices
negativas de las ecuaciones (y lo son efectivamente ahi donde el problema se nos presenta, es

presentado de tal manera que la naturaleza de la magnitud buscada no admite opuesto). Pero
de la misma manera que tenemos pocos escrúpulos al acoger los números fractionarios en el
seno de la arithmética general, mientras existe una multitud de cosas denombrables para las
cuales un número fractionario carece de sentido, de la misma manera no deberiamos rechazar a
los números negativos derechos idénticos a los de los números positivos,bajo pretexto que una
infinidad de cosas no admiten opuestos. La realidad de los números negativos está ampliamen-
te justificada, ya que encuentran en miles de otras ocasiones un soprte adecuado. En verdad,
desde hace mucho tiempo, un hecho está en lo succesivo establecido : solo los grandores ima-
ginarios que se oponen a los grandores reales (grandores imaginarios antiguamente, y a veces
todavia llamados torpemente imposibles) todavia no han adquerido derecho de cita, están solo
tolerados, se parecen por lo tanto más a un juego de signos vacios de contenido real, a los cua-
les rechazamos imperativamente un soprte imaginable, sin querer sin embargo desdeñar el pre-
ciado tributo que este juego de signos sirve a fin de cuentas al tesoro de las relaciones entre los
grandores reales. »
Ejercicios fuera de programa :

Ejercicio 1. En , se da z 2 =a 2 +ib 2 además z 2 =a 2 +ib 2 . Se define ≤ mediante :
z 1 ≤ z 2 ⇔ [(a 1 < a 2 ) ∨ ((a 1 = a 2 ) ∧ (b 1 ≤ b 2 ))]
a- Clasificar del más pequeño al más grande, los números complejos siguientes : i , 5
+ i , -6 ,-6 + 2i.
b- Comprobar que la relación ≤ así definida hace de  un conjunto ordenado (orden
lexicográfico).
c- Representar el conjunto de los números complejos z tales que (z ≤ 1+i).
d- (; ≤ ) ¿posee la propiedad del borne superior?
Ejercicio 2. Sea (K, ≤ ) un cuerpo ordenado, es decir un cuerpo conmutativo provisto con
una relación de orden total ( ≤ ) compatible, lo que quiere decir que comprueba
1- ∀(x, y, z) ∈ K 3 , x ≤ y ⇒ (x + z) ≤ (y + z)
2- ∀(x, y) ∈ K 2 ,(0 ≤ x ∧ 0 ≤ y) ⇒ (0 ≤ xy)
a- Mostrar que (x<0 ⇒ -x>0)
b- Mostrar que ( ∀x ∈ K,0 ≤ x² )
c- Mostrar que 1>0
d- Mostrar que ninguna relación de orden total definida en  es compatible con su es-
tructura de cuerpo.
1- Definiciones
Admitimos el resultado siguiente, que es la base de este capítulo
Teorema 1:
Existe un conjunto  que contiene , y que cumple:
-  posee una adición y una multiplicación que prolongan las de  y que siguen las
mismas reglas de cálculo.
- Existe un elemento i de  como i2 = - 1.

- Todo elemento z de  se escribe de manera única como z = a + ib ("a" y "b" reales).
Vocabulario • es el conjunto de los números complejos.

• Si z = a + ib ("a" y "b" reales, a es la parte real de z, escrita como Re (z);
b es la parte imaginaria de z, escrita como Im (z).
• La escritura z = a + ib es la forma algebraica de z.
Otras formas de escribirlos:

• z=|z|(cosθ + isenθ) con z que no es nula, es la forma trigonométrica
• z=|z|eiθ es la forma exponencial
Estructura de 
• (,+)
1- + es una ley de composición interna
2- Asociatividad
3- Existe un elemento neutro 0
4- Todo número complejo admite un opuesto
5- Conmutatividad
Se dice entonces que (,+) es un grupo conmutativo.
• (, × )
1- × es una ley de composición interna
2- Asociatividad
3- Existe un elemento neutro 1
4- Todo número complejo que no es nulo admite un inverso
5- × es distributiva con respecto a +
6- Conmutatividad
Se dice entonces que (,+, × ) es un cuerpo conmutativo.
2- Formula del binomio de Newton
Sean "a" y "b" dos números complejos y "n" un entero natural que no es nulo.
n n
n
(a+b)n= ∑ Ckn a n − k b k = ∑   a n − k b k
= k 0= k 0k
Newton Isaac (inglés, 1642-1727) Ilustre físico, filósofo, y,

a veces olvidamos, un célebre matemático. El final del siglo 17 mar-
ca el final de la inquisición y él supo aliar el progreso de la ciencia a
las ideas teológicas de la época.
Se dice que ocurrió cuando él observaba una manzana caerse
de un árbol cuando tuvo la idea de la teoría de la gravedad universal.
Newton formula la ley según la cual los cuerpos celestes se atraen
siguiendo una fuerza proporcional a sus masas e inversamente pro-
porcional al cuadrado de la distancia de los separa.

3- Formula de Moivre
Para todo real θ y para todo entero n, (eiθ)n=einθ.

(cos θ + i sen θ)n = cos (nθ) + i sen (nθ)
Abraham De Moivre
(1667-1754)
Aplicación: Expresión de cos (nθ) y de sen(nθ) en función de potencias de cosθ y de

sinθ.
Por ejemplo, cos(5θ =16cos5θ - 20cos3θ + 5cosθ.
4- Formula de Euler
eiα +e−iα eiα −e−iα

Para todo real α, cos α = con sen α = .
2 2i
Aplicación a la linearización: Sea α un real. Linearizar sin 5 ( α ) .
Utilizando el triángulo de Pascal para calcular los coeficientes binomiales, vamos a desarrollar
5
 e iα − e − iα 
  , enseguida bastará con reagrupar los términos de dos en dos:
 2i 
5
 e iα − e − iα
 1 iα − iα 5 1 5iα
 = 5 ( e − e )= 5 ( e − 5e + 10e − 10e + 5e − e )
3iα iα − iα −3iα −5iα

 2i 2 i 2 i
1
( )
= 5 ( e5iα − e −5iα ) − 5 ( e3iα − e −3iα ) + 10 ( eiα − e − iα )
2i
1  (e − e ) ( e3iα − e −3iα ) ( eiα − e − iα ) 
5iα −5iα
= 4  −5 + 10 
2  2i 2i 2i 
 
1
= 4 ( sen ( 5α ) − 5sen ( 3α ) + 10sen ( α ) )
2

5- Raíces cuadradas de un número complejo
Definición 1 :
Sea Z un número complejo. Se llama raíz cuadrada de Z todo número complejo z como:
z²=Z.
Observación: la notación z no tiene ningún sentido (excepto por supuesto si z es un real

positivo).
Teorema 2:
Todo número complejo que no es nulo admite exactamente dos raíces cuadradas.
Método de cálculo: la busqueda de las raices cuadradas del complejo Z = A+iB corresponde a
a² − b² = A

buscar los complejos z = a + ib tales que :  2ab = B .

a² + b² = A² + B²
6- Raíces nésimas de un número complejo
Definición 2:
Sea Z un número complejo con "n" como entero natural que no es nulo. Llamamos raíz nésima
de Z todo número complejo z tal que:
zn=Z.
1
Observación: la notación z n no tiene ningún sentido (excepto claro si z es un real positivo).
Teorema 3:
Sea n un entero natural que no es nulo. Todo número complejo que no es nulo admite exac-
tamente n raíces nésimas.
7- Raíces nésima de la unidad
Se escribe U n el conjunto de las raíces nésiimas de la unidad.
Teorema 4:
 2ikπ 
Sea n un entero natural que no es nulo. U n = e n / k ∈ , 0 ≤ k ≤ n − 1 .
 
Teorema 5:
Sea n un entero natural que no es nulo.
La suma de las raíces nésimas de la unidad es nula.

Propiedad:
2ikπ
con k {
∈ 0,..., n − 1}
Notamos M k el punto de afijo z k = e
n
.
Los n puntos M k son los vértices de un poligono regular centrado al origen y de radio 1.
2iπ
Caso particular: U 3 ={1, j, j²} avec j= e . De plus, j² = j .

3
8- Ecuación del segundo grado con coeficientes en 
Resolución de la ecuación de segundo grado az² + bz + c = 0, de coeficientes complejas y

a ≠ 0.
Sea ∆ = b²-4ac el discriminante de esta ecuación .
b
– si ∆= 0 entonces la ecuación admite − como solución única.
2a
−b ± δ
– si ∆ ≠ 0 entonces la ecuación admite dos soluciones distintas , donde δ es una
2a
raíz cuadrada de ∆.

Ejercicio 1.
1- Poner bajo la forma cartesiana los siguientes números complejos:
4 − 3i
z1 =(1 + i 3)(2 − i) ; z 2 = (1 + i)3 ; z 3 =
i −1
2- Dar el argumento de los siguientes números complejos:
2 2
z=
1 cos(θ) − isen(θ) ; z= 2 +i ; z=3 sen(θ) + i cos(θ)
2 2
Ejercicio 2. Calcular las raíces cuadradas de 100, −100,3 + 4i, −5 − 12i .
Ejercicio 3. Resolver en  :
z² + z +1 =0
Ejercicio 4.
1- Calcular las raíces cuartas de la unidad. Representarlos en el plano complejo.
2- Mostrar que el producto de 2 raíces nésimas de la unidad es una raíz nésima de la uni-
dad (Decimos que el conjunto de las raíces nésimas de la unidad es estable para la mul-
tiplicación.)
Ejercicio 5. Linearizar cos5 (x) y sen 6 (x) .

7 1
Ejercicio 1. 1- z1 =2+ 3+i(2 3-1) ; z 2 =-2+2i ; z 3 =- - i .
2 2
π π
2- -θ, , -θ.
4 2
Ejercicio 2. 1. 10, -10 ;

2. 10i, -10i ;
3. 2+i, -2-i ;
4. 2-3i, 2+3i
Ejercicio 3. j, j²
Ejercicio 4. ver el curso.
Ejercicio 5.
1 5 5 1 3 15 5
cos5 (x) = cos(5x) + cos(3x) + cos(x) y sen 6 (x) =
− cos(6x) + cos(4x) − cos(2x) +
16 16 8 32 16 32 8

EJERCICIOS
Ejercicio 1. Poner en forma algebraica los números complejos siguientes:

1− i a +i a+ib a − ib
=z1 ; z2
= con "a" real=
; z3 + con "a" y "b" reales ;
1+ i 1 − ai b+ia b − ia
cosθ + isenθ
= z4 con θ y también ϕ reales
cosϕ − isenϕ
20
1 + i 3 
Ejercicio 2. Calcular el módulo y el argumento de   .
 1− i 
Ejercicio 3. 1- Determinar en forma algebraica las raíces cuadradas de (-7-24i) y de (-3+4i).

2- Resuelva la ecuación: z² + (3+4i)z - 1 + 5i = 0.
3- ¿Cuáles son las formas algebraicas de las raíces cuartas de la unidad y de
(-7-24i)?
Ejercicio 4. Resolver en  las ecuaciones siguientes:

a- z² − (1 + i 3)z − 1 + i 3 = 0
b- z 4 − (5 − 14i)z 2 − 2(5i + 12) = 0
c- (3z² + z + 1)² + (z² + 2z + 2)² =0
Ejercicio 5. Sabiendo que P(z) = 4z 3 − 6i 3z 2 − 3(3 + i 3)z − 4 tiene una raíz real , resolver
en  la ecuación P(z) = 0.
Ejercicio 6. 1- Sea la ecuación : z5-1=0 (E).

Resolver la ecuación (E) en  calculando las raíces en forma de modulo y de argumento.
2- Determinar el polinomio Q tal que para toda z que pertenezca a , se tiene:
z5-1=(z-1)Q(z)
1
3- Resolver la ecuación Q(z)= 0 efectuando el cambio de incógnita Z=z + (para eso
z
usted podrá comenzar por poner z² como factor en Q(z)).
 2π   4π  π  2π   4π 
4- Deducir los valores exactos de cos , cos , cos  , s e n   , s e n   ,
 5   5  5  5   5 
π
sen  .
5
Ejercicio 7. Linearizar cos3 x.s e n 2 x donde x es un real.
Ejercicio 8. Calcular cos(5x) - respectivamente sen(5x) – como potencias de cos(x) – y res-

pectivamente sen(x) -.

n
Ejercicio 9. Calcular S = ∑e ikθ
con θ real, distinta de 2pπ (p entero).
k =0
n n
Deducir ∑ cos(kθ) y ∑ sen(kθ) .
k =0 k=0
Ejercicio 10. Siendo α, β, ρ números reales y "n" un entero natural que no es nulo, calcular:
n-1 n-1
A= ∑ ρ cos(α+kβ)
k=0
k
y B= ∑ ρ sen(α+kβ)
k=0
k
Ejercicio 11. 1- Siendo θ un número real comprendido entre 0 y 2π, determinar el módulo y
el argumento del número complejo:
α = 1+ cosθ + isenθ
1
2- Determinar los elementos z d e * tales que z, z + 1 así como tengan el mismo
z
módulo.
Ejercicio 12. Resolver las siguientes ecuaciones:

1- (z + i) n = (z − i) n donde n es un entero superior o igual a 2.
2- z + z + i(z + 1) + 2 = 0
Arg(z)= − Arg(z + 1) + 2kπ, k entero
3- 
 z =1
2iπ
Ejercicio 13. Sea j = e 3
y sean a, b, c tres complejos dados. Resolver el sistema (S) siguien-
te:
x + y + z = a

x + jy + j² z = b
x + j² y + jz = c

2iπ
Ejercicio 14. Sean los tres números complejos: ω =e 7 , u=ω+ω2+ω4 et v=ω3+ω5+ω6.
1- Mostrar que u et v son conjugués. Calcular u + v y deducir la parte real de u.
2- Calcular uv, después la parte imaginaria de u. Deducir el valor de:
 2π   4π   8π 
sen   + sen   + sen  
 7   7   7 
(Observación: en estas dos cuestiones, pedimos valores numéricos y no simplemente los resul-
tados en función de ω).

6 +i 2
( )
7
Ejercicio 15. Escribir en fomar exponencial: (1 − i ) , 1 + i 3 , y
5
. Con ayuda del
1− i
 5π   5π 
último, deducir cos   y sen   .
 12   12 
Corrección:
π
 1 1   π  π  −i
(1=
− i) 2 −i=  2  cos   − isen =  2e 4 .
 2 2  4  4 
5π
( )
5 −i
Entonces (1 − i ) =2 e
5
4 .
1 3 π
( )
1 + i 3 = 2  + i 
 = 2

 cos
π
  + i.sen
 π 
  = 2e
i
3.
2 2   3  3 
7π
( )
7 i
7
Entonces 1 + i 3 2 e
=. 3
π
−i
Tenemos (1 − i ) =2e 4
.
Por otro lado
 6 2  3 1  π  π  i
π
6 +i =
2 8  +i =  8  +i =  8  cos   + i.sen  =  8e 6 .
 8 8   2 2   6  6 
π
i
π π π
6 +i 2 8e i +i 6
5i
Entonces = = π
2e
= 2e
6 4 12 .
1− i −i
2e 4
 5π   5π  6 +i 2
Para determinar cos   y sen   , basta con transformar la escritura de . Para
 12   12  1− i
ello, multiplicamos el denominador por su conjugada:
(
6 + i 2 (1 + i ) 1 )
6 +i 2
1− i
=
2
=
2
6 − 2 +i 2 + 6 . ( ( ))
π
6 +i 2 i5   5π   5π  
Como = 2e = 2  cos   + i.sen    .
12
1− i   12   12  
 5π  6− 2  5π  6+ 2
Deducimos
= que cos   = y sen   .
 12  4  12  4
Ejercicio 16. Resolver en  las ecuaciones:

a- z² − 2iz + 2 − 4i =0
4
b- z = −119 + 120i
c- z² − 2eiα z + 1 =0 con α ∈ [ 0, π]
Corrección: a- Calculamos el discriminante ∆ = ( −2i ) − 4 ( 2 − 4i ) = −4 − 8 + 16i = −12 + 16i

2
Buscamos una raíz cuadrada de ∆ , es decir, que buscamos z=a+ib tal que z²= ∆ .

a² − b² = Re ( ∆ ) a² − b² = −12
 
z² = ∆ ⇔ ( a + ib ) = ∆ ⇔ 2ab = Im ( ∆ ) ⇔ 2ab = 16
2
 a² + b² = 20
( a² + b² ) =
2
∆ 
= 2a² 8= a² 4
  a = 2 a = −2
⇔ 2ab = 16 ⇔ ab =8 ⇔  ou 
   b = 4 b = −4
= 2b² 32 = b² 16
 2i + 2 + 4i
z1 = 2
= 1 + 3i
Las raíces de la ecuación son entonces : 
z =2i − 2 − 4i =−1 − i
 2 2
b- Primero, busquemos una raíz cuarta de −119 + 120i .

Para ello, comenzaremos por determinar una raíz cuadrada. Luego, de nuevo buscaremos una
raíz cuadrada de la que venimos de encontrar.
a² − b² =
−119

−119 + 120i ⇔ ( a + ib ) =
2
z² = −119 + 120i ⇔ 2ab = 120
a² + b² =
169

= 2a² 50 = a² 25
  a = 5 a = −5
⇔ 2ab =120 ⇔ ab = 60 ⇔  o
2b² 288 b² 144  b = 12 b = −12
=  = 
Escogemos z= 5 + 12i por ejemplo.
Determinemos una raíz de z :
a² − b² =5

5 + 12i ⇔ ( a + ib ) =
2
z² = 5 + 12i ⇔ 2ab = 12
a² + b² =13

= 2a² 18 = a² 9
  a = 3 a = −3
⇔ 2ab = 12 ⇔ ab =⇔ 6  o
2b² 8= b² 4  b = 2 b = −2
=  
Deducimos que α = 3 + 2i es una raíz cuarta de −119 + 120i .
4
4 z4 4
La ecuación z = −119 + 120i se escriba entonces z =α ⇔   =1 .
α
Esto nos lleva a determinar las raíces cuarta de la unidad.
 ikπ

Anotemos entonces ω1 , ω2 , ω3 , ω4 las raíces cuarta de la unidad  ωk =e 2  , las soluciones
 
de la ecuación son ω1α, ω2 α, ω3α, ω4 α .
c- Calculamos el discriminante ∆ = ( −2eiα ) − 4 = 4 ( e 2iα − 1) .

2
Buscamos una raíz cuadrada de ∆ .

Observemos primero que :

 π
∆ 4 (e − 1) 4e (e ) 4e
i  α+ 
= 2iα
= iα iα
− e= − iα iα
( 2isen (=
α )) iα
( α ) 8sen ( α ) e
8ie sen =  2
.
Como 8sen ( α ) es un real positivo, tenemos inmediatamente una raíz cuadrada carrée de ∆ :
α π α π
i +  i + 
8sen ( α )e  2 4
= 2 2sen ( α )e  2 4
Las raíces de la ecuación son entonces:

 α π
i + 
 iα
2e + ∆ 2e iα
+ 2 2sen ( α ) e  2 4 α π
i + 
z1 = = e + 2sen ( α )e  2 4 
=iα
2 2
 α π
 i + 
2e − ∆ 2e − 2 2sen ( α )e
iα iα  2 4 α π
i + 
z = = e − 2sen ( α )e
=iα  2 4
 2 2 2
Ejercicio 17. Resolvamos en  cada una de las ecuaciones :

1− i
a- z 4 =
1+ i 3
b- ( z + 1) =( z − 1)
n n
c- z 7 = z
3 2
 z+i  z+i  z+i
d-   +  +  +1 =0 (Podremos efectuar un cambio de variable…)
 z −i   z −i   z −i 
1− i
Corrección: a- Primeramente, busquemos una raíz cuarta de .
1+ i 3
π π
( )
−i i
Tenemos: (1 − i ) =2e 4
et 1 + i 3 =
2e 3 .
π
−i
1− i 2e 4
2 −127 π
Entonces tenemos = = π
e .
1+ i 3 i 2
2e 3
1 −7 π
1− i −
Así una raíz cuarta de es α =2 8 e 48 .
1+ i 3
4
1− i
4 z
La ecuación z = se escribe entonces z 4 =α 4 ⇔   =1 .
1+ i 3 α
Esto nos lleva entonces, a determinar las raíces cuarta de la unidad.
 ikπ

Anotemos entonces ω1 , ω2 , ω3 , ω4 las raíces cuarta de la unidad  ωk =e 2  , las soluciones
 
de la ecuación son ω1α, ω2 α, ω3α, ω4 α .
b- Primero, observemos que z = 1 no es una solución.

( z + 1)
n n
 z +1 
Esta ecuación es entonces equivalente a 1⇔ 
= 1.
 =
( z − 1)
n
 z −1 
z +1
Anotemos entonces Z = .
z −1

Las soluciones de la ecuación Zn = 1 son las raíces de la unidad. Anotémoslas ωk .
2kπ
i
Tenemos ωk =e n
para k ∈ {0, n − 1} .
z +1
Para encontrar las soluciones de la ecuación del comienzo, basta con resolver: = ωk
z −1
z +1
= ωk ⇔ z (1 − ωk ) = − (1 + ωk )
z −1
Es claro que para ω0 =, 1 no existen soluciones.
Por el contrario, para k ∈ {1, n − 1} , las soluciones son z = −

(1 + ωk )
(1 − ωk )
c- Sea z una solución de esta ecuación.
Pasando al módulo, obtenemos z 7 = z , lo que quiere decir:
7
( 6
)
z = z ⇔ z z − 1 = 0 ⇔ z = 0 o z =1 ⇔ z = 0 o z =1
6
Es fácil verificar que z = 0 es solución de la ecuación.

Supongamos z ≠ 0 .
De acuerdo con lo anterior, tenemos z = 1 entonces z = eiθ .
π
Como z es solución, tenemos ei7 θ = e − iθ ⇔ ei8θ = 1 ⇔ 8θ ≡ 0 [ 2π] ⇔ θ ≡ 0   .
4
π π 3π 5π 3π 7π
i i i i i i
Finalmente, las soluciones de la ecuación z 7 = z son : 0, 1, e 4 , e 2 , e 4 , eiπ , e 4 , e 2 , e 4
.
 z+i
d- Anotemos X =   , tenemos:
 z −i 
X 3 + X 2 + X + 1 =0
Es claro que X = 1 no es solución de esta ecuación.
X4 −1
Observemos además que para X ≠ 1 , tenemos = X3 + X 2 + X + 1 .
X −1
Para ver esto, ya sea calculamos la suma de términos de una sucesión geométrica, o ya sea
( a − b ) ( a n + a n −1b + a n −2 b 2 +  + ab n −1 + b n ) .
conocemos la fórmula: a n +1 − b n +1 =
 X4 −1 
Así, X 3 + X 2 + X + 1 = 0 ⇔ ( X ≠ 1) ∧  = 0  ⇔ ( X ≠ 1) ∧ ( X 4 =1) .
 X −1 
3 2
Las soluciones de la ecuación X + X + X + 1 = 0 son entonces, las raíces cuartas de la unidad
 ikπ

diferentes de 1. Las anotaremos ω1 , ω2 , ω3  ωk =e 2  .
 
z+i
Para encontrar las soluciones de la ecuación del principio , basta con resolver: = ωk .
z −i
z+i
= ωk ⇔ z (1 − ωk ) = −i (1 + ωk )
z −i
Como para k ∈ {1, 3} , ωk ≠ 1 , las soluciones son: z = −i
(1 + ωk ) .
(1 − ωk )

2π
i
Ejercicio 18. Anotemos ω =e 7 , A = ω + ω2 + ω4 et B = ω3 + ω5 + ω6 .
1- Calcular A + B y AB
2- Deducir A y B
Corrección : 1- Tenemos A + B = ω + ω2 + ω4 + ω3 + ω5 + ω6 = ω + ω2 + ω3 + ω4 + ω5 + ω6 .
ω7 − 1
Como ω ≠ 1 , tenemos 1 + ω + ω2 + ω3 + ω4 + ω5 + ω6 = .
ω −1
7
Como ω= e 2i=
π
1 entonces A + B + 1 =0 , lo que quiere decir A + B =−1 .
Por otro lado, tenemos:
AB = ( ω + ω + ω )( ω + ω + ω ) = ω + ω + ω + ω + ω + ω + ω + ω + ω
2 4 3 5 6 4 6 7 5 7 8 7 9 10
= ω4 + ω6 + 1 + ω5 + 1 + ω7 × ω + 1 + ω7 × ω2 + ω7 × ω3
= ω4 + ω6 + 1 + ω5 + 1 + ω + 1 + ω2 + ω3
=3 + A + B =2
2- De acuerdo con lo que precede, tenemos:

A + B = −1 B =−A − 1 B =−A − 1
 ⇔ ⇔ 2
AB = 2 A ( −A − 1) =2 A + A + 2 =0
Determinemos las soluciones de X 2 + X + 2 =0.
−1 ± i 7
Tenemos ∆ = 1 − 4 × 2 = −7 entonces las dos soluciones son .
2
 −1 + i 7  −1 − i 7
= A = A
 2  2
Tenemos entonces dos posibilidades  o .
 −1 − i 7  −1 + i 7
= B = 2 B 2
Para determinar la buena solución, basta con estudiar el signo de la parte imaginaria de A por
ejemplo :
 i 27π   i 47π   i 87π 
Im ( A=) Im ( ω + ω + ω=) Im ( ω) + Im ( ω ) + Im ( ω=) Im  e  + Im  e  + Im  e 
2 4 2 4
     
 2π   4π   8π   2π   6π   2π 
= sen   + sen   + sen   = sen   + 2sen   cos  
 7   7   7  7   7   7 
 6π   2π 
2sen   cos  
 7   7 
 −1 + i 7
A =
 2
Es claro entonces Im ( A ) ≥ 0 . Deducimos que  .
B = −1 − i 7
 2
Ejercicio 19. Calculando (1 + i ) para n ∈  de dos maneras diferentes, calcular:

n

n n n n n
n k n
n k
S 1 =   −   +   −   + ... = ∑=   i ∑   ( −1) 2
 0   2   4  =
6 k 1=k k 1 k
k pair k pair
n n n n n k n

n
n k +1
S 2 =   −   +   −   + ... = ∑ =
  i ∑ k 2 ( −1)
1  3 5 = 7 k
k 1= k 1  
k impair k impair
Corrección: Primeramente, podemos calcular (1 + i ) con ayuda del binomio de Newton :

n
n
n n
n n
n k n
n k n
n k +1
i) ∑  =
(1 += ∑  k  ik + ∑ ∑  ( ) ∑ k 2 ( )
n k
i =
  i −1 2 +i −1
=k 1= k
k 1 = k 1     k
= k 1  k = k 1  
k pair k impair k pair k impair
Tenemos entonces (1 + i ) =S1 + iS2 .

n
Pero podemos también calcular (1 + i ) con ayuda de la forma exponencial:

n
n
 i 
π π
 π  π
( 2 )= ( 2) ( 2)
n in n n
(1=
+ i )  2e=
n
4
 e 4
cos  n  + i sen  n 
   4  4
 π  π
2 ) cos  n  et S ( )
(=
n n
Deducimos que : S1
= 2 2 sen  n  .
 4  4

Capítulo 6
COMPLEMENTOS DE TRIGONOMETRÍA
En este capítulo, a y b designan dos reales.
1- Formula de adición
• cos(a+b) = cosa.cosb - sena.senb

• cos(a-b) = cosa.cosb + sena.senb
• sen(a+b) = sena.cosb + cosa.senb
• sen(a-b) = sena.cosb - cosa.senb
• cos(2a) = cos²a – sen²a= 2cos²a – 1 = 1 – 2sen²a
• sen(2a) = 2sena.cosa
tan a + tanb
• tan(a+b) = cuando los dos miembros existen.
1 - tana.tanb
tan a - tanb
• tan(a-b) = cuando los dos miembros existen.
1 + tana.tanb
2 tan a
• tan(2a) = cuando los dos miembros existen.
1 - tan²a
2- Transformación de producto en suma
1
• cosa.cosb =
2
( cos ( a + b ) + cos ( a − b ) )
1
• sena.senb = - ( cos ( a + b ) − cos ( a − b ) )
2
1
• sena.cosb = ( s e n ( a + b ) + s e n ( a − b ) )
2
1
• cosa.senb = ( s e n ( a + b ) − s e n ( a − b ) )
2
3- Transformación de suma en producto
Sean "p" y "q" dos reales.

p+q p−q
• cosp + cosq = 2 cos .cos
2 2

p+q p−q
• cosp – cosq = -2 s e n .s e n
2 2
p+q p−q
• senp + senq = 2 s e n .cos
2 2
p+q p−q
• senp – senq = 2 cos .s e n
2 2
Ver la ficha de ejercicio.
4- Resolución de la ecuación acos x + bsen x = c
con a, b, c tres reales, "a" y "b" que no son simultáneamente nulos.

Llevamo la ecuación a una ecuación de tipo: cos(x-φ)=cos(θ) dividiendo la ecuación inicial por
a² + b² .
Ver la ficha de ejercicio.
θ
5- Expresión de cos θ, sen θ, tan θ en función de t=tan  
2  
θ
Sea θ un real, tal que tan   existe.
2
1 − t²
• cos θ =
1 + t²
2t
• sen θ =
1 + t²
2t
• tan θ = cuando los dos miembros existen.
1 − t²

EJERCICIOS
Conversión de sumas en productos
El objetivo de esta ficha es transformar en productos sumas como cos p + cos q, sen p + sen q,
..., y aplicar los resultados obtenidos a la resolución de ecuaciones trigonométricas.
Las fórmulas
1. Con los números complejos

"p" y "q" son dos reales cualquiera, cos p + cos q es la parte real de eip+eiq y sen p + sen q es la
parte imaginaria de eip+eiq.
a) Mostrar que:
p+q p−q p+q p−q
cosp+cosq=2cos cos y senp+senq=2sen cos
2 2 2 2
p+q ip iq
Indicación: Poner como factor de ei 2 en e +e .
b) Deducir las fórmulas:
p+q p−q p−q p+q
cosp - cosq= -2sen sen y senp - senq=2sen cos
2 2 2 2
2. Utilizando las fórmulas ya establecidas

a) A partir de las fórmulas que dan cos (a + b) y cos (a - b), comprobar que:
cos (a + b) + cos (a - b) = 2 cos a cos b.
Luego poner a +b=p y a-b=q, luego encontrar la fórmula que da cosp + cosq.
b) Encontrar así mismo la fórmula que da sen p + sen q.
Aplicaciones a la resolución de ecuaciones
Resolver cada una de las siguientes ecuaciones:

a) cos 3x - cos 5x = sen 6x + sen 2x
b) senx + sen 2x + sen 3x = 0
c) cos 5x + 2 cos 3x + 3 cos x = 0
Indicación: b) Transformar sen x + sen 3x en un producto.
Respuestas sin simplificar:

kπ π 2kπ π
a- cos 3x - cos 5x = sen 6x + sen 2x ⇔ x = "o" x = + "o" x = - + 2kπ
4 6 3 2
con k ∈ .
kπ 2π 2π
b- senx + sen 2x + sen 3x = 0 ⇔ x = "o" u x = + 2kπ "o" x = - + 2kπ
2 3 3
con k ∈ .
π kπ π π
c- cos 5x + 2 cos 3x + 3 cos x = 0 ⇔ x = + "o" x = + kπ "o" x = ± +
4 2 2 3
2π
2kπ "o" x = ± + 2kπ con k ∈ .
3

Transformación de a cos θ + b sen θ
Numerosos problemas, en particular en Física, conducen a una ecuación acosθ+bsenθ =

c, en donde la incógnita es el número θ. En general, para resolver tal ecuación, se le escribe
con la forma r cos (θ-ϕ) = c, siendo " r" y "ϕ" conocidos, se sabe entonces encontrar θ-ϕ, así
como θ.
Vamos a ver cómo se puede operar para obtener la expresión r cos (θ-ϕ) = c
Transformación de a cosθ + b senθ (a, b, θ reales)
1. Utilizando los números complejos

El método que sigue se apoya en la observación siguiente: a cosθ + b senθ es la parte
real del complejo eiθ (a - ib).
a- Se supone que ambos "a" y "b" no son nulos.
Se plantea r=|a+ ib| y ϕ = arg(a + ib). Mostrar entonces que para todo real θ:
a cosθ + b senθ= r cos (θ-ϕ)
b- Aplicación: Utilizando la pregunta a, transformar cada una de las expresiones:
cosθ + 3 senθ ; cos3θ+sen3θ
2. Como un escalar
El método que sigue se apoya sobre la observación siguiente: a cosθ + b senθ es de la
forma xx’+yy’, y puede pues expresarse como un producto escalar. En una referencia
 
( )
ortonormal directa O, OI, OJ , consideremos los puntos M (cosθ; senθ) y N (a; b).
 
a- Comprobar que a cosθ + b senθ = OM.ON .
( )

 
b- Plantear r=ON y ϕ= OI, ON .

Deducir entonces de a que a cosθ + b senθ= r cos (θ-ϕ).
b
3. Planteando tanϕ= , a ≠ 0
a
a- Comprobar entonces que siempre existe un número ϕ real tal que tanϕ= b .
a
 b 
b-Escribiendo a cosθ + b senθ=a  cos θ + s e n θ  , comprobar que:
 a 
a cosθ + b senθ = a cos(θ-ϕ)
cosϕ
Resolución de ecuaciones a cos x + b sen x = c
1. Mostrar que la ecuación a cos x + b sen x = c no tiene solución cuando c2 > a2 + b2.
2. Resolver cada una de las siguientes ecuaciones:
a) cosx+ 3 senx= 1
b) 2cosx-3senx= -6
c) cos 3x + sen3x=1
d) 3 cos2 x + 2senxcosx - 3 sen2 x= 2 .
Respuestas sin simplificar:

 π 1 2π
a- cosx+ 3 senx= 1 ⇔ cos  x −  = ⇔ x = + 2kπ o bien x = 2kπ con k ∈ .
 3 2 3
b- 2cosx-3senx= -6 No hay solución
π 2kπ 2kπ
c- cos 3x + sen3x=1 ⇔ x = + o x= con k ∈ .
6 3 3
5π π
d- 3 cos2 x + 2senxcosx - 3 sen2 x= 2 ⇔ x = + kπ o bien x = - + kπ
24 24
con k ∈ .

Algunos ejercicios corregidos :
Ejercicio 1. Resolver en  las siguientes ecuaciones:

a- sen ( 3x ) = cos ( 2x )
b- 4 cos 2 ( x ) + 4 cos ( x ) − 3 =0
Corrección : a- sen ( 3x ) = cos ( 2x )

π 
⇔ sen ( 3x ) =sen  − 2x 
2 
π π 
⇔ 3x ≡ − 2x [ 2π] ou 3x ≡ π −  − 2x  [ 2π]
2 2 
π π
⇔ 5x ≡ [ 2π] ou 3x ≡ π − + 2x [ 2π]
2 2
π  2π  π
⇔ x ≡   ou x ≡ [ 2π]
10  5  2
π  2π 
⇔x≡
10  5 
b- 4 cos ² ( x ) + 4 cos ( x ) − 3 =0.
Anotameos evidentemente X = cos ( x ) , y obtenemos 4X² + 4X − 3 =0.
1 3
Las soluciones de esta ecuación son X = o X= − .
2 2
1 3
Este nos lleva a resolver: cos ( x ) = o cos ( x ) = − .
2 2
Es claro que la segunda ecuación no tiene solución.
1 π π π
Por otro lado, cos ( x )= ⇔ cos ( x )= cos   ⇔ x ≡ [ 2π] o x ≡ − [ 2π] .
2 3 3 3
π π
Entonces las soluciones de la ecuación inicial son: x ≡ [ 2π] o x ≡ − [ 2π] .
3 3
Ejercicio 2.
 2π   4π 
1- Demostrar que: cos ( x ) + cos  x +  + cos  x + =0.
 3   3 
π  π 
2- Simplificar: sen  − x  + cos  − x  .
6  3 
Corrección : 1-
*

 2π   4π   2π   2π 
cos ( x ) + cos  x +  + cos  x +  = cos ( x ) + cos ( x ) cos   − sen ( x ) sen  
 3   3   3   3 
 4π   4π 
+ cos ( x ) cos   − sen ( x ) sen  
 3   3 
1 3 1 3
=cos ( x ) − cos ( x ) − sen ( x ) − cos ( x ) + sen ( x )
2 2 2 2
=0
2-
π  π  π π π π
sen  − x  + cos  − x  = sen   cos ( x ) − sen ( x ) cos   + cos   cos ( x ) + sen   sin ( x )
6  3  6 6 3 3
1 3 1 3
= cos ( x ) − sen ( x ) + cos ( x ) + sen ( x ) = cos ( x )
2 2 2 2
Ejercicio 3. Sea x un real diferente de un múltiplo de π. Consideramos la expresión F(x)

definida por :
sen ( 7x )
F(x) = − 2 cos ( 2x ) − 2 cos ( 4x ) − 2 cos ( 6x )
sen ( x )
Mostrarque : F ( x ) = 1 .
Recordamos que 2sen ( a ) cos ( b ) =sen ( a+b ) +sen ( a-b ) .
Corrección :
sen ( 7x ) -2sen ( x ) cos ( 2x ) -2sen ( x ) cos ( 4x ) -2sen ( x ) cos ( 6x )
F(x) =
sen ( x )
sen ( 7x ) -sen ( 3x ) -sen ( -x ) -sen ( 5x ) -sen ( -3x ) -sen ( 7x ) -sen ( -5x )
=
sen ( x )
sen ( 7x ) -sen ( 3x ) +sen ( x ) -sen ( 5x ) +sen ( 3x ) -sen ( 7x ) +sen ( 5x ) s e n ( x )
=1 = =
sen ( x ) se n (x)

Capítulo 7
LOS POLINOMIOS
0- Presentación histórica
Viète François, francés, 1540-1603, es considerado, en Fran-

cia, como creador en el origen del cálculo algébrico "moderno". Escri-
bió todavia en Latín, a la manera de Bombelli, pero utilizando los
símbolos operativos actuales + y – para la suma y la diferencia, here-
dados del alemán Widmann.
En una ecuación, las consonantes (respectivamente las vocales)

son los parámetros conocidos (respectivamente los desconocidos). Uti-
lizó el término actual de "coeficiente" en una ecuación.
Viète resolvió completamente la ecuación de segundo grado
“ax2 + bx = c”. Afirmó poder asimilar los problemas de su época a la
resolución de ecuaciones y emitió, a justo título, la conjectura desde la
cual la trisección del ángulo está ligada a la ecuación de tercer grado
que resolvió en la forma x3+ ax = b cuando a y b son números positivos.
Las raíces negativas de una ecuación son consideradas como falsas pero las raíces
imaginarias ya han sido "inventadas" gracias al genio de Bombelli y Viète será también uno
de los primeros en presentir, seguido por Girard y Descartes, el teorema fundamental de
l’algebra que d'Alembert y después Gauss demostraron.
Observó igualmente, con Harriot, las relaciones, dichas alguna que otra vez de Viète,
existentes entre las soluciones y los coeficientes de una ecuación algébrica :
Estas relaciones serán estudiadas por Girard y Descartes, y por Lagrange y Cauchy,
quienes percibieron sus funciones en la resolución general de ecuaciones algébricas. Pero será
Galois quién mostrará en el siglo 19, por el medio de la teoría (naciente) de grupos termina-
dos, que las ecuaciones de grado superior a 5 no son generalmente solucionables por radicales
(es decir que las soluciones no se pueden expresar por el medio de combinaciones de raices
cuadradas, cúbicas,..., nesimas de coeficientes).
Evariste Galois asiste a la escuela solamente a par-

tir de sus doce años. Entra al Colegio Real Luis El Grande
del cual termina explusado porque él se niega a cantar en
la capilla. Luego de sus estudios secundarios brillantes
pero perturbadores y dos fracasos al ingreso de la Escuela
Politécnica, él entra a la Escuela Normal Superior. A pesar
de su inteligencia, sus profesores no lo toman en serio.
Con un carácter tempestuoso, sus ideas republicanas lo
conducen en prisión de la cual queda libre luego de enfermarse algunos meses más tarde. Eva-
riste Galois tiene entonces veinte años. El se enamora de una « infame coqueta », según sus

palabras, por quien tuvo que aceptar una provocación en duelo donde encontrará la muerte. La
noche anterior a s u muerte, el redacta apresuradamente todos sus descubirmientos. Sólo en
1870 los matemáticos comprenderán la importancia de sus descubrimientos.
En este capítulo,  designará tanto o al cuerpo conmutativo , o como al cuerpo conmutativo


1- Presentación de los polinomios
1- Definición
Nos situamos sobre un cuerpo conmutativo  (para nosotros  o ). Un polinomio

(formal) es definido por el dato de sus coeficientes a 0 , ...,a n elementos de . X siendo una
letra muda, notamos P = a 0 + a 1 X + ... + a n Xn o ∑a X

k ≥0
k
k
, siendo entendido que la suma com-
porta solo un número finito de a k no nulos.

a i Xi es un monomio de grado i.
Distinguimos a veces el polinomio P(X) (que, por construcción, es nulo si y solamente

si todos sus coeficientes son nulos (*)) de la función polinomial asociada :
P : →
n
x  ∑ a k x k =P(x)
k =0
Este es nulo si y solamente si: ∀x ∈ , P(x) = 0.

Por otro lado, podemos emplear X en otras funciones que solo en valores en . X
puede también ser remplazado por ejemplo por una matriz, o por un endomorfismo de un es-
pacio vectorial en  (ver los capítulos de álgebra lineal correspondientes).
Tenemos, evidentemente, la implicación:

P(X) = 0 ⇒ ∀x ∈ K, P(x) = 0
Pero la recíproca está lejos de ser una evidencia. Demostraremos que, mientras  es
igual a  o a , existe una equivalencia ; aquello que permite de confundir polinomio y fun-
ción polinomial. La frase P = 0 guardará, mientras tanto de preferencia, el sentido (*).
Propiedad : 1- Sea P un polinomio con coeficientes en  o en  Entonces, si la función po-

linomial asociada a P es idénticamente nula, P tiene todos sus coeficientes nulos.
2- Sean P y Q dos polinomios en  o en . Entonces, si las funciones polinomia-
les asociadas son iguales (que toman los mismos valores), los dos polinomios son iguales (que
tienen los coeficientes iguales).

Idea de la prueba (recurrencia finita):
1-  contiendo , supondremos que la variable x s ólo toma valores en . Sea P =
∑a X
k ≥0
k
k
tal que ∀x ∈ , P(x) = 0
Entonces, x = 0, obtenemos a 0 = 0.
Entonces ∀x ∈ , a 1 x+...+a n xn=0
∀x ∈ *, a 1 +...+a n xn-1=0.
Ya no podemos tomar x = 0, mientras tanto, podemos tomar el límite mientras x tiende
a 0, lo que da a 1 = 0. etc...
2- Se demuestra aplicando 1- a P-Q.
Notación: [X] es el conjunto de los polinomios con coeficientes en K.

[X], [X], …
Cuidado: No confundir [X] y (X). Este último conjunto es el conjunto de las fracciones
racionales con coeficientes en K que se estudiará en el capítulo siguiente.
Observación: El polinomio nulo es el polinomio donde todos sus coeficientes son nulos. Se
escribe 0 [X] o si no hay ambigüedad 0.
2- Grado y valoración
n
Sea P un elemento de [X] donde P no es nulo y donde P= ∑ a k X k .
k =0
El grado de P es el del entero mayor p tal que a p ≠ 0. Se escribe deg(P).
La valoración de P es el del entero menor p tal que a p ≠ 0. Se escribe val(P).
El polinomio nulo 0 [X] no tiene ni grado, ni valoración.

A veces las convenciones siguientes son utilisadas : deg(0 [X] )=- ∞ y val(0 [X] )=+ ∞ .
Teorema: Dos polinomios son iguales si, y solamente si poseen el mismo grado y los
mismos coeficientes.
2- Adición de polinomios
n1 n2
Definición: Sean P y Q dos polinomios donde P= ∑ a k X y Q= ∑ b k X k . Entonces,
k
k =0 k =0
n3
P+Q= ∑ (a k + b k )X k donde n3 = Max(n1 ,n2 ).
k =0
Propiedad: Sean P y Q dos polinomios que no son nulos de forma que la suma P+Q
no sea nula tampoco. Entonces deg(P+Q) ≤ Max(deg(P),deg(Q)) y
val(P+Q) ≥ Min(val(P),val(Q)).

Propiedad: ([X],+) es un grupo conmutativo.
3- Multiplicación de polinomios
n1 n2
Definición: Sean P y Q dos polinomios, P= ∑ a k X y Q= ∑ b k X k . Entonces
k
k =0 k =0
n1 + n 2 k
P.Q= ∑cX
k =0
k
k
con c k = ∑ a b =∑a b
i + j=k
i j
i =0
i k −i
Propiedad: Sean P y Q dos polinomios que no son nulos. Entonces

deg(P.Q)=deg(P)+deg(Q) y val(P.Q)=val(P)+val(Q).
Propiedad: ([X],+,.) es un anillo conmutativo.
Propiedad: Sean P y Q dos polinomios. P.Q=0 ⇔ P=0 ∨ Q=0 (Integridad).
4- División euclidiana
Teorema y definición : Sean A y B dos polinomios donde B no es nulo. Existe un par
único (Q,R) de polinomios tales que A=BQ+R con R=0 donde deg(R)<deg(B).
A es el dividendo, B el divisor, Q el cociente y R el resto.
Demostración : Para simplificar, tomaremos para esta demostración que el grado del poli-
nomio nulo es - ∞
Demostremos primero la unicidad :
Sea A = BQ + R = BQ' + R' con (deg R < deg B o R=0) y (deg R' < deg B o R’=0).
De B(Q - Q') = R' – R, deducimos deg B + deg(Q - Q') = deg(R' - R).
Como deg(R' - R) ≤ sup(deg R, deg R') < deg B.
De degB + deg(Q - Q') < degB, deducimos deg(Q - Q') = - ∞ ,
entonces que Q - Q' = 0 y luego que R'-R=O.
Demostremos ahora la existencia :
Sea B un polinomio de grado p y de coeficiente dominante b p.
- Si A = 0 o A ≠ 0 con deg A < p, tenemos A = 0.B + A entonces (Q, R) = (0, A) es
solución del problema.
- Supongamos la existencia del cociente y del resto de la división por B de todo poli-
nomio de grado inferior o igual a n y sea A de grado n + 1, de coeficiente dominante a n+l .
a
Sea A l = A - n +1 Xn+l-p B. Tenemos degA l ≤ n ; existe entonces (Q 1 , R l ) tal que :
bp
 a 
A 1 = BQ l + R l , deg R l < deg B de lo cual A =  Q1 + n +1 X n +1− p  B + R l .
 bp 
 
a
R = R l y Q = Q 1 + n +1 Xn+1-p da una solución.
bp
La existencia es entonces establecida por recurrencia para n = degA.

Práctica de la división euclidiana:
Ejemplo : A=X5+X4-X3+X-1, B=X3+X2+2.
A X5 + X4 - X3 +X-1 X3 + X2 + 2
X5+X4 + 2X2
11
2X 2 + X + 1 3X8-3X7+6X6-5X5+8X4-4X3+6X2-5X+
2
6X10-3X9+6X8-X7+5X6+5X5
-6X10-3X9+3X8
-6X9+9X8-X7
+6X9+3X8-3X7
12X8-4X7+5X6
-12X8-6X7+6X6
-10X7+11X6+5X5
+10X7+5X6-5X5
16X6
-16X6 -8X5+8X4
-8X5+8X4
+8X5+4X4-4X3
12X4 -4X3
-12X4 -6X3+6X2
-10X3+6X2
+10X3+5X2-5X
+11X2-5X
11 11
−11X 2 − X +
2 2
21 11
- X+
2 2
2
X
- 1
-X3 - 2X2 + X - 1 Q1 Q2
-X3 - X2 -2
2
- X +X +1
A=B(Q 1 +Q 2 ) + A 2 y deg(A 2 )<deg(B).

El cociente es X2-1, y el resto es –X2+X+1.
Observación : En algunos países de América Latina, el algoritmo de la división euclidiana es

el mismo que el utilizado anteriormente pero sólo la presentación del mismo varía.. Tienen
ustedes aquí a continuación un ejemplo de una tal presentación.
El resultado de esta división es:

6X10-3X9+6X8-X7+5X6+5X5=
 11   21 11 
(2X2+X+1)  3X8 -3X 7 +6X 6 -5X 5 +8X 4 -4X 3 +6X 2 -5X+ +- X +  .
 2   2 2

5- División según las potencias crecientes
Teorema y definición : Sean A y B dos polinomios con val(B)=0 (es decir el término
constante de B que no es nulo).
Sea n un entero natural.
Existe un par único (Q n, R n) de polinomios de manera que:
A=BQ n +Xn+1R n con Q=0 donde deg(Q) ≤ n (1)
Este teorema define la división según las potencias crecientes de A entre B de or-
den n.
Demostración:
1- Demostremos la unicidad.
Si BQ n + Xn+1R n = 0, la condición B(0) ≠ 0 muestra que Xn+1 debe dividir Q n ; como
deg (Q n) ≤ n, esto implica Q n = 0, de lo cual R n =0.
2- Demostremos la existencia.
Tomemos
p q
A= ∑ a k Xk y B =
k =0
∑b X
k =0
k
k
Por hipótesis, b0 ≠ 0.
Razonemos por recurrencia en n. Para n = 0, basta con tomar:
a A − BQ0
Q0 = 0 , R0 =
b0 X
Supongamos determinados Q n y R n verificando (1). Ya que B(0) ≠ 0, existe entonces una
R (0)
constante λ n+1 = n y un polinomio S tales que:
B(0)
R n = λ n+1 B+XS
La relación (1) implica entonces :
A=BQ n + λ n+1 Xn+1B+Xn+2R n S.
Basta entonces con tomar Q n+1 = Q n + λ n+1 Xn+1 y R n+1 = R n S para obtener (1) al orden n + 1.
La disposición práctica de un cálculo de división sigue paso a paso el siguiente razonamiento

constructivo.
Por ejemplo, he aquí la división de A = 1 + 2 X + X3 por B= 1 +X+2X2 al orden 3 :
1 + 2X + X3 1 + X + 2X2
X – 2X2 + X3 1 + X - 3X2 + 2X3
- 3X2 – X3
2X3 + 6X4
4X4 – 4X5
El cociente al orden 3 es 1 + X - 3X2 + 2X3, el resto es 4(1 - X) X4.

Podemos entonces escribir : A=B(1 + X - 3X2 + 2X3) + 4(1 - X) X4

6- Raíces de un polinomio
Definición: Sea "P" un elemento de [X] y "a" un elemento de . Decir que "a" es
una raíz de P significa P(a)=0.
Teorema. Sea "P" un elemento de [X] y "a" un elemento de . Se tiene que "a" es
una raíz de P si y solamente si P es divisible entre (X-a).
Definición: Sea "P" un elemento de [X] y "a" es una raíz de P. El orden de multi-
plicidad de a es del mayor entero p tal que (X-a)p divide P.
Teorema. Sea P un elemento de [X] de grado n. P admite como máximo n raíces,

cada raíz se cuénta con su orden de multiplicidad.
7- Derivadas sucesivas de un polinomio

n
Definición: Sea P un elemento de [X], P= ∑ a k X k con a n que no es nula (deg(P)=n).
k =0
n n
Se da P’= ∑ ka k X k −1 , P’’= ∑ k(k − 1)a k X k − 2 ,…
k =1 k =2
n
Teorema. Sea P un elemento de [X], P= ∑ a k X k con a n que no es nula (deg(P)=n).
k =0
Sea "j" un entero comprendido entre "0" y "n". Entonces, deg(P(j))=n-j y P (j)(0)=j !a j .
8- Formula de Taylor
Teorema: Sea P un elemento de [X] tal que deg(P)=n y que "a" sea un elemento de
n
X k (k )
. Entonces P(X+a)= ∑
k = 0 k!
P (a) .
n
(X − a) k (k )
Variante: P(X)= ∑
k =0 k!
P (a) .
9- Criterio de multiplicidad de una raíz
Teorema: Sea P un elemento de [X] donde P no es nulo y que además "a" sea un
elemento de K.
Se tiene la equivalencia entre "i"- y "ii"-
i- "a" es una raíz de P de multiplicidad k
ii- P(a)=P’(a)=…=P(k-1)(a)=0 y t P(k)(a) ≠ 0.
Ejemplo: Raíces de P= X 5 + 3X 4 + 4 X 3 + 4 X 2 + 3X + 1 .

10- Factorización en productos de factores irreductibles en [X]
Teorema de d’Alembert: Sea P un elemento de [X] que no es nulo, tal que

deg(P)=n. Entonces P admite exactamente n raíces, cada raíz se cuenta considerando su orden
de multiplicidad. Se dice que  es algebraicamente cerrado.
Conjeturado por Albert De Girard en 1629, este resultado no será demostrado más
que por Gauss en 1799, tras un intento casi conseguido por d’Alembert, pero también por
Euler y Lagrange. A este teorema, capital para el Algebra, la Arithmética y el Análisis, se le
llama teorema fundamental del Algebra, menos en Francia, donde se le relaciona con el nom-
bre de d'Alembert.
Jean le Rond d'Alembert (francés, 1717-1783) : Hijo natural

de un comisario en artillería, abandonado sobre las escaleras de una
capilla parisina, el futuro matemático es acogido por un vidriero quien
recibirá una pensión por la educación del niño que estudiará brillante-
ment el derecho, la medicina y las matemáticas.
Co fundador, , en 1751, junto con Diderot, de la Enclipedia,
llamada también «Diccionario razonado de las Ciencias, las Artes y los
Oficios », síntesis de los conocimientos filosóficos, literarios y científi-
cos de ese siglo fértil, llamado « siglo de las luces ».
n
Consecuencia: Sea P un elemento de [X] que no es nulo tal que deg(P)=n., P= ∑ a k X k .
k =0
n
Sean (x k ) k=1 a n las n raíces de P (distintas o no). P puede escribirse: P= a n ∏ (X − x k ) .
k =1
Consecuencia: La factorización de P en productos de factores irreductibles en [X].

Todo polinomio P de [X] se descompone de la forma :
p
P = a ∏ ( X − αi )
µi
i =1
Donde los α1 ,…, αp son las diferentes raíces de P de multiplicidades µ 1 ,…, µ p y a es el co-
eficiente del término de mayor grado de P.
p
Tenemos : ∑µ
i =1
i = deg(P).
11- Factorización en productos de factores irreductibles en [X]
Teorema: Sea P un elemento de [X]. Si z 0 es una raíz compleja de P de multiplici-

dad α, entonces z 0 es también una raíz de P con la misma multiplicidad α.

Consecuencia: Factorización de P en productos de factores irreductibles en [X].
Todo polinomio P de [X] se descompone en la forma :
p q
∏(X + b jX + c j )
νj
P = a ∏ ( X − αi )
µi 2
=i 1 =j 1
donde αi , 1 ≤ i ≤ p, son las diferente raíces reales de P de multiplicidades µ i , los b j y c j ,

1 ≤ j ≤ q, son reales tales que b j 2−4c j < 0 y a es el coeficiente del término de mayor grado de
P.
p q
Tenemos : ∑ µi +2 ∑ ν j =deg(P).
i =1 j=1
12- Relaciones entre coeficientes y raíces

n
Sea P un elemento de [X] que no es nulo tal que deg(P)=n, P= ∑ a k X k . Sea (xj ) j=1 a n
k =0
las n raíces de P (distintas o no). Entonces, para k entero incluido entre "1" y "n":
a
∑
i1 <...<i k
x i1 ...x ik = (−1) k n − k
an
n
a n −1 n
a0
En particular , ∑ xi = −
i =1 an
y ∏x
i =1
i = (−1) n
an

COMPLEMENTOS DE CURSO
ECUACIONES DE TERCER Y CUARTO GRADO
Histórico :
Los números complejos, tal como los utilisamos hoy en día, datan del siglo XIX. Eran
por lo tanto conocidos y utilizados desde hace muchos siglos bajo el nombre de números ima-
ginarios (término que ha quedado en la expresión "parte imaginaria"). Ellos aparecieron mien-
tra se intentaba resolver las ecuaciónes de 3er grado.
El primero que resolvió las ecuaciónes de 3er grado de tipo x3+ px = q (p > 0, q > 0)
parece que fue Scipione Del Ferro (1465 – 1526), profesor en la Universidad de Bologne. El
no publica su descubrimiento pero la transmite a su alumno Antonio Maria Fior. En 1531,
Tartaglia (1500 – 1557), ya sea por una luz de indiscreción, ya sea por su propia invención,
aprende también a resolver las ecuaciónes de 3er grado. Creyendo a una impostura, Fior lanza
un desafio público en Tartaglia.
Al final del plazo otorgado, Tartaglia había resolvido todas las ecuaciónes de Fior,
mientras que él había resolvido solo una ecuación de Tartaglia. La superioridad de Tartaglia
proviene del hecho que este último sabía resolver las ecuaciónes de tipo x3+ px2= q, cosa que
Fio no sabía hacer. En 1539, Tartaglia acepta revelar su secreto a Cardan (1501 – 1576) que
los publica poco después, a pesar de la ira de Tartaglia. Un alumno de Cardan, Ludovico Fe-
rrari (1522 – 1565), viene a resolver las ecuaciones de 4to grado.
Formulas do Cardan
Efectuando el cambio de incógnita x= X+ a , la ecuación se transforma en
3
«x3+px+q=0».
Las tres raíces de esta ecuación son:
1 1 1
x1 = (u+v) ; x 2 = (ju + j²v) ; x 3 = (j²u + jv)
3 3 3
con u = − 27 q+3i 3 −4p3−27q2 y con v = 3 − 27 q −3i 3 − 4p3 − 27q 2

3
2 2 2 2
conviniendo en escribir a como una de las raíces m-ésimas del número complejo a.
m
Ejercicio: Resolver la ecuación: x3 + 12x – 12 = 0.

Ustedes darán x=u+v, y luego la transformarán en una ecuación de segundo grado.

Ejercicio 1. Efectuar la división euclidiana de X 5 + 2X 3 − 3X − 2 por X 3 + X + 1 en [X].

Misma pregunta para X 5 + X 2 − 2 por X 3 − X 2 − X − 2 en [X].
Ejercicio 2. Descomponer en factores irreductibles en [X] y en [X] los siguientes polino-

mios:
P X3 + 1
1- = 2- Q = X 5 − X 4 − 8X 2 + 8X
Ejercicio 3. Consideramos el polinomio P = 2X 3 − 6X + 4 . Calcular P’ y verificar que una de

las raíces de P’ es también una raíz de P. Deducir la factorización de P en [X].

Ejercicio 1. X 5 + 2X 3 − 3X − 2= (X 2 + 1)(X 3 + X + 1) − X 2 − 4X − 3
X 5 + X 2 − 2= (X 2 + X + 2)(X 3 − X 2 − X − 2) + 6X 2 + 4X + 2
 1 + 3i  1 − 3i 
Ejercicio 2. 1- P = (X + 1)(X² − X + 1) en [X] y P =(X − 1)  X −  X −  en
 2  2 
[X].
2- Q = X(X − 1)(X − 2) ( X 2 + 2X + 4 ) en [X] y
( )(
Q X(X − 1)(X − 2) X + 1 − i 3 X+1+i 3 en [X].
= )
Ejercicio 3.=P’ 6X² − 6 , 1 y -1 son raíces de P’, verificamos que 1 es una raíz de P, es en-
tonces una raíz doble , entonces P se factoriza por (X − 1)² , tenemos P =2(X − 1)²(X + 2) .

EJERCICIOS
Ejercicio 1.
1. Efectuar la división euclidiana de A =X 4 + 2X 3 + 4X 2 + 2 por B = X 2 + (1 − i ) X + (1 + i ) .
2. Efectuar la división sugún las potencias crecientes al orden 3 de C = X 4 − 5X + 3 por

D= 2X 2 − X + 1 .
3. Determinar a y b tales que E = X 2 − aX + 1 divida F = X 4 − X + b .
Ejercicio 2. Sean los polinomios A= X 5 + X 4 + αX 3 + βX 2 + 5X − 2 y B=X3-2X+1. Efectuar

la división división euclidiana de A por B y determinar α y β para que B divida A.
Ejercicio 3. Sean S y T dos polinomios con coeficientes reales definidos por :

S X 7 + αX 6 + βX 5 − X 4 + 5X 3 − 2X 2
=
T= X 4 − 2 X 2 + X
Determinar dos polynomios A y B de [X] que respondan a : S=AT+X5B.
Deducir α y β para que T divida S.
Exercice 4.
1. Sea P ∈[X]. Sean a y b dos números complejos diferentes. Comprobar la siguiente equi-
valencia : P es divisible por ( X − a )( X − b ) ( a ) P=
⇔ P= (b) 0
3n + 2 3k +1
2. Mostrar que el polinomio X +X + X 3p es divisible por X 2 + X + 1 .
3. Para que valores del entero n P = ( X + 1) − X n − 1 es divisible por X 2 + X + 1 ?
n
Ejercicio 5. La formula de Taylor aplicada al orden n sobre un polinomio de grado n, produ-

ce un desarrollo de este polinomio según las potencias de (x - a) donde a es un real arbitrario.
Dar la expresión de este desarrollo.
Aplicación: Ordenar el polinomio P = X 3 - 9 X 2 + 7X + 15 según las potencias de (X-2).
Ejercicio 6. Explicar si hay unicidad para un polinomio P0 de [X] tal que P0 (1) = 3 ; P0 '(1)
= 4 ; P0 "(1) = 5 ; para todo entero k superior o igual a 3, P0(k ) (1) = 0.
Determinar entonces todos los polinomios P de [X] tales que P(1) = 3 ; P'(1) = 4 ; P"(1) = 5
Ejercicio 7. Polinomio de interpolación de Lagrange (Francés, 1736-1813):

Sea  un cuerpo conmutativo( =  ou ).
• Sean α1 , α 2 ,..., α n elementos de  dos a dos diferentes
• Sean β1 , β2 ,..., βn elementos de .

Buscamos un polinomio de grado ≤ n-1 tal que L ( α i ) =βi para 1 ≤ i ≤ n .
Consideramos el polinomio L definido por :
n
X − α1 X − α 2 X − α k −1 X − α k +1 X − αn
L (X) = ∑β
k =1
k × ×
α k − α1 α k − α 2
× ... × ×
α k − α k −1 α k − α k +1
× ... ×
αk − αn
Verificar que este polinomio cerrosponde con el problema propuesto.
L recibe el nombre de polinomio de interpolación de Lagrange.
Sea C el gráfico de x  sen(x) con x como elemento de [-π;π]. Determinar una función poli-
nomial P tal que el gráfico de P pase por los puntos de C con abscisas -π; -π /2; 0; π/2; π , P
siendo a lo sumo de grado 4.
Ejercicio 8. ¿Existen polinomios P de [X] de grado 5 tales que

[P + 2] sea divisible entre (X - 1)3
 3
[P - 2] sea divisible entre (X + 1)
Determinarlos, en caso afirmativo.
Ejercicio 9. Sea n ∈ *. Tenemos Pλ ( X=

) ( X − 2 ) − ( 2X − 3) + λ ( X n − 1) .
n n
1. Encontrar el conjunto de valores de λ ∈  por los cuales Pλ admite al 1 como raíz d' orden
al menos 2.
2. Por los valores de λ encontrados , cuál es el orden de multiplicidad de esta raíz ?
Ejercicio 10. Sea A =X 5 + aX 3 + 5X 2 + b , donde a y b son reales. Encontrar a y b para que A

admita una raíz de orden por lo menos 3 y factorisar A en este caso.
Ejercicio 11. Factorisar cada uno del polinomios siguientes en producto de polinomios irre-
ductibles en [X], y en [X] : P1 = X 4 + 1, P2 = X 5 − 1, P3 = X 4 + X 2 + 1 .
Ejercicio 12. Sea P el polinomio P ( X ) = X 4 − X 3 + 2X 2 − 2X + 4 .

Verificar que P (1 + i ) =
0 y deducir una factorisación de P en productos de factores irreducti-
bles en [X].
Ejercicio 13. Descomponer en productos de factores irreductibles los polinomios siguientes:

a- X 8 + X 4 + 1 en [X].
b- 2 X 3 − (5 + 6i) X 2 + 9iX + 1 − 3i en [X] sabiendo que admite una raíz real
c- X 6 − 3X 5 + X 4 + 4 X 2 − 12 X + 4 sobre [X] sabiendo que admite dos raíces reales
con una inversa de la otra
d- X 5 + 3X 4 + 4 X 3 + 4 X 2 + 3X + 1 en [X]
Ejercicio 14. Sea P = ( X − 2) 2 n + ( X − 1) n − 2 donde n es un entero superior o igual a 3. De-

terminar el resto de la división de P entre (X - 1).(X - 2), luego entre (X - 1)².

Ejercicio 15. Sea n un entero natural que no es nulo. Se da Pn =(1+X)n −(1−X)n.
1- Mostrar que Pn es divisible entre X, y determinar, según la paridad de n, el grado de
Pn .
2- Determinar los ceros de Pn en  (ustedes darán el resultado final en forma algebrai-
ca) y contar cuántos ceros distintos encuentran
3- Factorizar Pn en [X] luego en [X].
Ejercicio 16. Sea el polinomio P=(X²-1)n-X2n.

1. Calcular la suma y el producto de las raices de P en .
2. Determinar todas las raices de P en .
Ejercicio 17. Se considera a la familia de polinomios de [X] definida por recurrencia por:
Pn (X) = (1 + nX).Pn −1 (X) + X.(1 − X).Pn −1 ' (X) ∀n ∈ * et P 0 (X)=1
a- Calcular P1 , P2 , P3.
b- ¿Cuál es el término de más alto grado de Pn ?
c- Calcular Pn (1) y Pn (0).
1
d- Mostrar que para todo complejo z que no es nulo, Pn (z)= z n .Pn   . Deducir que las
z
raíces de P n(X) son opuestas dos a dos. Dar una raíz común a todos los Pn para n impar.

Ejercicio 18.
1- Efectuar la división euclidiana de X4 + 3X2 + X + 2 par X2 + 3X + 1.
2- Efectuar la división según las potencias crecientes al orden 3 de X2 + X + 1 por 3X2
+ 2X + 1.
Corrección : 1-
X 4 + 3X 2 + X + 2 X 2 + 3X + 1
− ( X 4 + 3X 3 + X 2 ) X 2 − 3X + 11
−3X 3 + 2X 2 + X + 2
− ( −3X 3 − 9X 2 − 3X )
11X 2 + 4X + 2
− (11X 2 + 33X + 11)
−29X − 9
Tenemos entonces: X + 3X + X + 2= ( X 2 + 3X + 1)( X 2 − 3X + 11) − 29X − 9
4 2
2- Para efectuar una división según las potencias crecientes, escribimos los polinomios en el
orden creciente de potencias, y despreciamos todos los términos de grado más grande que 3.
1 + X + X2 1 + 2X + 3X 2
− (1 + 2X + 3X 2 ) 1− X
−X − 2X 2
− ( −X − 2X 2 )
0
Tenemos entonces : 1 + X + X 2 = (1 + 2X + 3X 2 ) (1 − X ) + 0X 3 .
 x+y+z = −1 + i

Ejercicio 19. Resolver en  el siguiente sistema:  xy + xz + yz = −2 − i .
 xyz = −2i

Corrección : El problema es determinar las raíces del siguiente polinomio:
P ( X )= X 3 − ( −1 + i ) X 2 + ( −2 − i ) X + 2i
Observemos que 1 es una raíz evidente, podemos entonces poner ( X − 1) en factor:
P ( X ) = ( X − 1) ( X 2 + ( 2 − i ) X − 2i ) .
Nos queda entonces determinar las raíces de Q = X 2 + ( 2 − i ) X − 2i .
Tenemos ∆ =( 2 − i ) − 4 × ( −2i ) =4 − 1 − 4i + 8i =4 + 4i + i 2 =( 2 + i ) .
2 2
− (2 − i) + (2 + i) − (2 − i) − (2 + i)
Las raíces de Q son etonces x1 = = i et x 2 = = −2 .
2 2

 x+y+z = 1+ i

Finalmente, las soluciones del sistema  xy + xz + yz = −2 − i son 1, − 2, et i .
 xyz = −2i

Ejercicio 20. Sea P = (X + 1)7 – X7 –1.

1- Determinar el grado y la valuación de P.
2- Mostrar que P admite dos raíces evidentes, las cuales precisaremos el orden de mul-
tiplicidad.
3- Probar que j es una raíz doble de P.
4- Deducir la factorización de P en [X] luego en [X].
7
7  6
7 
Corrección : 1- Tenemos ( X + 1) = ∑   X k = X 7 + ∑   X k + 1 .
7
= k 0=k k 1k
6
7 
Entonces P= ( X + 1) − X 7 − 1= ∑   X k .
7
k =1  k 
Es claro que
= deg ( P ) 6=
et val ( P ) 1 .
2- Es fácil verificar que 0 y -1 son dos raíces de P.

Para determinar el orden de multiplicidad de esas dos raíces, calculamos la derivada de P :
P′ = 7 ( X + 1) − 7X 6
6
0 y -1 no son raíces de P′ entonces el orden de multiplicidad de esas raíces es 1.
3- P ( j) =( j + 1) − j7 − 1 =( − j2 ) − j − 1 =− j2 − j − 1 =− ( j2 + j + 1) =0 .
7 7
Por otro lado, P′ ( j) = 7 ( j + 1) − 7 j6 = 7 ( − j2 ) − 7 = 7 − 7 = 0 .

6 6
Deducimos que j es una raíz doble de P.
4- P es un polinomio de [X], entonces necesariamente para toda raíz α ∈  con orden de

multiplicidad k, la conjugada α es también una raíz de P de orden de multiplicidad k. Así j es
una raíz doble de P.
( )
2
Con todo lo anterior, podemos poner X ( X + 1)( X − j) X − j
2
en factor en P.
( )
2
Como P tiene grado 6, su factorización en [X] es: αX ( X + 1)( X − j) X − j
2
avec α ∈ 
6
7 
Con la ayuda de la siguiente escritura P = ∑   X k , es fácil darse cuenta por identificación
k =1  k 
que α =7 .
( )
2
Concluímos que P = 7X ( X + 1)( X − j) X − j en [X],
2
Para obtener la factorización de P en [X]., hay que reagrupar las raíces complejas ( no rela-
es) conjugadas :

( ) ( ( ))
2 2
P 7X ( X + 1)( X − j) X − j = 7X ( X − 1) ( X − j) X − j
2
=
2
  2π  
= 7X ( X + 1)  X 2 − 2 cos   X + 1 .
  3  
Xk n
∑
Ejercicio 21. Sea n un entero superior (o igual) a 2 y P =
k = 0 k!
.
Mostrar razonando por el absurdo que P no tiene raíz múltiple.
Corrección : Supongamos que P tiene una raíz múltiple (al menos doble). La anotamos α .
Como α es al menos una raíz doble, es también una raíz de la derivada.
X2 X n −1 Xn
Es fácil ver que : P′ =1 + X + + ... + ′
, lo que quiere decir que P= P + .
2! ( n − 1)! n!
αn
Reemplacemos X por α en la igualdad anterior, obtenemos P ( α )= P′ ( α ) + .
n!
αn
( α ) 0 et P=
Como por hipótesis P= ′ ( α ) 0 , entonce esto implica que = 0 ⇒ α= 0 .
n!
Pero P ( 0 ) = 1 entonces 0 no es una raíz de P, lo que contradice nuestra hipótesis.
Concluimos que P no tiene una raíz múltiple.
Ejercicio 22. 1- Encontrar las raíces del polinomio Q = X3 + X2 + X + 1.

2- Mostar que Q divide P = X59 + X50 + X41 + X20.
Corrección : 1- Las raíces de Q son las raíces cuarta de la unidad diferente de 1.

kπ
i
Particularmente, tenemos Q
= ( X − ω1 )( X − ω2 )( X − ω3 ) con ωk = e 2 .
2- Como los ωk pour k ∈ {1, 2,3} son distintos dos a dos, podemos mostrar que Q divide P
si y solamnete si ∀k ∈ {1, 2,3} P ( ωk ) =0 .
Verifiquemos entonces que ∀k ∈ {1, 2,3} P ( ωk ) =0 .
59 50  41  20 π   π
 i kπ   i kπ   i kπ   i kπ  ik  29 π+  ik  20 π+ 
P (=
ωk )  e 2  +  e 2  +  e 2  +  e 2=
ik ( 25 π )
+e ( )
ik 10 π
 e  2
+ e + e  2
       
3π π
ik ik
ikπ
=e + e + e + 1 =−i − 1 + i + 1 =0.
2 2
De donde obtenemos el resultado.
Ejercicio 23.
1- Sea α ∈ . Calcular cos ( 7α ) en función de cos α.
2- Sea P = 64X3 – 112X2 + 56X – 7.
 π
a- Encontrar las raíces de P bajo la forma cos²α, donde α ∈ 0,  .
 2
b- Factorizar P en [X].
Corrección : 1- Para desarrollar cos ( 7α ) en función de cos ( α ) , pasamos por los complejos:

cos
= ( ei7α ) Re (=
( 7α ) Re= e iα ) ( ) (
Re ( cos ( α ) + isen ( α ) )
7 7
)
Para calcular ( cos ( α ) + isen ( α ) ) , utilizamos la fórmula del binomio y observamos que los
7
únicos términos reales sont aquellos para los cuales la potencia de ( i sen ( α ) ) es par.
Enseguida, reemplazamos los senos con exponentes par por los cosenos.
( 7
) 7
 2
2 7
Re ( cos ( α ) +i sen ( α ) ) =cos 7 ( α ) +   cos5 ( α ) ( isen ( α ) ) +   cos3 ( α ) ( i sen ( α ) )
 4
4
7
+   cos ( α ) ( i sen ( α ) )
6
6
=cos 7 ( α ) +21cos5 ( α ) ( -sen 2 ( α ) ) +35cos3 ( α ) sen 4 ( α )
+7cos ( α ) ( -sen 6 ( α ) )
=cos 7 ( α ) -21cos5 ( α ) (1-cos 2 ( α ) ) +35cos3 ( α ) (1-cos 2 ( α ) )

2
-7cos ( α ) (1-cos 2 ( α ) )
3
=cos 7 ( α ) -21cos5 ( α ) +21cos 7 ( α ) +35cos3 ( α ) (1-2cos 2 ( α ) +cos 4 ( α ) )

-7cos ( α ) (1-3cos 2 ( α ) +3cos 4 ( α ) -cos 6 ( α ) )
=22cos 7 ( α ) -21cos5 ( α ) +35cos3 ( α ) -70cos5 ( α ) +35cos 7 ( α ) -7cos ( α )
+21cos3 ( α ) -21cos5 ( α ) +7cos 7 ( α )
=64cos 7 ( α ) -112cos5 ( α ) +56cos3 ( α ) -7cos ( α )
= ( 64cos 6 ( α ) -112cos 4 ( α ) +56cos 2 ( α ) -7 ) ×cos ( α )
( 7α ) 64 cos7 ( α ) − 112 cos5 ( α ) + 56 cos3 ( α ) − 7 cos ( α )
De donde: cos=
2- a- P ( cos 2=
( α ) ) 64 cos6 ( α ) − 112 cos 4 ( α ) + 56 cos 2 ( α ) − 7 .
 π
Como α ∈ 0,  , tenemos cos ( α ) ≠ 0 .
 2
cos ( 7α )
Así, de acuerdo con lo anterior, P ( cos 2 ( α ) ) = .
cos ( α )
cos ( 7α ) π π π
Entonces P ( cos 2 ( α ) ) = 0 ⇔ = 0 ⇔ cos ( 7α ) = 0 ⇔ 7α ≡ [ π] ⇔ α ≡   .
cos ( α ) 2 14  7 
 π π 3π 5π
Como α ∈ 0,  , las únicas posibilidades para α son , , .
 2 14 14 14
2-b- De acuerdo con lo que precede, tenemos (al menos) tres raíces distintas de P :
π  3π   5π 
cos 2   , cos 2   , cos 2  
 14   14   14 
Siendo P un polinomio de grado 3, deducimos que :
  π    3π    5π  
P= 64  X − cos 2    X − cos 2    X − cos 2   
  14    14    14  

Capítulo 8
LAS FRACCIONES RACIONALES
0- Preliminar
X8 + 3X 7 + 2X 6 + X 5 + 6X 4 + 6X 3 − 6X 2 − 6X − 3
Consideramos la fracción F = .
X 5 + 3X 4 + 2X 3 − 2X 2 − 3X − 1
a- Efectuando la división (Euclidiana) entre el numerador y el denominador,
X 3 + 3X
demostrar que: F = X 3 + 3 + .
(X − 1)(X + 1) 4
x 3 + 3x
b- Sea F1 (x) = , h=x+1.
(x − 1)(x + 1) 4
h 3 − 3h 2 + 6h − 4
Demostrar que F1 (h-1) = .
h 4 (h − 2)
c- Con la ayuda de una división de potencias crecientes, demostrar que:
1 1 1
2 2 2
F= X3 + 3 + 4
− 3
+ 2
− 4 + 4
(X + 1) (X + 1) (X + 1) (X + 1) (X − 1)
En este capítulo,  designará tanto al cuerpo conmutativo, como al cuerpo conmutativo.
1- Definiciones
P
Sean P y Q dos elementos de [X]. Entonces, F= es una fracción racional.
Q
Notación: (X) designa el conjunto de las fracciones racionales con coeficientes en.
La fracción racional F es irreductible porque P y Q no poseen ningún factor común de grado

superior o igual a 1.
P
Para lo siguiente, suponemos que la fracción F= es irreductible.
Q
Si "a" es un elemento de  , tal que Q(a)=0. Decimos que "a" es un polo de F.
Si "a" es una raíz de orden α de Q, decimos que "a" es un polo de orden α de F.
Efectuemos la división (euclidiana) entre P y Q:

∃!(E, R) ∈ [X]² / P = QE + R con R=0 donde deg(R) <deg(Q).

P R
De ahí: F = =E+ .
Q Q
El cociente E de la división de P dividido Q es la parte entera de F
R
y es la parte polar de F.
Q
P
En este párrafo, consideramos una fracción F = con deg(P)<deg(Q).
Q
Sea "a" un polo de orden α de F.
P
Existe un elemento Q 1 de [X] tal que: F = y Q 1 (a) ≠ 0.
(X − a)α Q1
P(x)
Podemos escribir: F(x)= .
(x − a)α Q1 (x)
Efectuamos el cambio de variables: h = x-a.
Luego efectuamos la división de P(a+h) dividido Q 1 (a+h) con las potencias crecientes (de h)
al orden α-1.
Volviendo a la variable x, obtenemos una fórmula de tipo:
α−1
ai R(x − a)
F(x) = ∑ α−i
+ con Q 1 (a) ≠ 0
i = 0 (x − a) Q1 (x)
α−1
ai
El término ∑ (x − a)
i =0
α−i
es la parte polar relativa al polo "a".
R(x − a)
El término tiene como polos eventuales los polos de F excepto "a".
Q1 (x)
2- Descomposición en elementos simples en (X)
Sea F un elemento de (X).

Sean x1, …, xr los polos de F, de respectivos ordenes α1 , …, αr .
r
Tenemos entonces la descomposición irreductible de Q : Q=k ∏ ( X − x j )
αj
j=1
Podemos obtener la expresión:

r αj
β j,i
F(x)=E(x) + ∑∑ (x − x )
=j 1 =i 1
i
j
Esta expresión (única) es la descomposición en elementos simples (de primera especie) de

F en (X).
3- Descomposición en elementos simples dentro de (X)
Sea F un elemento de (X).

r p
Tenemos la descomposición irreductible de Q : Q=k ∏ ( X − x j ) ∏(X )
αj γj
2
+ p jX + q j con
=j 1 =j 1
cualquier j de 1 a p, tenemos p j ²-4q j <0.
Podemos obtener una expresión de la forma :

r αj β j,i p γj
ci, j x + d i,j
F(x)=E(x) + ∑∑ i
+ ∑∑ i
=j 1 =i 1 (x − x j ) =j 1 =i 1 (x² + p j x + q j )
Con cualquier j de 1 a p, p j ²-4q j <0.

Esta expresión (única) es la descomposición en elementos simples de F dentro de (X).
E(x) es la parte entera de F.
r αj β j,i
∑∑
=j 1 =i 1 (x − x j )
i
está constituido de los elementos simples de primera especie (si existen).
p γj
ci, j x + d i,j
∑∑ (x² + p x + q )
=j 1 =i 1
i
está constituido de los elementos simples de segunda especie (si
j j
existen).

Ejercicio 1. Las siguientes fracciones racionales son irreductibles ? En el caso de que no sean
irreductibles, encontrar la expresión irreductible de la fracción racional, indicar sus ceros y
sus polos.
X-1 X 2 -1 X 2 -4X 2X8 -8X 7 +6X 6 -2X 2 +8X-6

(a) ; (b) ; (c) ; (d)
X 2 (X+1) X 2 -2X-3 2X 3 -4X 2 X 3 -2X 2 -5X+6
Ejercicio 2. Calcular las partes enteras de las siguientes fracciones racionales:
X5 X 2 -1 2X+1 X 3 -2X+5
(a) ; (b) 2 ; (c) ; (d)
(X 2 +1)(X-1) 2 X -2X-3 X(X 2 +1) 2 X+3
Ejercicio 3 . Indicar, sin efectuar cálculos, la forma de la descomposición en elementos

simples en (X) y en (X) de las siguientes fracciones racionales, dar las relaciones entre los
diferentes coeficientes.
X 2 -1 X2
(a) ; (b)
(X 2 + 2)X 3 (X 2 + 1) 2
Ejercicio 4. Descomponer en elementos simples las siguientes fracciones racionales en (X)

y en (X) :
X-3 1 X
(a) ; (b) ; (c)
(X 2 +4) (X+1)3 (X+1)3

Ejercicio 1. (a) La fracción es irreductible, cero: 1 ; polos : 0 (doble) y -1

X −1
(b) Forma irreductible: ; cero: 1 ; polo: 3
X −3
X−4
(c) Forma irreductible : ; cero : 4 ; polos : 0 y 2
2X 2 − 4X
2(X 6 − 1)
(d) Forma irreductible : ; ceros : las raíces sextas de 1 ; polo : -2
X+2
Ejercicio 2. (a) X + 2
(b) 1
(c) no hay parte entera
(d) X 2 − 3X + 7
Ejercicio 3. (a) Forma de la descomposición en (X) :

a b c d e
F= + 2 + 3 + +
X X X X −i 2 X +i 2
Además la fracción es real, entonces d = e y la fracción es impar, escribiendo:
F(−X) = −F(X) , obtenemos= b 0,= d e.
Forma de la descomposición en (X) :
a b c αX + β
F= + 2 + 3 + 2
X X X X +2
a, b y c son los mismos que los anteriores, el hecho de que la fracción es impar nos da esta
vez b=0, β=0 .
(b) Forma de la descomposición en (X) :
a a2 b b2
F= 1 + + 1 +
X − i (X − i) X + i (X + i) 2
2
Además la fracción es real entonces = a1 b= 1 y a2 b 2 , por otro lado, la fracción es par

entonces obtenemos demás: a1 = − b1 y a 2 = b 2 . Deducimos además que a1 es un imaginario
puro y que a 2 es real.
Forma de la descomposición en (X) :
α1X + β1 α 2 X + β2
= F +
X 2 + 1 (X 2 + 1) 2
Como la fracción es par, obtenemos α1 =α 2 =0 .
Ejercicio 4. (a) Al principio en (X) : F es un elemento simple !

1 3 1 3
+ i − i
En (X)
= : F 2 4 +2 4 .
X − 2i X + 2i
(b) En (X) como en (X), F es un elemento simple.

(c) Tenemos un polo múltiple, que es una raíz real entonces obtenemos la misma
1 1
descomposición en (X) y en (X)
= : F − .
(X + 1) (X + 1)3
2

EJERCICIOS
X4 + X2 + 2
Ejercicio 1. Descomponer dentro de (X) la fracción F(X) = 3 .
X + 5X 2 + 8X + 4
2
Ejercicio 2. Descomponer dentro de (X) la fracción F(X) = .
(X² + 1)(X + 1)²
X² - 4
(X - 1)² (X+ 1)²
2X 4 + 1
(X - 1) 3 (X 2 + 1)
Ejercicio 5. Descomponer dentro de (X) la fracción racional F definida por :

2X - 1
F(X) =
X(X + 1)² (X²+ X + 1)²
Ejercicio 6. Descomponer dentro de (X) la fracción racional F definida por :

X+3
(X + 1) (X 2 + 2X + 2)
7
Ejercicio 7.
1- Descomponer en elementos simples dentro de (X) la fracción racional siguiente :
2X 5 + 5X 4 + 4X 3 + 2X 2 − 3X − 2
F=
X 4 + 2X 3 + X 2
n
k 2 − 3k − 2
2- Determinar Lim ∑ 4 3 2
.
k =1 k + 2k + k
n →+∞

Ejercicio 8. Sea P el polinomio con coeficientes reales definido por :
P ( X ) =X 6 +2X 5 +3X 4 +αX 3 +3X 2 +2X+1
1- Determinar α para que -1 sea raíz de P.
Nos quedamos con este valor de α para la continuación.
2- Mostrar que -1 es raíz doble de P.
3- Mostrar que i es raíz múltiple de P.
4- Deducir una factorización de P en [X], luego en [X].
5- Con ayuda de lo precedido, determinar la decomposición en elementos simples en
(X) de :
4X
R (X) =
P (X)
Corrección:
1- -1 racine de P ⇔ P ( -1) =0 ⇔ ( -1) +2 ( -1) +3 ( -1) +α ( -1) +3 ( -1) +2 ( -1) + 1 ⇔ α=4
6 5 4 3 2
Nos quedamos con este valor de α para la continuación.

Tenemos entonces P ( X ) =X 6 +2X 5 +3X 4 +4X 3 +3X 2 +2X+1
2- De lo precedido, -1 es raíz de P entonces para verificar si -1 es raíz doble de P, basta con
verificar que -1 sea raíz de la derivada de P y que no sea raíz de la derivada segunda de P.
P es derivable , entonces tenemos :
Así, P′ ( -1) =6 ( -1) +10 ( -1) +12 ( -1) +12 ( -1) +6 ( -1) +2=0 .
5 4 3 2
Mostramos también que P" (-1) ≠ 0 .

Deducimos que -1 es raíz doble de P.
3- Tenemos por un lado que: P ( i ) =0 , y por el otro que, P′ ( i ) =0
Deducimos entonces que i es raíz al menos doble de P.
4- Con todo lo que precede, i es una raíz al menos doble de P.
P siendo un polinomio de coeficientes reales, deducimos que i=-i es también una raíz al
menos doble de P.
P siendo de grado 6, P tiene exactamente 6 raíces en  (contadas con sus orden de
multiplicidad). Hemos encontrado todas las raíces de P. Entonces P puede tener la siguiente
forma :
P ( X ) =A ( X+1) ( X-i ) ( X+i ) con A el coeficiente dominante.
2 2 2
Por identificación, tenemos claramente A=1 .

Concluimos que P ( X ) = ( X+1) ( X-i ) ( X+i ) en [X].
2 2 2
Para obtener la factorización en [X], basta con agrupar los términos con las raíces
conjugadas de dos a dos.
P ( X ) = ( X+1) ( X 2 +1) .
2 2
5- Gracias a la pregunta anterior, tenemos P ( X ) = ( X+1) ( X 2 +1)

2 2
4X 4X
Entonces R ( X ) = = .
P ( X ) ( X+1)2 ( X 2 +1)2

Para determinar la decomposición en elementos simples de R, tenemos dos posibilidades. El
primer método consiste en determinar la decomposición en [X], y luego volver a la
decomposición en [X]. El segundo método consiste en determinar directamente la
decomposición de R en [X].
Aquí, vamos a optar por el segundo método que en este caso nos da la solución con menos
cálculos.
La descomposición de R en [X] es del tipo:
a a2 a X+a a X+a 6
R (X) = 1 + + 3 2 4+ 5
( X+1) ( X+1) X +1 ( X 2 +1)2
2
Para determinar la parte polar asociada al polo -1 de orden 2, vamos a utilizar el método de
división con las potencias crecientes.
Comencemos haciendo el cambio de variable X+1=h ⇔ X=h-1 , obtenemos:
4 ( h-1) 4 ( h-1)
R (X) = =
( h ) ( h-1) +1 h ( h -2h+2 ) ( )
2 2 2 2 2 2
Debemos dividir 4 ( h-1) por ( h 2 -2h+2 ) =4-8h+8h 2 -4h 3 +h 4 con las potencias crecientes al
2
orden 1=2-1 :
-4+4h 4-8h+8h 2 -4h 3 +h 4
- ( -4+8h-8h 2 +4h 3 -h 4 ) -1-h
-4h+8h 2 -4h 3 +h 4
- ( -4h+8h 2 -8h 3 +4h 4 -h 5 )
4h 3 -3h 4 +h 5
Deducimos que tenemos:

-4+4h= ( h 2 -2h+2 ) ( -1-h ) +h 2 ( 4h-3h 2 +h 3 )
2
Lo que nos da:

( h -2h+2 ) ( -1-h ) +h ( 4h-3h +h 3 ) -1-h ) ( 4h-3h +h )
2
R (X) =
2 2 2
=
( +
2 3
h ( h -2h+2 ) ( h -2h+2 )
2 2
2 2 h2 2
1 1 ( 4h-3h +h )
2 3
=- - +
h h ( h -2h+2 )
2 2 2
Luego, reemplazando h por X+1 :
R ( X ) =- -
11
+
(
4 ( X+1) -3 ( X+1) + ( X+1)
2 3
)
( X+1) ( X+1) ( X 2 +1)
2 2
Además tenemos:
4 ( X+1) -3 ( X+1) + ( X+1) =X 3 +X+2
2 3

Entonces:
1 1 X 3 +X+2
R ( X ) =- - +
( X+1)
2
( X+1) ( X 2 +1)2
Para determinar la parte polar de segunda especia, efectuaremos la división euclidiana de

X 3 +X+2 por X 2 +1 :
X 3 +X+2 X 2 +1
- ( X 3 +X ) X
2
Tenemos entonces X 3 +X+2= ( X 2 +1) X+2

Lo que nos da:
R ( X ) =-
1
-
1
+
( X 2 +1) X+2
=-
1
-
1
+ 2
X
+
2
( X+1) ( X+1) ( X 2 +1) ( X+1) ( X+1) ( X +1) ( X 2 +1)
2 2 2 2
Finalmente, hemos obtenido la descomposición de R en elmentos simples en [X] :

1 1 X 2
R ( X ) =- - + 2 +
( X+1) ( X+1) ( X +1) ( X 2 +1)2
2

Capítulo 9
COMPLEMENTO SOBRE LOS REALES
Simple profesor, Weierstrass Karl Wilhelm Theodor,

alemán, 1815-1897, siguió sus estudios en Münster donde
Gudermann sería su profesor. Weierstrass enseñó las matemáticas
en diferentes liceos pero, animado por su antiguo profesor, sus pri-
meros trabajos sobre las integrales elípticas le llevaron a un estatus
de matemáticos en la universidad de Berlín. Lo consideramos gene-
ralmente como uno de los más grandes matemáticos del siglo19.
Consolidando con rigor los resultados de Cauchy relativos

al análisis numérico, sus trabajos precisarán también el estatuto de
los números irracionales, una noción todavía vaga desde el descu-
brimiento de estos últimos por los Pythagoristas (discípulos de Pythagoras). Weierstrass
pondrá un punto y final al difícil estudio de funciones y de integrales elípticas de las que Abel
creo al origen.
Weierstrass da por primera vez una construcción del conjunto de los números irracio-
nales, siempre intentando evitar la noción de límite con el fin de separar los números del aná-
lisis y de quedarse en el dominio de la aritmética: su construcción está basada en el desarrollo
decimal ilimitado no periódico de un número irracional (no racional).
Dedekind, Meray y Cantor se lanzaron a su vez sobre esta difícil construcción que los ma-
temáticos « esperaban » desde hace más de 2000 años, tras el descubrimiento de los irraciona-
les por los Pythagoristas (discípulos de Pythagoras).
Pitágoras de Samos (griego, -570 ?/-500 ?) Astrónomo, filoso-

fo, músico, este ilustre sabio, es conocido por los Pitagoracianos (o
Pitagorianos), sus discípulos. Personaje mítico por estos últimos. (él
sería el hijo de Apolo), funda su escuela en Crotona, la cual se vuelve
una secta con reglas de la vida muy severas. Se convierte en alguien
desagradable, ingrato, y será asesinado.
Para Pitágoras, la tierra es esférica y gira alrededor de ella
misma y alrededor del Sol. Esto hunde al mundo en el error durante
2000 años hasta la aparición de Galileo.

Con Weierstrass, entramos en un universo de rigor hasta hoy en dio ignorado, que po-
ne fin a sabias conclusiones de convergencia, de continuidad o de derivabilidad, como lo
hicieron imprudentemente Fourier y Cauchy. Le debemos la primera definición precisa ("por
los ε " como dicen los estudiantes) de la noción de límite de una serie (convergente) y de una
función así como la definición formal de la continuidad de una función.
1- El cuerpo de los reales
Teorema: (,+) es un grupo conmutativo.
Teorema: (*, × ) es un grupo conmutativo.
Teorema: (,+, × ) es un grupo conmutativo.
2-  y la relación de orden ≤
Definición: x ≤ y ⇔ y-x ∈ +.
Teorema.  es un cuerpo totalmente ordenado.
Teorema.  es arquimediano: ∀(x, y) ∈ (*+)²

∃n ∈ /nx>y.
Archimède
(hacia 282-217 a. J.C.)
Teorema.  está valorado. Quiere decir que el conjunto de los reales esta provisto de
la aplicación ‘valor absoluto’
Proposición: para todos reales x y y,

• |xy|=|x|.|y|
• ||x|-|y|| ≤ |x+y| ≤ |x|+|y|
• ∀α > 0, ∀x 0 ∈, x 0 < α ⇔ −α < x 0 < α
• ∀α > 0, ∀x 0 ∈, ∀x ∈ , x − x 0 < α ⇔ x 0 − α < x < x 0 + α
Estas dos ultimas propiedades son igualmente verdaderas si reemplazamos en toda la línea el
signo < por el signo ≤ .

3- Límite superior y límite inferior
Definición: Sea A una parte no vacía de .

M es un mayorando de A significa que ∀a ∈ A, a ≤ M .
Si existe un Máximo de A, se dice que A está mayorada.
M es un minorando de A significa que ∀a ∈ A, m ≤ a .
Si existe un mínimo de A, se dice que A está minorada
A está limitada si A está mayorada y minorada.

A admite un elemento mayor de M 0, significa que
- M 0 es elemento de A
- M 0 es un mayorando de A.
M 0 (si existe) es el máximo de A y se lo tiene en cuenta MaxA.

A admite un elemento menor de m0 significa que
- m0 es elemento de A
- m0 es un minorando de A.
m0 (si existe) es el mínimo de A y se lo tiene en cuenta MinA.

Siendo "S" el límite superior de A significa que "S" es el menor de los mayorandos de A. Se
escribe Sup A.
Siendo "I" el límite inferior de A significa que "I" es el mayor de los minorandos de A. Se
escribe Inf A.
Ejemplo : Sea A = ] 0,1[. Todos los reales negativos o nulos minoran A. El más grande de
esos minorandos es 0. Anotamos Inf A = 0. Todos los reales superiores o iguales a 1 mayoran
a A. El más pequeño de esos mayorandos es 1. Anotamos Sup A = 1. Notaremos que no se
trata ni de un mínimo ni de un máximo, ya que ni Inf A ni Sup A pertenecen a A.
Podemos escribir igualmente :

 ∀a ∈ A, a ≤ S
S=SupA ⇔ 
∀ε > 0, ∃a ∈ A, a > S − ε
La primera línea significa que S mayora a A, y la segunda significa que todo número inferior
a S (o sea de la forma S - ε con ε > 0) no mayora a A. Entonces S es el más pequeño de los
mayorados de A. Este último es llamado el contorno superior.
Igualmente :
 ∀a ∈ A, a ≥ I
I=InfA ⇔ 
∀ε > 0, ∃a ∈ A, a < I + ε
Teorema: Toda parte mayorada no vacía admite un límite superior.

Toda parte minorada no vacía admite un límite inferior.

Definición: Recta cabal
Definimos  añadiendo a  dos símbolos, - ∞ y + ∞ .
En el nuevo conjunto así definido, prolongamos la relación de orden usual sobre  por :
∀x ∈, −∞ < x < +∞
Podemos entonces designar el nuevo conjunto bajo la forma de intervalo [- ∞ ,+ ∞ ].
El interés de la recta cabal se basa en que numerosos resultados de  están liados al hecho de
poseer una parte de A borneado o no. De esta manera, si A está mayorada, podemos definir S
= Sup A. Si A no está mayorada, diremos Sup A = + ∞ . + ∞ no es nada más que el contorno
superior de A, pero en la recta cabal  .
Por otro lado, obtenemos, en la recta cabal, resultados más concisos.
A continuación una lista de resultados en , de los cuales algunos serán comprobados ulte-
riormente:
- Toda parte no vacía mayorada admite un contorno superior.
- Toda sucesión creciente mayorada converge hacia su contorno superior. Toda suce-
sión creciente no mayorada tiende hacia + ∞ .
- Toda sucesión decreciente minorada converge hacia su contorno inferior. Toda suce-
sión decreciente no minorada tiende hacia - ∞ .
- De toda sucesión contornada, podemos extraer una sub-sucesión convergente. De to-
da sucesión no borneada podemos extraer una sucesión con tendencia hacia + ∞ o - ∞ .
Estos resultado se enuncian en la recta cabal:

- Toda parte admite un contorno superior.
- Toda parte admite un contorno inferior.
- Toda sucesión creciente converge hacia su contorno superior.
- Toda sucesión decreciente converge hacia su contorno inferior.
- De toda sucesión, podemos extraer una sub-sucesión convergente.
Observación : La función parte entera E

Proposición : Sea x un real. Existe un único entero p, llamado parte entera de x tal
que:
p ≤ x<p+1.
Demostración :
Sea x > 0. Consideremos A = { n ∈  / n ≤ x}.
Este conjunto es una parte no vacía ( contiene 0) mayorado (por x mismo). El admite entonces
un contorno superior α. Mostremos que α es un entero y elemento de A. En efecto, α-1 no es
un mayorando de A entonces existe n elemento de A tal que α-1 < n ≤ α. Los enteros supe-
riores a n son entonces superiores a α y no pueden estar en A. n es entonces el elemento más
grande de A y es entonces igual a α. α es entonces no solamente el contorno superior sino el
máximo de la parte A. α no es otro que el entero p que buscamos. En efecto, p está en A en-
tonces p ≤ x, pero p+1 no está en A entonces x < p+1. Lo que prueba la existencia. Admita-
mos la unicidad que será demostrada justo después.
Anotemos p = E(x).

Para x<0, tomaremos p= -E(-x)-1 si x no es un entero, y x si x es entero. En el primero de los
casos tenemos:
E(-x) < -x < E(-x) + 1
-E(-x) - 1 < x < -E(-x)
Así, E(-3,5) =-4.
Resaltaremos que esta definición utilizada en Matemáticas no siempre corresponde a la pri-
mera idea de « parte entera ». En las calculadoras, encontrarán « dos funciones partes ente-
ras » : una que corresponde a aquella que estamos definiendo y la otra que propone como par-
te entera de x < 0, el valor-E(-x).
Demostremos ahora la unicidad.

Si q < p, con p y q enteros, entonces q+ l ≤ p ≤ x, y si q > p, entonces q ≥ p+ l > x, lo que
muestra que ningún número inferior o superior a p no puede verificar la definición de la parte
entera de x. Solo p conviene.
Aplicación : Escritura decimal de un real

Sea n un entero positivo. Todo real puede ser enmarcado de manera única bajo la forma :
d1 d d d +1
M+ + ... + nn ≤ x < M + 1 + ... + n n
10
  10
 10
 10
Valor aproximado por defecto Valor aproximado por exceso
donde M es un entero y los d i son cifras entre 0 y 9. Basta con considerar el enmarcado :
E(10nx) ≤ x < E(10nx) + 1
A propósito de la noción de intervalo:

Un intervalo se escribe |a,b| (*) donde | reemplaza [ o ]. a puede ser finito o valer - ∞ , b puede
ser finito o valer + ∞ . El intervalo es entonces el conjunto de reales comprendidos entre a y b,
eventualmente en el sentido abierto.
Proposición :I es un intervalo si y solamente si:

∀x ∈ I, ∀y ∈ I, x<z<y ⇒ z ∈ I
Una parte verificando esta propiedad es dicha convexa.
Otra formulación es la siguiente :
∀x ∈ I, ∀y ∈ I, x<y ⇒ [x, y] ⊂ I
Demostración :
Es evidente que un intervalo verifica la propiedad de convexidad.
Demostremos la recíproca. Sea I convexa. Mostremos que es de la forma (*). Si I está mino-
rada, tomemos a = Inf I si no, a = - ∞ . Si I está mayorada, tomamos b = Sup I si no, b = + ∞ .
Tenemos entonces I incluido en [a, b].
Sea z tal que a < z < b. En todos los casos, existen x e y elementos de I tales que:
a ≤ x<z<y ≤ b
Demostrémoslo para x :
Si a = - ∞ , esto significa que I no está minorada y entonces que z no minora I, y enton-
ces que existe x elemento de I tal que x < z.
Si a es finito, a es el más grande de los minorandos, entonces z no minora I, y entonces
existe x elemento de I tal que a ≤ x < z.
La propiedad de convexidad prueba que z e s elemento de I. As, ]a, b[ está incluido en I. El
hecho que a y b pertenezcan o no a I cerrará eventualmente uno de los contornos del intervalo
o de los dos.

4- Racional e Irracional
Definición: Un número racional es un número que puede escribirse como el cociente

de dos enteros.
Teorema. Un número real es un racional si y solamente si su desarrollo decimal ilimi-

tado es periódico.
Teorema: Sea ]a, b[ un intervalo no vacío. Entonces ]a, b[ encuentra  y c. Decimos
que  es denso en .
Demostración: Debemos demostrar que ]a, b[ contiene un racional y un irracional. Sean x e y

dos elementos de ]a, b[.
Si uno de ellos es racional y el otro irracional, no hay nada que demostrar.
Si los dos son racionales, basta con demostrar que:
i) Entre dos racionales, existe un irracional.
Si los dos son irracionales, basta con demostrar que :
ii) Entre dos irracionales, existe un racional.
i) Si x e y son dos racionales tales que x < y, entonces tomemos:

(y − x) 2
z=x+
2
z es un irracional comprendido entre x e y.
ii) Si x e y son dos irracionales tales que x < y, existe q entero tal que:
1
0< <y-x
q
1
(tomar q superior a , por ejemplo la parte entera de ese número aumentado de 1). Con-
y−x
sideremos ahora p = E(qx). Tenemos:
p ≤ qx<p+ 1 ≤ qx+ 1<qx+q(y-x)=qy
p +1
⇒x < <y
q
p +1
es un racional comprendido entre x e y.
q
Teorema. Todo real puede escribirse como límite de una secuencia de número racio-
nal.

Ejercicio 1. Demostrar, utilizando una disyunción de casos, que para todo real x e y, tene-
1 1
mos: max(x, y)
= (x + y + | x − y |) y min(x, y)
= (x + y − | x − y |)
2 2
Ejercicio 2. Sean a, b, c, x, y, z seis reales estrictamente positivos.

1- Demostrar que : ax + by + cz ≤ (a + b + c)(x + y + z) .
x y z
2- Demostrar que tenemos la igualdad si y solamente si : = = .
a b c
Ejercicio 3. Determinar el par de reales (x,y) que verifican y − sin(x) + y n + x n =

0 para todo
entero n.
Ejercicio 4. Demostrar las siguientes desigualdades:

1- ∀(a, b) ∈ *+ × *+, (a + b) < ( a + b) 2 .
2- ∀(a, b) ∈ *+ × *+, (a + b) < ( 3 a + 3 b)3 .
Ejercicio 5. Utilizando la fórmula del binomio de Newton, demostrar que, para todo entero n
no nulo y para todo real x estrictamente positivo, tenemos:
(1 + x) n ≥ 1 + nx
(Indicación: considerar los primeros términos...).
Ejercicio 6. Utilizando la fórmula del binomio de Newton, demostrar que, para todo entero n
2
no nulo, tenemos: n n < 1 +
n
Ejercicio 7. Para cada uno de los siguientes conjuntos, decir si está mayorado, minorado o
limitado. Dar, si existen, el elemento máximo, el límite superior, el elemento mínimo, el lími-
te inferior.
 1   1    2nπ  
= E  2
; x ∈]0,1[
=  ;F  2
; x=
∈ [0,1[  ; G sin   ; n ∈ 
1 + x  1 − x    7  
Ejercicio 8. Sean A y B dos conjuntos no vacíos. Demostrar que :

1- sup(A  B) = max(sup(A),sup(B)) ;
2- inf(A  B) = min(inf(A),inf(B)) .
Ejercicio 9. Determinar el conjunto de reales que son estrictamente superiores a dos veces
sus inversos.
Ejercicio 10. Sea a un real estrictamente positivo. Resolver la inecuación:

1 1
− < a.
1− x 1+ x

EJERCICIOS
Ejercicio 1. Sea x = 7, 314 . Determinar la formulación fraccionaria de x.
Ejercicio 2. Para cada uno de los conjuntos siguientes, decir si es sobreestimado, infravalo-
rado, limitado en . Dar, si existen, el elemento máximo, el límite sup, el elemento mínimo,
el límite inf (no pedimos justificación).
 1 
E 1 ={x ∈ /-2<x ≤ 2} ; E 2 ={x ∈ /-2<x ≤ 2} ; E 3 =  / x ∈]0,1[ 
1 + x² 
 1 
E4=  / x ∈ [0,1[  ; E 5 ={x ∈ /x² ≤ 17} ; E 6 ={x ∈ /x² ≤ 17}
1 + x² 
 1 
Ejercicio 3. Sea E la parte de  definida por: E = (−1) n + / n ∈ * .
 n 
1- Justificar la existencia del contorno superior y del contorno inferior de E. Después,
calcularlos justificando detalladamente las respuestas.
2- Este conjunto admite el elemento más pequeño ? el elemento más grande?
1 1 
Ejercicio 4. Sea A=  + / (n, m) ∈ *2  . Después de haber demostrado la existencia de
n m 
Sup(A) y de Inf(A), determinar sus contornos.
Ejercicio 5.
a- Sean E y F dos partes limitadas de  que no están vacías. Se supone que E ⊂ F. Mostrar que
Sup(E) ≤ Sup(F) y que Inf(E) ≥ Inf(F). Ustedes establecerán de antemano que estos bornes
existen.
b- Sean A y B dos partes limitadas de  que no están vacías Calcular en función de
Inf(A), Inf(B), Sup(A), Sup(B) : Sup(A+B), Min(A∪B), Max(A∪B). Ustedes establecerán de
antemano que estos bornes existen.
c- Se supone que A ∩ B ≠ ∅. Comparar los números siguientes:
Inf(A∩B), Sup(A∩B), Min(SupA,SupB), Max(InfA,InfB)
¿Pueden las desigualdades ser estrictas?
Ejercicio 6. Para todo entero "n" natural, se define el conjunto de reales

 n 
E=
n k + ; k entero natural no nulo 
 k 
a- Mostrar que E n admite un límite inferior y que:
 n
Inf( E n ) = Inf  k + 
1≤ k ≤ n  k
b- Mostrar que para todo entero n estrictamente positivo, Inf( E n ) ≥ 4n .¿En qué caso
se obtiene la igualdad?

Ejercicio 7. Sea A una parte de  no vacía tal que A y A c son partes abiertas de  (A abier-
ta ⇔ ∀a ∈ A , ∃ε > 0,]a − ε; a + ε[⊂ A ).
a- Demostrar que A no está agrandada.
b- Suponemos que A c no está vacío y sea además x0 elemento de A c .
Sea B = {t ∈ A / x 0 ≤ t} . Demostrar que B admite un límite inferior m tal que m > x0 .
c- Demostrar que m∉ A c y m∉A. Concluir.

Ejercicio 8. Sean A y B dos partes no vacías de  tales que : ∀ (a ; b)∈A×B : a ≤ b.

a- Justificar la existencia de Sup (A) y de Inf (B).
b- Demostrar que tenemos Sup (A) ≤ Inf (B) (Podemos razonar por lo absurdo)
Corrección : a- A es una parte no vacía.

Además, el conjunto de los mayorados de A contienen B y entonces es una parte no vacía, lo
que significa que A está mayorada.
Siendo A una parte no vacía y mayorada, ella admite un límite superior.
Hacemos el mismo razonamiento para demostrar que B admite un límite inferior.
b- Razonamos por lo absurdo.
Supongamos que sup(A)>inf(B).
Entre dos reales, siempre podemos encontrar otro real entonces : ∃ε > 0 ,
inf(B)<inf(B)+ε<sup(A)
Caracterizando el límite inferior, sabemos que : ∀ε > 0, ∃b ∈ B , inf(B)<b<inf(B)+ε.
Entonces, podemos deducir que : ∃b ∈ B , b<sup(A).
Entre dos reales, siempre podemos encontrar otro real entonces:
∃ε′ > 0 b < sup ( A ) − ε′ < sup ( A )
Caracterizando el límite superior, sabemos que :
∀ε′ > 0 ∃a ∈ A, sup ( A ) − ε′ < a < sup ( A )
Entonces, deducimos que : ∃a ∈ A, b < a .
Como esto es absurdo por hipótesis, tenemos: ∀ ( a, b ) ∈ A × B, a ≤ b .
Concluimos que : sup ( A ) ≤ inf ( B ) .
Ejercicio 9. Sea A una parte no vacía limitada de .

Demostrar que sup x − =
y sup A − inf A .
( x,y )∈A 2
Corrección : Siendo A limitada, ella admite un límite superior y un límite inferior.

ε
Por definición, tenemos por un lado: ∀ε > 0 ∃x ∈ A, sup ( A ) − ≤ x ≤ sup ( A ) .
2
ε
Y por otro lado, ∀ε > 0 ∃y ∈ A, inf ( A ) ≤ y ≤ inf ( A ) + .
2
ε
La segunda desigualdad se escribe también: − inf ( A ) − ≤ − y ≤ − inf ( A ) .
2
En particular, obtenemos combinando esos dos resultados que :
∀ε > 0 ∃ ( x, y ) ∈ A 2 ,sup ( A ) − inf ( A ) − ε ≤ x − y ≤ sup ( A ) − inf ( A )
Ahora, solo queda reemplazar x-y por x − y .
Hay que distinguir dos casos:
Caso 1- sup ( A ) − inf ( A ) − ε ≥ 0
Todos los términos de la desigualdad son positivos, podemos reemplazarlos por sus valores
absolutos.
Esto nos da entonces: sup ( A ) − inf ( A ) − ε ≤ x − y ≤ sup ( A ) − inf ( A ) .

Caso 2- sup ( A ) − inf ( A ) − ε < 0
Este caso no es importante.
En efecto, tomemos ε′ como en el anterior caso, entonces:
∃ ( x, y ) ∈ A 2 , 0 ≤ sup ( A ) − inf ( A ) − ε′ ≤ x − y =
x − y ≤ sup ( A ) − inf ( A )
En particular, ∃ ( x, y ) ∈ A 2 ,sup ( A ) − inf ( A ) − ε ≤ x − y ≤ sup ( A ) − inf ( A ) .
Entonces tenemos el resultado buscado.
De hecho, mientras queremos demostrar desigualdades de ese tipo, el problema se plantea
únicamente para ε próximo de 0.
Hemos entonces demostrado que :
∀ε > 0 ∃ ( x, y ) ∈ A 2 ,sup ( A ) − inf ( A ) − ε ≤ x − y ≤ sup ( A ) − inf ( A )
Esto significa caracterizando el límite superior que :
sup x − = y sup A − inf A
( x,y )∈A 2
Ejercicio 10. Sean X e Y dos conjuntos no vacíos, y f una aplicación de X × Y en  mayora-

da. Demostrar que :
 
Sup f ( x; y) = SupSup f ( x; y) 
( x , y ) ∈ X× Y x∈ X  y∈ Y 
Corrección : a- Esos límites superiores existen.

b- Anotemos F la función de X en  definida por : x  F( x ) = Sup f ( x; y).
y∈Y
 
Entonces SupSup f ( x; y)  = Sup F( x).
x∈ X  y∈ Y  x∈ X
Sea ( x 0 ; y 0 ) un elemento de X× Y.
 
Tenemos : f( x 0 ; y 0 ) ≤ F( x 0 ) ≤ Sup F( x) ≤ SupSup f ( x; y) 
x∈ X x∈ X  y∈ Y 
 
Entonces, Sup f ( x; y) ≤ SupSup f ( x; y) 
( x , y ) ∈ X× Y x∈ X  y∈ Y 
Mostremos la desigualdad inversa.
Tenemos: ∀( x; y) ∈ X × Y, Sup f ( x; y) ≥ f ( x; y)
(x,y)∈ X×Y
≥ F(x)
≥ Sup F( x)
x∈ X
 
≥ SupSup f ( x; y) 
x∈ X  y∈ Y 
Deducimos la igualdad:
 
Sup f ( x; y) = SupSup f ( x; y) 
( x , y ) ∈ X× Y x∈ X  y∈ Y 
Ejercicio 11. 1- Determinar E (n) para todo n ∈ .

Determinar E (x) para x ∈ [ n ; n +1 [ con n ∈.
Probar que para todo real x y todo entero relativo n, tenemos: E (x + n) = E (x) + n.

Hacer la representación gráfica de esta función en [ - 3 ; 3 ].
Probar que para todo x tenemos: x – 1 < E(x) ≤ x.
E (x)
Deducir el límite de cuando x tiende hacia + ∞ o hacia – ∞.
x
1
Calcular el límite de x E   cuando x tiende hacia 0.
x
2- Estudiar el límite cuando x tiende hacia 0 de las siguientes funciones:
x b a x
f (x) = E   y g (x) = E   donde a y b son dos reales estrictamente positivos.
a x x b
Corrección : 1- ∀n ∈ , n ≤ n < n + 1 entonces E ( n ) =n.

Sea x ∈ [ n, n + 1[ con n ∈ , alors n ≤ x < n + 1, entonces E ( x ) =n.
Sea x ∈  et n ∈ .
Tenemos: E ( x ) ≤ x < E ( x ) + 1 entonces E ( x ) + n ≤ x + n < E ( x ) + n + 1 .
Deducimos que : E ( x + n =
) E(x) + n .
Demostrar que para todo x, tenemos: x – 1 < E(x) ≤ x.
Por definición, tenemos E ( x ) ≤ x < E ( x ) + 1 entonces E ( x ) ≤ x y x − 1 < E ( x ) , y así tene-
mos: x − 1 < E ( x ) ≤ x .
1 E(x) 1 E(x)
Con lo que precede, tenemos para x > 0, 1 − < ≤ 1 y para x < 0, 1 − > ≥ 1.
x x x x
E(x)
Deducimos, por el teorema de gendarmes, que Lim = 1.
x →±∞ x
1 1 E (u)
Tomemos
= u entonces lim = xE   lim= 1.
x x →0
 x  u →±∞ u
n
E (10n x ) E (u)
Tomemos
= u 10 x entonces lim = lim
= 1.
n →∞ 10n x u →±∞ u
b b E (u) b E (u) b
2- Tomemos u =entonces lim f ( x ) = lim × = × lim = .
x x →0 u →±∞ a u a u →±∞ u a
x a E (u) a E (u) a
Tomemos u =entonces lim g ( x ) = lim × = × lim =.
b x →∞ u →∞ b u b u →∞ u b

Anexo
Indicaciones cronológicas, referencias
- Cerca de -30000 años : Técnica del corte.

- Siglo V a.C.: Pitágoras, irracionalidad del 2.
- Siglo III a.C.: Euclides funda el método axiomático, Arquímedes dona:
10 10
3+ ≤ π ≤ 3+
71 70
- Siglo I: Los chinos conocen los número negativos.
- Siglo III: Diofante calcula sobre las fracciones, en despecho a Euclides.
- Siglo IV: El cero es « inventado » en India.
- 1484 : N. Chuquet introduce los número negativos en Europa.
- 1545-1560 : Introducción de los números imaginarios por Cardan y Bombelli.
- 1637 : Descartes, Geometría analítica : un puente se crea entre el álgebra y l a geo-
metría.
- 1760 : Lambert demuestra que π es irracional.
- 1800 : Gauss introduce el plano complejo.
- 1843 : Hamilton « inventa » los cuaterniones .
- 1858 : Cayley, cálculo de matrices.
- 1830-1872 : Cauchy, Dedekind, definición precisa de los números reales.
- 1882 : Von Lindemann demuestra la trascendencia de π.
- Fin del siglo XIX- principios del XX: Cantor, Peano, Zermelo, etc...: teoría de los
conjuntos, definición de , números transfinitos.
- 1920-1930 : Heisenberg, Dirac: nacimiento de la mecánica cuántica. Los números no

conmutativos invaden la Física.
- Fin del siglo XX: La geometría no conmutativa lanza un nuevo puente entre el álge-
bra y la geometría.

Capítulo 10
FUNCION DE UNA VARIABLE REAL
0 – PRESENTACION HISTORICA
La noción de límite hizo su aparición en una obra del matemático inglés B. Robins ti-
tulada A Discourse Concerning the Nature and Certainty of Sir Isaac Newton’s Method of
Fluxions and Prime and U ltimate Ratios (1735). Robins intenta
precisar y aclarar la expresión un poco oscura de Newton « prime-
ras y últimas razones », hablando de límites hacia los cuales tien-
de, sin jamás alcanzarlos, relaciones de cantidades J. Jurin, se-
guidor de Newton ortodoxo y altivo, para quien las primeras y las
últimas razones efectivamente se alcanzaban (en el instante de
nacimiento o de desvanecimiento).
C. Maclaurin, en su obra Treatise of Fluxions (1742) re-
cupera la interpretación de las « primeras y últimas razones » de
Newton en términos de límites; sin embargo funda el Cálculo
infinitesimal sobre la noción de fluxión (velocidad instantánea) y
I. Newton no sobre la del límite. Por el contrario, d’Alembert, en su artículo
« Diferencial » de La Enciclopedia vol. IV, 1754, presenta la no-
ción de límite como la “verdadera metafísica del cálculo diferencial”: define la relación dife-
rencial dy /dx como el límite de la relación de los crecimientos terminados en y y en x cuan-
do estos crecimientos tienden hacia 0, e insiste en el hecho que no debemos separar las “dife-
renciales” dy y dx. Igual que sus predecesores Robins y Maclaurin, el lenguaje de
D’Alembert es integralmente geométrico, y la noción de límite no está claramente definida :
decimos simplemente que la relación considerada puede volverse tan cercana como quera-
mos de su límite, o que una “medida es el límite de otra medida cuando la segunda puede
acercarse de la primera lo más cerca que una cantidad establecida, tan pequeña como lo po-
damos suponer, sin que la medida que se acerca no pueda jamás sobrepasar la medida hacia
la cual se acerca, de manera que la diferencia de una cantidad con su límite sea absolutamen-
te insignificante” (observamos que, para d’Alembert, el límite se acerca de un solo lado).
Sin embargo, d’Alembert toma cuidado en establecer la unicidad del límite.
La puesta en macha de la noción de límite en el siglo XVIII se encontró con numero-
sos obstáculos: el lenguaje geométrico no otorgaba un dominio numérico homogéneo donde
desarrollar la teoría y la noción general de función no estaba todavía asimilada. Era por lo
tanto muy difícil de de concebir claramente cómo una medida o una relación variable tendían
hacia sus límites. El concepto de límite se esclareció progresivamente en el siglo XIX: a par-
tir de 1800, C. F. Gauss tenía una concepción extremadamente clara de la noción de una se-

rie de números reales (a n ) n , puesto que la definió (en una obre inédita Nociones fundamenta-
les sobre la teoría de las series) como el valor común a lim sup a n y lim inf a n cuando estos
dos límites extremos, definidos de manera precisa, coincidan. A. L. Cauchy impuso la no-
ción de límite en la base del cálculo infinitesimal ; la definición que daba era todavía un poco
confusa : « cuando los valores sucesivamente atribuidos a una misma variable se acercan in-
definidamente de un valor fijo, de manera para acabar por diferir de eso tan poco como que-
rremos, esta última se denomina límite de los demás » (resumen de las « lecciones » imparti-
das en la escuela real politécnica sobre el cálculo infinitesimal, 1823) ; pero introduce una
notación lim para el límite y demuestra con ejemplos numéricos cómo se comportan los lími-
tes.
La definición más precisa de límite que todavía damos en las clases remonta a Weiers-
trass (1815-1897), promotor del “estilo de los épsilon”. Para que la teoría sea totalmente cla-
ra, solo faltaba una teoría satisfactoria de los números reales, que permita establecer la exis-
tencia de un límite superior para una parte no vacía aumentada y demostrar el criterio de
Cauchy, admitido hasta entonces como una evidencia ; diversas teorías sobre los números
reales han sido elaboradas hacia 1860-1870 (Dedekind, Weierstrass, Cantor).
Cauchy (1789-1857) publica en 1821 su Curso de análisis que tie-

ne una gran audiencia y constituye la primera exposición rigurosa sobre
las funciones numéricas. Renovando el análisis funcional, él formaliza,
en particular, las nociones:
De límite : si los valores sucesivamente atribuidos a una varia-

•
ble se acercan indefinidamente de un valor fijo, de manera para
acabar por diferir de eso tan poco como querremos, entonces
este último es llamado límite de todos los demás.
• De función: mientras que las variables están ligadas entre ellas,
y que el valor de una de ellas esta dado, de manera que poda-
mos deducir los valores de todas las demás, concebimos de or-
dinario estas diversas cantidades expresadas por medio de una entre ellas, que toma el
nombre de variable independiente; y las demás cantidades expresadas por medio de la
variable independiente, son lo que llamamos las funciones de esta variable.
• De continuidad sobre un intervalo: (h designado para una cantidad infinitamente pe-
queña) : mientras que la función f(x) admita un valor único y finito para todos los va-
lores de x comprendidos entre dos límites dados, si la diferencia f(x + h) - f(x) está
siempre entre los límites una cantidad infinitamente pequeña, decimos que fx) es una
función continua de la variable x entre los límites en el que ella trata.
Intuitivamente y gráficamente, describimos la curva representante de f sin levantar el

lápiz: no hay “huecos”. En el esquema de la izquierda tenemos un arco de curva “continuo” y
a la derecha, hay discontinuidad en el punto x = 2.

• de derivabilidad (de una función continua) : si, mientras h se vuelve infinitamente pe-
queño comparado a las diferencias
∆y f (x + h) − f (x)
=
∆x h
Admite un límite finito, lo anotamos f'(x), es una función de x llamada la función derivada.
Estas definiciones permiten a Cauchy de ser el primero en establecer rigurosamente la

fórmula de Taylor precisando las condiciones de convergencia hacia la función desarrollada.
De todos modos, el conjunto  de números reales no está aún construido. Un número real, en
esta época, es un número no imaginario; entero, fraccionario o irracional. Los números π y e
son irracionales a partir de Euler y Lambert pero no son aún trascendentes. Habrá que espe-
rar Lindemann y Liouville. La confusión de los números reales conduce a Cauchy a conclu-
siones que pueden parecer como poco rigurosas, incluso falsas, como, por ejemplo, su resul-
tado sobre la suma de una serie de funciones.
Cauchy utiliza implícitamente que salvo en algunos puntos singulares, toda función
continua admite una derivada. Riemann, luego Bolzano y Weierstrass darán un ejemplo de
función continúa en todo punto de un intervalo y no siendo derivada en ningún punto.
Cauchy anuncia, ilustrándolo pero sin demostrar, el teorema de los valores intermedia-
rios:
Si una función f es continua entre los límites a y b y que se designa a k una cantidad
intermediaria entre f(a) y f(b), podremos satisfacer siempre la ecuación f(x) = k por al menos
un valor de x comprendido entre a y b.
1- Vocabulario
En este capítulo consideramos las funciones definidas en una parte de , con valores
en  (función de una variable real con valores reales) o a veces a valores en  (función de una
variable real con valores complejos).
Si f y g son dos funciones y λ un escalar, f + g es la función: x  f(x) + g(x). λf es la

función: x  λf(x). Estas dos operaciones confieren al conjunto de funciones definidas sobre
el mismo conjunto una estructura de espacio vectorial (ver el capítulo de Espacios Vectoria-
les) La función f g es la función: x  f(x)g(x). La función f o g e s la función x  f(g(x)).
La función |f| es la función: x  |f(x)|.
Una función f con valores reales es agrandada si : ∃ M ∈ , ∀x ∈ D f , f(x) ≤ M.
Una función f con valores reales es disminuida si: ∃ m ∈ , ∀x ∈ D f, f(x) ≥ m.
Una función f con valores reales es limitada si ella está agrandada y disminuida. Se
puede escribir también

∃ M ∈ , ∀x ∈ D f , |f(x)| ≤ M
Esta última definición se aplica a las funciones con valores complejos reemplazando el
valor absoluto por el módulo.
Una función f con valores reales admite un máximo si: ∃ x 0 ∈ D f, ∀x ∈ D f,

|f(x)| ≤ f(x 0 ).
Notamos f(x0 ) = Max f(x), o mejor aún, f(x0 ) = Max f.
x∈Df x
Una función f con valores reales admite un mínimo si: ∃ x 0 ∈ D f, ∀x ∈D f, |f(x)| ≥ f(x 0 ).
Notamos f(x 0 ) = Min f(x), o mejor aún, f(x 0 ) = Min f.
x∈Df x
Una función f con valores reales admite un extremo si ella admite un máximo y un
mínimo.
El máximo y el mínimo o el extremo son llamados locales reemplazando anteriormen-

te ∀x ∈D f por ∃α > 0, ∀x ∈ ]x 0 − α, x 0 + α[  Df .
Dicho de otro modo, la propiedad no está verificada que sobre un intervalo alrededor
de x0 y no sobre el conjunto de definición de f.
Una función con valores reales puede ser limitada sin admitir un máximo o un míni-
mo, pero solamente un límite superior o inferior (pensar en x  e-x en [0,+ ∞ [ que admite 1
como máximo y 0 como límite inferior pero no como mínimo). Estas limitaciones son notadas
respectivamente Sup f(x) o simplemente Sup f, y Inf f(x) o simplemente Inf f.
x∈Df x x∈Df
Una función f es par si :

1- D f es simétrico con relación a 0
2- ∀x ∈D f, f(-x) = f(x).
El conjunto de funciones pares es estable para las dos operaciones de adición de fun-
ciones y de multiplicación de escalares; se trata de un sub-espacio vectorial del espacio de
funciones (ver el capítulo de Espacios Vectoriales).
Una función es impar si :

1- D f es simétrico con relación a 0
2- ∀x ∈ D f, f(-x) = - f(x).
Se trata igualmente un sub-espacio vectorial del espacio de funciones. (ver el capítulo
de Espacios Vectoriales).
Una función es periódica de periodo T si : ∀x ∈ D f , f(x + T) = f(x).
Una función es lipschitziana de analogía k o k-lipschitziana si :

∀(x, y) ∈ D f2, |f(x) -f(y)| ≤ k |x –y|
(Lipschitz, matemático alemán, 1832-1903)
Decimos que la propiedad P es verdadera « alrededor » de ω mientras que:

- Para ω∈  : existe un α > 0 tal que P es verdadero en ]ω-α,ω[  ]ω,ω+α[
- Para ω = + ∞ : existe un α ∈  tal que P es verdadero en ]α;+ ∞ [

- Para ω = - ∞ : existe un α ∈  tal que P es verdadero en ]- ∞ ,α[.
En este capítulo, consideramos una función f de  en  donde el conjunto de definición D f es

un intervalo o una reunión de intervalos; x 0 es un real tal que x0 ∈ D f , o x0 es une borde de
D f.
2- Límites
Definición: el real x0 está adherido D f (o x0 pertenece a la adherencia de D f) significa :
∀ε > 0, ]x 0 − ε, x 0 + ε[  Df ≠ ∅
Ejemplo: La adherencia de ]-1,10] es [-1,10].
La pregunta sobre el límite de f en un real x 0 no cabe lugar sólo si x0 es un punto adherido a

D f.
Las definiciones “en francés” de los límites son las siguientes:

Sea x0 y l dos reales.
Lim f(x)= l significa que f(x) se puede aproximar al l tanto como se quiera con la sola
x →x0
condición de tomar x suficientemente próximo de x0 .

Lim f(x)= + ∞ significa que f(x) puede ser lo grande como se quiera con la sola condi-
x →x 0
ción de tomar x suficientemente próximo de x 0 .

Lim f(x)= l significa que f(x) se puede aproximar al l tanto como se quiera con la sola
x → +∞
condición de tomar x suficientemente grande .
Lim f(x)= + ∞ significa que f(x) puede ser lo grande como se quiera con la sola condi-
x → +∞
ción de tomar x suficientemente grande.
Definiciones análogas con - ∞ …
Estas definiciones transformadas al lenguaje matemático:

(
Lim f(x)= l ⇔ ∀ε > 0, ∃η>0, ∀x ∈ Df , x-x 0 < η ⇒ f (x) − l < ε
x →x0
)
Lim f(x)= + ∞ ⇔ ( ∀A > 0, ∃η>0, ∀x ∈ Df , x-x 0 < η ⇒ f (x) > A )
x →x 0
(
Lim f(x)= l ⇔ ∀ε > 0, ∃B>0, ∀x ∈ Df , x>B ⇒ f (x) − l < ε
x → +∞
)
Lim f(x)= + ∞ ⇔ ( ∀A > 0, ∃B>0, ∀x ∈ Df , x>A ⇒ f (x) > B )
x → +∞
Ejemplos: Demostrar con ayuda de la definición « con los ε » : Lim(2x + 4) =

6 y
x →1
5.
Lim(x² + 1) =
x →2
Observación

La expresión Lim f(x) = l (x0 finito o infinito, l real ) se traduce también por:
x →x0
Lim (f(x)-l)=0 o f(x) = l+ε(x) con Lim ε(x) = 0

x →x0 x →a
=  f (x) 1 pour x ∈ ]-∞, 1[

Ejemplos: Sea f la función definida por:  . Entonces,
f (x) x pour x ∈ ]1, +∞[
=
Lim f (x) = 1 .
x →1
= g(x) 1 pour x ∈ ]-∞, 1[


Sea g la función definida por:  g(1) = 2 . Entonces, Lim g(x) no existe, sin
x →1
=
g(x) x pour x ∈ ]1, +∞[
embargo Lim g(x) = 1 .
x →1
x ≠1
Teorema: El límite, si existe, es único.
Demonstración: Por lo absurdo en el caso donde x0 , l y l' sean finitos:

Sea f una función que admite l y l' como límite en x0 , y l ≠ l’.
1
Tomemos ε = l − l ' . Existe η 1 y η 2 reales estrictamente positivos tales que :
2
∀x ∈ ]x 0 − η1 , x 0 + η1 [ , f(x)-l < ε
∀x ∈ ]x 0 − η2 , x 0 + η2 [ , f(x)-l' < ε
Para x ∈ ]x 0 − η1 , x 0 + η1 [  ]x 0 − η2 , x 0 + η2 [ , tenemos:
|l-l’| ≤ |l-f(x)|+|f(x)-l’|<2ε
Obtenemos una contradicción.
3- Operaciones con los límites
Suma
Las funciones f y g t eniendo un límite (finito o infinito), la función f+g admite un límite en
cada uno de los casos descritos en la tabla siguiente :
Lim f l∈  +∞ -∞
Lim g
l’ ∈  l + l’ +∞ -∞
+∞ +∞ +∞ FI
-∞ -∞ FI -∞
Producto
Para las funciones f y g que tienen un límite (finito o infinito), la función f × g admite un límite
en cada uno de los casos descritos en la tabla siguiente ( ± ∞ significa + ∞ o - ∞ según el sig-

no del límite finito.)
Lim f l ∈ * +∞ -∞
Lim g
l’ ∈ * l.l’ ±∞ ±∞
+∞ ±∞ +∞ -∞
-∞ ±∞ -∞ +∞
Observación: Si f y g tienen un límite uno de los cuales es nulo y el otro infinito entonces se
tiene FI
Cociente
f
Para las funciones f y g que tienen un límite (finito o infinito), la función admite un límite
g
en el cuadro siguiente
Lim f l∈  +∞ -∞
Lim g
l’ ∈ * l ±∞ ±∞
l'
+∞ 0 FI FI
-∞ 0 FI FI
Observaciones : 1- Si l’= 0, se puede concluir que cuando g conserva un signo constante en

la proximidad del « punto » cuyo límite se busca, se tiene que:
1 1
si g(x)> 0, entonces tiende hacia + ∞ ; si g(x)<0, entonces tiende hacia - ∞
g( x ) g( x )
2- Regla de comparación entre potencia, logaritmo y exponencial :
ln x ex
para todo α>0, Lim α =0 y Lim α =+ ∞
x → +∞ x x → +∞ x
Formas indeterminadas
Las situaciones señaladas FI en los cuadros se llaman (de manera significativa) : formas inde-
0 ∞
terminadas. Generalmente se dice que son 4 : , , 0 × ∞, +∞-∞ .
0 ∞
Atención, las « formas » 1∞ , +∞ 0 y 00 son también formas indeterminadas.
4- Enunciados usuales acerca de los límites

x0 designa un número real o + ∞ o - ∞

a- Comparación
Hipótesis 1 Hipótesis 2 Conclusión

Desigualdades en la proximi- Comportamiento cuando x
dad de x0 tiende hacia x0
u(x) ≤ f(x) u tiende hacia + ∞ f tiende hacia + ∞
f(x) ≤ u(x) u tiende hacia - ∞ f tiende hacia - ∞
|f(x)-l| ≤ u(x) u tiende hacia 0 f tiende hacia l
u(x) ≤ f(x) ≤ v(x) u y v tienden hacia el mismo f tiende hacia l (Teorema de
límite l gendarmes)
f(x) ≤ g(x) f y g admiten límites en x0 Lim f(x) ≤ Lim g(x)
x →x0 x →x0
Observemos que en la conclusión del último resultado solamente se obtiene una desigualdad
amplia entre los límites, incluso si f(x)<g(x).
b- Límite de una función compuesta
Teorema : Sean x0 , l, l’ reales o + ∞ o - ∞ y las aplicaciones f y g :

f g
E →F→ 
Donde E en un intervalo que contiene x 0 , x0 eventualmente excluido
F es un intervalo que contiene l, l eventualmente excluido.
Si Lim f=l y si Lim g=l’, entonces Lim g  f=l’.
x0 l x0
c- Límite a la derecha, límite a la izquierda
Definiciones : Sea una función f cuyo conjunto de definición es Df y un real x0.

1.Si la restricción de f a D f  ]x 0 , + ∞ [ admite un límite (finito o no), este límite es llamado
límite de f a la derecha en x0 . Se escribe Lim f o también Lim+ f(x).
x 0+ x →x 0
2. Si la restricción de f a D f  ]- ∞ , x0 [ admite un límite (finito o no), este límite es llamado

límite de f a la izquierda en x 0 . Se escribe Lim
−
f o también Lim− f(x).
x0 x →x0
Queda claro que si f admite l como límite en x 0 , f admite l como límite a la izquierda y a la
derecha en x0 .
Teorema del limite monótono :

Sea f una función creciente en el intervalo ]a; b[.
- Si f esta mayorada, entonces f admite un límite a la izquierda finita en b.
- Si f no esta mayorada, entonces Lim− f (x) = +∞
x →b

5- Continuidad
Sea una función f definida en x0 y que admite un límite l en x0 :

Lim f(x 0 +h)=l
h →0
esto significa que, cualquiera que sea el real ε estrictamente positivo, podemos encontrar un
intervalo que contenga 0 en el cual:
|f(x 0 +h)-l| ≤ ε
en particular para h = 0 :
|f(x 0 )-l| ≤ ε
f (x 0 ) − l f (x 0 ) − l
Suponiendo |f(x 0 )-l| ≠ 0 . Si tomamos ε = , |f(x 0 )-l| ≤ , que es sólo posible
2 2
si f(x 0 ) = l.
Teorema :
Si una función f está definida en x 0 y admite un límite en x 0 , este límite es necesaria-
mente f(x0 ).
Definición : Si el límite de f mientras que x tiende hacia un valor x0 real es igual a

f(x 0 ), decimos que f es continua en x0 .
Observación 1 : Mientras que f está definida en x0, es equivalente de decir que el límite de f
existe en x0 y que f es continua en x0.
Observación 2 : la noción de continuidad aunque intuitiva es una noción esencial en matemá-

tica que debe ser manipulado con atención. Por ejemplo, la función f define sobre  como:
1 p
f(x)= si x= no nulo irreducible, q>0
q q
f(x)=1 si x=0
f(x)=0 si x es irracional
es discontinua sobre , continua sobre c…
Ejemplo : Tomando el ejemplo del parágrafo 2 :

= f (x) 1 pour x ∈ ]-∞, 1[
Sea f una función definida por :  .
=f (x) x pour x ∈ ]1, +∞[
=  g(x) 1 pour x ∈ ]-∞, 1[

Sea g una función definida por :  g(1) = 2 .
=
g(x) x pour x ∈ ]1, +∞[
La función g no es continua en 1 porque ella no posee limite en este real
En un principio f no posee problema de continuidad en 1 porque f no es definida en este real.
Pero, Lim f (x) = 1 . Entonces podemos prolongar la función f por continuidad en 1 poniendo :
x →1

=  f (x) 1 pour x ∈ ]-∞, 1[

=f (1) Lim= f (x) 1 . Entonces ahora la “nueva” función f está definida y
x →1

= f (x) x pour x ∈ ]1, +∞[
continua en 1.
Teorema: existe una equivalencia entre :

1- f tiende hacia l mientras que x tiende hacia x 0
2- Para toda sucesión (a n) n tendiendo hacia x 0 , (f(a n )) n tiende hacia l.
En el caso de las funciones continuas, esta equivalencia se expresa de la siguiente manera :
Teorema :existe una equivalencia entre :

1- f es continua en x0
2- Para toda sucesión (a n) n tendiendo hacia x 0 , (f(a n )) n tiende hacia f(x0 ).
Definiciones : Una función f continua a la derecha en x0 es una función definida en

x0 tal que su límite a la derecha en x0 es igual a f(x0).
Una función f continua a la izquierda en x 0 es una función definida en
x0 y tal que su límite a la izquierda en x 0 es igual a f(x 0 ).
Propiedades inmediatas : Sean f y g dos funciones de  en  y x 0 un elemento de

D f  D g tal que f y g sean continuas en x0 .
Entonces, f+g, fg, kf (donde k es una constante real) son continuas en x0 .
f
Si además g(x0 ) no es nula, es continua en x0 .
g
Sea f una función continua en x 0 y g una función continua en f(x 0 ). Tenemos :

Lim f=f(x 0 ) y Lim g=g(f(x0 ))
x0 ( )
f x0
De acuerdo al teorema sobre la composición de funciones que tengan límites, deduci-

mos:
Lim g  f=g(f(x0 ))
x0
entonces g  f es continua en x0 . De donde :
Propiedad : Si f es una función continua en x0 y si g es una función continua en f(x0),

entonces la función g  f es continua en x0.
Teorema : Sea f una función de  en  y x 0 un elemento de D f tal que f sea continua

en x0 . Entonces, f está limitada en la proximidad de x0 .
Teorema : Sea f una función de  en  y x 0 un elemento de D f tal que f sea continua

en x0 y f(x0 )>0. Entonces, f es estrictamente positiva en la proximidad de x0 .

6- Continuidad en un conjunto, en un intervalo
Definición : f es continua sobre un conjunto D mientras f es continua en todo punto

de D.
Teorema : La imagen de un intervalo I para una función continua es un intervalo.
Demostración : La propiedad a demostrar es equivalente a las siguientes:

i) ∀y ∈ f (I), ∀z ∈ f (I), [y,z] ⊂ f(I)
Esto proviene de la caracterización de intervalos como partes convexas de , visto en
el capítulo sobre las Reales.
ii) ∀a ∈ I, ∀b ∈ I, [f(a),f(b)] ⊂ f(I)
Esto proviene de i) posando y = f(a) y z = f(b).
iii) ∀a ∈ I, ∀b ∈ I, f(a) ≤ z ≤ f(b) ⇒ ∃c ∈ [a,b], z = f(c)
Solo hemos traducido ii la frase: [f(a), f(b)] ⊂ f(I)
iv) ∀a ∈ I, ∀b ∈ I, f(a) ≤ 0 ≤ f(b) ⇒ ∃c ∈ [a,b], f(c) = 0
Conlleva inmediatamente de iii con z = 0. Inversamente, iii se deduce razonando sobre
g = f - z.
v) ∀a ∈ I, ∀b ∈ I, f(a)<0<f(b) ⇒ ∃c ∈]a,b[, f(c)=0
Este último enunciado es conocido bajo el nombre de teorema de los valor intermediarios. Es
entonces este último que hay que demostrar.
Teorema de valores intermediarios : Sea f una función continua sobre un intervalo

que contiene a y b tal que f(a)f(b)<0. Existe entonces c e lemento de ]a,b[ u ]a,b[ tal que
f(c)=0.
Este teorema no tuvo una demostración hasta muy tarde. Necesita en efecto una con-
cepción clara de la continuidad, que apareció en el siglo XIX. En 1817, Bolzano (1781-1848)
rechaza las justificaciones usuales basadas en consideraciones ligadas a la geometría, al mo-
vimiento, al espacio, en un dominio que él considera puramente analítico. Observemos que la
definición de Cauchy a cerca de la continuidad fue publicada en 1821.
Demostración :
Sea A = {x ∈ [a, b] / f(x) ≤ 0}. A contiene a, entonces no está vacío, y está agrandada en b.
Admite entonces un límite superior c, c ≤ b.
Mostremos que c acuerda:
- Si f(c) < 0, entonces f es estrictamente negativa en una proximidad ]c-η, c+η[ de c,
η
entonces c+ pertenece a A, lo que contradice el hecho de que c sea el límite superior de A.
2
- Si f(c) > 0, entonces f es estrictamente positiva en una proximidad ]c-η, c+η[ de c.
No obstante, c siendo el límite superior de A, Existe un elemento x0 de A en ]c-η, c+η[, tal
que f(x0 ) ≤ 0, lo que es contradictorio con f(x 0 )>0.
Tenemos así f(c) = 0.
Teorema : La imagen por una función continua de un intervalo cerrado limitado es un

intervalo cerrado limitado.

Consecuencia : Sea f una función continua en el intervalo cerrado limitado [a, b].
Entonces f alcanza sus límites:
∃M ∈ , ∃m ∈ / f([a,b])=[m, M] et ∃x 0 ∈ [a, b], ∃x1 ∈ [a, b] / m=f(x 0 ), M=f(x 1 )
Definición: sean a y b dos reales distintos tales que a<b.

Sea I=[a, b]. I es un intervalo cerrado y limitado de .
Sea f una función definida sobre I.
Decimos que la función f es continua por pedazos sobre I si f es continua sobre I salvo en un
número finidos de puntos de I, puntos en el cuales f admite un límite a la derecha y un límite a
la izquierda finidas.
Esto significa que existe un número finido de valores de I, x1 =a<x 2 <…<x n-1 <x n =b tales que :
- ∀i ∈ {1, 2, ..., n-1} , f es continua sobre ]xi , xi+1 [
- f admite límites finidos a la derecha en xi y a la izquierda en x i+1
Observaciones:
1- La secuencia de valores x1 , x 2 ,…, x n-1 , x n es llamada ‘’subdivisión de I’’
2- Toda función continua sobre I es continua por pedazos sobre I
7- Continuidad y derivabilidad
Definición : Sea una función f de  en  definida sobre un intervalo conteniendo x0.

Decimos que f se puede derivar en el punto x0 si y solamente si existe un intervalo I
que contenga O tal que ∀h∈I , f(x0 +h)=a+bh+hε(h),
donde a y b son reales y ε una función definida sobre I tal que Lim ε(h) = 0.
h →0
El real b (en el cual admitimos la unicidad) es llamado número derivado de f en x0 .
Decimos también que a + bh + h ε(h) es un desarrollo limitado de orden 1 en la

proximidad de 0 de la función: h  f(x 0 + h).
Tomemos h = 0 en la igualdad anterior, tenemos: f(x 0 ) = a,
De acuerdo el teorema de los límites
Lim f(x 0 +h)=a+ Lim (bh)+ Lim hε(h)=a
h →0 h →0 h →0
entonces Lim f = f(x0 ) lo que significa que f es continua en x 0 . Enunciamos este resultado :
x0
Teorema :
Toda función que se pueda derivar en un punto es continua en ese punto.
Observación : La recíproca es falsa: una función puede ser continua en un punto sin ser que
se pueda derivar en ese punto, por ejemplo la función valor absoluto en 0.
Existen funciones continuas en x 0 que no admiten ninguna derivada a la derecha ni a la iz-
1
quierda de x 0 , por ejemplo x  x.sen   en x0 =0.
x

1
Gráfico de x  x.sen   .
x
8- Biyección
Propiedades generales sobre las biyecciones :

1- Sea f una biyección de A en B. Entonces f-1 es una biyección de B en A
2- Sea f una biyección de A en B y g una biyección de B en C. Entonces g  f es
una biyección de A en C y (g  f)-1=f-1  g-1.
Representación gráfica de una biyección y de su recíproca

Sea f une función de  en  tal que f sea biyectiva de D f sobre su imagen. El plano se
sitúa en una referencia ortonormalizada, las curvas representativas de f y de f-1 son simétricas
en relación a la recta de ecuación y=x (primera bisectriz).
Ejemplo :
y=x
y=f -1(x) y=f(x)
9- Continuidad y biyección
1- Composición de funciones variables
Sea f una función derivable en x0 y g una función derivable en f(x0 ). Estudiemos si

g  f es derivable en x 0 .

Ya que f es derivable en x0 , existe un intervalo I que contiene el 0 tal que:
∀ h∈I, f(x0 +h)=f(x0 )+hf ’(x 0 )+hε 1 (h) (1)
α siendo una función tal que Lim ε 1 (h) = 0.
h →0
Ya que g se puede derivar en f(x0 ), existe un intervalo J que contiene 0 tal que:
∀ k∈J, g[f(x 0 ) + k] = g[f(x 0 )] + kg’ [f(x0 )] + kε 2 (k) (2)
β siendo una función tal que Lim ε 2 (k) = 0.
h →0
De acuerdo (1), podemos tomar f(x0 +h)=f(x0 )+k con k= hf ’(x 0 )+hε 1 (h). La igualdad
(2) se puede escribir entonces :
g [f(x 0 + h)] = g [f(x0 )] + [hf ’(x 0 ) + hα(h)] g’[f(x 0 )] + hε 3 (h)
= g [f(x0 )] + hf ’(x 0 ) × g’[f(x0 )] + hε(h)
= g  f(x 0 ) + h[g’  f(x 0 ) × f’(x0 )] + hε(h) (3)
en donde ε 3 y ε son dos funciones de h de límite 0 cuando h tiende hacia 0.
El desarrollo limitado (3) nos muestra que g  f se puede derivar en x 0 , siendo el núme-
ro derivado g’  f(x 0 ) × f ’(x 0 ).
Si x 0 describe un intervalo, podemos concluir:
Teorema :
Si f se puede derivar sobre un intervalo y si g se puede derivar sobre la imagen por f de
este intervalo, entonces g  f se puede derivar sobre el mismo intervalo f y tenemos:
(g  f)’=(g’  f) × f ’
Observación : La demostración del teorema anterior fue hecho utilizando los “desarrollos
limitados de orden 1”. Hubiéramos podido demostrarlo utilizando la definición de un número
derivado por medio de una taza de variaciones.
2- Continuidad y biyección
Teorema : Sea f una función de  en , continua y estrictamente monótona sobre un

intervalo I. Entonces:
a- f es una biyección de I sobre f(I)
b- f -1 es continua, estrictamente monótona “de mismo sentido de variación que f”
c- si f se puede derivar en x0 elemento de I y f ’(x0 ) no nulo, entonces f -1 se puede
1
derivar en f(x 0 ) y : (f -1)’(f(x 0 ))= .
f '(x 0 )
Teorema : Sea f une función de  en , que se puede derivar sobre un intervalo I, de

derivada estrictamente positiva (o estrictamente negativa) salvo eventualmente en un número
finito de puntos. Entonces, f es una biyección de I sobre f(I).
Teorema : Sea f una función de  en , biyectiva de I sobre f(I), que se puede derivar
sobre I tal que f’ no se anula sobre I. Entonces f -1 se puede derivar sobre f(I) y :
1
(f -1) ’=
f ' f −1

Ejercicio 1. Sean f una aplicación de ]a,b[ en  y x o un real de ]a,b[. Demostrar que una
condición necesaria y suficiente para que f admita 0 como límite en x o es que |f| admita0 co-
mo límite en x o .
Ejercicio 2. 1- Utilizando la definición bajo la forma de una aserción cuantificada, demostrar

que la función identidad es continua en .
2- Deducir que para todo entero n la función x  x n es continua en .
3- Concluir que las funciones polinomiales son funciones continuas en .
Ejercicio 3. Estudiar el límite eventual de las siguientes funciones:

x2 −1 + x 1 − cos(x) 2
a- x  en x0 =1 b- x → en x 0 =0
x sen(2x)
x 2 − 10x + 25 sen(x)
c- x  en x0 =5 d- x  2 en x 0 =0
x −5 x −x
1
e- x  x 2 − 1 − x en +∞ f- x  x 2sen   en +∞
x
g- x  x − 1 − x + 2 en +∞ h- x  sen(x) ln(| x |) en x 0 =0
 x +1 
Ejercicio 4. Estudiar la función : x  ln  2 .
 x − 3x + 2 
1 + sen(x)
Ejercicio 5. Estudiar la función : x  .
2sen(x) − 1
Ejercicio 6. Estudiar la continuidad en  de la función f definida por : f (x) = x 2 si x ≤ 0 y

f (x) = x ln(x) si x>0.
Ejercicio 7. Aplicación del teorema de los valores intermediarios

Sea P un polinomio de coeficiente reales de grado impar.
1- Demostrar que podemos encontrar dos reales a y b tales que: P(a) × P(b) < 0.
2- Deducir que P tiene al menos una raíz real.
Ejercicio 8. Sea f una aplicación real y k un real positivo. Decimos que f es lipschitziana en
relación a k en  si :
∃k ∈+ ∀(x1 , x 2 ) ∈² | f (x1 ) − f (x 2 ) |≤ k | x1 − x 2 |
Decimo que f es lipschitziana si existe un real positivo k tal que f es lipschitziana en relación
a k.

1
1- Demostrar que la aplicación x  es lipschitziana en relación a 1 en 
1+ | x |
2- Demostrar que toda aplicación lipschitziana en  es continua en .
1
Ejercicio 9. Sean f y g las funciones definidas por : f : x  2x 2 − 3x + 1 y g : x  . Dar
x −1
el dominio de definición y el sentido de la variación de f  g y de g  f.

EJERCICIOS
Ejercicio 1. Estudiar el límite eventual de cada uno de las funciones siguientes en el punto x0
indicado:
1 1 3− x
1- f ( x ) = 2 − 2 ( x0 =
2) 2- g ( x )
= = ( x0 9)
x ( x − 2 ) x − 3x + 2 x 2 − 81
1 − cos x sen ( x 3 )
3- h ( x )
= = ( x0 0) 4- t ( x ) =
= ( x0 0)
sen 2 ( πx ) sen 2 ( x )
cos x  π
5- s ( x )
= =  x0 
π  2
x−
2
Ejercicio 2. Demostrar los siguientes resultados con ayuda de la definición:

a- Lim(2x + 1) =3
x →1
1 1
b- Lim =
x 2
x →2
c- Lim(2x 2 + 1) =
9
x →2
d- Lim 2x + 1 =3
x →4
Ejercicio 3. a- Estudiar y representar gráficamente la función:

f : x  x − E(x )
b- Para cuáles valores del real ‘a’ la función:
g(x) = [x - E(x)][x - E(x) - a]
¿es continua sobre ? ¿Cuál es entonces su gráfico?
Ejercicio 4. Estudiar la continuidad de las funciones siguientes a los puntos indicados:

 esen (x ) − 1
 si x ≠ 0
1- f1 (x) =  x en 0
 1 si x=0


 sen(x) si x<0

2- f 2 (x) =  0 si x=0
 1
exp  -  si x>0
  x

Ejercicio 5. Para cada una de las funciones siguientes, mostrar que es continua sobre su do-
minio de definición, y estudiar si es prolongable por continuidad sobre .
1
1- f1 (x) = e x −3
x 3 − 2x 2 − x + 2
2- f 2 (x) =
x −1
sen(2x)
3- f 3 (x) =
3x
1
4- f 4 (x) = x.sen  
x
Ejercicio 6. Sea f una función de  en 
1. Mostrar que si f es creciente y mayorada, entonces f admite un límite finito en

+ ∞.( Podemos considerar en conjunto f()).
2. ¿Qué pasa si f es una función creciente pero no mayorada?
Ejercicio 7. Sea f una función definida sobre . Sea g una función tal que Lim g ( x ) = 0 .
x →+∞
Suponemos que existe un real x 0 y un real M tales que para todo real x : x > x 0 ⇒ f ( x ) < M .
Mostrar que Lim f ( x ) g ( x ) = 0 .
x →+∞
Ejercicio 8. Sea f una función de [0;1] en , que se puede derivar y tal que f(0) y f(1) sean
iguales. Consideramos la función g siguiente:
  1
 f(2x) si x ∈ 0, 2 
  
g(x) = 
f(2x-1) si x ∈  1 ,1
  2 
1- Mostrar que g es continua sobre [0,1].
2- Bajo qué condición g se puede derivar sobre [0,1] ?
Ejercicio 9. Sean f, g y h las funciones definidas por:

x2 − x x x 3 − 2x 2 − x + 2
f (x) = g ( x ) = h (x) =
x −1 x2 − x 1− x
1- Mostrar que f es continua en 0. ¿Podemos prolongar la función f por continui-
dad en 1?
2- ¿Podemos prolongar g por continuidad en 0?
3- a ¿h es continua en 0?
b. Calcular : Lim h ( x ) y Lim h ( x ) .
x →−1 x →1
c. Definir la función k que prolonga h por continuidad sobre .
Ejercicio 10. Mostrar con ayuda de la definición que si una función f definida sobre E es
continua en x 0 , entonces |f| también lo es. Estudiar la recíproca.

Ejercicio 11. Mostrar que la ecuación "x²cos(x) + x sen(x) + 1 = 0" admite al menos una so-
lución real.
Ejercicio 12. Sea f una función continúa de  en  tal que Lim f (x) = +∞ y Lim f (x) = −∞ .
x →+∞ x →−∞
1- Mostrar que existe un real a < 0 tal que f (a) < 0 y un real b > 0 tal que f (b) > 0.
2- Mostrar que la ecuación f (x) = 0 posee por lo menos una solución.
3- Deducir que todo polinomio a coeficientes reales de grado impar posee por lo me-
nos una raíz efectiva.
f(x)
Ejercicio 13. Sea f : + → + una aplicación continua tal que Lim = l < 1. Mostar que:
x→+∞ x
∃x 0 ∈+/ f(x 0 )=x0
Ejercicio 14. Sean a, b dos reales tales que a ≤ b y f, g dos funciones definidas y continuas
sobre [a,b]. Suponemos que para todo real x de [a,b], f(x) > g(x). Demostrar que :
∃λ > 0 ∀x ∈ [a;b], f(x) ≥ g(x)+λ
π
Ejercicio 15. Tomamos a = y sea f la función real definida sobre]-a,a[ por f(x)=tan ( x 3 ) .
3
2
a- Mostrar que f admite una función recíproca g de la cual determinarán el con-
junto de definición.
b- Estudiar la derivabilidad de g. Expresar g'(u) en función de u y de g(u).
c- Determinar los gráficos de f y de g en una referencia ortonormalizada.
2x
Ejercicio 16. Sea f :  → [-1,1] definida por f (x) = .
x² + 1
1- Estudiar las variaciones de f. ¿f es inyectiva? sobreyectiva ?
2- Mostrar que la restricción de f a [-1,1] es una biyeccion. Determinar f -1.
π  1
Ejercicio 17. Sea f la función definida sobre I =  , π  por f (x) = .
2  sin(x)
1- Estudiar las variaciones de f, y mostrar que f es una biyeccion de I sobre un interva-
lo J a determinar. (No procuraremos calcular explícitamente f -1). ¿Cual es el sentido de varia-
ción de f -1 ?
2- ¿En cuales puntos de J la función f -1 es derivable?
( ) ( )
3- Determinar f -1 2 , f -1(2), y ( f −1 ) ' 2 , ( f −1 ) ' (2).
-1
4- Trazar los grafos de f y f en el plano ortonormal.
x −1
Ejercicio 18. Sea f la función definida sobre *+ por : f ( x ) = .
ln x
1- Determinar el conjunto de definición de f.
2- Mostrar que f es prolongable por continuidad en 0 y en 1 po r una función g
continua sobre [0;+∞[ .
3- ¿g es derivable en 0? ¿ La curva de g admite una asíntota en + ∞ ?
Ejercicio 19. Consideramos la función f definida sobre ]-1; +∞[ por :

 x − ln (1 + x )
 si x ≠ 0
f (x) =  x
0 sinon

Notamos Cf la representación grafica de f en una referencia ortonormal.
1- Mostrar que f es de clase derivable con derivada continua sobre ]-1; +∞[ y ex-
plicitar su derivada.
2- Determinar la ecuación de la tangente de la curva en el punto de abscisa 0. ¿La
curva admite tangentes horizontales?
3- Estudiar las variaciones de la función sobre ]− 1;+∞[ . Deducir el signo de la
función f.
4- Estudiar la existencia de asíntotas de la curva y trazar la curva Cf .
x +1
Ejercicio 20. Sea la función definida sobre I= ]1; +∞[ por: f : x  .
x −1
Demostrar que f es una biyeccion de I en I, y determinar su biyeccion reciproca.
2x
Ejercicio 21. Sea f :  → [-1,1] definida por f ( x ) = .
1+ x2
1- ¿f es inyectiva, sobreyectiva?
2- Mostrar que la restricción de f a [ −1,1] es una biyeccion. Determinar la expre-
sión de la función reciproca.

Ejercicio 22. Sea f una función definida en . Suponemos que existe un real x0 y un real M
tales que :
∀ x ∈ , x > x0 ⇒ | f (x) | < M
Sea g una función tal que : Lim g(x) = 0 .
x →+∞
Demostrar que Lim f (x)g(x) = 0 .

x →+∞
Corrección : lim g ( x ) =0 ⇔ ∀ε>0 ∃A ε ∈ , x ≥ A ε ⇒ g(x) < ε .

x →+ ∞
 
Sea entonces ε>0. Tomemos α =max  A ε , x 0  .
 M 
ε
Entonces tenemos : x ≥ α ⇒ f ( x ) g ( x ) ≤ f ( x ) g ( x ) < M
= ε.
M
Hemos entonces demostrado que ∀ε > 0, ∃α ∈ , x ≥ α ⇒ f ( x ) g(x) < ε , lo que significa jus-
tamente que lim f ( x ) g ( x ) = 0 .
x →+∞
3− x
Ejercicio 23. Estudiar el límite eventual de la función f :x  en el punto x0 =9.
x² − 81
0
Corrección : Se trata de un forma indeterminada de tipo .
0
Observamos que x 2 − 81 = ( x − 9 )( x + 9 ) = ( x −3 )( )
x + 3 ( x + 9 ) para x ≥ 0.
Tenemos entonces
   
 3− x   −1 = − 1 .
lim g ( x ) = lim = lim
x →9 x →9 
(x −3 )( )
x + 3 ( x + 9 )  x →9 
 ( )
x + 3 ( x + 9) 

108
Ejercicio 24. 1- Sea f una función de  en . Demostrar que si f es creciente y mayorada,

entonces f admite un límite finito en + ∞. (Podemos considerar el conjunto f()).
2- Que pasa si f es creciente pero no mayorada?
Corrección : 1- f() es un conjunto no vacío y mayorado entonces f() admite un límite sup
que anotaremos α.
Caracterizando el límite superior, tenemos: ∀ε > 0, ∃y ε ∈, f() y ε ≤ α ≤ y ε + ε .
Esto puede escribirse: ∀ε > 0, ∃x ε ∈, f ( x ε ) ≤ α ≤ f ( x ε ) + ε .
Además, como f es creciente, tenemos ∀x ≥ x ε f ( x ε ) ≤ f ( x ) , y como f ( x ) ∈ f(), f ( x ) ≤ α .
Deducimos que x ≥ x ε ⇒ f ( x ) ≤ α ≤ f ( x ) + ε , sea x ≥ x ε ⇒ α − f ( x ) ≤ ε .
Hemos entonces demostrado que ∀ε > 0, ∃x ε ∈, x ≥ x ε ⇒ α − f ( x ) ≤ ε , lo que significa
exactamente que lim f ( x ) = α .
x →+∞

2- f no mayorada significa que : ∀M ∈ , ∃x 0 ∈, f ( x 0 ) ≥ A .
Como f es creciente, x ≥ x 0 ⇒ f ( x 0 ) ≤ f ( x ) .
Deducimos entonces que ∀M ∈ , ∃x 0 ∈, x ≥ x 0 ⇒ f ( x ) ≥ A .
Eso significa exactamente que lim f ( x ) = +∞ .
x →+∞
Ejercicio 25. Sea φ la función definida por : φ (x) =

ln x ( ).
4
x4 −1
1- Determinar el dominio de definición de esta función.
2- Estudiar el límite eventual de φ en los puntos (-1), 0 y 1.
3- Podemos prolongar φ por continuidad en * ? en  ?
Corrección : 1- Tenemos Dφ = {-1, 0, 1}.

2- Antes que nada, observemos que lim φ ( x ) = lim φ ( x ) porque la función es
x →−1 x →−1
par.
ln ( x 4 ) ln ( X ) ln (1 + u )
lim =φ ( x ) lim = 4
lim = lim .
x →1 x →1 x − 1 X →1 X − 1 u →0 u
ln (1 + u )
Recordamos que lim =1
u →0 u
Deducimos que lim φ ( x ) = 1.
x →1
ln ( x 4 )
Por otro lado, tenemos: lim φ ( x ) = lim = lim ( − ln ( X ) ) = +∞ .
x →0 x 4 − 1 X → 0+
x →0
3- Podemos prolongar φ por continuidad en * tomando φ (1) =φ ( −1) =1

Por el contrario, no podemos prolongar φ en  todo entero.
Ejercicio 26. Estudiar la continuidad de las siguientes funciones en los puntos indicados:

 sen x si x<0

1- f(x) =  0 si x=0 en el punto x0 = 0
 -1
exp si x>0
 x
 1
 xE si x ≠ 0 1
2- g(x)=   x  en los puntos x0 =0 y x 0 =
 1 3
 si x=0
 0 si x racional
3- h(x)=  en los puntos x0 =0 y x 0 =1.
 x si x irracional
lim− f ( x ) lim
Corrección : 1- Tenemos= = −
sen ( x ) 0 .
x →0 x →0
 1
(
Además , lim+ f= x ) lim+ exp  −= lim exp ( −=
X) 0 .
x →0 x →0  x  X →∞

Deducimos que f es continua en 0.
1 E (X)
2- Tenemos lim g ( x )= lim xE  = lim = 1= g ( 0 ) entonces g es continua en
x →0 x →0
x X →±∞ X
0.
1 E (X) 2 1
Tenemos lim + g ( x ) = lim + xE   = lim− = ≠ 1 = g   entonces g no es continua
1
x → 
1
x →   x  X →3 X 3 3
 3  3
1
en .
3
0 si y racional
3- Sea y ∈ , tenemos h ( 0 ) − h ( y ) =  .
y sino
En particular, ∀ε > 0, y ≤ ε ⇒ h ( 0 ) − h ( y ) ≤ ε .
Entonces h es continua en 0.
Por el contrario, h no es continua en 1. Para probar esto, vamos a escribir la definición de esta
propiedad y la vamos a negar:
h continua en 1 ⇔ ∀ε > 0, ∃δ > 0, ∀y ∈ D h , 1 − y < δ ⇒ h (1) − h ( y ) < ε
(
Entonces h no es continua en 1 ⇔ ∃ε > 0, ∀δ > 0, ∃y ∈ D h , ( 1 − y < δ ) ∧ h (1) − h ( y ) ≥ ε )
0 si y racional
Sea y ∈ , tenemos h (1) − h ( y ) = .
y sinon
1
Sea entonces=ε et δ > 0 .
2
Podemos encontrar un elemento y irracional tal que 1 < y < 1 + δ .
Tenemos entonces por un lado 1 − y < δ y por otro lado, h (1) − h ( y )= y > 1 ≥ ε .
Deducimos entonces que h no es continua en 1.
Ejercicio 27. Sea f una función continua de [0, 1] en [0, 1].

Demostrar que la ecuación f(x) = x posee al menos una solución.
Podremos considerar la función g definida por g(x) = x – f(x).
Corrección : Anotemos g(x)=f(x)-x.

g es continua en [0, 1] porque compuesta por funciones continuas en [0, 1].
Supongamos que ¬ ( ∃x ∈ [ 0,1] g ( x ) =0 ) pues ∀x ∈ [ 0,1] g ( x ) ≠ 0 .
Como g es una función continua, esto implica que tiene un signo constante.
Podemos entonces suponerque ∀x ∈ [ 0,1] g ( x ) < 0 por ejemplo.
Observemos que si g(x)>0 entonces nos interesamos a la función (-g).
Así, ∀x ∈ [ 0,1] , x < f ( x ) .
Como para x=1, esto nos da 1<f(1) lo que es absurdo por hipótesis, porque f tiene valores en
[0, 1].
Concluímos que ∃x ∈ [ 0,1] , f ( x ) =x .
Ejercicio 28. Sea f una función definida en  y periódica.

1- Suponemos que lim f ( x ) = l ∈. Demostrar que f es constante.
x →∞

2- Suponemos que f es continua en . Demostrar que f está limitada.
Corrección : 1- Anotemos T el period de f y tomemos un real.

Tenemos ∀n ∈ , f ( a + nT ) =
f (a ) .
Hacemos tender n hacia +∞ , obtenemos : f (=
a ) lim f ( a + nT
= ) lim f ( X
= ) l.
n →+∞ X →+∞
Finalmente, ∀a ∈ , f(a)=l entonces f es una función constante.

2- Anotemos T el periodo de f (T>0).
f es continua en [0, T] entonces en particular, f está limitada y alcanza sus límites en este in-
tervalo.
Sea entonces m su mínimo en [0, T] y M su máximo. Sea a un real.
Existe un entero n tal que ( a + nT ) ∈ [ 0, T ] .
a a a
De hecho, ∀a ∈ , E   ≤ < E   + 1 .
T T T
a
Anotemos entonces n = −E   ( entier), tenemos entonces :
T
a
−n ≤ < −n + 1 ⇔ −nT ≤ a < −nT + T ⇔ 0 ≤ a + nT < T
T
Ahora, como ( a + nT ) ∈ [ 0, T ] , tenemos m ≤ f ( a + nT ) ≤ M .
Como f ( a + nT ) =
f ( a ) entonces m ≤ f ( a ) ≤ M .
Deducimos que f es limitada en .
Ejercicio 29. Consideramos una aplicación f continua de + en el mismo y que admite 0 co-
mo límite en +∞ .
Demostrar que para todo a ≥ 0 , existe b ≥ a en el cual f alcanza su máximo en [ a, +∞[ .
Corrección : Sea a ≥ 0 .
f teniendo valores en +, tenemos ∀x ∈ +, f ( x ) ≥ 0 .
Por hipótesis, tenemos lim f ( x ) = 0 y esto se escribe:
x →+∞
∀ε > 0, ∃A ≥ 0, ∀x ∈ +, ( x ≥ A ) ⇒ ( f ( x ) ≤ ε )
f es continua en [0, a] que es un intervalo cerrrado limitada, entonces f está limitada y alcanza
sus límites.
()
Entonces existe a ∈ [ 0, a ] tal que ∀x ∈ [ 0, a ] f ( x ) ≤ f a .
Anotemos ε =f ( a ) , con lo que precede, ∃A ≥ 0, ∀x ∈ +, ( x ≥ A ) ⇒ ( f ( x ) ≤ f ( a ) ) .
Si A ≤ a , entonces basta con tomar b=a.
Sino, tenemos A>a, pero f es continua en [a, A] que es un intervalo cerrado limitado entonces
f está limitada y alcanza sus bornes. En particular, existe b ∈ [ a, A ] en el cual f alcanza su
máximo en [a, A].
Además, ya que ∀x ≥ A, f ( x ) ≤ f ( a ) , tenemos también ∀x ≥ A f ( x ) ( ≤ f ( a ) ) ≤ f ( b ) .
Deducimos que f(b) es el máximo de f en [ a, +∞[ .

x 2 −3x + 2
1
Ejercicio 30. Consideramos la función f definida por f(x) =   .
3
1- Cuál es el conjunto de definición de f ?
2- En qué conjunto f se puede derivar?
3- Estudiar las variaciones de f.
4- Demostrar que la resticción de f en el intervalo [2 ;+∞[ realiza una biyección de
[2 ;+∞[ en un intervalo J que precisaremos.
5- Sin calcular f -1, estudiar el sentido de la variación y la derivabilidad de f –1.
6- Trazar el aspecto de la representación gráfica de la restricción de f y de f –1 en la
misma referencia.
7- Determinar f –1(x) para x ∈ J.
  1 
(
Corrección : 1- Tenemos f ( x )= exp  x 2 − 3x + 2 ln   = exp − x 2 − 3x + 2 ln ( 3) .
  3 
)
La función f está definida si y solamente si P(x) = x 2 − 3x + 2 ≥ 0 .
Podemos verificar que : x 2 − 3x + 2 = ( x − 1)( x − 2 ) .
Concluimos que Df = ]−∞;1]  [ 2; ∞[ .
( x ) exp − P ln ( 3) .
2- Hemos visto que f se escribe de ésta forma: f = ( )
Entonces f se puede derivar si y solamente si P se puede derivar, lo que quiere decir, si y
solamente si P no se anula.
Deducimos entonces que f se puede derivar en Df ′ = ]−∞;1[  ]2; ∞[ .
3- f se puede derivar en Df ′ y tenemos :
− ( 2x − 3) ln ( 3)
∀x ∈ Df ′ , f ′ ( x )
=
2 x − 3x + 2 2 (
exp − x 2 − 3x + 2 ln ( 3) )
Vemos entonces claramente que el signi de f ′ es el signo de − ( 2x − 3) .
Tenemos entonces la siguiente tabla de variaciones:
x 3
−∞ 1 2 +∞
2
2x − 3 - - + +
f ′(x) + -
f 1
4 f es estrictamente decreciente en [ 2; +∞[ y continua, entonces f realiza una biyección

de [ 2; +∞[ dans
= J f ([ 2; +∞[ ) .
Queda determinar J :
Primero, tenemos f ( 2 ) = 1 .
Por otro lado, lim f=
x →+∞ x →+∞
(
( x ) lim exp − x 2 − 3x + 2 ln=
( 3) ) lim exp ( −X ln=
X →+∞
( 3) ) 0 .
Deducimos entonces que J = ]0 ;1]

1
5- Si f ′ ( f −1 ( x ) ) no se anula, tenemos: ( f −1 )′ ( x ) = .
f ′(f −1
( x ))
Con lo que precede, si x ∈ J , entonces f −1 ( x ) ∈ [ 2; +∞[ , y entonces f ′ ( f −1 ( x ) ) no se anula.
Deducimos entonces que en J, el signo de ( f −1 )′ es el mismo que aquel de f ′ . (cf. resultado de

curso).
Tenemos entonces la siguiente tabla de variaciones:
x 0
1
-
( f )′ (x)
−1
+∞
−1
f
6- El aspecto de la representación gráfica de la restricción f y de f –1 en la misma refe-

rencia es:
7- Anotamos y = f ( x ) con x ∈ J ( y entonces y ∈ ]0,1]) y queremos expresar x en fun-

ción de y.
f (x) ⇔ y =
y= ( )
− x 2 − 3x + 2 ln ( 3)
exp − x 2 − 3x + 2 ln ( 3) ⇔ ln ( y ) =
No sabemos resolver esta ecuación directamente, debemos elevar al cuadrado:
( x 2 − 3x + 2 ) ( ln ( 3) )
− x 2 − 3x + 2 ln ( 3) ⇒ ( ln ( y ) ) =
2 2
ln ( y ) =
2 2
 ln ( y )   ln ( y ) 
( ln ( y ) ) = ( x − 3x + 2 ) ( ln ( 3) )
2 2 2 2 2
⇔ x − 3x + 2 =   ⇔ x − 3x + 2 −   = 0
 ln ( 3 )   ln ( 3 ) 
2
 ln ( y ) 
Para simplificar los cálculos, tomamos: α = , debemos entonces resolver:
 ln ( 3) 
 
x 2 − 3x + 2 − α = 0
Se trata de una ecuación de segundo grado, el discriminante de este polinomio es:
∆ = 9 − 4 ( 2 − α ) = 1 + 4α

3 − 1 + 4α 3 + 1 + 4α
Tenemos entonces dos
= soluciones: x1 = et x 2 .
2 2
2
 ln ( y ) 
Reemplazando α por  , obtenemos:
 ln ( 3) 
 
2
 ln ( y ) 
3 − 1+ 4 
3ln ( 3) − ( ln ( 3) ) + 4 ( ln ( y ) ) 3ln ( 3) + ( ln ( 3) ) + 4 ( ln ( y ) )
2 2 2 2
 ln ( 3) 
x1 = = o x2
2 2 ln ( 3) 2 ln ( 3)
Sabemos que tenemos una única solución y para determinarla vamos verificarla tomando va-
lores particulares para x e y :
Tomemos y = 1 , entonces vamos a tener = x f= −1
( y) 2 .
( ln ( 3) ) ( ln ( 3) )
2 2
3ln ( 3) − 3ln ( 3) +
Tenemos
= x1 = 1y
= x2 = 2.
2 ln ( 3) 2 ln ( 3)
( ln ( 3) ) + 4 ( ln ( y ) )
2 2
3ln ( 3) +
Concluimos que f −1
( y) = .
2 ln ( 3)
Ejercicio 31. 1- La función parte entera E posee la propiedad del valor intermediario ?
2- Buscar una función discontinua en [0 ; 1] que poseda la propriedad del valor
intermediario.
Corrección : 1- No, de hecho podemos tomar como ejemplo y = 1,5 .

Tenemos E (1) ≤ y ≤ E ( 2 ) y por lo tanto no existe c ∈  tal que y = E ( c ) ya que y no es un
entero..
 1
 x si 0 ≤ x <
2- f ( x ) =  2.
 2 − 2x si 1 ≤ x ≤ 1
 2

Capítulo 11
FUNCIONES ELEMENTALES
0- Ejemplo de la cadena
Galileo fue sin duda el primero en interesarse a la cadena, que asimiló a un arco de
parábola. Jean Bernoulli, Huygens y Leibniz encontraron (independientemente) en respuesta
al desafío lanzado por Jakob Bernoulli, su verdadera naturaleza en 1691: engendrada por un
coseno hiperbólico.
Consideremos un cable homogéneo, flexible, atado en A y B. En su posición de equi-
librio, el cable pende en un plano vertical. Establezcamos en este plano un referencial de ejes
 
normalizados (O, i, j ), donde O designa el punto más bajo del cable y notemos g el campo de
gravitación terrestre (pesantez). Sea M(x,y) un punto del cable.
x x
-
e k +e k
x
x e y están entonces ligados por la relación : y=k = k.ch   donde ch desig-
2 k
na el Coseno Hiperbólico.
La cadena es de una importancia capital porque permite

calcular las flechas (es decir la distancia del arco a la cuerda)
que dar a los cables suspendidos a fin de que las tensiones en
los puntos de enganche no sean excesivas. En efecto, desde
que buscamos a t ender por mucho un cable entre dos pilones,
las tensiones se vuelven considerables.

En el caso de las líneas ferroviarias eléctricas, mitigamos a la flecha redhibitoria por
un cable portador principal de la catenaria (cable que conduce la corriente que alimenta la
locomotora, del latín catena=cadena) : el cable superior sufre una flecha aceptada, lo que dis-
minuye las tensiones entre los dos pilones.
La catenaria queda de este modo bien lineal, gracias a los enganches auxiliares múlti-
ples a un cable auxiliar. De hecho, el antiguo nombre de la cadena fue la catenaria, nombre
que no se ha modificado en inglés (catenary).
Notemos en fin que la cadena es la ruedecilla del foco de una parábola : lugar de su
foco cuando gira sin deslizar, sobre una recta.
1- Logaritmos y exponenciales
x dt
Definición: La función definida en *+ por x  ∫ es la función logaritmo nepe-
1 t
riano (logaritmo de base e). Se escribe ln.
1
x  ln(x) es la primitiva de x  definida en ]0, + ∞ [ y que se anula en x = 1.
x
1
Su derivada x  siendo estrictamente positiva, ln es entonces estrictamente creciente. La
x
a 1
derivada de x  ln(ax) valiendo: = , ln(ax) es igual a ln(x) + Cte. El valor de Cte es ob-
ax x
tenido tomando x=1, de lo que resulta la célebre relación :
ln(ax) = ln(x) + ln(a)
Esta relación, transformando el producto en adición, ha permitido, desde el siglo XVII
hasta la introducción de las calculadoras a bajo precio en 1980, acelerar notablemente las po-
sibilidades de cálculo de los matemáticos. De esta manera, Laplace se maravilla « los loga-
ritmos, admirables instrumentos , que, reduciendo a unas cuantas horas el trabajo de varios
meses, duplica, si podemos decirlo, la vida de los astrónomos, y les ahorra los errores y los
desagrados inseparables de los largos cálculos».

Propiedad: ln es una biyección de *+en . Su biyección reciproca es la función ex-
ponencial, que se escribe exp, biyección de  en *+.
e
y=x
y=exp(x)
y=ln(x)
Definición: Se define el logaritmo de base a (donde a es real estrictamente positivo

ln x
distinto de 1) como log a x= .
ln a
Se trata de una biyección de *+en . Su biyección recíproca es la función exponen-

cial de base a, que se escribe exp a , biyección de  en *+.
Como la restricción de exp a hasta coincida con la función definida sobre  por:
n  a , se escribe exp a (x)=ax.
n
a>1
a<1
Funciones logarítmicas de base a

a>1
a<1
Funciones exponenciales de base a
2- Potencias
Definición: ∀a ∈ *+, ∀b ∈ , ab=eb.ln a
Observación: No confundir la función potencia: x  xa con la función exponencial (de base

a): x  ax.
α>1
α=1
0<α<1
α=0
α<0
Función potencia x  xα
ex xa
Crecimiento comparado: Lim = +∞ y Lim = +∞ .
x →+∞ x a x →+∞ ln x

3- Función arco seno
 π π
Definición: La función seno es una biyección de  − ,  en [-1,1]. Su biyección
 2 2
 π π
recíproca es la función arco seno de [-1,1] en  − ,  .
 2 2
Observación : Por qué arc y no ángulo ? Simplemente porque en el círculo trigonométrico

(centrado en el origen y de radio 1), arcsen(x) representa la medida del arco AM definido por
 que mide x.
el ángulo AOM
He aquí una tabla de valores :

3 2 1 1 2 3
x -1 - - - 0 1 senθ
2 2 2 2 2 2
π π π π π π π π
arcsen(x) - - - - 0 θ
2 3 4 6 6 4 3 2
 π π
Propiedades: 1- ∀x ∈  − ,  , ∀y ∈ [-1,1] , y=sen x ⇔ x= arcsen y
 2 2
 π π
2- ∀x ∈  − ,  , arcsen (sen x)=x
 2 2
3- ∀x ∈ [-1,1] , sen (arcsen x)=x
4- ∀x ∈ [-1,1] , cos (arcsen x)= 1 − x²
  3π    π
Ejercicio: Determinar arcsen  sen    , arcsen(sen x) por x elemento de  −π, −  .
  4   2
Propiedad: arcsen es estrictamente creciente, impar, continua sobre [-1,1].
1
Teorema: arcsen es derivable sobre ]-1,1[ y ∀x ∈] − 1,1[ , (arcsen x)’= .
1 − x²
Observación: arcsen no es derivable en-1 y 1. En los puntos de abscisa 1 y 1, el grafo de arc-

sen admite tangentes verticales.

Representación gráfica de la función arco seno
arco seno
sen
4- Función arco coseno
Definición: La función coseno es una biyección de [0,π] en [-1,1]. Su biyección recí-

proca es la función arco coseno de [-1,1] en [0,π].

3 2 1 1 2 3
x -1 - - - 0 1 cosθ
2 2 2 2 2 2
5π 3π 2π π π π π
arccos(x) π 0 θ
6 4 3 2 3 4 6
Propiedades: 1- ∀x ∈ [ 0, π] , ∀y ∈ [-1,1] , y=cos x ⇔ x= arccos y

2- ∀x ∈ [ 0, π] , arccos (cos x)=x
3- ∀x ∈ [-1,1] , cos (arccos x)=x
4- ∀x ∈ [-1,1] , aen (arccos x)= 1 − x²
Propiedad : arccos es estrictamente decreciente, continua sobre [-1,1].
1
Teorema: arccos es derivable en ]-1,1[ y ∀x ∈] − 1,1[ , (arccos x)’= - .
1 − x²
Observación: arccos no es derivable en-1 y 1. En los puntos de abscisa 1 y 1, el grafo de arc-

cos admite tangentes verticales.

Representación gráfica de la función arco coseno
arcco coseno
coseno
5- Función arco tangente
 π π
Definición: La función tangente es una biyección de  − ,  en . Su biyección
 2 2
 π π
recíproca es la función arco tangente de  en  − ,  .
 2 2

1 1
x -∞ - 3 -1 - 0 1 3 +∞ tanθ
3 3
π π π π π π π π
arctan(x) - - - - 0 θ
2 3 4 6 6 4 3 2
 π π
Propiedades: 1- ∀y ∈ , ∀x ∈  − ,  , y=tan x ⇔ x= arctan y
 2 2
 π π
2- ∀x ∈  − ,  , arctan (tan x)=x
 2 2
3- ∀x ∈ , tan (arctan x)=x
Propiedad : arctan es estrictamente creciente, impar, continua sur .
1
Teorema: arctan es derivable en  y ∀x ∈ , (arctan x)’= .
1 + x²
1 π
Propiedad: Para todo real x que no es nulo, arctan x + arctan = sgn(x)
x 2

Representación gráfica de la función arco tangente
tan
arctan
6- Función seno hiperbólico
ex − e− x
Definición: Para todo real x, sh x = .
2
Representación gráfica de la función seno hiperbólico
Propiedad: sh es estrictamente creciente, impar, continua  sobre y derivable sobre .

Para todo x real, sh’(x) = ch(x).
7- Función coseno hiperbólico
ex + e− x
Definición: Para todo real x, ch x = .
2

Representación gráfica de la función coseno hiperbólico
Dicho esto, abramos nuestro Petit Larousse : « La catenaria y la curva según la cual se
tiende un hilo homogéneo, pesado, flexible e inextensible, suspendido por sus extremidades a
dos puntos fijos. ».
Propiedad : ch es par, continua sobre  y derivable sobre .

Para todo x real ch’(x) = sh(x).
Propiedad fundamental: Para todo real x, ch²x – sh²x = 1.
8- Función tangente hiperbólica
sh x
Definición: Para todo real x, th x = .
ch x
Representación gráfica de la función tangente hiperbólica
Propiedad : th es estrictamente creciente, impar, continua sobre  y derivable sobre

.
1
Para todo real, th’(x) = 1-th²(x)= .
ch²(x)

9- Parametraje de la hipérbola
10- Trigonometría hiperbólica
Fórmulas de adición:
ch(a+b) = ch a ch b + sh a sh b
ch(a-b) = ch a ch b - sh a sh b
sh(a+b) = sh a ch b + ch a sh b
sh(a-b) = sh a ch b - ch a sh b
th a + th b
th(a+b) =
1 + th a th b
th a - th b
th(a-b) =
1 - th a th b
Fórmulas de duplicación:
ch 2a=ch² a + sh² a=2ch2 a - 1=1 + 2 sh² a
sh 2a =2 sh a ch a
2th a
th 2a=
1 + th 2 a
11- Función argsh
Definición: La función sh es una biyección de  en . Su biyección recíproca es la

función argsh de  en .
Propiedades: 1- ∀x ∈ , ∀y ∈ , y=sh x ⇔ x= argsh y

2- ∀x ∈ , argsh (sh x)=x
3- ∀x ∈ , sh (argsh x)=x
Propriedad : argsh es estrictamente creciente, impar, continua sobre .

1
Teorema: argsenh es derivable en  y ∀x ∈ , (argsh x)’= .
1 + x²
(
Expresión logarítmica: Para todo real x, argsh x = ln x + 1 + x² . )
Representación gráfica de la función argsh
12- Función argch
Definición: La función ch es una biyección de + en [1,+ ∞ [. Su biyección recíproca

es la función argch de [1,+ ∞ [ en +.
Propiedades: 1- ∀x ∈ +, ∀y ∈ [1,+ ∞ [ , y=ch x ⇔ x= argch y

2- ∀x ∈ +, argch (ch x)=x
3- ∀x ∈[1,+ ∞ [, ch (argch x)=x
Propiedad : argch es estrictamente creciente, continua sobre [1,+ ∞ [.
1
Teorema: argch es derivable en ]1,+ ∞ [ ∀x ∈ ]1,+ ∞ [, (argch x)’= .
x² − 1
Observación: argch no es derivable en 1. En el punto de abscisa 1, el grafo de argch admite

una tangente vertical.
(
Expresión logarítmica: Para todo elemento de [1,+ ∞ [, argch x = ln x + x² − 1 . )
Representación grafica de la función argch

13- Función argth
Definición: La función th es una biyección de  en ]-1,1[. Su biyección recíproca es

la función argth de ]-1,1[ en .
Propiedades: 1- ∀x ∈ , ∀y ∈ ]-1,1[, y=th x ⇔ x= argth y

2- ∀x ∈ , argth (th x)=x
3- ∀x ∈]-1,1[, th (argth x)=x
Propiedad : argth es estrictamente creciente, impar, continua sobre ]-1,1[.
1
Teorema: argth es derivable en ]-1,1[ además ∀x ∈ ]-1,1[, (argth x)’= .
1 − x²
1  1+ x 
Expresión logarítmica: Para todo elemento de ]-1,1[, argth x = ln  .
2  1− x 
Representación gráfica de la función argth


1- e 2x − 5e x + 6 =0.
2- ln(x + 2) + ln(x − 4)
= 2 ln(x + 1).
2
3- ln(x −= 1) ln(2x − 1) − ln(2).
(Determinar el conjunto de definición de la ecuación antes de efectuar algún cálculo.)
Ejercicio 2. Sea f la función definida por: f (x) =

x − 2 x + 1.
Demostrar que f es continua en [0, +∞[ y que posee 2 intervalos de monotonía. Definir la bi-
yección recíproca de f en cada uno de ellos.
Ejercicio 3. Estudiar la función definida por: f (x) = ln(ch(x)) .
1
Ejercicio 4. Estudiar la función definida por: f (x) = th   .
x
Ejercicio 5. Dar una expresión simplificada de las siguientes expresiones:

sin(2 arcsin(x)) ; cos(2 arccos(x)) ; cos(arctan(x))
 3 1
Ejercicio 6. Establecer las siguientes relaciones: 2 arccos   = arccos   ;
 4 8
1  4
2 arctan   = arctan   .
 2  3
Ejercicio 7. Demostrar que para todo entero n y para todo real x tenemos:
n
 1 + th(x)  1 + th(nx)
  =
 1 − th(x)  1 − th(nx)
 2x 
Ejercicio 8. Estudiar la función f definida por: f (x) = arcsen  2 
.
 1+ x 
Ejercicio 9. Llamamos función cotangente hiperbólica el cociente de la función coseno

hiperbólico por la función seno hiperbólico. Estudiar esta función.
 2x 
Ejercicio 10. Sea f la función definida por: f (x) = arctan  2 
.
 1− x 
1- Estudiar la función f.
2- Dar una expresión simplificada de f.

EJERCICIOS
Ejercicio 1.
  −11π     7π     19π  
1- Calcular sin (arcsin(-0,2)), arcsen  sen    , arccos  cos    , arctan  tan  .
  4    3    6 
2- Dar una expresión simplificada por las expresiones siguientes: sen(2arcsen(x)) ;
cos(2arccos(x)) ; cos(arctan(x)).
3- Estudiar la función f : x  arccos(cos(x)) (Dominio de definición, continuidad, paridad, la
periodicidad, derivabilidad, derivada, variaciones, representación gráfica).
Ejercicio 2. Se recuerdan las definiciones siguientes :

  π π 
x = arcsen(t) ⇔=  t sen x ∧  − ≤ x ≤ 
  2 2 
x = arccos(t) ⇔ (t = cos(x) ∧ (0 ≤ x ≤ π) )
  π π 
x = arctan(t) ⇔ =
 t tan x ∧  − < x <   )
  2 2 
Demostrar las relaciones siguientes precisando su dominio de validez:
t
sen(arcsen(t))=t ; cos(arcsen(t))= 1− t² ; tan(arcsen(t))=
1 − t²
1 − t²
sen(arccos(t))= 1− t² ; cos(arccos(t))=t ; tan(arccos(t))=
t
t 1
sen(arctan(t))= ; cos(arctan(t))= ; tan(arctan(t)) = t
1+ t ² 1+ t²
t = sen(x) ⇔ ∃k ∈, ( x = arcsen t + 2kπ) ∨ ( x = π - arcsen t + 2kπ )
t = cos(x) ⇔ ∃k ∈, ( x = arccos t + 2kπ) ∨ ( x = - arccos t + 2kπ)
t = tan(x) ⇔ ∃k ∈, ( x = arctan t + kπ)
Ejercicio 3. Construir el gráfico de la función definida por: f(x)=arccos(cos 2x).
Ejercicio 4.
  2π     5π    2   1 
1. Calcular arccos  cos  −   , arcsen  sen    , arcsen  −  y sen  arcsen    .
  3    4   2    3 
2. Dar una expresión mas simple de las funciones siguientes :
a- cos ( arctan x ) b- sen ( arctan x ) c- tan ( arccos x )
 π π
3. Simplificar arcsen ( sen ( 2x ) ) para x ∈  − ;  .
 2 2

Ejercicio 5. a- Determinar el conjunto de definición y construir el gráfico de la función:
 1 − x²   2x   2x 
f : x  2arccos   + arcsen   − arctan  
 1 + x²   1 + x²   1 − x² 
Indicación: podrán poner t = arctan(x).
2π
b- Resolver la ecuación: f(x) = .
3
Ejercicio 6. Calcular las derivadas de las siguientes funciones, precisando sus dominios de
definición:
a. arccos x ( ) b. x 2 arctan ( x 2 ) c. arctan ( sen2x )
 x −1   x-1 
(
d. ln arctan ( x 2 ) ) e. arctan  
 x +1 
f. arcsen  
 x+1 
π
Ejercicio 7. Resolver la ecuación: arctan(2x) + arctan(x) = .
4
Ejercicio 8. Consideramos la curva (C) por ecuación:

 2x 
y=f(x)= arctan 
 1 − x² 
1- Determinar los conjuntos de definición y de derivación de f.
2- Calcular f ’(x). Comparar f ’(x) con la derivada de la función x  arctan(x). Dedu-
cir una expresión más simple de la restricción de f a cad a intervalo donde f ’ es
continua.
3- Trazar (C).
Ejercicio 9. Por este ejercicio, podrán utilizar el resultado siguiente que se demostrará en el
capítulo «Cálculo diferencial».
Sean “a” y “b” dos reales tales que “a” sea estrictamente inferior a “b”, “f” una función real
definida y continua en [a,b] tal que f sea derivable en todo punto de ]a,b[excepto quizá en x 0
elemento de [a,b].
f (x) − f (x 0 )
Si Lim f ' ( x) existe en ∪{+∞,-∞} y vale l, entonces Lim existe y vale l.
x → x0 x→x 0 x − x0
(El recíproco de la propiedad es falso).
Sea “f” la función definida por f(x) = arcsen ( 3x − 4x 3 ) .
1- Determinar el dominio de definición de f así que las variaciones de f sin utilizar la
derivabilidad de f.
2- Estudiar la derivabilidad de f.
3- a- Deducir de f '(x) la expresión de f(x) en función de arcsen(x).
b- Se da t = arcsen(x). Sin utilizar la derivada de f, encontrar el resultado de la pre-
gunta 3-a-.
Indicación : Podremos mostrar que: sen(3t)=3sent – 4sen3t.
Ejercicio 10. Se recuerdan las definiciones siguientes:

x = argsh(t) ⇔ t = sh(x)
x = argch(t) ⇔ t = ch(x)) ∧ ( x ≥ 0)
x = argth(t) ⇔ t = th(x)

Demostrar las relaciones siguientes precisando su dominio de validez:
1 1 + t 
argsh(t)= ln( t + 1 + t ² ) ; argch(t)=ln( t + t ² − 1) ; argth(t)= ln 
2 1 − t 
t
sh(argsh(t))=t ; ch(argsh(t))= 1+ t² ; th(argsh(t))=
1+ t ²
t² − 1
sh(argch(t))= t² − 1 ; ch(argch(t))=t ; th(argch(t))=
t
t 1
sh(argth(t))= ; ch(argth(t))= ; th(argth(t))=t
1− t ² 1− t²
Ejercicio 11. Simplificar las expresiones siguientes:
 1 + ch(x) 
y = argch 
2
 et z=argsh 2x 1+x² ( )
 
2 1
Ejercicio 12. a- Mostrar que para todo real x que no es nulo, th(x)= − .
th(2 x) th( x)
n
b- Deducir el valor de ∑2 k
th(2 k x) para n entero natural.
k =0
Ejercicio 13. Calcular las derivadas de las funciones siguiente precisando sus dominios de
definición:
1
a- argth ( −4x ) b- argch x c- argch x d- x argsh   e- argth ( x + 1)
x
Ejercicio 14. Resolver las ecuaciones siguientes :

1
a- ch x = 2 b- 5ch x − 4sh x =
3 c- argth x = argth
x
1  1
d- argth x = argch argch x argsh  x − 
e.- =
x  2
Ejercicio 15.
1. Dar una otra expresión en función de x de las funciones siguiente:
f ( x ) = ch ( argsh x ) g ( x ) = th ( argsh x ) h ( x ) = sh ( 4 argsh x )
2. Simplificar las expresiones siguientes:
 1 + ch x   1 + th x   ch x − 1 
i ( x ) = argch   j ( x ) = ln   k ( x ) = argth  
 2   1 − th x   ch x + 1 
1
Ejercicio 16. Consideramos la función f definida sobre [ 0; +∞[ por : f ( x ) = .
ch ( x )
2
1. Mostrar que f realiza una biyeccion de [ 0; +∞[ sobre un intervalo J a determinar.

2. Notamos f −1 la biyeccion reciproca:
a. Estudiar sin cálculos la continuidad, el sentido de variación y la derivabilidad de
f −1 sobre J
b. Representar f y f −1 en una misma referencia ortonormal.
3. Para y ∈ J , calcular f −1 ( y ) .

4. Para el y convenientemente elegido, calcular de dos maneras diferentes ( f −1 ) ' ( y ) .

  3π     π    3π  
Ejercicio 17. 1- Calcular arcsen  sen    , arccos  cos  −   y arctan  tan    .
  2    2    4 
 5π 5π 
2- Simplificar la expresión φ(x) = arctan (tan x ) con x ∈  − ,  .
 2 2
π π
3- Simplificar f(x) = arcsen(sen(3x)) y g(x) = arccos(cos(3x)) para x ∈ - ; .
 2 2
Trazar las curvas representativas de estas dos funciones.
4- Expresar en función de x luego de haber dado el dominio de definición de la
función considerada:
a- tan (arcsenx)
b- cos (arctan x).
5- Estudiar completamente siguiente la función: g (x) = arcsen (cos x)
  3π     π  π
Corrección : 1- arcsen  sen    = arcsen  sen  −   = − ,
  2    2  2
  π    π  π
arccos  =
cos  −   arccos=  cos   
  2    2  2
  3π     π  π
arctan  tan    = arctan  tan  −   =−
  4    4  4
 π π
2- Tenemos φ ( x ) = α con α ∈  − ,  et x ≡ α [ π] .
 2 2
 5π 3π 
x + 2π si x ∈  − , − 
 2 2
 3π π 
x + π si x ∈  − , − 
 2 2
π π
Deducimos que : φ=( x ) x si x ∈  − ,  .
 2 2
 π 3π 
x − π si x ∈  , 
2 2 
 3π 5π 
x − 2π si x ∈  , 
 2 2
 π π  3π 3π 
3- Tenemos x ∈  − ,  ⇔ 3x ∈  − ,  , de donde :
 2 2  2 2

 3π π   π π
−π − 3x si 3x ∈  − , −  −π − 3x si x ∈  − , − 
 2 2  2 6
 π π  π π
f ( x ) 3x si 3x ∈  − ,  = 3x si x ∈  − , 
=
 2 2  6 6
 3π  π π
π − 3x si 3x ∈  π,  π − 3x si x ∈  , 
 2 6 2
 π π
3x + 2π si x ∈  − , − 
 3π   2 3
3x + 2π si 3x ∈  − , −π 
 2   π 
−3x si x ∈  − , 0 
−3x si 3x ∈ [ −π, 0]  3 
g(x) = .
3x si 3x ∈ [ 0, π]  π
3x si x ∈ 0, 
 3π   3
−3x + 2π si 3x ∈  π, 
 2 π π
−3x + 2π si x ∈  , 
3 2
4- a- El dominio de definición es ]−1,1[ .

sin ( arcsen ( x ) ) x
Tenemos tan
= ( arcsen ( x ) ) =
cos ( arcsen ( x ) ) cos ( arcsen ( x ) )
.
Para determinar cos ( arcsen ( x ) ) en función de x, utilizamos la relación cos 2 ( θ ) + sen 2 ( θ ) =1 .

cos 2 ( arcsen ( x ) ) =1-sen 2 ( arcsen ( x ) ) =1-x 2 ⇒ cos ( arcsen ( x ) ) =
1− x2
x
De donde: tan ( arcsen ( x ) ) = .
1− x2
4-b- El dominio de definición es ]−∞, ∞[ .

1
Recordamos que cos 2 ( θ ) = , de donde:
1 + tan 2 ( θ )
1 1
cos 2 ( arctan ( x ) )
= =
1 + tan ( arctan ( x ) ) 1 + x 2
2
 π π 1
Como cos ( x ) ≥ 0 para x ∈  − ,  , deducimos que cos ( arctan ( x ) ) = .
 2 2 1+ x2
5- Sea g ( x ) = arcsen ( cos ( x ) ) .
Claramente tenemos Dg = .
g es 2π − periódica y es también par.
Podemos entonces restringir el intervalo de estudioen [ 0, π] .
−sen ( x ) −sen ( x )
g se puede derivar en ]0, π[ y tenemos ∀x ∈]0,
= π[, g′ ( x ) = .
1 − cos 2 ( x ) sen ( x )
La función siendo positiva en ]0, π[ , deducimos que la función g es decreciente en [ 0, π] . Por
paridad, obtenemos la siguiente tabla de variación :
x π π
−π − 0 π
2 2
g’(x) + -
g(x)
La representación gráfica de la función es la siguiente:

(
a- arcsen (2x) – arcsen 3x = arcsen (x))
π
b- arctan (x +1) + arctan (x – 1) =
4

Corrección : a- arcsen ( 2x ) -arcsen ( ) (
3x =arcsen ( x ) ⇒ sen arcsen ( 2x ) -arcsen ( 3x )) =
x.
(
Como, sen arcsen ( 2x ) -arcsen ( ))
3x
= sen ( arcsen ( 2x ) ) cos ( arcsen ( 3x ) ) -cos ( arcsen ( 2x ) ) sen ( arcsen ( 3x ))

= 2x 1 − 3x 2 − x 3 1 − 4x 2 .
Debemos entonces resolver :
x= 2x 1 − 3x 2 − x 3 1 − 4x 2
⇔ x= 0 o 1= 2 1 − 3x 2 − 3 (1 − 4x 2 )
Para resolver : 1 = 2 1 − 3x 2 − 3 (1 − 4x 2 ) , introducimos la función :
f ( x ) = 2 1 − 3x 2 − 3 (1 − 4x 2 ) − 1
y la estudiamos para determinar las soluciones de f ( x ) = 0 .
 1 1   1 1  1 1
Tenemos Df = − ,   − ,  = − ,  .
 3 3   2 2  2 2
 1 1  1 1 ′ −6x 4 3x
f (x)
f se puede derivar en  − ,  y tenemos : ∀x ∈  − ,  ,= + .
 2 2  2 2 1 − 3x 2
1 − 4x 2
6x 4 3x 36x 2 48x 2
Entonces, f ′ ( x ) = 0⇔ = ⇒ = .
1 − 3x 2 1 − 4x 2 1 − 3x 2 1 − 4x 2
3x 2 4x 2
Y 2
= 2
⇔ 3x 2 (1 − 4x 2 )= 4x 2 (1 − 3x 2 ) ⇔ 3x 2= 4x 2 ⇔ x= 0 .
1 − 3x 1 − 4x
Recíprocamente , tenemos f ′ ( 0 ) = 0 .
Deducimos la tabla de variaciones de la función f :
x 1 1
− 0
2 2
f ’(x) - +
f(x) 0 0
-1
1 1
Con la tabla de variaciones concluimos que : f ( x ) =0⇔x= o x=− .
2 2
Podemos también determinar las raíces de la ecuación: 1 = 2 1 − 3x 2 − 3 (1 − 4x 2 ) sin pasar
por un estudio de funciones :
1= 2 1 − 3x 2 − 3 (1 − 4x 2 ) ⇒ 1= 4 (1 − 3x 2 ) + 3 (1 − 4x 2 ) − 4 3 (1 − 4x 2 )(1 − 3x 2 )
−4 3 (1 − 4x 2 )(1 − 3x 2 ) ⇒ 12x 2 − 3 =
⇒ 24x 2 − 6 = −2 3 (1 − 4x 2 )(1 − 3x 2 )
⇒ (12x 2 − 3)= 12 (1 − 4x 2 )(1 − 3x 2 ) ⇒ 144x 4 − 72x 2 + 9= 144x 4 − 84x 2 + 12

2
⇒ 12x 2 =
3

1 1 1
Como, 12x 2 = 3 ⇔ x 2 = ⇔ x = o − .
4 2 4
Por el contrario, en este caso, debemos verificar que los valores encontrados son soluciones
de la ecuación: 1 = 2 1 − 3x 2 − 3 (1 − 4x 2 ) .
Recíprocamente, verificamos que los valores encontrados por uno de los dos métodos son
soluciones.
1 1
( )
Finalmente, las soluciones de arcsen ( 2x ) -arcsen 3x =arcsen ( x ) son 0, , − .
2 2
b- arctan está definida en  entonces buscamos las soluciones en .

Calculamos tan ( arctan ( x+1) +arctan ( x-1) ) utilizando la relación:
tan(a) + tan(b)
tan ( a + b ) =
1 − tan(a) tan(b)
−2x
tan ( arctan ( x+1) +arctan ( x-1) ) = .
−2 + x 2
π −2x
Así, arctan ( x+1) +arctan ( x-1) = ⇒ 1
=
4 −2 + x 2
u tan v ⇔ u ≡ v [ π] , y
Cuidado, esto no es una equivalencia ! (porque tan =
u = v ⇒ u ≡ v [ π] )
−2x
2
= 1 ⇔ −2x = −2 + x 2 ⇔ x 2 + 2x − 2 = 0
−2 + x
Encontramos las raíces del polinomio x 2 + 2x − 2 = 0 : x1 =−1 + 3 y x 2 =−1 − 3 .
Hay que verificar que las raíces convienen ya que no hemos razonado por equivalencia.
π 3π
Tenemos arctan ( x1 +1) +arctan ( x1 -1) = y arctan ( x 2 +1) +arctan ( x 2 -1) = − .
4 4
Deducimos que la solución de la ecuación del principio es únicamente x1 =−1 + 3 .
Ejercicio 19. 1- Linearizar f(x) = (ch x ) 5 y g(x) = (sh x ) 5. Deducir una primitiva de cada
una de estas funciones.
chx + chy = 5
2- Resolver en  el siguiente sistema:  .
 shx + shy = 3
n n
3- calcular las siguientes sumas: S n = ∑ ch ( kx ) y T n = ∑ sh ( kx ) .
k =1 k =1
Corrección :
 ( ex + e− x ) 
5
1
1 − f ( x=
) 
2  2
) 215 e5x + e−5x + 5 ( e3x + e−3x ) + 10 ( ex + e− x )
= 5 ( e5x + 5e3x + 10e x + 10e − x + 5e −3x + e −5x= ( )
 
1 1 5 5
= 5 ( 2ch ( 5x ) + 10ch ( 3x ) + 20ch ( x ) ) = ch ( 5x ) + ch ( 3x ) + ch ( x )
2 16 16 8
1 5 5
Una primitiva de f es entonces
= : F(x) sh ( 5x ) + sh ( 3x ) + sh ( x ) .
80 48 8

 ( ex − e− x ) 
5
1 1 5x −5x
g ( x=
) 
2
= 5 ( e5x + 5e3x + 10e x − 10e − x − 5e −3x − e −5x=
 2
) 2 5 (
e − e + 5 ( e3x − e −3x ) + 10 ( e x − e − x )
 
1 1 5 5
= 5 ( 2sh ( 5x ) + 10sh ( 3x ) + 20sh ( x ) ) = sh ( 5x ) + sh ( 3x ) + sh ( x )
2 16 16 8
1 5 5
: G (x)
Una primitiva de g es entonces= ch ( 5x ) + ch ( 3x ) + ch ( x ) .
80 48 8
2- Sumando y restando estas dos ecuaciones, verificamos que el sistema es equivalente al si-
e x + e y = 8
guiente:  − x − y .
e + e = 2
8
Tenemos : e − x + e − y =2 ⇔ ( e x + e y ) =2e x e y ⇔ e x e y = =4 .
2
e + e y =
x
8
Debemos entonces resolver el siguiente sistema :  x y .
e e = 4
x
Efectuamos el cambio de variable siguiente: = u e= y v ey .
u + v =8
El sistema se escribe :  .
uv = 4
Las soluciones de este sistema son las raíces del polinomio: X 2 − 8X + 4 .
Tenemos ∆= 82 − 42= 48 , y las raíces son entonces :
8+ 4 3 8−4 3
x1 = = 4 + 2 3 y x1 = = 4−2 3
2 2
ch ( x ) + ch ( y ) =5
Concluimos que las soluciones del sistema 
sh ( x ) + sh ( y ) =
3
son ln 4 + 2 3 y ( )
(
ln 4 − 2 3 . )
n n n
1 − e nx
3- Observamos que Sn + Tn = ∑ ( ch ( kx ) + sh ( kx ) ) = ∑ ( e kx ) = ∑ ( e x ) = e x ×
k
=k 1 =k 1=k 1 1 − ex
n n n
1 − e − nx
∑ ( ch ( kx ) − sh ( kx ) ) = ∑ ( e− kx ) = ∑ ( e− x ) = e− x ×
k
Por otro lado, Sn − Tn = .
=k 1 =k 1=k 1 1 − e− x
Para concluir , basta de ver que :
1 1
Sn=
2
( (Sn + Tn ) + (Sn − Tn ) ) et Tn= 2
( (Sn + Tn ) − (Sn − Tn ) )
Obtenemos entonces :
1  e x − e(
n +1) x
1  x 1 − e nx −x 1 − e − nx  1 − e − nx  1  e x − e( n +1) x − 1 + e − nx 
Sn=  e × + e × =  + =  
2 1 − ex 1 − e− x  2  1 − e x ex − 1  2 1 − ex 
Y del mismo modo :
1 − e − nx  1  e x − e( n 1) x 1 − e − nx  1  e x − e( n +1) x + 1 − e − nx 
+
1  x 1 − e nx −x
Tn= e × −e × =  − x =  
2 1 − ex 1 − e − x  2  1 − e x e −1  2 1 − ex 
Ejercicio 20. Demostrar que : ∀ x ∈  , 2arctan (th x) = arctan (sh (2x)).

Corrección : Anotemos f ( x ) =2arctan ( th ( x ) ) y g ( x ) =arctan ( sh ( 2x ) ) .
f y g son dos funciones continuas y se pueden derivar en .
Por un lado, tenemos:
th ′ ( x ) 1 1 1 2
f ′(x) = 2 2× 2
= × 2× 2
= = .
1 + th ( x )
2
ch ( x ) 1 + th ( x )
2
ch ( x ) + sh ( x ) ch ( 2x )
2
sh ′ ( 2x ) ch ( 2x ) ch ( 2x ) 2
Por otra parte, g′ ( x ) =
2 2×
= 2× 2
= =.
1 + sh ( 2x )
2
1 + sh ( 2x )
2
ch ( 2x ) ch ( 2x )
Tenemos entonces : ∀x ∈ , f ′ ( x ) = g′ ( x ) entonces f y g son dos primitivas de la misma fun-
ción.
Deducimos que f ( x ) =g ( x ) + c con c ∈ .
Como, f ( 0 )= 0= g ( 0 ) entonces c = 0 y así ∀x ∈ , f ( x ) = g ( x ) .

Capítulo 12
COMPARACIÓN DE FUNCIONES
En la parte que sigue en este capítulo, excepto mención contraria, x 0 designa tanto a un real
como + ∞ , o bien - ∞ .
1- Funciones Despreciables
Definiciones: 1- Sean "f" y "g" dos funciones definidas en la proximidad del real x0 ,
excepto quizá en x 0 .
El que f sea despreciable con respecto a “g” en la proximidad del real x0 significa que
∀ε > 0, ∃η>0, ∀x ∈ Df ∩ Dg , x-x 0 < η ⇒ f (x) < ε g(x)
2- Sean "f" y "g" dos funciones definidas en la proximidad de + ∞ .
El que f sea despreciable con respecto a “g” en la vecindad de + ∞ significa que
∀ε > 0, ∃A>0, ∀x ∈ Df ∩ Dg , x>A ⇒ f (x) < ε g(x)
3- Sean "f" y "g" dos funciones definidas en la vecindad de - ∞ .
El que f sea despreciable con respecto a ”g” en la vecindad de - ∞ significa
∀ε > 0, ∃A>0, ∀x ∈ Df ∩ Dg , x<-A ⇒ f (x) < ε g(x)
Sea x0 un real, o bien + ∞ , o también - ∞ .Si “g” no se anula en la vecindad de x0 excepto
f (x)
quizá en x 0 , las definiciones anteriores pasan a ser: Lim =0.
x → x 0 g(x)
Notación de Landau: f = o(g).

x0
Landau Edmund (1877-1938) es un matemático alemán que

enseña en Göttingen y fue en esta célebre universidad uno de los
primeros universitarios que tuvo que abandonar sus investigaciones
por ser víctima de los nazis (nacional-socialismo de Hitler, 1933).
Sus trabajos sostienen en teoría números (de los cuales la
famosa función ζ de Riemann) y sobre las funciones de variables
complejas.
Observación: Los físicos utilizan la notación f g.

x0
Propiedad: Sean f1 , f2 , g tres funciones definidas en la proximidad de x0 , λ 1 y λ 2 que

son dos reales.
Si f1 = o(g) , f2 = o(g), entonces λ 1 f1 + λ 2 f2 = o(g)
x0 x0 x0
Propiedad: Sean f, g dos funciones definidas en la proximidad de x 0 .

f-g = o(f) si y solamente si f-g = o(g)
x0 x0
Propiedad: Sean f, g, h tres funciones definidas en la proximidad de x0 .

Si f = o(g) como también g = o(h), entonces f = o(h)
x0 x0 x0
Observación: f = o(1) ⇔ Lim f = 0

x0 x0
Propiedad: Sean f, g y h funciones definidas próximos de x0 .

Si f = o(h) y g = o(h), entonces f+g = o(h).
x0 x0 x0
Propiedad: Sean f y h dos funciones definidos próximos de a, tales que f = o(h).

x0
Si g es una función borneada próximo de a, entonces f = o(h).

x0
En particular, para todo k, tenemos k f = o(h).

x0
Propiedad: Si α<β, entonces xα = o(xβ) y xβ =+ o(xα).

+∞ 0
2- Funciones equivalentes
Definición: Sean f, g dos funciones definidas en la proximidad de x0 . El que "f" y "g"
sean equivalentes significa que f-g = o(f).
x0
Si g no se anula en la proximidad de x0 excepto quizás en x 0 , la definición anterior pasa a ser:

f (x)
f y g son equivalentes significa Lim =1.
x → x 0 g(x)
Notación: f  g
x0
Propiedad: Sea f una función definida y derivable en x 0 real tal que f ’(x 0 ) no sea
nula.
Entonces, f(x)-f(x 0 )  f ’(x0 )(x-x 0 ).
x0
Algunas equivalencias clásicas:

Cerca de 0 :
sin x  x
0
cos x  1
0
tan x  x
0
x²
1-cos x 
0 2
x
e 1
0

ex-1  x
0
ln(1+x)  x
0
(1+x)α-1  αx
0
n
∑a
k =p
k x k  a p xp con a p ≠ 0
0
Cerca de + ∞ :
n
∑a
k =p
k x k  a n xn con a n ≠ 0
+∞
Observación: Cuidado con las funciones equivalentes a 0.
Propiedad: Sean f, g dos funciones definidas en la proximidad de x 0 .

Si f  g , y si Lim g=l elemento de   {+∞, −∞} , entonces Lim f=l.
x0 x0 x0
Propiedad: Sea f una función definida en la proximidad de x 0 excepto eventualmente

en x0 , y l un real no nulo.
f  l ⇔ Lim f =
l
x0 x0
Propiedad: Sean f1 , f2 , g 1 , g 2 cuatro funciones definidas en la proximidad de x 0 .

Si f1  g 1 y f2  g 2 , entonces f1 f2  g 1 g 2 .
x0 x0 x0
Propiedad: Sean f, g dos funciones definidas en la proximidad de x 0 , g no se anula en

la proximidad de x 0 Salvo tal vez en x0 .
1 1
Si f  g, entonces  .
x0 f x0 g
Propiedad: Sean f1 , f2 , g 1 , g 2 cuatro funciones definidas en la proximidad de x 0 , g 2

no se anula en la proximidad de x 0 salvo tal vez en x0 .
f1 g
Si f1  g 1 y f2  g 2 , entonces  1.
x0 x0 f2 0 g2
x
Propiedad: Sean f, g dos funciones definidas en la proximidad de x0 , g estrictamente

positiva en la proximidad de x0 .
Si f  g, entonces f estrictamente positiva en la vecindad de x0 .
x0
Propiedad: Sean f, g, h tres funciones definidas en la proximidad de x0 .

Si f  g y h = o(g), entonces f+h  g.
x0 x0 x0
Utilizamos a veces este teorema de la forma siguiente: f+o(f)  f.

x0

Propiedad: Sean f1 , f2 , g tres funciones definidas en la proximidad de x 0 , c 1 y c 2 dos
reales tales que f1  c 1 g y f 2  c 2 g.
x0 x0
Si c 1 +c 2 ≠ 0, entonces f1 +f2  (c 1 +c 2 )g.

x0
Si c 1 +c 2 =0 , entonces f1 +f2 = o(g).

x0
3- Complementos
1- Cambio de variable: (Compatibilidad con la composición a la derecha)

Sean f, g dos funciones definidas en la proximidad de x0 , ϕ una función definida en la
proximidad de t 0 tales que f(x)  g(x) y Lim ϕ(t)=x0 . Entonces f  ϕ(t)  g  ϕ(t).
x →x0 t →t0 t →t0
2- Compatibilidad con los logaritmos:

Sean f, g dos funciones definidas en la proximidad de x 0 tales que f(x)  g(x) y
x →x0
Lim g=l real positivo distinto a 1 o igual a + ∞ , entonces lnf  lng.

x0 x0
3- Compatibilidad con las exponenciales:

a- Sean f, g dos funciones definidas en la proximidad de x0 tales que f(x)  g(x) y
x →x0
f g
Lim (f-g)=0, entonces e  e .
x0 x0
b- Sean f, g dos funciones definidas en las proximidades de x0 de manera que

f(x)  g(x) y g borneado en las proximidades de x 0 , entonces ef  eg.
x →x0 x0
4- Compatibilidad con las potencias:

Sean f, g dos funciones definidas y estrictamente positivas en la proximidad de x 0 .
- Para todo α de *, f  g ⇔ fα  gα
x0 x0
+
- Para todo α de * , f = o(g) ⇔ fα = o(gα)
x0 x0
-
- Para todo α de * , f = o(g) ⇔ g = o(fα) α
x0 x0
5- Crecimiento comparado
∀α > 0, ∀β ∈ , ( ln(x) ) = o ( x α )
β
+∞
β  1 
∀α > 0, ∀β ∈ , ln(x) =+ o  α 
0 x 
∀m > 0, ∀γ > 0, ∀α ∈ , x α = o e mx
+∞
( ) γ

Ejercicio 1. Demostrar las siguientes reglas (que hay que conocerlas):

a- Si en la proximidad de a (real o infinito) tenemos f (x)  g(x) y si lim f (x) = λ con
a x →a
+
λ ∈  , λ ≠ 1 , entonces en la proximidad de a, tenemos: ln(f (x))  ln(g(x)) .
a
b- Si en la proximidad de a (real o infinito) tenemos f (x)  g(x) y si lim f (x) = +∞ ,
a x →a
entonces en la proximidad de a, tenemos : ln(f (x))  ln(g(x)) .
a
c- Si lim f (x) = 1 , entonces en la proximidad de a tenemos ln(f (x))  f (x) − 1 .
x →a a
Ejercicio 2. Demostrar las siguientes equivalencias:

x2
a- En la proximidad de 0, tenemos : cos(x) − 1  − (con ayuda de sen(x)  x ).
0 2 0
ex ex
b- En la proximidad de +∞ , tenemos: ch(x)  y sh(x)  . Adaptar para −∞ .
+∞ 2 +∞ 2
Ejercicio 3. Calcular los siguientes límites:

βx
 α
a- lim 1 +  (α y β son reales no nulos).
x →+∞  x
ln ( sen(x) )
b- lim (cos(x)) .
x →0
c- lim x 2 (ln(x))3 e− x .
x →+∞

EJERCICIOS
Ejercicio 1. Para cada uno de los pares de funciones, determinar si una de las dos es
despreciable delante de la otra a la vecindad de a, o si las funciones son equivalentes (o si no
es ninguno de estos casos).
1. f(x)= x , g(x)=ln(x) y a=+ ∞
2. f(x)=sen(x), g(x)=ln(x) y x=+ ∞
3. f(x)=x4+5x+1, g(x)=ex(ln(x))² y a=+ ∞
4. f(x)=2+sen(x), g(x)=2+cos(x) y a=+ ∞
5. f(x)=2sen(x), g(x)=x(1+ex) y a=0
sh(x) 1
6. f(x)= 3 , g(x)= y a=0
x x
−x² -2x
7. f(x)= e , g(x)=e y a=+ ∞
8. f(x)=ex-1, g(x)=x(ln(x))3 y a=0
Ejercicio 2. Sean “a” y “b” dos funciones definidas y estrictamente positivas en una
proximidad del real u. Se supone que “a” y “b” son equivalentes en la proximidad de u.
a- ¿Qué pueden decir con respecto a la equivalencia de ln(a) y ln(b) en la proximidad de u ?
b- ¿Qué pueden decir con respecto a la equivalencia de exp(a) y exp(b) en la proximidad de
u?
Ejercicio 3.
1. Sea f (x) = x2 y g(x) = x2 + 3x para x ∈ .
f  g ? ef  eg ?
+∞ +∞
1 1
2. La misma cuestión para f (x) = y g(x) = .
2x + 5x² x²
3. Que se puede deducir de eso?
Ejercicio 4.
1- Determinar un equivalente en la proximidad de 0 de cada una de las siguientes
funciones :
f1 ( x ) = ln ( cos x ) f 2 ( x ) = tan ( 2 tan x ) 3x − 3x 2

f 3 ( x ) =+
1 sen 2 x − 1 f4 ( x ) =
2x + x 2
2- Deducir el limite eventual cuando x tiende hacia 0 de la siguiente función :
ln ( cos x ) tan ( 2 tan x ) 3x − 3x 2

F ( x )= × ×
1 + sen 2 x − 1 tan x 2x + x 2
Ejercicio 5. Para cada expresión, dar un equivalente simple.

1. x5-2x2+x en + ∞ y en 0

x 3 + 2x − x
2. 3 2
en + ∞ y en 0+
4x + x + 7
3. 3 x + 1 + 4 cos(x) en + ∞ y en 0
4. 5e2x+ln(x)-x en + ∞ y en 0+
5. sen(x)+2x+ 1 + x -1 en + ∞ y en 0
6. x + 2 − x en + ∞ y en 0+
 x +1 
7. ln   en + ∞
 x 
π
8. arccos(x)- en 0
2
3 π
9. cos(x)- en
2 6
10. ln(2x3-3x2+1) en 0 y en + ∞
Ejercicio 6. Determinar los límites de les funciones siguientes en los puntos indicados.
1 − cos(x) (1-e x )sen(x)
= x en x 0 0= ; x en x 0 0
x(2 − x)tan(x) x 2 + x3
x(2x²−3x +1)tan(πx ) en x 0 = 1 ; x tan(x)tan(2x) en x 0 = π
2 2
x x
a −b
x en x 0 = 0 y con a>0 , b>0
x
 πx 
tan  
 x  2a 
Ejercicio 7. Determinar para “a” real que no es nulo, que Lim  2 −  .
x →a
 a
Ejercicio 8. Determinar Lim tan 3x

x→ π 2
( ( ) tan(3x)
.
6
Ejercicio 9. Determinar los límites de las funciones siguientes en los puntos indicados:
sen(x).ln(1 + x²) ln[cos(ax)]

x en 0 ; x  en 0 con b que no es nulo
x.tan(x) ln[cos(bx)]
1 1
( cos(x) ) sen²x en 0 ; x  ( cos(x) ) tan(2x) en 0
1
π
( sen(x) ) 2x-π en ; x  |sen(x)|tan(x) en 0
2
sen(x)
π  x  x-sen(x)
tan(x)|cos(x) en ; x 
2  sen(x) 
1
( sen(x) + cos(x) ) x en 0
x.ln(x)
 ln(x + 1) 
Ejercicio 10. Determinar Lim 
x →+∞ ln(x) 

xe x + x 9 − 2 x ln( x)
Ejercicio 11. Determinar Lim .
x →+∞
x3 + ( )
x 3 + x 2 − x 3 ch( x)
Ejercicio 12.
x
 x 
1- f ( x ) =   . Determinar Lim f ( x ) . Notamos l este limite.
 sh x  x →0
2-Prolongamos f por continuidad, poniendo f(0)=l.

Mostrar de dos maneras diferentes que f es derivable en 0.
x 1
 x x
3- Mostrar que sh x  e x . Deducir que ln    − x después determinar
+∞ 2
 sh x  +∞
Lim f ( x ) .
x →+∞
 1 
Ejercicio 13. Sea λ un real fijo. Consideramos la función f λ (=
x ) x λ  1 + − 1 definido
 x 
sobre *+.
1- Determinar los equivalentes simples f λ ( x ) en la proximidad de 0 y de +∞ .
2- Para que valores de λ la función f es prolongable por continuidad (a la derecha) en 0 ?
3- Para que valores de λ la función f es derivable a la derecha en 0 ?
Ejercicio 14. Sea f definida por f (x) = ln(ch x).

1- Precisar el dominio de definición de f y dar su cuadro de variaciones.
2- Dar un equivalente simple de f en 0.
3- Mostrar que en + ∞ , tenemos f (x)  xk donde k es un real que hay que determinar.
4- Mostrar que Lim ( f (x) − x k ) =
− ln(2) . Que podemos deducir de eso para la curva
x →+∞
de f ?
5- Trazar la curva representativa de f.
xλ
Ejercicio 15. Sea λ un real. Definimos la función fλ por fλ (x) = .
(x² + 1) arctan(x)
1- Dar equivalentes simples de fλ a la vecindad de 0+ y de + ∞ .
2- Para cuales valores de λ la función fλ es prolongable por continuidad a la derecha
en 0 ?
3- Mostrar que para λ ≥ 2, este prolongamiento es derivable a la derecha en 0.

Ejercicio 16. 1- Comprobar que : x + x² - 1 ∼ 2x en la proximidad de +∞.

2- Deducir un equivalente de argch x y argsh x en la proximidad de (+ ∞).
Corrección: 1- Anotemos f ( x ) =+
x x2 −1 y g ( x ) =
2x .
f (x)
Basta con demostrar que : lim = 1.
x →+∞ g ( x )
f ( x ) x + x2 −1 1 x2 −1 1 1 1
Tenemos = = + = + − 2 , entonces
g(x) 2x 2 4x 2
2 4 4x
f (x) 1 1
lim =+ =1.
x →+∞ g ( x ) 2 4
( )
2- Tenemos argch ( x ) = ln x + x 2 − 1 ,entonces de acuerdo con lo que precede :
argch ( x )  ln ( 2x )  ln ( x ) .
+∞ +∞
Del mismo modo que en la pregunta anterior, verificamos que x + x 2 + 1  2x , y ( ) +∞
( )
deducimos que : ln x + x 2 + 1  ln ( 2x ) , entonces argsh ( x )  ln ( 2x )  ln ( x ) .
+∞ +∞ +∞
xλ
Ejercicio 17. Sea λ un real fijo. Definimos la función f λ por : f λ (x) =
( x² + 1) arctan(x)
para todo x de *+.
1- Dar equivalentes simples de f λ (x) en la proximidad de 0 y de + ∞
2- Para qué valores de λ f se puede prolongar por continuidad a la derecha en 0 ?
3- Demostrar que para λ ≥ 2, esta prolongación se puede derivar a la derecha en 0 .
π
Corrección : 1- Tenemos arctan ( x )  x y arctan ( x )  , y por otro lado,
0 +∞ 2
(x 2
+ 1)  1 y ( x 2 + 1)  x 2 .
0 +∞
2 λ− 2
Deducimos entonces que : f λ ( x )  x λ−1 y f λ ( x ) 
x .
π0 +∞
2- f se puede prolongar por continuidad a la derecha en 0 si y solamente si

λ −1 ≥ 0 ⇔ λ ≥ 1 .
0 si λ > 1
En este caso, anotamos f λ ( 0 ) = .
1 si λ =1
3- Sea λ ≥ 2 , tenemos entonces f λ ( 0 ) = 0 .
f λ ( x ) − f λ ( 0 ) f λ ( x ) x λ−1
Así = =  x λ− 2 , y ya que λ ≥ 2 , x  x λ− 2 tiene un límite a la
x −0 x 0 x
derecha finito en 0.
Entonces la prolongación se puede derivar a la derecha en 0.

Ejercicio 18. Consideramos las siguientes funciones de  en :
argth (x 3) 1 1
g 1 (x) = g 2 (x) = x (ln |x|)3 g 3 (x) = 5 exp  - 
x x  x² 
1 1
g 4 (x) = x² argsh (x) g 5 (x) = x 3 ln |x| g 6 (x) = exp – 
x  |x|
Clasificar todas estas funciones en la proximidad de 0, adoptando la siguiente notación:
g i  g j si y solamente si g i = o (g j ) en la proximidad de 0
Corrección : Primero intentaremos encontrar equivalentes.

x3
Sabemos que argth ( x )  x . Deducimos que g1 ( x )  = x 2 .
0 0 x
Del mismo modo, tenemos argsh ( x )  x , entonces g 4 ( x )  x 2 x = x 3 .

0 0
g1 x
Tenemos :  , entonces g1  g 2 .
(
g 2 ln ( x ) 3
0
)
g5
De plus,  x ln ( x ) , entonces g 5  g1 .
g1 0
g 1
Por otro lado, 4  , entonces g 4  g 5 .
g 5 0 ln ( x )
1
g 1 −
Ahora, 6  4 e x , entonces g 6  g 4 .
g4 0 x
1 1
g 1 − 2+ 1 1 1
Por último, 3  4 e x x , y tenemos − 2 +  − 2 , entonces g 3  g 6 .
g6 0 x x x 0 x
La relación  siendo evidentemente transitiva, concluimos que g 3  g 6  g 4  g 5  g1  g 2 .

Capítulo 13
CÁLCULO DIFERENCIAL
Procedente de su Auvernia natal, Michel Rolle (francés, 1652-1719) comienza su ca-
rrera en Paris como simple copista. Se opuso al cálculo diferencial del cual Varignon era, en
Paris, el ardúo defensor. En su "Tratado de álgebra" (1690) sobre la resolución de las ecua-
ciones, Rolle aborda un tema fundamental: el problema de la separación de las raíces. Consis-
te en aislar las soluciones de una ecuación, es decir de determinar las cercanias disconjuntas
que contengan una y solo una solución de la ecuación. Aplicamos entonces diversos algorit-
mos que reposan sobre la continuidad, la monotonía, la convexidad, etc.
Formulación de Rolle (1691) : sea f(x) = 0 Una ecuación algébrica entera (polinomio).
No puede existir mas de una raiz (real) entre dos raices consecutivas de su derivada (i.e. la
derivada de f).
La noción de función derivada existe claramente desde Leibniz. No es por entonces
que está todavia definida en tanto que límite de la tasa de crecimiento, que será el hecho de
d'Alembert. Decir que f se anula, es decir que la tangente al gráfico en un punto situado entre
a y b es paralelo al eje de las abcisas.
1- Teorema de Rolle
Teorema: Sea f una función definida y continua en [a,b], derivable en ]a,b[ tal que
f(a)=f(b). Entonces, existe un elemento c de ]a,b[ tal que f ’(c)=0.
3
Ejemplo : con f : x  arctan((x-1)²+5) - , a=-2 y b=4
2

Observaciones acerca de la demostración del Teorema de Rolle:
Es falso creer que, si c es un máximo, entonces f es creciente a la izquiera de c, entonces de-
creciente después. f(c) es ciertas veces el valor máximo, pero f puede no ser monótona, ni a la
x² 1
izquierda ni a la derecha. Tomar por ejemplo la función f definida por: f(x)= - - x²sen² .
2 x
2- Teorema de los aumentos finitos
Teorema: Sea f una función definida y continua en [a,b], derivable en ]a,b[. Entonces
existe un elemento c de ]a,b[ tal que f(b) – f(a)=f ’(c)(b-a).
Aplicación:
1- Sean “a”, “b” dos reales tales que “a” sea estrictamente inferior a "b", "f" una fun-
ción real definida y continua en [a,b] tal que f sea derivable en todo punto de ]a,b[ excepto
quizá en x 0 elemento de [a,b].
f (x) − f (x 0 )
Si existe Lim f ’(x) en ∪{+∞,-∞} y vale l, entonces Lim existe y vale l.
x →x0 x→x 0 x − x0
 1
= f(x) x².sen   si x ≠ 0
2- Estudiando la función g de finida por  x , demostramos
 f(0)=0

que la recíproca de la propiedad en 1- es falsa.
Particularmente, si Lim f ’(x) no existe, no podemos concluir sobre la existencia de f ’(x0 ).
x →x0
Gráfico de la función f

Teorema: desigualdad de los crecimientos finitos
Sea una función f derivable sobre [a, b].
1- Si m ≤ f ’ ≤ M sobre [a, b], entonces m(b-a) ≤ f(b)-f(a) ≤ M(b-a).
2- Si |f ’| ≤ M sobre [a, b], entonces |f(b)-f(a)| ≤ M(b-a).
Prueba :
Método 1 :
Suponemos que existen dos reales m et M tales que m ≤ f ’ ≤ M sobre [a,b].
Considerando las funciones definidas sobre [a, b] :
g : x  f(x)-mx y h : x  f(x)-Mx.
Para todo x de [a, b], tenemos :
g’(x)=f ’(x)-m ≥ 0 y h’(x)=f ’(x)-M ≤ 0
entonces g es creciente y h decreciente sobre [a, b] donde :
g(a) ≤ g(b) et h(a) ≥ h(b)
es decir :
f(a)-ma ≤ f(b)-mb et f(a)-Ma ≥ f(b)-Mb
lo que podemos escribir :
m(b - a) ≤ f(b) - f(a) ≤ M(b - a)
En particular si |f ’| ≤ M sur [a, b], tenemos : - M(b-a) ≤ f(b)-f(a) ≤ M(b-a)
Es decir : |f(b)-f(a)l ≤ M(b - a).
Método 2 : caso particular del teorema de los crecimientos finitos..
Teorema: Sea f una función continua sobre [a, b] y derivable sobre ]a, b[. tenemos las
siguientes equivalencias :
2- Sentido de variación de una función con valores reales
f creciente entre [a, b] ⇔ ∀t ∈ ]a,b[, f '(t) ≥ 0
f decreciente entre [a, b] ⇔ ∀t ∈ ]a,b[, f '(t) ≤ 0
f constante entre [a, b] ⇔ ∀t ∈ ]a,b[, f '(t) = 0.
Demonstración : El sentido ⇒ proviene de un pasaje al límite entre las tasas de crecimiento

de signo constante. Puede ser demostrado desde el curso de Primero.
La recíproca es admitida en el liceo. Ella utiliza en efecto el teorema de las tasas de
crecimiento finito. Si f ’ es de signo constante (o nulo), es el mismo para todas las tasas de
f (y) − f (x)
crecimiento ya que este último es igual a f '(c) con c entre x e y.
y−x
Observación : Es falso creer que f '(x 0 ) > 0 ⇒ f es estrictamente creciente entre un intervalo
conteniendo x0 . Basta con la estricta positividad entre todo un intervalo, pero la positividad en
un punto único no basta.
1
Considerar por ejemplo f(x) = x + 2x2 sen en 0. Tenemos f '(0) = 1, pero f ' no es de signo
x
constante en ninguna proximidad de 0.

Si f se puede derivar y si f ' > 0, f es estrictamente creciente. La recíproca es falsa. Puede ser
que f sea estrictamente creciente y que se puede derivar y que f se anule. Basta con tomar f(x)
= x3. El equivalente es el siguiente :
Notemos Z el conjunto de las x donde f ’ se anula.
f estrictamente creciente ⇔ f ' ≥ 0 y Z no contiene ningún intervalo ]a, b[ con a < b
En efecto, decir que f es creciente sin serlo estrictamente, quiere decir que existe x < y tal que
f(x)= f(y), o también que f es constante sobre un intervalo o también que f se anula sobre un
intervalo o enfín que Z contiene un intervalo abierto.
Corolario : Sea f una función continua sobre el intervalo I, derivable salvo en un nu-
mero finito de puntos de I. Si f ’ es de signo constante y solo se anula en un numero finito de
puntos del intervalo I, entonces f es estrictamente monótona.
Teorema de los crecimientos finitos generalizados

Sean f y g do s funciones definidas y continuas sobre [a,b], derivables sobre ]a,b[, g’ no se
anula sobre ]a,b[.
entonces, existe c elemento de ]a,b[ tal que :
f (b) − f (a) f '(c)
=
g(b) − g(a) g '(c)
Regla de Hospital (Francés 1661-1704)

Sea I intervalo, a un elemento de I y l un elemento de  .
Sean f y g dos funciones continuas sobre I y derivables sobre
I\{a} con g’(x) ≠ 0 para todo x elemento de I\{a}. Entonce :
f '(x) f (x) − f (a)
Lim l ⇒ Lim
= l
=
x → a g '(x) x → a g(x) − g(a)
Guillaume de l’Hospital
Variante : Sea I intervalo, a un elemento de I y l un elemento de  .

f (x) 0
Entonces el cálculo del límite de un cociente Lim con una forma indeterminada , con
x → a g(x) 0
f y g dos funciones continuas sobre I y derivables sobre I\{a} con g’(x) ≠ 0 para todo x ele-
f '(x) f (x)
mento de I\{a}. Si Lim = l , entonces Lim =l.
x → a g '(x) x → a g(x)
Esta regla aparece por la primera vez en 1696 en el tratado Análisis de los infinitamente pe-
queños de Guillaume de L’Hospital, que es el primer libro sobre el cálculo diferencial. El li-
bro está realizado gracias a Jean Bernoulli, quien había hecho el descubrimiento dos años an-
tes.
3- Funciones de clase Cn
Definición: Sea I un intervalo. Una función de clase C0 en I es una función continua
en I. El conjunto de las funciones de clase C0 en I se escribe C0(I).
Una función de clase C1 en I es una función derivable con derivada conti-
nua en I. El conjunto de las funciones de clase C1 en I se escribe C1(I).
Sea “n” un elemento de . Una función de clase Cn en I es una función
derivable n veces y de derivada nésima continua en I. El conjunto de las funciones de clase Cn
en I se escribe Cn(I).
Una función de clase C∞ en I es una función indefinidamente derivable en
I. El conjunto de las funciones de clase C∞ en I se escribe C∞ (I).
 1
= f(x) x².sen   si x ≠ 0
Ejemplo : La función f definida por  x (véase párrafo 2) es un
 f(0)=0

0
ejemplo de función de clase C , que se puede derivar y de derivada no continua.
1
x 2sen  
f ( x ) - f ( 0)  x  =xsen  1  .
Demostración : Tenemos =  
x x x
1 1
Ya que -1 ≤ sin   ≤ 1 , tenemos -x ≤ xsen   ≤ x ( ya que x ≥ 0 ) y entonces por el teorema
x x
1
de gendarmes lim xsen   =0 .Deducimos que f se puede derivar en 0 y tenemos f ' ( 0 ) =0
x →0
x
1 1
Por otro lado, sabemos que f se puede derivar sobre * con derivada x  2xsen   -cos   .
x x
1 1
Tenemos que lim xsen   =0 y sabemos que x  cos   no tiene límite en 0.
x →0
x x
1 1
Deducimos entonces que x  2xsen   -cos   no tiene límite en 0 y así que f ' no es con-
x x
tinua en 0.

Propiedad: Sea “n” un elemento de . Sean “f” y “g” dos funciones de clase Cn (resp.
C∞ ) y sean α y β dos reales. Entonces αf+βg es una función de clase Cn (resp. C∞ ).
Formula de Leibniz: Sea “n” un elemento de . Sean “f” y “g” dos funciones de cla-
se C (resp. C∞ ). Entonces fg es una función de clase Cn (resp. C∞ ).
n
n n
n
Además, (fg)(n)= ∑ Ckn f (k ) g (n − k ) = ∑   f (k ) g (n − k ) .
= k 0= k 0k
Demostración : Se efectúa por recurrencia en n.

- Fundación Está evidentemente verificada para n = 0 y para n = 1, para el cual reco-
nocemos que : (fg)' = f ' g + fg '.
- Herencia : Si la fórmula es verdadera al rango n y que las funciones se pueden deri-
var n+l veces, vemos que (fg)(n) se puede derivar y con derivada:
n
(fg)(n+l)= ∑ Cpn ( f (p +1) g (n − p) + f (p) g (n − p +1) )
p =0
n n
= ∑ Cpn f (p +1) g (n − p) + ∑ Cpn f (p) g (n − p +1)
p =0 p =0
n +1
= ∑ ( Cpn −1 + Cnp ) f (p) g (n − p +1) cambiando de índice p+ l → p en la primera suma
p =0
n +1
= ∑ Cpn +1f (p) g (n − p +1)
p =0
(Utilizamos el hecho que Cpn = 0 si p < 0 o p > n).
La demostración, así que la naturaleza de la fórmula, es entonces comparable a aq uella del

desarrollo del binomio de Newton. No es una casualidad : la fórmula de Leibniz permite de
deducir la fórmula del binomio de Newton. Basta con tomar f(x) = e ax y g(x) = ebx y de apli-
car la fórmula de Leibniz en x = 0.
4- Formula de Taylor-Lagrange
TAYLOR Brook, inglés, 1685-1731

Ecléctico, se dedicó a la música, a la pintura y a la philosophía.
Fue alumno, en Cambridge, de John Machin. Fuera de algunos traba-
jos geométricos dirigidos sobre la perspectiva, le debemos principal-
mente la publicación (1715-1717) de su tratado sobre el desarollo en
serie de funciones : Methodus incrementorum directa et inversa. Fue
miembro de la Royal Society de Londres (el equivalente a la academia
de las ciencias francesa) desde 1712.
La fórmula de Taylor, dicha también de Taylor-Lagrange, es en
realidad el término de trabajos ya empezados por Gregory, Newton,
Leibniz et Jacques Bernoulli.
Teorema: Sea “n” un elemento de . Sea “f” una función de clase Cn en [a,b] tal que
f(n+1) existe en ]a,b[. Entonces, existe c elemento de ]a,b[ tal que:

n
(b − a) k (k ) (b-a) n+1 (n +1)
f(b)= ∑ f (a) + f (c)
k =0 k! (n + 1)!
Fórmula de Taylor-Lagrange al orden n
Observación: Para n=0, se encuentra de nuevo la fórmula de los aumentos finitos.
Otra formulación con las mismas hipótesis:

n
hk h n+1 (n +1)
- con a=x, b=x+h, h>0: f(x+h)= ∑ f (k ) (x) + f (c)
k = 0 k! (n + 1)!
- con b=a+x, x>0: Existe θ elemento de ]0,1[ tal que:
n
xk x n+1 (n +1)
f(a+x)= ∑ f (k ) (a) + f (a + θx)
k = 0 k! (n + 1)!
- con a=0, b=x, x>0: Existe θ elemento de ]0,1[ tal que:
n
xk x n+1 (n +1)
f(x)= ∑ f (k ) (0) + f (θx)
k = 0 k! (n + 1)!
Formula de Mac-Laurin
5- Formula de Taylor-Young
Teorema de Taylor-Young:
Sea f una función definida en la vecindad del real “a” tal que f(n)(a) existe para un entero natu-
ral n. Entonces,
n
(x − a) k (k )
f(x)= ∑ f (a) + o ( (x-a) n )
k =0 k!
Fórmula de Taylor-Young al orden n
6- Posición de una curva con relación a su tangente en la vecindad de un

punto.

Ejercicio 1 : Sea I un intervalo abierto de  y a ∈ I .

Sea f una aplicación de I en  que se puede derivar.
Recordamos que si f se puede derivar en a entonces f es continua en a.
Demostrar que la implicación recíproca es falsa dando contra- ejemplos de funciones conti-
nuas en un punto pero que no se pueden derivar en ese punto.
Ejercicio 2 : Calcular las derivadas de las siguientes funciones (indicaremos el dominio de la

derivabilidad de la función):
 x2 −1 
f (x) =ln( x + 1), f (x) = ln( 6x -1(4x + 5)3 ), f (x) = ln  3 2 ,
 x +1 
 
x 2 +1
f (x) = e , f(x) = x(x + 1 + x 2 ), f(x) = x2 x
Ejercicio 3 : Mostrar que si la función f se puede derivar en un punto x0 entonces:

f (x + h) − f (x 0 − h)
∆(h) = 0
2h
admite un límite cuando h tiende hacia 0.
La recíproca es verdadera ?
Ejercicio 4 : Consideremos la función polinomial P definida por: P(x) = x 3 − 8x 2 + 5x + 3 .

Escribir P(x) con ayuda de las potencias (x − 2) .
Ejercicio 5 : 1- Utilizando el teorema de los crecimientos finitos, mostrar que para todos los
 π 2π  1
reales distintos x e y del intervalo  ;  , sen(x) − sen(y) ≤ x − y .
3 3  2
2- Utilizando el teorema de los crecimientos finitos, mostrar que para todo x ≥ 0 ,
x
tenemos : 2 ≤ arctan(x) ≤ x .
x +1
Ejercicio 6 . Para x real, anotamos g(x)= x4-24x2 +x+1. Con ayuda de la fórmula de Taylor
aplicada a la función polinomio g en 2, estudiar la forma local de la curva que representa g en
la proximidad del punto de abscisas 2.

Ejercicio 1 : x  x es un contra-ejemplo.
Ejercicio 2 :
1
1. f se puede derivar sobre ]−1; +∞[ , si x ∈ ]−1; +∞[ , f '(x) = .
2(x + 1)
1  1  84x + 3
2. f se puede derivar sobre  ; +∞  , si x ∈  ; +∞  , f '(x) = .
6  6  (6x − 1)(4x + 5)
4x
3. f se puede derivar sobre ]−∞; −1[ ∪ ]1; +∞[ , si x ∈ ]−∞; −1[ ∪ ]1; +∞[ , f '(x) = .
3(x 4 − 1)
x x 2 +1
4. f se puede derivar sobre , si x ∈ , f '(x) = e .
x2 +1
( ).
2
x + 1+ x2
5. f se puede derivar sobre , si x ∈ , f '(x) =
1+ x2
6. f se puede derivar sobre , si x ∈ , f '(x)= (1 + x ln(2))2 x .
Ejercicio 3 : lim ∆(h) =

f '(x 0 ) , la recíproca es falsa, x  x con x 0 = 0 es un contra-
h →0
ejemplo.
Ejercicio 4 : Aplicamos la fórmula de Taylor-Lagrange al orden 3 para P entre x y 2. Obte-

nemos, para todo x ∈ , P(x) = −11 − 15(x − 2) − 2(x − 2) 2 + (x − 2)3 .
Ejercicio 5 : Aplicación directa de la desigualdad de los crecimientos finitos.
Ejercicio 6 : Utilizamos la desigualdad de los crecimientos finitos para f : x  x entre

10000 y 10001 :
f es continua sobre [10000 ; 10001] y se puede derivar sobre ]10000 ; 10001[, además:
1
∀x ∈]10000 ; 100001[,| f '(x) |≤
200
1
entonces | 10001 − 100 |≤ .
200

EJERCICIOS
Ejercicio 1. Estudiar la derivabilidad de las funciones siguientes. ¿Son ellas de clase C1?
 → 
 →  
  →   1
f x g h α  x  x α sen   si x ≠ 0 α ∈ {1, 2,3}
 x  1+ x
3
 x  x − 1  x
  0  0
Ejercicio 2. Calcular la derivada enésima de la función x  (x - 1)3ex.
 a x si 0<x<x 0
Ejercicio 3. Sean a ∈ , x0 > 0 y f : *+ →  tal como : f(x)=  .
 x² + 12 si x ≥ x 0
Dar una condición necesaria y suficiente para a y x 0 para que f sea de clase C1 en +.
Ejercicio 4. Sea f una función no constante, n veces derivable sobre [ a; b ] . Mostrar que si f
posee n+1 ceros diferentes en [ a; b ] , entonces existe c ∈ ]a; b[ tal que f ( n ) ( c ) = 0 .
Ejercicio 5. Sea f un función definida y continua entre el segmento [0,1] y tal que
f(0)=f(1)=0. Suponemos , entre otros, que la función f se puede derivar entre [0, 1[ y que
f’(0)=0.
Consideramos la función g de [0, 1] de  definida por:
 f (x)
 para x ∈ ]0, 1]
g(x) =  x
 0 para x=0
Mostrar que la función g verifica las hipótesis del Teorema de Rolle y deducir que existe a∈
f (a)
]0, 1[ tal que f ’(a) = . Interpretar este resultado gráficamente.
a
Ejercicio 6. Evaluar un mayorando del error cometido tomando 100 como valor aproximado
de la raíz cuadrada de 10 001.
1 1
Ejercicio 7. Mostrar que por todo entero n ≥ 1 tenemos : < ln(n + 1) – ln(n) < .
n+1 n
1 1 1
Deducir que la suma S n = 1 + + + …. + tiende hacia + ∞ cuando n tiende hacia + ∞.
2 3 n
Ejercicio 8.
x
1- Mostrar que si x ∈ ]0;1[ , entonces tenemos : x < arcsin x < .
1− x2

x
2- Mostrar que si x > 0 , entonces tenemos : < arctan x < x .
1+ x2
3- Mostrar que si x es un real tal que x > 0 , entonces tenemos :
3x 3x 2 x 3 3
3x 3x 2
1+ + − < (1 + x ) 2 < 1 + +
2 8 16 2 8
2
3x 3x 3
Para cuales valores de x, 1 + + es un valor cercano de (1 + x ) 2 con una precisión de
2 8
–3
10 ?
Ejercicio 9. a- Sea I un intervalo abierto, y f una aplicación de I en , que se puede derivar

sur I. Suponemos que f admite k ceros distintos en I (k ≥ 2).
Demostrar que f admite al menos k – 1 ceros distintos.
Puede darse que f ' admite estrictamente más de k – 1 ceros?
Si f se puede derivar dos veces en I, que podemos decir del nombre de ceros de f " ?
b- Aplicación : Sean n entero≥ 2, y a y b dos números reales.
Demostrar que la función f definida sobre  por f(x) = x n – ax + b admite:
- por lo mucho dos raíces reales si n es par,
- por lo mucho tres raíces reales si n es impar
c- SeaP un polinomio con coeficientes reales de grado n con raíces reales. Mostrar que
es lo mismo para P ’. (distinguir el caso en el cual todas las raíces de P son simples del caso
donde ellas no lo son).
Ejercicio 10. Calcular los límites de las funciones en los puntos indicados:
 π
sen  x − 
 3 π
= 1- f1 (x) = en x 0
1 − 2cos(x) 3
x −1
2- f 2 (x) = m en x 0 = 1 (siendo m un real no nulo)
x −1
sen²(x) − sen²(a)
3- f 3 (x) = en x 0 = a ≠ 0
x² − a²
a x − bx
4- f 4=(x) en=
x 0 0 (a ≠ b;a>0;b>0)
x
Ejercicio 11. Calcular la derivada nesima de las siguientes funciones:

1- f(x) = cos(x)
2- g(x) = x.cos(x)
3- h(x) = xn-1 ln(x)
n
Ejercicio 12. Derivando n veces la igualdad: e3x=exe2x, mostrar que : ∑2 k
C kn = 3 n .
k =0
Ejercicio 13. Se dice que f es de clase Cn si f tiene derivadas continuas del orden n.
1- a- Mostrar que si f es de clase C2 y si f "( x 0 ) no es nulo, el gráfico de f se situa en
la vecindad de x 0 de un solo lado con relación a su tangente en x 0 .
b- Mostrar que si además f '( x 0 ) es nulo, entonces f presenta un extremum local en
x 0.

c- Mostrar que si f y f ' son continuas en [a;b], si f " existe y es positiva en
]a;b[,entonces el gráfico (Γ) de f en [a;b] se sitúa por encima de cada una de sus tangentes.
2- ¿Qué se puede concluir en el caso en que f es de clase Cn (n>2) y donde f "( x 0 ) es
nulo ?
Ejercicio 14. Sea f una función derivable dos veces sobre un intervalo I y a, b, c elementos
de I tales que a < b < c .
Mostrar que existe al menos un punto d de I tal que :
c−a f ′′ ( d )
f (c) = f (a ) +
b−a
( f ( b) − f (a )) +
2
( c − a )( c − b )
Método : Podemos utilizar la función φ definido por :
x−a λ
φ ( x) = f ( x) − f (a) −
b−a
( f ( b ) − f ( a ) ) − ( x − a )( x − b ) para un real λ conveniente.
2
Ejercicio 15. Sea f una función de clase C² sobre [ a; b ] y tal que:

( a ) f=
f= ( b ) f ′=
( a ) f ′=
(b) 0
Mostrar que existe un real c ∈ ]a; b[ tal que f ′′ ( c ) = f ( c ) .
φ ( x)
Podemos introducir la función φ definido por := ( f ′ ( x ) − f ( x )) e x
.
Ejercicio 16. Mostrar que la aplicación f de  en  definida por:

  1
exp −  si x ≠ 0
f(x) =   x² 
 0 si x = 0
es de clase C∞ y que para todo entero n, f (n) (0) = 0.
Ejercicio 17. Sea f :  →  una función derivable dos veces. Suponemos que f y f ′′ están
borneados y proponemos:
M 0 = sup f ( x ) y M 2 = sup f ′′ ( x )
x∈ x∈
Con la ayuda de la formula de Taylor aplicado a un intervalo de  conveniente, mostrar que :

2M 0 hM 2
∀x ∈ , ∀h ∈ *+, f ′ ( x ) ≤ +
h 2
Deducir que : sup f ′ ( x ) ≤ 2 M 0 M 2 .
x∈
Ejercicio 18. Para todo real x >0, se plantea :

 x3 
Ax =  θ ∈ ]0;1[/sh(x) x
= + .ch(θx) 
 6 
Mostrar que A x es un conjunto con un sólo elemento. Se plantea A x = {θ(x)}. Calcular
Lim θ(x)
x →0
Ejercicio 19. a- Demostrar, utilizando una función auxiliar, que si f es derivable en [a;a+2h]
y admite una derivada segunda en ]a;a+2h[, tenemos:
f(a + 2h) - 2f(a + h) + f(a) = h² f "(a + 2θh) donde θ es elemento de ]0;1[

b- Supongamos f de clase C3 y f (3) (a) ≠ 0. Determinar Lim θ(h).
h →0
Elementos de solución:
a- Sea A = f(a + 2h) - 2f(a + h) + f(a)
= [f(a + 2h) - f(a + h)] - [f(a + h) - f(a)]
Tomemos φ(x) = f(x + h) - f(x). Obtenemos entonces: A = φ(a + h) - φ(a).
Como φ verifica las hipótesis del teorema de los crecimientos finitos, existe θ 1 elemento de
]0;1[ tal que A = h.φ '(a + θ 1 h).
Como φ'(x) = f '(x + h) – f '(x), tenemos: A = h[f '(a + θ 1 h + h) – f '(a + θ 1 h)].
Comof ' verifica las hipótesis del teorema de los crecimientos finitos, existe θ 2 elemento de
]0;1[ tal que A = h².f"(a + θ 1 h + θ 2 h).
θ +θ
Tomemos θ = 1 2 .
2
Entonces θ es elemento de]0;1[ y f(a + 2h) - 2f(a + h) + f(a) = h².f"(a + 2θh).
b- f siendo una función de clase C3, podemos aplicar la Fórmula de Taylor a la igual-
dad anterior al orden 2 para el miembro de la izquierda y al orden 0 para el miembro de la
derecha.
Tenemos así la existencia de θ 3 , θ 4 , θ 5 elementos de ]0;1[ tales que:
 (2h) 2 (2h)3 (3) 
 f(a) + 2hf '(a) + f"(a) + f (a + 2θ3 h) 
 2! 3! 
 h2 h3 
−2  f(a) + hf '(a) + f"(a) + f (3) (a + θ4 h)  + f(a)
 2! 3! 
2 (2) 2 (3)
= h f (a) + h 2θhf (a + 2θθ5 h)
4 (3) 1
f (a + 2θ3 h) − f (3) (a + θ4 h)
De donde : θ = 3 (3)
3 .
2f (a + 2θθ5 h)
Como f (3) es continua y f (3) (a) no nulo, por el pasaje al límite en 0 :
1
Lim θ(h) =
h →0 2

DOS MÉTODOS DE INTEGRACIÓN NUMÉRICA
1- FÓRMULA DE LOS TRAPECIOS
Sea “f” de clase C² en [a,b] y “g” la ecuación de la recta tal que g(a)=f(a) y g(b)=f(b).
b b
Nos aproximamos entonces a la integral I = ∫ f (t)dt mediante el número J = ∫ g(t)dt .
a a
1) Calcular J.
2) Se desea aumentar el error de método |I-J|. Para eso, se considera la función
x x −a
ϕ(x)= ∫ f (t)dt − (f(x) + f(a)) - K (x-a)3, donde K es la constante determinada por la
a 2
condición ϕ(b) = 0.
a) Calcular ϕ' et ϕ".
b) Mediante la utilización repetida del teorema de Rolle, probar la existencia
f "(c)
de c elemento de ]a,b[ tal que K= -
12
3
(b − a)
c) Deducir I = J - f "(c) .
12
3) Se discretiza el intervalo [a,b] en los n+1 puntos xi = a+i b−a , i=0,…,n. Probar
n
que se puede escribir:
b (b−a)
I= ∫ f (t)dt = ( f(a) + 2f(x l ) + … + 2f(x n-l ) + f(b)) + ε n
a 2n
(b−a)3
con |ε n | ≤ M 2 y M 2 = Sup f "
12n² [a,b]
Formula de los trapecios

Indicar previamente por qué M 2 existe.
4- Aplicación numérica: ¿A partir de qué valor de n se puede afirmar que la utilización
1 dt
de la fórmula para acercar ln2 = ∫ garantiza un error de método inferior a 10-6 ?
0 1+ t

2- FORMULA DE SIMPSON
SIMPSON Thomas, inglés, 1710 - 1761. Discípulo de Newton, enseñó matemáticas
en la academia de Woolwich. Se inició al cálculo infinitesimal estudiando los escritos de
L'Hospital y publicó un importante tratado : nuevo tratado de las fluxiones (1737), dicho de
otra manera sobre las derivadas según Newton (por oposición a las de Leibniz).
Método de integración aproximado de Simpson : en el cálculo de una cuadratura
(area por debajo de una curva), consiste en reemplazar tres puntos consecutivos de un arco de
curva por un arco de parábola. Este método muy eficaz es generalmente utilizado en las calcu-
ladoras "de bolsillo" actuales.
Se desea ardientemente mejorar el método anterior acercando el gráfico de f por una

parábola, en vez de por una recta. Para ello:
Sea “f” de clase C4 en [a,b] y “g” el polinomio de Lagrange de grado inferior a 2 tal que
g(a)=f(a), g(b)=f(b) y g(c)=f(c) donde c= a+b .
2
1) Expresar g(x). Dar g(x) en función de u, con x = c + u b−a .
2
 f (a) + f (b)  f (b) − f (a)
Respuesta: g(x)= u 2  − f (c)  + u + f (c)
 2  2
b  b−a
2) Calcular J = ∫ g(x)dx . se dará x = c + u 
a
 2 
Respuesta: J=(f(a)+f(b)+4f(c)) b−a
6
3) Para aumentar el error de método |I-J|, se considera la función:
ϕ(t) = ∫ f (x)dx - t (f(c+t) + f(c-t) + 4f(c)) – Kt5,
c+ t
c−t 3
 b−a 
donde K es la constante determinada por la condición ϕ   = 0.
 2 
 b−a
a) Calcular ϕ(i), i= 1,2,3; probar la existencia de η elemento de  0, tal
 2 
f (4)(γ)
que ϕ(3)(η) = 0, y luego deducir la existencia de γ elemento de ]a,b[ tal que K = - .
90
2 4 t
Respuesta parcial: ϕ’(t)= [f(c+t)+f(c-t)]- f(c)- [f ’(c+t)-f ’(c-t)]-5Kt4.
3 3 3
1 t
ϕ’’(t)= [f’(c+t)-f’(c-t)]- [f ’’(c+t)+f ’’(c-t)]-20Kt3.
3 3
t
ϕ(3)(t)=- [f(3)(c+t)-f(3)(c-t)]-60Kt2.
3
(b − a)5 (4)
b) Deducir I = J − f (γ) .
2880
4) Mostrar que, n siendo un entero par:
b (b−a)
I = ∫ f (t)dt = ( f(a) + 4f(x l ) + 2f(x2 ) + 4f(x 3 ) +…+2f(x n-2 ) + 4f(x n-1 ) + f(b)) + ε n
a 3n
(b−a)5
con |ε n| ≤ M y M 4 = Sup f (4)
180n 4 4 [a, b]
Formula de Simpson

Usted indicará antes por qué M 4 existe.
5) Aplicación numérica : Reanudar la aplicación numérica que ilustra el método de los
trapecios.
1
Ejemplo : Un valor aproximado de ∫ exp(x²)dx
0
es 1,4626517 (los 7 de cimales son exac-
tos).
Comparemos este valor a aquello obtenidos por la suma de Riemann (véase capítulo de Inte-
gral de Riemann), el método de Trapecios y el método de Simpson.
N 2 4 8 16 32 64
Riemann 1,14201271 1,27589363 1,36231966 1,41072400 1,43624595 1,44933827
Trapecios 1,57158317 1,49067886 1,46971228 1,46442031 1,46309410 1,46276235
Simpson 1,46371076 1,46272341 1,46265632 1,46265203 1,46265176 1,46265175
 1
Constatamos entonces, que para n=64, el método de Riemann  en  da sólo dos decimales
 n
exactos, el método de Trapecios da cuatro, y el método de Simpson da siete ( y más).

Ejercicio 20. Estudiar el límite eventual de cada una de las siguientes funciones en el punto
x0 :
1 − cos x
1- u(x) = en x0 = 0
sen²(πx)
sen ( x 3 )
2- v(x) = en x0 = 0
sen 2 (x)
0
Corrección : 1- Se trata de una forma indeterminada de tipo .
0
Tomemos f ( x ) =
1 − cos ( x ) y g ( x ) =
sen 2 ( πx )
Tenemos f= ( 0 ) g= ( 0 ) 0 , y además f ′ ( x ) = sen ( x ) y g′ ( x ) =
2π cos ( πx ) sen ( πx ) .
No podemos aplicar la regla de Hospital directamente ya que
f ′(x) sen ( x ) 0
lim = lim es una forma indeterminada de tipo .
x →0 g′ ( x ) x → 0 2 π cos ( πx ) sen ( πx ) 0
′ ( 0 ) g=
Por el contrario, tenemos f= ′ ( 0 ) 0 , podemos entonces aplicar la regla de Hospital a
las funciones f ′ y g′ .
f ′′ ( x ) =cos ( x ) y g′′ ( x ) =2π2 cos 2 ( πx ) − sen 2 ( πx )  .
f ′′ ( x ) cos ( x ) 1
Así lim lim
= .
x → 0 g′′ ( x )
x → 0 2π  cos
2

2
( πx ) − sen 2
( πx ) 
 2 π 2
Finalmente, de acuerdo con la regla de Hospital aplicada a las funciones f ′ y g′ , tenemos:

f ′(x) 1
lim = 2 , y de acuerdo con la regla de Hospital aplicada a las funciones f y g , obte-
x →0 g′ ( x ) 2π
f (x) 1
nemos: lim
= u(x) lim
=
x →0 x →0 g ( x ) 2π 2
0
2- Se trata de una forma indeterminada de tipo .
0
Igual que antes, vamos a utilizar la regla de Hospital.
=
Tomemos f ( x ) sin
= ( x 3 ) y g ( x ) sin 2 ( x ) .
( 0 ) g=
Tenemos f= 0 , y además f ′ ( x ) 3x
( 0) = = 2
cos ( x 3 ) y g′ ( x ) 2 cos ( x ) sin ( x ) .
f ′(x) 3x 2 cos ( x 3 )
No podemos aplicar la regla de Hospital directamente ya que lim = lim
x →0 g′ ( x ) x → 0 2 cos ( x ) sen ( x )
0
es una forma indeterminada de tipo .
0
′ ( 0 ) g=
Por el contrario, tenemos f= ′ ( 0 ) 0 , podemos entonces aplicar la regla de Hospital a
las funciones f ′ y g′ .
6x cos ( x 3 ) − 9x 4sen ( x 3 ) y g′′ ( x ) =
f ′′ ( x ) = 2 cos 2 ( x ) − sen 2 ( x )  .

f ′′ ( x ) 6x cos ( x 3 ) − 9x 4sen ( x 3 )
Así lim
= = 0.
lim
x → 0 g′′ ( x )
( ) ( )
x → 0 2  cos 2 x − sen 2 x 

Finalmente, de acuerdo con la regla de Hospital aplicada a las funciones f ′ y g′ , tenemos:
f ′(x)
lim = 0 , y de acuerdo con la regla de Hospital aplicada a las funciones f y g , obtene-
x →0 g′ ( x )
f (x)
mos: lim = 0 lo que quiere decir lim v(x) = 0 .
x →0 g ( x ) x →0
Ejercicio 21. Sean x e y dos reales que verifican 0 < x < y . Demostrar que :
y−x
x< <y
ln y − ln x
Podremos aplicar el teorema de los crecimientos finitos a la función g definida por :
g ( t ) = ln t .
Corrección : Anotemos g ( t ) = ln t , esta función es continua en el intervalo [ x, y ] y se puede

derivar en ]x, y[ .
De acuerdo con el teorema de los crecimientos finitos, existe c elemento de ]x, y[ tal que :
g ( y ) − g ( x=
) g′ ( c )( y − x )
1 y−x
Sabiendo que ∀t ∈ *+, g′ ( t ) = , la relación que precede nos da c = y siendo
t ln y − ln x
dado que c ∈ ]x, y[ , esto nos conduce a la desigualdad buscada.
Ejercicio 22. Demostrar que para todo real estrictamente positivo x:

x2 x2 x3
x– < ln (1 + x) < x– +
2 2 3
2
x
Para qué valores de x, x – es un valor aproximado de ln (1 + x) a 10 –3 cerca?
2
Corrección : Anotemos f (= x ) ln (1 + x ) .
De acuerdo con la fórmula de Taylor Lagrange al orden 2, luego 3 para la función f en el in-
tervalo [ 0,x ] , obtenemos :
x2 x 3 ( 3)
f ( x ) =f ( 0 ) + xf ′ ( 0 ) + f ( 0 ) + f ( c1 ) , c1 ∈ ]0, x[
′′
2 6
por otro lado tenemos :
x2 x3 x4
f ( x ) =f ( 0 ) + xf ′ ( 0 ) + f ′′ ( 0 ) + f (3) ( 0 ) + f ( 4) ( c 2 ) , c 2 ∈ ]0, x[
2 6 24
2
Un cálculo simple nos da f ( 0 ) =0, f ′ ( 0 ) =1, f ′′ ( 0 ) =-1, f (3) ( 0 ) =2 así que f (3) ( c1 ) = ,
( c1 + 1)
3
−6
f ( 4) ( c2 ) = .
( c2 + 1)
4

x2 x3 x 2 x3 x4
Deducimos entonces que : f ( x ) =x − + y f ( )
x =x − + − .
2 3 ( c1 + 1)3 2 3 4 ( c 2 + 1)4
 x2  x3
Particularmente, esto implica por un lado que: f ( x ) −  x −=  > 0 , y por otro
( )
3
 2  3 c1 + 1
 x 2 x3  x4
lado: f ( x ) −  x − +  = − < 0 , que es el resultado que buscamos.
( )
4
 2 3  4 c 2 + 1
Podíamos también demostrar cada una de las desigualdades estudiando el signo de las funcio-
nes obtenidas por la diferencia de los dos términos.
x2 x 2 x3 x 2 x3
Ya que x − < ln (1 + x ) < x − + , deducimos que : 0 < ln (1 + x ) − x + < .
2 2 3 2 3
x2
Así x − es un valor aproximado de ln (1 + x ) a 10−3 cerca si :
2
3 1
x
≤ 10 ⇔ x ≤ 3 × 10 ⇔ x ≤ 33 × 10−1
−3 3 −3
Ejercicio 23. Estudiar completamente la función f definida en * por f(x) = |x ln|x| |.
Corrección : De un comienzo debemos observar que lim f ( x ) = 0 , podemos entonces pro-

x →0
longar f por continuidad en  anotando f(0)=0.

La función f es par, podemos entonces restringir el estudio a *+.
f se puede derivar en *+\{1}.
Derivabilidad de f en 0 :
f ( x ) − f ( 0 ) x ln x f ( x ) − f ( 0)
= entonces lim+ = lim+ ln x = +∞ y
x x x →0 x x →0
f ( x ) − f ( 0)
lim− = lim− − ln x = −∞ .
x →0 x x →0
Deducimos que f no se puede derivar en 0. Sin embargo, el gráfico de f, C f, admite semi-

tangentes verticales a la derecha y a la izquiera en el punto de abscisas 0.
Derivabilidad de f en 1 :
f ( x ) − f (1) x ln x
=
x −1 x −1
x −1 f ( x ) − f (1) x ln x
Recordamos que lim = 1 , entonces tenemos lim+ = lim = 1y
x →1 ln ( x ) x →1 x −1 x →1 x − 1
+
f ( x ) − f (1) x ln x
lim− lim− −
= −1 .
=
x →1 x −1 x →1 x −1
Deducimos que f no se puede derivar en 1. Sin embargo, C f admite semi-tangentes de pen-
diente -1 y 1 a la derecha y a la izquiera respectivamente en el punto de abscisas 1.
− x ln x si x ∈ ]0,1[
En *+\{1}, f se puede derivar y tenemos f ( x ) = .
x ln x si x ∈ ]1, ∞[

− ( ln x + 1) si x ∈ ]0,1[
Deducimos que f ′ ( x ) = .
( ln x + 1) si x ∈ ]1, ∞[
Para x ∈ ]1, ∞[ , tenemos : ( ln x + 1) ≥ 0 entonces f ′ ( x ) ≥ 0 .
Para x ∈ ]0,1[ , ( ln x + 1) ≥ 0 ⇔ ln ( x ) ≥ −1 ⇔ x ≥ e −1 .
Podemos entonces trazar la tabla de variaciones de f en *+ :
x 0 e −1 1 +∞
f ′ + - +
f
Con ayuda de la paridad deducimos la tabla de variaciones de f en .

Con ayuda de lo que sabemos acerca de las semi-tangentes, obtenemos el aspecto de la curva :

Capítulo 14
DESARROLLOS LIMITADOS
Brillante alumno de Simson y de Newton , Maclaurin Colin (o
Mac-Laurin) (escocés, 1698-1746) obtuvo a los 19 a ños una cátedra
de enseñanza de las matemáticas en la universidad de Aberdeen y
enseñaría ulteriormente en Edimburgo. Está al origen de los desarollos
en serie entera de las funciones numéricas por el método de los
coeficientes indeterminados ("Tratado de las fluxiones ", 1742),
prolongamiento de los trabajos de Newton y de Taylor.
Las fórmulas de Taylor y de Maclaurin son las herramientas
privilegiadas para obtener un desarollo limitado de una función sobre
un intervalo.
Un ejemplo de desarollo de Taylor convergente, pero no hacia la
función inicial, fue dado por Cauchy por el medio de la función :
1
−
x  e (Ver Ejercicios del capítulo “Cálculo Diferencial”).
x²
Los desarollos limitados se utilizan en la aproximación polinomial de las funciones, el

estudio de limites en un punto y el comportamiento local.
1- Definición
Definición: Sea f una función definida en la vecindad de un real x 0 excepto quizá en
x0 .
El hecho que f admita un desarrollo limitado de orden n en la vecindad de x 0 significa que
existe (n+1) reales a 0 , …, a n tales que:
n
f(x)= ∑ a (x − x
i 0 )i + o ( (x-x 0 ) n )
i =0
Observación: Nosotros podemos extender la definición precedente a una función
definida a la derecha de x 0 o a la izquierda de x 0 .
Definición: El polinomio que aparece en las escrituras de desarrollos limitados se

llama la parte regular o polinomial de estos desarrollos.
Observación a propósito de las equivalencias: El primer término no nulo del

desarrollo limitado de una función es un equivalente de esta función.

Observación con respecto a la fórmula de Taylor-Young
Toda función f de clase Cn−1 sobre [0, x] (resp. [x, 0]) y tal que f(n)(0) existe, admite un dl de
orden n en 0 que es :
n
f (k ) (0) k
f(x) = ∑ x + o ( xn )
k =0 k!
Algunos desarrollos limitados clásicos en la vecindad de 0:

x x2 xn
e x =1 + + + ... + + o(x n )
1! 2! n!
x3 x5 x 2n +1
sen x = x − + + ... + (−1) n + o(x 2n +1 )
3! 5! (2n + 1)!
x2 x4 x 2n
cos x = 1 − + + ... + (−1) n + o(x 2n )
2! 4! (2n)!
x3 x5 x 2n +1
senh x = x + + + ... + + o(x 2n +1 )
3! 5! (2n + 1)!
x2 x4 x 2n
cosh x =+
1 + + ... + + o(x 2n )
2! 4! (2n)!
2 3
x x xn
ln(1 + x) = x − + + ... + (−1) n +1 + o(x n )
2 3 n
α α ( α − 1) α(α − 1)...(α − n + 1) n
(1 + x)α =1 + x + x 2 + ... + x + o(x n )
1! 2! n!
2- Desarrollo limitado, continuidad y derivabilidad
1- Desarrollo limitado de orden 0

Propiedad: Si f está definida en la proximidad de 0 (salvo quizás en 0), las dos propiedades
siguientes:
1- f admite un dl de orden 0 en 0 de la forme f(x) = a 0 + o(1)
2- Lim f (x) = a 0
x →0
f es eventualmente prolongable por continuidad con f(0) = a 0 .
Desde ahora en adelante, las funciones no definidas en 0, que admiten un dl en 0, serán
prolongados por continuidad.
2- Desarrollo limitado de orden 1

Propiedad: Las dos propiedades siguientes son equivalentes :
1- f admite un dl de orden 1 en 0 de la forme f(x) = a 0 + a 1 x + o(x)
2- f es derivable en 0, f ’(0) = a 1 y la ecuación de la tangente en el punto (0, a 0 ) es
y = a0 + a1 x
3- Observaciones:
a- Un desarrollo de Taylor-Young al orden n es un desarrollo limitado al orden n.
b- Un desarrollo limitado al orden n no es necesariamente un desarrollo de Taylor-Young al
orden n.

 3 1
cos(t) + t sen   si t ≠ 0
Ejemplo: La función f(t) =  t admite un desarrollo limitado al orden
1 si t=0

2 en 0 pero, como la función no se puede derivar 2 veces en 0, elle no admite un desarrollo de
Taylor-Young al orden 2 en 0. Ver ejecicio.
4-Aplicación: Posición de una curva con respecto a su tangente.

Sea f una función que admite un desarrollo limitado en x 0 a un orden n>1 de la forma:
f(x)=a 0 + a 1 (x-x 0 ) + a n (x-x0 )n + o ( (x-x 0 ) n ) con a n ≠ 0
podemos deducir que la ecuación de la tangente al gráfico de f en x0 es y= a 0 + a 1 (x-x0 ).
Siguiendo la paridad de n el signo de a n , podemos precisar la posición del gráfico de f con
respecto a su tangente en las cercanías de x 0 .
3- Propiedades
En este párrafo, f es una función que admite un desarollo limitado de orden n en 0.
1- Unicidad
Propriedad: El desarollo limitado es único.
Consecuencia: Si f es de clase Cn-1 sobre [0, x] (resp. [x, 0]), si f(n)(0) existe y si f admite en 0
n
un dl de orden n de la forme f(x) = ∑a k x k + o ( x n ) entonces para todos enteros k de [0, n],
k =0
(k )
f (0)
ak = .
k!
2- Paridad
Propriedad : Si f es una función par (respectivamente impar), la patre polinomial (regular) de
su desarollo limitado en 0 es un polinomio par (respectivamente impar).
3- Desarollo limitado por restricción

Propriedad : Sea p un entero natural inferior a n. f admite un desarollo limitado de orden p.
Su parte polinomial (regular) se obtiene « por restricción » a los términos de grado inferior a p
de la parte polinomial (regular) del desarollo limitado de orden n.
4- Desarollo limitado por división de una potencia de la variable

Propriedad : Si el desarollo limitado de f en 0 es de la forma :
f(x)=a p xp+…+a n xn+o(xn) (p ≤ n)
f (x)
Entonces la función g definida por g(x)= p admite un desarollo limitado de orden (n-p) :
x
g(x)=a p +a p+1 x1+…+a n xn-p+o(xn-p)
5- Integración de un desarrollo limitado

Propriedad : Sea f tal que admita un desarollo limitado en 0 de orden n : f(x)=P n (x) + o(xn).
x
Si f es integrable sobre [0,x] o [x,0], entonces la función x  ∫ f (t)dt admite en 0 un
0
desarollo limitado de orden (n+1) determindo por :

x x
∫0
f (t)dt = ∫
0
Pn (t)dt + o(x n+1 )
Aplicación : Desarrollo limitado de arctan en 0.
Observación : Hay que resaltar que el desarrollo limitado de arctan permitió al final del siglo
XVII un avance espectacular en el cálculo de decimales de π, basado hasta entonces en el
método de Arquímedes (s. III a.C) que aproxima un círculo por un polígono en el cual se
calcula la longitud del perímetro o del aire. Arquímedes utiliza un polígono de 96 lados, Al-
Kashi (s. XV) un polígono de 3 × 228 lados, Ludolph van Ceulen ( ≈ 1600) un polígono de 262
lados, obteniendo para este último unos treinta decimales. Este método fue abandonado para
el provecho de otros métodos que daban expresiones de π bajo la forma de arctan.. Citemos
particularmente , la fórmula de Machin (1706) que el lector se encangará de comprobar:
π = 4 arctan 1 - arctan 1
4 5 239
Machin obtiene así una centena de decimales. Conocemos actualmente (2003) más de 1000
mil millones de decimales de π.
6- Observación sobre la derivación de un desarrollo limitado

Propiedad : Sea f tal que admite un desarollo limitado en 0 de orden n : f(x)=P n(x) +  (xn)
Si f es derivable al entorno de 0 y f ’ admite un desarollo limitado de orden (n-1) en 0 :
f ’(x)=Q n-1 (x) + o(xn-1), entonces Q n-1 = Pn '
4- Cálculo práctico
En este párrafo, f y g son dos funciones que admiten desarollos limitados de orden n en 0.
1- Combinación lineal
Propriedad : (αf+βg) admite un desarollo limitado de orden n en 0 de l cual obtenemos la
parte polinomial (regular) sumando las dos partes polinomiales (regulares) de αf y βg.
2- Producto
Propriedad : (fg) admite un desarollo limitado de orden n en 0 del cual obtenemos la parte
polinomial (regular) efectuando el producto de las dos partes polinomiales (regulares) de f y
de g y guardando únicamente los monomios de grado inferior (o igual) a n.
3- Quociente
Propriedad : Suponemos de más que la valuación de la parte polinomial (regular) de g es
nula.
f
Entonces admite un desarollo limitado de orden n en 0 de l cual la parte polinomial
g
(regular) es el quociente de la división según las potencias crecientes al orden n de la parte
polinomial (regular) de f por la parte polinomial (regular) de g.
4- Composición
Propriedad : Suponemos además que la valución de la parte polinomial (regular) de f no es
(
nula Lim f = 0 .
0
)

Entonces g  f admite un desarollo limitado de orden n en 0. Su parte polinomial(regular) se
obtiene componiendo las partes polinomiales (regulares) de f y de g y guardando únicamente
lo monomios de grado inferior (o igual) a n.
5- Desarrollo generalizado (asintótico)
1- Desarrollo generalizado
Sea f una función definida en la proximidad de x 0 tal que la función: x  (x-x0 )αf(x) admite
un desarrollo limitado de orden n en x 0 .
n
(x-x 0 )αf(x)= ∑ a k ( x − x 0 ) + o ( (x − x 0 ) n )
k
k =0
Tenemos entonces el desarrollo generalizado de f en x 0 :
1  n 
α ∑ k (
a x − x 0 ) + o ( (x − x 0 ) n ) 
k
f(x)=
(x − x 0 )  k =0 
2- Extremidad infinita
Designamos para f una función de variable real y por C f la curva representativa de f
en un plano munido de una referencia (O ; i ; j ).

→  →
Las extremidades infinitas de C f corresponden a los casos siguientes:
1- Lim f(x)= ±∞ con x 0 real: C f admite una asítota vertical de ecuación x = x0.
x →x0
2- Lim f(x)=L con L real : C f admite una asíntota horizontal de ecuación y = L.

x →±∞
3- Lim f(x)= ±∞ : un estudio más profundo es necesario.

x →±∞
Existen dos métodos posibles:

f (x)
a- Buscamos Lim para comparar f(x) a x en la proximidad de ±∞ . Podemos
x →±∞ x
hacer la siguiente clasificación:
f (x)
• si Lim = ±∞ , decimos que C f admite una extremidad parabólica vertical.
x →±∞ x
Ejemplos: f (x) = x2, f ( x ) = e x .

f (x)
• si Lim = 0, decimos que C f admite una extremidad parabólica horizontal.
x →±∞ x
Ejemplos: f ( x ) = x , f ( x ) = ln( x ) .
f (x)
• si Lim =a (con a ∈*)
x →±∞ x
– si Lim (f(x) – ax)=b, C f admite una asíntota de ecuación y=ax + b
x →±∞

– si Lim (f(x) – ax)= ±∞ , C f admite una extremidad parabólica de dirección y=ax
x →±∞
Ejemplo: f(x) = 2x + ln x
b- Buscamos un desarrollo asintótica de f en ± ∞

(que además permite estudiar la posición de Cf con relación a la asíntota).

Ejercicio 1 : Simplificar al máximo las siguientes escrituras :

1. (1 + 3x − x 2 + o(x 3 )) + (−2 + 5x 2 − x 4 + o(x 4 ))
2. (2x − 5x 2 + 4x 3 + o(x 5 )).(−1 + 7x − x 2 + 3x 3 + 2x 4 + x 5 + o(x 5 ))
2x + 4x 2 + o(x 4 )
3.
x − x 2 + o(x 2 )
Ejercicio 2 : Determinar un desarrollo limitado al orden n de f en a en los siguientes casos:

1. f (x) =2x + 3x 3 − x 4 , a =0, n =2 luego n =5. Misma pregunta para a=3.
2
2. f (x) = ln(1 − x) + x 2 + , a = 0, n = 6 .
1 + x3
3. f =(x) cos(3x),= a 0,= n 5.
4. f (x) = sen(x) 1 + x , a = 0, n = 4 .
ex
5. f =
(x) , a 0,=
= n 3.
1+ x
π
6. f=
(x) tan(x),
= a = , n 4.
4
3x 3 + x 2 + x + 1
Ejercicio 3. Para x un real conveniente, anotamos f (x) = .
x 2 − 2x + 1
1 1
Mostrar que en la proximidad de −∞ y de +∞ tenemos: f (x) = 3x + 7 + 12   + o   .
x x
Interpretar geométricamente este resultado.

Ejercicio 1 :
1. −1 + 3x + 4x 2 + o(x 3 )
2. −2x + 19x 2 − 41x 3 + 39x 4 − 15x 5 + o(x 5 )
3. 2 + 6x + o(x)
Ejercicio 2 :
1. cuando =a 0, = n 2, f (x)= 2x + o(x 2 ) ,
cuando a = 0, n = 5, f (x) = 2x + 3x 3 − x 4 + o(x 5 )
cuando a =3, n =2, f (x) =6 − 25(x − 3) − 26(x − 3) 2 + o((x − 3) 2 ) ,
cuando a =3, n =5, f (x) =6 − 25(x − 3) − 26(x − 3) 2 − 9(x − 3)3 − (x − 3) 4 + o((x − 3)5 )
x 2 7x 3 x 4 x 5 11x 6
2. f (x) = 2 − x + − − − + + o(x 6 )
2 3 4 5 6
9 2 81 4
3. f (x) = 1 − x + x + o(x 5 )
2 24
1 2 7 3 1 4
4. f (x) = x + x − x − x + o(x 4 )
2 24 48
1 1
5. f (x) = 1 + x 2 − x 3 + o(x 3 )
2 3
 π 
2
π 8
3
π  10  π
4
 π 
4
6. f (x) =
1+ 2 x −  + 2 x −  +  x −  +  x −  + o   x −  
 4  4  3 4 3 4  4  


EJERCICIOS
APLICACIONES DEL CURSO
Ejercicio 1. a- Sea f una función que admite un desarrollo limitado de orden 1 en la vecindad
de t 0 . Mostrar que f es derivable en t 0 .
b- Mostrar que la existencia de un desarrollo de orden n estrictamente superior a 1 en
la vecindad de t 0 no implica la existencia de f (n) (t 0 ) ni tampoco la existencia de otra derivada
diferente a f '( t 0 ).
 3 1
cos(t) + t sen   si t ≠ 0
Indicación : Usted podrá utilizar la función f(t) =  t .
1 si t=0

Ejercicio 2. Descubrir el error en el cálculo siguiente del desarrollo limitado de orden 2 en 0

sen(x)
de la función f : x  y corregirla.
x + x²
1- sen(x) = x + o(x²)
2- La división según las potencias crecientes de x por (x + x²) da :
x = (x + x 2 )(1 - x) + x 3
3- De ahí : f(x) = 1 - x + o(x²).
Ejercicio 3. a- Sea f la función definida por :

 2 3 1
1 + x + x + x sen   si x ≠ 0
f(x) =  x
1 si x=0

1- Mostrar que en la proximidad 0 tenemos : f ( x ) =1 + x + x 2 + o ( x 2 ) .
Deducir que f es derivable en 0. Determinar f ’(0).
2- Mostrar que f ' no admite desarrollo limitado de orden 1 en 0
1
b- Sea g la función definida por g(x) = . Mostrar que g admite en 0 un
(1 − x)²
desarrollo limitado de cualquier orden. Determinarlo.
Ejercicio 4. Sea f la función definida por f(t) = (ln|t|).t².

a- Mostrar que podemos prolongar f en 0 por continuidad. Llamamos también f la
prolongación por continuidad.
b- Mostrar que f se puede derivar en 0. Determinar f '(0).
c- Mostrar que f no tiene un desarrollo limitado de orden estrictamente superior a 1.
Ejercicio 5. Determinar el desarrollo limitado en la proximidad de 0 de orden 3 de las

funciones siguientes:
x 1 ln(1 + x) x
f1 (x)
= ; f 2 (x)
= ; f 3 (x)
= ; f 4 (x)
= x ; f 5 (x)
= 1 + sen(x) ;
sen(x) cos(x) 1+ x e −1
f 6 (x)
= 1 + cos (x)

Ejercicio 6. Determinar el desarrollo limitado en la vecindad de 0 de orden 3 de las
funciones siguientes:
x 1
f1 (x)= ecos(x) ; f 2 (x)= e cos(x) ; f 3 (x)= (1 + x) x
ln x
Ejercicio 7. Calcular el desarrollo limitado al orden 4 en la proximidad de 1 de .
x2
Método : suponemos x = 1 + u con u en la proximidad de 0.
Ejercicio 8. Determinar el desarrollo limitado en la proximidad de 1 al orden 3 de la función

f(x) = x .
Ejercicio 9. Calcular el desarrollo limitado al orden 3 de :

sen x
a- f ( x ) = arctan ( x ) en la proximidad de 2. b- g ( x ) = en la proximidad de π.
5 − 4 cos x
Ejercicio 10. Sea f la función definida por:

e x² − 1
f(0) = 0 ; ∀x ∈ *, f(x) =
x
Mostrar que f admite una función recíproca f , definida sobre , y dar el desarrollo limitado
-1
de f -1 al orden 5 en la proximidad de 0.
x ( e x + 1) − 2 ( e x − 1)
Ejercicio 11. Sea f la función definido por f ( x ) = . Determinar el límite
x3
de f en 0, la ecuación de la tangente en 0 también la posición de la tangente con respecto a la
curva representativa de f.
Ejercicio 12. Estudiar, según los valores del parámetro “a”, la forma y la posición respecto a
su tangente, de la función mencionada abajo en la vecindad de 0:
 1 − ax + x²  3 + x
f(x) = ln −
 1 + ax − x²  1 + x
Cada caso deberá estar ilustrado por un dibujo.
Ejercicio 13. consideramos la función g definido por : g ( x ) = 1 + 2x − cos x − senx .
1- Calcular el desarrollo limitado al orden 4 en la proximidad de 0 de g(x).

Deducir un equivalente de g en la proximidad de 0.
g(x)
2- calcular el limite eventual de en 0.
x3
Ejercicio 14. consideramos la función f definido por : f (=

x) x 2 − x + 1 + 3 x 3 + λx 2 + 1 .
1- Calcular un desarrollo asintótico de f(x) en la proximidad de − ∞ .

2- Calcular λ para que L im f ( x ) = 0 .
x →−∞

EJERCICIOS
ESTUDIOS DE LAS FUNCIONES
Ejercicio 15. Se considera a la familia de funciones f definidas por:

x + ax 3
f:x  arctan(x) −
1 + bx 2
donde “a” y “b” son dos reales.
1- Escribir el desarrollo limitado de orden 7 de f en la vecindad de 0.
4 3
2- Se propone estudiar la función f obtenida por a = yb= .
15 5
a- Deducir de la pregunta 1-, el aspecto de la curva representativa (C) de f en la
vecindad de 0.
π 1
b- Se recuerda que para x > 0, arctan(x) = - arctan   .
2 x
Deducir el desarrollo generalizado de f en la vecindad de (+∝), con la forma:
γ 1
f(x) = α + βx + + o  
x x
luego el aspecto de (C) en la vecindad de (+∝).
3- Acabar el estudio de f.
4- Dibujar (C).
Ejercicio 16. Se considera la función real f definida para toda x que no es nula por
1
−
=f(x) e x x² + x + 1 arctan(x)
1- Mostrar que para todo real x estrictamente positivo,
1 π
arctan(x) + arctan   =
x 2
1
¿Cuál es el valor de arctan(x) + arctan   para x estrictamente negativa?
x
2- Determinar los números reales a, b, c tales que:
c 1
f(x) = ax + b + + o   en la vecindad de (+∝).
x x
Determinar de la misma manera los reales α,β,γ tales que:
γ 1
f(x) = αx + β + + o   en la vecindad de (-∝).
x x
3- Sea (Γ) la curva de ecuación "y = f(x)". Determinar las asíntotas de (Γ) y la
posición relativa de (Γ) respecto a sus asíntotas.

1− x2 x +1
Ejercicio 17. Suponemos f ( x ) = ln .
x x −1
1. Propiedades generales de la función f :
a- Donar el dominio de definición Df de f.
b- Mostrar que f es par.
1
c- Expresar f   en función de f(x).
x
2. Estudio de f en la proximidad de 0 y de +∞ :
a- Determinar el desarrollo limitado al orden 2 en la proximidad de 0 de f.
Dar la forma de la curva Cf representando f en una referencia ortonormal en la proximidad
del punto de abscisa 0.
b- Encontrar un desarrollo asintótico de f en la proximidad de + ∞ y - ∞ de precisión
 1 
o  2  . Interpretar geométricamente.
x 
3. Estudio de f en la proximidad de 1 :
a- Dar un equivalente (la más simple posible) de f ( x ) en la proximidad de 1.
b- Cual es la forma de Cf en la proximidad del punto de abcisa 1.
4. Estudio de las variaciones de f :
a- Aplicando el teorema de los crecimientos finitos a ϕ definido por :
 1+ x  2x
ϕ(x) = ln   , mostrar que : ∀x ∈ ]0;1[ ϕ ( x ) − >0
 1− x  1+ x2
b- Mostrar que f (prolongado por continuidad) es decreciente sobre [0;+∞[ .
5. Grafico
Representar Cf .
Ejercicio 18. Estudiar las variaciones y dibujar la curva representativa de la función definida
por :
ln|x − 2|
f(x) =
ln|x|
Observación: El gráfico dado por una calculadora o por un programa informático de cálculo
no da a primera vista una buena idea de la curva como podrán darse cuenta estudiando f …

t² + 1 1t
Ejercicio 19. Estudiar la función f definida por : f(t) = e (Ejercicio con calculadora).
t −1
Elementos de solución:
- f es definida, continua y derivable en \{0,1}.
- Estudiar en 0:
f (t) − f (0)
Lim f = −∞ , Lim f = 0 , se da f(0)=0, Lim− =0
0 +
0 −
t →0 t −0
f es derivable a la derecha en 0 y f’d(0)=0.
- Estudiar en 1:
2e
f(t) ~ de ahí los límites en 1.
1 t −1
- Estudiar en + ∞ y - ∞ :
Un desarrollo generalizado de f da:
7 1
f(t)=t+2+ + o   pues la recta ∆ con ecuación y=t+2 es asíntota al gráfico Cf de f
2t t
en + ∞ y - ∞ . Se deduce también la posición relativa de ∆ y Cf.
1
ϕ(t)
- Para todo t elemento de \{0,1}, f’(t)= e t con ϕ(t)=t4-3t3-t+1.
t²(t − 1)²
Para estudiar el signo de ϕ, se estudian sus variaciones usando el signo de ϕ’
Para estudiar el signo de ϕ’, se estudian sus variaciones usando el signo de ϕ’’.
Se encuentra que ϕ se anula 2 veces: una vez en β comprendida entre 0 y 1 y una vez
en α comprendida entre 1 y + ∞ .
Un valor próximo a α es 3,07 y de f(α) es 6,97.
Un valor próximo a β es 0,56 y de f(β) es –17,80.
1
x² + 1 x
Gráfico de la función f(x)= e (cuidado con la escala)
x −1

x
Ejercicio 20. Sean f y g definidas por: f(x) = x3 – 2x2 – 1 y g(x) = x2 +1
x −1
1- Mostrar que la ecuación f(x) = 0 admite una solución única  real. Deducir de eso el
signo de f.
2- Estudiar las variaciones de g y dar su cuadro de variación.
3- Calcular el desarrollo limitado, a la orden 2, a la vecindad de 0, de g.
Deducir de eso la forma de la curva que representa g a la vecindad del punto de abscisa 0
y hacer un dibujo.
c 1
4- Calcular los reales a, b y c tales que : g(x) = ax + b + + o  
+∞ x x
Interpretar geométricamente el resultado obtenido.
Hacer un trabajo análogo a la vecindad de - .
5- Deducir la curva representativa de g. Admitiremos que  2,2 y g( )  4

ln (x)
Ejercicio 21. Calcular el desarrollo limitado al orden 4 en la proximidad de 1 de .
x2
Método : anotaremos x = 1 + u con u en la proximidad de 0.
ln (1 + u )
Corrección : Anotemos x=1+u entonces f ( x ) = .
(1 + u )
2
1
Como sabemos que =−1 u + u 2 − u3 + u 4 − u5 + o ( u5 ) .
(1 + u ) 0
−1
Entonces, derivando, obtenemos: − 1 + 2u − 3u 2 + 4u 3 − 5u 4 + o ( u 4 ) .
=
(1 + u )
2 0
1
Por lo cual: 1 2u + 3u 2 − 4u 3 + 5u 4 + o ( u 4 ) .
=−
(1 + u )
2 0
1 1 1
Por otro lado, tenemos: ln (1 + u ) = u − u 2 + u3 − u 4 + o ( u 4 ) .
0 2 3 4
Deducimos entonces que :
ln (1 + u ) 1 1 1
f (x) =
(1 + u )
2
=− ( 
 2 3
) 4

1 2u + 3u 2 − 4u 3 + 5u 4 + o ( u 4 )  u − u 2 + u 3 − u 4 + o ( u 4 ) 

1 1 1  1 1   1 
= u − u 2 + u 3 − u 4 − 2u  u − u 2 + u 3  + 3u 2  u − u 2  − 4u 4 + o ( u 4 )
2 3 4  2 3   2 
1 1 1 2 3
= u − u 2 + u 3 − u 4 − 2u 2 + u 3 − u 4 + 3u 3 − u 4 − 4u 4 + o ( u 4 )
2 3 4 3 2
5 13 77
= u − u 2 + u3 − u 4 + o ( u 4 )
2 3 12
Finalmente, esto nos da:
5
2
2 13
3
3 77
f ( x ) =x − 1 − ( x − 1) + ( x − 1) − ( x − 1) + o ( x − 1)
12
4 4
( )
43 50 64 77
= − x − 28x 2 − x 3 − x 4 + o ( x − 1)
12 3 3 12
4
( )
De hecho, tenemos una segunda solución que es un poco más rápida:
Queremos calcular el desarrollo limitado del cociente de :
1 1 1
ln (1 + u ) = u − u 2 + u 3 − u 4 + o ( u 4 ) por (1 + u ) =+
2
1 2u + u 2 .
0 2 3 4
Podemos entonces para ello, efectuar la división según las potencias crecientes de la parte
polinomial del numerados por la parte polinomial del denominador porque la valuación de
(1 + u )
2
es 0.

1 1 1
u − u 2 + u3 − u 4 1 + 2u + u 2
2 3 4
5 13 77
−u − 2u 2 − u 3 u − u 2 + u3 − u 4
2 3 12
5 2 1
− u 2 − u3 − u 4
2 3 4
5 2 5
u + 5u 3 + u 4
2 2
13 3 9 4
u + u
3 4
13 3 26 4 13 5
− u − u − u
3 3 3
77 13
− u 4 − u5
12 3
Encontramos el mismo resultado que con el método anterior.
Ejercicio 22. 1- Calcular el desarrollo limitado al orden 3 en la proximidad de 2 de

( )
arctan x .
2- Calcular el desarrollo limitado al orden 5 en la proximidad de 0 de
sh(ln(1+x)).
3- Calcular el desarrollo limitado al orden 3 en la proximidad de 0 de
x – ln (1 + x)
.
e x – cos x
Corrección : 1- Sabemos que para x en la proximidad de 2, tenemos:

arctan ( x)=
( x − 2) ( x − 2)
2 3
arctan ( )2 + ( x − 2 ) arctan ′ ( 2) +
2
arctan ′′ ( 2) +
2
arctan ′′′ ( 2 ) + o (( x − 2) )
3
1 −2x 2 ( 3x 2 − 1)
Como,
= arctan ′ ( x ) = , arctan ′′ ( x ) = y arctan ( x )
′′′ .
(1 + x 2 ) (1 + x 2 )
2 3
1+ x2
1 −2 2 10
Entonces,
= arctan ′ 2 ( ) 3
=, arctan ′′ 2( )9
arctan ′′′ 2
y=
27
. ( )
Finalmente obtenemos :
arctan
= ( )
x arctan ( 2 ) + 13 ( x − 2 ) −
9
2 2 5
( x − 2) + ( x − 2) + o ( x − 2) .
27
3 3
( )
2- Primero calculamos el desarrollo limitado de ln (1 + x) al orden 5 :
1 1 1 1
ln (1 + x ) =
0
x − x 2 + x3 − x 4 + x5 + o x5
2 3 4 5
( )
3
u u5
Recordamos que : sh ( u ) =u + +
0 6 120
+ o u5 . ( )
Deducimos entonces que :

3
 1 1 1 1  1 1 1 1 1 
sh ( ln (1 + x ) ) =  x − x 2 + x3 − x 4 + x5  +  x − x 2 + x3 − x 4 + x5 
0
 2 3 4 5  6 2 3 4 5 
5
1  1 2 1 3 1 4 1 5
 x − x + x − x + x  + o(x )
5
+
120  2 3 4 5 
Evidentemente, no vamos a desarrollar completamente cada una de esas expresiones. De
hecho, ya que estamos en el orden 5, podemos directamente reemplazar
5
 1 2 1 3 1 4 1 5 5
 x − x + x − x + x  por x , los otros términos tiene potencias estrictamente
 2 3 4 5 
superiores a 5.
3
 1 1 1 1 
Del mismo modo,  x − x 2 + x 3 − x 4 + x 5  se vuelve:
 2 3 4 5 
1 1 1 3 7
x3 − 3× x 4 + 3× x5 + 3× x5 = x3 − x 4 + x5 .
2 3 4 2 4
Finalmente deducimos que :
1 1 1 1 1 3 7  1 5
sh ( ln (1 + x ) ) = x − x 2 + x3 − x 4 + x5 +  x3 − x 4 + x5  + x + o ( x5 )
0 2 3 4 5 6 2 4  120
1 1 1 1
= x − x 2 + x3 − x 4 + x5 + o ( x5 )
0 2 2 2 2
1 2 1 3 1 4
3- Tenemos ln (1 + x ) = x − x + x − x + o ( x 4 ) entonces :
0 2 3 4
1 1 1
x − ln (1 + x )= x 2 − x 3 + x 4 + o ( x 4 ) ,
0 2 3 4
1 1 1 
lo que quiere decir x − ln (1 + x=) x 2  − x + x 2 + o ( x 2 ) 
0
2 3 4 
1 1 1 1 1
por otro lado, e x =1 + x + x 2 + x 3 + x 4 + o ( x 4 ) y cos ( x ) = 1− x 2 + x4 + o ( x4 ) .
0 2 6 24 0 2 24
x 1  1 
Por lo cual: e x − cos ( x ) = x + x 2 + x 3 + o ( x 4 ) = x 1 + x + x 2 + o ( x 3 )  .
0 6  6 
1 1 1 1
Así: x
= =
e − cos ( x ) 0  1 0x 1 2 3 
x 1 + x + x 2 + o ( x 3 )  1 + x + x + o ( x ) 
 6   6 
1 1
Como, =1 − u + u 2 + o ( u 2 ) , entonces anotando u= x + x 2 , se obtiene :
1+ u 0 6
1   1 
2
1 1  1  1 
= × 1 − x − x 2 +  x + x 2  + o ( x 2 )  = × 1 − x − x 2 + x 2 + o ( x 2 ) 
e − cos ( x ) x 
x 0  6  6  
 x 
0 6 
1  5 
= × 1 − x + x 2 + o ( x 2 ) 
0 x 6
 
Finalmente concluimos que :

x − ln (1 + x ) 2  1 1 1 1 5 
= x  − x + x 2 + o ( x 2 )  1 − x + x 2 + o ( x 2 ) 
e − cos ( x )
x 0
2 3 4 x 6 
1 1 1  5 
=  x − x 2 + x 3 + o ( x 3 )  1 − x + x 2 + o ( x 2 ) 
0
2 3 4  6 
Lo que nos da:
x − ln (1 + x ) 1 1 1 1 1 5 1 5
= x − x 2 + x3 − x 2 + x3 + x3 + o ( x3 ) = x − x 2 + x3 + o ( x3 )
e − cos ( x ) 2
x 0 3 4 2 3 12 0 2 6
x
Ejercicio 23. Definimos la función f en * por f(x) = .
ex – 1
1- Calcular el desarrollo limitado de f(x) al orden 2 en la proximidad de 0. Qué
podemos deducir de f y de su representación gráfica Cf ?
2- Demostrar que Cf admite dos asíntotas.
1 1
Corrección : 1- Tenemos e x =1 + x + x 2 + x 3 + o ( x 3 ) , entonces:
0 2 6
 1 1 
1 x 1 + x + x 2 + o ( x 2 ) 
e x −=
0
 2 6 
x 1
Por lo cual : x = .
e −1 0 1 + 1 x + 1 x2 + o x2
2 6
( )
1
Como, =1 − u + u 2 + o ( u 2 ) entonces,
1+ u 0
2
x 1 1 1 1  1 1 1 1 1
x
=1− x − x2 +  x + x2  + o ( x2 ) = 1− x − x2 + x2 + o ( x2 ) = 1− x + x2 + o ( x2 )
e −1 0 2 6 2 6  0 2 6 4 0 2 12
1
Gráficamente, esto significa que Cf tiene el aspecto de la recta de ecuación y = 1 − x en la
2
proximidad de zéro.
2- Estudio en la proximidad de +∞ :
x
Tenemos = lim f ( x ) lim
= x
0.
x →+∞ x →+∞ e − 1
Deducimos que la recta de ecuación y = 0 es una asíntota de la curva Cf en +∞ .

Estudio en la proximidad de −∞ :
x
Tenemos lim f ( x ) = lim x = +∞ .
x →−∞ x →−∞ e − 1
f (x) 1
Entonces, primero hay que estudiar lim = lim x = −1 .
x →−∞ x x →−∞ e −1
Luego hay que estudiar :
 x   x + x ( e x − 1)   xe x 
lim ( f (=
x ) + x ) lim  x = + x  lim  =  lim = 0
x →−∞ x →−∞ e − 1
  x →−∞  ex − 1  x →−∞  e x − 1 

Concluimos que la recta de ecuación y = − x es una asíntota de la curva C f en −∞ .
1
Ejercicio 24. Sea f la función definida en * por : f(x) = x + 2 –  arctan x.
 x

1- Demostrar que f admite en 0 un límite finito que determinaremos.
2- Demostrar que la prolongación de f en 0 se puede derivar. Estudiar la posición de la
curva en relación a la tangente en el punto de abscisas 0.
3- Estudiar en la proximidad de +∞ la existencia de una asíntota así que la posición de
la curva en relación a ésta.
Igualmente en la proximidad de – ∞.
Corrección : 1- Sabemos que arctan ( x )  x ,
0
 1
entonces : f ( x )   x + 2 −  x= x 2 + 2x − 1 → − 1 .
0
 x x →0
Podemos entonces prolongar f por continuidad en 0 anotando f ( 0 ) = −1

 1
 x + 2 −  arctan ( x ) + 1
f ( x ) − f ( 0)  x
2- Tenemos: = .
x x
1 3
Sabemos que arctan ( x ) =− x x + o ( x 3 ) entonces :
3
 1  1 
x + 2 −  x − x 3 + o ( x 3 )  + 1 x 2 + 2x − 1 − 2 x 3 + 1 x 2 + o ( x 3 ) + 1
f ( x ) − f ( 0 )  x  3  3 3
=
x 0 x 0 x
4 2
2x + x 2 − x 3 + o ( x 3 )
4 2
= 3 3 =+2 x − x2 + o ( x2 ) .
0 x 0 3 3
f ( x ) − f ( 0)
Así, lim =2.
x →0 x 0
Concluímos que la prolongación de f en 0 se puede derivar en 0, y obtenemos f ′ ( 0 ) = 2 .

f ( x ) − f ( 0) 4 4
Además, =+ 2 x + o ( x ) , entonces f ( x ) − ( f ( 0 ) + 2x ) = x 2 + o ( x 2 ) .
x 0 3 0 3
Como la ecuación de la tangente no puede ser otra que « y=f(0)+2x » entonces deducimos que
la curva está siempre por encima de su tangente.
3- Para el estudio de las asíntotas, recordamos lo siguiente:
1 π
∀x ∈ *, arctan ( x ) + arctan   = sgn(x)
x 2
Estudio en la proximidad de +∞ :
 1
Tenemos: lim f ( x ) = lim  x + 2 −  arctan ( x ) = +∞ .
x →+∞ x →+∞
 x
 1
 x + 2 −  arctan ( x )
f (x)  x π
Entonces tenemos primero= que estudiar : lim lim
= porque
x →+∞ x x →+∞ x 2
 1 π
 x + 2 −  arctan ( x ) +∞  x.
 x 2
Luego estudiamos:

 π   1 π   1  π  1  π 
lim  f ( x ) −=x  lim   x + 2 −  arctan ( x ) −=x  lim   x + 2 −   − arctan    − x 
x →+∞
 2  x →+∞   x 2  x →+∞   x  2  x  2 
π 1  1  1 
= lim   2 −  − arctan   x + 2 −  
x →+∞ 2 x
   x  x 
π 1  1
Tenemos lim   2 −   = π y podemos hacer un desarrollo asíntotico de arctan   :
x →+∞ 2
  x  x
1 1 1
arctan  = + o   , lo que nos da :
 x  +∞ x x
  1  1   1 1 
lim  −arctan   x + 2 −   =lim  −  x + 2 −   =−1 .
x →+∞
  x  x   x →+∞  x  x 
 π 
Deducims entonces que lim  f ( x ) − x  = π − 1 .
x →+∞
 2 
π
Concluímos que la recta de ecuación « = y x + ( π − 1) » es una asíntota a la curva C f en +∞ .
2
Estudio en la proximidad de −∞ :
 1
Tenemos: lim f ( x ) = lim  x + 2 −  arctan ( x ) = +∞ .
x →−∞ x →−∞
 x
 1
f (x)  x + 2 −  arctan ( x ) π
x
Tenemos entonces que estudiar antes lim = lim  = − porque
x →−∞ x x →−∞ x 2
 1 π
 x + 2 −  arctan ( x ) −∞
− x .
 x 2
Luego hay que estudiar:
 π   1 π   1  π  1  π 
lim  f ( x ) += x  lim   x + 2 −  arctan ( x ) += x  lim   x + 2 −   − − arctan    + x 
x →−∞
 2  x →−∞   x 2  x →−∞   x  2  x  2 
 π 1  1  1 
= lim  −  2 −  − arctan   x + 2 −   .
x →−∞
 2 x  x  x 
 π 1  1
Tenemos lim  −  2 −   = −π y podemos hacer un desarrollo asíntotico de arctan   :
x →−∞
 2 x  x
1 1 1
arctan  = + o   , lo que nos da :
 x  −∞ x x
  1  1   1 1 
lim  −arctan   x + 2 −   =lim  −  x + 2 −   =−1 .
x →−∞
  x  x   x →−∞  x  x 
 π 
Deducimos entonces que : lim  f ( x ) − x  = −π − 1 .
x →−∞
 2 
π
Concluímos que la recta de ecuación « = y x − ( π + 1) » es una asíntota a la curva Cf en −∞ .
2

Capítulo 15
SUCESIONES DE REALES
I- Acerca de las sucesiones
Definición: una sucesión es una función de  en .

La imagen de n para u es escrito u n. La sucesión ( u n )n∈ ou (u n ) n y a veces si no hay
ambigüedad (u n ).
a. Sucesiones aritméticas y geométricas
El cuadro siguiente reúne los principales resultados que deben conocerse sobre las sucesiones.
Sucesión aritmética de razón Sucesión geométrica de razón

“r”, teniendo como primer “q” teniendo como primer
término “u 0 =a” termino “u 0 =a”
Caracterización por una u n+1 =u n +r u n+1 =q.u n
relación de recurrencia
Caracterización por una u n = rn + a u n =a.qn
fórmula explícita
Suma de N términos N(N − 1) 1−q N
consecutivos Na + r a× (si q ≠ 1)
2 1−q
Ejemplo :
Una utilización muy común de las sucesiones geométricas interviene en los préstamos
con créditos. Un prestamista dispone de una cantidad M que él va a prestar con una tasa de
interés mensual t. El que pide el préstamo desea recibir esta suma M a cam bio de un pago
mensual de una cantidad a, durante n mensualidades. Cuál es el valor de a en función M, t y
de n ?
Del punto de vista del prestamista, la tasa de interés corresponde a l o que el podrá
ganar ahorrando su dinero. Así, el capital M se volvería M(1+t) al cabo del primer mes ,
M(l+t)2 al cabo del segundo, ..., M(l+t)n al cabo de los n meses. El puede consentir el
préstamo de la cantidad M solamente si los rembolsos regulares le permitieran obtener un
capital equivalente a M (l+t)n al cabo del n mes, y a horrando sus rembolsos en condiciones
comparables. Así, recibiendo una cantidad a al cabo de un mes, y ahorrando esta cantidad a la
tasa t, él tendrá a(l+t)n-1 al cabo del n-1 mes restante. Recibiendo otra cantidad a a l cabo de
dos mese, tendrá a(l+t)n-2 al cado de n-2 meses restantes, etc... La última cantidad recibida , al
enésimo mes es a y no aporta ningún interés. Su capital final será entonces:
n-1 n-2 (1 + t) n − 1
a(1+t) + a(1+t) + ... + a(l+t) + a = a
t
que debe ser igual a M(1+t)n, de donde proviene la relación:

Mt
a=
1 − (1 + t) − n
Otra explicación de esta fórmula será dada en aplicación de las sucesiones aritmético-
geométricas.
Indiquemos, por otro lado, que existen dos métodos para pasar del tiempo mensual t a
la tasa anual T :
1- El método exacto de la tasa actuarial (teniendo en cuenta los intereses
acumulados) :
1 +T=(1 +t)12
Así, una tasa anual de 6% corresponde a una tasa mensual de 0,4868 %.
T
2- El método de tasa proporcional consiste a anunciar la fórmula t = (utilizando los
12
intereses acumulado). Así, una tasa proporcional anunciada al 6% corresponde a u na tasa
mensual de 0,5 %, y entonces a u na tasa anual actuarial real de 6,17 % = 1,00512 - 1. El
prestamista tiene ventaja cuando habla de tasa proporcional. Y el que pide préstamo tendrá
que hacer la conversión a la tasa actuarial que es la que será aplicada verdaderamente.
Aplicación numérica : préstamo de 40 000 Euros con una tasa anual del 6% sobre 10 años.
El monto mensual de rembolsos es de 440,90 Euros en tasa actuarial, y de 444,08 en tasa
proporcional. La diferencia es mínima, pero, en 120 meses, esto representa incluso 381,60
Euros.
A propósito de las sucesiones aritmético-geométricas :

Tal sucesión tiene la forma:
∀ n, u n+1 = au n + b
Observaciones: con b = 0, volvemos a encontrar las sucesiones geométricas.
Con a = 1, volvemos a encontrar las sucesiones aritméticas.
Una solución particular es obtenida en la sucesión constante l tal que l = al + b. Este valor l
es, por otro lado, el límite eventual de la sucesión si ella converge. Sea (v n) la sucesión
auxiliar definida por:
∀ n, v n =u n -l
Tenemos entonces :
∀ n, v n+l = a.v n
tenemos:
v n = an v 0
y
u n = l + an (u 0 - l)
La sucesión converge entonces, si y solamente si |a| < 1 o u 0 =l.
Ejemplo :
Un prestamista dispone de una cantidad M que cuenta prestar a una tasa de interés
mensual t. El que desea el préstamo pide recibir esta cantidad M a ca mbio de un pago
mensual de una cantidad a, durante n mensualidad. Cuál es el valor de a en función de M,t y
de n?

Al momento de pagar la kesima mensualidad, el que pidió el préstamo ha pagado una
parte del capital. Sea C k-1 el capital que falta por pagar después del k-1esimo pago, de manera
que C 0 =M y C n=0. El pago de la mensualidad a consiste, por un lado, a rembolsar la parte del
capital C k-1 - C k , y por el otro, a pagar intereses sobre el capital C k-1 durante un mes, de
manera que:
a = C k-1 - Ck + tC k-1
Entonces, C k = (l+t)C k-1 - a
Reconocemos en (C k ) k una sucesión aritmético-geométrica, con punto fijo l = (l+t)l - a, sea
a
l= .
t
a  a
De donde : C k -  Ck −1 − 
= (l+t)
t  t
a  a
⇒ Ck - = (1+t)k(C 0 - t) = (1+t)k  M − 
t  t
a  a
⇒ - = (1 +t)n  M −  ya que C n = 0
t  t
Mt
⇒a = .
1 − (1 + t) − n
b. Sucesiones crecientes, sucesiones decrecientes
Definición: Sea (un)n una sucesión de números reales. Se dice que:

• La sucesión (u n ) n es creciente cuando u n ≤ u n+1 para todo entero n.
• La sucesión (u n ) n es decreciente cuando u n ≥ u n+1 para todo entero n.
• La sucesión (u n ) n es monótona cuando es creciente o decreciente.
Técnicas: Tres técnicas permiten esencialmente estudiar la monotonía de una

sucesión..
1. La técnica funcional
Se aplica a las sucesiones cuyo término general es de la forma u n = f(n) (donde f es una
función). Esta técnica consiste en estudiar las variaciones de f.
2. La técnica algebraica
Consiste:
- sea estudiar el signo de la diferencia u n+1 -u n
u
- o bien comparar el cociente n +1 a 1 si u n >0.
un
3. El razonamiento por recurrencia.
c. Sucesiones mayoradas, minoradas
Definición: Sea (un)n una sucesión de números reales. Se dice que:

• La sucesión (u n ) n está mayorada si existe un real M tal que u n ≤ M para todo entero n.
• La sucesión (u n ) n está minorada si existe un real m tal que m ≤ u n para todo entero n.
• La sucesión (u n ) n está borneada si es a la vez agrandada y disminuida.

II- Comportamiento asintótico
a- Generalidades
Sucesión convergente:
Una sucesión convergente es una sucesión que admite un límite finito 1, es decir:
(
∀ε > 0, ∃N ε ∈, ∀n ∈ , n ≥ N ε ⇒ u n − l ≤ ε )
Una sucesión convergente admite un límite único.
Sucesión divergente:
Se dice que una sucesión es divergente si no es convergente.
En este caso puede:
- tener un límite infinito
- o no tener límite
Teorema:. Toda sucesión convergente es limitada.
Observación: la recíproca es falsa. Ejemplo: u n =(-1)n.
b. Operaciones
Todos los resultados que conciernen a las operaciones sobre los límites se extienden a las
sucesiones.
Teorema: Sean (un)n y (vn)n dos sucesiones convergentes hacia los reales l y l’,
respectivamente. Entonces
1- La sucesión (u n +v n ) n converge hacia (l + l’)
2- Sea α un real. La sucesión (αu n ) n converge hacia αl
3- La sucesión (u n .v n) n converge hacia (l.l’)
u 
4- Si para todo entero n, vn no es nulo y si l’ no es nulo, la sucesión  n  converge
 v n n
l
hacia .
l'
c. Comparación
1era hipótesis: desigualdades 2da hipótesis: comportamiento conclusión

(a partir de un determinado al infinito
rango)
un ≥ 0 (u n) n converge hacia l l≥0
vn ≤ u n (u n) n converge hacia l l’ ≤ l
(v n) n converge hacia l’
un ≤ vn (u n) n tiende hacia + ∞ (v n ) n tiende hacia + ∞
vn ≤ u n (u n) n tiende hacia - ∞ (v n ) n tiende hacia - ∞
|v n -l| ≤ u n (u n) n converge hacia 0 (v n ) n tiende hacia l

un ≤ wn ≤ vn (u n) n y (v n ) n convergen hacia (w n ) n converge hacia l
el mismo límite l (teorema de los gendarmes)
d. Imagen de una sucesión por aplicación de una función
Teorema: Sea f una función definida y continua en un intervalo I y (un)n una sucesión
de puntos de I. Si Lim un =a y Lim f(x)=l entonces Lim f(un) = l (con a y l finitos o infinitos).
x →a
e. Sucesiones monótonas, borneadas
Teorema: 1- Toda sucesión real creciente y mayorada a p artir de un cierto rango

convergen.
2- Toda sucesión real decreciente y minorada a p artir de una cierta fila
converge.
f. Sucesiones y equivalencias
Teorema: Si (u n ) n y (v n ) n son dos sucesiones equivalentes y si una de ellas posee un

limite finito o infinito, la otra posee el mismo limite.
Atención: la reciproca de este teorema es falsa.
III- SUCESIONES ADYACENTES
Definición: Se dicen que dos sucesiones (u n ) n y (v n ) n son adyacentes si por

definición:
a- (u n ) n es creciente
b- (v n ) n es decreciente
c- Lim(v n -u n )=0
Teorema: Dos sucesiones adyacentes convergen y tienen el mismo límite.
Aplicación: Método de dicotomía.
IV- SUCESIONES EXTRAIDAS
Definición: Sea (u n) n una sucesión de reales.

La sucesión (v n ) n se dice extraída de (u n ) n si por definición existe una aplicación ϕ
estrictamente creciente de  en  tal que para todo entero natural n, v n =u ϕ(n) .
Teorema: Si la sucesión (u n ) n converge hacia l, entonces toda sucesión extraída de

(u n) n converge hacia l.
Teorema: Sea (u n ) n una sucesión tal que las dos sucesiones extraídas (u 2n+1 ) n y (u 2n ) n
convergen hacia un mismo real l, entonces la sucesión (u n ) n converge hacia el real l.

V- SUCESIONES RECURRENTES
Localización del problema: Sea I un intervalo Sea f una función de I en I.

u ∈ I
Se considera la sucesión definida por:  0 .
u
 n +1 = f (u n ) para todo entero natural n
Estudio de la sucesión (u n) n .
Interpretaciones gráficas:

Teorema: Sea f una función creciente de I en I. Sea la sucesión definida por:
 u0 ∈ I

u n +1 = f (u n ) para todo entero natural n
1- Si u 0 ≤ u 1 , entonces la sucesión (u n ) n es creciente.
2- Si u 0 ≥ u 1 , entonces la sucesión (u n ) n es decreciente.
Definición: Sea f una función. Las soluciones de la ecuación «f(x)= x» son por
definición los puntos fijos de f.
Teorema: Sea f una función continua de I en I. Sea la sucesión definida por:

u 0 ∈ I

u n +1 = f (u n )para todo entero natural n
Si la sucesión (u n ) n converge hacia el real l de I, entonces l es un punto fijo de f.
 1
 u 0 = 5  v0 =
Ejemplo : Sean (u n ) n y (v n ) n las 2 sucesiones definidas por :  y  4 .
u n +1 = u n v = v
 n +1 n
Estudio de la monotonía y de la convergencia (u n ) n y (v n) n .
Representación de (u n ) n Representación de (vn ) n
Teorema del punto fijo: Sea f una función definida y derivable en I= [a,b] que
comprueba:
1- Para todo x de I, f(x) es elemento de I,
2- Existe un real k de ]0,1[ tal que para todo x de I, |f ’(x)| ≤ k(entonces decimos que f
es k-contratante),
Entonces existe un único real α de I tal que f(α)=α.
u ∈ I
Además la sucesión definida por: 0
u n +1 = f (u n ) para todo entero natural n
converge y tiene por límite α.
Tenemos: |u n-α| ≤ kn|b-a| para todo entero natural n.

Ejercicio 1 : Calcular las siguientes sumas:

8 n
12n + k n n
n
∑ (3k + 1) ; ∑ 2
k 0 6n − 3
; ∑ (3k + k − 1) ; ∑ k
= k 0= k=
0 =k 0  
Ejercicio 2 : Consideremos la sucesión ( u n )n∈ , para n entero natural, expresar u n en

función de u 0 .
1. u n +1 = 3u n
2. u n +1 = u n + 2n + 1
3. u n +1 = −2u n + 3
4. u n +1 = (u n ) 2
Ejercicio 3 :
1. Gracias a la definición , mostrar que la sucesión ( u n )n∈ de término general
2
un = converge.
n +1
2. Gracias a la definición, mostrar que la sucesión ( u n )n∈ de término general u n = n 2
diverge hacia +∞ .
1 n
Ejercicio 4 : Definimos para n entero natural no nulo, u n = ∑ 2
.
k =1 k
1. Escribir los términos u1 , u 2 , u 3 y u 4 , por otro lado, escribir con ayuda del signo ∑
el término u n 2 − u n , para n entero dado.
2. Dar (sin calcularlos) los cuatro primeros términos de la sucesión extraída ( u n 2 ) .
n
3. Cuál es la monotonía de la sucesión ( u n )n∈* ?
Ejercicio 5 : Estudiar la convergencia de la sucesión ( u n )n∈* donde u n está dado por:

n  π
1. u n = sen  n 
2  2
n +1
2. u n = (−1) n
n
3. u n= ln(n + 1) − ln(n)
3n 2 + cos(n)
4. u n =
4(n + 1) 2 + sen(3n)
5. u n =−
n n2 − n
1
6. u n = n .
n
∑  
k =0  k 

25n(n + 1) 3n +1 − 3 + n(n − 1)
Ejercicio 1 : 117 ; ; ; 2n
2 ( 6n − 3)
2
2
Ejercicio 2 :
1. u n = 3n u 0
n
2. u n = u 0 + ∑ (2k + 1) = u 0 + (n + 1) 2 − 1
k =1
n
3. u n =(−2) (u 0 − 1) + 1
2n
4. u n = ( u 0 )
Ejercicio 4 :
2
5 49 205 n
1
1. =
u1 1,= u2
4
, u3
=
36
,=
u4
144
; si n es un entero, u n 2 − u n =∑
k= n +1 k
2
.
2. Los cuatro primeros términos son u1 , u 4 , u 9 y u16 .

1
3. Si n es un entero, u n +1 −=un > 0 entonces la sucesión ( u n )n∈* es
(n + 1) 2
estrictamente creciente.
Ejercicio 5 :
1. La sucesión es divergente (Las sucesiones extraídas ( u 4n )n y ( u 4n +1 )n son
convergentes con límites diferentes).
2. La sucesión es divergente. (Las sucesiones extraídas ( u 2n )n y ( u 2n +1 )n son
convergentes con límites diferentes).
3. ( u n )n∈* tiende hacia 0.
3
4. ( u n )n∈* (Poner n 2 en factor en el numerador y en el denominador).
tiende hacia
4
1
5. ( u n )n∈ converge hacia .
2
1
6. Simplificando obtenemos u n = n , entonces ( u n )n∈ converge hacia 0.
2

EJERCICIOS
3n − 1
Ejercicio 1. Se considera la sucesión ( u n ) n definida por u n = para todo entero natural
2n + 3
n.
a- Mostrar que la sucesión ( u n ) n es creciente y agrandada.
3
b- Demostrar utilizando la definición de límite de una sucesión que Lim u n = .
n →+∞ 2
n
 n + 1
Ejercicio 2. Mostrar que la sucesión con término general   converge hacia e.
 n 
Ejercicio 3. Estudiar la convergencia de las siguientes sucesiones definidas por su término

general:
n +1
a- u n = (−1) n e- u n = n.( n + a ) − n
n
n +1
b- u n = f- u n = n + 3 1 − n 3
n
n n  nπ 
c- u n = g- u n = .s e n  
n +1 2  2 
sen 2 (n) − cos3 (n)
d- u n = n − n ² − n h- u n =
n
1
Ejercicio 4. Sea la sucesión (u n ) n definida por u n+1 = 1 + y u 0 =1.
un
El propósito es mostrar la convergencia de (u n ) n y de determinar su límite por tres métodos
distintos.
1+ 5
Mostrar que el límite eventual de (u n ) n solo puede ser α = (Número de oro).
2
1
1- a- Mostrar que: ∀n ∈ , u n +1 − α ≤ u n − α .
α
b- Deducir que (u n ) n converge hacia el número de oro.
2-a- Estudiar el signo de u n+1 -α en función del de u n-α y el signo de u n+1 - u n en
función del de u n - u n-1 .
b- Mostrar por recurrencia que: ∀p ∈ , u 2p ≤ α y ∀p ∈ , u 2p+1 ≥ α .
c- Mostrar que (u 2p ) p es una sucesión creciente y que (u 2p+1 ) p es una sucesión
decreciente y que estas dos sucesiones extraídas de (u n ) n son sucesiones convergentes.
d- Mostrar que los límites de (u 2p ) p y (u 2p+1 ) p son iguales.
e- Mostrar que entonces (u n ) n es una sucesión convergente.
3- Seaβ la segunda raíz de la ecuación: x²=x+1.

un − α
a- Sea la sucesión (v n) n definida por
= vn ∀n ∈ . La sucesión (v n) n esta
un − β
definida ?
b- Mostrar que la sucesión (v n ) n es una sucesión geométrica.
c- Deducir que la sucesión (u n ) n converge hacia α.
Ejercicio 5. Sea “a” un real positivo. Se considera la sucesión ( u n ) n definida por ∀n ∈ ,

1 a² 
u n +1
=  u n +  con u 0 >0. Estudiar la convergencia de la sucesión ( u n ) n .
2 un 
Ejercicio 6. Estudiar la convergencia de la sucesión ( u n ) n definida por:

1+ un ²
∀n ∈ , u n+1 =
2
1
Ejercicio 7. Sea f la función definida por: f(x) = - x - . Consideramos la sucesión ( u n ) n
x
definida por u= 0 1 et ∀n ∈, u n+1 =f(u n ).
1- Estudiar las variaciones de f. Determinar eventualmente las asymptotes y los puntos
 1  1 
fijos de f. Trazar el grafo de f en  −5, −    ,5 (Unidad: 1 cm).
 5 5 
2- Representar gráficamente los u n para n elemento de {0, 1, 2, 3, 4, 5, 6, 7}.
3- Determinar los conjuntos (f  f)([1 ;+ ∞ [) y (f  f)(]- ∞ ;-2]). Deducir de eso las
inclusiones: (f  f)([1 ;+ ∞ ) ⊂ [1 ;+ ∞ [ y (f  f)(]- ∞ ;-2]) ⊂ ]- ∞ ;-2].
4-a- Mostrar que la sucesión ( u 2 n ) n es creciente y que la sucesión ( u 2 n+1 ) n es
decreciente.
b- Cuáles son los límites eventuales de ( u 2 n ) n y de ( u 2 n+1 ) n ? Concluir.
Ejercicio 8. El objetivo de este ejercicio es estudiar la sucesión ( u n ) n definida por :

∀n ∈ , u n+1 = ln( 1 + 2 u n )
a- Estudiar el signo de la función ϕ definida por ϕ :x  ln(1+2x) – x.
b- Estudiar la convergencia de la sucesión ( u n ) n .
Ejercicio 9. Nos proponemos calcular un valor aproximado de la solución positiva de la

ecuación “x²+x-1=0”.
1 
1-a- Demostrar que en el intervalo  ,1 , esta ecuación admite una única raíz,
2 
llamada r.
1
b- Demostrar que es equivalente a la ecuación: “g(x) = x” donde g(x)= .
x +1
2- Definimos una sucesión (u n) n por u 0 = 1 y ∀n ∈ , u n+1 =g(u n ).
a- Con ayuda del teorema del punto fijo, demostrar que (u n ) n converge hacia r.
b- determinar un valor cercano de r con una precisión de 10-2.
2 3 4 5 6
4 4 4 4 4
Donamos:   ≈ 0,1975;   ≈ 0,0878;   ≈ 0,039;   ≈ 0,0173;   ≈ 0,0077.
9 9 9 9 9

ex
Ejercicio 10. Sea f : [0, + ∞ [ →  la función definida por f(x) = . Consideramos la
x+2
1
secuencia numérica ( u n )n∈ definida por su primer termo u 0 = y por la relación de
2
recurrencia ∀ n ∈ , u n+1 = f(u n ).
1- Mostrar que, para todo n ∈ , u n ∈ [0,1].
2- Mostrar que existe un real único ∈ [0, 1] tal que f (l) = l.
3- Probar, con la ayuda de la desigualdad de los crecimientos terminados, que:
2
Para todo n ∈ , |u n+1 -l| ≤ |u n -l|
3
4- Deducir que Lim u n = l, y dar un valor acercado de l a 10-3 cerca.
n →+∞
u 0 = −2

Ejercicio 11. Sea ( u n )n la sucesión definida por :  2u n .
∀n ∈ , u n +1 =3 − u
 n
2x
1- Consideramos la función f definida por f ( x ) = y I = [ −3;0] .
3− x
Las condiciones de aplicación del teorema del punto fijo están reunidas?
2- Deducir la convergencia de la sucesión ( u n )n también su límite α.
3- A partir de qué valor de n, u n es un valor cercano de α con una precisión de 10 –3 ?
Ejercicio 12. Método de Newton

Sea f una función de clase C² en [a,b] tal que f(a)f(b)<0, f ’ y f ’’ de signo constante y que no
se anulan en [a,b]. Sea C f el gráfico de f.
1- Trazar unos esbozos de C f haciendo aparecer las propiedades de f (hay 4 casos de
figura).
2- Mostrar que la ecuación f(x)=0 admite una raíz única r en [a,b].
Se supone en adelante para fijar las ideas que f(a)<0, f ’ y f ’’>0 en [a,b].
3- Se define geométricamente la sucesión (u n ) n de la siguiente forma:
u 0 =b
la recta de ecuación x=u n corta C f en un punto M n . La tangente a C f que va de
M n corta Ox en el punto de abscisa u n+1 .
Representar gráficamente la sucesión (u n ) n , luego calcular u n+1 en función de u n .
4- Se supone en esta pregunta n fijo con r<u n ≤ b.
a- Mostrar que u n+1 <u n .
b- Probar la existencia de c elemento de ]a,b[ tal que:
(r − u n )²
f(r)=f(u n )+(r-u n )f ’(u n )+ f ’’(c) (1)
2
c- Observando que f(r)=0, mostrar que r<u n+1 .
5- Probar la convergencia de (u n ) n hacia r.

6- Sea ε n =|u n -r| el error de método cometido cuando se detiene la iteración en la nésima
f ' ' (c) 1 n
etapa. Mostrar, utilizando (1), que ε n+1 = ε n ², luego que ε n ≤ (Kε 0 ) 2 , con
2f ' (u n ) K
M
K= 2 , M 2 = Sup f " , m1 = Inf f ' .
2m 1 [a,b] [ a ,b ]
3
Aplicación numérica: f(x)= x3-5, a= , b= 2. ¿Cuánto es necesario prever de iteraciones para
2
obtener 5 con 1000 decimales exactos? (¡con un calculador perfecto!)
3
an
Ejercicio 13. Se considera la sucesión ( u n ) n definida por u n = donde :
bn
∀n ∈*, a n = 2a n −1 + 3b n −1 y b n =
a n −1 + 2b n −1 con a 0 > 0 y b 0 > 0
a- Mostrar que para todo entero n, a n y b n son estrictamente positivos.
b- Determinar u n+1 en función de u n .
c- Estudiar la convergencia de la sucesión ( u n ) n .
Ejercicio 14. Sea la sucesión ( u n ) n tal que ( u 2 n+1 ) n , ( u 2 n ) n , ( u 3n ) n convergen. Mostrar que
la sucesión ( u n ) n converge.
Ejercicio 15. El objetivo de este ejercicio es estudiar la sucesión ( u n ) n definida por :

5 4
u 0 = y ∀n ∈ , u n+1 =1+
2 1+ un
a- Representar gráficamente los primeros términos de esta sucesión
b- Estudiar la convergencia de la sucesión ( u n ) n .
Ejercicio 16. Sea 0 < b < a. consideramos las sucesiones imbricadas definidas por u 0 = a ,
v 0 = b y para todo n :
u + vn 2u n v n
u n +1 = n y v n +1 =
2 u n + vn
1- Demostrar que 0 < u n y 0 < v n para todo entero n. Deducir que u n > v n .
2- Demostrar que la sucesión ( v n )n es creciente y que ( u n )n es decreciente.
1
3- Verificar que para todo entero n, 0 < u n +1 − v n +1 < ( u n − vn ) .
2
4- Deducir que las sucesiones ( u n )n y ( v n )n∈ son adyacentes.
5- Mostrar que la sucesión ( u n v n )n es constante y deducir el límite de las sucesiones
( u n )n y ( v n )n∈ .
Ejercicio 17. Sucesión de Fibonacci

Consideramos la sucesión (u n ) n definida por u 0 = u1 = 1 y u n + 2 = u n +1 + u n , ∀n ∈.
1-a- Determinar los límites posibles de la sucesión (u n ) n .
b- Mostrar que (u n ) n es creciente y que ella tiende hacia + ∞ .
2- Demostrar por recurrencia la relación (1) siguiente:
(1) Para todo entero n no nulo, u n ²-u n+1 u n-1 =(-1)n

u n+1
3- Anotamos, para todo entero n, v n = .
un
a- Utilizando la relación (1), desarrollar v n+1 -v n en función de u n y de u n+1 .
b- Deducir que las sucesiones (v2p ) p y (v2p+1 ) p son adyacentes.
c- Mostrar que (vn ) n es convergente y determinar su límite.
Ejercicio 18. para todo entero n ≥ 2 , definimos la función fn :  →  para f n ( x ) = x n − x − 1

para x real.
1- Mostrar que existe un único real x n > 1 tal que f n ( x n ) = 0 .
2- Mostrar que f n +1 ( x n ) > 0 .
3- Deducir que la sucesión (x n ) n converge.
Ejercicio 19. Para todo n ∈ , escribimos x n la solución de la ecuación « tan x = x »sobre el

 π π 
intervalo I n =  − + nπ; + nπ  .
 2 2 
El fin de este ejercicio es determinar un desarrollo generalizado de la sucesión ( x n )n .
1- Justificar la existencia y la unicidad de x n y dar un equivalente de x n en +∞ .
 π π
2- Suponemos u n = x n − nπ . Verificar que u n ∈ I0 = − ;  y demostrar que
 2 2
u n = arctan ( x n ) .
Deducir que la sucesión ( u n )n converge y determinar su límite.
π 1
3- suponemos v n= − u n . Verificar que tan v n = . Deducir un equivalente de vn
2 tan x n
en +∞ .
4- Deducir de las preguntas precedentes un desarrollo generalizado de la sucesión ( x n )n .

Algunos métodos numéricos de resolución
de la ecuación f(x)= 0
1 DICOTOMÍA
Sea f continua en [a,b] y tal que f(a)f(b)<0.

1- Mostrar que existe al menos una raíz de la ecuación f(x) = 0 en ]a,b[.
2- El método de dicotomía consiste en localizar una raíz eligiendo uno de los intervalos
 a + b a + b 
[a 1 ,b1 ]= a , o , b  tal que f(a 1 )f(b1 ) ≤ 0, luego a iterar. Sea [a n ,b n ] el intervalo
 2   2 
obtenido en la nésima etapa.
a) Mostrar que las sucesiones (a n ) n y (b n ) n convergen hacia una raíz r de la ecuación

f(x)=0.
b) Dar un mayorando ε n del error de método cometido dando para un valor próximo
de r, el valor medio de [a n ,b n ].
c) Aplicación numérica: ¿Cuántas iteraciones son necesarias prever si se quiere un
valor con una exactitud de 10-15 para 3 5 , utilizando f(x)=x3-5, a = 3 , b = 2 ?
2
2 TEOREMA DEL PUNTO FIJO
1- Sea ϕ contratante en [a,b] y admite entonces un punto fijo único r y sea (u n ) n la sucesión
recurrente: u 0 ∈ [a,b], u n+1 =ϕ(u n).
Citar la expresión de un mayorando del error de método |u n -r|.
2- Sea f∈ C1[a,b] tal que la ecuación f(x) = 0 admita una raíz única r en [a,b]. r es entonces
punto fijo de toda aplicación ϕ de la forma
ϕ(x) = x + λf(x), (λ ≠ 0).
a) Por qué sería juicioso de escoger λ tal que ϕ’(r) = 0?
En la práctica podemos escoger λ = −1 donde x0 es una aproximación de r.
f '( x 0 )
b) Aplicación numérica: Aplicar el método para encontrar 3

5 con un 10-15 de
proximidad.

Ejercicio 20. Determinar los límites eventuales de las sucesiones de término general:
n
k 2n +1 + 3n +1 n
k 1
1- u n = ∑ 2 2- v n = n n 3- w
= n ∑ ( −1) k
k =1 n 2 +3 k =0 3
n
k
Corrección : 1- u n = ∑ 2
k =1 n
1 n
1 n ( n + 1) 1
De hecho, tenemos : u=
n
n2
∑=
k
k =1 n 2
×
2
entonces lim u n = .
n →+∞ 2
n +1 n +1
2+3
2- v n =
2 + 3n n
Factorizamos el numerador y el denominador por el término preponderante :

  2 n +1    2 n +1 
3n +1    + 1    + 1
 3  
vn =
2n +1 + 3n +1
=   = 3×   3  .
n n
2 +3  2
n
  2
n

3n    + 1    + 1
 3  
   3  
n n +1
2 2
Sabemos que : =
lim   lim =
  0 entonces lim v n = 3 .
n →∞ 3
  n →∞  3  n →+∞
k 1
n
3- w=n ∑
k =0
( −1) k
3
1
Reconocemos la suma de términos de una sucesión geométrica de razón − .
3
n
 1
1−  − 
 3 = 3 1 −  − 1   , de donde lim w = 3 .
n
Tenemos entonces: w=    
 1  4   3  
n n
n →+∞ 4
1−  − 
 3
1 xn
Ejercicio 21. Para todo n ∈ , llamamos I n = ∫ dx . Mostrar que la sucesión ( I n )n
0
1+ x2
decrece y que lim I n = 0 .
n →+∞
xn
Corrección: Observemos primero que la aplicación: x  es continua en [ 0;1]
1+ x2
entonces la integral I n está bien definida. Por el contrario, no podemos expresar fácilmente
los términos de la sucesión en función de n.
Calculamos entonces I n +1 − I n :
1 x n +1 1 xn 1x n +1 − x n 1 x n ( x − 1)
I n +1 − I n
= ∫
0
1+ x2
dx − ∫
0
=
1+ x2
dx ∫0 1= + x2
dx ∫0
1+ x2
dx

x n ( x − 1)
En [ 0;1] , ≤ 0 , entonces I n +1 − I n ≤ 0 , y la sucesión es decreciente.
1+ x2
Particularmente, es evidente que I n ≥ 0 . Se trata entonces de una sucesión decreciente y
minorada, entonces ella converge.
1
1  x n +1 
1 1
Además, en [ 0;1] , I n ∫ x dx =
≤ 1 entonces : I n =≤  n + 1 =
n
.
1+ x 2 0
 0 n + 1
Deducimos, de acuerdo con el teorema de gendarmes que la sucesión ( I n )n tiende hacia 0.
u 2n + 1
Ejercicio 22. Estudiar la sucesión ( u n )n definida por: u 0 ∈ + y ∀n ∈ , u n +1 = .
2
1+ x2
Corrección : Llamamos: f ( x ) = .
2
La función f está definida y se puede derivar de + en +, y tenemos que para todo x de +,
f ′(x) = x .
Esta función es entonces creciente de + en + entonces la sucesión ( u n )n es monótona.
1 + u 02
≥ u 0 . En efecto, ( u 0 − 1) ≥ 0 ⇔ u 02 + 1 ≥ 2u 0 .
2
Por otro lado, tenemos=
: u1
2
La sucesión ( u n )n∈ es entonces creciente. Debemos entonces distinguir dos casos:
u 0 ∈ [ 0;1] :
En este caso, verificamos por una recurrencia inmediata que: u n ≤ 1 .
1 + u 2n 1 + 1
En efecto, es verdad al rango 0 y si u n ≤ 1 entonces u n +1 = ≤ = 1.
2 2
La sucesión ( u n )n es creciente y mayorada, deducimos que elle converge. Llamamos α su
límite.
u 2n + 1
Pasando al límite en la relación u n +1 = , obtenemos:
2
1 + α2
⇔ 1 − 2α + α 2 = 0 ⇔ ( α − 1) = 0 ⇔ α = 1 .
2
α=
2
Concluimos que la sucesión converge hacia 1.
u 0 ∈ ]1; +∞[ :
Esta vez, debemos estudiar si la sucesión es mayorada.
Observemos que : u 2n + 1= ( u n − 1) + 2u n . Por otro lado, tenemos: u 0 = 1 + α con α > 0 .
2
α2
Deducimos que: u n +1 ≥ + u n . Por una recurrencia inmediata, verificamos que :
2
α2
un ≥ n + u0
2
Particularmente, la sucesión no está mayorada, y deducimos que : lim u n = +∞ .
n →+∞

Ejercicio 23. Vamos a estudiar la sucesión ( u n )n definida por:
3 1 2 
u0= y ∀n ∈ , =
u n +1  un + 
2 2 un 
1 2
1- Consideramos la función f definida en I = [1; 2] por : f =
(x) x + .
2 x
Las condiciones de aplicación del teoremas del punto fijo estás reunidas ?
2- Deducir la convergencia de la sucesión ( u n )n así que su límite α.
3- Desde qué valor de n, u n es un valor cercano de α a 10 –3 aproximativamente?
1 1
Corrección : 1- La función f está definida en I, y tenemos, para todo x de I, f ′ ( x )= − .
2 x2
1 1 2
Además, para x ∈ I , ≤ ≤ 1 , entonces 1 + 1 ≤ x + ≤ 2 + 2 , y así 1 ≤ f ( x ) ≤ 2 , entonces
2 x x
f ( I) ⊂ I .
1 1 1 1 1 1 1 1
Por otro lado, para x ∈ I , ≤ 2 ≤ 1 , entonces −1 ≤ − 2 ≤ − et − ≤ − 2 ≤ .
4 x x 4 2 2 x 4
1
Deducimos que: para x ∈ I , f ′ ( x ) ≤ .
2
Las condiciones para aplicar el teorema del punto fino estás todas verificadas.
2- De acuerdo con la pregunta anterior, podemos aplicar el teorema del punto fijo:
Existe un único α ∈ I tal que f ( α ) =α , y la sucesión ( u n )n converge hacia α .
No queda más que determinar la valor del real α :
1 2 1 1 1 1
f ( α ) = α ⇔  α +  = α ⇔ α + = α ⇔ = α ⇔ α2 = 2 ⇔ α = 2 o α = − 2
2 α 2 α α 2
Siendo dado que α ∈ I , concluimos que α = 2 .
3- De acuerdo con el teorema del punto fijo , tenemos la relación:

n
1 1
un − α ≤   2 −1 = n .
2 2
1
u n es entonces un valor cercano de α a 10 –3 aproximativamente de que n
≤ 10−3 :
2
1 ln10
n
≤ 10−3 ⇔ 2n ≥ 103 ⇔ n ln 2 ≥ 3ln10 ⇔ n ≥ 3
2 ln 2
ln10
Sabiendo que 3  9,97 , escogemos n ≥ 10 .
ln 2
Ejercicio 24. Para todo entero n ∈ *, consideramos la aplicación f n : [ 0;1] →  definida
por:
f n ( x ) = x n − (1 − x )
3
1- Mostrar que para todo n ∈ *, existe un único α n ∈ ]0;1[ tal que : f n ( α n ) =
0.
2- Mostrar que : para todo entero n ≥ 2 , f n −1 ( α n ) > 0

3- Deducir que la sucesión ( α n )n converge hacia un límite α ∈ ]0;1] .
Demostrar por lo absurdo que α =1 .
Corrección : 1- La función f n es continua y se puede derivar en [ 0;1] , y tenemos :

f n′ ( x )= nx n −1 + 3 (1 − x ) .
2
Particularmente, para x elemento de ]0;1[ , f n′ ( x ) > 0 , y entonces la función es estrictamente

creciente en [ 0;1] . Además, fn función [ 0;1] .
Por otro lado, tenemos : f n ( 0 ) = −1 , y f n (1) = 1 , entonces 0 ∈ f ( 0 ) ;f (1)  .
Concluimos que existe un único α n ∈ ]0;1[ tal que : f n ( α n ) = 0.
2- Por definición, tenemos: f n ( α n ) = (1 − α n ) .
3
0 y esto implica que : α nn=
Obtenemos entonces: f n −1 ( α n ) = α nn −1 − (1 − α n ) = α nn −1 − α nn = α nn −1 (1 − α n ) .
3
Sabiendo que α n ∈ ]0;1[ , deducimos que : f n −1 ( α n ) > 0 .

3- De acuerdo con la pregunta anterior, tenemos : f n −1 ( α n ) > 0 .
Como por definición, f n −1 ( α n −1 ) =
0 , y hemos visto en la pregunta 1 que la función f n −1 es
estrictamente creciente en el intervalo [ 0;1] .
Deducimos que: α n −1 < α n , lo que quiere decir que la sucesión (αn) n es creciente.
Por otro lado, siendo dado que α n ∈ ]0;1[ , ella es mayorada por 1.
Concluimos que ella converge hacia un real α ∈ [ 0;1] .
Particularmente, la sucesión siendo estrictamente creciente, tenemos α n ≤ α para todo n ∈ ,
y así 0 < α .
Entonces, α ∈ ]0;1] .
Demostramos por el absurdo que α =1 .
Supongamos que α ≠ 1 , tenemos 0 < α < 1 .
De acuerdo con lo que precede, tenemos entonces α n ≤ α < 1 para todo n ∈ .
(1 − α n )
3
Como por definición, tenemos : α nn= , y ya que α nn ≤ α n , deducimos que
lim (1 − α n ) = 0 .
3
n →+∞
Como lim (1 − α n ) = (1 − α )
3 3
, concluimos que α =1 , lo que contradice nuestra hipótesis.
n →+∞

Capítulo 16
INTEGRAL DE RIEMANN
Bernhard Riemann (1826-1866), matemático alemán,

alumno de Gauss, ha destacado brillantemente en distintos cam-
pos; es imposible avanzar seriamente en Matemáticas sin encon-
trar su nombre: integral de Riemann, superficie de Riemann, y
conjeturada de Riemann (« problema monumental y capital » -
todavia sin resolver).
Bernhard Riemann
1- Integral de una función escalera

Definición: Sea I=[a,b]. El que una función f definida en I sea en escalera significa que existe
una subdivisión a=c 0 <c 1 <c 2 <…<c n-1 <c n =b de I tal que la restricción de “f” a cada intervalo
]c i ,c i+1 [, para i = 0 hasta n-1, sea constante.
∀i=0 à n-1, ∃λi∈ , ∀x∈]ci ,ci +1[ , f(x)=λ i
Notación: C es el conjunto de las funciones en escalera.
b n −1
Definición: Sea f un elemento de C. Se plantea ∫ f(x)dx =∑λi(ci +1−ci ) .
a
i =0
2- Función integrable en un intervalo cerrado [a,b]

Sea f una función con bornes en [a,b].
Se plantea: C -(f)={g ∈ C/ ∀ x ∈ [a,b], g(x) ≤ f(x)}
C + (f)={h ∈ C/ ∀ x ∈ [a,b], h(x) ≥ f(x)}.

y
y=h(x)
y=g(x)
y=f(x)
x
O a c1 b
Se dice que f es integrable según el concepto de Riemann cuando

b b
Sup ∫
g∈C- (f ) a
g(x)dx = Inf ∫ h(x)dx .
h∈C+ (f) a
b b b
Se plantea entonces que ∫ f(x)dx = Sup ∫
a g∈C- (f ) a
g(x)dx = Inf
h∈C+ (f ) a∫ h(x)dx .
Notacion: Llamaremos I(D) el conjunto de funciones integrables en un conjunto D.
Teorema. Las funciones continuas, continuas por partes o m onótonas en [a,b] son
integrables en [a,b].
Observación: 1- Sea “f” la función indicadora de .

Mostrar que si "u" y "v" son dos funciones en escalera tales que u ≤ f ≤ v ,entonces
u ≤ 0 y v ≥ 1.
Deducir que “f” no es integrable en [a,b].
2- Existen funciones discontinuas que admiten primitivas. Por ejemplo, estu-
 1
 x² sin por x ≠ 0
diar la función F definida sobre  por: F(x) =  x . F se puede derivar en 0
 0 por x = 0
de función derivada f sobre , pero f no es continua en 0.
El problema precedente nos muestra que, de entre las

funciones no continuas, algunas tienen primitivas y o tras no.
La pregunta : « ¿Cuales son las funciones que admiten primiti-
va ? », pregunta estrechamente atada a l a teoria de la integra-
ción, suscita a finales del siglo XIX numerosos trabajos. Hay
que abonar en cuenta del matemético francés Henri Lebesgue
(1875-1941) el haber determinado las « felices elegidas de la
consulta comprometida ».
Henri Lebesgue

3- Propiedades
1- Linearidad
b b b
∀(f , g) ∈ I²([a, b]), ∀(α,β) ∈ ², ∫a
(αf + βg)(t)dt = α ∫ f (t)dt + β ∫ g(t)dt
a a
2- Integral y valor absoluto

b b
∀f ∈ I([a, b]), ∫ a
f (t)dt ≤ ∫ f (t) dt
a
3- Positividad
b
∀f ∈ I([a, b]), (a ≤ b) , ( ∀x ∈ [a, b], f(x) ≥ 0 ) ⇒ ∫ f(t)dt ≥ 0
a
4- Integral y desigualdad
b b
∀(f , g) ∈ I²([a, b]), (a ≤ b) , ( ∀x ∈ [a, b], f(x) ≤ g(x) ) ⇒ ∫ f(t)dt ≤ ∫ g(t)dt
a a
5- Relación de Chasles
b c b
∀f ∈ I([a, b]), ∀c ∈ [a, b], ∫ a
f(t)dt =∫ f(t)dt +
a ∫
c
f(t)dt
6- Teorema : Sea f una función continua, positiva sobre [a,b]. Si existe x 0 elemento
b
de [a,b] tal que f(x0 )>0, entonces ∫a
f(t)dt >0.
Corolario : Sea f una función continua, positiva sobre [a,b].

b
∫a
f(t)dt =0 ⇒ ∀x ∈ [a, b], f(x)=0
4- Fórmula de la mediana
Teorema: Fórmula de la mediana

Sean "f" y "g" dos funciones integrables en [a,b] tales que:
1- f continua en [a,b]
2- g positiva en [a,b]
b b
Entonces existe c elemento de [a,b] tal que ∫ f(t)g(t)dt =f(c)∫ g(t)dt .
a a
Observación : Con g(x)=1 para todo x de [a,b], la propiedad se convierte :

Sea f una función continua sobre [a,b]. Existe c elemento de [a,b] tal que :
1 b
b − a ∫a
f (c) = f (t)dt
Este valor es llamado valor medio de f entre [a,b].
En un anexo, usted puede ver ejemplo de aplicationes de esta noción.

µ
a b b
L’aire grisée est : (b-a)µ L'aire grisée est ∫
a
f (t)dt
5- Sumatoria de Riemann
Definición: Sea f una función definida en [a,b] .
Sea una subdivisión a = x 0 <x 1 <x2 <…<x n-1 <x n= b. El paso de la subdivisión es
h= Sup(x i − x i −1 ) .
1≤i ≤ n
Sea, para i=1 hasta n, ξi un elemento de [xi-1 ,x i ].

n
Se llama suma de Riemann al real ∑ (x
i =1
i − x i −1 )f (ξi ) .
Teorema: Sea f una función integrable en [a,b].

n b
Lim ∑ (x i − x i −1 )f (ξi ) =∫ f (t)dt
h →0 a
i =1
donde h designa el paso de la subdivisión.
Caso particular: Sea f una función integrable en [a,b].
n → +∞ n
n
Lim b−a ∑f a + j b−a =∫ f(t)dt
j=1 n a
b
( )

6- Primitiva de una función continua
Teorema: Sea I un intervalo de .

Sea “f” una función de I en  continua.
Sea “a” un elemento fijo de I.
Sea F la función de I en  definida por :
x
F(x)= ∫ f(t)dt
a
Entonces, F es de clase C1 en I y F ’=f.
x
Observación: si f no es continua, nada permite de decir que F definida por F(x)= ∫ f(t)dt se
a
puede derivar.
Ejemplo: Entre [0,2], sea f(x)= 1 entre [0,1] y f(x)= 0 entre ]1,2]. Tenemos entonces F(x)= x
entre [0,1] y F(x)=1 entre [1,2]. F es continua pero no se puede derivar en x=1.
Teorema : Sea I un intervalo de .

Sea f una función de I en  continua.
Sea a un elemento fijado de I.
Sea u una función derivable de un intervalo J en I.
Sea T la función de J en  definida por :
u (x )
T(x)= ∫ f (t)dt
a
Entonces, T es derivable sobre J y ∀x ∈ J, T ’(x)=u’(x)f(u(x)).
b
f (t)dt = [ G(t) ]a donde G es
b
Teorema : Sea f una función continua sobre [a,b]. Entonces ∫
a
una primitiva cualquiera de f sobre [a,b].

Tabla de primitivas
f
∫ f (t)dt tiene una constante (aditiva) cercana
entre los intervalos donde la función
se puede derivar
xr para r ≠ -1 x r +1
r +1
1 ln|x|
x
lnx xln|x| - x
1 arctan x
1 + x²
1 1 x
arctan
a² + x² a a
1 arcsin x
1 − x²
1 x
a>0, arcsen
a² − x² a
1 ln x + x² + h
x² + h
1 1 x −1
ln
x² − 1 2 x +1
1 1 x −a
ln
x² − a² 2a x + a
1 tan x
cos ²x
1 1
−
sen²x tan x
tan x - ln|cos x|
1 x
ln tan
sen x 2
1  x π
ln tan  + 
cos x 2 4

b
Ejercicio 1. Sean a y b dos reales tales que a < b . Calcular ∫
a
x dx con la ayuda de la defini-
ción de la integral.
Ejercicio 2. Mostrar que el producto de dos funciones que se pueden integrar en un intervalo
[a , b] es también una función que se puede integrar en [a , b] (comenzar por el caso donde
las dos funciones tienen valores positivos).

EJERCICIOS
Ejercicio 1. Se considera la secuencia (g n ) n de la función en escalera en [0;1] definida por :

 1
 0 si x> n
g n (x)= 
 n si x ≤ 1
 n
Sea f una función continua en [0;1]. Demostrar que la secuencia ( u n ) n definida por :
u n = ∫0f(x).g n (x)dx
1
converja hacia f(0).
Ejercicio 2. Utilizando una fórmula de la mediana, encontrar un equivalente cuando x → +∞

−t
x +1 e
de x  ∫ dt .
x 1 + t²
Ejercicio 3. Determinar el límite a la derecha en 0 de la función I definida para x estricta-

mente positiva por:
1
-
x² e t
I(x) = ∫ x t
dt
Ejercicio 4. Para n>0, se toma:

1 1 1 n
1
un =+ +... + =∑
n +1 n + 2 n + n k =1 n + k
Estudiar el límite de esta secuencia.
Ejercicio 5. Para n>0, se plantea:

22 42 (2n) 2 n
4k 2
=un +
n 3 + 23 n 3 + 43
+ ... + =
n 3 + (2n)3
∑ 3
k =1 n + 8k
3
Estudiar el límite de esta secuencia.
Ejercicio 6. Para n >0, se plantea:

1 n p n
1 k
= un = ∑
n² p=1 np
y v n ∑k=1 n+k 2n+k
e
Poner de manifiesto que estas dos secuencias convergen y determinar sus límites.

Ejercicio 7. Calcular la derivada de las siguientes funciones : (con F continua sobre )
x b b 2x
F1 ( x ) = ∫ e t dt F2 ( x ) = ∫ F3 ( x ) = ∫ e t dt F4 ( x ) = ∫ e t dt
2 2 2 2
e t dt
a x −3 a x
∫ (x − f ( t ) ) dt
x2 x 2 +1 x 2
F5 ( x ) = ∫ f ( t ) dt F6 ( x ) = ∫ f ( t ) dt 7 (x)
2
F=
x 2x −1 0
1
 1 1
Ejercicio 8. Sea 0<a<b y f continua en  ;  y sea F: x  ∫1x f ( t )dt .
b a b
1
1- Mostrar que F es de clase C en [a; b].
2- Calcular F’.
1 1
3- Calcular F para f: t  3 s e n   y b=π.
t t
1
Ejercicio 9. Sea g una función continua sobre . Tomamos G(x)= ∫ x
ln x
g(t)dt .
1- Determinar los conjuntos de definición, de continuidad y de derivación de G.
2- Calcular la derivada de G sobre su conjunto de derivación.
cos(t) 4x
Ejercicio 10. Sea f la función definida por f(x)= ∫ dt .
t x
1. Mostrar que f es definida en * y de clase C1 en *.

2. Mostrar que f es par.
3. Con la ayuda de la fórmula de la media, mostrar que Lim f(x)=ln(4) .
x →0
4. Prolongamos f apoyándose en f(0)=ln(4) . Mostrar que f prolongada es de clase C1

en .
5. Con la ayuda de una integración por partes, mostrar que Lim f(x)=0 .
x →+ ∞

1
Ejercicio 10. Sea f una función continua en [ 0;1] . Llamamos I n = ∫ x n f ( x ) dx con n ∈ N*.
0
Calcula lim I n .
n →∞
Correción: Sabemos que una función continua en un intervalo cerrado es limitado.

Llamemos M = sup f ( x ) .
x∈[ 0,1]
1
1  x n +1 1 M 1
Tenemos para todo n : I n ≤ ∫ x f ( x ) dx =
∫ x f ( x ) dxn
≤ M ∫ x dx M
= ×   =. n n
0 0 0
 n + 1 0 n + 1
Deducimos =que : lim I n 0= donc lim I n 0 .
n →∞ n →∞
Ejercicio 11. Sea f una función continua en [ a, b ] .
( f ( x ) ) dx ( f ( x ) ) dx ∫ (f ( x ))
b 2 b 3 b 4
Suponemos que ∫= ∫= dx . Mostrar que f es constrante en
a a a
[a, b] .
(( f ( x )) )
2 2
Podremos utilizar la función g definida por:
= g ( x) − f ( x) .
((f ( x )) )
2 2
Correción: Llamemos
= g(x) − f (x) .
Tenemos entonces: g ( x ) =f 4 ( x ) − 2f 3 ( x ) + f 2 ( x ) .
b
Utilizando la linearidad de la integral y la hipótesis, obtenemos ∫ g ( x ) dx = 0 .
a
Como g es una función positiva, esto implica que g es nula en [ a, b ] , entonces f vale sea 1 sea
0.
Como f es continua sobre ese intervalo, ella es necesariamente constante.
b b
Ejercicio 12. Sea f una función continua en [ a, b ] . Suponemos que ∫ f = ∫ f . Mostrar que
a a
f es de signo constante.
Corrección : Tenemos dos posibilidades:

b
 b b

• ∫a f ≥ 0  ie: ∫a f = ∫a f  :
En este caso, llamamos: g= (x) f (x) − f (x) .
g es una función positiva y continua , y
b b b b b
∫ g ( x ) dx = ∫ f ( x ) dx − ∫ f ( x ) dx = ∫ f ( x ) dx − ∫ f ( x ) dx =
a a a a a
0
Entonces g es nula en [ a, b ] , esto implica que f es positiva en [ a, b ] .
f < 0  ie: − ∫ f  :
b b b
• ∫ a  ∫
a
f=
a 

(x) f (x) + f (x) .
Est avez, llamamos: g=
g es una función positiva y continua , y
b b b b b
∫ g ( x ) dx = ∫ f ( x ) dx + ∫ f ( x ) dx = ∫ f ( x ) dx − ∫ f ( x ) dx = 0.
a a a a a
Entonces g es nula en [ a, b ] , lo que implica que f es negativa en [ a, b ] .

Finalmente, hemos demostrado que f es de signo constante en [ a, b ] .

Anexo 1
Histórico
El cálculo del aire tiene su origen en la antigüedad. Arquímedes sabe comparar el aire
delimitado por una parábola con el de un triángulo. Sabe igualmente que :
1- El perímetro de un círculo es porporcional a su diámetro.
2- El aire de un disco es proporcional al cuadrado de su radio.
Como el coeficiente de proporcionalidad π es el mismo ?. Cómo demostrarlo ? Ar-
químedes compara un círculo con un triángulo rectángulo en el cual uno de sus lados es el
radio del círculo y el otro tiene una longitud igual al perímetro del círculo. El utiliza para esto
un método dicho exhaustivo
Llamemos C al aire del círculo y T áquel del triángulo. Para mostrar la igualdad (en ai-
re) de esas dos figuras, efectúa un doble razonamiento por el absurdo, suponiendo primero
que el triángulo es más pequeño (T < C). Construye entonces un polígono de aire P tal que T
< P < C inscribiendo en el círculo una sucesión de polígonos de 3 x 2n lados de manera que el
aire de uno de los dos sea superior al aire del triángulo. Es posible ya que T < C. Basta con
elegir un polígono donde el aire sea suficientemente cercano de C. Demuestra luego que ese
polígono tiene un aire inferior a T llegando así a una contradicción. Basta con observar que
ese polígono está constituído de triángulos donde la suma de longitudes de las bases es infe-
rior al perímetro del círculo y donde la altura es inferior al radio. El aire P del polígono es
entonces inferior a T. Primera contradicción.
Supone luego que el triángulo tiene un aire superior al del círculo (T > C). El circuns-
cribe entonces al círculo una sucesión de polígonos regulares de manera a que el aire de uno
de los dos sea inferior al aire del triángulo (T > P > C). El muestra enseguida que ese polígono
tiene un aire superior a T. De hecho, la suma de las longitudes de las bases de los triángulos
constiyentes del polígono es superior al perímetro del círculo, y la altura es igual al radio. El
aire P del polígono es entonces superior al aire T del triángulo. Segunda contradicción.
De donde la única conclusión posible es que: C = T.
En 1635, Cavalieri (1598-1647), con el fin de acelerar las demostraciones del método
exhaustivo desarrolla la teoría de los indivisibles. Para probar la igualdad de dos aires, el veri-
fica la igualdad de las líneas que constituyen las dos superficies. Demos un ejemplo muy sim-
ple que permite de entender el funcionamiento y el interés de este método. Consideremos un
rectángulo y un paralelogramo de misma base y misma altura.
A B C D
A cada segmento [AB] del rectángulo correspondiendo al segmento [CD] del paralelo-
gramo de misma longitud. El método de los indivisibles concluye que los segmentos corres-
pondientes siendo iguales, es lo mismo para los aires de las dos figuras. La demostración del

resultado de Arquímedes, por el método de los indivisibles, consiste por ejemplo a trazar un
círculo de radio R, así que para todos los círculos de mismo centro de radio r, inferior a R, los
segmentos paralelos entre ellos, tangentes a cad a círculo y de longitud la circunferencia de
cada círculo. Al igual que los círculos van a llenar el disco de radio R, lo mismo harán los
segmentos que van a llenar el triángulo anunciado..
El aire del triángulo será igual al aire del disco.
Este método , bien artesanal, comparado con los métodos modernos, es, sin embargo,
extremamente eficaz. Podemos hacernos una idea leyendo « El tratado de la Ruleta » de Pas-
cal (1623-1662), en el cual, Pascal calcula los centros de gravedad de curvas, de superficies,
de volúmenes, cosas que no podríamos hacer actualmente sin cálculo integral. Pascal hace un
paso más que Cavalieri diciendo que una superficie es la suma de sus líneas. El dice « Yo no
tendré ninguna dificultad en usar esta expresión, la suma de las ordenadas, que parece no ser
geométrica para aquellos que no entienden la doctrina de los indivisibles, y que se imaginan
que es pecar contra la geometría en lugar de desarrollar un plano por un número definido de
líneas ; lo que viene de su falta de inteligencia, ya que por ello entendemos otra cosa que no
es la suma de un número indefinido de rectángulos hechos de cada ordenada con cada una de
las pequeñas porciones iguales de diámetro, donde la sume es ciertamente un plano, que no
difiere del espacio del semi-círculo sino de una cantidad menor que alguna dada »
Los métodos precedentes presentan el grave error de no poder dar un valor a un aire,
sino solamente de comparar dos aires entre ellos. Es así que es prioritario conocer el valor de
un aire antes de probar que este aire posede efectivamente un valor deseado.
Los trabajos de Pascal han influenciado bastante a Leibniz (1646-1716), inventor con
Newton (16421727) del cálculo diferencial e integral. Para Leibniz y Newton, la integración
es la operación opuesta a la derivación. Para calcular la integral de una función f buscamos
una primitiva de f.
Este aspecto presenta dos dificultades:

En el transcurso del siglo XVIII, los trabajos de Fourier (1768-1830) necesitan un
cálculo integral cada vez más profundo, donde la búsqueda de primitiva y la limitación de las
funciones continuas son insuficientes.
Para el profesor de ahora, esta presentación se basa en el hecho que toda función con-
tinua admite una primitiva, que resta a demostrar.
Contrariamente, Cauchy (1789-1857) resulve este último punto definiendo la integral

de una función f continua independientemente de la existencia de una primitiva, luego demos-
trando que la integral así obtenida es efectivamente una primitiva de f. Para definir su integral,

n
Cauchy divide [a, b] en n intervalos y él considera la suma ∑l f(t )
k =1
k k donde lk es la longitud
de un pequeño intervalo y t k un extremo del intervalo. Luego, él tiende n hacia + ∞ . Este paso
a sido criticado luego ya que las demostraciones utilizadas por Cauchy presentant algunos
defectos. Por otro lado, la integral de Cauchy solo se aplica a las funciones continuas.
Fue Riemann (1826-1866) quien introdujo la primera noción de ntegral, reconocida

aún válida en nuestros días, mejorando el desarrolo de Cauchy. La integral de Riemann es
suficientemente poderosa para definir una integral para todas las funciones siguientes:
Las funciones continuas
Las funciones monótonas
La función sen 1
x
()
La función x  0 si x∉
1 si x = p irreducible, q > 0
q q
Sin embargo, ella no es muy completa tampoco ya que no permite de atribuir un valor
a la integral de la función de Dirichlet :
x  0 si x∉
x  1 si x ∈ 
Es aún más asombroso que este función parece apenas diferente de la última función integral
en el sentido de Riemann dada anteriormente en ejemplo.
La integral de Riemann pone igualmente problemas delicados mientra se trata de saber

si, siendo dada una sucesión de funciones (fn ) convergiendo hacia f (en un sentido preciso), la
integral de f n converge hacia la integral de f.
Estos defectos conducieron a Lebesgue (1875-1941) a introducir una nueva noción de

integral, tal que:
- La función de Dirichlet es Lebesgue-integrable
- Un ejemplo de función positiva no Lebesgue-integrable existe bajo condición de uti-
lizar un axioma (llamado axioma de la opción), y no puede ser definido explicitamente.
- La integral de Lebesgue está particularmente adaptada al problema de convergencia
de sucesiones de funciones.

Anexo 2
Ejemplos de aplicación de la noción de valor medio
Ejemplo 1 : Consideremos las temperaturas tomados en el transcurso de una jornada. Divi-

n
dimos la jornada en n intervalos iguales. La temperatura media es 1 ∑T(h k ) , donde h k es el
n k =1
kesimo instante de medida, por ejemplo, h k = k , si la unidad es la jornada. Mientras más gran-
n
de es n, T es más precisa. Plus n est grand et plus la fonction T est précise. Limitadamente,
1
podemos modelizar Y por una función continua. Su valor media es ∫ T(t)dt
0
que no es otro
n
()
que el límite de la sume de Riemann 1 ∑T k mientras n tiende hacia + ∞ .
n k =1 n
Ejemplo 2 : El marégrafo de Marsella está encargado de medir la altura del mar. Un pozo
comunica con el mar para amortizar las olas. En esos pozos se encuentra un flotador. Medi-
mos la altura a la que sitúa el flotador en relación a una referencia fija. Un hilo ligado al flota-
dor pose un cursor que permite de determinar esta altura. Pero un mecanismo astucioso, en
funcionamiento desde hace más de un siglo, permite entre otros, de calcular altura media del
mar. He aquí la descripción simplificada.
hilo
flotador
Eje del
tambor
mar
rueda
Tambor cilíndrico
dando vueltas a
una velocidad
constante
Una pequeña rueda, conectada por un hilo tirante al flotador, Une petite roue, reliée
par un fil tendu au flotteur, da vueltas por frotamiento contra un cilindro girando a una veloci-
dad constante. Sea x la distancia de la rueda al eje del cilindro. X corresponde a la altura del
flotador. Mientras el flotador esté más alto, más la rueda está lejos del eje del tambor y más x

es grande. Mientras el flotador este abajo, más la rueda está cercana al eje del tambor y más x
es pequeño. La altura del flotador así que x dependen de t. La altura media sobre un intervalo
de tiempo [a,b] es calculada por 1 ∫ x(t)dt . Como la velocidad de rotación de la rueda es
b
b−a a
proporcional a x, Cad avez que x aumenta, la rueda gira mas rápido. Si el tambor gira a una
velocidad constante Ω y si el radio de la rueda es R, su velocidad de rotación ω es ω = Ωx .
R
El número de vueltas de la pequeña rueda es una primitiva de ω y es entonces proporcional a
una primitiva de x. Ese número de vueltas indica entonces , con una constante multiplicativa
cercana, el valor medio de x y por consecuencia la altura media del mar.
Desde hace poco, ese sistema viene acompañado con un sistemo electrónico, calculan-
do, con un intervelo regular, la altura del mar. Ese sistema suma igualmente los datos recogi-
dos y procede entonces a una suma de Riemann. Permite entonces igualmente de calcular un
valor medio de la altura del agua.
Ejemplo 3 : La potencia disipada por efecto Joule en corriente alternativa es RI², con
I=I 0 sen(ωx). La potencia media puede ser medida entre un periodo y vale:
2π
ω
∫ ω RI sen²(ωt )dt
2
0
2π 0
El cálculo conduce a 1 R I02 .

2
En un dipolo sumiso a una tension U = U 0 sen(ωt+ϕ), la potencia media vale:
2π
ω
2π ∫ω I U
0
0 0 sen(ωt ) sen(ωt + ϕ )dt
lo que da 1 I 0 U 0 cosϕ.
2

Capítulo 17
CÁLCULO PRÁCTICO
DE INTEGRALES Y DE PRIMITIVAS
A- CÁLCULO DE INTEGRALES
1- Integración por partes
Teorema: Sean "u" y "v" dos funciones de clase C1 en [a,b].

b b
∫ a
u(x)v '(x)dx = [u(x)v(x)]ab - ∫a
u'(x)v(x)dx
b b
∫
a
uv ' = [uv]ab - ∫
a
u'v
2- Cambio de variable
Teorema: Sean I y J dos intervalos.
Sea ϕ una función de J en I de clase C1 sobre [α,β].
Sea f una función de I en  continua sobre I.
ϕ (β ) β
Entonces, ∀ ( α, β ) ∈ J² , ∫ f (x)dx = ∫ (f  ϕ)(t)ϕ'(t)dt
ϕ( α ) α
Otra versión : Sea f una función continua sobre [a,b] y sea ϕ una función de [α,β]sobre [a,b]
b β
de clase C1 con ϕ(α)=a et ϕ(β)=b. entonces, ∫ f (x)dx = ∫ (f  ϕ)(t)ϕ'(t)dt
a α
1
Ejemplo1 : Calculo de ∫ 0
1 − x²dx utilizando el cambio de variable x=sen(t).
 x = sin(t)
dx = cos(t)dt
  π
0, 2  en [ 0,1]
1
 x = 0 si t=0 y sen es una función de clase C de

 x=1 si t= π
 2
π
1
∫ 1 − x²dx = ∫ cos ²(t) dt 2
0 0
π
Entonces solamente es necesario de linealizar cos2(t) para encontrar .
4
1
Ejemplo 2 : Calculo de ∫ 0
1 + x²dx utilizando el cambio de variable x=sh(t).

 x = s h(t)
 dx = c h(t)dt

 y sh es una función de clase C1 de [0, argsh(1)] en [0,1].
 x = 0 si t=0
 x=1 si t=argsh(1)
1 argsh (1)
∫0
1 + x²dx = ∫0
c h²(t) dt
1 + ch(2t)
linealizamos ch2(t) en
2
. Recordamos que argsh(t) = ln t + t² + 1 y que ( )
ch(argsh(t))= 1 + t² para concluir que el integral es :
argsh (1)
1 1

2 2

t + sh(2t) 
0
=
1
2
1
arg sh(1) + ch(arg sh(1))=
2
1
2
ln 1 + 2 + 2 . ( ( ) )
En cambio de variable x = tanθ es igualmente posible, pero el integral será mas difícil a inte-
grar.
B- CÁLCULO DE PRIMITIVAS
Notación : Sea f una función continua sobre un intervalo I.
t  ∫ f (t)dt designa una primitiva de f sobre I. ∫ f (t)dt está definida a una constante de dife-
rencia .
x²
Ejemplo : ∫ x.dx= 2
+ cste .

Teorema: Sean "u" y "v" dos funciones de clase C1 en un intervalo I.
∫ u(x)v '(x)dx = u(x)v(x) - ∫ u'(x)v(x)dx
∫ uv ' = uv - ∫ u'v
2- Cambio de variable
Teorema: Sean I y J dos intervalos de .

Sea f una función continua sobre I y ϕ una función de clase C1de J en I.
1- Si F es una primitiva de f sobre I.
∫ (f  ϕ)(t)ϕ'(t)dt
=
 x =ϕ (t )

∫ f (x)dx = F(x)+cste=F(ϕ(t))+cste
dx =ϕ '(t )dt
F  ϕ es una primitiva de la función ( f  ϕ ) .ϕ ' sobre J.

2- Si G es una primitiva de ( f  ϕ ) .ϕ ' sobre J donde ϕ es una biyeccion de clase C1de J
en I.

∫ f (x)dx =
 x=ϕ (t) ∫ (f  ϕ)(t)ϕ'(t)dt = G(t) + cste = G(ϕ−1 (x)) + cste
 -1
 t=ϕ (x )
dx =ϕ '(t )dt

G  ϕ-1 es una primitiva de f sobre I.
3- Primitivas de una fracción racional
Sea F una fracción racional definida en un intervalo I. Nos proponemos determinar las
primitivas de F en I.
1- Se divide F en elementos simples de 1a y 2a especie (y su parte entera).
2- Primitivas de los elementos simples de 1a especie de la forma b con “a” y “b”
(x −a)n
reales y “n” entero natural.
i- Para n=1, ∫ b dx =b.ln|x-a| + cte
x −a
ii- Para n ≥ 2, ∫ b n dx = - 1 b + cte
(x −a) n −1 (x −a)n −1
mx +p
3- Primitivas de los elementos simples de 2a especie de la forma con m, p,
(ax²+bx +c)n
a, b, c reales y ∆=b²-4ac<0.
mx + p
Se busca G(x)= ∫ dx
(ax²+ bx +c)n
i- Se escribe ax²+bx+c bajo la forma canónica:
 b 
2
∆ 
ax²+bx+c=a  x +  − .
 2a  4a² 
ii- Se plantea α= - b y β= −Δ
2a 2a
iii- El cambio de variable se efectúa con u= x−α . Se obtiene:
β
1 mβu + mα + p
G(x)= 2n −1 n ∫ du
β a (u² + 1) n
u 1
4- Queda por determinar las primitivas siguientes: ∫ n
du y ∫ du .
(u² + 1) (u² + 1) n
u u 1 dt
i- Para ∫ n
du , se plantea t=u²+1. Se obtiene: ∫ n
du = ∫ n
(u² + 1) (u² + 1) 2 t
1 dt 1
Para n=1, ∫ = ln t + cte
2 t 2
1 dt 1 1
Para n ≥ 2, ∫ n =- n −1
+ cte.
2 t 2(n − 1) t
1
ii- Para ∫ du = I n(u)
(u² + 1) n
1
Para n=1, I 1 (u) = ∫ du = arctan u + cte
u² + 1

u² + 1 − u² u²
Para n ≥ 2, I n(u)= ∫
(u² + 1) n
du =I n-1 (u) - ∫
(u² + 1) n
du .
u² u 2u
∫ (u² + 1)n du = ∫ u (u² + 1)n du y se integra por partes con f(u)=u, f ’(u)=1, g’(u)= 2(u² + 1)n y
1 1
g(u)=- .
2(n − 1) (u² + 1) n −1
2n − 3 1 u
Se obtiene: I n (u)= I n −1 (u) + .
2n − 2 2(n-1) (u² + 1) n −1
1 2x
Ejemplo: Calculo de I= ∫ dx .
x² + x + 1
0
2x
La fracción racional es un elemento simple de segunda especie.
x² + x + 1
1 2x 1 2x + 1 − 1 1 2x + 1 1 1
I= ∫ dx = ∫ dx = ∫ dx - ∫ dx
0 x² + x + 1 0 x² + x + 1 0 x² + x + 1 0 x² + x + 1
1 2x + 1
dx = [ ln(x² + x + 1) ]0 =ln(3).
1
Tenemos: ∫
0 x² + x + 1
1 1
Para el cálculo de J= ∫ dx .
0 x² + x + 1
1 1 1 1 1 1 4 1 1
J= ∫ dx = ∫ 2
dx = ∫ dx = ∫ dx
0 x² + x + 1 0
 1 3 0
34 1
2
 3 0   2x + 1  2 
x +  +   x +  + 1 
  3 
+ 1
 2 4 4  3  2  


4 3 1 3 2 3 1 2
[arctan(u)] 1 .
3
= ∫1 2 dx = ∫ dx =
3 3 ( u + 1) 2 3 3 ( u + 1)
1 2
3 3
2  2  π π
2x
( 3 ) − π2  = ln(3)-
1
Conclusion: I= ∫ dx =ln(3)-  2 arctan 2 − .
0 x² + x + 1 3 3 3 2
π
I = ln(3)- .
3 3
4- Primitivas de una fracción en seno y coseno
5- Integral abeliana
ABEL Niels Henrick, noruego, 1802-1829. Los trabajos de este
gran matemático, víctima de la tuberculosis apenas de 27 años, no fue-
ron reconocidos hasta después de su muerte. Su memoria fundamental
sobre las funciones elípticas, presentada por Hachette (1826) a la Aca-
demia de Ciencias de París, fue desestimada por Gauss y Legendre y
perdida, y felizmente encontrada por Cauchy pero luego de la muerte
de Abel.
Sería Jacobi quien comprenderá todo el genio del joven matemáti-
co. Es con éste último que Abel recibira, a título póstumo, el gran pre-
mio de matemáticos del Instituto de Francia (1830).

COMPLEMENTOS
DEMOSTRACIÓN DE LAS NORMAS DE BIOCHE
Declaración:
1- Sea “a” un número real. Demostrar que toda función G, definida en el intervalo
[-a,a] por
P(s e n x,cos x)
G(x) =
Q(sen x,cos x)
donde P(u, v) y Q(u, v) son polinomios con dos indeterminadas "u" y "v" puede escribirse:
L (cos x) + sen x. M1 (cos x)
G(x) = 1
L 2 (cos x) + sen x. M 2 (cos x)
donde L1 (v), M 1 (v), L2 (v) , M 2 (v) son polinomios en v.
2- Demostrar que en el supuesto de que todo elemento x de [- a, a], G(x) = - G(- x), la
función G es de la forma G(x) = S(cos x) sen x donde S es una función racional.
3- Deducir una observación útil para reconocer que la integral:

b
∫a
G(x)dx
puede ser calculada con ayuda del cambio de variable s = cos x.
¿Cuáles son las observaciones similares para reconocer que esta integral puede calcu-
larse con ayuda del cambio de variable s = sen x o s = tan x ?
Solución:
1- El polinomio P(u, v) puede escribirse en la forma:
P(u, v) = ∑
0≤ p ≤ m
a pq u p vq
0≤ q ≤ n
donde a pq es el coeficiente del monomio upvq de este polinomio. Separemos los monomios
que contienen “u” elevados a una potencia impar de los monomios que contienen “u” eleva-
dos a una potencia par. Tenemos:
P(u, v) = ∑
0≤ 2r ≤ m
a 2r,q u 2r vq + ∑
0≤ 2r +1≤ m
a 2r +1,q u 2r +1vq
0≤ q ≤ n 0≤ q ≤ n
Si u = sen x y v = cos x tenemos u2 + v2 = 1. Sea L1 (v) el polinomio:
∑
0≤ 2r ≤ m
a 2r,q (1 − v²) 2r vq
0≤ q ≤ n
y M 1 (v) el polinomio:
∑
0≤ 2r +1≤ m
a 2r +1,q (1 − v²) 2r +1 vq
0≤ q ≤ n

entonces para u = senx y v= cosx obtenemos P(u, v) = L 1 (v) + uM 1 (v).
Demostraríamos de manera similar que existen dos polinomios L2 (v) y M 2 (v) tales que para u
= senx y v= cosx tengamos:
Q(u, v) = L2 (v) + uM 2 (v)
y por lo tanto:
L (cos x) + sen x. M1 (cos x)
G(x) = 1
L 2 (cos x) + sen x. M 2 (cos x)
2- Supongamos que para todo el elemento x de [- a, a] tengamos G(x) = - G(-x).

La función coseno es una función par y la función seno una función impar. Tenemos pues:
L1 (cos x) + sen x. M1 (cos x) L (cos x) - sen x. M1 (cos x)
=- 1
L 2 (cos x) + sen x. M 2 (cos x) L 2 (cos x) - sen x. M 2 (cos x)
para todo elemento x de [- a, a].
Por lo tanto:
L1 (cosx)L2 (cosx)+senx[M 1 (cosx)L 2 (cosx)-L1 (cosx)M 2 (cosx)]-sen²xM 1 (cosx)M 2 (cosx)
= - L1 (cosx)L2 (cosx)+senx[M 1 (cosx)L2 (cosx)-L1 (cosx)M 2 (cosx)]+sen²xM l (cosx)M 2 (cosx)
para todo elemento x de [- a, a].
Tenemos entonces la relación:
L1 (cos x) L2 (cos x) - sen²xM 1 (cos x) M 2 (cos x) = 0
Para todo elemento x de [- a, a].
Supongamos que el polinomio L2 no sea idénticamente nulo, entonces tendremos:
s e n ²xM1 (cos x)M 2 (cos x)
L1 (cos x) =
L 2 (cos x)
Y por consecuencia:
s e n xM1 (cos x)
G(x) =
L 2 (cos x)
Si el polinomio L 2 es idénticamente nulo entonces necesariamente el polinomio M 1 es idénti-
camente nulo, porque M 2 no puede ser idénticamente nulo en mismo tiempo que L2 .
Tenemos entonces:
L1 (cos x) L1 (cos x)
G(x) = = sen x
s e n xM 2 (cos x) (1 − cos ²x)M 2 (cos x)
Así, si G(x) = - G(- x) para todo elemento x de [- a, a], existe una función racional S tal que
G(x) = sen x. S(cos x).
b
3- Deducimos del 2- que la integral ∫ a
G(x)dx puede calcularse en “a” haciendo el
cambio de variable cos x = s, si G(x) = - G(- x), o bien si el elemento diferencial G(x)dx es
invariante por la transformación x  - x.
Dado que las notaciones y las hipótesis son los de la pregunta anterior, tenemos entonces:
b b
∫a
G(x)dx = ∫a
s e n x S(cos x)dx
Así que si S es una primitiva de la función racional S, tenemos:
b
∫ a
G(x)dx = S (cos b) - S (cos a)
Demostraríamos así mismo que la integral propuesta puede calcularse haciendo el cambio de
variable sen x = s (resp. tan x = t) si el elemento diferencial G(x) dx no varia con la transfor-
mación x  π - x (resp. x  π + x).

Ejercicio 1 . Sea a un real estrictamente positivo y sea f una función continua en [ −a , a ] .

a a
Mostrar que si f es par entonces ∫
−a
f (t) dt = 2 ∫ f (t) dt . Mostrar que si f es impar entonces
0
a
∫−a
f (t) dt = 0 .
2 1 1
Ejercicio 2 . Calcular ∫ 2
3
2
x x −1
dx de dos maneras : poniendo x = , luego poniendo
t
−1
x= .
u
Ejercicio 3. Calcular las derivadas de las funciones de variable x definidas por:

5
x 2 x²
f (x) = ∫ (sin t)5 dt , g(x) = ∫ (ch t) 2 dt , h(x) = ∫ arctan(u)du ,
0 x x
=k(x) ∫
sin x
cos x ( ∫ ln(1 + u )du ) dt

t
0
2
Ejercicio 4. Calcular las siguientes primitivas en el intervalo conveniente (que hay que preci-
1 cos3 (x)
sar): ∫
(x − 1)(x 2 + 1)
dx ; ∫ sin 5 (x) dx (en ]0 , π[ , de cuatro maneras distintas) ;
1
∫ x x 2 − 1 dx (dos cálculos diferentes según el intervalo).

EJERCICIOS
Ejercicio 1. Calcular :
1 1 1 x
=I ∫ (2x + 3)
15
; J
dx= ∫ (2x + 3)
2
x10 dx ; K = ∫ dx
0 0 0 (2x + 3) 4
Ejercicio 2. Calcular las integrales siguientes:

π
x x
∫1
ln(t)dt para x estrictamente positiva, ∫0
arctan(t)dt ; ∫
0
2
e − x cos(x)dx
Ejercicio 3. Calcular ∫ cosh(x).sen(2x)dx .
ln(x 2 + 4x + 5)
Ejercicio 4. Calcular ∫ dx en un intervalo que no contiene (-1).
(x + 1) 2
arctan(x)
1
Ejercicio 5. Calcular ∫
0 x² + 1
dx .
Ejercicio 6. Sea f una función continúa en un intervalo [ a, b ] .

b b
1. Mostrar con la ayuda de un cambio de variable que ∫a
f(x)dx= ∫ f(a+b-t)dt . Deducir
a
3π
de eso el valor de I= ∫ ln(tan(x))dx .
π
8
8
b b
2. Mostrar que si f(a+b-x)=f(x) para todo x ∈ [ a, b ] , entonces ∫ x f(x) dx = ∫ f(x) dx .
a a
xsin(x) π
Deducir de eso el valor de K= ∫ dx .
0 1+cos 2 (x)
Ejercicio 7. Calcular las siguientes integrales con la ayuda de los cambios de variable indica-
dos:
=
1
I ∫ 1 − t² dt con t=cos(x)
2 x
J=∫ dx con u=x²+1
0 1 (x² + 1)²
3 arctan(x) e² 1
K=∫ dx con u=arctan(x) L=∫ dx con u=ln(x)
0 1+x² e x.ln(x)
∫ x . ( x + 1)
1 −
2 3
M= 4 dx con u=x 3 + 1
0

2x
∫
1
Ejercicio 8. Calcular 2 dx .
0 x + x +1
Ejercicio 9.Determinar una primitiva de las siguientes funciones precisando cada vez el in-
tervalo utilizado:
x4 1 x6
1) F ( x ) = 2) G ( x ) = 3) H ( x ) =
( x + 1)
2
(x 2
+ 1) ( x − 1)
4
(x 2
− 1)( x 2 + 1)
2
dt
Ejercicio 10. Establecer una relación entre I(n) y I(n+1) con I(n) = ∫ . Calcular I(2) y
(t − 1) n
2
I(3).
 π π 1
Ejercicio 11. Determinar una primitiva en  − ,  de : x  utilizando el cambio de
 2 2 cos( x)
variable u=sen(x).
1
Ejercicio 12. Determinar una primitiva en ]0,π[ de : x  utilizando el cambio de
sen(x)
variable u=cos(x).
 π π 1
Ejercicio 13. Determinar una primitiva en  − ,  de : x  utilizando el cam-
 2 2 1+sen 2 (x)
bio de variable u=tan(x).
 π π 1
Ejercicio 14. Determinar una primitiva en  − ,  de : x  donde "a" es un real
 2 2 a+sen(x)
x
estrictamente superior a 1 utilizando el cambio de variable t=tan   .
2
π
cos3 (x).sen 3 (x)
Ejercicio 15. Determinar ∫0
2
1 + sen 2 (x)
dx utilizando el cambio de variable u=cos(x).
∫ cos (x).sen (x) dx en [0,π] ; ∫ cos (x).sen

6 3 2 4
Ejercicio 16. Determinar (x) dx .
dx
Ejercicio 17. Calcular ∫ x2 + x + 2
.
dx
Ejercicio 18. Determinar ∫ (1 + x² ) 1- x² .
Ejercicio 19. Sean "a" un número real estrictamente superior a 2 y "x" un número real supe-
rior a "a". Calcular las integrales:

x t +1 x t2
=I ∫a t 2 − 3t + 2 dt y J
= ∫ a
4 + 9t 2
dt
x + 2
Ejercicio 20. Determinar ∫ x² - 5x + 6
dx .
2 x2 +1
Ejercicio 21. Calcular I = ∫ 1
x x4 − x2 +1
dx utilizando el cambio de variable
u=x- 1.
x
b 1
Ejercicio 22. Calcular la integral ∫a 3
x − 3x + 2
dx don de [a ;b] ⊂ ]-2 ;1[.
2x dt
Ejercicio 23. Se considera la función F : x  F(x) = ∫
x
t + t 2 +1
4
a- Mostrar que para todo real t estrictamente positivo,

1 1 1
2 ≤ 4 ≤ 2
t + 1 t + t2 +1 t
Deducir que para todo real x estrictamente positivo,
1
arctan(2x) - arctan(x) ≤ F(x) ≤
2x
X
b- Se plantea H(X) = ∫ ( arctan(2x) − arctan(x) ) dx . Calcular H(X) y determinar:
0
H(X)
Lim
X→+ ∞ ln(X)
1
Podrán utilizar la fórmula para X > 0, arctan(X) + arctan   = π .
X 2
X
c- Se plantea G(X) = ∫ 1
F(x)dx . Dar un equivalente de G(X) cuando X tiende hacia más
infinito.

Ejercicio 24. Sean a y b dos reales tales que a < b.
Sea f una función continua en [a ; b] tal que ∀ x ∈ [a ; b] f (a + b – x) = f(x).
b a+b b
Mostrar con ayuda de un cambio de variable que tenemos: ⌠ ⌡a x f(x) dx = 2 ⌠ ⌡a f(x) dx .
b
Corrección : Llamemos I = ∫ xf ( x ) dx .
a
Con ayuda del cambio de variable : u = a + b − x . Este cambio de variable es de clase C1. Te-
nemos:
a b
∫ ( a + b − u ) f ( a + b − u )( −du=) ∫ ( a + b − u ) f ( u ) du
I
=
b a
b b b
Esto se escribe aún: I = ( a + b ) ∫ f ( u ) du − ∫ uf ( u ) du =
a
( a + b ) ∫ f ( u ) du − I .
a a
b (a + b) b
Esto implica entonces que : 2I = ( a + b ) ∫a f ( u ) du ⇔ I = ∫ f ( u ) du .
2 a
Ejercicio 25. Calcular las integrales con ayuda de cambios de variables :

1 3 arctan(x) ⌠ e2 1
I=⌡⌠0 2
1 – t dt ⌠ π/4
J = ⌡0 tan x dx K= ∫ dx L= dx
⌡e x lnx
A E
1 + x²
EA A A E
Corrección : Observación:
b
Hay esencialmente dos maneras de definir un cambio de variable para la integral ∫ f ( x ) dx .
a
• La primera solución consiste en reemplazar la variable de la integral por una función

dependiendo de otra variable : x = u ( t ) . En este caso, basta con que la solución sea de clase
C1 en un intervalo [ α, β] en [ a, b ] ,y que ella verifique: u ( α ) =a y u ( β ) =b .
f ( x ) dx = ∫ f ( u ( t ) ) u ′ ( t ) dt .
b β
Obtenemos entonces: ∫ a α
• El segundo método consiste en definir una nueva variable como función de la variable
de la integral, quiere decir llamar: t = g ( x ) . Esta vez, la función g tiene que ser biyectiva en
el intervalo [ a, b ] en [ α, β] (lo que significa también que el cambio de variable es biyectivo!).
Y volvemos al primer método, llamando: t = g −1 ( x ) (ie : u = g −1 ).
′
∫ f ( x ) dx = ∫ f ( g ( t ) )( g ) ( t ) dt .
b β
−1 −1
Obtenemos entonces:
a α
Este método es interesante si por un lado, la función g aparece en la integral y s i además,
podemos fácilmente demostrar que se trata de una biyección en el intervalo considerado.
1
- I
= ∫ 0
1 − t 2 dt
 π
Llamemos t = cos ( u ) . La aplicación u  cos u es de clase C1 de 0;  en [ 0;1] verificando
 2
π
cos ( 0 ) 1,=
= cos   0 , obtenemos entonces:
2

π
I =∫ 1 − t 2 dt =∫π 1 − cos 2 ( u ) × ( − sin ( u ) du ) =− ∫π 1 − cos 2 ( u ) sin ( u ) du =∫ 2 sin 2 ( u ) du .
1 0 0
0 0
2 2
Observemos que podemos reemplazar 1 − cos 2 ( u ) por sin ( u ) porque estamos en el interva-
 π
lo 0,  .
 2
1 − cos ( 2u )
Para terminar el cálculo integral, basta con darse cuenta que: sin 2 ( u ) = .
2
π
1 − cos ( 2u )
π
1 π2 1 π2 π 1  sin ( 2u )  2 π
∫ ( )
2 ∫0 2 ∫0
De donde: I = 2
du = du − cos 2u du =−   =
2 0 4 2  2 0 4
π π
sin ( x )
=- J ∫=
4
tan ( x ) dx ∫ 4
dx
0 0 cos ( x )
Llamemos x = Arccos ( u ) . Este cambio de variable es de clase C1. P P
π 2
Tenemos u = cos ( x ) , du = − sin ( x ) dx y para=
x 0,= yx
u 1= =,u .
4 2
π
sin ( x ) 2
−1 1 1 1  2 1
∫0 cos ( x ) ∫1 u du =
De donde: J = 4
dx =
2
ln ( u )  2
∫ 22 u du = − ln 
=  = ln 2 .
2  2  2
3 arc tan ( x )
- K=∫ dx
1+ x2
0
Llamemos u = Arctan ( x ) . Este cambio de variable es de clase C1. P P
dx π
Tenemos x = tan ( u ) , du = y para=
x 0,=
u 0 y=
x 3,=
u .
1+ x2 3
π
arc tan ( x ) π π 3
3  2 32  3 2  π  2
1
De donde:
= K ∫ 0 1+ x2
= dx ∫=
0
udu
3
∫=u 2
du u 
 3=
0
3
  .
0 3  3 
1e2
- L=∫ dx
x ln x
e
Llamemos u = ln x . Este cambio de variable es de clase C1. P P
dx
Tenemos x = e u , du = y para= x e,= u 1 y= x e 2=, u 2.
x
e2 1 21
du [ ln u ]1 ln 2 .
2
De donde:
= L ∫ = dx ∫= =
e x ln x 1 u
Ejercicio 26. Calcular las siguientes integrales :

1 x cos x 1
1- I1 = ∫ 2
dx 2- I 2 = ∫ xf ′′ ( x ) dx ( f es de clase C 2 en [0 ; 1])
−1 x + 1
P P
0
π
3- I3 = ∫ sin ( px ) sin ( qx ) dx (n, p y q elementos de )
−π

x cos ( x )
1
Corrección : 1- I1 = ∫ dx .
−1 x 2 + 1
x cos ( x )
La función x  es impar. Como la integral de una función impar en un intervalo
x2 +1
simétrico en relación a 0 es nulo. Para verificarlo, basta con cortar la integral en dos de la si-
guiente manera:
1 x cos ( x ) 0 x cos ( x ) 1 x cos ( x )
∫=
x +1
−1
dx ∫
2 2
−1 x + 1
dx + ∫
0 x2 +1
dx y de aplicar el cambio de variable: u=-x en
el primer término.
Finalmente, I1 = 0
1
2- I 2 = ∫ xf ′′ ( x ) dx
0
Con ayuda de una integración por partes (verificamos simplemente las hipótesis) tenemos:
1 1 1
I 2 =  xf ′ ( x )  0 − ∫ f ′ ( x ) dx = f ′ (1) − f ( x )  0 = f ′ (1) − f (1) + f ( 0 )
0
π
3- I3 = ∫ sin ( px ) sin ( qx )dx
−π
Para calcular esta integral, hay que descomponer el producto de seno en suma de senos y de
cosenos.
π
Observemos que la función por integrar es par, tenemos I 4 = 2 ∫ sin ( px ) sin ( qx )dx .
0
−1  p+q   p − q 
sin ( px ) sin ( qx )
Tenemos: =  cos  x  − cos  x  .
2   2   2 
De donde
π
 p+q 
π  p − q   2 p+q  2  p − q 
− ∫  cos 
I3 = x  − cos  x  dx =
− sin  x− sin  x  .
0
  2   2  p + q  2  p−q  2 0
 π
Como, sin  n  = ( −1) si n es un entero.
n
 2
 2 2 p −q 
( −1) − ( −1)  = 0 porque ( −1) = ( −1) .
p+q p −q p+q
De donde, I3 =−
p + q p−q 
π
dt
Ejercicio 27. Siendo dado θ ∈ [ 0; π[ , calcular ∫ 2
(Podremos llamar
0 1 + cos θ cos t
t=2arctan(u) ).
Corrección : Utilizamos la indicación t=2arctan(u) .

 π
Podemos observar que este cambio de variable es biyectivo de 0;  en [0 ;1] por-
 2
 π t  π t
que t ∈ 0;  entonces ∈ 0;  , y así u = tan .
 2 2  4 2

t  π
Además, la aplicación t  tan es de clase C1 en 0;  .
2  2
t 2 2 1− u2
Recordamos que cos = t 2 cos 2 = −1 −1
= =
− 1 , y por otro lado,
2 t
2 2
2 1 + tan 1 + u 1 + u
2
2du
dt = .
1+ u2
Deducimos que :
du
π π
dt tan  
1+ u2 1 du 1 du
∫02 1 + cos θ cos t ∫=
= 4
tan ( 0 ) 1− u 2 ∫0
= ∫
1 + u + cos θ (1 − u ) 0 1 + cos θ + u (1 − cos θ )
2 2 2
.
1 + cos θ
1+ u2
1 − cos θ
Para simplificar las notaciones, llamamos: α = 1 + cos θ , y β = .
1 + cos θ
Observemos que β está bien definida porque θ ∈ [ 0; π[ .
π
dt 1 1 du
Obtenemos : ∫0
2
= ∫
1 + cos θ cos t α 0 1 + βu 2
.
1
Efectuemos ahora el cambio de variable: v= βu ( β >0), tenemos du = dv entonces:
β
1
π
dv
dt 1 1 du 1 β β 1 β dv 1 Arc tan β
[ Arc tan v ]0
β
∫0
2
= = ∫
1 + cos θ cos t α 1 + βu
0 2
α
=∫0 1+ v 2
α β
=∫0 1+ v 2
α β
=
α β
Ejercicio 28. Determinar una primitiva de las siguientes funciones precisando cada vez los
intervalos utilizados:
1 sin x 1 + cos x
1- f ( x ) = 2- g ( x ) = 3- h ( x ) =
cos ( x ) ( cos ( x ) )
5
sin x − 1
1 sin 3 x 1
4- j ( x ) = 5- k ( x ) = 6- l ( x ) =
cos ( x ) − cos ( 3x ) 1 + cos x
3
sin x cos x
1
Corrección : 1- f ( x ) = .
cos ( x )
Utilizamos un intervalo en el cual la función f está definida, o sea un intervalo de tipo
 kπ ( k + 1) π 
Ik =  ,  con k elemento de .
 2 2 
De acuerdo con las reglas de Bioche, podemos utilizar el cambio de variable: t = sin ( x ) que
es un cambio de variable biyectivo de clase C1 de Ik en un intervalo.
P P R R
dx cos xdx cos xdx dt

Tenemos;= = 2 2
, y dt = cos xdx entonces ∫ f ( x ) = ∫ .
cos x cos x 1 − sin x 1− t2
dt
Para calcular ∫ , hacemos una descomposición en elementos simples :
1− t2

2 1 1 dt dt dt 1+ t
= 2
+ d’où ∫ 2
=∫ +∫ =− ln 1 − t + ln 1 + t + C =ln +C.
1− t 1− t 1+ t 1− t 1− t 1+ t 1− t
Finalmente, deducimos que :
1+ t 1 + sin x  x π
∫ f ( x =) ln 1 − t + Cste= ln 1 − sin x + Cste= ln tan  2 + 4  + Cste
sin x
2- g ( x ) =
( cos ( x ) )
5
π π 
Del mismo modo que precede, utilizamos un intervalo de tipo I k =  + kπ, + ( k + 1) π  con
2 2 
k elemento de .
Sabemos que la derivada de x  cos x es x  − sin x , reconocemos entonces una función de
u′ 1
la forma − 5 con u = cos ( x ) , entonces una primitiva de g es G = (x) + Cste .
u cos 4 x
1 + cos x
3- h ( x ) =
sin x − 1
Utilizamos un intervalo en el cual el denominador no se anula, un intervalo de tipo
π π 
I k =  + 2kπ, + 2 ( k + 1) π  con k elemento de .
2 2 
x
Para determinar una primitiva de h, efectuamos el cambio de variable : t = tan   que es un
2
1
cambio de variable biyectivo de clase C de I k en un intervalo.
P P R R
1− t2 2t 2
Sabemos que : cos ( x ) = 2
, sin ( x ) = 2
y dx = dt .
1+ t 1+ t 1+ t2
Obtenemos entonces:
1− t2 2
+1
1 + cos x 1+ t 2 2 1+ t2 2 −4
∫ h ( x )
= ∫ sin x − 1 dx= ∫ 2t × dt= ∫ × dt= ∫ dt .
−1 1 + t 2
−
1 + t 2
− 2t 1 + t 2
(1 + t 2
) (1 − t )
2
1+ t2 1+ t2
Una descomposición en elementos simple nos da :
4 2t 2 2
= − +
(1 + t 2 ) (1 − t ) (1 + t ) ( t − 1) ( t − 1)2
2 2
Deducimos que :
 2t 2 2   2 
∫ h ( x ) =− ∫  (1 + t 2 ) ( t − 1) ( t − 1)2 
 − +  dt =− 
 ln (1 + t 2
) − 2 ln ( t − 1) −
(
+C
t − 1) 
  
2
=− ln (1 + t 2 ) + 2 ln ( t − 1) + +C
( t − 1)
1
4- j ( x ) =
cos ( x ) − cos ( 3x )

Podemos verificar fácilmente con ayuda de las fórmulas de trigonometría usales que :
cos (=
3x ) cos x − 4sin 2 x cos x de donde cos x − cos ( 3x ) =
4sin 2 x cos x , y a sí
1
j( x ) = 2
.
4sin x cos x
Debemos utilizar un intervalo I en el cual ni el seno ni el coseno se anulan.
De acuerdo con las reglas de Bioche, llamamos: t = sin x que es un cambio de variable biyec-
tivo de clase C1 de I en un intervalo, lo que nos da dt = cos xdx .
P P
dx cos xdx
tenemos: = entonces:
sin x cos x sin 2 x cos 2 x
2
1 cos xdx dt
= ∫ j ( x ) dx ∫ 4sin
= 2
x cos x
dx ∫= 2 2
4sin x cos x ∫ 4t (1 − t 2 )
2
1
Efectuamos la descomposición en elementos simples de y obtenemos:
t (1 − t 2 )
2
1 1 2 2
=2 + −
t (1 − t ) t
2 2
t +1 t −1
Finalemente, deducimos que :
1 1 2 2  1 1 
∫ j ( x ) dx = 4 ∫  t 2 + t + 1 − t − 1  dt = 4  − t + 2 ln ( t + 1 ) − 2 ln ( t − 1 )  + C , sea:
1 1 
∫ j ( x ) dx = 4  − sin x + 2 ln ( sin x + 1 ) − 2 ln ( sin x − 1 )  + C
sin 3 x
5- k ( x ) =
1 + cos x
Utilizamos un intervalo I en el cual el coseno no vale -1. Observamos que :
k (x) =
(1 − cos 2 x ) sin x
.
1 + cos x
Llamamos u = cos ( x ) que es un cambio de variable biyectivo de clase C1 de I en un intervalo P P
(Reglas de Bioche) entonces du = − sin xdx , obtenemos entonces:

(1 − cos 2 x ) sin xdx (1− u2 ) u2 cos 2 x
∫ k ( x ) dx =∫ 1 + cos x =∫
1+ u
( −du ) =− ∫ (1 − u )du =−u + + C =− cos x +
2 2
+C
1
6- l ( x ) = 3
sin x cos x
Utilizamos un intervalo I en el cual ni el seno ni el coseno se anulan. Tenemos:
cos x
l(x) = .
sin x cos 2 x
3
Llamamos u = sin ( x ) que es un cambio de variable biyectivo de clase C1 de I en un intervalo P P
(Reglas de Bioche) entonces du = cos xdx , obtenemos entonces:

cos xdx du
= ∫ l ( x ) dx ∫= 3 2
sin x cos x ∫ u (1 − u 2 )
3
Haciendo una descomposición en elementos simples, obtenemos :

1 1 1 1 1
= + 3− −
u (1 − u ) u u 2 ( u + 1) 2 ( u − 1)
3 2
Deducimos que :
1 1 1 1  1 1 1
∫ l ( x ) dx= ∫  u u 3 2 ( u + 1) 2 ( u − 1)  du= ln u − 2u 2 − 2 ln ( 1 + u ) − 2 ln ( u − 1 ) + C
 + − −
 
1 1 1
De donde: ∫ l ( x= ) dx ln sin x − 2
− ln ( 1 + sin x ) − ln ( sin x − 1 ) + C
2sin x 2 2
Ejercicio 29. Integrales de Wallis

π
Llamamos: I n = ∫ 2 sin n ( x ) dx para n ∈ .
0
1- Calcular I0 y I1 .
2- Demostrar que la sucesión ( I n )n es estrictamente decreciente y minorada.
3- Con ayuda de una integración por partes, demostrar que para todo entero natural n,
tenemos:
( n + 2 ) In +2 =
( n + 1) In +1 (1)
4- Deducir la expresión de I n en función de n, distinguiendo el caso n par del caso n
R R
impar.
5- A partir de la relación (1), demostrar que la sucesión (U n ) n definida por: R R R R
U n = nI n I n −1 es constante para n > 0.

Deducir el lite de la sucesión ( I n )n .
I n +1 π
6- Mostrar que la relación tiene como límite 1. Deducir que : I n  .
In +∞ 2n
1×3×5×…× (2p – 1) 1
7- Deducir finalmente que : plim p = .
→ +∞ 2×4×6×…×(2p) π
A EA E
A A
π π
π π
Corrección : 1- Tenemos=I0 ∫=
2
dx ∫0
y I1 = 2
sin xdx [
= − cos x ] 1.
2 =
0 2 0
 π
2- ∀x ∈  0,  0 ≤ sin x < 1 entonces sin n +1 x < sin n x .
 2
Deducimos entonces que : I n +1 < I n lo que quiere decir que la sucesión es estrictamente decre-
ciente.
 π
Por otro lado, como ∀x ∈  0,  , 0 ≤ sin n x , tenemos I n ≥ 0 .
 2
La sucesión, siendo decreciente y minorada, podemos deducir que ella converge. Llamamos I
su límite.
3-
π π π π
∫ sin ∫ (1 − cos
( x ) dx = x ) sin ( x ) dx =
∫ sin ( x ) dx − ∫ x × cos x sin n ( x ) dx
n +2 2 n n
In +2 = 2 2 2 2
cos

0 0 0 0
v
  
u′

π
π π
 sin n +1 x  2 sin n +1 x
In − ∫ ()
n + 1  0 ∫0
n
In +2 = 2
cos
 x × cos x sin x dx I
= n −  cos x × − 2
sin x × dx
0
v
  n +1
u′
1 π2 n + 2 1
=In −
n +1 ∫0
sin xdx = In −
n +1
In +2
De donde : ( n + 2 ) I n + 2 =
( n + 1) In .
4- Supongamos primero que n es par: n=2p.
De acuerdo con la relación (1), tenemos: 2 ( p + 1) I 2( p +1) =( 2p + 1) I 2p ⇔ I 2( p +1) =

( 2p + 1) I .
2 ( p + 1)
2p
Aplicamos de nuevo la relación a (n-2) con el objetivo de obtener una expresión de I 2p , esto
nos da:
= I 2( p +1)
( 2p + 1) × ( 2p − 1) I
2 ( p + 1) 2p 2( p −1)
Continuamos :
I 2=
( 2p + 1) × ( 2p − 1) × ( 2p − 3) ...= × I
( 2p + 1) × ( 2p − 1) × ( 2p − 3) × ....1 × I
( )
2 ( p + 1) 2 ( p − 1) 2 ( p + 1) × 2p × 2 ( p − 1) × ... × 2
p +1 0 0
2p
( 2p + 2 )( 2p + 1)( 2p )( 2p − 1)( 2p − 2 )( 2p − 3) × ....1 × I
( 2 ( p + 1) ) × ( 2p )2 × ( 2 ( p − 1) ) × ... × 22
2 2 0
= 2 p +1 =
( 2p + 2 )! × I ( 2p + 2 )! × π
2 ( ) ( ( p + 1) !) 22( p +1) ( ( p + 1) !) 2
2 0 2
De donde
= : I 2p
( 2p )! × π .
22p ( p!) 2
2
Tratamos de igual manera el caso n impar.

Obtenemos:
2 ( p + 2 ) 2 ( p + 1) 2 ( p ) 2 ( p + 2 ) × 2 ( p + 1) × 2 ( p ) × ....2
I 2p +3
= × × ...
= × I1 ×I
2p + 3 2p + 1 2p − 1 ( 2p + 3) × ( 2p + 1) × ( 2p − 1) × ... ×1 1
( 2=
( p + 2 ) ) × ( 2 ( p + 1) ) × ( 2 ( p ) ) × ....2 ( ( p + 2 )!)
2 2 2 2
2 2( p
+ 2)
×I
( 2p + 4 )( 2p + 3)( 2p + 2 )( 2p + 1) 2p ( 2p − 1) × ... ×1 1 ( 2p + 4 )!
22( p +1) ( ( p + 1) !)
2
De donde : I 2p +1 = .
( 2p + 2 )!
5- De acuerdo con la relación (1), tenemos ( n + 1) I n +1 = nI n −1 .
Observemos que de acuerdo con la pregunta anterior, , I n jamás es nulo, entonces U n tampo-
co.
U n +1 ( n + 1) I n +1I n ( n + 1) I n +1 (=
n + 1) n
Tenemos entonces:
= = = 1.
Un nI n I n −1 nI n −1 n ( n + 1)
Concluímos que la sucesión (U n ) n es constante y para todo entero natural n,
π
U=n U=1 I1=
I0 .
2

π
Tenemos entonces: I n I n −1 = .
2n
Hemos visto en la pregunta 2, que la sucesión (I n ) n converge hacia I, podemos entonces pasar
al límite en la relación precedente, lo que nos da: I 2 = 0 de donde I = 0 .
n
I
I n +1 n + 1 n −1 n2 I
6- De acuerdo con la relación 1, tenemos : = = 2 × n −1 .
In n −1
In −2 n − 1 In −2
n
I n +1 n2
Llamamos Vn = entonces , con lo que venimos de ver, tenemos Vn = 2 Vn − 2 .
In n −1
Tenemos entonces según n sea par o impar :
( 2p + 1) V
2
4p 2
V2p = 2 V2( p −1) y V2p +1 = .
( 2p + 1) − 1 ( )
2 2 p −1 +1
4p − 1
Consideremos entonces las sucesiones (a p ) p y (b p ) p definidas=
R R R por: a p V=
R R R
2p y b p
R R V2p +1 .
( 2p + 1) b
2
4p 2
Tenemos: a p =
= a ( A ) y bp p −1 ( )
B entonces está claro que las dos
4p 2 − 1 ( p −1) ( 2p + 1) − 1 ( )
2
sucesiones son crecientes.

Por otro lado, ya que la sucesión (I n ) n es decreciente, ellas están mayoradas por 1
 I n +1 
=Vn ≤ 1 .
 In 
Como sabemos que una sucesión creciente y mayorada es convergente, entonces estas dos
sucesiones son convergentes.
Pasando al límite en las relaciones (A) y (B), vemos que estas dos sucesiones tienen mismo
límite 1.
Hemos demostrado que = lim V2p lim
= V2p +1 1 , podemos concluir entonces que
p →∞ p →∞
I n +1
lim Vn = 1= lim .
n →∞ n →∞ In
I n +1
1 = lim implica que I n  I n +1 entonces I n +1I n  I n2 .
n →∞ I +∞ +∞
n
π π π
Como hemos visto en la pregunta 5 que : I n +1I n = entonces I 2n   y así
2 ( n + 1) +∞ 2 ( n + 1) 2n
+∞
π
In  .
+∞ 2n
7- Esta relación proviene inmediatamente de la expresión de I 2p y de la equivalencia
precedente:
I
Tenemos lim 2p = 1 y reemplazando I 2p por su expresión encontramos el resultado.
p →∞ π
4p

Capítulo 18
INTEGRALES GENERALIZADAS
1- Funciones localmente integrables
Definición: Sea I un intervalo (abierto, cerrado, semi-abierto) de . Sea f una función

de I en . El que f sea localmente integrable en I significa que f es integrable en todo interva-
lo cerrado incluido en I.
Teorema: Una función continua en I es localmente integrable en I.
Definición: Sea f una función localmente integrable en [a,b[ (b real o infinito).

x
Plantemos para todo elemento x de [a,b[, F(x)= ∫ f (t)dt .
a
b
Si Lim− F(x) existe y tiene como valor al real l, entonces se plantea ∫ f (t)dt =l y se dice que
x →b a
b
la integral generalizada ∫ f (t)dt converge (hacia l), sino decimos que la integral generalizada
a
b
∫a
f (t)dt diverge.
Definición: Sea f una función localmente integrable en ]a,b] (a real o infinito).

b
Plantemos para todo elemento x de ]a,b], F(x)= ∫ f (t)dt .
x
b
Si Lim+ F(x) existe y tiene como valor al real l, entonces se plantea ∫ f (t)dt =l y se dice que
x →a a
b
la integral generalizada ∫ f (t)dt converge (hacia l), sino decimos que la integral generalizada
a
b
∫a
f (t)dt diverge.
+∞ +∞ a
Atención : La idea de definir ∫ f (t)dt por : ∫ f (t)dt = Lim ∫ f (t)dt es falsa. Para con-
−∞ −∞ a →+∞ − a
vencernos basta con examinar el siguiente ejemplo :
a a²
a  t²  a²  t²   a4 a2 
a →+∞ ∫− a a →+∞ ∫− a
Lim
= tdt Lim
= 0 et Lim tdt = Lim = Lim  −  = +∞
a →+∞  2  a →+∞  2 
  −a   − a a →+∞  2 2 
+∞
Qué valor tomamos para ∫ −∞
tdt ?

+∞
Respuesta : La integral ∫−∞
tdt diverge.
-a a -a a²
Observaciones: a- Sea f una función localmente integrable en ]a,b[ ("a" y "b" reales o infini-
tos).
b
La integral ∫ f (t)dt converge si y solamente si para c e lemento de ]a,b[ las dos integrales
a
c b b c b
∫a
f (t)dt y ∫ f (t)dt convergen y en este caso, ∫ f (t)dt = ∫ f (t)dt + ∫ f (t)dt .
c a a c
Se puede mostrar que este resultado es independiente del real c.
+∞
b- Sea f un elemento de C0 ([a;+∞[) . Que la condición " ∫ f(t) dt converja” no
a
implica que " Lim f = 0".
+∞
Ejemplo: Sea f la función definida por: ∀n ∈*,

  1
 si t ∈  n , n+ 2n  , f (x) =−2n t + 1 + 2n n
  
  1 
 si t ∈  n - n , n  , f (x)= 2n t + 1 − 2n n
  2 
  1 1
si t ∈  n-1+ n-1 , n- n  , f (t) = 0
  2 2 
+∞
f comprueba que ∫
0
f (t)dt converge y es igual a 1 y que Lim f no existe.
+∞
c-Prolongación por continuidad
b
Sea f una función real continua sobre [a,b[. Estudio de ∫a
f (t)dt .

Si Lim− f (t) = l ∈ , entonces prolongamos f por continuidad en b tomando f(b)=l.
t →b
b
En ese caso, la integral ∫a
f (t)dt es la integral de una función continua definida sobre [a,b] y
el problema de convergencia no interviene más…
2- Método de cálculo
1- Utilización de una primitiva
2- Cambio de variable «generalizada»
Teorema: Sea ϕ una biyeccion de clase C1 de ]α, β[ sobre f (]α, β[). Notamos a= Lim+ ϕ(t) y
t →α
b= Lim− ϕ(t) .
t →β
Sea f una función continua sobre ]a, b[ ou ]b, a[.

b β
Entonces las integrales generalizadas ∫a
f (x)dx et ∫
α
f (ϕ(t))ϕ '(t)dt son de la misma naturali-
za, y si ellas convergen, ellas son iguales.
Teorema: Sean "u" y "v" dos funciones de ]a,b[ en  de clase C1 tales que:
A= Lim+ u(x)v(x) y B= Lim− u(x)v(x) existen
x →a x →b
b b
Entonces las integrales generalizadas ∫a
u(t)v '(t)dt y ∫a
u '(t)v(t)dt son de la misma natura-
leza.
b b
Si convergen, entonces ∫ a
u(t)v '(t)dt =B-A- ∫ u '(t)v(t)dt .
a
b
Observación : Si la integral ∫ u(t)v '(t)dt converge, tenemos entonces:
a
b b
∫ u(t)v '(t)dt =  u(t)v(t) -∫ u '(t)v(t)dt 

a a
3- Las integrales de Riemann
Teorema: Sea "a" un real estrictamente positivo.

+∞ dt
∫a t α converge si y solamente si α>1
Teorema: Sea "b" un real estrictamente positivo.
b dt
∫0 t α converge si y solamente si α<1

Teorema: Sea "c" un real estrictamente superior al real a.
c dt
∫a (t − a)α converge si y solamente si α<1
1
Idea: Localización de los gráficos de las funciones x  con relación al gráfico de la fun-
xα
1
ción x  .
x
4- Comparación con funciones positivas

Teorema: Sean "f" y "g" dos funciones localmente integrable positivas definidas en
[a,b[ tales que para toda x de [a,b[, f(x) ≤ g(x).
b b
1- Si ∫
a
f (t)dt diverge, entonces ∫
a
g(t)dt diverge
b b
2- Si ∫ g(t)dt converge, entonces ∫ f (t)dt converge.
a a
5- Integral absolutamente convergente y semi-convergente

b
Definición: Se dice que la integral generalizada ∫a
f (t)dt es absolutamente conver-
b
gente si por definición ∫ a
f (t) dt es convergente.
b
Propiedad: Sea f una función localmente integrable. Si ∫a
f (t) dt converge, entonces
b b b
∫a
f (t)dt converge y ∫ a
f (t)dt ≤ ∫ f (t) dt .
a

b b
Definición: Si la integral generalizada ∫
a
f (t)dt converge sin que ∫a
f (t) dt converja,
b
se dice que ∫a
f (t)dt es semi-convergente.
6- Criterio de Riemann en la vecindad del infinito

Teorema: Sea "a" un real estrictamente positivo.
Sea f una función localmente integrable en [a,+ ∞ [.
+∞
a- Si existe un real α>1 tal que Lim tαf(t)= 0, entonces ∫ f (t)dt es absolutamente
t →+∞ a
convergente
k
b- Si existen reales k que no son nulos y α tales que f(t)  , entonces
+∞ tα
+∞
- ∫ a
f (t)dt es absolutamente convergente si α>1
+∞
- ∫ f (t)dt es divergente si α ≤ 1
a
+∞
c- Si existe un real α ≤ 1 tal que Lim tαf(t)=+ ∞ (o - ∞ ), entonces ∫ f (t)dt es diver-
t →+∞ a
gente.
7- Criterio de Riemann en la vecindad de un real a
Teorema: Sean "a" y "b" dos reales.

Sea f una función localmente integrable en ]a,b].
b
a- Si existe un real α<1 tal que Lim+ (t-a)αf(t)=0, entonces ∫ f (t)dt es absolutamente
t →a a
convergente
k
b- Si existen dos reales k que no son nulos y α tales que f(t)  , entonces
a (t − a)α
b
- ∫ a
f (t)dt es absolutamente convergente si α<1
b
- ∫ f (t)dt es divergente si α ≥ 1
a
b
c- Si existe un real α ≥ 1 tal que Lim+ (t-a)αf(t)=+ ∞ (o - ∞ ), entonces ∫ f (t)dt es di-
t →a a
vergente.
8- Integrales generalizadas y equivalencia
Teorema : Sea f y g dos funciones localmente integrable, estrictamente positivas so-

b b
bre [a,b[ tales que: f  g. Entonces las integrales generalizadas
b ∫a
f (t)dt y ∫ a
g(t)dt tienen la
misma naturaleza.

f (t)
Demostración : Como Lim = 1 , existe c ∈ [a,b[ tal que :
t →b g(t)
1 f (t) 3
∀t ∈ [a, b[, t ∈ [c, b[⇒ ≤ ≤
2 g(t) 2
1 3
Entonces, ∀t ∈ [a, b[, t ∈ [c, b[⇒ g(t) ≤ f (t) ≤ g(t)
2 2
b b
Tenemos entonces: ∫ a
g(t)dt converge ⇒ ∫ c
g(t)dt converge
b
⇒∫ f (t)dt converge
c
b
⇒∫ f (t)dt converge
a
3
La segunda implicación proviene de la desigualdad f (t) ≤ g(t) , y la primera y la tercera son
2
evidentes.
b b
Del mismo modo : ∫a
f (t)dt converge ⇒ ∫a
g(t)dt converge.
1
Est avez gracias a la desigualdad: g(t) ≤ f (t) .
2
Conclusión : las integrales tienen la misma naturalera.
Observación : Hay que ser muy rigoruso en la utilización de equivalencias para establecer la
naturaleza de las integrales. Es claro que el resultado anterior sigue siendo justo si las funcio-
nes son estrictamente negativas. Pero el resultado es falso cuando las funciones cambian de
signo (ver ejercicios).
9- Función Gamma de Euler
En 1755, Euler publica un tratado de cálculo diferencial e integral (completado en

1768 : Instituciones calculi integralis) donde encontramos las « funciones de Euler » o fun-
ciones eulerianas de las cuales la más conocida, la función Γ (el G griego : gamma, así deno-
minado por Legendre) definida para todo x > 0 por :
+∞
Γ(x) = ∫ t x-1e-t dt
0
Si n es entero natural, entonces :
Γ(n) = (n - 1)!
Prueba: 1- Para encontrar el conjunto de definición de Γ, hay que estudiar en qué condicio-
+∞
nes para x la integral ∫0
t x −1e − t dt converge.
[0, ∞[ si x ≥ 1
La función t  t x −1e − t es continua en .
]0, ∞[ sino
Debemos distinguir dos casos :
- x ≥1 :

t →+∞
Tenemos un problema en +∞ . Como tenemos t 2 ×= t x −1e − t t x +1e − t  → 0 entonces de
acuerdo con el criterio de Riemann, esta función se puede integrar en la proximidad de +∞ .
+∞
Deducimos entonces que si x ≥ 1 , entonces la integral ∫ 0
- x <1 :
Tenemos un problema en +∞ y en 0.
En +∞ , tenemos lo mismo que antes, convergencia de la integral.
t 1
En 0, tenemos t x −1e − t  t x −1 = 1− x y esta función se puede integrar en 0 si y solamente si
0 t
1− x < 1 ⇔ 0 < x .
+∞
Deducimos entonces que si 0 < x < 1 , entonces la integral ∫ 0
Finalmente, concluímos que el dominio de definición de Γ es *+.
2- Mostremos que para todo real x>0, Γ (x+1) = x Γ(x).

+∞ B
( x + 1)
Sea x>0, Tenemos Γ = ∫ 0
t x e − t dt lim ∫ t x e − t dt .
=
B→∞ 0
x -t 1
Como t  t y t  -e son C . Entonces :
 t x × ( −e − t )  − ∫ xt x −1 ( −e − t ) dt =
B B B B B
∫0
t x e − t dt =
IPP  0 0 −Bx e − B + ∫ xt x −1e − t dt =
0
−Bx e − B + x ∫ t x −1e − t dt
=
0
(
Entonces, Γ ( x + 1) =lim −Bx e − B + x ∫ t x −1e − t dt =x ∫
B→∞
B
0 ) +∞
0
t x −1e − t dt =xΓ ( x ) .
Sea entonces n un entero natural. De acuerdo con lo que precede, tenemos Γ ( n + 1) =nΓ ( n ) .
Es fácil entonces verificar por recurrencia que Γ ( n + 1) =
n!.
+∞ +∞ +∞
De hecho, Γ ( 0 + 1) =∫ t 0 e − t dt =∫ e − t dt = −e − t  =1 =0!.
0 0 0
Además, si suponemos que Γ ( n ) =( n − 1) ! entonces ya que Γ ( n + 1) =nΓ ( n ) , obtenemos:

Γ ( n + 1)= n ( n − 1) != n!
Menos célebre, pero práctica para la integración de funciones racionales, es la función

euleriana β :
1 Γ(p)Γ(q)
β(p,q)= ∫ t p −1 (1 − t)q −1 dt =
0 Γ(p + q)
Euler demostró la fórmula dicha de los complementos :
π
si 0 < p < 1 , entonces : Γ(p).Γ(1 − p) =
sin(pπ)
1
Consecuencia con p = :
2
+∞
π =2 ∫ e − x ² dx
0
Es la integral dicha de Gauss.

Ejercicio 1. Con ayuda de la definición de la convergencia de una integral impropia, estudiar

la convergencia (y dar eventualmente el valor) de las siguientes integrales:
+∞ 1 1 1 1 1 1 +∞ 1 +∞ 1 1
∫0 e dt ; ∫0 1 − u 2 du ; ∫0 x dx ; ∫0 32 dx ; ∫0 x dx ; ∫1 32 dx ; ∫0 ln(u) du
−t
x x
2 1
Ejercicio 2. Mostrar la convergencia de ∫1
(2 − t)(t − 1)
dt , luego calcular esta integral.
+∞
Ejercicio 3. Sea n ∈ *. Mostrar que I n = ∫ t n −1e − t dt converge, luego calcular I n expresada
0
en función de I n −1 .
1
Ejercicio 4. Sea n ∈ . Mostrar que J n = ∫ (ln(t)) n dt converge, luego calcular J n .
0

EJERCICIOS
+∞ x +1 a x +1
Ejercicio 1. Estudiar la naturaleza de la integral ∫-∞ x² + 1
dx . Calcular Lim ∫
a → + ∞ -a x² + 1
dx .
Ejercicio 2. 1- Sea f una función de clase C1 , decreciente en [a;+ ∞ [ tal que Lim f sea nulo.
+∞
+∞ +∞
Integrando por partes, mostrar que ∫a
f(x).sen(x) dx y ∫a
f(x).cos(x) dx convergen.
sen²(x) +∞
2- Mostrar que
x∫ π
2
dx es divergente.
Indicación : Expresar sen²x en función de cos(2x).

+ ∞ sen(x) + ∞ cos(x)
3- Mostrar que ∫π dx y ∫π dx son convergentes. ¿Son absolutamente
2 x 2 x
convergentes?
4- Sea “a” un real estrictamente positivo. Estudiar:
+ ∞ sen(x) + ∞ sen(x)  sen(x) 
∫a x dx y ∫a x . 1+ x  dx
Concluir.
Ejercicio 3. Estudiar la naturaleza de las integrales generalizadas siguientes determinando los

π
1 +∞
∫ ln(x) dx ; ∫ ∫
- αx
límites correspondientes e dx ; 2
tan(x) dx .
0 0 0
Ejercicio 4. Estudiar la naturaleza de las integrales generalizadas siguientes:

1 1 + ∞ cos(x) + ∞ sen(x)
∫0 sen  x  dx ; ∫0 1 + x² dx ; ∫0 3 dx
x2
Ejercicio 5. Sea α y β dos reales tales que : 0<α ≤ β. Estudiar la naturaleza de:
+∞ 1
∫0 x α + x β dx .
Ejercicio 6. Estudiar la naturaleza de las integrales generalizadas siguientes:
+∞ 1 2 1 +∞ 1  1  +∞ 1 +∞ arctan(x)
∫2 ln(x)
dx ; ∫
1 ln(x)
dx ; ∫
1  x - arcsen  x   dx ;
  
∫0 senh(x) + 1
dx ; ∫ 2 x3
dx
Ejercicio 7. Determinar el campo de definición de la función Γ definida por:

+∞
Γ(α) = ∫0
t α-1e-x dx
Calcular Γ(α) para el entero natural α que no es nulo.

Ejercicio 8. Sea "a" un real.
1
∫
+∞
1- Estudiar la convergencia de I a = dx . a
1 x x² - 1
En lo que sigue del ejercicio, se elige "a" tal que I a converja.
2- Calcular I 1 y I 2 .
a
3- Mostrar que I a +2 = I .
a +1 a
Indicación: podrán utilizar una integración por partes de I a .
4- Sea n un entero natural. Calcular I n .
π
Ejercicio 9. Estudiar y eventualmente calcular ∫2
cos(x).ln ( tan(x) ) dx .
0
ln(u)
Ejercicio 10. 1- Para u >0, se plantea f(u) = . Calcular ∫ f (u)du en ]0;+ ∞ [.
(1 + u) 3
2- Mostrar que la integral impropia I 1 = ∫0f(u) du existe.
+∞
3- Calcular I 1 con auxilio del punto 1 de este mismo ejercicio-.

α-1
+ ∞ t ln(t)
4- Para α real que no es nulo, se plantea Iα = ∫ dt . Calcular Iα con auxilio
0 (1+t α )3
del punto 3 de este mismo ejercicio- (distinguirán los casos α > 0 y α< 0).
ln(u)
∫
1
Ejercicio 11. Probar la convergencia luego calcular I = du .
0 1- u
1
∫ arccos(x) dx .
1
Ejercicio 12. Determinar la naturaleza de la integral generalizada siguiente: 0
t.ln(t) +∞ +∞ t 3 .ln(t)
Ejercicio 13. Se consideran las integrales: I = ∫1 (1+t²)² dt y J = ∫0 (1+t 4 )3
dt .
Mostrar que I y J son convergentes y calcular sus valores.
x²
-t²-
Ejercicio 14. Sea ϕ(t,x)=e , (t,x)∈]0,+∞[×[0,+∞[ .
t²
1- Mostrar la convergencia de las integrales generalizadas:

+∞ +∞ ∂ϕ
∫0 ϕ(t, x)dt y ∫0 ∂x (t, x)dt para toda x ∈ [0,+∞[
2- Se plantea f(x)= ∫0ϕ( t , x)dt .
+∞
a- Probar que ∀u ∈ [0,+∞[, 0 ≤ 1- e -u ≤ min(1, u) .

dt
b- Deducir que ∀x ∈ [0,+∞[, |f(x) - f(0)| ≤ ∫ e -t² dt + x ² ∫
x +∞
.
0 x t²
c- Mostrar entonces que f es continua en 0 + .
∂ϕ
3- Se admite que f es derivable en ]0,+∝[ y ∀x ∈]0,+∞[, f' (x) = ∫0
+∞
( t , x)dt .
∂x
Mostrar con ayuda de un cambio de variable que se tiene: ∀x ∈]0, +∞[, f '(x)=-2f(x) .

π
∫
+∞
4- Deducir la expresión de f en [0,+∝[ sabiendo que e − t ² dt = .
0 2
Elementos de corrección:
1- Sea x un elemento de [0, +∞[ . La función t  ϕ(t,x) es localmente integrable en
]0, +∞[ .
Se puede prolongar por continuidad esta función en 0 planteando ϕ(0,0)=1 y ϕ(0,x)=0 si x no
1
es nulo. Entonces ∫ ϕ(t, x)dt
0
es convergente.
+∞
Lim t² ϕ(t,x)=0. Pues según los criterios de Riemann,
t →+∞ ∫
1
ϕ(t, x)dt converge.
∂ϕ 2x
Tenemos que (t,x)= - ϕ(t,x).
∂x t²
∂ϕ 1 ∂ϕ
- Para x=0, tenemos que (t,0)=0, de ahí ∫ (t, 0)dt converge.
∂x 0 ∂x
1
∂ϕ ∂ϕ
- Para x ≠ 0, tenemos que Lim+ t 2 (t, x) = 0 y Lim t 2 (t, x) = 0. Pues según los
t →0 ∂x t →+∞ ∂x
+∞ ∂ϕ
criterios de Riemann, ∫ (t, x)dt converge.
0 ∂x
2- a- La desigualdad ∀u ∈ [0, +∞[, 0 ≤ 1-e-u ≤ u se obtiene estudiando la función :

u  e − u + u − 1 . Las otras no plantean dificultad.
+∞  −
x²

b- |f(x)-f(0)|= ∫ e − t² 1 − e t²  dt
0
 
x²
≤ ∫0 e− t² Min 1,  dt
+∞
 t² 
≤ ∫0 e− t² Min 1, x²  dt + ∫x e− t² Min 1, x²  dt
x +∞
 t²   t² 
≤ ∫0 e− t² dt + ∫x x² e− t² dt .
x +∞
t²
+∞ dt
Entonces ∀x ∈ [0,+∞[, |f(x) - f(0)| ≤ ∫ e -t² dt + x ² ∫
x
0 x t²
x
≤ ∫0 e− t² dt + x.
c- Por paso al límite, se deduce que f es continua en 0.
x
3- El cambio de variable es u= .
t
π − 2x
4- Se obtiene el resultado: ∀x ∈ [0, +∞[, f(x)= e integrando la ecuación diferen-
2
cial obtenida en el punto 3-de este ejercicio.
Ejercicio 15. Sea la función :

sen²(tx) +∞
F:x ∫ dt
t²(1+t²) 0
1- Demostrar que F está definida en  y es par.

2- Derivabilidad:
2-1- Demostrar la desigualdad siguiente:
∀(x, t, h) ∈ 3, sen² ( t(x+h) ) − sen²(tx) − thsen(2tx) ≤ h²t²
2-2- Mostrar que :
+∞ sen(2tx)
G:x ∫ dt
0 t(1+t²)
está definida en .
2-3- Estudiando:
F( x + h) − F( x)
Lim − G ( x) ,
h h→ 0
demostrar que F es derivable en , con derivada G.
Ejercicio 16.
+∞ dt
1- Mostrar que la integral I = ∫0 1+ t4
es convergente. Para la continuación, supone-
π 2
mos que I = .
4
+∞ dt
2 – Consideramos la integral J = ∫
0
t (1 + t² )
.
a- Mostrar que J es convergente.

b- Utilizar, después de haberle justificado, el cambio de variable u = t para calcular
el valor de J.
+∞ arctan(t)
3 - Para α > 0, consideramos la integral K(α) = ∫ dt .
0 tα
a- Para cuales valores de α la integral K(α) es convergente ?
3
b- Calcular K   .
2
Ejercicio 17.
1 t −1
1 – Porque la integral J = ∫0 ln(t)
dt puede ser considerada como una integral ordina-
ria?
x t x² 1
2-a- Mostrar que para todo x ∈ ]0,1[, ∫
0 ln(t)
dt = ∫
0 ln(u)
du .
−1 x
b- Deducir de eso que J = Lim− ∫ dt .
x →1 ln(t) x²
3 - Sea t ∈ ]0,1[. Determinar un encuadramiento de - ln(t) integrando las desigualdades

1 1
1 ≤ ≤ 2 para todo u ∈ [t, 1]..
u u
x −1
4 – Deducir de eso un encuadramiento de ∫ dt y el valor de J.
x ² ln(t)
Ejercicio 18.

+∞
1 - Mostrar la convergencia de I = ∫0
e − t ² dt .
1e − x (1+ t ² )
2 - Sea f la función definida en  por f (x) = ∫0 1 + t² dt .
a- Mostrar que Lim f (x) = 0.
x →+∞
1
b- Mostrar que f es derivable en  y que f '(x) = ∫ e − x (1+ t ² ) dt f(x) (podremos aplicar el
0
teorema de la media sobre el índice de incremento de f).
(∫ )
x 2
3 - Para x ∈ , definimos F(x) = f (x2) + e − t ² dt .
0
Mostrar que F es constante. Deducir de eso el valor de I.

Ejercicio 19. Estudiar la convergencia de las siguientes integrales (sin calcular sus valores):
1 ln (1 + t )
+∞ 1 ln x
J1 = ∫
1
J 2 = ∫ ( ln t ) dt
2
J3 = ∫ dx +∞
0 t
dt 0
2
x ( ln x )
5 J 4 = ∫2 x2
dx
J5 = ∫
+∞ (x 2
+ 1) dx
J6 = ∫
1 dt
J7 = ∫ 4
π
dt
J8 = ∫
1 ln t
dt
0
x4 + x2 +1
0
1− t2 0
tan t 0
t
1 arctant +∞ sin t
+∞ +∞
J11 = ∫ tα
+∞
J 9 = ∫ sin  2  dt J10 = ∫ dt 3
dt J12 = ∫ dt
1
t  2 t 3 + ln t 0
t 2 0 1+ t2
ln (1 + x α ) +∞
J14 = ∫ α
dt 1 1 +∞ sin x
J15 = ∫ sin  dx J16 = ∫
1
J13 = ∫ dx
0 xβ
dx 1
t (1 + t β ) 0
x 0 x
Corrección : Para estudiar la convergencia de cada una de las integrales propuestas, hay que
estudiar primero la continuidad de la función por integrar. Si la función no es continua en uno
de los límites, entonces hay un problema en ese límite y debemos resolver ese problema gra-
cias a los resultados conocidos. Sino no podemos hacer nada y la función se puede integrar.
1 ln (1 + t )
1- J1 = ∫ dt
0 t
ln (1 + t )
La función: t  es continua en ]0,1] . Tenemos un problema en 0.
t
t ln (1 + t ) t ln (1 + t )
Como, tenemos ln (1 + t )  t de donde  1 , la función: t  se puede enton-
0 t 0 t
1 ln (1 + t )
ces prolongar por continuidad en 0, y así la integral ∫ dt converge.
0 t
1
2- J 2 = ∫ ( ln t ) dt
2
0
La función: t  ( ln t ) es continua en ]0,1] . Tenemos un problemos en 0.

2
( ) ( ( )) → 0
2 2
t ( ln ( t ) ) =
2 1 1 1
Como, tenemos = t 4 ln ( t ) 4t 4 ln t 4 t →0
de donde
 1 
( ln ( t ) )
2
= o  .
 t
1
La función: t  t se puede integrar en 0, deducimos que la integral J 2 = ∫ ( ln t ) dt con-
2
0
verge.
+∞ 1
3- J 3 = ∫ dx
x ( ln x )
2 5
1
La función: x  es continua en [ 2, +∞[ . Tenemos un problema en +∞ .
x ( ln x )
5
1 3
x 4
x →∞ x 4
x →∞
Tenemos:  → +∞ , entonces  → +∞ , entonces de acuerdo con
( ln ( x ) ) x ( ln ( x ) )
5 5
el criterio de Riemann, esta integral diverge.

ln x
+∞
4- J 4 = ∫ dx
x2
2
ln x
La función : x  es continua en [ 2, +∞[ . Tenemos un problema en +∞ .
x2
ln x x →∞
( )
x
Como sabemos que  → 0 entonces ln x = o x .
x ∞
ln x x  1  1
Así, 2
= o  3  , y como: x  3 se puede integrar en la proximidad de +∞ , deduci-
x ∞
x 2  x 2
+∞ ln x
mos por un teorema de comparación que la integral J 4 = ∫ dx converge.
2 x2
2
+∞ x +1
5- J 5 = ∫ dx
0
x + x2 +1
4
x2 +1
La función : x  es continua en [ 0, +∞[ . Tenemos un problema en +∞ .
x4 + x2 +1
x2 +1 x x2 x
Tenemos:   1 > 0 , y como x  1 no se puede integrar en la proximidad
x 4 + x 2 + 1 +∞ x 4 +∞
+∞ x2 +1
de +∞ , deducimos por un teorema de comparación que la integral J 5 = ∫ dx no
0
x4 + x2 +1
converge.
1 dt
6- J 6 = ∫
0
1− t2
1
La función : t  es continua en [ 0,1[ . Tenemos un problema en 1.
1− t2
1 1 1 u 1 1
Tenemos= : =  > 0 , y como u  se puede inte-
1 − t 2 u = 1− t −u 2 + 2u u ( 2 − u ) 0 2u 2u
grar en la proximidad de 0, deducimos por un teorema de comparación que la integral
1 dt
J6 = ∫ converge.
0
1− t2
π
dt
7- J 7 = ∫ 4
0
tan t
1  π
La función : t  es continua en  0,  . Tenemos un problema en 0.
tan t  4
1 t 1 1
Tenemos :  > 0 , y c omo u  se puede integrar en la proximidad de 0, dedu-
tan t 0 t u
π
dt
cimos por un teorema de comparación que la integral J 7 = ∫ 4 converge.
0
tan t
1 ln t
8- J 8 = ∫ dt
0
t
ln t
La función : t  es continua ]0,1] . Tenemos un problema en 0.
t

3 ln t 1
t →0 ln t  1  1
Tenemos : t 4 × = t 4 × ln t  → 0 entonces = o  3  y como t  3 se puede
t t t 4  t 4
integrar en la proximidad de 0, deducimos por un teorema de comparación que la integral
1 ln t
J8 = ∫ dt converge.
0
t
+∞ 1
9- J 9 = ∫ sin  2  dt
1
t 
1
La función : t  sin  2  es continua en [1, +∞[ . Tenemos un problema en +∞ .
t 
1t 1 1
Tenemos : sin  2   2 > 0 , y como t  2 se puede integrar en la proximidad de +∞ , dedu-
t  t ∞ t
+∞ 1
cimos por un teorema de comparación que la integral J 9 = ∫ sin  2  dt converge.
1
t 
+∞ arctan t
10- J10 = ∫ 3 dt
2 t + ln t
arctan t
La función : t  3 es continua en [ 2, +∞[ . Tenemos un problema en +∞ .
t +lnt
arctan t t π 1
Tenemos : 3  3 > 0 , y como t  3 se puede integrar en la proximidad de +∞ ,
t + ln t 2t +∞ 2t
+∞ arctan t
deducimos por un teorema de comparación que la integral J10 = ∫ 3 dt converge.
2 t + ln t
+∞ sin t
11- J11 = ∫ 3
dt
0
t 2
sin t
La función : t  3 es continua en ]0, +∞[ . Tenemos un problema en 0 et en +∞ .
t 2
sin t 1 1
Tenemos : 3 ≤ 3 y como t  3 se puede integrar en la proximidad de +∞ , deduci-
t 2 t 2 t 2
sin t
mos por un teorema de comparación que t  3 se puede integrar en la proximidad de
t 2
+∞ .
sin t t t t 1 1
Por otro lado, tenemos 3  3  > 0 y como t  se puede integrar en la proximidad
0
t 2 t 2 0 t t
sin t
de 0, deducimos por un teorema de comparación que t  3 se puede integrar en la proxi-
t 2
midad de 0.
+∞ sin t
Finalmente, concluímos que la integral J11 = ∫ 3
dt converge.
0
t 2
α
+∞ t
12- J12 = ∫ dt
0 1+ t2
Hay que estudiar la convergencia en función del valor del parámetro α.

tα [0, +∞[ si α ≥ 0
Primero, tenemos : t  es continua en .
1+ t 2
]0, +∞[ sino
• α≥0 :
Tenemos un problema en +∞ .
t α t α− 2 1
Como tenemos :  t > 0 y t  t α− 2 = 2−α se puede integrar si y solamente si
2 +∞
1+ t t
2 − α > 1 lo que quiere decir si y solamente si α < 1 .
α
+∞ t
Deducimos que si 0 ≤ α < 1 , entonces la integral J12 = ∫ dt converge.
0 1+ t2
• α≤0 :
Tenemos un problema en +∞ et en 0.
En +∞ , tenemos lo mismo que antes, convergencia si y solamente si α < 1 que es el caso.
tα t α
En 0, tenemos :  t > 0 y esta función se puede intergar si y solamente si α > −1 .
1+ t2 0
α
+∞ t
Deducimos entonces que si −1 < α < 0 , entonces la integral J12 = ∫ dt converge.
0 1+ t2
α
+∞ t
Finalmente, concluímos que la integral J12 = ∫ dt converge si y solamente si
0 1+ t2
−1 < α < 1 .
1 ln (1 + x )
α
13- J13 = ∫ dx
0 xβ
ln (1 + x α )
La función : x  es continua en ]0;1] , hay un problema entonces en 0.
xβ
Buscamos un equivalente de esta función en 0, en función de los parámetros:
x ln (1 + x α ) x 1
Si α > 0 , lim x = 0 y tenemos ln (1 + x )  x , de donde
α α α
 β−α > 0 .
x →0 0 xβ 0 x
Así f se puede integrar en ]0;1] si y solamente si β − α < 1 .
ln (1 + x α ) x ln 2
Si α =0 , tenemos ln (1 + x ) = α
ln 2 , de donde  β >0.
xβ 0 x
Así f se puede integrar en ]0;1] si y solamente si β < 1 .
x
Finalmente, si α < 0 , lim x α = +∞ y tenemos ln (1 + x α )  ln x α =
α ln x , de donde
x →0 0
ln (1 + x α
)  α ln x > 0 .
x
β
x 0 xβ
Así f se puede integrar en ]0;1] si y solamente si β < 1 .
+∞ 1
14- J14 = ∫ dt
1
t (1 + t β )
α
Hay que estudiar la convergencia en función del parámetro α .

1
Primero, tenemos: t  es continua en [1, +∞[ .
t (1 + t β )
α
Tenemos un problema en +∞ .
1 t 1 1
Como tenemos : α  > 0 y t  α+β se puede integrar si y solamente si
t (1 + t ) t
β +∞ α+β
t
α + β > 1.
+∞ tα
Deducimos entonces la integral J14 = ∫ dt converge si y solamente si α + β > 1 .
0 1+ t2
1 1
15- J15 = ∫ sen  dx
0
x
1 1 1
Tenemos : ∫ sen   dx ≤ ∫ dx = 1 . Entonces, J 15 es absolutamente convergente.
0
x 0
1 1
Deducimos que la integral J15 = ∫ sen  dx converge.
0
x
+∞ sen x
16- J16 = ∫ dx
0 x
sin x
La función : x  es continua en ]0; +∞[ y se puede prolongar por continuidad en 0.
x
+∞ sen x
Basta con estudiar la convergencia de ∫ dx .
1 x
b
sen x b  − cos t  b cos t
Integrando por partes (hipótesis verificadas), tenemos : ∫1 x
= dx  t  ∫1 t 2 dt .
1
−
cos b +∞ sen x +∞ cos t

Como lim = 0 , las integrales ∫ dx y ∫ dt tienen misma naturaleza.
b →∞ b 1 x 1 t2
cos u 1 +∞ cos ( u )
Como tenemos : 2
≤ 2 en [1; +∞[ entonces ∫ du es convergente.
u u 1 u2
+∞ sen x
Concluímos que la integral J16 = ∫ dx es convergente.
0 x
+∞ ln x
Ejercicio 20. 1- Mostrar que la integral I = ⌠
 dx es convergente.
⌡0 (x+2)²
2- Con ayuda de una integración por partes, determinar una primitiva de F en
ln x
]0; +∞[ de la función .
( x + 2)
2
3- Determinar los límites de F(x) cuando x tiende hacia 0+ y hacia + ∞. Deducir la

valor de I.
ln x
Corrección : La función : x  es continua en ]0, +∞[ . Tenemos entonces un pro-
( x + 2)
2
blema en 0 y uno en +∞ .

3 ln x x ln x x →+∞
En +∞ , tenemos x 2
 → 0 , entonces de acuerdo con el criterio de Rie-
( x + 2)
2 +∞
x
mann, deducimos que la función se puede integrar en +∞ .
ln x x 1
En 0, tenemos  ln x > 0 , y x  ln x se puede integrar en 0 (aplicar el criterio de
( x + 2) 0 4
2
Riemann). Finalmente, la integral I es convergente.

x ln t
2- Sea F la primitiva de f que vale 0 en 1, tenemos entonces: F ( x ) = ∫ dt .
( t + 2)
1 2
1
Vamos a hacer una integración por partes, llamando:
= t y v′(t)
u(t) ln= , entonces
( t + 2)
2
1 1
u ′(t) = y v(t) = − . Las funciones u y v son de clase C1.
t ( t + 2)
x
x ln t  ln t  x −1 ln x x 1
Obtenemos: ∫ dt =  −  −∫ dt =
− +∫ dt .
1
( t + 2)
2
 ( t + 2 ) 1 (
1 t t+2
) ( x + 2 ) (
1 t t+2
)
1 1 1 1 
Es fácil verificar que : =  −  , tenemos entonces:
t ( t + 2) 2  t t + 2 
x 1 1 x1 1  1 x1 1 x 1 1 1
dt = [ ln t ]1 − ln ( t + 2 ) 1
x x
∫1 t ( t + 2)
dt = ∫  −
1 
2  t t+2
dt = ∫ dt − ∫
2 t
1 2 t+2
1 2 2
1 1 1
=ln x − ln ( x + 2 ) + ln 3
2 2 2
ln x 1 1 1
Finalmente, obtenemos: F ( x ) = − + ln x − ln ( x + 2 ) + ln 3
( x + 2) 2 2 2
ln x 1 1 1
3- De acuerdo con la pregunta anterior, F ( x ) =− + ln x − ln ( x + 2 ) + ln 3 .
( x + 2) 2 2 2
ln x 1 x 1
Por una lado, esto puede escribirse F ( x ) =
− + ln + ln 3 y así tenemos :
( x + 2) 2 x + 2 2
1
ln 3 lim F ( x ) =
2 x →+∞
x 1 1
Por otro lado, podemos también escribir
= : F(x) ln x − ln ( x + 2 ) + ln 3 y así:
2 ( x + 2) 2 2
x  1 1 1 1
lim F ( x ) = lim  ln x  − ln ( 2 ) + ln 3 = − ln ( 2 ) + ln 3
x →0 4
x →0
  2 2 2 2
F siendo una primitiva de f, tenemos :
+∞ 1  1 1  1
∫0 f ( x ) =
dx lim F ( x ) − lim+ F (=
x →∞ x →0
x)
2
ln 3 −  − ln ( 2 ) + ln=
 2 2
3
 2
ln ( 2 )
1
De donde finalmente: I = ln ( 2 ) .
2

Capítulo 19
ESPACIO VECTORIAL
Grassmann Hermann Günther (alemán, 1809-1877) fue

profesor de matemáticas en Stettin (entonces ciudad prusiana, en
Pomérania, sobre el estuario de l'Oder, hoy polonesa: Szczecin),
Phísico y linguista (estudió el sanskrit). Estudiando el fenómeno de
las mareas, fue llevado a desarollar el cálculo vectorial. Sus trabajos
portan esencialmente sobre el nuevo concepto de espacios vectoriales
abstractos de dimensión superior a 3.Publicósus resultados en 1844
en un tratado titulado « La ciencia de los grandores extensivos o de la
teoría del espacio » (completada en 1863). En la misma época, el
irlandés Hamilton introdujo el concepto moderno de vector.
Le debemos las primeras nociones :
• de independencia lineal;
• de suma de sub-espacios;
• de producto lineal, correspondiendo al producto escalar actual :
• de producto exterior, que se convertirá, en dimensión 3 , con Gibbs y Clifford,
en nuestro producto vectorial usual;
• El importate teorema de las dimensiones, que lleva su nombre:
Dim(F+G)=Dim(F) + Dim(G) – Dim(F  G)
Pero es sobre Peano que recaerá el mérito de definir de manera axiomática y más clara el
concepto de espacio vectorial sobre un cuerpo de escalares.
1- Espacio vectorial
Definición : Sea  un cuerpo conmutativo igual a  o a .

Un espacio vectorial en  (o -espacio vectorial) es un conjunto E provisto de una ley in-
terna + (es decir una aplicación de E × E en E) y de una ley externa × (es decir una aplicación de
 × E en E)que comprueba que
- (E,+) es un grupo conmutativo

- ∀(k1 , k 2 ) ∈², ∀u ∈ E, (k1 + k 2 ) × u = k1 × u + k 2 × u
- ∀k ∈ , ∀(u1 , u 2 ) ∈ E², k × (u1 + u 2 ) =k × u1 + k × u 2
- ∀(k1 , k 2 ) ∈², ∀u ∈ E, k1 × (k 2 ×=
u) (k1k 2 ) × u
- ∀u ∈ E , 1 × u=u
Los elementos de  son llamados escalares, y los elementos de E son llamados vecto-
res.
Es fácil verificar que n, el conjunto de sucesiones o el conjunto de funciones consti-

tuyen un espacio vectorial. De hecho, la definición serviría sólo para esos conjuntos de base.
Otros criterios son enseguida utilizados para mostrar que un conjunto es un espacio vectorial.
En lo que concerne la regla « 1 × u=u », hay que tomar consciencia que la regla no vie-
ne de ella misma. 1 es el neutro del producto de , no hay ninguna razón para que adopte una
actitud comparable en lo que implica el producto externo. Es el único resultado de un produc-
to por un escalar que es dado por los axiomas.
Resultan axiomas que :

a- ∀u ∈ E, 0 × u=0 E
donde 0 es el neutro de (,+) y 0 E el neutro de (E,+).
b- ∀k ∈ , k × 0 E = 0 E
c- (-1) × u = -u où -1 es el simétrico de 1 en (,+) y -u el simétrico de u en (E,+).
d- k × u = 0 E ⇒ k= 0 o u = 0 E
Demostración :
a- l × u = u =(1+0) × u = 1 × u+0 × u = u+0 × u ⇒ u = u+0 × u ⇒ 0 × u = 0 E
b- k × 0 E = k × (0 × u) = (k.0) × u = 0 × u = 0 E
c- 0 E = 0 × u = [1 + (-1)] × u = u + (-1) × u ⇒ (-1) × u = -u
1 1
d- Si k × u = 0 E y si k ≠ 0, entonces × (k × u) = × 0 E ⇒ 1 × u = 0 E ⇒ u = 0 E .
k k
2- Subespacio vectorial
Definición: Sea E un -espacio vectorial y F una parte de E.

F es un subespacio vectorial de E si y solamente si F es un -espacio vectorial (provisto de
las leyes inducidas por las leyes de E).
Teorema: Sea E un -espacio vectorial y F una parte de E.

F es un subespacio vectorial si y solamente si:
1- F no está vacío
2- F es estable para la ley interna de E
3- F es estable para la ley externa de E
Ejemplo:

Sea E=3 considerado como un -espacio vectorial.
Entonces P definido por su ecuación cartesiana: 3x+2y+z=0 es decir
P={(x,y,z) ∈ 3/3x+2y+z=0}es un subespacio vectorial de E.
 x + y + 2z =0
Así mismo, D definido por  , es decir D= {(x,y,z) ∈ 3/x+y+2z=0 ∧ x-y-
 x−y−z = 0
z=0}es un subespacio vectorial de E.
Teorema: La intersección de 2 subespacios vectoriales de E es un subespacio vectorial de E.
Observación: La reunión de 2 subespacios vectoriales de E no es en general, un subespacio

vectorial de E. (ver ejercicio).
3- Subespacio vectorial engendrado
Definición: Sea E un -espacio vectorial y A una parte no vacía de E. El subespacio vecto-

rial engendrado por A es el más pequeño subespacio vectorial de E que contiene A.
Se escribe Vect(A) (o A ).
Observación: Vect(A)=  F .
F sev
A⊂F
Teorema: Sea E un -espacio vectorial y x1 ,…,x n unos elementos de E.

Vect({x1 ,…,x n}) es el conjunto de las combinaciones lineales de x1 ,…,x n .
n 
Vect({x1 ,…,x n})= ∑ λ i x i / ∀i=1 à n, λ i ∈  
 i =1 
4- Suma de dos subespacios vectoriales
Definición: Sean F y G dos subespacios vectoriales de un espacio vectorial E.

Se da F+G={v 1 +v 2 /v1 ∈ F, v 2 ∈ G}.
Teorema: Con las notaciones anteriores, F+G es un subespacio vectorial de E.
Teorema: F+G es el más pequeño subespacio vectorial de E que contiene F y G:

F+G=Vect(F  G)
Definición: Sean F y G dos subespacios vectoriales de un espacio vectorial E.

Se dice que la suma F+G es directa si por definición F  G={0 E }. Se escribe entonces F ⊕ G.
Teorema: La suma F+G es directa si y solamente si todo vector de F+G se descompone de

manera única como la suma de un elemento de F y de un elemento de G.
Ejemplo 1 :

E=3. Tenemos i=(1,0,0), j=(0,1,0) et k=(0,0,1).Tenemos E=Vect({i,j,k}).
Sean F=Vect({i, j – i}) y G=Vect({k, j + k})
La suma no es directa puesto que :
-i+j+k= − j+k = −
i+  i+ j+ k
∈F ∈G ∈F ∈G
Ejemplo 2 :
E=3. Tenemos i=(1,0,0), j=(0,1,0) et k=(0,0,1).Tenemos E=Vect({i,j,k}).
Sean F=Vect({i, j + k}) et G=Vect({j - k – i}).
La suma F+G es directa y F+G=3 puesto que :
xi +yj+zk= 1 (y+2x z)i+ 1 (y+z)(j+k)+ 1 (y-z)(j-k-i)
2 2 2
y no hay otra posibilidad.
Remarca : En los 2 ejemplos precedentes es màs fàcil de demostrar que la suma es directa si
se determina que F  G.
Definición: Sean F y G dos subespacios vectoriales de un espacio vectorial E. F y G son su-

plementarios si por definición F ⊕ G=E.
5- Familias libres, familias vinculadas
Definición: Sea E un -espacio vectorial. Sea {v 1 , v2 ,…,v p } una familia de p vectores de E.

La familia {v1 , v 2 ,…,v p } es libre si por definición toda combinación lineal nula de sus vecto-
res, tiene todos sus coeficientes nulos.
p
∀ ( λ i )i =1 à p ∈ p, ∑ λ v=
i =1
i i 0E ⇒ ∀=
i 1 à p, λ=
i 0
Se dice entonces que los vectores de esta familia son linealmente independientes.
Una familia que no es libre se llama vinculada..

Se dice mientras que los vectores de esta familia son linealmente dependientes.
p
∃ ( λ i )i =1 à p ∈ p, ( λ i )i =1 à p ≠ (0, 0,..., 0) ∧ ∑λ v
i =1
i i 0E
=
Observación : No confundir no todos nulos y todos no nulos.
Propiedades: 1- Toda familia extraída de una familia libre es una familia libre.
2- Toda familia que contiene una familia vinculada está vinculada.
3- Toda familia que contiene 0 E está vinculada.
4- En una familia vinculada, existe (al menos) un vector que puede expresar-
se como combinación lineal de los demás.
6- Familias generatrices
Definición: Sea E un -espacio vectorial. Sea {v 1 , v2 ,…,v p } una familia de p vectores de E.

La familia {v 1 , v 2 ,…,v p } es generatriz si por definición todo elemento de E puede escribirse
como una combinación lineal de los elementos de esta familia.
p
∀v ∈ E, ∃ ( λ1 ,..., λ p ) ∈ p/v= ∑ λ i vi
i =1
Observación : 1- La familia {v 1 , v 2 ,…,v p } es generadora de E si y solamente si

E=Vect({v1 ,v2 ,…,v p}).
2- Sean F y G dos sub-espacios vectoriales de un espacio vectorial E con
F=Vect({u 1 ,u 2 ,…,u p }) y G=Vect({v1 ,v 2 ,…,v q }).
Entonces, F+G=Vect({u 1 ,u 2 ,…,u p,v 1 ,v 2 ,…,v q }).
Dicho de otra manera, la reuniôn de una familia generadora de F y de una familia generadora
de G es una familia generadora de F+G
Teorema: Sea E un -espacio vectorial no reducido a {0 E }.

Si E posee una familia generatriz finita, entonces se puede extraer de esta familia a una fami-
lia generatriz y libre.
7- Bases
Definición: Sea E un -espacio vectorial. Una base de E es una familia libre y generatriz.
Aplicaciones: 1- Reanudar el ejemplo del apartado 2 y determinar una base de P y una base
de D.
2- Sea E=3 considerado como un -espacio vectorial.
 x + y − 2z =
0

Sea F, definido por 2x − y + z =0 . Mostrar que F es un subespacio vectorial de
8x − y − z =0

E. Determinar una base de F.
8- Dimensión
Definición: Un espacio vectorial E esta dicho de dimensión finito si él posee una familia ge-
neratriz finita.
En el caso contrario, E esta dicho de dimensión infinita.
Teorema: Sea E un -espacio vectorial de dimensión finita. Todas las bases de E tienen el
mismo número de elementos. Este número es la dimensión de E, escrita Dim(E).
Convención: Dim({0 E })=0.
Teorema: Sea E un -espacio vectorial de dimensión finita y F un subespacio vectorial de E.

- F es de dimensión finita y Dim(F) ≤ Dim(E).
- Dim(F)=Dim(E) si y solamente si E=F.

9- Caracterización de una base de dimensión finita
Teorema. Sea E un -espacio vectorial de dimensión finita n.

1- Toda familia libre de E posee un máximo de n elementos
2- Toda familia generatriz de E posee al menos n elementos
3- Toda familia libre de E que tiene n elementos es una base de E
4- Toda familia generatriz de E con n elementos es una base de E.
En la práctica, los puntos3 y 4 se utilizan así:

Sea E un -espacio vectorial de dimensión n y sea F una familia de vectores de E.
Les siguientes propiedades son equivalentes :
1- F es una base de E
2- F es una familia libre de n vectores
3- F es una familia generadora de n vectores
Definición: Sea E un -espacio vectorial de dimensión finita "n" y sea B=(e1 ,…,e n) una
base de E.
n
∀u ∈ E, ∃!(x1 ,..., x n ) ∈ n /u= ∑ x i ei
i =1
(x1 ,…,x n ) son los componentes de u en la base B.
Teorema de la base incompleta:

Sea E un -espacio vectorial de dimensión finita n que no es nulo de base B=(e 1 ,…,e n ).
Sea S={u 1 ,…,u p } una familia libre de p vectores. (p ≤ n).
S puede completarse por (n-p) vectores de la base B para formar una base de E.
Ejemplo : Sea E=4 abastecido de la base canónica (e 1 , e 2 , e 3 , e 4 ). Consideramos los vecto-
res w 1 (1, 2, 0, 0) y w 2 =(-1, 1, 0, 0). {w 1 ,w 2 } es un sistema libre.
Complétons le en une base de 4.
{w 1 ,w 2 ,e 1 } está ligado.
{w 1 ,w 2 ,e 2 } está ligado.
{w 1 ,w 2 ,e 3 } está libre.
{w 1 ,w 2 ,e 3 ,e 4 } está libre, entonces es una base de 4.
Teorema. Formula de Grassmann: Sea E un -espacio vectorial.

Sean F y G dos subespacios vectoriales de E de dimensión finita.
Entonces Dim(F+G)=Dim(F) + Dim(G) – Dim(F  G).
Prueba:
1- Si F  G={0 E } :
Sea (f) i=1àn una base de F y (g j ) j=1àm una base de G.
Entonces, F+G=Vect{f1 ,…,fn ,g 1 ,…,g m}.
Mostremos que {f1 ,…,fn ,g 1 ,…,g m }es una familia libre.
n m n m n m
∑α f
i =1
i i + ∑ β i g i =0 E ⇒
i =1
i i
=i 1 =i 1
∑α f =−∑ βi g i ∈ F  G . Por lo que ∑α f
i =1
i i = −∑ β i g i = 0 E.
i =1

Se deduce que para i=1 hasta n, α i =0 y para i=1 hasta m, β i =0. De lo cual se deduce el resul-
tado.
2- Si F  G ≠ {0 E } :
Sea (e i ) i=1àn una base de F  G, completar (refiéranse al teorema de la base incompleta) en una
base (e 1 ,…,e n ,ε 1 ,…,ε q) de F y (e 1 ,…,e n ,ν 1 ,…,ν p ) de G.
Sea H el subespacio vectorial de E con base (ν 1 ,…,ν p ).
Mostremos que F  H={0 E } (para utilizar el punto 1-).
Sea "u" elemento de F  H.
n q p
∃(α i )i =1àn ∈ n ∃(βi )i =1àq ∈ q/ u= ∑ α i e i + ∑ β i ε i (1) et ∃( γ i ) i =1àp / u = ∑γ ν i i (2).
i =1 i =1 i =1
Entonces u es elemento de G (por ejemplo como combinación lineal de elementos de G) y de
F.
n
Entonces, ∃(λ i )i =1àn ∈  : u= ∑ λ i e i (3).
n
i =1
n q
Realizando la igualdad entre (1) y (3), se deduce que ∑ (α i − λ i )e i + ∑ β i ε i =0 E .
i =1 i =1
Como (e 1 ,…,e n ,ε 1 ,…,ε q ) es una base de F (por lo tanto libre), se tiene que para toda i=1 hasta
q, β i =0.
n
(1) Se transforma en u= ∑ α i e i (4).
i =1
p n
Realizando la igualdad entre (4) y (2), se deduce que ∑ γ i ν i - ∑ α i e i =0E .
i =1 i =1
Como (e 1 ,…,e n ,ν 1 ,…,ν p ) es una base de G (por lo tanto libre), se tiene que para toda i=1 has-
ta n, αi =0 y que para toda i=1 hasta p, γ i =0.
Entonces u=0 E .
Se obtiene así que Dim(F+H)=DimF + Dim H.

Lo que da F+H=F+G (familia generatriz de igualdad).
Así Dim(F+G)=n+q+p=(n+q)+(p+n)-n=DimF + DimG – Dim(F  G).
De donde se deduce el resultado.
Teorema. Sea E un -espacio vectorial de dimensión finita.

Sean F y G dos subespacios vectoriales de E.
Las propiedades siguientes son equivalentes:
1- E=F ⊕ G
2- E=F+G y Dim(E)=Dim(F) + Dim(G)
3- F  G={0 E } y Dim(E) = Dim(F) + Dim(G)
10- Rango de una familia de vectores
Definición: Sea E un -espacio vectorial.

Sea F={v1 ,…,v p } una familia de p vectores de E.
El rango de F es la dimensión de Vect({v1 ,…,v p }).

Notación: rg(F).
Observación: rg(F) ≤ p.
Propiedad: rg(F)=p si y solamente si F es libre.
Consecuencia : Sea E un -espacio vectorial de dimensión finita n y sea F={v1 ,…,vn } una
familia de n vectores de E.
rg(F)=n si y solamente si F es una base de E
Método de los ceros escalonados

Propiedades:
1- rg({v1 ,…,v p})=rg({λ 1 v1 ,…,v p }) con λ 1 elemento de *
 p

2- rg({v1 ,…,v p})= rg   v1 + ∑ λ i vi , v 2 , ..., v p   con λ 2 ,…,λ p elementos de 
 i=2 
3- rg({v1 ,…,v p})=rg({v1 ,…,v p ,0 E })
4- El rango de una familia de vectores no depende del orden de los vectores.
Aplicaciones:
Sea E=3 provisto de su base canónica (i,j,k).
1- Sean u=(0,1,1), v=(1,1,1), w=(-1,1,2) y n=(1,2,0).

Mostrar que rg({u,v,w,n}) es 3. Determinar una base de E formada con ayuda de los vectores
u, v, w, n.
2- Sean a=(1,1,0), b=(1,2,1), c=(5,8,3) y d=(-1,-4,-3).
Sea F=vect({a, b, c, d}).
Determinar una base de F formada con ayuda de los vectores a, b, c, d.

Ejercicio 1. En 2, definimos las dos siguientes leyes de composición:

∀ ((x,y) ,(x’,y’)) ∈ 2 × 2, (x,y) + (x’,y’) = (x+x’ ,y+y’)
∀λ∈, λ•(x,y) =(λ2x,λ2y)
(2, +, • ) es un espacio vectorial real ?
Ejercicio 2. En 2, definimos las dos siguientes leyes de composición:

∀ ((x,y), (x’,y’)) ∈ 2 × 2, (x,y) + (x’,y’) = (x+x’,y+y’)
∀λ∈, λ(x,y) =(λx,0)
2
( , + ,  ) es un espacio vectorial real?
Ejercicio 3. EnE =+* × , definimos las dos siguientes leyes de composición:

∀ ((x,y), (x’,y’)) ∈ E2, (x,y) ⊕ (x’,y’) = (xx’,y+y’)
∀λ∈, λ(x,y) =(xλ,λy)
(E, ⊕ ,  ) es un espacio vectorial real?
Ejercicio 4. Los siguientes sub-conjuntos son de sub-espacios vectoriales de (3, + , . ) ?

1- F1 = { (x,y,z) ∈ 3/z = 0}
2- F2 = { (x,y,z) ∈ 3/x<0}
3- F3 = { (x,y,z) ∈ 3/x =1}
4- F4 = { (x,y,z) ∈ 3/x = y e y = 2z}.
Ejercicio 5. Los siguientes sub-conjuntos de [X] son de sub-espacios vectoriales ?

1- F1 = { P ∈ [X] / P(0) = 0}
2- F2 = { P ∈ [X] / P= 0 donde deg (P)  2}
3- F3 = { P ∈ [X] / P(0) = P(1)}
4- F4 = { P ∈ [X] / P+P’ = 1}.
Ejercicio 6. En 3, el vector V=(1,2,3) pertenece al sub-espacio vectorial F 1 engendrado por:

V 1 =(0,1,0) y V 2 = (1,1,1) ?
Misma pregunta con F2 engendrado por V 3 =(-1,-1,0) y V 4 = (0,1,3) ?
Ejercicio 7. En 2, mostrar que F1 ={(x,x) / x ∈ } y F2 ={(x,-x) / x ∈ }son suplementarios.
Ejercicio 8. En 3, los siguientes sistemas son libres? Generadores de 3 ? bases de 3 ?

S 1 = {(1,0,0) (0,1,0)}, S 2 = {(0,0,0) ; (1,0,0) ; (0,1,0) ; (0,0,1)}, S 3 = {(1,2,3)},

S 4 = {(1,1,0) ; (0,1,1) ; (1,0,1)}.
Ejercicio 9. En  conjunto de funciones de  en , los siguientes sistemas son libres o liga-

dos ?
 1   1 
F1 ={cos, sin}, F2 = exp,  , F3 = exp, , ch 
 exp   exp 
Ejercicio 10. 1- Determinar dim( 4 [X]).

2- Determinar dim(E) con E ={acos+bsin / (a,b) 2}
Ejercicio 11. En 3, determinar una base de F = {(x,y,z) ∈ 3 / x = y = 2z}.

EJERCICIOS
Ejercicio 1. el conjunto 2 proveniente de las operaciones ⊕ y  definidas debajo, es un -

espacio vectorial ?
1. (x ; y) ⊕ (x’ ; y’) = (y + y’ ; x + x’) et α  (x ; y) = ( α y ; α x).
2. (x ; y) ⊕ (x’ ; y’) = (x + x’ ; y + y’) et α  (x ; y) = ( α x ; α y).
3. (x ; y) ⊕ (x’ ; y’) = (x + x’ ; y + y’) et α  (x ; y) = ( α x ; 0).
Ejercicio 2. los siguientes subconjuntos 2 son subespacios vectoriales ?

A
= {( x, y ) ∈  2
= 0}
/ 3x − 2y B
= {( x, y ) ∈  2
= 1}
/ 3x − 2y C ={( x, y ) ∈ 2 / xy ≥ 0}
D = {( x, y ) ∈  2
/ x = 0} E= {( x, y ) ∈  2
/ x ≤ y} F= {( x, y ) ∈  2
/ x < 0}
Ejercicio 3. Dentro de los siguientes subconjuntos [X], precisar aquellas que son un sub-
espacios vectoriales :
G1 = {P ∈  [ X ] / deg ( P ) =
3} G2 = {P ∈  [ X ] / deg P ≤ 3}  {0[X]}
{P ∈  [ X ] / P ( 0 ) =
G3 = 0}
P (1) = {P ∈  [ X ] / P ( 2 ) =
G4 = 2P (1)}
Ejercicio 4. Sea F(,) el conjunto das aplicaciones de  en . Admitimos que F(,) es

un -espacio vectorial. Indicar los subconjuntos de F(,) de los subespacios vectoriales
siguientes.
F1 {f :  →  / ∀x ∈ , f ( −=
= x ) f ( x )} F2 ={f :  →  / ∀x ∈ , f ( − x ) =−f ( x )}
F3
= {f :  →  / ∀x ∈ , f ( x ) ≥ 0} F4
= {f :  →  / ∀x ∈ , f (=
x ) 0}
Ejercicio 5.
Los sub-conjuntos siguientes del conjunto  das aplicaciones de  en  son sub-espacios
vectoriales de  ?
F1 = { f∈  / f (1) + f (-1) = 0 }
F2 = { f∈  / f (1) + f (-1) = 1 }
F3 = { f∈  / ∀x∈, f (2x) = f (x) }
F4 = { f∈  / ∀x∈, f (x -1) = f (x )- f (1) }
Ejercicio 6. Los siguientes conjuntos son -espacios vectoriales?

E = { f :  →  / f(1) = 1}
F = { f :  →  / f(1) = 0}
G = {f : *+ →  / ∃(α, β) ∈ ², ∀x ∈ *+, f(x) = αex+βln(x)}
Ejercicio 7. Sean F1 y F2 dos subespacios vectoriales de un espacio vectorial E dado.

a - Determinar una condición necesaria y suficiente para que F = F1 ∪ F2 sea un subes-
pacio vectorial de E.
b - en el caso general, poner de manifiesto que F1 + F2 es el más pequeño subespacio
vectorial de E que contiene F.
Ejercicio 8. E 1 , E 2 , E 3 son tres subespacios vectoriales de un espacio vectorial E. Demostrar

que (E 1 ⊂ E 3 ) ⇒ [E 1 + (E 2 ∩ E 3 ) = (E 1 + E 2 ) ∩ E 3 ].
Ejercicio 9. E 1 , E 2 , E 3 son tres subespacios vectoriales de un espacio vectorial E que prue-

ban que E 1 + E 3 = E 2 + E 3 ; E 1 ∩ E 3 = E 2 ∩ E 3 ; E 1 ⊂ E 2 . Mostrar que E 1 = E 2 .
Elementos de respuesta.
Basta con poner de manifiesto que E 2 se incluye en E 1 .
Sea x un elemento de E 2 .
Por ello, x es elemento de E 2 + E 3 .
Entonces, x es elemento de E 1 + E 3 .
Existe entonces x1 elemento de E 1 y x3 elemento de E 3 tales que x=x 1 +x 3 .
Como x1 es elemento de E 1 , es también elemento de E 2 .
Entonces x3 =x- x1 es elemento de E2.
Además x 3 es elemento de E 2 ∩ E 3 , por lo tanto también de E 1 ∩ E 3 .
Por ello, x3 es elemento de E 1 .
Como x=x1 +x3 , x es elemento de E 1 .
De donde se llega al resultado.
Ejercicio 10. Sea  considerado como -espacio vectorial.

a- {3 , 5} ¿es una familia libre o generatriz?
{ }
b- 1, 2 ¿es una familia libre o generatriz?
c- {1, 2, 3} ¿es una familia libre?
Ejercicio 11. Dentro de las siguientes familias de elementos de E, precisar aquellas que son
libres, generatrices, bases :
1. E = 2 A = {(1, 2 ) , ( 2,3) , ( 3, 4 )}
2. E =  3 [X] {
B = 1, ( X - 2 ) , ( X - 3) , ( X - 4 )
2 3
}
3. E = C∞ () C = {f1 : x  cos ( x ) , f 2 : x  cos ( 2x ) , f 3 : x  cos ( 3x )}
Ejercicio 12. Sea un -espacio vectorial E.

1- Demostrar que si los vectores v1 y v 2 de E son de manera lineal independientes,
ocurre lo mismo para los vectores v1 + v 2 et v1 - v2 .
2- Demostrar que si los vectores v1 , v2 y v 3 son lineal independientes, ocurre lo mis-
mo con v 1 + v2 + v 3 , v1 - v2 + v3 y v 1 + v 2 - v 3 .
3- Sea E= 3 [X]. Mostrar que {1, X - 1, X3 +X2 - 1, (X2 - 1)(X - 1)} es una base de E.

Ejercicio 13. Considerando como -espacio vectorial y siendo z un elemento de , ¿cuál
es la condición para que (z, z ) sea una base de  ?
Escribir u = x + iy (con "x" e "y" reales) en dicha base (con z = α + iβ).
Ejercicio 14. Consideramos los tres vectores de 3 :

v1 = (1,1,1) ; v2 = (-1,2,3) ; v3 = (7,-8,-13)
1- Determinar el rango de la familia {v 1 ,v 2 ,v 3 }. Dar una combinación lineal nula, con
coeficientes no todos nulos, de esos vectores.
2- Sea F el subespacio vectorial engendrado por {v1 ,v2 ,v3 }. Determinar una base de F.
3- Sea G = {(x,y,z) ∈ 3/x – 4y + 3z = 0}. Mostrar que G es un subespaio vectorial de
3. Daru na base de G.
4- Mostrar que F y G son iguales.
Ejercicio 15. En el -espacio vectorial de las aplicaciones de  en , mostrar que si

λ1 , λ 2 , λ 3 , son tres reales distintos 2 à 2 , la familia de las aplicaciones x  e λ1x , x  e λ2 x ,
x  e λ3x es libre.
Ejercicio 16. En 4, damos los vectores :

a=(1,2,0,1), b=(2,1,3,1), c=(2,4,0,2), t=(1,2,1,0), u=(-1,1,1,1), v=(2,-1,0,1), w=(2,2,2,2)
F es el subespacio engendrado por a, b y c. G es el subespacio engendrado por t, u, v y w.
Encontrar una base de F, una base de G, una base de F+G y una base de F  G .
Ejercicio 17. En el espacio vectorial 4, se considera que

V1 = (1,2,0,1) ; V2 = (1,0,2,1) ; V3 = (2,0,4,2) ; W1 = (1,2,1,0) ; W2 = (-1,1,1,1)
W3 = (2,-1,0,1) ; W4 = (2,2,2,2).
1- Demostrar que las siguientes familias son libres
{ V1 ,V2 } ; { W1 ,W2 ,W3 } ; { V1 ,V2 ,W1 ,W2 }.
2- Sea E el subespacio vectorial de 4 engendrado por { V1 ,V2 ,V3 }.
a- Determinar una base de E.
b- Determinar un espacio suplementario a E.
3- Sea F el subespacio vectorial de 4 engendrado por { W1 ,W2 ,W3 ,W4 }. Determinar
una base de F.
4- Determinar E + F.
5- a- Mostrar que V1 + V2 ∈ E ∩ F .
b- Determinar una base de E ∩ F.
Ejercicio 18. Sean F={(x,y,z) ∈ 3/x+y+z=0} y G={(x,y,z) ∈ 3/x-y=0 ∧ x+z=0}.

1- F y G son subespacios vectoriales de 3 ?
2- Son subespacios vectoriales suplementarios?
Ejercicio 19.
1- Determinar una base del subespacio vectorial de 4 definido por :
E 1 = {(a,b,c,d) ∈ 4, a = 2b-c et d = a+b+c}.
2- Anotamos E 2 = Vect{(3,1,0,3),(-1,1,1,0)}.

Mostrar que E 1 y E 2 son suplementarios en 4.
Ejercicio 20. Sea E el sub-conjunto de 4 determinado por :

 3x + 2 y − 4 z + t = 0

x + y + z − t = 0
2 x + y + 2 z + 2 t = 0

Demostrar que E es un sub-espacio vectorial. Cual es la dimensión de E? Determinar una base
de E.
Ejercicio 21. Sea (Pn ) n una secuencia de polinomios de [X] tales que para todo entero n, el
grado de Pn es n. Mostrar que para todo entero n, {Pi }i = 0 à n es una parte generatriz de  n [X].
Deducir que es une base de  n [X].
Ejercicio 22.
1. Demonstrar que la familia  = ((0,1,2),(-1,0,1),(3,2,0)} es una base de 3.
2. Cuáles son las coordenadas del vector u = (0,2,1) en la base canónica de3 ?
Cuáles son las coordenadas del vector u = (0,2,1) en la base  ?
Ejercicio 23. Sean α 0 , α 1 ,..., α n (n+1) reales distintas de dos en dos (n ∈ *).
Se considera k como un entero comprendido entre 0 y n : P k = ∏ (X − α ) .
i =0 à n
i
i≠k
a- Mostrar que ( P0 , P1 ,..., Pn ) es una base del espacio vectorial  n [X].

b- Sea P un elemento de  n[X]. Determinar las componentes de P en la base
( P0 , P1 ,..., Pn ).
Ejercicio 24. E es el conjunto de aplicaciones de  en  provisto de su estructura de espacio

vectorial en .
a- Sea G = { f: → / ∃(a, b, c) ∈ 3, ∀ x∈, f(x) = a.cos(x) + b.sen(x) + c.sen(x).cos(x)}.
Mostrar que G es un subespacio vectorial de E cuya dimensión debe precisarse.
b- Sea H={f: → / ∃(a, b, c) ∈ 3, ∀ x∈, f(x) = a.cos(2x) + b.sen(2x) + c.sen(2x).cos(2x)}.
Mostrar que H es un subespacio vectorial de E cuya dimensión debe precisarse.
¿Cuál es la dimensión de (G∩H)?
c- Determinar la dimensión, enseguida una base de (G + H).
Ejercicio 25. E es el -espacio vectorial formado por secuencias de números complejos.

Sean “p” y “q” dos números complejos que no son simultáneamente nulos. Se llama S al con-
junto de secuencias (u n ) n tales que :
∀n ∈ , u n + 2 + p.u n +1 + q.u n =
0
a- Mostrar que S es un subespacio vectorial de E cuya la dimensión se va a determinar.
b- Si p²- 4q ≠ 0, encontrar dos secuencias de S linealmente independientes cuyo
término general tiene la forma s n . Para (u n ) n elemento de S, expresar u n en función de
u 0 , u 1 ,p, q, n.

c- Si p²-4q = 0, existe una secuencia única de S que no es nula, con término general de
la forma s n . Determinar s. Mostrar que las sucesiones v y w con término general s n y n s n son
elementos de S. Determinar una base de S y escriban la forma general de un elemento de S.
Ejercicio 26. Determinar el rango de la familia { a1 ,a 2 ,a 3 ,a 4 } de vectores de 5 referenciada

con respecto a su base canónica ( e1 ,e 2 ,e3 ,e 4 ,e5 ) con
 a1 = 2e1 + 3e 2 -3e3 +4e 4 +2e5
a = 3e1 +6e 2 -2e3 +5e 4 +9e5
 2

a 3 = 7e1 +18e 2 -2e3 +7e 4 +7e5
a 4 = 2e1 + 4e 2 -2e3 +3e 4 + e5
Ejercicio 27. En el espacio vectorial 4 dado con respecto a su base canónica, comprobar que
los vectores
a = (1,2,-1,-2) ; b = (2,3,0,-1) ; c = (1,3,-1,0) ; d = (1,2,1,4)
forman una familia libre. Deducir que esta familia forma una base de 4. Calcular las coorde-
nadas del vector u, con coordenadas (7,14,-1,2) en la base canónica, en la base (a, b, c, d).
Ejercicio 28. En el espacio vectorial 4 referenciado con respecto a s u base canónica, se

consideran los siguientes vectores
V 1 = (0,1,0,1) ; V 2 = (1,0,1,0) ; V 3 = (2,0,-1,1) ; V 4 = (-3,3,3,1) ;V 5 = (7,-4,-2,-1) .
a- Determinar el rango de la familia { V1 ,V2 ,V3 ,V4 ,V5 }.
b- Sea el sistema de ecuaciones
 x 2 + 2x 3 − 3x 4 + 7x 5 = a
 x + 3x 4 − 4x 5 = 3
1

 x 2 − x 3 + 3x 4 − 2x 5 = 2
 x 1 + x 3 + x 4 − x5 = 1
¿Para qué valores del parámetro real "a", existen soluciones para este sistema?

Ejercicio 29.
En 2, definimos una ley de adición y una ley de multiplicación para un real de la siguiente
manera :
(a ; b) + ( c ; d ) = (a + c ; b + d) y λ. (a ; b) = (λ² a ; λ² b)
Tenemos una estructura de –espacio vectorial ?
Corrección: Recordemos antes que nada la definición de un espacio vectorial:

(E ;+ ;.) es un K-espacio vectorial si y solamente si, tenemos:
( E, + ) grupo commutativo (1)
⋅ : K × E → E ( 2)
( λ + µ ) .x = λ.x + µ.x ( 3)

λ. ( x + y ) = λ.x + λ.y ( 4 )
∀ ( λ, µ, x, y ) ∈ K 2 × E 2 
( λ.µ ) .x = λ. ( µ.x )( 5 )
1.x = x 6
 ( )
Para demostrar que un conjunto es un K-espacio vectorial, evidentement tenemos que verifi-
car todas las propiedades. Sin embargo, para demostrar que no es un K-espacio vectorial, bas-
ta con demostrar que una de las propiedades no es verificada. Particularmente, incluso basta
con dar un contra ejemplo.
Por otro lado, para mostrar que tenemos un sub K-espacio vectorial, basta con verificar que el
espacio es estable mediante la combinación lineal, lo que quiere decir :
( F, +,.) sub Kev de ( E, +,.) ⇔ ∀ ( λ, x, y ) ∈ K × F2 λ.x + y ∈ F
En lo que sigue, si no está precisado, λ y µ serán elementos de K.
En el ejercicio:
Tomemos= λ 2 y= µ 1.
Entonces tenemos ( λ + µ )(=
a, b ) 3=
( a, b ) ( 9a,9b ) y
λ ( a, b ) + µ =
( a, b ) 2 ( a, b ) + 1=
( a, b ) ( 4a, 4b ) + =
( a, b ) ( 5a,5b ) .
Está claro entonces que ( 3) no está verificada, y así, que no tenemos una estructura de -
espacio vectorial.
Ejercicio 30.
Sea E = *+ × .
Definimos una adición en E y una ley de multiplicación por un real de la siguiente manera :
(a ; b) + (c ; d) = (ac ; b + d) y λ (a ; b) = (a λ ; λ b)
Tenemos una estructura de –espacio vectorial?
Correción: Verifiquemos primero que ( E, + ) es un grupo conmutativo.

Comencemos buscando el elementro neutro llamado e :
Por definición del elemento neutro, tenemos ∀α = ( a, b ) ∈ E e + α = α .
Esto nos da ( e1 , e 2 ) + ( a, b=) ( a, b ) ⇔ ( e1a, e2 + b=) ( a, b ) ⇔=
e (1, 0 ) .

1 
=
Sea entonces α ( a, b ) ∈ E , es claro que =
β  , −b  ∈ E es el inverso de=
α ( a, b ) ∈ E por
a 
la ley +.
1  a
De hecho, tenemos α=
+β ,= ( a, b ) + 

b e .
−b   , b −=
a  a 
Finalmente es claro que ∀(α, β) ∈ E², α + β ∈ E .
La conmutatividad proviene de la conmutatividad del producto y de la adición en .
(1) está entonces verificada.
(2) está también claramente verificada.
Las propiedades que quedan no son inmediatas pero unos cálculos rápidos nos demuestran
que ellas son también verdaderas y que así obtenemos una estructura de -espacio vectorial :
( λ + µ ) .x = ( λ + µ ) . ( x1 , x 2 ) = ( x1λ+µ , ( λ + µ ) x 2 ) = ( x1λ x1µ , λx 2 + µx 2 ) = ( x1λ , λx 2 ) + ( x1µ , µx 2 ) = λx + µx
λ. ( x + y ) = λ. ( x1 y1 , x 2 + y 2 ) = (( x y ) , λ ( x
1 1
λ
2 )
+ y 2 ) = ( x1λ y1λ , λx 2 + λy 2 ) = ( x1λ , λx 2 ) + ( y1λ , λy 2 ) = λx + λy
( λ.µ ) .x = ( x1λ.µ , ( λ.µ ) x 2 ) = (( x 1 )

µ λ
)
, λ ( µx 2 ) = λ. ( x1µ , µx 2 ) = λ. ( µx )
=1.x (=
x ,1x )
1
1
2 x
Ejercicio 31.
Entre los siguientes sub-conjuntos de [X], precisar aquellos que son sub-espacios vectoria-
les:
A = {P ∈ [X], P (0) = 1} B = {P ∈ [X], deg (P) ≥ 8 }
C = {P ∈ [X], P + P’ + P’’ = 0} D = {P ∈ [X], P (1) = P (2)}
Corrección : Antes de nada, observemos que ∀ ( λ, P, Q ) ∈  × ([X])², λP + Q ∈ [X].
- Sea ( λ, P, Q ) ∈  × A². Entonces ( λP + Q )( 0 ) = λP ( 0 ) + Q ( 0 ) = λ + 1

Como para λ =2 , ( λP + Q )( 0 ) = 3 ≠ 1 entonces A no es un sub-espacio vectorial [X].
- Sea ( λ = 1, P = X8 , Q = −X8 ) ∈  × B². Entonces λP+Q es el polinomio nulo, entonces

( λP + Q ) ∉ B , entonces B no es un sub-espacio vectorial de [X].
- Sea ( λ, P, Q ) ∈  × C². Entonces
( λP + Q ) + ( λP + Q )′ + ( λP + Q )′′ =λP + λP′ + λP′′ + Q + Q′ + Q′′ =λ ( P + P′ + P′′) =0 .

Entonces C es un sub-espacio vectorial de [X].
- Sea ( λ, P, Q ) ∈  × D². Entonces ( λP + Q )(1) =λP (1) + Q (1) =λP ( 2 ) + Q ( 2 ) =λ

( P + Q )( 2 ) .
Entonces D es un sub-espacio vectorial de [X].
Ejercicio 32.

1- Entre los siguientes sub-conjuntos de 3, determinar aquellos que son sub-espacios vecto-
riales:
P 1 = {(x ; y ; z) ∈  3, z = 0)} P 2 = {(x ; y ; z) ∈  3, z = 1)}
P 3 = {(x ; y ; z) ∈  3, x – y ≥ 0)} P 4 = {(x ; y ; z) ∈  3, x = 0)}
2- Determinar P 1 ∪ P 4 , P 1 ∩ P 4 , P 1 + P 4 , un suplementario de P 1 en 3, un suplementa-
rio de P 1 ∩ P 4 en P 1 , y luego en 3.
Corrección: 1-
- Sean α = ( α1 , α 2 , α 3 ) ∈ P1 , β = ( β1 , β2 , β3 ) ∈ P1 et λ ∈  entonces tenemos:
λα + β = λ ( α1 , α 2 , 0 ) + ( β1 , β2 , 0 ) = ( λα1 , λα 2 , 0 ) + (β1 , β2 , 0 ) = ( λα1 + β1 , λα 2 + β2 , 0 ) ∈ P1 .
Entonces P1 es un sub-espacio vectorial.
- Sean α = ( α1 , α 2 , α3 ) ∈ P2 , β = (β1 , β2 , β3 ) ∈ P2 et λ ∈ , entonces tenemos:

λα + β = λ ( α1 , α 2 ,1) + ( β1 , β2 ,1) = ( λα1 , λα 2 , λ ) + ( β1 , β2 ,1) = ( λα1 + β1 , λα 2 + β2 , λ + 1) .
Como para λ = −1, ( λα1 + β1 , λα 2 + β2 , λ + 1) ∉ P2 y P2 no es un sub-espacio vectorial.
- Sean α = ( α1 , α 2 , α3 ) ∈ P3 , β = (β1 , β2 , β3 ) ∈ P3 et λ ∈ , tenemos entonces:

λα + β = ( λα1 + β1 , λα 2 + β2 , λα 3 + β3 ) .
Como, λα1 + β1 − ( λα 2 + β2 ) = λ ( α1 − α 2 ) + ( β1 − β2 ) .
Tomemos entonces: α = ( 2,1, 0 ) ∈ P3 , β = (1,1, 0 ) ∈ P3 y λ = −1 ∈ .
Obtenemos λα1 + β1 − ( λα 2 + β2 ) = −1 < 0 y así λα + β ∉ P3 .
Entonces P3 no es un sub-espacio vectorial.
- Sean α = ( α1 , α 2 , α3 ) ∈ P4 , β = (β1 , β2 , β3 ) ∈ P4 y λ ∈, tenemos entonces:

λα +=
β λ ( 0, α 2 , α 3 ) + ( 0, β2 , β3=
) ( 0, λα 2 , λα3 ) + ( 0, β2 , β3=) ( 0, λα 2 + β2 , λα3 + β3 ) ∈ P4 .
Entonces P4 es un sub-espacio vectorial.
2- Tenemos
P4  P1 = {(x,y,z) ∈ 3/x=0 ∨ z=0}
P4  P1 = {(x,y,z) ∈ 3/x=0 ∧ y=0}={(0,y,0)/y ∈ }.
Además,
P 4 +P 1 ={X=(x,y,z) ∈ 3/ ∃A ∈ P1 , ∃B ∈ P4 , X=A+B}
={ ( a1 , a 2 + b 2 , b3 ) ∈ 3/ ( a1 , a 2 , 0 ) ∈ P1 , ( 0, b 2 , b3 ) ∈ P4 }
= { ( a1 , a 2 + b 2 , b3 ) ∈ 3/ ( a1 , a 2 , b 2 , b3 ) ∈ 4}=3.
Sea K={ ( x, y, z ) ∈ 3/x=0 ∧ y=0} = {( 0, 0, z )} .

Entonces K  P1 = {( 0, 0, 0 )} y

1 ={ X
K+P= ( x, y, z ) ∈3/ ∃A ∈ P1 , ∃B ∈ X ,
X=A+B}={ ( a1 , a 2 , b3 ) ∈ 3/ ( a1 , a 2 , 0 ) ∈ P1 , ( 0, 0, b3 ) ∈ X }=3.
Deducimos que K es un suplementario de P1 en 3.
Hemos visto que P4  P1 = { ( 0, y, 0 ) ∈ 3}.

Sea E={ ( x, y, z ) ∈ 3/ y = 0 ∧ z = 0 }= {( x, 0, 0 )} .
Entonces E  P4  P1 = {( 0, 0, 0 )} y
1 ={ X
E + P4  P= ( x, y, z ) ∈3/ ∃A ∈ P4  P1 , ∃B ∈ E , X=A+B}
={ ( b1 , a 2 , 0 ) ∈ 3/ ( 0, a 2 , 0 ) ∈ P4  P, ( b1 , 0, 0 ) ∈ E }={ ( x, y, 0 ) ∈3}=P 1 .
Deducimos entonces que E es un suplementario de P4  P1 en P1 .
Finalmente, sea F={ ( x, y, z ) ∈ 3/y=0}.

Verificamos fácilmente que F es un suplementario de P4  P1 en 3.
Exercice 33.
Sea E = 3. Consideramos: E 1 = {(a ; b ; c) ∈ 3 / a = b = c} y E 2 = {( a ; b ; c) ∈ 3 / a = 0}.
Mostrar que : E = E 1 ⊕ E 2 .
Corrección: Empezamos verificando que E1 y E 2 son sub-espacios vectoriales de E.

Sean
= A ( a, a, a ) ∈=E1 , B ( b, b, b ) ∈ E1 y λ ∈ , entonces tenemos :
λA + B =λ ( a, a, a ) + ( b, b, b ) =( λa + b, λa + b, λa + b ) ∈ E1 , entonces E1 es un sub-espacio
vectorial.
Del mismo modo, =
sean A ( 0, a1 , a 2 ) =
∈ E 2 , B ( 0, b1 , b 2 ) ∈ E 2 y λ ∈ , tenemos entonces:
λA + B =λ ( 0, a1 , a 2 ) + ( 0, b1 , b 2 ) = ( 0, λa1 + b1 , λa 2 + b 2 ) ∈ E 2 , entonces E 2 es un sub-espacio
vectorial.
Ahora, demostramos que esos dos sub-espacios vectoriales son suplementarios.

Primero, tenemos:
E1  E 2= {( a, b, c ) / a= b= c y a= 0}= {( a, b, c ) / a= b= c= 0}= {( 0, 0, 0 )} .
Por otro lado,
E1 + E 2 ={X =( x, y, z ) / X =A + B con A ∈ E1 , B ∈ E 2 }
={ ( a, a + b 2 , a + b3 ) ∈ 3/ ( a, a, a ) ∈ E1 , ( 0, b 2 , b3 ) ∈ E 2 }
={ ( a, a + b 2 , a + b3 ) ∈ 3/ ( a, b 2 , b3 ) ∈ 3}.
Esencialmente hay dos métodos para mostrar que E1 + E 2 = 3.
La primera solución consiste a verificar que el siguiente cambio de variable es biyectivo, lo
que quiere decir, verificar que podemos expresar las antiguas coordenadas en función de las
nuevas de manera única y recíprocamente:

=  x a= a x
 
 y =a + b 2 ⇔ b 2 =y − x
z = b =
 a + b3  3 z−x
3
Esto equivale a mostrar directamente que  ⊂ E1 + E 2 .
La segunda solución consiste a escribir esta suma bajo la forma de un espacio vectorial en-
gendrado por tres vectores libres:
Vect ( (1,1,1) , ( 0,1, 0 ) , ( 0, 0,1) ) .
E1 + E 2 =
Finalmente, concluímos que E
= E1 ⊕ E 2 .
Ejercicio 34.
Entre las siguientes familias de elementos de E, precisar aquellas que son libres, generadoras,
bases :
1- E =3
A = {(1 ; 0 ; 1) ; ( -1 ; 1 ; 2 ) ; (-2 ; 1 ; 2 )}
B = {(1 ; 0 ; 1) ; ( 2 ; 0 ; 3 ) ; ( -1 ; 1 ; 1 ) ; ( 0 ; 0 ; 1 )}
2- E =  2 [X]
C = {1 ; X – α ; (X – α )²} con α ∈ 
D = {X² + 3X – 1 ; X² – X + 5 ; -7X² + 9X – 17}
3- E = C0(,)
F = {f1 : x  x² ; f2 : x  ex ; f3 : x  sin x}
Corrección: 1- Sean α, β, γ tales que :

− 2γ 0
α − β = α=−γ 0 =α 0
  
α (1, 0,1) + β ( −1,1, 2 ) + γ ( −2,1, 2 ) = 0 ⇔ β + γ =0 ⇔ β =−γ ⇔ β =0
α + 2β +
= 2γ 0 =α 0 =γ 0
  
Entonces la familia es libre.
3 siendo un espacio vectorial de dimensión 3, deducimos que esta familia es una base de 3
y entonces ella es generadora.
3 siendo un espacio vectorial de dimensión 3, no pueden existir cuatro vectores de 3 libres.

Entonces la familia es ligada.
Es fácil verificar que la familia B′ = ( (1, 0,1) , ( 2, 0,3) , ( 0, 0,1) ) es libre entonces es una familia
generadora de 3. Pero tenemos Vect ( B′ ) ⊂ Vect ( B ) ⊂ 3 entonces B es una familia genera-
dora.
2- Sean a,b,c tales que:

a + b ( X − α ) + c ( X − α ) = 0 ⇔ a − αb + α 2 c + ( b − 2cα ) X + cX 2 = 0 .
2
Por identificación, esto implica que a= b= c= 0 entonces la familia es libre.

Como  2 [X] es de dimensión 3, deducimos que C es una base de E y entonces esta familia es
generadora.
Sean a, b, c tales que a ( X 2 + 3X − 1) + b ( X 2 − X + 5 ) + c ( −7X 2 + 9X − 17 ) =
0.
Esto es equivalente a:

( a + b − 7c ) X 2 + ( 3a − b + 9c ) X − a + 5b − 17c =0
( a + b − 7c ) = 0 a =−b + 7c a =−b + 7c a =− b + 7c a =0
    
⇔ ( 3a − b + 9c ) = 0 ⇔ −3b + 21c − b + 9c = 0 ⇔ −4b + 30c = 0 ⇔ −4b + 30c = 0 ⇔ b = 0
−a + 5b − 17c =0 b − 7c + 5b −=
17c 0 6b −=24c 0 = b 4c = c 0
    
Deducimos que la familia D es libre.
Como  2 [X] es de dimensión 3, deducimos que D es una base de E y entonces que esta fami-
lia es generadora.
3- Sean a, b, c tales af1 + bf 2 + cf 3 =

0.
Esto significa que para todo real x, tenemos ax 2 + be x + c sin x = 0.
Para determinar los valores de a, b y c, debemos obtener al menos tres ecuaciones no ligadas
(si esto es posible !) gracias a la relación ax 2 + be x + c sin x =
0 . Para ésto, el método más
simple consiste en escoger valores particulares para x pero podemos también para algunos
casos « derivar » la relacion con el fin de obtener ecuaciones más simples.
Por ejemplo aquí, derivemos una vez la relación, obtenemos: 2ax + be x + c cos x = 0 (1) .
0 ( 2) .
Si la derivamos nuevamente, tenemos : 2a + be x − c sin x =
Si la derivamos una vez más, tenemos : be x − c cos x = 0 ( 3) .
Tomemos entonces x=0 en las tres anteriores ecuaciones, obtenemos el sistema :
b + c = 0 (1) a = 0
 
2a += b 0 ( 2 ) ⇔ =b 0
 c = 0
b − c = 0 ( 3) 
Deducimos entonces que esta familia es libre.
Aquí, no es el método más simple pero hay que acordarse de este método porque nos puede
ser muy útil en algunos casos.
Volvemos a la relación principal : ax 2 + be x + c sin x =
0.
π
Tomando x = 0 , obtenemos b = 0 , luego x = π , nos da c = 0 , y finalmente x = , nos da
2
a = 0.
Sin embargo, hay que estudiar el carácter generador de esta familia. Aquí vemos fácilmente
que esta última no es generadora. De hecho, si hubiera sido el caso, nuestro espacio sería de
dimensión 3 pero sabemos que E = C0(,) es un espacio vectorial de E de dimensión infinita
y entonces la familia no puede ser generadora.
Ejercicio 35.
Calcular el rango de las siguientes familias de 4 :
1- u 1 = (1 ; 2 ; -4 ; 3) ; u 2 = (2 ; 5 ; -3 ; 4) ; u 3 = (6 ; 17 ; -7 ; 10 ) ; u 4 = (1 ; 3 ; -3 ; 2)
2- u 1 = (1 ; 2 ; 6 ; -1) ; u 2 = (3 ; 6 ; 5 ; -6) ; u 3 = (2 ; 4 ; -1 ; -2 )
3- u 1 = (a ; 1 ; 1 ; 0 ) ; u 2 = (1 ; a ; 1 ; 0) ; u 3 = (1 ; 1 ; a ; 0) con a ∈ .
Corrección : 1-

1 2 6 1 1 0 0 0 1 0 0 0 1 0 0 0
 2 5 17 3  2 1 5 1 2 1 0 0 2 1 0 0 
      
rg=
  rg =  rg=
  rg  
−4 −3 −7 −3 −3 5 17 1  −3 5 −8 −4  −3 5 −8 0
 3 4 10 2   4 −2 −8 −1  4 −2 2 1   4 −2 2 0 
Entonces la familia es de rango 3.
1 3 2 1 0 0  1 0 0
2 6 4 2 0 
0   0 
   2 0
2-=
rg   rg =   rg  
 6 5 −1  6 −13 −13  6 −13 0
−1 −6 −2  −1 −3 0  −1 −3 3 
a 1 1 0 0 0  0 0 0 
1 a 1     0 
 a 1 1  a 0
3 − rg  = rg   C ←=aC −C rg  2 
1 1 a 1 a 1  i i 1 1 a − 1 a − 1 
0 0 0  1 1 a  1 a − 1 a 2 − 1
0 0 0 
a 0 0 
 
= rg  2 
C3 ←( a +1) Ci − C2 1 a −1 0
 
1 a − 1 ( a − 1) ( a + 1) − ( a − 1) 
2
 
0 0 0 
a 0 0 
 
= rg  2 
 1 a − 1 0 
1 a − 1 a ( a − 1)( a + 2 ) 
Observemos que el cálculo anterior sólo es válido si pour un lado tenemos
a ≠ 0 ( Ci ← aCi − C1 ) , y por otro lado si a ≠ −1( C3 ← ( a + 1) C3 − C2 ) .
Debemos entonces distinguir diferentes casos según el valor de a :
- a=0 :
0 0 0  0 0 0  0 0 0  0 0 0  0 0 0
a 1 1  0 1 1  1 1 0  1 0 0   0 
        1 0
rg=  rg=   rg =  C ←C −C rg  =  C ←C + C rg  
1 a 1  1 0 1  1 0 1  2 2 1 1 −1 1  3 3 2 1 −1 0
1 1 a  1 1 0  0 1 1  0 1 1  0 1 2 
- a=-1 :
a 1 1  0 0 0  0 0 0 0 0 0
1 a 1  a 0 0    −1 0 0 
   −1 0 0   
rg 
=  rg  = 2  rg=   rg  
1 1 a  1 a − 1 a − 1   1 0 −2   1 −2 0 
0 0 0  1 a − 1 a 2 − 1  1 −2 0   1 0 −2 
Entonces la familia es de rango 3 también.
- a ∉ {0, −1} :

En este caso tenemos :
a 1 1  0 0 0 
1 a 1  a 0 0 
   
rg   = rg  2 
1 1 a  1 a − 1 0 
0 0 0  1 a − 1 a ( a − 1)( a + 2 ) 
Debemos resolver: a ( a − 1)( a + 2 ) =
0 , y a 2 − 1 =0.
a ( a − 1)( a + 2 ) = 0 ⇔ a ∈ {0,1, −2} , y a 2 − 1 = 0 ⇔ a ∈ {−1,1} .
Nos queda entonces por estudiar el caso a = 1 y a = −2 .
- Si a = 1 , tenemos:
a 1 1  0 0 0 
1 a 1  1 0 0 
   
rg   = rg  
1 1 a  1 0 0 
0 0 0  1 0 0 
- Si a = −2 , tenemos :
a 1 1   0 0 0
1 a 1  −2 0 0 
   
rg   = rg  
1 1 a   1 3 0
0 0 0   1 −3 0 
En todos los otros casos, la familia es de rango 3.

Capítulo 20
APLICACIONES LINEALES
Cayley Arthur (inglés, 1821-1895) fue abogado de origen.

Será profesor de matemáticas en la universidad de Cambridge y
miembro de la Royal Society of London (La academia de las cien-
cias inglesa) cerca de la cual publicará gran número de sus trabajos,
fundamentalmente sobre las geometrias no euclidianas.
Pero la obra maestra de Cayley será el desarollo (desde 1843) de
una nueva rama de las matemáticas : el álgebra lineal y sus trans-
formaciones, nacidas del estudio de los sistemas de ecuaciones li-
neales.
1- Aplicaciones lineales
Definición: Sean E y F dos -espacios vectoriales.

Se dice que una aplicación f de E en F es lineal si por definición comprueban las dos condi-
ciones siguientes
1- ∀(u, v) ∈ E², f(u+v)=f(u)+f(v) (o + es la ley interna)

2- ∀k ∈ , ∀u ∈ E, f(k.u)=k.f(u) (donde designa la ley externa).
Notación: El conjunto de aplicaciones lineales de E en F se escribe L(E,F).
Observación : Una aplicación lineal es también llamada morfismo de los espacios vectoria-
les.
Casos particulares:
- Cuando f es biyectiva, f es un isomorfismo de E en F.
- Cuando E = F, f es un endomorfismo.
El conjunto de los endomorfismos de E se escribe End(E) u L(E).
- Cuando E = F y f son biyectivas, f es un automorfismo de E.
- Cuando F = , f es una forma lineal.
Propiedades: Sea f una aplicación lineal de E en F.

1- f(0 E )=0 F

 n  n
2- ∀(k1 ,..., k n ) ∈ n, ∀(u1 ,..., u n ) ∈ E n , f  ∑ k i u i  =
∑ k i f (u i )
=  i 1=  i1
2- Imagen e imagen recíproca de un subespacio vectorial por aplicación li-

neal
Teorema. Sea f un elemento de L(E, F) y o de G un subespacio vectorial de E. Entonces,
f(G)={f(u)/u G } es un subespacio vectorial de F.
Definición: Sean E y F dos conjuntos, f una aplicación de E en F y H una parte de F.

La imagen recíproca de H por aplicación de f es f –1(H)={x E/f (x) H }.
Teorema. Sean f un elemento de L (E, F) y H un subespacio vectorial de F. Entonces f –1(H)

es un subespacio vectorial de E.
3 Imagen y núcleo de una aplicación lineal

Definición: Sea f un elemento de L(E, F). La imagen de f es por definición f (E). S e le
escribe como Im (f).
Im(f)={f(u)/u E }
Teorema. De acuerdo con la notación anterior, Im (f) es un subespacio vectorial de F.
Definición: Sea f un elemento de L(E, F). El núcleo de f es por definición f -1({0 F }). Y se
escribe como Ker (f).
u ∈ Ker(f) ⇔ f(u)=0 F
Teorema. De acuerdo con las notaciones anteriores, Ker (f) es un subespacio vectorial de E.
Ejemplo : Sea f la aplicación lineal de 4 en 3 definida por : f(a,b,c,d)=(x,y,z) con

x = a + b + c

= y b + d
z
= a + c − d

Determinar Im(f) y Ker(f).
Teorema. Sea f un elemento de L(E, F).

1- f es inyectiva si y sólo si Ker(f)={0E }
2- f es sobreyectiva si y sólo si Im(f)=F.
4 Caso en que E es de dimensión finita
Teorema. Sean E y F dos -espacios vectoriales, E de dimensión finita "n" elemento de *.
Sea B=(e 1, …,e n ) una base de E.
Sea f un elemento de L(E, F).

f está totalmente determinado por los n vectores f(e 1 ), …, f(e n ).
Teorema. Sean E y F dos -espacios vectoriales, E de dimensión finita n elemento de *.

Sea B= (e 1 ...,e n) una base de E. Sea f un elemento de L(E, F).
Entonces Im(f)=Vect({f(e 1 ), …, f(e n )}).
Definición: Sea f un elemento de L(E, F). El rango de f, que se escribe rg (f), es la dimen-
sión de Im (f).
Teorema del rango. Sean E y F dos -espacios vectoriales, E de dimensión finita n elemento
de *. Sea f un elemento de L(E, F).
Dim(Ker(f)) + rg(f) = Dim(E)
Dim(Ker(f)) + Dim(Im(f)) = Dim(E)
Teorema : Sean E y F dos espacios vectoriales tales que E tenga una dimensión finita.
Sea f de E en F una aplicación lineal.
1-f inyectiva ⇔ f transforma cualquier base de E en une familia libre de F.
⇔ existe una base B de E que tiene como imagen para f una familia libre de F.
2-f sobreyectiva ⇔ f transforma cualquier base de E en una familia generatriz de F
⇔ existe una base B de E que tiene como imagen para f una familia generatriz de F.
3-f biyectiva ⇔ f transforma cualquier base de E en una base de F
⇔ existe una base B de E que tiene como imagen para f una base de F.
Teorema: Caracterización analítica de una aplicación lineal

Suponemos que E y F los dos son de dimensión finita p y n respectivamente.
Sean B 1 = (e 1 ,…,e p) una base de E, y B 2 = (f1 ,…, f n ) una base de F.
n
Notamos ( a1j ,..., a nj ) las coordenadas de f(e j ) en la base B 2 : f(e j ) = ∑a f .
i,j i
i =1
p
Sea u un vector de E de coordenadas (x 1 ,…,x p ) en la base B 1 : u = ∑x e
k =1
k k y (y1 ,…,yn ) las
n
coordenadas de f(u) en la base B 2 : f(u) = ∑y f
i =1
i i .
 y1 = a11x1 +  + a1p x p

Entonces obtenemos:   .
y = a n1x1 +  + a np x p
 n
5 Caso de un endomorfismo con E de dimensión finita
Teorema. Sea E un -espacio vectorial de dimensión finita n elemento de .

Sea f un elemento de End (E).
Las propiedades siguientes son equivalentes.
1- f es inyectiva
2- f es suprayectiva
3- f es biyectiva.

6- Estudio de L (E, F)
Teorema: Sean E y F dos -espacios vectoriales. Anotemos como + la ley de composición

interna de L(E, F) y la ley externa.
(L(E,F),+) es un grupo conmutativo.
(L(E,F),+,.) es un -espacio vectorial.
7- Composición de aplicaciones lineales
Teorema. Sean E, F y G tres -espacios vectoriales.

Sean f un elemento de L(E, F) y g un elemento de L(F, G).
Entonces g  f es un elemento de L(E,G).
Prueba: Sean f un elemento de L(E,F) y g un elemento de L(F,G).

Sean x e y dos vectores de E y λ un escalar.
λy ) f ( g ( x + λy ) )=
( f  g )( x += f ( g ( x ) + λg ( y ) )
por linearidad de g
= f ( g ( x ) ) + λ=
f (g ( y)) ( f  g )( x ) + λ ( f  g )( y )
par linearidad de f
8- Proyectores e involuciones
Definición : proyección y simetría paralelamente a un subespacio vectorial.

Sean E un -espacio vectorial, F y G dos subespacios suplementares de E (E = F ⊕ G).
Entonces tenemos: ∀x ∈ E, ∃!(x F , x G ) ∈ F × G / x = x F + x G
Llamamos proyección sobre F paralelamente a G la aplicación p de E en E definido por :
p(x)=x F .
Llamamos simetría en comparación a F paralelamente a G la aplicación s de E en E definido
por: s(x) = xF -x G .
Proposición :
1- las proyecciones y las simetrías son endomorfismos de E.
2- una proyección p verifica p  p = p y una simetría s verifica s  s = Id E .
3- F = Im p = {x ∈ E/p(x) = x}=Ker(Id E -p) et G = Ker p = Im(Id E - p).
4- F = Ker(s - Id E ) = Im(s + Id E ) et G = Im(s - Id E ) = Ker(s + Id E )
Proposición :
1- sea p un endomorfismo de E verificando p  p = p.
p es un proyector. Notamos F = Im p y G = Ker p.
Entonces tenemos E = F ⊕ G y p es la proyección sobre F paralelamente a G.
2- Sea s un endomorfismo de E verificando s  s=Id E . s es una involución.
Notamos F=Ker(s-Id E ) y G=Ker(s + Id E ).
Entonces tenemos E = F ⊕ G y s es la simetría en comparación a F paralelamente a G.

ANEXO
PROYECCIONES Y SIMETRÍA VECTORIALES
1. . Proyecciones y simetrías vectoriales en el plano P

Definición : Sean D1 y D2 dos rectas que no son paralelas y que tienen vectores característi-
 
cos respectivos i y j .
  
Todo vector u del plano se divide de manera única en la suma de un vector u1 colineal a i y
    
de un vector u 2 colineal a j : u = u1 + u 2 .
D2

 u
u2
D1
 
u1 = p u ()
 
−u 2 ()
s u
 
La proyección p sobre D 1 así como sobre D 2 se define por p u = u1 . ()
  
()
La simetría "s" con relación a D 1 , así como sobre D 2 se define entonces por: s u = u1 - u 2 .
Ilustración : p proyección sobre (∆’) como sobre (D).
(D)
C (∆)
B
A
(∆’)
A’ B’ C’
 
Propiedades : 1- Para todo vector u y v y para todo real k,
     
( ) () () ( )
p u + v = p u + p v , p ku =k p u
 
()
2- Para todo vector u y v y para todo real k,
     
( ) () () ( )
s u + v = s u + s v , s ku =k s u ()

   
Ilustración: Con p proyección ortogonal sobre la recta (OC) con u = OA , v = AB ,
   
()
p u = OA1 y p v = A1B1 ()
B
O A1 B1 C
Propiedad : p  p=p y s  s=id, donde id designa la aplicación de identidad del plano.
Observación: Los elementos característicos de p y de s, D 1 y D 2 , están definidos por:

     
{
- D1 = u ∈ P / p u = () }
u y D 2= u ∈ P / p u = 0 { () }
     
{
- D1 = u ∈ P / s u = () }
u y D 2= u ∈ P / s u = −u { () }
2. Proyecciones y simetrías vectoriales en el espacio E

   
( )
Definición : Sea P un plano de base i, j y D una recta que no está incluida en P con vector
característico k , es decir que i, j, k no son coplanarios.
 
Todo vector u del plano se divide de manera única en la suma de un vector u1 coplanario a
     
( )
i, j y de un vector u 2 colineal a k : u = u1 + u 2 .
 
La proyección p 1 sobre D como en P se define entonces por: p 1 u = u 2 . ()
  
La simetría s 1 con relación a D como en P se define entonces por: s 1 u = u 2 - u1 . ()
Ilustración : p proyección sobre D y sobre P.

v
P 
u
  D
u' v'
 
Propiedades: 1- Para todo vector u , v y para todo real k,
     
( ) () ()
p 1 u + v = p 1 u + p 1 v y p 1 ku =k p 1 u
 
( ) ()
2- Para todo vector u , v y para todo real k,

     
( ) () () ( )
s 1 u + v = s 1 u + s 1 v y s 1 ku =k s 1 u ()
Ilustración: p proyección sobre la recta (xx’) y sobre el plano P.

A4
A2 A3
A5
P
A1
x’
x
A’1 A’2 A’3 A’4 A’5
Propiedad : p 1  p 1 =p 1 y s 1  s 1 =id donde id designa la aplicación de identidad del espacio.
Observación : Los elementos característicos de p 1 y de s 1 , P y D, están definidos por:

     
{
- D= u ∈ E / p1 u = () }
u y P= u ∈ E / p1 u = { 0 () }
     
{
- D= u ∈ E / s1 u = () }
u y P= u ∈ E / s1 u = { −u () }
 
La proyección p 2 sobre P como en D se define entonces por p 2 u = u1 . ()
  
La simetría s 2 con relación a P como en D se define entonces por s 2 u = u1 - u 2 . ()
 
Propiedades : 1- Para todo vector u , v y para todo real k,
     
( ) () ()
p 2 u + v = p 2 u + p 2 v y p 2 ku =k p 2
 
( ) (u)
2- Para todo vector u , v y para todo real k,
     
( ) () ()
s 2 u + v = s 2 u + s 2 v y s 2 ku =k s 2 ( ) (u)
Propiedad : p 2  p 2 =p 2 y s 2  s 2 =id donde id designa la aplicación de identidad del espacio.
Observación : Los elementos característicos de p 2 y de s 2 , P y D, están definidos por:

     
{
- P= u ∈ E / p 2 u = () }
u y D= u ∈ E / p 2 u = { 0 () }
     
{
- P= u ∈ E / s 2 u = () }
u y D= u ∈ E / s 2 u = { −u () }

Ejercicio 1. Las siguientes aplicaciones son lineales ? Entre aquellas que lo son, precisar
eventualmente si se trata de formas lineales o de endomorfismos.
f1 : Ñ3ØÑ f2 : Ñ3ØÑ f3 : Ñ3ØÑ2 f4 : Ñ3ØÑ3
(x,y,z)#x+2y (x,y,z)#xy (x,y,z)#(x+2y,x-y) (x,y,z)#(x+y,y+z,z+x)
Ejercicio 2. Las siguientes aplicaciones son lineales?

f1 : Ñ[X]ØÑ[X] f2 : Ñ[X]ØÑ[X] f3 : Ñ[X]ØÑ[X]
P # 2P+P’ P # XP+P’’ P # P2
Ejercicio 3. En E espacio vectorial de una base B = (e1,e2,e3 ) sea f endomorfismo de E defi-

nido por : f(e1) = 2e1-e2+e3 ; f(e2) = e1+e2-2e3 ; f(e3) = e1+e2+e3.
Determinar las coordenadas de f(V) para V = x e1+ye2+ze3.
Ejercicio 4. Sea f : Ñ3ØÑ2, (x,y,z) # (3x+2y,y-z).

Determinar la imagen de la base canónica B = (e1,e2,e3 ) de Ñ3 en función de la base canónica
B’ = (1,2) de Ñ2.
Ejercicio 5. Determinar la imagen y el núcleo de f1 y f3 del ejercicio 1.
Ejercicio 6. Determinar la imagen y el núcleo para f y g :

f : Ñ4[X]ØÑ4[X] g : Ñ2[X]ØÑ2[X]
P # P’ P # XP’+P
Ejercicio 7. Sea f : Ñ3ØÑ3 ; (x,y,z) # (x-y+2z , x+y+z , 0 ).

Demostrar que : Ñ3 = Imf ∆ Kerf.
Tenemos f  f = f ?
Ejercicio 8. En Ñ3, sean E1 ={(x,y,z)  Ñ3 / x+y+z =0 }y E2 ={ (x,y,z)  Ñ3 / x=y=z }.

1- Demostrar que ( V1= (-1,1,0) , V2= (-1,0,1) ) es una base de E1.
2- Demostrar que ( V3 = (1,1,1) ) es una base de E2.
3- Demostrar que todo vector de Ñ3 se descompone de una manera única bajo la forma
de la suma de un vector de E1 y de un vector de E2 y deducir que Ñ3 =E1∆E2.
4- Sea p la proyección en E1 paralelamente a E2. Calcular p(x,y,z).
5- Sea s la simetría en relación con E1 paralelamente a E2. Calcular s(x,y,z).

334
Ejercicio 1. f1 forma lineal, f2 no lineal, f3 lineal, f4 endomorfismo.
Ejercicio 2. f1 lineal, f2 lineal, f3 no lineal.
Ejercicio 3. f(V) = (2x+y+z)e 1 +(-x+y+z)e 2 +(x-2y+z)e 3 .
Ejercicio 4. f(e 1 ) = 3ε 1 ; f(e 2 ) = 2ε 1 + ε 2 ; f(e 3 ) = -ε 2 .
Ejercicio 5. Im(f1 ) =  y Ker(f1 ) = { (-2y, y, z) / (y,z) � 2 }

Im(f3 ) = 2 y Ker(f3 ) = { (0,0,z ) / z �  }.
Ejercicio 6. Im(f) =  3 [X] y Ker(f) = { funciones constantes }

Im(g) =  2 [X] y Ker(g) = { función nula }.
Ejercicio 7. f  f f.
2 1 1 1 2 1 1 1 2 
Ejercicio 8. p(x,y,z) =  x − y − z, - x + y − z, - x − y + z 
3 3 3 3 3 3 3 3 3 
1 2 2 2 1 2 2 2 1 
s(x,y,z) =  x − y − z, - x + y − z, - x − y + z  .
3 3 3 3 3 3 3 3 3 

EJERCICIOS
Ejercicio 1.
1- Las aplicaciones siguientes de 3 en él mismo son lineales? Para las que son, de-
terminar su núcleo y su imagen y precisar si son inyectivas, sobreyectivas, biyectivas.
a- f((x,y,z))=(x,0,z)
b- g((x,y,z))=(y+z,x+z,x+y)
c- h((x,y,z))=(x,xy,x+z)
2 - Mismas cuestiones con las aplicaciones siguientes de 2 en 3.
a- f((x,y))=(x+1,y+1,x+2)
b- g((x,y))=(x,x-y,x+y)
c- h((x,y))=(2x-y,6x-3y,4x-2y)
3 - Mismas cuestiones con las aplicaciones siguientes de [X] en él mismo.
a- f(P)=PP’
b- g(P)=X²P
c- h(P)=3P" + 2P' + P
Ejercicio 2. Dentro de las siguientes aplicaciones, indicar aquellas que son lineales
Para aquellas que los son, precisar su núcleo, su imagen.
1. f1 : 3 → 3 definido por ( x, y, z )  ( e x , 2y, x − z ) .
2. f2 : 3 → 2 definido por (x, y, z)  (x − y + z, 2x + y − 3z) .
3. f3 : 2 → 2 definido por (x, y)  ( 4x − 6y, −6x + 9y ) .
4. f4 : 3 → 2 definido por ( x, y, z )  ( x − y + z 2 , 2x − z )
5. f5 :  4 [X] →  2 [X] definido por P  2P′′
6. f6 : [X] → [X] definido por P  P (1 + P )
7. f7 : C∞ () → C∞ () definido por f  f 2 − ef
Ejercicio 3. En E espacio vectorial proveído de una base  = (e 1 ,e 2 ,e 3 ) sea f el

endomorfismo de E definido por: f(e 1 ) = 2e 1 -e 2 +e 3 ; f(e 2 ) = e 1 +e 2 -2e 3 ; f(e 3 ) = e 1 +e 2 +e 3 .
Determinar las coordenadas de f(V) para V = x e 1 +ye 2 +ze 3 .
Ejercicio 4. Sea f : 3→ 2 definido por (x,y,z)  (3x+2y,y-z).

Determinar la imagen de la base canónica  = (e 1 ,e 2 ,e 3 ) de 3 en función de la base canónica
’ = (ε 1 ,ε 2 ) de 2.
Ejercicio 5. Sea f la aplicación de 3 en 3 definida por:

 x' = x - y

(x,y,z)  f(x,y,z) = (x',y',z') con  y' = y - z
 z' = - x + z

a- ¿Es f lineal?
b- Determinar una base de Ker(f) e de Im(f).
Ejercicio 6. Sea f la aplicación lineal de 4 en 3 definida por :

 f (e1 ) = ε1 + ε2
f (e ) = ε + 2ε 2 + ε3
 2 1

f (e3 ) = ε1 + 5ε 2 − 2ε3
f (e 4 ) = ε1 + 3ε 2 + 2ε3
donde ( e 1 ,e 2 ,e 3 ,e 4 ) es la base canónica de 4
(ε 1 , ε 2 , ε 3 ) es la base canónica de 3.
Determinar Ker(f) e Im(f). (Ustedes darán una base y una ecuación de estos espacios).
Ejercicio 7. Sea u : 3 → 3 definido por (x, y, z)  (5x + 2y − z, −8x − 3y + 2z,3x − y − 5z) .

1. Mostrar que la aplicación u es lineal.
2. Mostrar que V={(x,y,z) ∈ 3/x-5y=0} es un subespacio vectorial de 3.
3. Determinar u(V), imagen de V para u y dar una base de este espacio .
Ejercicio 8. Sea T : 2 →  una aplicación lineal que verifica T(1,1)=3 et T(0,1)=-2.

1. La familia B={(1,1), (0,1)} forma una base de 2 ?
2. Sea t de coordenadas (x, y) en la base B. Exprimir T(t).
3. Dar el núcleo y la imagen de T.
Ejercicio 9. Sea E, F, G tres -espacios vectoriales, f ∈ L(E,F) et g ∈ L(F,G). Mostrar que :

1. Ker ( f ) ⊂ Ker ( g  f ) . 2. Im ( g  f ) ⊂ Im ( g )
Ejercicio 10. Sea E =  3 [X] proveído de su base canónica B=(1,X,X2,X3).

Tomamos E 0 = {P ∈ E/ P(0) = 0} y E 1 = {P ∈ E/ P(1) = 0}.
1- Seaλ un real. Mostrar que la aplicación φ λ : P  P(λ) es una aplicación lineal no
nula de E en . Deducir que E 0 , E 1 y E 0  E 1 son subespaciones vectoriales de E. Cuál es la
dimensión de E 0 ?
2- Sea u : E →  1 [X] definida por u(P) =P(0)X + P(1).
2-1- Mostrar que u es lineal. Determinar el rango de u. u es sobreyectiva ?
2-2- Mostrar que Ker u = E 0  E 1 . Aplicar el teorema del rango a u para determinar
dim Ker u. Mostrar que Ker u es el conjunto de múltiplos de un polinomio que habrá de de-
terminar , luego dar una base de Ker u.
3- Con la ayuda de las dimensiones, mostrar que E = E 0 + E 1 . La suma es directa ?
Ejercicio 11. Sean E y F dos espacios vectoriales tales que E tenga una dimensión finita.
Sea f de E en F una aplicación lineal. Mostrar las siguientes propiedades:
1-f inyectiva ⇔ f transforma cualquier base de E en une familia libre de F

⇔ existe una base B de E que tiene como imagen para f una familia libre de F.
2-f sobreyectiva ⇔ f transforma cualquier base de E en una familia generatriz de F
⇔ existe una base B de E que tiene como imagen para f una familia generatriz de F.
3-f biyectiva ⇔ f transforma cualquier base de E en una base de E'
⇔ existe una base B de E que tiene como imagen para f una base de F.
Ejercicio 12. Sean u, v dos endomorfismos del espacio vectorial E.

1- a- Mostar que Ker(u) ⊂ Ker(v  u).
b- Mostar que Ker(v  u) = Ker(u) ⇔ [Im(u) ∩ Ker(v) = { 0 E }].
2- a- Mostar que Im(v  u) ⊂ Im(v).
b- Mostar que Im(v  u) = Im(v) ⇔ E = Im(u) + Ker(v).
Indicación: para ⇒ , mostrarán que para todo vector x de E, existe un elemento "y" de E tal
que x = u(y) + [x - u(y)] con (x - u(y)) elemento de Ker(v).
3- a- Mostrar que (u  u = u) ⇒ E = Im(u) ⊕ Ker(u).
b- Mostrar que esto es falso cuando se considera la aplicación de 2 en 2 definida
en la base canónica ( e 1 ,e 2 ) de 2 por :
u( e 1) = (0,0) ; u( e 2 ) = a. e 2 donde "a" es un real fijo distinto de 0 y de 1
Ejercicio 13. E es un espacio vectorial de dimensión finita.

Sea "u" un proyector de E (es decir un endomorfismo de E tal que u  u = u).
a- Mostrar que (Id - u) es un proyector.
b- Mostrar que Im(Id - u) = Ker(u) y que Ker (Id - u) = Im(u).
c- Mostrar que Ker(u) ⊕ Im(u) = E.
d- Sean F y G subespacios vectoriales de E tales que F ⊕ G = E. Definir el único pro-
yector "u" tal que F = Ker(u) y que G = Im(u).
Ejercicio 14. Se dice que un endomorfismo v es involutivo si v  v = Id.

Sea "u" un proyector de E. Se considera v = 2u - Id.
Mostrar que v es involutivo. Estudiar el recíproco.
Dar una interpretación geométrica de este resultado en 3.
Ejercicio 15. 1- Sea "p" el endomorfismo del -espacio vectorial 3 definido por :
 y z y z
p(x,y,z)=  x,x + − ,x − + 
 2 2 2 2
Mostrar que p es una proyección vectorial. Determinar los elementos característicos de p.
2- Sea s el endomorfismo del -espacio vectorial 3 definido por :
1 1 
s(x,y,z)
=  (5x + 2y − 4z),y, (4x + 4y − 5z) 
3 3 
Mostrar que s es una simetría vectorial. Determinar los elementos característicos de s.
Ejercicio 9 a- Construir un endomorfismo f de 3 tal que 3 no sea la suma directa de Im(f)

y de Ker(f).
b- Construir un endomorfismo g de 3 tal que 3 = Ker(g) ⊕ Im(g) y tal que g no
sea un proyector.

Ejercicio 16.
1- Las siguientes aplicaciones de 3 en él mismo son lineales ?
Para aquellas que lo son, determinar su núcleo y su imagen.
F (x ; y ; z) = (x ; 0 ; z)
G (x ; y ; z) = (y + z ; x + z ; x + y)
H (x ; y ; z) = (x ; xy ; x + z)
2- Mismas preguntas con las siguientes aplicaciones de 2 en 3 :
F (x ; y) = (x + 1 ; y + 1 ; x + y + 2)
G (x ; y) = (x ; x – y ; x + y)
H (x ; y) = (2x – y ; 6x – 3y ; 4x – 2y)
3- Mismas preguntas con las siguientes aplicaciones de [X] en él mismo:
F (P) = P P’
G (P) = X 2 P
H (P) = 3 P’’ + 2 P’ + P
Corrección: Recordamos que una aplicación lineal f es una aplicación que verifica :
∀ ( X, Y, λ ) ∈ E × E × , f ( X + λ= Y ) f ( X ) + λf ( Y )
Omitiremos algunas veces a continuación los cuantificadores (para no hacer la lectura pesada)
1- F (x ; y ; z) = (x ; 0 ; z)
F ( ( x1 , y1 , z1 ) + λ ( x 2 , y 2 , z 2 =
) ) F ( x1 + λx 2 , y1 + λy 2 , z1 + λz 2=) ( x1 + λx 2 , 0, z1 + λz 2 )
= ( x1 , 0, z1 ) + λ ( x=
2 , 0, z 2 ) F ( x1 , y1 , z1 ) + λF ( x 2 , y 2 , z 2 )
Entonces F es una aplicación lineal.
Tenemos :
Ker
= F {( x, y, z ) / F ( x, y,= z ) 0= 3 }
{( x, y, z ) / ( x, 0,=z) ( 0, 0,=0 )} {( 0, y,=0 )} Vect {( 0,1, 0 )}
Y ImF={ F ( x, y, z ) / ( x, y,=
z ) ∈ } 3
( x, 0, z )} Vect {(1, 0, 0 ) , ( 0, 0,1)} .
{=
G (x ; y ; z) = (y + z ; x + z ; x + y)
G ( ( x1 , y1 , z1 ) + λ ( x 2 , y 2 , z=
2 )) G ( x1 + λx 2 , y1 + λy 2 , z1 + λz 2 )
= ( y1 + λy2 + z1 + λz 2 , x1 + λx 2 + z1 + λz 2 , x1 + λx 2 + y1 + λy2 )
= ( y1 + z1 , x1 + z1 , x1 + y1 ) + λ ( y2 + z 2 , x 2 + z 2 , x 2 + y2=) G ( x1 , y1 , z1 ) + λG ( x 2 , y2 , z 2 )
Entonces G es una aplicación lineal.
Ker G = {( x, y, z ) / G ( x, y, z ) = 03 } =
{( x, y, z ) / ( y + z, x + z, x + y ) = ( 0, 0, 0 )}
{( x, y, z ) / y =
= −z, x =
−z, 2x = 0} = {( 0, 0, 0 )}
De acuerdo con el teorema del núcleo, tenemos
rang G = dim Im G = dim E − dim Ker G = 3 − 0 = 3 .
Siendo Im G un sub espacio vectorial de 3, deducimos que Im G = 3.
Podemos así ver que: Im G = Vect {( 0,1,1) , (1, 0,1) , (1,1, 0 )}
H (x ; y ; z) = (x ; xy ; x + z)

H ( ( x1 , y1 , z1 ) + λ ( x 2 , y 2 , z=
2 )) H ( x1 + λx 2 , y1 + λy 2 , z1 + λz 2 )
= (x 1 + λx 2 , ( x1 + λx 2 )( y1 + λy 2 ) , x1 + λx 2 + z1 + λz 2 )
= (x 1 + λx 2 , x1 y1 + λ ( x1 y 2 + x 2 y1 ) + λ 2 x 2 y 2 , x1 + λx 2 + z1 + λz 2 )
Et, H ( x1 , y1 , z1 ) + λH ( x=
2 , y2 , z2 ) ( x1 , y1x1 , z1 + x1 ) + λ ( x 2 , y 2 x 2 , z 2 + x 2 )
= ( x1 + λx 2 , x1y1 + λx 2 y2 , x1 + z1 + λ ( x 2 + z 2 ) )
Entonces H no es una aplicación lineal a priori.
Para demostrarlo, basta con dar un contra ejemplo :
H (1,1, 0 ) + H (1, 2, 0 ) =(1,1,1) + (1, 2,1) =( 2,3, 2 ) ≠ ( 2, 6, 2 ) =H ( 2,3, 0 ) .
2- F (x ; y) = (x + 1 ; y + 1 ; x + y + 2)
F ( ( x1 , y1 , z1 ) + λ ( x 2 , y 2 , z=
2 )) F ( x1 + λx 2 , y1 + λy 2 , z1 + λz 2 )
= ( x1 + λx 2 + 1, y1 + λy2 + 1, x1 + λx 2 + y1 + λy 2 + 2 )
Or, F ( x1 , y1 , z1 ) + λF ( x 2 , y 2 , z 2=) ( x1 + 1, y1 + 1, x1 + y1 + 2 ) + λ ( x 2 + 1, y 2 + 1, x 2 + y 2 + 2 )
= ( x1 + λx 2 + 1 + λ, y1 + λy 2 + 1 + λ, x1 + λx 2 + y1 + λy 2 + 2 + 2λ )
Y en particular tenemos:
F ( ( 0, 0, 0 ) + 1× (1,1,1
= ) ) F (1,1,1
= ) ( 2, 2, 4 ) ≠ F ( 0, 0, 0 ) + F (1,1,1
= ) (1,1, 2 ) + ( 2, 2, 4 ) .
Entonces F no es una aplicación lineal.
G (x ; y) = (x ; x – y ; x + y)
G ( ( x1 , y1 , z1 ) + λ ( x 2 , y 2 , z=
2 )) G ( x1 + λx 2 , y1 + λy 2 , z1 + λz 2 )
= ( x1 + λx 2 , x1 + λx 2 − y1 − λy2 , x1 + λx 2 + y1 + λy 2 )
= ( x1 , x1 − y1 , x1 + y1 ) + λ ( x 2 , x 2 − y2 , x 2 + y2 )
= G ( x1 , y1 , z1 ) + λG ( x 2 , y 2 , z 2 )
Tenemos :Ker G= {( x, y ) / G ( x, y )= 03 }={( x, y ) / ( x, x − y, x + y )= ( 0, 0, 0 )}
= {( x, y ) / x = 0, x = y, x = − y}
= {( 0, 0, 0 )}
Por otro lado, tenemos ImG={ ( x, x − y, x + y ) /(x,y) ∈ 2}= Vect {(1,1,1) , ( 0, −1,1)} .
H (x ; y) = (2x – y ; 6x – 3y ; 4x – 2y)
H ( ( x1 , y1 , z1 ) + λ ( x 2 , y 2 , z=
2 )) H ( x1 + λx 2 , y1 + λy 2 , z1 + λz 2 )
= ( 2x1 + 2λx 2 − y1 − λy 2 , 6x1 + 6λx 2 − 3y1 − 3λy 2 , 4x1 + 4λx 2 − 2y1 − 2λy 2 )
= ( 2x1 − y1 , 6x1 − 3y1 , 4x1 − 2y1 ) + λ ( 2x 2 − y2 , 6x 2 − 3y 2 , 4x 2 − 2y 2 )
= H ( x1 , y1 , z1 ) + λH ( x 2 , y 2 , z 2 )
Entonces H es una aplicación lineal.
Tenemos :Ker H = {( x, y ) / H ( x, y ) = 03 } = {( x, y ) / ( 2x − y, 6x − 3y, 4x − 2y ) = ( 0, 0, 0 )}
= {=
( x, y ) / =
2x y, 6x= 4 x 2y} {=
3y,= ( x, y ) / 2x y}

Ker H es entonces la recta de ecuación 2x = y .
Por otro lado, tenemos:
ImH={ ( 2x − y, 6x − 3y, 4x − 2y ) /(x,y)
= ∈ 2}= Vect {( 2, 6, 4 ) , ( −1, −3, −2 )} .
Es fácil ver que la familia {( 2, 6, 4 ) , ( −1, −3, −2 )} es ligada y así Im H = Vect {( 2, 6, 4 )} .
3- F ( P1 + λP2=
) ( P1 + λP2 )( P1 + λP2 )=′ ( P1 + λP2 ) ( P1′ + λP2′=) (
P1P1′ + λ 2 P2 P2′ + λ P1P2′ + P2 P1′ )
Particularmente, F ( X + λ ×1)= ( X + λ )(1)= X + λ , et F ( X ) + λF (1)= X + λ × 0= X .
Entonces F no es una aplicación lineal.
G (P) = X²P.
G ( P1 + λ=
P2 ) X 2 ( P1 + λ=
P2 ) X 2 P1 + λX=
2
P2 G ( P1 ) + λG ( P2 )
Tenemos : Ker =G P / G= { ( P ) 0=
[ X ] } {
P /=X 2 P 0= [ X ] } { }
0 [ X ] .
Por otro lado, tenemos: ImG={X²P/P ∈ [X]}=X²[X].
H (P) = 3 P’’ + 2 P’ + P
Podemos directamente decir que H es lineal porque sabemos que la derivación es lineal, que
la multiplicación por un escalar de una aplicación lineal es lineal y que la suma de aplicacio-
nes lineales es lineal.
Tenemos: Ker= {
H P / H (=P ) 0[X=] }
{P / 3P′′ + 2P′ +=
P 0} .
Para determinar el núcleo de esta aplicación, debemos encontrar las aplicaciones polinomiales
soluciones de la ecuación diferencial: 3y′′ + 2y′ + y =0 (E) .
Observemos que el polinomio nulo es solución de esta ecuación.
n
Sea P un polinomio de grado n ≥ 0 , tenemos P = ∑ a k X k con a n ≠ 0 .
k =0
Así, P verifica (E) si y solamente si :
n n n
3∑ k ( k − 1) a k X k − 2 + 2∑ ka k X k −1 + ∑ a k X k =
0
=k 2 =k 1=k 0
n −2 n −1 n
⇔ ∑ 3 ( k + 2 )( k + 1) a k + 2 X k + ∑ 2 ( k + 1) a k +1X k + ∑ a k X k =
0
=k 0 =k 0=k 0
n −2
⇔ ∑ ( 3 ( k + 2 )( k + 1) a k + 2 + 2 ( k + 1) a k +1 + a k ) X k + ( 2na n + a n −1 ) X n −1 + a n X n =
0
k =0
Por identificación, obtenemos en particular a n = 0 , lo que contradice nuestra hipótesis.

Deducimos que el polinomio nulo es la única solución.
Podíamos encontrar este resultados más rápidamente razonando sobre el grado del polinomio
3P′′ + 2P′ + P .
De hecho, deg ( 3P′′ + 2P′ + P ) =
deg P entonces P verifica (E) si y solamente si P=0.
Tenemos entonces Ker H = {0} .
Por otro lado, tenemos: ImH={ 3P′′ + 2P′ + P / P ∈ [X]}.
Aquí, podemos intuir que Im H = [X]. Vamos a demostrar este resultado.

Sabemos que [X] está engendrada por la familia {Xn/n ∈ }. Sabiendo además que
Im H ⊂ [X], nos basta con demostrar que todo elemento de la familia {Xn/n ∈ } pertenece
también a Im H.
Sea entonces n ∈ .
Para mostrar que Xn ∈ Im H , hay que mostrar que: ∃P ∈ [X], X n = 3P′′ + 2P′ + P .
Supongamos que existe un tal elemento P. Ya que deg ( 3P′′ + 2P′ + P ) =
deg P , debemos nece-
n
sariamente tener =
deg P deg
= X n n , sea P = ∑ a k X k con a n ≠ 0 .
k =0
De acuerdo con lo que precede, hemos visto que si P es de esta forma entonces :
n −2
3P′′ + 2P=
′+P ∑ ( 3 ( k + 2 )( k + 1) a
k =0
k +2 + 2 ( k + 1) a k +1 + a k ) X k + ( 2na n + a n −1 ) X n −1 + a n X n .
Entonces por identificación obtenemos :

a n = 1

2na n + a n −1 =
0
3 k + 2 k + 1 a + 2 k + 1 a + a k 0 para k ∈ 0, n − 2
 ( )( ) k + 2 ( ) k +1 =
a n = 1

⇔ a n −1 = −2n
a = 0 para k ∈ 0, n − 2
 k −3 ( k + 2 )( k + 1) a k + 2 − 2 ( k + 1) a k +1 =
Los coeficientes del polinomio P están entonces bien definidos de manera única.
Recíprocamente, tomando un polinomio P cuyos coeficientes verifican el sistema anterior,
obtenemos un polinomio que satisface a 3P′′ + 2P′ + P = Xn .
Finalmente, concluimos que Im H = [X].
Ejercicio 17. Consideramos E el espacio vectorial de funciones de de  en  de clase C∞.

Tomamos: D(f) = f " .
Mostar que D es una aplicación lineal de E en E. Precisar Ker (D) y Im (D).
Corrección : Antes de nada, observemos que D está definido de E en E ya qua la derivada de

una función de clase C∞ sigue siendo C∞.
La linealidad proviene de la linealidad de la derivación y del hecho que la composición de dos
funciones lineales sigue siendo lineal.
Podemos también verificar la linealidad de D demostrando que : D ( f + =λg ) D ( f ) + λD ( g ) .
Por definición tenemos Ker D = {f ∈ E / D ( f ) =0E } = {f / f ′′ =

0} ={ f / ∀x ∈ , f "(x) =0}.
Es fácil ver que:
KerD=’ f /=f ′ a, a ∈ }={ f / f ( x ) =
ax + b, ( a, b ) ∈ ²}={ x  ax + b / ( a, b ) ∈ ²}
Es un espacio vectorial de dimensión 2.
Por otro lado, Im

= D {f ′′ / f ∈ E}
Sabemos que Im D es un sub espacio vectorial de E.
Incluso tenemos Im D = E .

De hecho, sea g ∈ E . Llamemos f ( x ) = ∫
∞
0
x
( ∫ g ( u ) du ) dt .
0
t
Siendo g de clase C , es claro que f está bien definida y pertenece a E.

f ′ ( x ) = 
t x x
Además,
=
 ∫0
g ( u ) du
 t = x ∫0
g ( u ) du=y f ′′ ( x ) ∫0 g ( u ) du g ( x ) , sea f ′′ = g .
=
Hemos demostrado Im D ⊃ E por lo cual Im D = E .
Ejercicio 18.Sea f la aplicación lineal de 4 en 3 definida por:

f ( e1 ) = ε1

f ( e 2 ) = −ε1

f ( e3 ) = ε2
f e =
 ( 4) −ε 2
donde ( e1 , e 2 , e3 , e 4 ) designa la base canónica de 4 y ( ε1 , ε 2 , ε3 ) la base canónica de 3.
Determinar una base de Ker f y de Im f
Corrección:
= Sea u ( x, y, z, t ) ∈4 entonces:
f ( u ) = f ( xe1 + ye 2 + ze3 + te 4 ) = xf ( e1 ) + yf ( e 2 ) + zf ( e3 ) + tf ( e 4 ) = xε1 − yε1 + zε 2 − tε 2
= ( x − y ) ε1 + ( z − t ) ε 2 = ( x − y, z − t, 0 )
Por definición tenemos:Kerf={ ( x, y, z, t ) ∈ 4/ f ( x, y, z, t ) = 0 }={ ( x, y, z, t ) ∈ 4= / x y,= z t }.
Es un espacio de dimensión 2 e incluso tenemos:
Kerf={ ( x, x, z, z ) ∈4}= Vect {(1,1, 0, 0 ) , ( 0, 0,1,1)} .
Por otro lado, Imf={ ( x − y, z − t, 0 ) ∈ 3/ ( x, y, z, t ) ∈ 4}
= Vect {(1, 0, 0 ) , ( −1, 0, 0 ) , ( 0,1, 0 ) , ( 0,
= −1, 0 )} Vect {(1, 0, 0 ) , ( 0,1, 0 )} .
Ejercicio 19. Sea E un -espacio vectorial y u y v dos elementos de L(E).

1- Mostrar la equivalencia de las siguientes propiedades:
i- u ° v = u y v ° u = v
ii- u y v son dos proyectores y Ker (u) = Ker (v)
2- Deducir la equivalencia de las siguientes propiedades:
i- u ° v = v y v ° u = u
ii- u y v son dos proyectores e Im (u) = Im (v).
Corrección : Mostremos primero: i ⇒ ii .

u  u (=
= u  v )  u u=
 ( v  u=
) u  v u entonces u es un proyector.
Del mismo modo,
= vv (=v  u )  u v= ( u  u=
) v  u v entonces v es un proyector.
x ) v ( u (=
( x ) ( v  u )(=
Sea x ∈ Ker u entonces v= x ) ) v= ( 0 ) 0 entonces x ∈ Ker v .
Por otro lado, si x ∈ Ker v entonces u= x ) u ( v (=
( x ) ( u  v )(= x ) ) u=
( 0 ) 0 entonces
x ∈ Ker u .
Deducimos entonces que Ker u = Ker v .
Mostremos ahora: ii ⇒ i .
Tenemos: v ( v ( x ) − x ) =
0 entonces v ( x ) − x ∈ Ker v =Ker u .

Así, u ( v ( x ) − x ) =
0 y esto significa que u  v = v .
Del mismo modo, tenemos u ( u ( x ) − x ) =
0 entonces u ( x ) − x ∈ Ker u =Ker v .
Así, v ( u ( x ) − x ) =
0 y esto significa que v  u = u .
Finalmente concluimos que : i ⇔ ii .
2- Aquí tenemos dos posibilidades : ya sea demostramos el resultado directamente, o

sino utilizamos el siguiente resultado visto en un ejercicio en TD : para un proyector u, tene-
mos Im (u) = Ker (Id – u).
Llamemos u =− Id u y v =− Id v .
Tenemos entonces u  v = ( Id − u )  ( Id − v ) = Id − u − v + u  v = u − v + u  v ,
 
Y del mismo modo, v  u = Id − v − u + v  u = v − u + v  u .

Deducimos que : ( u  v =∧v) ( v  u = u ) ⇔ u  v =∧(u ) (
v  u =
v . )
Reconocemos entonces las hipótesis de la primera pregunta, lo que nos permite deducir que:
( u  v =∧
v) ( v  u = (
u ) ⇔ u  v =∧
u ) (
v  u =
v ⇔ u, ) ( ) (
 v son dos proyectores ∧ Ker u = Ker v )
Según el ejercicio viste en TD, tenemos
= Ker u Im= u y Ker v Im v , entonces :
( u  v =∧
v) ( v  u = u ) ⇔ u, (
 v son dos proyectores ∧ ( Im u =)
Im v )
También hemos visto que si u es proyector entonces Id − u lo es también, es fácil verificar que
se trata de una equivalencia: u  u =u ⇔ ( Id − u )  ( Id − u ) =Id − u .
Finalmente concluimos que :

( )
 Id − v son dos proyectores ∧ ( Im u =Im v )
( u  v =v ) ∧ ( v  u =u ) ⇔ Id − u,
⇔ ( u, v son dos proyectores ) ∧ ( Im u =
Im v )
Observación:
En este ejercicio, la demostración directa es más rápida que la solución propuesta. Sin embar-
go, es interesante ver las relaciones que podemos encontrar entre propiedades diferentes, so-
bretodo en el caso donde las demostraciones directas son complicadas.
Ejercicio 20. Sea E un espacio vectorial y f ∈ L(E) tal que : ∀x ∈ E ( x, f ( x ) ) está ligada.
Mostrar que si f no es nula, ∃λ ∈ *, ∀x ∈ E, f ( x ) =λx (Decimos que f es una homotecia).
Corrección: Supongamos que f no es nula, entonces esto significa que: ∃x 0 ∈ E / f ( x 0 ) ≠ 0 .

En particular, x 0 es no nulo también porque f es una aplicación lineal f ( 0E ) = 0E .
Esto significa entonces que existe λ 0 ∈* tal que f ( x 0 ) = λ 0 x 0 .
Consideremos entonces y ∈ E , tenemos dos posibilidades:
- La familia {x 0 , y} está ligada:
En ese caso, ∃α ∈ / y = αx 0
Entonces por linealidad, tenemos: f ( y ) = αf ( x 0 ) = αλ 0 x 0 = λ 0 y .

- La familia { x0 , y} es libre:
Por hipótesis, f ( x 0 + y ) y x 0 + y están ligados, lo que quiere decir que existe λ1 ∈ tal que :
f ( x0 + y) =
λ1 ( x 0 + y ) =
λ1x 0 + λ1 y
Como, por linealidad, tenemos: f ( x 0 + y ) =
f ( x0 ) + f ( y) =
λ0 x 0 + f ( y ) .
Utilizando una vez más la hipótesis hecha para f, sabemos que f ( y ) e y están ligados, lo que
quiere decir que existe λ 2 ∈ tal que : f ( y ) = λ 2 y .
Tenemos entonces: f ( x 0 + y ) = λ 0 x 0 + λ 2 y .
Combinando estas dos relaciones, obtenemos :
λ1x 0 + λ1 y = λ 0 x 0 + λ 2 y ⇔ ( λ 0 − λ1 ) x 0 + ( λ 2 − λ1 ) y = 0
λ − λ1 = 0 λ 0 = λ1
La familia { x0 , y} siendo libre, implica que :  0 ⇔ .
λ 2 − λ1 = 0 λ 2 = λ1
Deducimos entonces que : f ( y ) = λ 0 y .
Finalmente, en cualquier caso, vemos que : f ( y ) = λ 0 y , lo que significa que f es una homote-
cia de razón λ 0 . Concluimos que f es sea nula, sea una homotecia.

Capítulo 21
MATRICES
Paralelamente a los trabajos de Grassmann,

Cayley despejó la noción de espacio vectorial de
dimensión n, introdujo, junto a Sylvester James Joseph
(inglés, 1814-1897), la noción de matriz (el término será
introducido por este último en 1850) y expuso la utilidad
haciendo uso de los determinante (de los cuales el
iniciador fue Cauchy) en una teoría más ancha dicha de
los invariantes (1858) : entendemos por aquí las
propiedades matriciales invariantes por transformación
Sylvester lineal como, por ejemplo, el determinate, el trazado (suma
de los elementos diagonales).
1- Matrices
Definición : Sea  igual a  o .

Una matriz M de tipo (n,p) con coeficientes en  es un arreglo de np elementos de  de tipo:
 a11 a12  a1p 
 
 a 21 a 22  a 2p 
M= =(a i,j ) i,j
   
 
 a n1 a n 2  a np 
Notación: M n,p () designa al conjunto de las matrices de tipo (n, p) con coeficientes en .
Observación: El coeficiente a i,j se escribe también a ij .
Casos particulares:
- Matrices cuadradas M n ()
- Matrices diagonales: D=(a i,j ) i=1 a n y j=1 a n es diagonal si y sólo si para toda "i" y "j"
de 1 hasta n, i distinto de j, a ij =0.
- Matriz identidad o unidad.

Suponemos: δi,j =1 para i=j, 0 si i ≠ j.
I n es la matriz de M n() de termino general δ i,j es decir que todos los coeficientes son nulos
salivo aquellos de la diagonal que vale 1.
2- Estudio de Mn,p()
1- Igualdad de dos matrices

2- Adición de dos matrices
(M n,p(),+) es un grupo conmutativo.
3- Multiplicación de una matriz por un escalar

(M n,p(),+,.) es un -espacio vectorial.
4- Base y dimensión de M n,p()
Dim(M n,p())=np.
3- Matrices simétricas et antisimétricas
Definición: Sea A=(a i,j ) i,j un elemento de M n,p(). La transpuesta de A, que se escribe tA
es la matriz B=(b j,i ) j,i definida por bi,j =a j,i .
Observación: De acuerdo con la notación anterior, B es elemento de M p,n ().
1 4
 1 2 3 t  
Ejemplo : A=   , A=  2 5  .
 4 5 6 3 6
 
Propiedades: Sean A y B dos elementos de M n,p () y sea k un elemento de .

t
(A+B)=tA + tB et t(kA)=ktA
En el resto de este párrafo trabajamos en M n ().
Definición: Una matriz A de M n () se dice que es simétrica si por definición tA=A. Se dice
que es antisimétrica si por definición tA=-A.
Notaciones: El conjunto de las matrices simétricas de M n() se escribe S n ().

El conjunto de las matrices antisimétricas de M n ()se escribe A n ().

Propiedad: S n() ⊕ A n()=M n ().
4- Producto matricial
Definición: Sean A un elemento de M m,n () y B un elemento de M n,p ().

El producto A.B es la matriz C elemento de M n,p () definida por:
n
∀j 1 à p , c i,j = ∑ a i,k b k, j
∀i 1 à m,=
=
k =1
Observación: En resume, decimos que el producto entre dos matrices se realizan “línea por
columna”
jème columna de B
↓
 b1, j 
 
  
 b qj 
 
  
   n 
 
i ème línea de A →  a i,1  a i,n   ∑a i,k b k, j 
   k =1 
   

 
Propiedades:
- Distributividad: ∀A1 ∈M n,p (), ∀A 2 ∈ M n,p (), ∀B ∈M p,q (),
(A1 +A2 ).B=A 1 .B+A2 .B.
∀A ∈ M n,p(), ∀B1 ∈ M p,q (), ∀B2 ∈ M p,q (),
A.(B 1 +B 2 )=A.B 1 +A.B 2 .
- Asociatividad: ∀A ∈ M m,n (), ∀B ∈M n,p (), ∀C ∈ M p,q(), (A.B).C=A.(B.C).
- Transposición: ∀A ∈ M n,p (), ∀B ∈M p,q (), t(A.B)=tB.tA
 1 0  0 0   0 0 
- No integridad :   = .
 0 0  0 1   0 0 
- No conmutatividad
- Producto y potencia : Si A ∈ M n(), definimos A0 = I n y para n ∈ , An+1 = A(An) =
(An)A.
La asociatividad de la multiplicación en M n() hace que:
Para todos naturales p y q; Ap+q = ApAq y (Ap)q = Apq
Si A ∈ M n () y B ∈ M n (), verificando AB = BA, entonces (AB)p = ApBp y
p p p
p p
p
(A + B)p = ∑ Ckp A k Bp − k = ∑ Ckp Bk A p − k = ∑   A k Bp − k = ∑   Bk A p − k
k =0 k =0 k =0  k  k =0  k 
Formula del binomio de Newton

5- Estudio de Mn()
Teorema: (M n (),+,.) es un anillo unitario.
Definición: A elemento de M n () es inversible si por definición existe B elemento de

Mn() tal que A.B=B.A=I n donde I n designa la matriz unitaria de Mn ().
En este caso se escribe B=A-1.
Observación : Si A.B=I n , entonces BA=I n . Y entonces B=A-1.

Al mismo tiempo, si BA=I n , entonces A.B=I n . Y entonces B=A-1.

Ejercicio 1. Determinar las matrices A y B de  2 () que verifican:

1 3  2 6 
2A –B =   y A+B =  
 2 −1  2 −5 
Ejercicio 2 . Verificar la asociatividad del producto matricial calculando A(BC) y (AB)C

para :
 1 0 −1  1 −1 −2 0 
 1 2 −1    
A =  , B = 3 0 2  , C =  2 3 0 1
0 3 1   1 −1 2   0 1 1 2
   
 −1 2  2
Ejercicio 3. Sea la matriz A =   . Demostrar que A -5A +4I = 0.
 −5 6 
 1 5 
Deducir que A  − A + I  = I, y luego la matriz A-1.
 4 4 
Ejercicio 4 . Sea a u n real. Calcular A2, A3 y luego por recurrencia An para A =

 ch(a) sh(a) 
 .
 sh(a) ch(a) 
 0 1 1
 
Ejercicio 5. Para la matriz A =  1 0 1  probar que A2= A +2I y luego por recurrencia que :
 1 1 0
 
n
A = a n A+b n I
Dar las relaciones que unen a n+1 y b n+1 a a n y b n .
Ejercicio 6. Verificar la fórmula de la transportación de un producto de 2 matrices A y B en

1 0 1
 1 0 −2   
las matrices : A =   , B =  0 −1 2  .
2 3 1   1 2 3
 
 1 2 −1 0 
Ejercicio 7. Calcular A tA para la matriz A =  .
 3 0 −3 2 
Demostrar que para una matriz A cualquiera, el producto A tA es una matriz simétrica.

 1 3  1 3
Ejercicio 1. A =   yB=  .
 4/3 −2   2/3 −3
 ch(na) sh(na) 
Ejercicio 3. An=  .
 sh(na) ch(na) 

EJERCICIOS
Ejercicio 1. Sea E el conjunto de matrices cuadradas de orden tres con coeficientes reales de
la forma :
a b c 
 
M(a; b;c) =  3c a - 3c b 
 
 3b -3b + 3c a - 3c 
Siendo a, b y c reales.
a- Encontrar tres matrices I, J, K de E, independientes de a, b, c tales que toda matriz
de E se escriba bajo la forma M(a;b;c) = aI + bJ + cK.
b- Mostrar que E proviene de la adición de matrices y de la multiplicación por un
escalar es un subespacio vectorial de M 3 (). Cuál es su dimensión?
c- Calcular J², J.K, K.J, K².
Ejercicio 2. Calcular los productos A.B y B.A cuando se tienen los casos siguientes:
a- A = (1 2 –1 3) y B = t(-1 0 2 1)
 -1 1 0 0 
1 2 1 0 0 0  2 1 0 0
1 1 0 0 0 0   
  3 5 0 0
b- A =  0 0 0 1 -1 5  ; B = 
 0 0 0 2 -2 -1 0 0 2 -4 
 
   0 0 5 -2 
 0 0 0 1 -3 4   
0 0 1 1
1 0 2
 
Ejercicio 3.Sea.= A  0 −1 1  .
 1 −2 0 
 
3
Calcular A -A. Deducir que A es invertible y determinar su inversa.
1 1 1 1 
 
1 1 −1 −1
Ejercicio 4. Sea B =  . Calcular B2. Deducir que B es invertible y
1 −1 1 −1
 
1 −1 −1 1 
determinar su inversa.

Ejercicio 5. Sea A la matriz de M 3 () definida por :
 1 1 1
A =  0 1 1
 
 0 0 1
Se plantea B = A - I 3 .
a- Calcular B n para cualquier entero n.
b- Deducir A n para cualquier entero n.
Ejercicio 6. Sea M la matriz de M 4 () definida por :

1 a b c 
0 1 d e 
M = 
 0 0 1 f 
 
 0 0 0 1
Se plantea N = M – I 4 .
a- Calcular Nn para cualquier entero n.
b- Deducir Mn para cualquier entero n.
Ejercicio 7. Sea A la matriz de M 2 () definida por :

 5 -4 
A = 
 4 -3
Calcular A 100 .
Ejercicio 8. Consideramos las matrices M(a,b) y A siguientes :

a b b 0 1 1
M(a,b)=  b a b  y A=  1 0 1  donde a y b son dos reales
 
b b a 1 1 0
   
1. Mostrar que A es invertible y calcular su inversa. (podríamos calcular A²-A)
2. Sea E el conjunto de matrices de la forma M(a,b).
Mostrar que E es un subespacio vectorial de M 3 () donde daríamos una base.
3. Mostrar que el producto de dos elementos de E están todavía en E.
4. Determinar todas las matrices M de E tales que:
a) M 2 = M b) M 2 = I c) M 2 = 0

 1 −2 −6 
Ejercicio 8. Sea la matriz A =  −3 2 9  .
 2 0 −3 
 
1- Calcular A² y A3.
2- Deducir las potencias sucesivas de A.
3- A es invertible?
 −5 −6 −6   1 −2 −6 
Corrección: 1- Tenemos A =  9 10 9  y A =  −3 2 9  .
 2  3
 −4 −4 −3   2 0 −3 
   
3
Observamos que : A = A .
2- Sea n un entero natural. De acuerdo con lo anterior, para n ≥ 3 , tenemos:
A n = A n −3 × A 3 = A n − 2
Mediante una recurrencia inmediata, vemos que: A n = A n − 2p para n − 2p ≥ 1 .
Distinguimos dos casos:
- n par :
n 2p + 2 y así tenemos:=
En este caso, existe p tal que = A n A= n − 2p
A2 .
- n impar :
n 2p + 1 y así tenemos:=
En este caso, existe p tal que = A n A= n − 2p
A.
3- De acuerdo con la pregunta 1, tenemos: A 3 = A lo que quiere decir: A ( A 2 − I ) =
0.
Supongamos entonces que A es invertible, esto significa que existe una matriz B tal que:
AB
= BA = I.
Multiplicando en la izquierda la relación anterior por B, obtenemos:
BA ( A 2 − I ) = 0 ⇔ A 2 − I = 0 ⇔ A 2 = I
Como esto es absurdo,
Concluimos que A no es invertible.
3 2 2
Ejercicio 9. 1- Sea A =   . Mostrar que: A – 4A + I 2 = 0.
1 1
Deducir que A es invertible y calcular su inverso.
a b
2- Más generalmente, sea A =   ∈M 2 (). Mostrar que :
c d
A2 – (a + d)A + (ad – bc)I 2 = 0
Deducir una condición necesaria y suficiente para que A sea invertible y una expresión de A-1
en ese caso.
Corrección : 1-
11 8   3 2   1 0  11 − 12 + 1 8 − 8 + 0   0 0 
A 2 − 4A =
+ I2   − 4 + =   =   .
 4 3  1 1   0 1   4 − 4 + 0 3 − 4 +1  0 0 
Con lo que precede tenemos:
A 2 − 4A + I 2 =0 ⇔ − A 2 + 4A =I 2 ⇔ A ( − A + 4I 2 ) =( − A + 4I 2 ) A =I 2 .

Esto permite de concluir que A es invertible y que su inverso es ( −A + 4I 2 ) .
2  a 2 + bc ab + cd 
2- Tenemos: A =  2  entonces:
 ac + bd d + bc 
 a 2 + bc ab + cd  a b 1 0
A2 − ( a + d ) A
= + ( ad − bc ) I 2   − (a + d)   + ( ad − bc )  
c d 0 1
2
 ac + bd d + bc 
 a 2 + bc − a ( a + d ) + ( ad − bc ) ab + bd − b ( a + d )  0 0
=   
 ac + cd − c ( a + d ) d + bc − d ( a + d ) + ( ad − bc )   0 0 
2
Obtenemos el resultado.
Con lo que precede tenemos:

A 2 − ( a + d ) A + ( ad − bc ) I 2 = 0 ⇔ − A 2 + ( a + d ) A = ( ad − bc ) I2 ⇔ A ( −A + ( a + d ) I2 ) = ( ad − bc ) I2
Supongamos que ad − bc ≠ 0 entonces, con la relación anterior, deducimos que A es
1
invertible y su inverso es
ad − bc
( −A + ( a + d ) I2 ) .
Recíprocamente, supongamos que A es invertible.
Esto significa que existe B tal que AB= I=( BA ) .
Así tenemos: BA ( −A + ( a + d ) I 2 )= ( ad − bc ) B ⇔ −A + ( a + d ) I2 = ( ad − bc ) B .
a + d 0 
Supongamos ahora que ad − bc = 0 , esto implica que : A =( a + d ) I2 = .
 0 a + d
a=+d a = a 0
 b 0
= b 0=  0 0
Por identificación obtenemos:  ⇔ sea A =  .
= c 0= c 0 0 0
a=
+d d = d 0
Como A siendo invertible, esto es absurdo (la matriz nula no es invertible). Entonces
ad − bc ≠ 0 .
Finalmente, concluimos que A es invertible si y solamente si ad − bc ≠ 0 .

Capítulo 22
MATRICES Y APLICACIONES LINEALES
1 Matrices y vectores
Definición:  un - espacio vectorial de dimensión “n” elemento de *.

Sea B= (e 1 ,…,e n) una base de E.
Sea “u” un vector de E
n
Existe un n-uplet único (x1...,xn) de n tal que u = ∑ x i ei .
i =1
 x1 
 
Se plantea X=    ∈ M n,1 (). X=mat(u,B).
x 
 n
Observación: no confundir matriz y componente de un vector.
Propiedad: Existe un isomorfismo entre E y M n,1 ().
2 Matrices y aplicaciones lineales
Definición: Sea E un - espacio vectorial de dimensión “n” elemento de * y sea

B1 = (f1 ,…,fp) una base de E.
Sea F un - espacio vectorial de dimensión p elemento de * y sea B 2 = (f1 ...,fp ) una base
de F.
Sea φ una aplicación lineal de E en F.
p
Demos φ(e j )= ∑ a ijf i para j=1 à n.
i =1
 a11  a1j  a1n 

 
Pongamos M=(a i,j ) i=1 a p y j=1 a n =      ∈ M p,n().
 a p1  a pj  a pn 
 
M=mat(φ,B 1 ,B 2 ).

φ(e1 )  φ(e j )  φ(e n )
a  a1n  f1
a1j
Observe que M =  11 
     
 a p1  a pj  a pn  f p

Teorema. Sea E un - espacio vectorial de dimensión “n” elemento de * y sea
B1 =(e1 ,…,e n) una base fija de E.
Sea F un - espacio vectorial de dimensión “p” elemento de * y sea B 2 =(f1 ,…,fp ) una base
fija de F.
La aplicación T de L(E,F) en M p,n() que a un elemento φ de L(E,F) asocia el elemento
M=mat(φ,B 1 ,B 2 ) de M p,n () es un isomorfismo.
Consecuencia: Dim L(E,F)=Dim M p,n ()=pn=DimE.DimF
Ejemplo: Sea φ la aplicación lineal de 3 en 2 definida por

=a x + y
(x,y,z)  φ(x,y,z)=(a,b) con  .
b = x + y − z
Sean B 1 la base canónica de 3 y B 2 la base canónica de 2.
Determinar M 1 =mat(φ,B 1 ,B 2 ).
Sean u= (1,1,0), v= (1, -1, 0) y w= (0,1,1). B 1 ’=(u, v, w) es una base de 3.

Sean e 1 =(1,1) y e 2 =(1,-1). B 2 ’=(e 1, e 2 ) es una base de 2.
Determinar M 2 =mat(φ,B 1 ’,B 2 ’).
3 - Imagen de un vector dada por una aplicación lineal
Sea E un - espacio vectorial de dimensión “n” elemento de * y sea B 1 =(e 1 ,…,e n ) una
base de E.
Sea F un - espacio vectorial de dimensión “p” elemento de * y sea B 2 =(f1 ,…,fp ) una base
de F.
Sea φ una aplicación lineal de E en F de matriz M=mat(φ,B 1 ,B 2 ).
n
 x1 
Sea «u» un vector de E; u= ∑ x je j y sea X= mat(u,B 1 ) =    ∈ M n,1 ().
j=1 x 
 n
p
 y1 
 
Pongamos v=φ(u). v es un elemento de F. v= ∑ yi f i y sea Y=    ∈ M p,1 ().
i =1
 yp 
 
Y=mat(v,B 2 ).
Entonces
Y=MX

Ejemplo: Con los datos del ejemplo del apartado anterior, calcular en la base B2’ las
coordenadas de la imagen dada por φ del vector “x” con coordenadas (1,2,3) en B 1 ’.
4- Composición de aplicaciones lineales
Sea E un -espacio vectorial de dimensión «n» elemento de * y sea B 1 =(e 1 ,…,e n ) una base
de E.
Sea F un -espacio vectorial de dimensión «p» elemento de * y sea B 2 =(f1 ,…,fp ) una base
de F.
Sea G un -espacio vectorial de dimensión «q» elemento de * y sea B 3 =(g 1 ,…,g q ) una
base de G.
Sean φ 1 ∈ L(E,F), φ 2 ∈ L(F,G), φ 3 =φ 2  φ 1 ∈ L(E,G).
φ1 φ2
E →F→G
Sean M 1 =mat(φ 1 ,B 1 ,B 2 ), M 2 =mat(φ 2 ,B 2 ,B 3 ), M 3 =mat(φ 3 ,B 1 ,B 3 ).
Entonces,
M 3 =M 2 .M 1
5- Formulas de cambio de bases
Notación: M(f,B 1 ,B 2 ) o M B 1 ,B 2 es la matriz de la aplicación lineal f de E cuya base es B 1

en F cuya base es B 2 .
1- Para las coordenadas de un vector.
Sea E un espacio vectorial de dimensión finita cuyas bases son B y B ’.

Sea P la matriz en cuya iésima columna está formada con las coordenadas de a’ i en la base B.
P se conoce como la matriz de paso de B (Antigua base) hacia B ’ (nueva base).
Se tiene entonces que P=M(id E ,B ’,B) y P-1=M(id E ,B,B ’) donde las columnas de P-1 están
hechas con las coordenadas de las a i en B ’.
Sea «u» un elemento de E, X la matriz columna con coordenadas de “u” en B (X=mat(u,B))
y X' la matriz columna con las coordenadas de “u” en B ’ (X’=mat(u,B ’)).
Se tiene entonces que
X’=P-1X et X=PX’
2- Para la matriz de una aplicación lineal:
Sea E un espacio vectorial provisto con dos bases B 1 y B 1 ’.

Sea F un espacio vectorial provisto con dos bases B 2 y B 2 ’.
Sea f una aplicación lineal de E hacia F.
Se plantea A=M(f,B 1 ,B 2 ) y A'=M(f,B 1 ’,B 2 ’).

Sea P la matriz de paso de B 1 hacia B 1 ’.
Sea Q la matriz de paso de B 2 hacia B 2 ’.
Se tiene entonces
A’=Q-1AP y A=QA’P-1
Y se dice que A y A’ son equivalentes.
Caso particular
E=F, B 1 =B 2 , B 1 ’=B 2 ’ y «f» endomorfismo de E.
A=M(f,B 1 ,B 1 ), A’=M(f,B 1 ’,B 1 ’) y P matriz de paso de B 1 hacia B 1 ’.
Se tiene entonces que
A’=P-1AP y A=PA’P-1
Y se dice que A y A’ son similares
Ejemplos:
1- Sea f la aplicación lineal de 3 en 2 definida por f(x, y, z)=(a, b) y
a = x + y + z

b = x − y − z
Sean B 1 =(i,j,k) la base canónica de 3 y B 2 =(e 1 ,e 2 ) la base canónica de 2.
=i' 2i + j

Sean i’, j’ y k’ definidas por =j' i + j

= k ' i + k
e '
= e1 + e 2
y e 1 ’, e 2 ’ definidas por  1 .
e2 '
= e1 − e 2
Pongamos B 1 ’=(i’,j’,k’) y B 2 ’=(e 1 ’,e 2 ’). B 1 ’ es una base de 3 y B 2 ’ es una base de 2.
a- Determinar M=mat(f,B 1 ,B 2 ).
b- Determinar M’=mat(f,B 1 ’,B 2 ’).
2- Sea E=3 proveído de su base canónica B=(i, j, k).

x − y =0
Se considera P definido por x+y+z=0 y D definida por  .
2x + y + z =0
Sea p la proyección en P en paralelo a D.
Determinar M=mat(p,B).

Ejercicio 1. Sea E espacio vectorial de dimensión 3 munida de una base  = (e 1 ,e 2 ,e 3 ) y sea

’=(e’ 1 ,e’ 2 ,e’ 3 ) con e’1 = e 1 , e’2 =e 1 +e 2 , e’ 3 = e 1 +e 2 +e 3 .
1- Demostrar que ’ es una base de E y escribir P la matriz de pasaje de  à ’.
2- Determinar P-1 buscando una matriz Q = (bij ) tal que PQ = I.
3- Determinar P-1 calculando e 1 ,e 2 ,e 3 en función de e’1 ,e’2 ,e’3 y escribiendo que P-1 es
la matriz de pasaje de ’ a .

 1 −1 0 
Ejercicio 1. P =  0 1 −1 .
-1
0 0 1 
 

EJERCICIOS
Ejercicio 1. Sean f y g dos aplicaciones lineales definidas por:

  3   2
2 3
→ →
f y g
( x, y )  ( x + y, x − y, 2x ) ( x, y, z )  ( 2y − z, x + y + z )
1- Determinar la matriz Mat B,C (f ) en cada uno de los casos siguientes:
(a) B y C on las bases canónicas respectivas de 2 et 3.
(b) B = ((1,1), (1, −1)) y C es la base canónica de 3.
(c) B = ((1,1), (1, −1)) y C= ((1,1,1), (0,1,1), (0, 0,1)) .
2- Determinar la expresión de de f  g con la ayuda de sus expresiones, y encontrar
este resultado con la ayuda de sus matrices.
3- Misma cuestión para g  f .
Ejercicio 2. Consideramos las funciones f1 y f 2 definidas por:

∀x ∈ f1 (x) = e 2x y f 2 (x) = xe 2x
Sea E={αf1 +βf2 , (α,β) ∈ 2}.
1- Mostrar que E es un espacio vectorial real de base B= (f1 , f 2 ) .
2- Sea φ la aplicación definida por φ(f ) = f ′ . Mostrar que φ es un endomorfismo de
E, y determinar su matriz M en la base B
3- Escribiendo = A 2I 2 + B , calcular A n para todo n ∈ .
 → 
4- Deducir la derivada enésima la función: f  2x
 x  (3x + 1)e
Ejercicio 3. Sea f el endomorfismo de 2 donde la matriz en la base canónica es:

17 −45 
F= 
 6 −16 
Suponemos g=f-2Id y h=f+Id.
1. Determinar la matrices asociadas a los endomorfismos g y h.
2. Determinar el núcleo de g y el de h. Determinaremos una base de cada uno de estos
espacios.
3. Con la ayuda de la pregunta precedente, determinar dos vectores v1 y v2 (no nulos) tales
que:
f ( v1 ) = 2v1 y f ( v 2 ) = − v 2 .
4. Demostrar que la familia {v1 , v 2 } es una base de 2 y determinar la matriz de pasaje P de
la base canónica a esta nueva base.
5. Calcular P-1 después P-1 FP. Que representa este producto?

Ejercicio 4. B = ( e1 , e 2 , e3 ) designa la base canónica de 3.
 3 −1 1 
3  
Sea f el endomorfismo de  donde la matriz en la base B es A =  2 0 1  .
 1 −1 2 
 
Sea B ’ = ( ε1 , ε 2 , ε3 ) con
= ε1 ( 0,1,1=
) , ε2 (1,1, 0=
) , ε3 (1,1,1) .
1. Mostrar que B ’ es una base de 3.
2. Expresar f(ε 1 ) et f(ε 2 ) en la base B ’ y verificar que f ( ε3 ) =ε 2 + 2ε3 .
3. Deducir la matriz en esta nueva base.
Ejercicio 5. Sea f el endomorfismo de 3 donde la matriz en la base canónica es:

 5 8 −7 
 
F =−  2 −3 2 
 2 4 −4 
 
Suponemos g=f+Id, h=f+2Id y k=f-Id.
1. Determinar las matrices asociadas a los endomorfismos g, h y k.
2. Determinar los núcleos de g, h y k.
3. Con la ayuda de la pregunta precedente, determinar tres vectores v1 , v2 y v 3 (no nulos)
tales que :
f(v 1 )=-v 1 , f(v 2 )=-2v 2 y f(v 3 )=v3
4. Demostrar que (v1 , v2 , v3) es una base de 3 y determinar la matriz F’ de f en esta base.
Que puede constatar?
Ejercicio 6. E es un espacio vectorial de dimensión n.

1- Definimos la traza de una matriz M cuadrada de orden n (notada Tr(M)) como la
suma de los términos diagonales de esta matriz.
Si A y B son dos matrices cuadradas de orden n , admitimos que Tr(AB) = Tr(BA).
Mostrar que las trazas de las matrices de un endomorfismo f con relación a las diversas bases
de E son iguales. Definimos así la traza del endomorfismo f.
2- Sea f un proyector de (E). Si  1 y  2 son respectivamente las bases de Im(f) y
Ker(f), justificar que  = 1 ∪ 2 es una base de E.
Dar la matriz asociada a f en esta base. Mostrar que la traza de f es igual al rango de f.
Ejercicio 7. E es el -espacio vectorial de los polinomios con un grado máximo de 5 y del

polinomio nulo.
1- Sea f la aplicación definida en E por :
Para todo P(X) elemento de E , f(P(X)) = P(X+1) + P(X-1) - 2P(X)
1-1- Mostrar que f es un endomorfismo de E.
1-2- Escribir la matriz de f en la base canónica de E.
1-3- Determinar Im(f), rg(f), Ker(f).
2- Sea F = {P(X) ∈ E / P(0) = P'(0) = 0}.
2-1- Mostrar que F es un subespacio vectorial de E. Encuentre una base de F.
2-2- Se escribe g la restricción de f a F, es decir g: F → E ; P(X)  f(P(X)).
Determinar Im(g), rg(g), Ker(g).

Ejercicio 8. Se coloca en el -espacio vectorial  4 [X].
a- Mostrar que para todo P elemento de  4 [X], P(1+X)-P(1-X) es divisible por X.
P(1 + X) − P(1 − X)
b- Se considera la aplicación ϕ : P  ϕ(P) = . Mostrar que ϕ es un
2X
endomorfismo de  4 [X].
( )
c- Determinar la matriz de ϕ en la base 1, X, X 2 , X 3 , X 4 .
d- Determinar una base de Ker( ϕ ),así como una base de Im( ϕ ).
Ejercicio 9. En el -espacio vectorial  4 [X], se consideran las aplicaciones siguientes:

φ(P(X))=P(X+1) y Ψ(P(X))=P(X-1)
a- Mostrar que φ y ψ son unos automorfismos de  4 [X].
φ+ψ
b- Determinar la matriz M de en la base ( 1, X, X 2 , X 3 , X 4 ).
2
c- Mostrar que M puede invertirse. Deducir que:
∀Q ∈ 4 [X], ∃!P ∈  4 [X], P(X+1) + P(X-1) = 2Q(X)
d- Sea Pn el único polinomio de  4 [X] tal que Pn (X + 1) + Pn (X - 1) = 2X n . Mostrar
que para n elemento de {0;1;2;3;4}, Pn ' = nPn−1.
e- Determinar Pn para n elemento de {0,1,2,3,4} y deduzca en M −1 .
Ejercicio 10. El espacio vectorial  n [X] está provisto con su base canónica B igual a
k
{X /0 ≤ k ≤ n} . Para k incluido entre 0 y n, escribamos E k el polinomio:
E k (X) = C kn X k .(1 − X) n− k
a- Mostrar que el conjunto de los E k es una base B’ de  n [X].
b- Escribir la matriz de paso P de B hacia B’ y aclarar P -1 .
Ejercicio 11. Se considera el espacio vectorial 3 referido con respecto a su base ortonormal
canónica B=(i, j, k).
 -1 0 0
 
1- ¿Cuál es la aplicación lineal cuya matriz en relación a B es A =  0 1 0 ?
 
 0 0 1
2- Sea P el plano de ecuación "x - y + z = 0 ". Sea s la simetría ortogonal en relación
con P. Determinar una base B' de 3 tal que s admite A como matriz en B'.
3- a- Determinar la matriz de s en B.
b- Determinar la matriz mat(s,B’,B).

Problema recapitulativo
Sea E un -espacio vectorial de dimensión 3. Se escribe id el endomorfismo identidad de E y

0 el endomorfismo nulo.
1- f es un endomorfismo de E, a y b dos reales distintos.
Se escribe g = f - a.id, h = f - b.id, F = Ker(g), G = Ker(g  g), H = Ker(h).
1- 1- Mostrar que G ∩ H = {0 E }.
(Se utilizará g = f - a.id y h = f - b.id)
1- 2- Se supone que g  g  h = 0 y g  h ≠ 0. Mostrar que F ⊂ G y que la
inclusión es estricta.
1- 3- Se supone además que F ≠ {0 E } y H ≠ {0 E }. Utilizando las
dimensiones de F, G, H, mostrar que G y H son complementarios en E y precisar las
dimensiones de F, G y H.
1- 4- Sea v un vector de G que no pertenece a F; mostrar que “g(v)” y “v” son
linealmente independientes y constituyen una base de G.
1- 5- Siendo u un vector que no es nulo de H, mostrar que (g(v),v,u) es una
base de E. Escribir la matriz M de f en esta base.
(Se utilizará f = g + a.id y f = h + b.id).
2- Se supone ahora que con respecto a una base B dada de E, el endomorfismo f tiene
como matriz:
 8 -1 -5
 
A =  -2 3 1 
 
 4 -1 -1
2- 1- Calcular los productos matriciales :
(A - 4I).(A - 2I) y (A - 4I)².(A - 2I)
y deducir los dos números reales « a » y « b » para los cuales se comprueban las hipótesis de
la pregunta 1-2-.
2-2- Determinar un vector de base de F con primera coordenada 1 en la base B.
Determinar un vector v de G que no pertenece a F, cuyas dos primeras coordenadas sean 1 en
la base B. Determinar un vector de base, u, de H, con primera coordenada 1 en B. Escribir la
matriz M de f en la base B'= (g(v),v, u).
2- 3- Siendo P la matriz de paso de B a B', calcular P, P -1 , M n para n entero
natural que no es nulo. Expresar A n en función de las matrices anteriores ; el calculo explícito
no se pide.

Ejercicio 12. Consideramos el espacio vectorial E =  3 [X] y la aplicación f definida por

f(P)=P'–P.
1- Mostrar que f es un endomorfismo de E.
2- Determinar Ker f e Im f.
3- Cuál es la matriz M de f en la base canónica de E ?
4- Demostrar que M es invertible.
Corrección: 1- f es una aplicación lineal por linealidad de la derivada y de la suma.

Por otro lado, tenemos deg(P′) ≤ deg(P) y deg ( A − B ) ≤ max ( deg(A), deg(B) ) entonces
deducimos que deg ( f ( P ) ) ≤ deg(P) ≤ 3 y entonces que f ( P ) ∈ E .
Concluimos entonces que f es un endomorfismo de E.
2- Por definición tenemos: Ker f = {P ∈ E / f ( P ) =0} .
Sea entonces P ∈ Ker f y supongamos que P ≠ 0 .
Tenemos deg (= f ( P ) ) deg(P) ≥ 0 , pero como f ( P ) = 0 , esto es absurdo, entonces P=0.
Concluimos que K er f = {0} .
Por otro lado, de acuerdo con el teorema del rango, tenemos : dim= E rg f + dim Ker f ,
entonces, con lo anterior, esto implica que dim E = rg f , y así que Im f = E .
También hubiéramos podido utilizar el razonamiento siguiente : como K er f = {0} , f e s
inyectiva. f siendo un endomorfismo inyectivo, deducimos que f es biyectiva y entonces
Im f = E .
3- La base canónica de E es {1, X, X 2 , X 3 } , y la matriz M de f en esta base se obtiene
escribiendo las imágenes de los elementos de la base en línea y los de la base en columnas:
f (1 ) f ( X ) f ( X ) f ( X )
2 3
 −1 1 0 0  1
 
 0 −1 2 0  X
M=
 0 0 −1 3  X 2
  3
 0 0 0 −1 X
4- Para demostrar que M es invertible, podríamos verificar, resolviendo un s istema
lineal de 4 ecuaciones con 4 incógnitas, que existe una matriz N tal que MN = I .
No obstante, podemos simplemente observar que f es una biyección (ver pregunta 2-) f siendo
biyectiva, es invertible y entonces la matriz M asociada a f es también invertible.
Ejercicio 13. Sea E un -espacio vectorial de dimensión 3 y B = (e 1 ; e 2 ; e 3 ) una base de E.

 1 –1 2 
Sea f el endomorfismo de E cuya matriz en la base B es M =  –2 1 –3 .
 –1 1 –2 
1- Determinar una base de Ker f y de Im f.
2- Anotamos u = e 1 + e 2 . Mostrar que B ’ = (u ; f(u) ; f 2(u)) es una base de E.
4- Cuál es la matriz T de f en esta base ?
5- Calcular T 2 y T 3. Deducir M n para todo entero natural n no nulo.
Corrección : Por definición tenemos:

x  0   x − y + 2z   0   x − y + 2z = 0
          x − y + 2z =0
X=  y  ∈ K er f ⇔ MX=  0  ⇔  −2x + y − 3z =  0  ⇔ −2x + y − 3z= 0 ⇔ 
z  0   − x + y − 2z   0   −2x + y − 3z = 0
         − x + y − 2z =0
x =y − 2z x = y − 2z  x = −z
⇔ ⇔ ⇔
−2y + 4z + y=
− 3z 0 = y z y = z
Anotemos v=-e 1 +e 2 +e 3 . Deducimos entonces que Ker f = Vect ({v} ) , es un espacio vectorial
de dimensión 1.
Por otro lado, tenemos por definición:
  x ' = x − y + 2z 
  
Im f = x 'e1 + y 'e 2 + z 'e3 /  y ' =−2x + y − 3z  . Anotemos w 1 =e 1 -2e 2 -e 3 et w 2 =2e 1 -3e 2 -2e 3 .
  z ' =− x + y − 2z 
  
Entonces, Imf=Vect({w 1 ,w 2 }).
Es un sub-espacio vectorial de dimensión 2 cuya base es (w 1 ,w 2 ).
Hubiésemos podido también utilizar los ceros escalonados…
2- f siendo una aplicación lineal , tenemos: f ( u ) = f ( e1 + e 2 ) = f ( e1 ) + f ( e 2 ) .
Conociendo la matriz de f en la base B, tenemos: f ( u ) = −e 2 .
Deducimos entonces que f 2 ( u ) = f (f ( u )) = f ( −e 2 ) = −f ( e 2 ) =e1 − e 2 − e3 .
Para mostrar que B’ es una base de E, basta con mostrar que es una familia libre.
Sean entonces λ1 , λ 2 , λ 3 tales que λ1u + λ 2 f ( u ) + λ 3f 2 ( u ) = 0 .
λ1u + λ 2 f ( u ) + λ 3f 2 ( u )= 0 ⇔ λ1 ( e1 + e 2 ) − λ 2 e 2 + λ 3 ( e1 − e 2 − e3 )= 0
⇔ ( λ1 + λ 3 ) e1 + ( λ1 − λ 2 − λ 3 ) e 2 − λ 3e3 = 0
Por libertad de la familia ( e1 , e 2 , e3 ) , deducimos:
λ1 + λ 3 = 0 λ1 =0
 
λ1 − λ 2 − λ 3 = 0 ⇔ λ 2 = 0
λ =0 λ =0
 3  3
Entonces la familia B’ es libre, y es una base de E.
3- Para expresar la matriz T de f en esta base, hay que calcular f 3 ( u ) :
f 3 ( u )= f ( f 2 ( u ) )= f ( e1 − e 2 − e3 )= 0 .
Concluimos entonces que :
f (u) f (u) f (u)
2 3
0 0  u 0
 
T = 1 0  f ( u )0
0 1  f 2 ( u0)
 
0 0 0 0 0 0
4- Tenemos T =  0 0 0  , y T =  0 0 0  .
2   3
1 0 0 0 0 0
   

B’ y B siendo dos bases de E, sabemos que existe una matriz invertible que permite de pasar
de una base a otra. Llamemos P la matriz de pasaje de la base B a la base B’ :
u f (u) f 2 (u)
 1 0 1  e1
 
P=  1 −1 −1 e 2
 0 0 −1 e
  3
Tenemos entonces M = PTP −1 .
Es fácil ver por recurrencia inmediata que : M n = PT n P −1 .
Para calcular M n , entonces basta con calcular T n .
De acuerdo con lo que precede tenemos T n = 0 para n ≥ 3 , de por lo cual M n = 0 para n ≥ 3 .
1 0 1
Sólo queda calcular M²que vale  −1 0 −1 .
 −1 0 −1
 
Observemos que aquí no era necesario determinar explícitamente la matriz P.
Ejercicio 14. Sea f la aplicación lineal de 2 en 3 definida por f(x ; y) = (x ; x + y ; x).

1- Determinar la matriz de f relativamente a las bases canónicas B 1 y B 2 de 2 y 3
respectivamente.
2- Sea B'1 = ((2 , 3) ; (-1 , 7) ). Mostrar que B'1 es una base de 2, luego escribir la
matriz de pasaje P de B 1 a B'1.
3- Sea B'2 = ( (2 , 0 , 1) ; (1 , 1 , 1) ; (2 , 1 , 0) ). Mostrar que B'2 es una base de 3,
luego escribir la matriz de pasaje Q de B 2 a B'2.
3- Calcular Q-1. Deducir la matriz N de f relativamente a las bases B'1 y B'2 .
Corrección : La base canónica B1 de ² es ((1,0), (0,1)), y tenemos:

=f (1, 0 ) (1,1,1
= ) y f ( 0,1) ( 0,1, 0 )
Deducimos entonces que la matriz de f relativamente a las bases B1 y B2 es :
f ( e1 ) f ( e 2 )
1 0  e1
 
M = 1 1  e2
1 0  e
  3
2- Sea B'1 = ( (2 ; 3) ; (-1 ; 7) ).
Para mostrar que B1′ es una base de ², basta con mostrar que la familia es libre.
Sean entonces λ, µ dos reales tales que : λ ( 2,3) + µ ( −1, 7 ) = 0 .
 2λ − µ = 0  2λ = µ λ = 0
λ ( 2,3) + µ ( −1, 7 )= 0 ⇔  ⇔ ⇔
3λ + 7µ = 0 17µ = 0 µ = 0
Deducimos entonces que la familia es libre, y entonces que es una base de ².
P es la matriz de pasaje de la base B 1 a B' 1 ; tenemos:
 2 −1
P= 
3 7 

3- Del mismo modo que antes, para mostrar que tenemos una base basta con mostrar
que la familia es libre.
Sean entonces λ, μ, ν tres reales tales que : λ ( 2, 0,1) + µ (1,1,1) + ν ( 2,1, 0 ) = 0 .
2λ + µ + 2ν = 0 −3µ = 0 λ = 0
  
λ ( 2, 0,1) + µ (1,1,1) + ν ( 2,1, 0 ) = 0 ⇔ µ + ν = 0 ⇔ ν = −µ ⇔ µ = 0
λ + µ = 0 λ = −µ ν = 0
  
Deducimos entonces que la familia es libre, y entonces que es una base de 3.
Q es la matriz de pasaje de B 2 a B'2 ; tenemos:
 2 1 2
 
Q =  0 1 1
 1 1 0
 
4- Para calcular Q −1 , hay que escribir Y=QX y expresar X en función de Y, lo que
quiere decir que debemos resolver el siguiente sistema con incógnita X :
 2 1 2   x1   y1   2x1 + x 2 + 2x 3  y1 2x1 + x 2 + 2x 3 =y1
       
QX =Y ⇔  0 1 1   x 2  = y 2  ⇔  x 2 + x3  =y 2 ⇔  x2 + x 3 =y 2
 1 1 0 x   y   x1 + x 2  
  3   3    y3  x1 + x 2 = y3
 1
 x 2 = 3 ( − y1 + 2y 2 + 2y3 )
2 ( y3 − x 2 ) + x 2 + 2 ( y 2 − x 2 ) = y1 −3x 2 = y1 − 2y 2 − 2 y3 
   1
⇔ x3 = y2 − x 2 ⇔ x 3 = y2 − x 2 ⇔  x 3 = ( y1 + y 2 − 2y3 )
   3
 x= y3 − x 2  x= y3 − x 2
1 1
 1
 x1 = 3 ( y1 − 2y 2 + y3 )

Concluímos entonces que el inverso de Q es la matriz:
 1 −2 1 
−1 1 
Q =  −1 2 2 
3 
 1 1 −2 
La matriz N de f relativamente a las bases B' 1 y B' 2 es: N = Q −1MP .
Esto nos da entonces :
 1 −2 1  1 0   −6 −14 
1    2 −1 1  
N=  −1 2 2  1 1   =  12 11  .
3   3 7  3  3 7 
 1 1 −2  1 0  
2 1 1 0
Ejercicio 15. Mostrar que las matrices A =  1 2  y B =  0 3  son las matrices de un mismo
endomorfismo relativamente a bases diferentes.
Corrección : Decir que las matrices representan el mismo endomorfismo en bases diferentes,
significa que A y B son semejantes, quiere decir que existe una matriz inversible P tal que
tenemos :
A = P −1BP
Esto es equivalente a: PA = BP .

Observemos que la segunda relación nos da un sistema más fácil ya que no tenemos que
invertir la matriz.
Todo el problema está entonces en demostrar la existencia de una matriz P que verifique la
relación enunciada anteriormente.
a b
Llamamos: P =  .
c d
Tenemos entonces :
 a b   2 1   2a + b a + 2b   1 0  a b   a b 
= PA =    =  y BP =    .
 c d   1 2   2c + d c + 2d   0 3  c d   3c 3d 
Obtenemos entonces :
2a= +b a =a+b 0
 
 2a + b a + 2b   a b  a + 2b =b a + b =0 a =− b
PA = BP ⇔  =  ⇔ ⇔ ⇔
 2c + d c + 2d   3c 3d  2c= + d 3c −c=+d 0 = c d
c=
+ 2d 3d =
c−d 0
La matriz siendo invertible, tenemos también la siguiente condición suplementaria: detP ≠ 0.
Como, det P ≠ 0 ⇔ ad − bc ≠ 0 .
a = − b
a = − b 
= PA BP =  c d
Entonces :  ⇔ c = d ⇔  .
det P ≠ 0 2ac ≠ 0 a ≠ 0

d ≠ 0
1 −1
Una solución al sistema es, por ejemplo, la matriz : P =  .
1 1 
Concluimos que las matrices A y B representan la misma aplicación en bases diferentes.

Capítulo 23
DETERMINANTES
1- Forma n-lineal alternada
Definición. Sea E un -espacio vectorial de dimensión n entero natural que no es nulo.

Una aplicación φ de En en  es una forma n-lineal si por definición φ es lineal con relación a
cada una de sus variables.
Una forma n-lineal es alternada si por definición cambia de signo cuando se permutan 2 de
sus variables:
φ(…,u i ,…,u j ,…) = - φ(…,u j ,…,u i ,…)
Observaciones:
1- Una forma n-lineal alternada se anula cuando dos de sus variables son planas.
2- Una forma n-lineal alternada se anula cuando una de las variables es una
combinación lineal de otras variables.
2- Expresión de una forma n-lineal alternada relativamente a una base

1- De dimensión 2:
Sea E un -espacio vectorial de dimensión 2 y φ una forma n-lineal alternada en E.
Sea B=(e 1 ,e 2 ) una base de E.
Se consideran dos vectores “u” y “v” de E con coordenadas respectivas en B (x, y) y (x’, y’).
Entonces, φ(u, v)=(xy’-yx’)φ(e 1 ,e 2 ).
2- De dimensión 3
Sean E un -espacio vectorial de dimensión 3 y φ una forma n-lineal alternada sobre E.
Sea B=(e 1 ,e 2 ,e 3 ) una base de E.
Consideramos tres vectores u, v y w de E de respectivas coordenadas en B (x,y,z), (x’,y’,z’)
y (x’’,y » »,z’’).
Entonces, φ(u,v,w)=(xy’z’’+yz’x’’+zx’y’’-xz’y’’-yx’z’’-zy’x’’)φ(e 1 ,e 2 ,e 3 ).
3- De dimensión n entero natural que no es nulo

Sean E un -espacio vectorial de dimensión n y φ una forma n-lineal alternada en E.
Entonces φ está enteramente determinada por su valor en una base de E.

3- Determinantes de n vectores en una base fija
Definición: Sea E un -espacio vectorial de dimensión n entero natural que no es nulo.

Sea B =(e 1 ,…,e n ) una base fija de E.
El determinante en la base B es la única forma n-lineal alternada que toma el valor 1 en B.
Se escribe det B .
Observación: det B (e 1 ,…,e n)=1.
a- Estudio del determinante de dimensión 2
Sea E un -espacio vectorial de dimensión 2.

Sea B=(e 1 ,e 2 ) una base de E.
Se consideran dos vectores «u» y «v» de E con matrices con coordenadas respectivas en
x x'
B   y   .
 y   y '
x x'
Entonces, det B (u,v)=xy’-yx’= .
y y'
b- Estudio del determinante de dimensión 3
Sea E un -espacio vectorial de dimensión 3.

Sean B=(e 1 ,e 2 ,e 3 ) una base de E.
Se consideran tres vectores «u», «v» y «w» de E con matrices con coordenadas respectivas en
 x   x '   x "
B  y  ,  y '  y  y"  .
 z   z '   z" 
     
x x ' x"
Entonces, det B (u,v,w)=xy’z’’+yz’x’’+zx’y’’-xz’y’’-yx’z’’-zy’x’’= y y ' y" .
z z' z"
Observación: Regla de Sarrus (franceses, 1798-1861)

Procedimiento mnemotécnico: escribimos a la derecha del determinante las dos primeras
columnas ( o debajo las dos primeras líneas). Para obtener el valor D, sumamos el producto de
los te términos diagonales p1 + p2 + p3, como indicado, y le restamos la suma p4 + p5 + p6.

p4 p5 p6
x x' x" x x'
y y' y" y y'
z z' z" z z'
p1 p2 p3
CUIDADO : esta regla sólo es valida para un espacio vectorial de dimensión 3. No está
generalizada para un espacio vectorial de dimensión estrictamente superior a 3.
c- Expresión de una forma n-lineal alternada relativa a una base
Sea E un -espacio vectorial de dimensión n entero natural que no es nulo.

Sea φ una forma n-lineal alternada en E.
∀ (u 1 ,…,u n ) ∈ En, φ(u 1 ,…,u n )=det B (u 1 ,…,u n ).φ( e 1 ,…,e n ).
d- Teorema. Sea E un -espacio vectorial de dimensión n entero natural que no es

nulo.
Sean u 1 ,…,u n n vectores de E.
Las propiedades siguientes son equivalentes:
a- {u 1 ,…,u n} es una base de E
b- det B (u 1 ,…,u n ) ≠ 0
4- Determinante de una matriz
 a11  a1n 
 
Definición: Sea A un elemento de M n (). A= ( a i, j )i =1 à n =    .
j=1 à n  
 a n1  a nn 
Sea E un - espacio vectorial de dimensión n entero natural que no es nulo.
 a1j 
n
 
Se plantea para todo j=1 hasta n, u j = ∑ a ijei , es decir mat(u j ,B)=    .
i =1
 a nj 
 
Por definición, det(A)=det B (u 1 ,…,u n ).
Observaciones: 1- Este número, det(A), no depende de la base elegida ya que solamente los
datos de los vectores intervienen.

2- det(I n)=1.
a11  a1n
Notación: det(A)=   .
a n1  a nn
Propiedad: Sean A y B dos elementos de M n ().

det(AB) = det(A).det(B)
Demostración :
(Hacer un cálculo directo para n = 2 o 3)
Consideremos A y B dos matrices n × n.
Podemos considerarlas como las matrices de dos endomorfismos de n, f y g.
Notamos B=(e 1 , ..., e n) la base canónica de n.
La jésima columna de A es igual a f(e j ) ; la de B es igual a g(e j ) ; la de AB es igual f  g(e j ).
La función definida por:
Φ(V 1 , ..., V n ) = det B (f(V 1 ), ..., f(V n ))
es una forma n-lineal alternada.
Ella es entonces proporcional a d et B (V 1 , ..., V n ), el coeficiente de proporcionalidad siendo
Φ(e 1 ,...,e n).
Tenemos entonces:
Φ(V 1 , ..., V n) = Φ(e 1 , ..., e n ). det B (V 1 , ..., V n )
⇔ det B (f(V 1 ), ..., f(V n )) = det B (f(e 1 ), ..., f(e n )).det B (V 1 , ..., V n )
Como det B (f(e 1 ), ..., f(e n )) no puede ser otro que det(A).
Así :
det B (f(V 1 ), ..., f(V n )) = det(A). det B (V 1 , ..., V n ).
Tomemos ahora V i = g(e i ). Obtenemos:
det B (f(g(e l )), ..., f(g(e n ))) = det(A).det B (g(e 1 ), ..., g(e n ))
Como det B (f(g(e l )), ..., f(g(e n ))) = det(AB) y det B (g(e 1 ), ..., g(e n )) = det(B)
Así :
det(AB) = det(A).det(B)
Consecuencia: Sea A un elemento de M n ()y m un entero natural.

det ( A m ) = det(A)m
Observación: Sean A y B dos elementos de M n (). En general,

det(A+B) ≠ det(A)+det(B)
Teorema: Sea A un elemento de M n ().

A se puede invertir si y solamente si det(A) ≠ 0.
1
En este caso, det ( A −1 ) = .
det(A)
Observación : Sea E un -espacio vectorial de dimensión n entero natural no nulo.

Sea B una base de E.

 a1j   a11  a1n 
   
Sea vj el vector de E tal que mat(v j ,B) =    para j=1 a n. Anotamos A=    .
 a nj  a 
   n1  a nn 
Las siguientes propiedades son equivalentes :
1- det(A) ≠ 0
2- (v1 , v2 , …,v n ) es una base de E
5- Cálculo práctico
Propiedad: Sea A un elemento de M n (). det(A)=det ( t A ) .
 a11  a1n 
 
Definición: Sea A un elemento de M n (). A= ( a i, j )i =1 a n =    .
j=1 a n  
 a n1  a nn 
Sea ∆ i0 j0 el determinante de la matriz cuadrada de orden (n-1) obtenido suprimiendo la línea
i0 y la columna j0 de det(A). ∆ i0 j0 es el menor del coeficiente a i0 j0 y ( −1) 0
i + j0
∆ i0 j0 es el
adjunto del coeficiente a i0 j0 .
Desarrollo de un determinante con ayuda de los adjuntos:

Sea A un elemento de M n (). Entonces para todo i0 y j0 incluido entre 1 y n:
n n
det(A)= ∑ (−1)i0 + j a i0 j∆ i0 j =
j=1
∑ (−1)
i =1
i + j0
a ij0 ∆ ij0
6-Propiedades de los determinantes
Propiedades :
1- Un determinante es nulo si una línea (respectivamente una columna) es una
combinación lineal de las otras líneas (respectivamente de las otras columnas).
2- Un determinante cambia de signo si permutamos 2 líneas ( o 2 columnas ).
3- Puesta en factor por la n-linealidad
De esta manera, para todos α ∈  y A ∈ M n (), det(αA) = αndet(A).
4- El determinante no cambia si añadimos a 1 línea (respectivamente 1 columna) una
combinación lineal de las otras líneas (respectivamente columnas).
5- El determinante de una matriz triangular es igual al producto de los términos de su
diagonal.
7- Matriz inversa
Propiedad : Sea A un elemento de M n ().

A es invertible si y solamente si det(A) ≠ 0.

1 t
En ese caso, A-1= ( comA ) donde comA es la matriz de M n() obtenida a partir de
det(A)
A reemplazando cada término a ij por su adjunto (-1)i+j∆ ij .
comA es la matriz de adjuntos de A
8- Rango de una matriz
Propiedad : Sea A un elemento de M np(). Denominamos rango de A, notado rg(A), el

rango de la familia de vectores columna de A.
Caso particular : si A es elemento de M n (). rg(A)=n si y solamente si det(A) ≠ 0.
9- Determinante de un endomorfismo
Definición : Sea f un endomorfismo de E -espacio vectorial. El determinante de f es el

determinante de una matriz de f en una base establecida (misma base de salida que de
llegada).
Teorema : Sea E un -espacio vectorial de dimensión n entero natural no nulo, y sea f un

endomorfismo de E de matriz A en una base de E.
Las propiedades siguientes son equivalentes :
1- f es un automorfismo
2- det(f) ≠ 0
3- det(A) ≠ 0
4- A es invertible.

1 4 5
Ejercicio 1 . Calcular el determinante
= ∆1 2 0 −2 desarrollándolo según la 2da
3 −1 6
columna, luego según la 2da línea.
1 2 3
Ejercicio 2. Mostrar, sin desarrollar, que el determinante ∆ 2 =2 3 4 es nulo.
3 4 5
1 1 1
Ejercicio 3 . Transformar ∆ 3 =2 3 4 en un determinante de una matriz triangular.
3 5 6
Deducir el valor de ∆ 3 .
 2 3 −1
Ejercicio 4. Calcular el inverso de la matriz A=  0 −1 −1 .
2 1 2 
 
1 1 1 1 a α 0 β
1 −1 1 1 0 b 0 γ
Ejercicio 5 . Calcular los determinantes: D1 = , D2 = ,
1 1 −1 1 δ η c λ
1 1 1 −1 0 0 0 d
a b c d
−1 x 0 0
D3 = .
0 −1 x 0
0 0 −1 x

EJERCICIOS
Ejercicio 1. a- Encontrar dos matrices A y B tales que :

det(A + B) ≠ det(A) + det(B)
1 2 
b- Sea A =  . Demostrar que el conjunto de las matrices B comprobando que
3 4
det(A+B)= det(A)+det(B) es un subespacio vectorial del espacio vectorial de las matrices
2 × 2 . Determinar una base de este subespacio vectorial.
Ejercicio 2. Cuáles son los valores posibles del determinante de la matriz A de M n () en
los siguientes casos? :
a- A diagonal d- A idempotente (es decir A² = A)
b- A triangular e- A involutiva (es decir A² = I)
c- A nilpotente (es decir ∃p ∈  /A = 0M n (  ) ) f- A antisimétrica de carácter impar
p
Ejercicio 3. Calcular los siguientes determinantes :

1 −1 0 1 d 1 1 1
2 1 −1
2 13 a b 1 2 1 3 1 d 1 1
D1 = D2 = D3 5 −2 2
= D4 = D5 =
−3 −20 c d 4 1 2 3 1 1 d 1
−1 3 0
5 1 2 1 1 1 1 d
Ejercicio 4.Dado E=3 y sean tres vectores de E :

= V1 (1,=2, m ) , V2 (=2,1, m ) , V3 ( 3m, 0,1)
Para que valores de m estos vectores están ligados?
Ejercicio=
5. Sean u1 (1,1,
= a, 0 ) , u 2 (1,
= a,1, 0 ) , u 3 (=
a,1,1, 0 ) , u 4 ( 0,1,1, a ) .
Para que valores de a la familia {u1 , u 2 , u 3 , u 4 } de 4 es libre?
1 λ λ2 λ3
λ3 1 λ λ2
Ejercicio 6. Sea ∆ = .
λ2 λ3 1 λ
λ λ2 λ3 1
1- Designemos por K1 ,K 2 ,K 3 y K 4 los vectores columnas de ∆. Aclarar, con la ayuda
de ∆, el determinante δ=det(K1 +K3 , K2 , K 3 -K1 , K 4 ).
2- Calcular δ.

3- Deducir el valor de ∆.
a b c d
 − b a −d c 
Ejercicio 7. Sea A =   . Calcular AtA. Deducir det(A).
 − c d a − b 
 
 −d −c b a
Ejercicio 8. Calcular el determinante siguiente de orden n:

n n −1 n − 2   3 2 1
n −1 n − 2 n − 3   2 1 0
n−2 n−3 n−4   1 0 0
    1 0  0
   1 0 0
  1 0 0
 1 0 0
1 0      0
Ejercicio 9. Sea
x un parámetro real y sea D(x) el determinante
5− x 1 −1
siguiente: 2 4 − x −2
1 −1 3 − x
1- Calcular D(0).
2- Mostrar que D(x) es un polinomio de grado 3.
3- Calcular D(x). (Indicación: sustituir por ejemplo C 1 por C 1 +C 2 ) y determinar para
cuales valores de x el se anula.
 m 2 −9 −4 
 
B  2m −3 −4  con m ∈ . Para que valores de m esta matriz es
Ejercicio 10. Sea =
 8 3m −8 
 
invertible?
Ejercicio 11. Sea n un entero no nulo. A todo polinomio P de  n [X], asociamos Q(P)
cociente de su división por X, y R(P) resto de su división por X n .
Demostrar que la aplicación f definida sobre  n [X] por : f(P)= Q(P) + X.R(P) es un
endomorfismo de  n [X]. Determinar la matriz M de f en la base canónica.
M es invertible?
Ejercicio 12. Sea E un espacio vectorial de dimensión 3, sea (e l , e 2 , e 3 ) una base de E y sea
m ∈ .
Sean V l = e l + 2e 2 + me 3 , V 2 = 2e 1 + e 2 + me 3 y V 3 = 3me 1 + e 3 .
¿Para cuál valor de m forman estos vectores una familia ligada?

Ejercicio 13. ¿Las matrices siguientes son inversibles? Si sí, calcular su inverso con la ayuda
de la comatriz:
 1 −5 7  1 3 5  1 1 1 
   m +1 3      con j= 3
2iπ
A=  7 1 −5  , B=   , C=  2 7 1  , D=  1 j j²  e
 −5 7 1   1 m − 1  0 1 −9  1 j² j 
     
λ 0 0
 
Ejercicio 14. Calcular cuando es posible la inversa de la matriz=
A 0 λ 1.
 0 −1 λ 
 
Ejercicio 15. Sea A la matriz:

13 −8 −12 
 
12 −7 −12 
 6 −4 −5 
1- ¿Se puede invertir A? En caso afirmativo, determinar A -1 .
2- Determinar para todo entero natural n, A n en función de A.

 3 0 −3 
1 4   
Ejercicio 16. Sea A =   y B = 2 1 6 .
 2 −3   0 −1 0 
 
1- Calcular el determinante de A.
2- Calcular el determinante de B de tres maneras diferentes :
a- mediante la regla de Sarrus.
b- desarrollando según 1era columna.
c- desarrollando según 1era línea.
Corrección : 1- Tenemos det( A) =−3 ×1 − 4 × 2 =−11

2- a- mediante la regla de Sarrus.
De acuerdo con la regla de Sarrus, tenemos:
det B = 3 × 1× 0 + 2 × ( −1) × ( −3) + 0 × 0 × 6 − 0 × 1× ( −3) − 2 × 0 × 0 − ( −1) × 6 × 3
=6 + 18 =24
2-b- Desarrollando según la primera columna tenemos :
1 6 0 −3 0 −3
det B = ( −1) × 3 × + ( −1) × 2 × + ( −1) × 0 ×
1+1 2 +1 3+1
−1 0 −1 0 1 6
= 3 × 6 − 2 × ( −3) = 18 + 6 = 24
2-c- Desarrollando según la primera línea tenemos :
1 6 2 6 2 1
det B = ( −1) × 3 × + ( −1) × 0 × + ( −1) × ( −3) ×
1+1 1+ 2 1+ 3
−1 0 0 0 0 −1
= 3 × 6 + ( −3) × ( −2 ) = 18 + 6 = 24
Ejercicio 17. Sea f la aplicación lineal de 3 en 3 definida por:

f ( x, y, z ) = ( x + y, − x + y − z, − x − y + z )
Llamamos A su matriz asociada en la base canónica de 3.
1- Determinar A.
2- Calcular det(A). Qué podemos deducir sobre f ?
3- Determinar f −1 ( x, y, z ) .
1 1 0
Corrección : 1- A =  
 −1 1 −1 .
 −1 −1 1 
 
2- Utilizando la regla de Sarrus tenemos :
det ( A ) =1×1×1 + ( −1) × ( −1) × 0 + ( −1) × 1× ( −1) − ( −1) × 1× 0 − ( −1) × ( −1) × 1 − 1× ( −1) × 1
=1 + 1 − 1 + 1 =+2
Deducimos que la aplicación f es biyectiva.
3- Para determinar la aplicación recíproca de f, hay que determinar el inverso de la
matriz A.

 0 −1 −1
1
Tenemos: A −1 =  2 1 1  .
2 
2 0 2 
1
Entonces obtenemos: f −1 ( x, y, z ) = ( − y − z; 2x + y + z; 2x + 2z ) .
2
Ejercicio 18. Sea n u n elemento de \{0,1] y a 1 , a 2 ,..., a n elementos de un cuerpo

conmutativo .
El objetivo de este ejercicio es de calcular el siguiente determinante, dicho de Vandermonde :
1 a1 a12   a1n-1
1 a 2 a 22   a n-1 2
     
Vn =
     
     
1 a n a n2   a n-1 n
1- Definimos la aplicación de  en  por:

1 a1 a12   a1n-1
1 a2 a 22   a n-1
2
     
Pn ( X ) =
     
1 a n −1 a 2n −1   a nn −−11
1 X X2   X n-1
Demostrar que Pn es un polinomio perteneciente a  n-1 [X] cuyo coeficiente dominante es
Vn −1 .
(Podremos para ello desarrollar el determinante según la última línea.)
2- Explicar por qué los elementos a i para i ∈ 1; n − 1 son las raíces del polinomio Pn .
3- Gracias a las preguntas anteriores, deducir una expresión factorizada de Pn .
4- Calcular Pn ( a n ) , y deducir una relación entre Vn −1 y Vn .
5- Con ayuda de las preguntas anteriores, demostrar que

= : Vn ∏ (a
1≤i < j≤ n
j − ai ) .
Corrección : Desarrollemos el determinante Pn ( X ) según la última línea:

a1 a12  a1n −1 1 a12  a1n −1 1 a1  a1n −1
a a 22  a2n −1
1 a 22  a2n −1
1 a2  a n2 −1
Pn ( X ) = (−1) n +1 ×1× 2 + (−1) n + 2 × X + (−1) n + × X 2 +
        
a n −1 a 2n −1  a nn −−11 1 a 2n −1  a nn −−11 1 a n −1  a nn −−11
1 a1  a1n − 2
1 a2  a n2 − 2
+ (−1) n + n × X n −1
  
1 a n −1  a nn −−12
Los determinantes que aparecen son los elementos del cuerpo , y tenemos entonces un
polinomio de grado como máximo (n-1).
Por otro lado, esta relación nos permite ver que el coeficiente dominante de Pn es:
1 a1  a1n − 2
1 a2  a n2 − 2
= Vn −1
  
1 a n −1  a nn −−12
2- Reemplazando X por a i para i ∈ 1; n − 1 en Pn ( X ) , es claro que vamos a tener dos
líneas idénticas entonces ligadas.
Como sabemos que si dos líneas (o dos columnas) están ligadas en un determinante, entonces
este determinante es nulo.
Esto implica que Pn ( a i ) = 0 , esto significa justamente que los elementos a i para i ∈ 1; n − 1
son dos raíces de Pn . Gracias al grado de este polinomio, podemos afirmar que obtenemos así
todas las raíces de ese polinomio.
3- Por hipótesis los elementos a i para i ∈ 1; n − 1 son todos distintos, el polinomio Pn
posee entonces , de acuerdo con la pregunta 2, (n-1) raíces distintas, podemos entonces
factorisarlo bajo la forma :
n −1
α∏ ( X − a i ) donde α es el coeficiente dominante de Pn .
Pn ( X ) =
i =1
n −1
De acuerdo con la pregunta 3, concluimos que:
= Pn ( X ) Vn −1 ∏ ( X − a i ) .
i =1
4- Por definición de Pn , tenemos: Pn ( a n ) = Vn .

n −1
que : Vn Vn −1 ∏ ( a n − a i ) .
De acuerdo con la pregunta anterior, deducimos=
i =1
5- Vamos a hacer una demostración por recurrencia. Llamaos H ( n ) la propiedad:
=Vn ∏ (a
1≤i < j≤ n
j − ai )
1 a1
Fundación: Paran=2, tenemos V=
2 = a 2 − a1 y admite además,
1 a2
∏ (a
1≤i < j≤ 2
j − a i ) =a 2 − a1 .
Entonces, H(2) está verificada.

Herencia : Sea n un entero natural superior a 2. Supongamos H ( n ) .
n −1
De acuerdo con la anterior pregunta, tenemos
= : Vn Vn −1 ∏ ( a n − a i ) .
i =1

Utilizando la hipótesis de recurrencia, esto nos da :
n −1
Vn
= ∏ (a − a ) × ∏ (an =
j i
1≤i < j≤ n −1=i 1
− ai ) ∏ (a
1≤i < j≤ n −1
j − ai ) × ∏ (an =
− ai )
1≤i ≤ n
∏ (a
1≤i < j≤ n
j − ai ) .
Entonces, H(n+1) está verificada.
Concluimos por recurrencia que para todo entero natural n ≥ 2 , tenemos:

=Vn ∏ (a
1≤i < j≤ n
j − ai )

Capítulo 24
SISTEMA DE ECUACIONES LINEALES
1- Definición e interpretaciones
 a11x1 + a12 x 2 +  + a1p x p b1

=
    

Definición: (S)  a i1x1 + a i2 x 2 +  + a ip x p bi
=
    

a n1x1 + an2x2 +  + a np x p bn
=
Interpretación vectorial
Sea E un -espacio vectorial de dimensión n entero natural que no es nulo.

Sea B una base de E.
 a1j 
 
Sea vj el vector de E tal que mat(vj ,B) =    para j=1 hasta p.
 a nj 
 
 b1 
Sea b el vector de E tal que mat(b,B) =    .
b 
 n
(S) tiene soluciones si y solamente si b es una combinación lineal de los vj con j=1 hasta p.
Interpretación matricial
 a11  a1p   x1   b1 
     
Sean A=     , X=    y B=    .
 a n1  a np   xp  b 
     n
Entonces (S) ⇔ AX=B
Interpretación con las aplicaciones lineales
Sea E un -espacio vectorial de dimensión p provisto con la base B.

Sea F un -espacio vectorial de dimensión n provisto con la base B ’.

 a11  a1p 
 
Sea f un elemento de L(E,F) de matriz A=mat(f,B,B ’)=    .
 a n1  a np 
 
 b1 
Sea b el elemento de F de matriz B=mat(b,B ’)=    .
b 
 n
(S) tiene unas soluciones si y solamente si b es un elemento de Im(f).
Definiciones: Si (S) admite al menos una solución, se dice que (S) es compatible.
Si no, se dice que (S) es incompatible.
Cuando los coeficientes b 1 ,…,b n son nulos, se dice por definición que (S) es homogéneo.
Propiedad: El conjunto de las soluciones de un sistema homogéneo es un espacio vectorial

sobre .
 a11  a1p 
 
Definición: El rango del sistema (S) es el rango de la matriz A= ( a i, j )i =1 a n =    .
j=1 a p  
 a n1  a np 
2- Sistema de Cramer
Cramer Gabriel (suizo, 1704-1752), profesor de matemáticas y

de filosofía en Ginebra, amigo de su compatriota Jean Bernoulli. Sus
trabajos llevan esencialmente sobre las curvas algebraicas y sobre la re-
solución de sistemas lineales : : " Introducción al análisis de las lineas
curvas algebraicas " (1750).
 a11x1 + a12 x 2 +  + a1n x n = b1

    

Definición: Sea (S)  a i1x1 + a i2 x 2 +  + a in x n = bi .
    

a n1x1 + a n 2 x 2 +  + a nn x n =
bn
(Número de ecuaciones = número de incógnitas)
 a11  a1n 
Sea A= ( a i, j )i =1 a n =   
 .
j=1 a n  
 a n1  a nn 
El sistema (S) se llama sistema de Cramer si A se puede invertir.

Volviendo de nuevo a la interpretación vectorial,
det(v1 ,..., v j−1 , b, v j+1 ,..., v n )
xj= para j=1 hasta n
det(v1 ,..., v j−1 , v j , v j+1 ,..., v n )
Fórmulas de Cramer
3- Méthode de Gauss
El método de eliminación de Gauss es un método de resolución sistemático de un sis-
tema lineal (S) de tipo (n , p). El permite una discusión sobre la existencia eventual de una
solución, seguido en el caso donde la existencia está establecida, de un cálculo de su forma
general. El método está compuesto de dos etapas: una primera etapa dicha de eliminación,
seguido de una segunda etapa (eventualmente) dicha de remontada.
Etapa de eliminación
Esta primera etapa apunta a escribir un sistema triangular equivalente al sistema (S) en una
forma escalonada utilizando las siguientes operaciones elementales:
– multiplicación de una ecuación por un escalar no nulo.
– adición de un múltiplo de una ecuación a una otra ecuación.
--Intercambio de ecuaciones y o intercambio de columnas.
Si después de esta etapa, obtenemos una ecuación no compatible, entonces el sistema (S) es
incompatible.
Etapa de remontada
El sistema obtenido después de la etapa precedente es un sistema triangular superior donde la
resolución se efectúa partiendo de la última ecuación, después montando hasta la primera
ecuación. Para esto utilizaremos eventualmente parámetros.

3x + 2y − z = 1

Ejercicio 1. Sea el sistema de ecuaciones:  x − y + z =0 . Mostrar que es un sistema de
 x + y − 2z =−1

Cramer.
Resolver con las fórmulas de Cramer.
3x + 4y + z + 2t =3

Ejercicio 2. Resolver en  el sistema: 6x + 8y + 2z + 5t = 7 .
9x + 12y + 3z + 10t =13

x + y + z + t = 4

Ejercicio 3. Resolver en  el sistema:  x − y − z + 2t =1.
 x + 2y − z − t =1

2x + y + z + t = 3
 x + 2y + z + t = 1

Ejercicio 4. Resolver en  el sistema:  x + y + 2z + t = 2.
 x + y + z + 2t = 4

 x − y + z − t =0

EJERCICIOS
2 2 3
 
Ejercicio 1. a- Calcular la inversa de la matriz A=  1 −1 0 .
 
 −1 2 1
 2 x + 2 y + 3z = 1

b- Resolver el sistema  x − y = 4
− x + 2 y + z = 2

Ejercicio 2. Resolver el sistema en 3:

2 x + 4 y − z = 1

 x − 3y + 2 z = 2
2 x − y + z = 5


 x + y = 4

 3y + 4 z = 1
2 x + 2 y = 8


 x − 3y − 2z = −1
2 x + y − 4z = 3


 x + 4y − 2z = 4
 5x + 6y − 10z = 10
Ejercicio 5.
Resolver los sistemas siguientes por las fórmulas de Cramer:
 x − y + 3z = 8
3x + 7y = 14   x − my =
a
(S 1 )  , (S 2 ) 2x + y + z = 3 , (S 3 ) 
5x + 3y = 8  x + 2y − z = −3 mx + y =b

Ejercicio 6. Resolver los siguientes sistemas con la ayuda de las formulas de Cramer :

4x + y − 9z =−7  5x − y + z = 3
 
 1 b.  y − 2z =0
a. 2x − 3y + z =−2
4 10x + 3y − 10z =
2
 
 4y + 6z = −4
Ejercicio 7. con la ayuda del algoritmo del pivote de Gauss, resolver el siguiente sistema:
a + b − c − d + e = 0

2a + b − 4c + 4e = 0
 a + 2b − 3c + d − e = 0

Donaremos una base del conjunto de las soluciones.
x − y + z − t = 6
 2x + 2y + 4z = 2

Ejercicio 8. Resolver en  el siguiente sistema :  .
 − x − 3z − 3t = 0
 3x + 5y − 2z + 3t = −4
Ejercicio 9. Sean «a» y «b» dos reales. Resolver el sistema en 4:

 x + y + z + 2at = a

 x + by + z + t = 2b
2 x + 2 y + 2 z + 2 t = 1

Ejercicio 10. Discutir el sistema lineal con dos parámetros “m” y”n” :
 y z
x + 2 + 3 = 1
 x y z
 + + = 1
 2 3 4
 x + y + mz = n
 3 4
Ejercicio 11. Discutir según los valores del parámetro λ el sistema:

 2(λ + 1) x + 3y + λz = λ + 4

 (4λ − 1) x + (λ + 1) y + (2λ − 1) z = 2λ + 4
(5λ − 4) x + (λ + 1) y + (3λ − 4) z = λ−1

Ejercicio 12. Solucionar y discutir el sistema con cuatro incógnitas x, y, z, t, en el cuerpo de

los complejos (h, λ parámetros):
 hx + y + z + t = 1
 x + hy + z + t = λ
 2
 x + y + hz + t = λ
 x + y + z + ht = λ3
Ustedes darán s= x+y+z+t y calcularán las soluciones, cuando existen, en función de s, cuyo
valor habrán precisado previamente.

Ejercicio 13. Sea (S) el siguiente sistema con incógnitas x, y, z y con el parámetro λ :
 2x + λy − z = 5

(S)(λ − 5) x + 3y + 7 z = 7
 x + 3y + 2 z = 4

1- Determinarλ para que (S) sea un sistema de Cramer.
2- Mientras (S) es de Cramer, determinar la incógnita y.
Resolver (S) mientras el sistema no es de Cramer.

Ejercicio 14. Discutir y resolver el siguiente sistema ( S ) :

 2x + λy − z =5

(λ − 5)x + 3y + 7z = 7
 x + 3y + 2z = 4

Comenzaremos por determinar para qué valores de λ el sistema es de Cramer.
Corrección : Antes de determinar las soluciones, hay que comenzar por estudiar el determi-
nante del sistema para determinar los valores de λ para los cuales el sistema no será de Cra-
mer (si existe).
El determinante del sistema es:
2 λ −1
det ( S) = λ − 5 3 7 = 12 + 7λ − 3 ( λ − 5 ) + 3 − 42 − 2λ ( λ − 5 ) = −2λ 2 + λ ( 7 − 3 + 10 ) − 27 + 15
Sarrus
1 3 2
= −2λ 2 + 14λ − 12 = −2 ( λ 2 − 7λ + 6 )
Debemos entonces resolver la ecuación λ 2 − 7λ + 6 = 0 .

7 + 25 7 − 25
Hay dos soluciones: λ=1 = 6 y λ 2= = 1.
2 2
Finalmente, hay que distinguir tres casos :
Caso 1 : λ =1
= 2x + y − z 5 = 2x + y − z 5
 
(S) ⇔ −4x + 3y + 7z = 7 L ←⇔ L 2 + 2L1
5y + 5z = 17
 L3 ← 2L3 − L1 
2
 x + 3y + 2z 4
= = 5y + 5z 3
Es claro que el sistema es incompatible, entonces en ese caso, tenemos el conjunto de solu-
ciones igual a ∅ .
Caso 2 : λ =6
 14
 x=−3t +
2x
= + 6y − z 5 2x
= + 6y − z 5 5
  
(S) ⇔  x + 3y + 7z = 7 L ←⇔2L 2 − L1
15z = 9 ⇔ y= t t ∈
x= L ← 2L3 − L1 
2

 + 3y + 2z 4 3 = 5z 3  z=
3
 5
Caso 3 : λ ∉ {1;6}
En este caso el sistema es de Cramer, entonces sabemos que hay una única solución.
Sabiendo que el sistema es de Cramer, tenemos dos métodos para resolverlo.
El primero consiste en resolver el sistema inicial de manera usual (por el método del pivote de
Gauss, por substitución,…).
La otra solución consiste a utilizar las fórmulas de Cramer. Esto es más rápido ya que tene-
mos directamente la forma de la solución. Sin embargo, para obtener la solución bajo la forma
explícita, hay que calcular igual números de determinantes que de incógnitas, y mientras más
grande sea el número de incógnitas , más grande es el tamaño de los determinantes …

Primer método : Resolución directa
Aquí vamos a utilizar el método de Gauss, pero contrariamente a los casos anteriores, vamos a
comenzar por eliminar z porque los coeficientes de z son constantes e independientes de λ .
= 2x + λy − z 5 = 2x + 6y − z 5 = 2x + 6y − z 5
  
(S) ⇔ ( λ − 5) x + 3y + 7z = 7 L ←⇔ L 2 + 7L1
 ( λ − 5 + 14 ) x + ( 3 + 7λ ) y = 7 + 35 ⇔ ( λ + 9 ) x + ( 3 + 7λ ) y = 42
 x + 3y + 2z = L3 ← L3 + 2L1 
2

 4 = 5x + ( 3 + 2λ ) y 14 = 5x + ( 3 + 2λ ) y 14
Ahora, podemos seguir mediante substitución para resolver las dos últimas ecuaciones:
 
2x + 6y − z = 2x + 6y − z = 5
5 
 ( λ + 9 ) − 3 + 2λ y + 14 + 3 + 7λ y= 42
(S) ⇔ ( λ + 9 ) x + ( 3 + 7λ ) y= 42 ⇔  ( ( ) ) ( )
  5
 x = 1 ( − ( 3 + 2λ ) y + 14 )  1
 5  x = 5 ( − ( 3 + 2λ ) y + 14 )
 
2x + 6y − z = 5 2x + 6y − z = 5
 
  ( λ + 9 )( 3 + 2λ )  14 ( λ + 9 )  −2 14 ( λ + 9 )
⇔ y  − + ( 3 + 7λ )  y= 42 − ⇔  ( λ 2 − 7λ + 6 ) y= 42 − ...
  5  5 5 5
  1
 x = 5 ( − ( 3 + 2λ ) y + 14 )
1
 x = ( − ( 3 + 2λ ) y + 14 )
 5
(terminar …)
Obtenemos finalmente la solución del sistema en función del parámetro λ .
Segundo método : Fórmulas de Cramer

Utilizamos directamente las fórmulas de Cramer :
5 λ −1 2 5 −1 2 λ 5
1 1 1
x= 7 3 7 = y λ −5 7 7 = z λ −5 3 7
det ( S) det ( S) det ( S)
4 3 2 1 4 2 1 3 4
Quedan todavía tres determinantes por calcular. Estos últimos siendo de tamaño 3 × 3 , pode-
mos calcularlos directamente con la regla de Sarrus (recordamos que
det ( S) = −2 ( λ 2 − 7λ + 6 ) ).
Obtenemos finalmente:
14λ − 84 7λ − 42
x= = − 2
−2 ( λ − 7λ + 6 )
2
λ − 7λ + 6
14λ-84 7λ − 42
y= − =
−2 ( λ − 7λ + 6 ) λ − 7λ + 6
2 2
4λ ²-42λ +108 2λ ² − 21λ + 54

z= − =
−2 ( λ − 7λ + 6 )
2
λ 2 − 7λ + 6
Podemos ver en este ejemplo la ventaja de utilizar las fórmulas de Cramer.

Capítulo 25
REDUCCIÓN DE LAS MATRICES CUADRADAS
En este capítulo, E designa un - espacio vectorial de dimensión n, entero natural que no es

nulo, B=(e 1 ,…,e n ) una base de E, f un endomorfismo de E de matriz A en B.
1- Definiciones
1- Valor propio y vector propio

x es un vector propio asociado a f para el valor propio λ elemento de  si por
definición x no es nulo y f(x)=lx. y f(x)=λx.
Se dice entonces que λ es el valor propio asociado a x.
Propiedad: λ es un valor propio de f si y solamente si det(f-λId)=0

si y solamente si det(A-λI)=0.
2- Polinomio característico
El polinomio característico de f (respectivamente A) es el polinomio P f
(respectivamente P A ) definido por P f(λ)=det(f-λId).
Propiedad: Los valores propios son las raíces del polinomio característico.
 1 −1 −1
 
Ejemplo: Sea A=  1 3 1  . Determinar los valores propios de A.
 −1 −1 1 
 
2- Subespacio propio
Definición : Sea f un endomorfismo de E y λ un valor propio de f.

El subespacio propio de E asociado al valor propio λ es por definición E λ =Ker(f-λId).
Observación: E λ es el conjunto de los vectores propios asociados al valor propio λ unión

{0 E }.
Propiedad: De acuerdo con las notaciones anteriores, Eλ es un subespacio vectorial de E y

1 ≤ Dim(E λ ) ≤ n.
 1 −1 −1
Ejemplo: Sea A=  1 3 1  . Determinar los subespacios propios de A.
 −1 −1 1 
 
3- Diagonalización
Definición: Se puede diagonalizar f si por definición existe una base de E formada con
vectores propios de f.
Propiedad: Si λ 1 , λ 2 , …, λ p son p valores propios distintos de f, entonces:

p
E λ1 + ... + E λp =E λ1 ⊕ ... ⊕ E λp =⊕ E λk
k =1
Caso particular: Si f admite n valores propios distintos, entonces f se puede diagonalizar.
 4 −1 −2 
Ejemplo: M=  0 2 −1  .
 2 −1 0 
 
Teorema: Sean λ 1 ,…,λ p los p valores propios distintos de f (p ≤ n).

p
f se puede es diagonalizar si y solamente si E= ⊕E λi .
i =1
4- Orden de multiplicidad de un valor propio

Definición: El orden de multiplicidad de un valor propio de f es el orden de multiplicidad
de este valor considerado como raíz del polinomio característico de f.
Propiedad: Sea λ 0 un valor propio de f de multiplicidad α. Entonces, 1 ≤ Dim( E λ0 ) ≤ α.
Teorema: E designa un -espacio vectorial de dimensión n entero natural que no es nulo, f

un endomorfismo de E.
f se puede diagonalizar si y solamente si se comprueban las dos condiciones siguientes:
1- El polinomio característico de f, P f, se divide, es decir que P f admite n raíces
(distintas o confundidas) en .
2- La dimensión de cada subespacio propio es igual al orden de multiplicidad del
valor propio correspondiente.
 1 −1 −1
 
Ejemplo: Tomar de nuevo la matriz A=  1 3 1  y estudiar su diagonalización.
 −1 −1 1 
 

Interpretación geométrica : Sea E=² considerada como un -espacio vectorial con su base
canónica B=(i, j).
 5 1
 2 − 2
Sea f el endomorfismo de E definida por su matriz: A=mat(f,B)=  .
− 1 5
 
 2 2
f es diagonalizable.
Podemos escoger: e 1 =i+j, e 2 =-i+j.
Entonces, B’=(e 1 , e 2 ) es una base de ² y en esta base, la matriz de f es:
 2 0
D=mat(f,B’)=  
 0 3
 1 1
1 −1 -1  2 2  -1
Observación: Con P=   , P =  1 1  , tenemos: D=P AP.
1 1  − 
 
 2 2
Qué interpretación geométrica podemos hacer sobre f?
Sea E 2 (resp. E 3 ) la recta de base e 1 (resp. e 2 ).
Sea u un vector. Construyamos geométricamente f(u).
Descomponemos u en : u=u 1 +u 2 con u 1 elemento de E 2 y u 2 elemento de E 3 .
Obtenemos: f(u)= f(u 1 +u 2 )=f(u 1 )+f(u 2 )=2u 1 +3u 2 porque f restringido a E 2 (resp. E 3 ) es una
homotecia de razón 2 (resp. 3).
f(u)
E3 E2
j
e2 e1
i

5- Aplicaciones
1- Reconocer la naturaleza de una aplicación lineal
Sea f un endomorfismo de matriz A en relación a una base B de E.
Suponemos que A es diagonalizable y semejante a una matriz D. Además suponemos que la
estructura de D permite reconocer un tipo de endomorfismo particular: Por ejemplo una
simetría vectorial o una proyección vectorial o una mezcla de simetrías o proyecciones con
una homotecia vectorial. Entonces podemos deducir la naturaleza de f.
2- Potencia mésima de una matriz

Sea A una matriz diagonalizable. Existe una matriz P invertible y una matriz D diagonal tales
que A = PDP-1.
Entonces para todos enteros m, positivos : Am = PDmP-1.
Como D es diagonal, Dm se calcula fácilmente y nos queda solamente 2 productos de matrices
a realizar para calcular Am.
 1 −1 −1
m  
Ejemplo: Calcular A para m entero natural con A=  1 3 1  .
 −1 −1 1 
 
3- Sistema de ecuación diferencial lineal

 dx
 dt = 4x − y − 2z

 dy
Ejemplo: Resolver el sistema de ecuación diferencial
=  2y − z
 dt
 dz
= 2x − y
 dt
4- Secuencia
6- Complemento: triangularizacion

Ejercicio 1. Determinar los valores propios y los sub-espacios propios de las matrices:
 0 1 1
 3 1  
A=   y B =  1 0 1
 2 4  1 1 0
 
Ejercicio 2. Determinar en  luego en  los valores propios y los sub-espacios propios de la

 0 0 1
 
matriz: A =  1 0 0  .
 0 1 0
 
Ejercicio 3. Determinar si las siguientes matrices son diagonalizables:

 5 −1 1   −2 0 0 
   
A =  −1 1 −3 y B =  0 1 3 
 1 −3 1   1 0 1
   
Ejercicio 4. Determinar una base de vectores propios para las matrices:

 0 −1 0   2 −4 1 
   
A =  −1 0 0  y B =  6 −8 1 
 1 1 1  24 −24 2 
   
 1 1
Ejercicio 5. Calcular An para A =  .
 2 0
1
Ejercicio 6. Sea la sucesión recurrente (u n ) n definida por: ∀n ∈  \{0,1} , u n = ( u n-1 + u n-2
2
), u 0 =1 y u 1 =2.
1 1 u
 un     n −1  .
1- Mostrar que   =  2 2  
 u n −1   1 0   u n − 2 
 
1 1
2- Sea A =  2 2  . De n ∈ *, calcular A .
n-1
 
1 0 
1  1 
n −1
5
3- Deducir: u n =  5 +  −   luego lim u n = .
3   2   3

Ejercicio 1. Para A : λ 1 = 5, E 5 = vect( V=(1,2))

λ 2 = 2, E 2 = vect( V=(1,-1)).
Para B : λ1 = 2, E 2 = vect( V=(1,1,1))
λ 2 = -1, E -1 = vect( (1,-1,0), (1,0,-1) ).
Ejercicio 2. En , λ 1 = 1, E 1 = vect( V=(1,1,0))

En , λ 1 =1 y λ 2 =j, E j = vect( (j,1,j2) , (j2,1,j)).
Ejercicio 3. A sí, B no.
1 0 1
 
Ejercicio 4. Para A : P=  −1 0 1
0 1 −1

1 0 1
 
Para B : P =  1 1 1 .
4 4 0 

 2n +1 +(−1)n 2n −(−1)n 
Ejercicio 6. An = 1  n +1 .
3 2 +2(−1)n +1 2n +(−1)n 2 

EJERCICIOS
APLICACIONES DEL CURSO
Ejercicio 1. Se considera en un espacio vectorial E de dimensión n un endomorfismo f que se

puede diagonalizar, pues posee solamente dos valores propios distintos λ 1 y λ 2 de
subespacios propios asociados E1 y E 2 .
Llamamos ϕ 1 el proyector de E en E 1 en paralelo a E 2
ϕ 2 el proyector de E en E 2 en paralelo a E 1 .
¿Porqué ϕ 1 y ϕ 2 están bien definidos?
Determinar ϕ 1 + ϕ 2 ; ϕ 1  ϕ 2 ; ϕ 2  ϕ 1 ; λ 1 ϕ 1 + λ 2 ϕ 2 .
Ejercicio 2. Sea u un endomorfismo de un espacio vectorial E de dimensión finita sobre .

Justificar si las aserciones siguientes son verdaderas o falsas:
- λ valor propio de u ⇒ λ2 valor propio de u2 = u  u.
- x vector propio de u ⇒ x vector propio de u2.
- u diagonalizable ⇒ u2 diagonalizable.
Ejercicio 3. Sea E un espacio vectorial sobre de dimensión n y sea f ∈ L(E). Suponemos

que f admite un solo valor propio λ 0 ∈  y que f es diagonalisable. Determinar la aplicación f,
y deducir la matriz de f en cualquier base.
Ejercicio 4. Sea A ∈ M.(). On Suponemos que existe k tal que Ak = I n .

1 - ¿Cuáles son los valores propios posibles de A en  ? en  ?
2 - Si A es en M n () y es diagonalisable en , mostrar que A es la matriz de una
simetría.
Ejercicio 5. Las siguientes matrices son diagonalizables en M3 ()? Y en M3 () ?

 5 −3 2   4 −5 0   2 2 0  2 1 −2 
       
M1  6 −4 4 
= M2 =  2 2 0  M 3 =−
 2 −4 2  =
M 4  2 3 −4 
 4 −4 5  0 0 1  0 2 2  1 1 −1 
       
En el caso donde las matrices son diagonalizables en M3 (), dar una base de vectores
propios.
 5 −1 1 
 
Ejercicio 6. Sea A =  1 3 −1. Mostrar que A es diagonalisable. Dar una matriz D
 
 2 −2 4 
diagonal similar à A y P matriz invertible tal que D=P-1 AP. Determinar P-1.

 i −1 −i 1
 
 −1 1 −1 1
Ejercicio 7. Sea A= . Mostrar que A es diagonalisable. Dar una matriz D
 −i −1 i 1
 
 1 1 1 1
diagonal similar à A y P matriz invertible tal que D=P-1 AP.
Ejercicio 8.
1. Mostrar que los vectores u = ( 3, 0,1) , v = ( −2, −1, −1) y w = (1, 0, 0 ) forman una base
de 3.
2. Sea f el endomorfismo de 3 donde la matriz en la base canónica es:
 −1 −2 6 
 
A =  −1 0 3 
 −1 −1 4 
 
a. Determinar f(u), f(v) y f(w). Deducir la matriz M de f en la base (u,v,w).
b. Verificar que 1 es valor propio triple de M y comprobar que f no es
diagonalizable.
1 α β 
 
Ejercicio 9. Discutir las posibilidades de diagonalizar M =  0 1 γ  en la base canónica.
 0 0 −1
 
Ejercicio 10. ¿Se puede diagonalizar la matriz siguiente? Si es el caso, diagonalizarla.

 
 0 a a² 
 
1 0 a
a 
1 1 
 0 
 a² a 
0 1 1 1 1 1
 
1 0 1 1 1 1
1 1 0 1 1 1
Ejercicio 11. Sea M=   . Designamos por u el endomorfismo de 6 por el
1 1 1 0 1 1
1
 1 1 1 0 1
1
 1 1 1 1 0 
cual la matriz en la base canónica de 6 es M y por id la identidad de 6.
1- Determinar Ker(u+id). Dar una base ε así que su dimensión.
2- Deducir que (-1) es n valor propio de u, de orden por lo menos 5.
3- Calcular el 6imo valor propio de u. Determinar el subespacio propio asociado al
cual daremos una base η. u es diagonalizable ? Decir por qué ε ∪ η es una base B’
de 6.

4- Escribir la matriz M’ de u en la base B’. Calcular det(u) y deducir que u e s
invertible.
5- Mostrar que u  u=5id + 4u. Deducir la matriz M-1.
Ejercicio 12. ¿ Se puede diagonalizar la matriz siguiente en  o en ?

 0 -2 0 
 
M =  1 0 -1
 
0 2 0 
Determinar M n en M 3 (),donde n es un entero natural que no es nulo.
 3 1
Ejercicio 13. Encontrar una solución de la ecuación X n =   para n fijo en  y X
1 3
incógnita en M 2 ().
Ejercicio 14. a- Mostrar que si X es un vector propio asociado al valor propio λ de un

endomorfismo “u” de un espacio vectorial que no es nulo E, entonces X es un vector propio
de todas las potencias u n de u donde n es un entero natural que no es nulo.
b- Sea E un -espacio vectorial de dimensión 4 y u un endomorfismo de E con
matriz :
 0 1 0 0
 2 0 -1 0
M =  
 0 7 0 6
 
 0 0 3 0
en una base dada B = ( e 1 ,e 2 ,e 3 ,e 4 ) de E.
1- ¿Se puede diagonalizar la matriz M? Determinar los subespacios propios de u.
2- ¿Se puede diagonalizar la matriz M n , donde n es un entero natural que no es nulo?
Determinar los subespacios propios de u n .
Ejercicio 15. Resolver el sistema diferencial:

 dx
 dt = 4x − 3y + 9z

 dy
 = − 3x + 4y − 9z
 dt
 dz
 dt = − 3x + 3y − 8z

Ejercicio 16. Sea la secuencia "doble" definida por :

 u n+1 = −10u n − 28v n

 v n+1 = 6u n + 16v n
Determinar u n y v n en función de u 0 , v 0 y n.

Ejercicio 17. Sea f el endomorfismo de 3 donde la matriz en la base canónica es :
2 2 0
1 
=A  1 3 −1 .
2 
 −1 1 3 
 2 0 0
 
1. Mostrar que la matriz A es semejante a la matriz T =  0 1 1  .
0 0 1
 
2. Deducir los valores propios de f. f es diagonalizable ?
Ejercicio 18. Consideramos el endomorfismo f de 3 donde la matriz en la base canónica

es :
 3 2 4
 
A=  −1 3 −1 
 −2 −1 −3 
 
1. Verificar que los valores propios de f son -1 et 2, y determinar la multiplicidad de cada
valor.
2. Demostrar que f no es diagonalizable.
3. Suponemos u=(-1,0,1) y v=(-2,-1,1). Verificar que E −1 = Vect ({u} ) y que
E 2 = Vect ({v} ) .
H Ker ( f − 2 Id ) .
2
4. Sea
=
Verificar que v ∈ H después determinar una base {v,w} de H conteniendo el vector v.
5. Verificar que la familia {u,v,w} es una base de 3 después determinar la matriz de f en
esta base. Que puede constatar?
 1 3 − 1
 
Ejercicio 19. Mostrar que la matriz M=  − 1 − 3 1  es similar a la matriz
 
 2 −2 2 
 0 1 0
 
T=  0 0 1 .
 
 0 0 0
 0 1 0  2 1 0
   
Ejercicio 20. Mostrar que la matriz A=  − 4 4 0 es similar a la matriz T=  0 2 0 .
   
 − 2 1 2  0 0 2

Ejercicio 21. Consideramos la matriz A asociada a un endomorfismo f de 3 relacionada a su
1 0 0 
 
base canónica: A=  0 0 −1
0 1 2 
 
1- Mostrar que λ = 1 es el único valor propio de A.
2- Determinar el espacio propio Eλ dando una base. A es diagonalizable?
3- Sea B = (e l , e 2 ) una base de E λ tal que el = (1, 0, 0) y e2 = (0,1, -1).
a- Completar B en una base (e l , e 2 , e 3 ) de 3 en la cual la matriz del endomorfismo f
se escribe:
1 0 0
A’=  0 1 1 
0 0 1
 
n
b- Tomaremos e 3 = (0, -1, 0). Calcular A para n ≥ 0 ( utilizando A’ y una
demostración por recurrencia).

PROBLEMA DE SÍNTESIS
Problema Sea E un -espacio vectorial de dimensión 2, y u un elemento de L(E). El

endomorfismo de identidad se escribe Id .
1- Se supone que u n o se puede diagonalizar, pero posee un valor propio doble λ 1 .
Mostrar que el subespacio propio E λ1 es de dimensión 1. Sea B=(e 1 ,e 2 ) una base de E tal que
λ µ
e 1 pertenece a E λ1 . Mostrar que M B ( u) =  1  con µ que no es nulo. Sea B’=(µe 1 ,e 2 ).
0 λ1
Dar M B’ (u).
 α β
2- Se supone ahora que u no posee valores propios (reales). Sea A=   la matriz
 γ δ
de u en una base. Se recuerda que la traza de A, escrita Tr(A), es α+δ. Se plantea a=½ tr(A), y
v=u-aid. Mostrar que tr(A-aI)= 0, que v no posee valores propios y que su polinomio
característico P(λ) se escribe:
P(λ)=λ²+b² con b que no es nulo
Mostrar que si Q(λ) es el polinomio característico de v², tenemos a Q (λ²)=P(λ)P(-λ) y que
 v( x) 
Q(λ)=(λ+b²)². Sea x un vector propio de v² para el valor propio -b². Mostrar que B=  x, 
 b 
es una base de E. Dar M B (v) y M B (u).
3- Deducir de lo anterior que para todo u de L(E), existe una base B de E tal que
λ 1  a − b
M B (u) es diagonal, o bien de la forma  1  , o bien de la forma   con b que no
0 λ1 b a 
es nulo.

Solución abreviada
1- Tenemos 1 ≤ dimE λ1 < 2 . Pues, dimE λ1 =1.

u(e 1 )=λ 1 e 1 , de ahí la 1era columna.
El 2do λ 1 de la diagonal procede del hecho que λ 1 es un valor propio doble (y de la traza …)
µ no es nulo porque u no se puede diagonalizar.
λ 1
Se obtiene: M B’ (u)=  1 
 0 λ1 
2- tr(A-aI)=tr(A) – atr(I)=0.
λ 2 valor propio de v si y solamente si λ 2 + a valor propio de u: Absurdo.
No hay término en λ en P(λ) porque la traza es nula.
Como no hay valor propio real, el término constante es estrictamente positivo; se puede pues
escribirlo b² con b que no es nulo.
Q(λ²) = det(v² - λ²id) = det(v - λid).det(v + λid) = P(λ).P(-λ) = (λ²+b²)².
Se trabaja en el cuerpo , entonces Q(λ)=(λ + b²)².
 v( x ) 
Si x ,  es una familia vinculada, x sería un vector propio. Absurdo. De ahí el resultado.
 b 
v( x )  v( x )  1 1
Tenemos v(x)=b y v  = v²(x)= (-b²x)=-bx.
b  b  b b
0 − b
Entonces M B (v)=   .
b 0 
v( x )
Tenemos u(x)=(v+aid)(x)=v(x)+ax=ax+b
b
 v ( x )   v ( x )  v ²( x) v( x ) v( x )
Además u   =(v+aid)  = +a =-bx+a .
 b   b  b b b
a − b
Entonces M B (u)=   .
b a 
3- Basta con hacer la distinción entre diagonalizable, no diagonalizable con un valor propio
doble y sin valor propio doble.

Ejercicio 22. Trabajamos en E=3. Las siguientes matrices son diagonalizables en M 3 () ?
en M 3 () ?
 0 −1 0  0 1 1  1 −1 2 
1- M1 =      
 −1 0 −1 ; 2- M 2 =  1 0 1  ; 3- M 3 = −2 1 −3  ;
 0 −2 0  1 1 0  −1 1 −2 
     
 1 1 0
4- M 4 =  −1 2 1  .
 1 0 1
 
Determinar una base de vectores propios para M 2 .
Corrección: Para determinar si esas matrices son diagonalizables o no, comencemos

buscando los valores propios de cada una de esas matrices, y para ello determinaos las raíces
del polinomio característico.
1- Tenemos :
− X −1 0
− X −1 −1 0
P1 ( X ) =det ( M1 − X Id ) =−1 − X −1 = −X +
segun1era linea −2 −X −2 −X
0 −2 −X
−X ( X 2 − 2 ) + X =
= −X ( X 2 − 3)
−X 3 + 3X =
Este polinomio admite tres raíces simples 0, 3, − 3 .
Deducimos que la matriz M 1 es diagonalizable en M 3 (), y entonces en M 3 ().
2- Tenemos:
−X 1 1 −X + 2 −X + 2 −X + 2 1 1 1
P2 ( X ) =det ( M 2 − X Id ) = 1 −X 1 = 1 −X 1 =( −X + 2 ) 1 −X 1
L1 ← L1 + L 2 + L3
1 1 −X 1 1 −X 1 1 −X
1 0 0
= ( −X + 2 ) 1 −X − 1 0 =( −X + 2 )( X + 1)
2
C2 ← C2 − C1
C3 ← C3 − C1
1 0 −X − 1
Este polinomio admite una raíz simple 2, y una raíz doble (-1).
No podemos entonces concluir directamente, tenemos que estudiar la dimensión del sub
espacio asociado al valor propio (-1) que lo llamamos E -1 .
Por definición, tenemos
= a E −1 Ker ( M 2 + Id ) , entonces tenemos:
 y + z =− x x
  
u ∈ E −1 ⇔ M 2 u + u =0 ⇔ M 2 u =− u ⇔  x + z =− y ⇔ x + y + z =0 con mat(u)=  y  .
 x + y =− z z
  
Deducimos que E −1 es un espacio de dimensión 2 (es un plano!).
Concluimos que la matriz M 2 es diagonalizable en M 3 (), y entonces en M 3 ().
Busquemos ahora una base de vectores propios para M 2 .

De acuerdo con lo que venimos de ver, tenemos:
E
= −1 {( x, y, − x − y ) ∈=
E} {x (1, 0, −1) + y ( 0,1, −=
1)} Vect {(1, 0, −1) , ( 0,1, −1)} .
La familia {(1, 0, −1) , ( 0,1, −1)} es obviamente libre, entonces es una base de E −1 .
Por otro lado, tenemos

= E 2 Ker ( M 2 − 2Id ) .
 y + z = 2x 2x + 2y + 2z = 2x + 2y + 2z
  x = y
u ∈ E 2 ⇔ M 2 u =2u ⇔  x + z =2y ⇔  x =−z + 2y ⇔ .

L1 ← L1 + L 2 + L3
  z=y
=  x + y 2z −=z + 2y + y 2z
De donde
= E2 {=
( y, y, y )} Vect {(1,1,1)} .
Finalmente, concluimos que una base de vectores propios para M 2 está dada por la familia:
{(1, 0, −1) , ( 0,1, −1) , (1,1,1)} .
3- Tenemos:
1 − X −1 2
P3 ( X ) =
det ( M 3 − X Id ) = −2 1 − X −3
−1 1 −2 − X
(1 − X ) ( −2 − X ) − 4 − 3 + 2 (1 − X ) + 3 (1 − X ) + 2 ( 2 + X ) =
2
= −X3 .
Sarrus
Este polinomio admite una raíz triple 0.
- Primer método: Para saber si esta matriz es diagonalizable, determinaremos la
dimensión de E 0 = Ker ( M 3 ) . Terminar…
- Segundo método: Si M 3 fuera diagonalizable, entonces ella sería semejante la matriz
nula. Absurdo. Entonces, M 3 no es diagonalizable.
4- Tenemos:
1− X 1 0
P4 ( X ) = det ( M 4 − X Id ) = −1 2 − X 1 = (1 − X ) ( 2 − X ) + 1 + (1 − X )
2
Sarrus
1 0 1− X
= ( X − 2 ) ( X 2 − 2X + 2 ) .
El polinomio X 2 − 2X + 2 posee un discriminante negativo, lo que significa que no tiene
raíces reales. Deducimos que M 4 no es diagonalizable en M 3 ().
Por el contrario, el discriminante no es nulo, entonces esto significa que él posee dos raíces
complejas distintas.
El polinomio característico P 4 posee entonces tres raíces simples en , y concluimos que la
matriz M 4 es diagonalizable en M 3 ().
Ejercicio 23. Sea u el endomorfismo de 3 cuya matriz en la base canónica es:

 
1 2 4
 
1
A= 1 2
2 
1 1 
 1 
4 2 
1- Calcular det A .
2- Determinar el rango de A.
3- Cuál es la dimensión de Ker u ? Determinar una base en este espacio.
4- Calcular los valores propios de A y mostrar que A es diagonalizable.
5- Determinar una base de vectores propios de A y dar la matriz de pasaje P de la base
canónica a esta base. Calcular P −1 .
6- Deducir la expresión de A n para n ≥ 1.
Corrección: 1- Por la regla de Sarrus (por ejemplo), encontramos det A = 0 .

Podemos también observar que al menos dos líneas o dos columnas están ligadas (la tercera y
la segunda columna) y entonces det A = 0 .
2- Utilizamos el método de los ceros escalonados:
 1 2 4  1 0 0
   
= rang A rg = 1/ 2 1 2  = rg 1/ 2 0 0  1 .
C ← C − 2C
1/ 4 1/ 2 1  C32 ←C32 − 4C11 1/ 4 0 0 
   
Esto significa que dim Im u = 1 .
3- De acuerdo con el teorema del rango, tenemos:= dim E dim Im u + dim Ker u .
Entonces, de acuerdo con al pregunta precedente, deducimos que : dim Ker u = 3 − 1 = 2 .
Una base de Ker u está entonces constituida de dos vectores libres de Ker u .

 x + 2y + 4z = 0
 1 2 4  x   0  
     1
AX =0 ⇔ 1/ 2 1 2  y  = 0  ⇔  x + y + 2z =0 ⇔ x + 2y + 4z =0
 1/ 4 1/ 2 1  z   0  2
     1 1
 4 x + 2 y + z = 0
De donde Ker u ={( x, y, z ) / x + 2y + 4z =0} ={( −2y − 4z, y, z )} =Vect {( −2,1, 0 ) , ( −4, 0,1)}
La familia {( −2,1, 0 ) , ( −4, 0,1)} es obviamente libre, entonces es bien una base de Ker u .
1− X 2 4
4 − PA ( X )= det ( A − X Id )= 2 = (1 − X ) + 1 + 1 − (1 − X )(1 + 1 + 1)
3
1/ 2 1− X
Sarrus
1/ 4 1/ 2 1 − X
= 1 − 3X + 3X 2 − X 3 + 2 − 3 + 3X = 3X 2 − X 3 = X 2 ( 3 − X )
Los valores propios de A son 0 y 3 de multiplicidad 2 y 1 respectivamente.
A es diagonalizable si y solamente si si dim E 0 = 2 .
Como, por definición, E 0 = Ker u entonces de acuerdo con la pregunta
precedente, dim E 0 = 2 y así A es diagonalizable.
5- Para determinar una base de vectores propios de A, hay que determinar una base de
E3 :


−2x + 2y + 4z = 0
 −2 2 4  x  0  − x + y + 2z =0
     1 
( A − 3I ) X =0 ⇔ 1/ 2 −2 2   y  = 0  ⇔  x − 2y + 2z =0 ⇔  x − 4y + 4z =0
     2 
1/ 4 1/ 2 −2   z   0  1 1  x + 2y − 8z =
0
 4 x + 2 y − 2z =
0
− x + y + 2z =0
  x = 4z
⇔ −3y + 6z= 0 ⇔ 
3y − 6z = 0  y = 2z

De donde: =
E3 {( x, y, z ) =
/x 4z,=
y 2z
=} {( 4z, 2z, z=
)} Vect {( 4, 2,1)} .
Deducimos que la familia {( 4, 2,1) , ( −2,1, 0 ) , ( −4, 0,1)} es una base de vectores propios de A y
la matriz de pasaje asociada es :
 4 −2 −4 
 
P = 2 1 0 
1 0 1 
 
Para calcular P −1 , podemos utilizar la transpuesta de la matriz de adjuntos y obtenemos:
1 2 4
−1 1 
P = −2 8 −8 
12  
 −1 −2 8 
6- Tenemos la relación A = PDP −1 donde D es la siguiente matriz diagonal:
 3 0 0
 
D = 0 0 0
0 0 0
 
Mediante una recurrencia inmediata, tenemos entonces: A n = PD n P −1 .
 3n 0 0 
 
Como, también tenemos: D n =  0 0 0 
 0 0 0
 
 4 −2 −4   3 0 0   1 2 4 
n
1   
Concluimos que:=A n PD n= P −1  2 1 0   0 0 0   −2 8 −= 8  3n −1 A .
12    
 1 0 1   0 0 1   −1 −2 8 

Capítulo 26
A PROPOSITO DE LA REDACCION
Uno de los problemas para los estudiantes (fuera de los problemas puramente
matemáticoas) es la redacción.
Qué escribimos ? Qué cosas no podemos escribir ? Es que mi demostración es correcta
y es que ha sido redactada correctamente ?....
El objetivo de este capítulo no consiste en responder globalmente todas esas preguntas
sino el de simplemente dar ejemplos (reales) de las hojas de exámenes con el fin de dar una
idea de lo que es posibile (y conveniente) de escribir en una redacción.
A través los ejercicios y los problemas de examénes de años anteriores (basados en el
mismo programa) ofrecemos de manera similar a las hojas de examen. No se trata de modelos
perfectos de redacción que hay que seguir al pie de la letra, sino simplemente de ejemplos …

Ejercicio 1.
Sea n un entero natural estrictamente positivos.
n(n+1)(n+2)
Mostrar que : (1×2)+(2×3)+(3×4)+......+n(n+1)= .
3

Ejercicio 2. Sea u un endomorfismo de un espacio vectorial E de dimensión finita sobre .
Justificar si las siguientes implicaciones son verdaderas o falsas :
- λ valor propio de u ⇒ λ2 valor propio de u2 = u ou.
- x vector propio de u ⇒ x vector propiode u2.
- u diagonalizable ⇒ u2 diagonalizable.

  
Ejercicio 3.  3 tiene por base canónica B = i, j, k . ( )
 1 1 0 
3 1  
Notamos f al endomorfismo de  tal que Mat (f,B )= M =  1 1 0 .
2
 1 -1 2 
1- Dar una base de Kerf , de Imf.
2- Calcular M 2 . Qué podemos deducir ?
 
3- Tomamos u = k ; v = i + j + k y w = i - j - k .
( )
3-1- Demostrar que la familia B ’= u, v, w es una base de  3 . Escribir la matriz de
paso P de B a B ’.

3-2- Desarrollar i , j et k en función de u , v y w .
3-3- Deducir la matriz de paso Q de B ’a B . Podemos obtener Q de otra manera ?

Ejercicio 4. Consideramos la sucesi’on de polinomios P n definida por:
P0 (X)=1 P1 (X)=X et Pn+1 (X)=2XPn (X)-Pn-1 (X) para n ≥ 1.
1-1- Calcular P 2 ,P 3 ,P 4 .
1-2- Determinar para n en * el grado de P n y su término de grado más alto.
2-1- Mostrar por recurrencia sobre el entero natural n, que para x>1 , Pn (x) ≤ Pn+1 (x) .
2-2- Deducir que : para n entero natural, x>1 ⇒ Pn (x)>0 .
2-3- Admitiremos que Pn tiene la misma paridad que n.
Mostrar entonces que las raíces de P n están entre [-1, 1].
3- Para x ∈ [−1, 1] ,tomamos : x = cos θ , θ ∈ [0, π ] .
3-1- Mostrar que para todo n en , tenemos : P n (cos θ. ) = cos(n θ ).
Deducir que para x entre [-1, 1], P n (x) = cos (n arccos (x)).
3-2- Resolver la ecuación: cos (n arccos (x))=0 . Deducir que para n ∈ * y x ∈  :
n −1   ( 2k + 1) π  
n-1 ∏  x − cos   
P n (x) = 2  2n
k =0   

 π
Ejercicio 5. (Extracto) Sea f la función definida sobre 0,  par : f (x) = ln(cos x) .
 2
 π
1- Mostrar que f es un bijección de 0,  sobre un intervalo a determinar. Dar su
 2
-1 -1
bijección recíproca f y calcular (f )’ de dos maneras diferentes
x2
2-1- Mostrar que existe un real θ entre ]0, 1[ tal que : f(x) = ln(cos x) = − .
2 cos 2 (θ x)
A continuación, admitiremos la unicidad de este real θ. Definimos así una función u :
θ = u ( x) .
2-2- Desarrollaru(x) en funciónde x.

Ejercicio 6. 1. Sea a un real estrictamente positivo.
+∞ cos u
1.1 Mostrar que ∫ du existe
a u²
+∞ sin u
1.2 Utilizando una integración por partes, demostrar que ∫a u
du existe.
cos u
+∞
Admitimos, del mismo modo: ∫
a u
du existe.
+∞ sin u
1.3 Demostrar que ∫ du existe.
0 u
2. Sean a y x dos reales estrictamente positivos.
Utilizando un cambio de variables, demostrar:
x sin t a + x sin u a + x cos u
∫0 t+a dt = cos a ∫a u du - sin a ∫a u du
+∞ sin t +∞ sin u +∞ cos u
Deducir que ∫ dt existe y vale : cos a ∫ du - sin a ∫ du .
0 t+a a u a u
1 cos u
3. Demostrar que ∀a ∈ ]0,1[ , 0 ≤ ∫ du ≤ − ln a .
a u
+∞ cos u +∞ sin t +∞ sin u
Deducir que Lim sin a ∫ du = 0 luego que Lim ∫ dt = ∫ du .
a →0 a u a →0 0 t+a 0 u


MATEMÁTICAI Amerinsa

Cargado por

Información del documento

Título original

Derechos de autor

Formatos disponibles

Compartir este documento

Compartir o incrustar documentos

Opciones para compartir

¿Le pareció útil este documento?

¿Este contenido es inapropiado?

Copyright:

Formatos disponibles

MATEMÁTICAI Amerinsa

Cargado por

Copyright:

Formatos disponibles

MATEMATICAS

Auteur de la Ressource Pédagogique

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 2

Post Scriptum.: S i detectan errores de mecanografiado o si tienen observaciones,

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 3

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 4

Cap. 0 : ALGUNOS CONCEPTOS FUNDAMENTALES 7

Cap. I : TEORÍA DE CONJUNTOS 13

Cap. II : LA LÓGICA MATEMÁTICA 22

Cap. III : LA DEMOSTRACIÓN MATEMÁTICA 43

Cap. IV : FUNCIÓN, APLICACIÓN, BIYECCIÓN 52

Cap. V : COMPLEMENTOS SOBRE LOS NÚMEROS COMPLEJOS 65

Cap. VI: COMPLEMENTOS EN TRIGONOMETRÍA 81

Cap. VII: LOS POLINOMIOS 88

Cap.VII: LAS FRACCIONES RACIONALES 107

Cap. IX: COMPLEMENTOS SOBRE LOS REALES 117

Cap. X: FUNCION DE UNA VARIABLE REAL 130

Cap. XI: FUNCIONES ELEMENTALES 157

Cap. XII: COMPARACIÓN DE FUNCIONES 181

Cap. XIII: CÁLCULO DIFERENCIAL 191

Cap. XIV: DESARROLLOS LÍMITES 211

Cap. XV: SUCESIONES DE REALES 231

Cap. XVI: INTEGRAL DE RIEMANN 250

Cap. XVII: CÁLCULO PRÁCTICO DE PRIMITIVAS Y DE INTEGRALES 266

Cap. XVIII: INTEGRALES GENERALIZADAS 285

Cap. XIX: ESPACIO VECTORIAL 304

Cap. XX: APLICACIONES LINEALES 327

Cap. XXI: MATRICES 346

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 5

Cap. XXIII: DETERMINANTES 371

Cap. XXIV: SISTEMA DE ECUACIONES LINEALES 385

Cap. XXV: REDUCCIÓN DE MATRICES CUADRÁTICAS 394

Cap. XXVI: A PROPOSITO DE LA REDACCION 411

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 6

Inyección o correspondencia inyectiva de E en F

Suprayección o correspondencia suprayectiva de E sobre F

Biyección o correspondencia biyectiva de E sobre F

Composición de las aplicaciones

2. El compuesto de dos inyecciones es una inyección.

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 7

Una aplicación f: E → E es una involución si y solamente si se cumple alguna de las propie-

Restricción de una aplicación. Prolongación

El grupo (G, *) es conmutativo si y solamente si la ley * es conmutativa (cualesquiera que

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 8

- Espacio vectorial o espacio vectorial en 

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 9

• Sea el plano P cuya ecuación es ax+by+cz+d=O, (a, b, c) ≠ (0, 0,0).

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 10

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 11

Formulas de multiplicación por dos

Transformación de productos en sumas

Transformación de sumas en productos

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 12

Peano Giuseppe (1858-1932) es un matemático italiano, así

• los símbolos de los conjuntos ∈ , ⊂ , ,  (pero el signo ⊂ es más seguramente fruto

© [G. ATHANAZE], [2011], INSA de Lyon, tous droits réservés. 13

3. El conjunto vacío es un conjunto que no contiene ningún elemento. Se representa con la

4. Un conjunto unitario es un conjunto que posee un único elemento.

Sean A y B dos conjuntos. Se dice que A está incluido en B si todo elemento de A es

Atención: No confundir entre “pertenece” e “incluido”.

Sea A un conjunto. El conjunto de sus sub-conjuntos (de sus partes) es el conjunto de

Observación: Si el cardinal (número de elementos) de A es finito e igual al entero n, entonces el

Igualdad de dos conjuntos

El grupo (G, ) es conmutativo si y solamente si la ley es conmutativa (cualesquiera que