LGEBRA

1.- RESOLUCIN DE SISTEMAS. MTODO DE GAUSS

El mtodo Gauss consiste en convertir la matriz asociada a un sistema de ecuaciones en
otra matriz equivalente triangular superior, haciendo ceros debajo de la diagonal
principal.
|
|
|
|

\
|

|
|
|
|

\
|

i
h
g
f 0 0
e d 0
c b a
...
b
b
b
a a a
a a a
a a a
j i
F F
3
2
1
33 32 31
23 22 21
13 12 11


Para ello se utilizan tres tipos de transformaciones elementales:
o Intercambiar filas.
o Sumar y/o restar filas.
o Multiplicar filas por un nmero para luego sumarlas o restarlas.
Es importante seguir un orden para no estropear los ceros ya conseguidos. Por
ejemplo, en un primer paso se puede hacer ceros los trminos a
21
y a
31
, y en el
siguiente, el trmino a
32
.
Una vez conseguida la matriz triangular superior, se transforma en ecuacin la tercera
fila para calcular z; despus se sustituye este valor en la ecuacin correspondiente a la
segunda fila averiguando el valor de y; y finalmente, se sustituyen ambos valores en la
ecuacin asociada a la primera fila para obtener x.
Con el mtodo de Gauss tambin se pueden discutir (clasificar) sistemas de ecuaciones,
estudiar el rango de una matriz o calcular su inversa (mtodo de Gauss-Jordan); pero,
en general, resulta ms cmodo utilizar determinantes.
Mtodo de Gauss-Jordan.- Consiste en considerar la matriz identidad, I, adosada a la
derecha de la matriz A y, mediante transformaciones elementales, conseguir que la
matriz identidad quede situada a la izquierda, obteniendo as la matriz inversa adosada
a su derecha:

( )
A I
s elementale ciones Transforma

( )
1
I A

2.- RESOLUCIN DE PROBLEMAS

Normalmente se trata de resolver un problema de enunciado con tres incgnitas.
Debemos definirlas correctamente, plantear un sistema de tres ecuaciones y
resolverlo por el mtodo de Gauss o aplicando la regla de Cramer. Finalmente se
interpreta la solucin obtenida. En principio no procede aplicar el T
ma
de Rouch-
Frbenius porque se supone que la solucin es nica (compatible determinado). Otras
veces debemos plantear ecuaciones que dependen de algn parmetro; en estos casos
s es preciso estudiar cundo tienen solucin.




3.- MATRICES QUE CONMUTAN

El ejercicio suele consistir en calcular uno o ms parmetros para que el producto de
dos matrices A y B sea conmutativo. Para resolverlo, calculamos las matrices A B y
B A , e imponemos como condicin que ambas sean iguales: A B B A = . Igualando
trmino a trmino, normalmente generaremos un sistema de ecuaciones, y
resolvindolo, conseguiremos la solucin.


4.- GRANDES POTENCIAS DE UNA MATRIZ

Dada una matriz cualquiera, A, nos pueden pedir calcular:
o Una gran potencia de esa matriz, por ejemplo, A
124
.
o Su n-sima potencia, es decir, A
n
.
En ambas situaciones debemos ir calculando las sucesivas potencias de A: A
2
, A
3
,...
En el primer caso llegar un momento en que volvamos a obtener A o la matriz
identidad, I, con lo que, aplicando la regla de la divisin y las propiedades de las
potencias, resulta sencillo decidir cul es la matriz A
124
.
En el segundo caso debemos analizar como van evolucionando los trminos de las
sucesivas matrices para dejarlos en funcin de n, como trmino general de una
sucesin.


5.- USO DE MATRICES PARA PROBLEMAS DE ENUNCIADO

Se trata de utilizar matrices como forma de representacin de situaciones de
contexto real, y hacer las operaciones adecuadas entre ellas (suma, transposicin,
producto,...). Para hacer estas operaciones es imprescindible tener en cuenta las
dimensiones de cada matriz y los conceptos que representan cada una de esas
dimensiones.


6.- CLCULO DE DETERMINANTES

o Determinantes de orden tres (regla de Sarrus):
11 12 13
21 22 23 11 22 33 12 23 31 21 32 13 13 22 31 12 21 33 23 32 11
31 32 33
a a a
a a a a a a a a a a a a a a a a a a a a a
a a a
= + +

o Determinantes de orden superior a tres. Conviene hacer ceros previamente,
aplicando la siguiente propiedad de los determinantes: Si a una fila (o columna) le
sumamos el producto de una paralela por un nmero, el determinante no vara. Despus
se desarrolla por una fila o columna. Por ejemplo:
11 1n
11 11 12 12 1n 1n
n1 nn
a a
a A a A ... a A
a a
= + + +

7.- RANGO DE UNA MATRIZ

El rango de una matriz es el nmero de filas (o columnas) linealmente independientes.
Coincide con el mximo orden de sus menores no nulos. Para calcularlo se puede
comenzar detectando un menor de orden dos no nulo e ir amplindolo a rdenes
mayores hasta decidir el rango. Tambin coincide con el nmero de filas (o columnas)
distintas de cero tras aplicar el mtodo de Gauss. Es un ejercicio tpico estudiar el
rango de una matriz dependiendo de los diferentes valores que tome un parmetro.



8.- DISCUSIN DE SISTEMAS

Se trata de discutir (clasificar) y/o resolver un sistema de ecuaciones lineales
dependiendo de los valores que tome un parmetro. Se procede de la siguiente forma:
1.- Se toma la matriz (A|B) formada por la matriz de coeficientes A y la matriz de
trminos independientes B. Se estudia el rango de la matriz A en los diferentes casos
y se compara con el rango de la matriz AB.
2.- Se aplica el T
ma
de Rouch-Frbenius (comparacin de rangos):
o Si rango (A) = rango (AB) = n de incgnitas SISTEMA COMPATIBLE
DETERMINADO. (Solucin nica: los planos se cortan en un punto).
o Si rango (A) = rango (AB) < n de incgnitas SISTEMA COMPATIBLE
INDETERMINADO. (Infinitas soluciones: los planos cortan en una recta o
coinciden).
o Si rango (A) rango (AB) SISTEMA INCOMPATIBLE. (No tiene
solucin, los planos no tienen ningn punto en comn).

Si el sistema es homogneo (todas las ecuaciones estn igualadas a cero), no se utiliza
la columna B, y se aplica:
o Si rango (A) = n de incgnitas SISTEMA COMPATIBLE
DETERMINADO (Solucin trivial: 0 z y x = = = ).
o Si rango (A) < n de incgnitas SISTEMA COMPATIBLE
INDETERMINADO (Infinitas soluciones).



9.- REGLA DE CRAMER

La solucin de un sistema de ecuaciones compatible y determinado es:
A
A
x
x
= ;
A
A
y
y
= ;
A
A
z
z
= ;
donde
x
A es la matriz que resulta de sustituir en A la columna de coeficientes de x
por la de trminos independientes. Y, anlogamente,
y
A y
z
A se obtienen sustituyendo
en A la columna de los coeficientes de la incgnita correspondiente por la columna de
trminos independientes.




Tambin se puede utilizar la regla de Cramer para resolver sistemas compatibles
indeterminados de la siguiente forma:
Sea AB, la matriz asociada al sistema de ecuaciones
11 12 13 1
21 22 23 2
31 32 33 3
A
a a a b
AB a a a b
a a a b
| |
|
=
|
|
\

En este caso ran (A) = ran (AB) = 2 < n de incgnitas = 3. Utilizamos un menor de
orden dos distinto de cero, por ejemplo,
11 12
21 22
a a
0
a a
; entonces despreciamos la
tercera fila (ecuacin) pues no forma parte del menor; llamamos z = , y formamos la
matriz asociada a un nuevo sistema de dos ecuaciones con dos incgnitas:
1 13 11 12
2 23 21 22
A
b a a a
b a a a

| |
|
|

\

que podremos resolver aplicando la regla de Cramer.


10.- CLCULO DE LA MATRIZ INVERSA POR DETERMINANTES

Para que una matriz cuadrada, A, tenga inversa, A
-1
, es necesario que su determinante
sea distinto de cero; en este caso se dice que A es regular y:
11 21 31
1
12 22 32
13 23 33
Traspuesta de la
matriz de adjuntos
A A A
1
A A A A
A
A A A

| |
|
=
|
|
\

con
i j
ij ij
A ( 1)
+
=


11.- ECUACIONES MATRICIALES

Consiste en resolver ecuaciones cuya incgnita es una matriz X. Para conseguirlo
utilizamos la matriz inversa y tenemos en cuenta que el producto de matrices no es
conmutativo (se multiplican ambos miembros por la derecha o ambos miembros por la
izquierda, segn interese):
1. A X = B A
-1
A X = A
-1
B I
d
X = A
-1
B X = A
-1
B
2. X A = B X A A
-1
= B A
-1
X I
d
= B A
-1
X = B A
-1



12.- FORMA MATRICIAL DE UN SISTEMA DE ECUACIONES
Cualquier sistema de ecuaciones lineales se puede expresar como ecuacin matricial:
11 12 13 1 11 12 13 1
21 22 23 2 21 22 23 2
31 32 33 3 31 32 33 3
" " "
A X B
a x a y a z b a a a x b
a x a y a z b a a a y b
a x a y a z b a a a z b
| | | | | | + + =
| | |
+ + = =

| | |

| | |
+ + =
\ \ \


y resolverse como tal, empleando la matriz inversa de A.

GEOMETRA
1.- BASE EN lR
3


Dados los vectores

x ,

y ,

z ,,

w y los nmeros a, b, c,, g, la expresin

+ + + + w g ... z c y b x a se llama combinacin lineal de esos vectores.
Dos vectores son linealmente dependientes si alguno de ellos se puede expresar
como combinacin lineal de los dems. En caso contrario se llaman linealmente
independientes.
o Dos vectores alineados (proporcionales) son L.D.
o Dos vectores no alineados son L.I.
o Tres vectores coplanarios son L.D.
o Tres vectores no coplanarios son L.I.
Tres vectores no coplanarios,

x ,

y ,

z , forman una base ) z , y , x (

porque cualquier
otro vector se puede expresar como combinacin lineal de ellos.
Si los vectores

x ,

y ,

z son perpendiculares entre s, la base ) z , y , x (

se llama
ortogonal. Si adems tienen mdulo 1, se dice que la base es ortonormal.
Dada una base ) z , y , x (

, cualquier vector

v se puede expresar de forma nica como

combinacin lineal de sus elementos:

+ + = z c y b x a v . Se escribe ) c , b , a ( v =

y
se llaman coordenadas del vector

v respecto a la base .


2.- PRODUCTOS DE VECTORES.

Producto escalar: ) v , u ( cos v u v u



= y tambin
3 3 2 2 1 1
v u v u v u v u + + =

.
Se aplica para:
o Calcular el mdulo de un vector:
2
3
2
2
2
1
u u u u u u + + = =

.
o Calcular el ngulo entre dos vectores:
|
|
|
|

\
|

=


v u
v u
cos arc .
o Calcular la proyeccin de

u sobre

v :
2
3
2
2
2
1
3 3 2 2 1 1
u u u
v u v u v u
v
v u
) v sobre u ( P
+ +
+ +
=

.
o Como criterio de perpendicularidad: 0 v u v u =

.

Producto vectorial: El resultado es un vector perpendicular a ambos:
) y x y x , z x z x , z y z y (
z y x
z y x
k j i
b a
1 2 2 1 1 2 2 1 1 2 2 1
2 2 2
1 1 1
+ = =



Adems, su mdulo es = sen b a b a

y coincide con el
rea del paralelogramo determinado por los vectores a

y b

.




Producto mixto: Se llama producto mixto de tres vectores al nmero que resulta
de hacer ) w v ( u

:
[ ]
3 2 1
3 2 1
3 2 1
w w w
v v v
u u u
) w v ( u w , v , u = =



Su valor absoluto coincide con el volumen del paraleleppedo definido por
w y v , u




3.- APLICACIONES DE VECTORES A PROBLEMAS GEOMTRICOS.

Coordenadas de un vector que une dos puntos.- Si ) z , y , x ( A
1 1 1
y ) z , y , x ( B
2 2 2
son
dos puntos, el vector que une A con B es ) z z , y y , x x ( AB
1 2 1 2 1 2
=

.

Puntos alineados.- Tres puntos ) z , y , x ( A
1 1 1
, ) z , y , x ( B
2 2 2
y ) z , y , x ( C
3 3 3
estn
alineados si

AB y

BC son paralelos (proporcionales), es decir:

2 3
1 2
2 3
1 2
2 3
1 2
z z
z z
y y
y y
x x
x x

.
Punto medio de un segmento.- El punto medio, PM, del segmento

AB es:
|

\
|
+ + +
=
2
z z
,
2
y y
,
2
x x
PM
2 1 2 1 2 1
AB

Punto simtrico.- Si ) z , y , x ( A
/
es el punto simtrico de ) z , y , x ( A
1 1 1
respecto al
punto ) z , y , x ( B
2 2 2
, entonces B es el punto medio del segmento
/
AA , es decir:
; x
2
x x
2
1
=
+
; y
2
y y
2
1
=
+
. z
2
z z
2
1
=
+



4.- ECUACIONES DE LA RECTA.

Una recta r queda determinada por un punto ) p , p , p ( P
3 2 1
de la recta y un vector
) d , d , d ( d
3 2 1
=

paralelo a dicha recta (vector director).

Ecuacin vectorial de la recta:
) d , d , d ( ) p , p , p ( ) z , y , x ( r
3 2 1 3 2 1
+ = .

Ecuaciones paramtricas de la recta:

+ =
+ =
+ =

3 3
2 2
1 1
d p z
d p y
d p x
r
Ecuacin continua de la recta:
3
3
2
2
1
1
d
p z
d
p y
d
p x
r

=

.




Tambin se puede expresar una recta como interseccin de dos planos:
Ecuacin implcita de la recta:

= + + +
= + + +
0 d z c y b x a
0 d cz by ax
/ / /


En este caso, podemos conseguir puntos de la recta resolviendo el sistema y su
vector director se consigue haciendo el producto vectorial ) c , b , a ( ) c , b , a ( d
/ / /
=

.


5.- POSICIONES RELATIVAS ENTRE RECTAS.

Dos rectas en el espacio pueden ser coincidentes, paralelas, pueden cortarse en un
punto o pueden cruzarse. Para estudiar posiciones relativas entre dos rectas, r y s,
utilizaremos rangos. Consideramos las matrices:
|
|
|

\
|
=
3 3
2 2
1 1
M
/
3 3
/
2 2
/
1 1
/
p q
p q
p q
d d
d d
d d
M


donde conocemos

) d , d , d ( d
) p , p , P(p
r
3 2 1
3 2 1

) d , d , d ( d
) q , q , Q(q
s
/
3
/
2
/
1
3 2 1

.
Entonces:
o Si = = 1 ) M ( ran ) M ( ran
/
r y s coinciden.
o Si = = 2 ) M ( ran 1 ) M ( ran
/
r y s son paralelas.
o Si = = 2 ) M ( ran ) M ( ran
/
r y s se cortan.
o Si = = 3 ) M ( ran 2 ) M ( ran
/
r y s se cruzan.


6.- ECUACIONES DEL PLANO.

Un plano queda determinado por un punto ) p , p , p ( P
3 2 1
del plano y dos vectores
paralelos al mismo y linealmente independientes entre s (no proporcionales):
) u , u , u ( u
3 2 1
=

y ) v , v , v ( v
3 2 1
=

, llamados vectores posicionales.

Ecuacin vectorial del plano:
) v , v , v ( ) u , u , u ( ) p , p , p ( ) z , y , x (
3 2 1 3 2 1 3 2 1
+ + = .

Ecuaciones paramtricas del plano:

+ + =
+ + =
+ + =

3 3 3
2 2 2
1 1 1
v u p z
v u p y
v u p x

Ecuacin implcita del plano:
0 d cz by ax = + + +

En este caso, el vector ) c , b , a ( n =

es un vector normal (perpendicular al plano ).

Adems
o Si conocemos un punto del plano, P, y dos vectores posicionales, v y u

,
es fcil conseguir la ecuacin implcita de la siguiente manera:
0
p z v u
p y v u
p x v u
3 3 3
2 2 2
1 1 1
=

.

o Si conocemos un punto del plano P y su vector normal ) c , b , a ( n =

, la
ecuacin implcita es
0 ) p z ( c ) p y ( b ) p x ( a
3 2 1
= + + .

En este caso, tambin se puede imponer que el punto P , y debe cumplir
su ecuacin, es decir, sustituir las coordenadas del punto en la ecuacin
del plano y calcular d.


7.- POSICIONES RELATIVAS ENTRE PLANOS.

Dos planos en el espacio pueden ser coincidentes, paralelos o cortarse en una recta.
Para distinguir cada caso consideramos los planos

= + + +
= + + +
0 d c y b x a
0 d cz by ax
/ / / /
2
1

y las matrices
|
|

\
|
=
/
M
/ / /
/
d
d
c b a
c b a
M

.
Entonces
o Si = = 1 ) M ( ran ) M ( ran
/

1
y
2
son coincidentes.
o Si = = 2 ) M ( ran 1 ) M ( ran
/

1
y
2
son paralelos.
o Si = = 2 ) M ( ran ) M ( ran
/

1
y
2
se cortan en una recta.

Tres planos en el espacio pueden ser coincidentes (S.C.I.), paralelos (S.I.), dos
paralelos cortados por un tercer plano (S.I.), las tres caras de un prima de base
triangular (S.I.), pueden cortarse en una recta (S.C.I.) o pueden cortarse en un punto
(S.C.D.). Formando un sistema de ecuaciones y aplicando el T
ma
de Rouch podremos
distinguir cada uno de los casos.


8.- POSICIONES RELATIVAS ENTRE RECTA Y PLANO.

En el espacio, una recta r puede estar contenida en un plano , puede ser paralela a
ese plano o lo puede cortar en un punto.

La recta r est contenida en el plano .- En este caso se deben cumplir dos
condiciones:
1. El vector director de la recta y el vector normal del plano son
perpendiculares: 0 n d n d
r r
=

.
2. Un punto cualquiera, P, de la recta r tambin pertenece al plano .




La recta r es paralela a plano .- En este otro caso se debe cumplir:
1. El vector director de la recta y el vector normal del plano son
perpendiculares: 0 n d n d
r r
=

.
2. Un punto cualquiera, P, de la recta r no pertenece al plano .
La recta r corta al plano en un punto P.- En este caso el vector director de la
recta y el vector normal al plano forman un ngulo distinto de 90. Podemos
calcular el punto de corte estableciendo un sistema de ecuaciones entre las
ecuaciones de la recta y las del plano.


9.- DISTANCIA ENTRE PUNTOS, RECTAS Y PLANOS.

Distancia entre dos puntos P y Q.- Coincide con el mdulo del vector que los une:
2
1 2
2
1 2
2
1 2
) z z ( ) y y ( ) x x ( PQ ) Q , P ( dist + + = = .

Distancia de un punto P y una recta r.- Si Q es un punto de la recta r, la distancia
entre P y r coincide con la altura del paralelogramo determinado por los vectores

QP y
r
d

, es decir, con el resultado de dividir el rea del paralelogramo entre la

longitud de su base:
r
r
d
d QP
) r , P ( dist

.

Distancia de un punto P a un plano .- Si ) z , y , x ( P
0 0 0
y la ecuacin implcita del
plano es 0 d cz by ax = + + + , entonces:
2 2 2
0 0 0
c b a
d z c y b x a
) , P ( dist
+ +
+ + +
= .
Distancia entre dos rectas r y s.- Distinguiremos dos casos:
o Si las rectas son paralelas, tomamos un punto P
r
de la recta r y se cumplir:
) s , P ( dist ) s , r ( dist = .

o Si las rectas se cruzan, la distancia entre ellas coincide con la altura del
paraleleppedo determinado por los vectores

PQ y d , d
s r

, es decir, con el
resultado de dividir el volumen del paraleleppedo entre el rea de su base:
s r
s r
d d
PQ , d , d
) s , r ( dist

.
Distancia de una recta r a un plano .- Si la recta r corta al plano , la distancia
entre ellos es cero. Si la recta r es paralela al plano (o est contenida en l)
) , P ( dist ) , r ( dist
r
= .
Distancia entre dos planos
1
y
2
.- Si los planos 1 y 2 se cortan, la distancia
entre ellos es cero. Si no se cortan es porque son paralelos o coinciden. En este
caso:
) , P ( dist ) , ( dist
2 2 1
1
=

o ) , P ( dist ) , ( dist
1 2 1
2
=




10.- NGULOS ENTRE RECTAS Y PLANOS.

ngulo entre dos rectas.- El menor ngulo que forman dos rectas es el mismo que
el que forman sus vectores directores:

|
|
|

\
|

=
s r
s r
d d
d d
cos arc




ngulo entre dos planos.- El ngulo que forman dos planos
1
y
2
es el mismo que el
que forman sus vectores normales:
|
|

\
|

=
2 1
2 1
n n
n n
cos arc




ngulo entre una recta y un plano.- El ngulo que forman una recta r y un plano es
complementario del que forman el vector director de la recta y el vector normal
del plano:

=
n d
n d
) 90 ( cos
r
r

|
|
|

\
|

n d
n d
sen arc
r
r

11.- REAS Y VOLMENES.

rea de un paralelogramo. rea de un tringulo.- El rea de un paralelogramo
determinado por los vectores

AC y AB es el mdulo de su producto vectorial:
REA DEL PARALELOGRAMO =

AC AB .
Por lo tanto, el rea del tringulo de vrtices A, B y C ser la mitad del rea del
paralelogramo, es decir:
REA DEL TRINGULO =

AC AB
2
1
.
Volumen del paraleleppedo. Volumen del tetraedro.- El volumen del paraleleppedo
determinado por tres vectores

AD y AC , AB es el valor absoluto del producto
mixto de estos tres vectores:
VOLUMEN DEL PARALELEPPEDO =
(

AD , AC , AB
Por lo tanto, el volumen del tetraedro de vrtices A, B, C y D es
VOLUMEN DEL TETRAEDRO =
(

AD , AC , AB
6
1

Otra versin de esta frmula sencilla de recordar es:
VOLUMEN DEL TETRAEDRO =
4 4 4
3 3 3
2 2 2
1 1 1
z y x 1
z y x 1
z y x 1
z y x 1
6
1

donde x
i
, y
i
, z
i
son las coordenadas de A, B, C y D, respectivamente.



1.- SOBRE LMITES DE UNA FUNCIN

Comparacin de lmites infinitos.
Si =
+
) x ( f lm
x
y =
+
) x ( g lm
x
, se dice que f(x) es un infinito de orden
superior a g(x) si se cumple que:
=
+ ) x ( g
) x ( f
lm
x
, o lo que es lo mismo, 0
) x ( f
) x ( g
lm
x
=
+
.
(Las funciones EXPONENCIALES (base mayor que 1) son infinitos de orden
superior a las POTENCIAS que, a su vez, son infinitos de orden superior a los
LOGARITMOS).
Lmites en -.
A menudo resulta cmodo aplicar ) x ( f lm ) x ( f lm
x x
=
+
.

Indeterminaciones: . ; 0 ; 1 ; ;
0
0
; 0 ;
0 0

Lmites de la forma 1

. Es muy til aplicar la siguiente propiedad:

Si 1 ) x ( f lm
x
=
+
y + =
+
) x ( g lm
x
, entonces [ ]
[ ] ) x ( g 1 ) x ( f lm
) x ( g
n
n
e ) x ( f lm

+
+
= .

Lmites laterales.
0
x c
0
x c
lm f(x) lmf(c )
, 0
lm f(x) lmf(c )

>

= +

.
No obstante, se puede utilizar la calculadora para justificar fcilmente el valor de
los lmites laterales.
Adems, segn los diferentes tipos de indeterminaciones se siguen procedimientos
algebraicos sencillos (factorizar y simplificar, multiplicar y dividir por el
conjugado, efectuar la resta de fracciones algebraicas,...) que permiten calcular el
valor del lmite.


2.- CONTINUIDAD DE UNA FUNCIN EN UN PUNTO.

Una funcin f es continua en un punto x
0
si verifica:

1) ). x ( f lm ) x ( f lm , decir es ), x ( f lm
0 0 0
x x x x x x
+

=
2) lR k k ) x ( f lm ) x ( f
0
x x
o
= =

Si la funcin est definida a trozos

<
=
0 2
0 1
x x si ) x ( f
x x si ) x ( f
) x ( f
entonces

) x ( f ) x ( f lm ) x ( f lm
) x ( f ) x ( f lm ) x ( f lm
0 2 2
x x x x
0 1 1
x x x x
0 0
0 0
= =
= =


+

3.- TEOREMAS DE CONTINUIDAD EN INTERVALOS

TEOREMA DE BOLZANO.
Si f(x) es continua en a,b (

y signo de f(a) signo de f(b), entonces
( ) 0 ) c ( f / b , a c = .






COROLARIO DEL TEOREMA DE BOLZANO.
Si f y g son continuas en a,b (

, f(a) g(a) < y f(b) g(b) > , entonces
( ) ) c ( g ) c ( f / b , a c = .







TEOREMA DE LOS VALORES INTERMEDIOS.
Si f(x) es continua en a,b (

entonces toma todos los valores intermedios entre
f(a) y f(b), es decir, [ ] ( ) k ) c ( f / b , a c ) b ( f ), a ( f k = .






TEOREMA DE WEIERSTRASS.
Si f(x) es continua en a,b (

entonces tiene un mximo y un mnimo absoluto en ese
intervalo, es decir, [ ] [ ] ) c ( f ) x ( f ) d ( f , b , a x / b , a d , c .









4.- DEFINICIN DE DERIVADA

Derivada de una funcin f en un punto x
0
:
h
) x ( f ) h x ( f
lm ) x ( f
0 0
0 h
0
+
=

La definicin de funcin derivada es similar:
h
) x ( f ) h x ( f
lm ) x ( f
0 h
+
=

TASA DE VARIACIN INSTANTNEA VELOCIDAD INSTANTNEA DERIVADA
EN UN PUNTO PENDIENTE DE LA RECTA TANGENTE


5.- DERIVABILIDAD DE UNA FUNCIN EN UN PUNTO.

Una funcin f es derivable en un punto x
0
si verifica:
1) f es continua en x
0
.
2) Existe la derivada en x
0
, es decir, coinciden sus derivadas laterales:
) x ( f ) x ( f
0 0
+
=


6.- DERIVADAS MS FRECUENTES.

{ } [ ] [ ] ) x ( f ) x ( f n ) x ( f D
1 n n
=




f(x) f(x) x x
D e f(x) e ; D e e
( (
= =




f(x) f(x) x x
D a f(x) a lna; D a a lna
( (
= =



[ ]
) x ( f
) x ( f
) x ( f ln D =

[ ] ) x ( g ) x ( f ) x ( g ) x ( f ) x ( g ) x ( f D + =


( )
2
) x ( g
) x ( g ) x ( f ) x ( g ) x ( f
) x ( g
) x ( f
D

=
(

[ ] ) x ( f cos ) x ( f ) x ( f sen D =

[ ] ) x ( f sen ) x ( f ) x ( f cos D =

[ ] [ ] ) x ( f tg 1 ) x ( f ) x ( f tg D
2
+ =

[ ]
[ ]
2
) x ( f 1
) x ( f
) x ( f sen arc D

=

[ ]
[ ]
2
) x ( f 1
) x ( f
) x ( f cos arc D

=
[ ]
[ ]
2
) x ( f 1
) x ( f
) x ( f tg arc D
+
=


7.- DERIVACIN LOGARTMICA

Es un proceso que nos permite calcular la derivada de la funcin de la forma
( )
) x ( g
) x ( f y = (la base y el exponente dependen de x)
y consiste en aplicar los siguientes pasos:

1. Tomamos logaritmos a ambos lados de la igualdad
( )
) x ( g
) x ( f ln y ln =

2. Aplicamos la propiedad 3 de los logaritmos al segundo miembro
( ) ) x ( f ln ) x ( g y ln =

3. Derivamos ambos miembros de la igualdad
( )
) x ( f
) x ( f
) x ( g ) x ( f ln ) x ( g
y
y
/
/
/
+ =

4. Despejamos la derivada sustituyendo y por su valor
( ) [ ]
) x ( g
/
/ /
) x ( f
) x ( f
) x ( f
) x ( g ) x ( f ln ) x ( g y
(
(

+ =








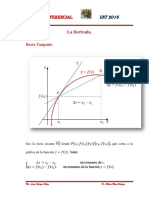
8.- ECUACIN DE LA RECTA TANGENTE

Se trata de calcular la ecuacin de la recta tangente a la curva y = f(x) en el punto
de abscisas x
0
. Por tratarse de una recta, su ecuacin en forma de punto-pendiente
ser
( )
0 0 t
x x m y y : r = .
Se calcula la segunda coordenada del punto: ) x ( f y
0 0
= ,

y la pendiente de la recta
tangente:
/
0
m f (x ) = . Se sustituyen ambos valores y ya tenemos la ecuacin.

Otra versin del problema consiste en averiguar el punto donde la recta tangente
tiene cierta pendiente m. En este caso resolvemos la ecuacin
/
0
m f (x ) = , cuya nica
incgnita es la primera coordenada del punto, x
0
, y posteriormente calculamos la
segunda y
0
.


9.- CRECIMIENTO Y DECRECIMIENTO. EXTREMOS RELATIVOS.

Tambin se llama estudio de la monotona de una funcin.
f(x) es creciente en un intervalo (a,b)
/
f (x) 0 > ( ) b , a x .

f(x) es decreciente en un intervalo (a,b)
/
f (x) 0 < ( ) b , a x .

Si
/
0
f (x ) 0 = y
//
0
f (x ) 0 < , entonces f tiene un mximo relativo en el punto
(x
0
,f(x
0
)).
Si
/
0
f (x ) 0 = y
//
0
f (x ) 0 > , entonces f tiene un mnimo relativo en el punto
(x
0
,f(x
0
)).
Para saber si es mximo o mnimo relativo, tambin se puede dividir la recta real en
intervalos (representando en ella las soluciones de la ecuacin
/
0
f (x ) 0 = ) y estudiar
el signo de la derivada:
o Si la funcin cambia de creciente a decreciente es un mximo relativo.
o Si la funcin cambia de decreciente a creciente es un mnimo relativo.


10.- CURVATURA. PUNTOS DE INFLEXIN

Tambin se llama estudio de la curvatura de una funcin.
Si
//
0
f (x ) 0 x (a,b) > , entonces f es cncava en (a,b) .

Si
//
0
f (x ) 0 x (a,b) < , entonces f es convexa en (a,b) .

Si
//
0
f (x ) 0 = y adems
///
0
f (x ) 0 , entonces f tiene un punto de inflexin en
(x
0
,f(x
0
)).

Tambin podemos estudiar el signo de la segunda derivada a ambos lados del
candidato a punto de inflexin (soluciones de la ecuacin
//
0
f (x ) 0 = ) y si cambia de
cncava a convexa o viceversa, efectivamente se trata de un punto de inflexin.





11.- PROBLEMAS DE OPTIMIZACIN

Son problemas en los que debemos optimizar (encontrar el mximo o el mnimo) una
funcin que viene descrita a travs de un enunciado. La dificultad suele estar en
determinar correctamente la funcin. Normalmente se utilizan una o dos variables.
En el caso de dos variables, dividimos el procedimiento en cuatro apartados:
1. Descripcin de las variables. Relacin entre las variables (frmula).
2. Funcin objetivo (a optimizar).
3. Planteamiento y resolucin.*
4. Interpretacin del resultado.
*(Se forma un sistema de ecuaciones con la funcin f(x, y) y la ecuacin que
relaciona las variables. Aplicando el mtodo de sustitucin se consigue una funcin,
f(x), con una sola variable de la que buscaremos sus mximos o mnimos a travs de
su derivada)


12.- REGLA DE LHPITAL

Sean f y g dos funciones derivables en un entorno del punto a.
Si |

\
|
=
0
0
) x ( g
) x ( f
lm
a x
y =

) x ( g
) x ( f
lm
/
/
a x
, entonces =
) x ( g
) x ( f
lm
a x
=

) x ( g
) x ( f
lm
/
/
a x

Si al aplicar esta regla volvemos a tener una indeterminacin del tipo |

\
|
0
0
podemos
repetir el proceso.
La regla de LHpital tambin se aplica para indeterminaciones del tipo
|

\
|

.
Incluso, algunas expresiones del tipo ( ) o ( )

1 , se pueden expresar en forma de

cociente para poder aplicar esta regla.


13.- TEOREMAS DE DERIVABILIDAD EN INTERVALOS.

TEOREMA DE ROLLE.

Sea f una funcin continua en a,b (

y derivable en
( ) b , a . Si ) b ( f ) a ( f = entonces existe al menos un
valor ( ) b , a c tal que 0 ) c ( f
/
= . Son puntos de
tangente horizontal (mximos o mnimos relativos)


TEOREMA DEL VALOR MEDIO.
Si f es continua en a,b (

y derivable en ( ) b , a ,
entonces existe al menos un punto ( ) b , a c tal que
a b
) a ( f ) b ( f
) c ( f
/

= . Es decir, habr un punto

intermedio c en el que la tangente sea paralela a
segmento AB .



14.- ASNTOTAS DE UNA FUNCIN

Asntotas verticales: Las asntotas verticales de una funcin racional son los
valores de x que anulan su denominador. Su ecuacin es de la forma x = k. Con
ayuda de la calculadora se deben estudiar los lmites laterales alrededor de k.
Si se trata de una funcin logartmica es preciso analizar el comportamiento de la
funcin en los extremos de su dominio.
Asntotas horizontales: Las asntotas horizontales de una funcin son de la forma
) x ( f lm y
x
= .
(Si se trata de una funcin racional, el grado del numerador es menor o igual que el
grado del denominador).
Si una funcin tiene asntotas horizontales, no puede tener asntotas oblicuas.
Asntotas oblicuas: Son de la forma y = m x + n donde
[ ] mx ) x ( f lm n y
x
) x ( f
lm m
x x
= =


(Si se trata de una funcin racional, el grado del numerador es una unidad mayor
que el grado del denominador, y la mejor forma de calcular la ecuacin de la
asntota es dividir numerador entre denominador. La ecuacin ser y = cociente de
la divisin).


15.- REPRESENTACIN DE FUNCIONES

Los aspectos ms importantes a tener en cuenta son:
Dominio (Dom f): son los valores que puede tomar x
Puntos de corte con los ejes:
o x = 0 Puntos de corte con el eje Y
o y = 0 Puntos de corte con el eje X
Asntotas y ramas infinitas.
Crecimiento y decrecimiento. Extremos relativos.
Curvatura. Puntos de inflexin.


16.- INTEGRALES INMEDIATAS MS FRECUENTES.


n 1
n
a x
a x dx C
n 1
+

= +
+

n 1
n
f(x)
f(x) f(x) dx C
n 1
+
(

( = +

+

/ f(x) f(x)
1
f (x) a dx a C
lna
= +

/ f(x) f(x)
f (x) e dx e C = +

/
f (x)
dx ln f(x) C
f(x)
= +

/
f (x) senf(x)dx cosf(x) C = +

/
f (x) cosf(x)dx senf(x) C = +

/ 2
f (x) 1 tg f(x) dx tgf(x) C
(
+ = +

/
2
f (x)
dx arc tg f(x) C
1 f(x)
= +
( +

/
2
f (x)
dx arc sen f(x) C
1 f(x)
= +
(

/
2
f (x)
dx arc cos f(x) C
1 f(x)

= +
(

17.- MTODOS DE INTEGRACIN

Integracin por partes:
Se aplica la frmula
udv u v vdu =


y se suele utilizar con funciones producto de una potencia de x por una funcin
logartmica, trigonomtrica o exponencial. Tambin se utiliza este mtodo para
integrar la funcin logaritmo o la funcin arcotangente.

Integracin mediante cambio de variable:
Se define el cambio de variable z f(x) = ; se calcula
/
/
dz
dz f (x)dx dx
f (x)
= = ;
se sustituye en la integral para conseguir otra que sea inmediata, y finalmente se
deshace el cambio de variable.
Integracin de funciones racionales:
Si el numerador es mayor o igual que el denominador, se hace la divisin y se
aplica la regla de comprobacin de la divisin:
D(x) r(x)
c(x)
d(x) d(x)
= +
Despus se integran ambos miembros:
D(x) r(x) r(x)
dx c(x) dx c(x)dx dx
d(x) d(x) d(x)
(
= + = +
(



o Si el divisor tiene n races simples, la ltima integral se descompone de la
siguiente forma:
n 1 2
1 2 n
A A A r(x)
dx ... dx
d(x) x x x x x x
| |
= + + +
|
|

\


o Si el divisor tiene n races mltiples, la ltima integral se descompone de
la siguiente manera:
( ) ( )
n 1 2
2 n
1
1 1
A A A r(x)
dx ... dx
d(x) x x
x x x x
| |
|
= + + +
|

|

\


En ambos casos se obtienen integrales inmediatas.


18.- INTEGRAL DEFINIDA. REGLA DE BARROW

Si F(x) es una primitiva de f, para calcular la integral definida se aplica la regla de
Barrow:
[ ] ) a ( F ) b ( F ) x ( F dx ) x ( f
b
a
b
a
= =

19.- CLCULO DE REAS.

o El rea que encierra una curva y f(x) = , el eje X y las rectas x a = y x b = es
1 2
1 2
x x b
a x x
A f(x) dx f(x) dx f(x) dx = + +

,
siendo x
1
y x
2
los puntos de corte de la funcin con el eje X en el intervalo a,b (

.













o Para calcular el rea entre dos curvas se plantea la integral de la diferencia de
ambas (en valor absoluto), y se toman como lmites de integracin los puntos de
interseccin entre ellas (soluciones de la ecuacin f(x) g(x) = ).









20.- CLCULO DE VOLMENES DE REVOLUCIN.

o El volumen del cuerpo de revolucin que engendra la funcin
y f(x) = , considerada en el intervalo a,b (

, al girar sobre el
eje X es

b 2
a
V f(x) dx ( =





o El volumen del cuerpo de revolucin que engendra la funcin
y f(x) = , considerada en el intervalo a,b (

, al girar sobre
el eje Y es
b 2
a
V g(y) dy ( =


donde g(y) se consigue despejando x en la expresin
y f(x) = , es decir, x g(y) = .