Código asignatura Nombre asignatura

68031029 Cálculo (I. Mecánica)

Fecha alta y origen Convocatoria
04/11/2013
Equipo Docente
Febrero 2012 (2ª Semana)
 E.T.S. INGENIEROS INDUSTRIALES. U.N.E.D
CÁLCULO. Ingeniería Mecánica. Modelo B
PRUEBA PRESENCIAL 2a SEMANA. FEBRERO 2012.

PREGUNTAS CORTAS

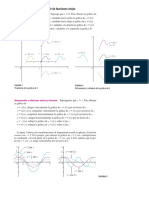
1. (1 PUNTO) Sea f (x) : [−1, 1] → R una función continua tal que f (−1) = −3 y f (1) = 3. Razone si es
cierto que la ecuación f (x) = 0 tiene una única solución en el intervalo [−1, 1]. Apóyese en la gráfica de una
función con estas características si lo considera necesario.
Solución: Cumple las condiciones del Teorema de Bolzano (página 51 del libro “Cálculo para Ingenieros”),
y por eso, sabemos que tiene al menos una solución en este intervalo. Pero no tiene que ser única, como se
muestra con la gráfica de la función f (x) = 3sen 5πx
2 :

-1 -0.5 0 0.5 1
x
-1

-2

-3

¡ ¢ ¡ 5π ¢ ¡2¢ ³ 2´
5π 5
Tenemos f (−1) = 3sen − 5π 2 = −3, f (1) = 3sen 2 = 3 y además, f (0) = 0, f 5 = 3sen 2 = 0,
por lo que la raíz no es única.
2. (1 PUNTO) ¿Es derivable en x = 0 la función dada por f (x) = |x2 sen x|? Justifique la respuesta.
Solución: Sí lo es, porque existe el el límite
¯ 2¯
f (h) − f (0) |h2 sen h| − 0 ¯h ¯ · |sen h|
lim = lim = lim = lim h · |sen h| = 0.
h→0 h h→0 h h→0 h h→0

3. (1 PUNTO) Estudie si la sucesión de funciones fn (x) = xn definidas en el intervalo [0, 1] converge puntual-
mente y uniformemente en este intervalo.
Nota: Estudie la continuidad de la función límite puntual para estudiar la convergencia uniforme.
Solución: La función límite puntual es f (x) = 0 en [0, 1) y f (1) = 1 porque cuando x ∈ [0, 1) se cumple que

lim xn = 0.
n→∞

Y en x = 1, tenemos limn→∞ 1n = limn→∞ 1 = 1. Como no es una función continua y las funciones de la

sucesión son continuas, la convergencia no puede ser uniforme (teorema 1.6, página 60 del libro “Cálculo para
ingenieros”).
4. (1 PUNTO) Calcule el producto escalar de (1, 2, 3, 4) y (−1, −2, −3, −4) y la norma de estos dos vectores.
Solución: (1, 2, 3, 4) · (−1, −2, −3, −4) = 1 (−1) + 2 (−2) + 3 (−3) + 4 (−4) = −1 − 4 − 9 − 16 = −30.
 √ √
k(1, 2, 3, 4)k = 12 + 22 + 32 + 42 = 30.
√
k(−1, −2, −3, −4)k = k− (1, 2, 3, 4)k = k(1, 2, 3, 4)k = 30.
EJERCICIOS
5. (3 PUNTOS) Determíne el valor de la integral
Z π
I= cos2 x sen xdx
0

aplicando la regla del trapecio en 4 intervalos. Compárese con el valor real.

Solución: Al dividir el intervalo en 4 partes iguales, resultan los subintervalos [0, π4 ], [ π4 , π2 ], [ π2 , 3π 3π

4 ], [ 4 , π].
Según la regla del trapecio, con el recinto de integración dividido en 4 subintervalos, resulta
Z π Z π Ã 3 µ ¶!
2 π f (0) + f (π) X kπ
I= f (x) dx = cos x sen xdx ≈ + f .
0 0 4 2 4
k=1

Ahora calculamos
à √ !2 √ √
³π´ 2 2π π 2
f (0) = cos2 0 sen 0 = 0, f = cos2 sen =
= ,
4 2 2 4 44
µ ¶ µ ¶ Ã √ !2 √ √
2π ³π´ π π 3π 3π 3π 2 2 2
f =f = cos2 sen = 0, f = cos2 sen = − = ,
4 2 2 2 4 4 4 2 2 4
f (π) = cos2 π sen π = 0.

Entonces, con estos valores, tenemos

3 µ ¶ √ √ √
X kπ 2 2 2
f =0+ +0+ +0= ,
4 4 4 2
k=1
à 3 µ ¶! à √ ! √
π f (0) + f (π) X kπ π 0+0 2 π 2
I= + f = + = .
4 2 4 4 2 2 8
k=1

La integral es inmediata si observamos que la derivada del coseno (que está elevado al cuadrado) es el seno
cambiado de signo. Así, su valor real es
Z π ¯π
1 3 ¯
¯ 1 1 2
I= cos x sen xdx = − cos x¯ = − cos3 π + cos3 0 = .
2
0 3 0 3 3 3

6. (3 PUNTOS) Sea f la función dada por

f (x, y) = x + y,

y sea S la circunferencia de ecuación x2 + y 2 = 1. Determine dónde se alcanzan el máximo y el mínimo

absolutos de la función f en S.

Solución: Aplicamos el método de los multiplicadores de Lagrange, y construimos la función auxiliar

¡ ¢
F (x, y, λ) = f (x, y) + λg (x, y) = x + y + λ x2 + y 2 − 1 ,
si escribimos la condición como g (x, y) = x2 + y 2 − 1 = 0. Observamos, además, que los puntos que cumplen
esta condición son los de la circunferencia de centro (0, 0) y radio 1, que es un conjunto cerrado y acotado.
Esto significa que en este conjunto se van a alcanzar los extremos absolutos (teorema de los valores extremos,
página 268 del libro “Cálculo para ingenieros”).
Para encontrarlos, tenemos que resolver el sistema que nos da ∇F (x, y, λ) = 0, que es

∂F
(x, y, λ) = 1 + 2λx = 0,
∂x
∂F
(x, y, λ) = 1 + 2λy = 0,
∂y
∂F
(x, y, λ) = x2 + y 2 − 1 = 0.
∂λ
Restando las dos primeras ecuaciones, resulta 2λ (x − y) = 0

2λ (x − y) = 0 =⇒ λ = 0 ó x = y.

Si λ = 0, entonces las dos primeras ecuaciones no son ciertas, y es una contradicción. Por tanto, los extremos
se deben alcanzar en los puntos donde x = y. Sustituimos esta igualdad en la tercera ecuación:
√
2 2 2 2 1 2
x + x − 1 = 0 ⇐⇒ 2x = 1 ⇐⇒ x = ⇐⇒ x = ± .
2 2
³√ √ ´ ³ √ √ ´
Entonces, los posibles extremos absolutos se alcanzan en los puntos 22 , 22 y − 22 , − 22 . Como son dos
puntos y sabemos que en este conjunto f alcanza un máximo absoluto y un mínimo absoluto, calculamos el
valor de f en estos puntos y sabemos cuál se alcanza en cada uno:
Ã√ √ ! √ √ à √ √ ! √ √
2 2 2 2 √ 2 2 2 2 √
f , = + = 2, f − ,− =− − = − 2.
2 2 2 2 2 2 2 2
³√ √ ´
2 2
Ya podemos afirmar que f alcanza el máximo absoluto, dentro del conjunto indicado, en 2 , 2 y el
³ √ √ ´
mínimo absoluto en − 22 , − 22 .