Lima, 19 de marzo de 2019

Universidad del Pacífico

Departamento académico de Economía
Matemáticas IV – Sección D
Profesor: Kevin Gershy-Damet Vargas
Primer semestre de 2019

Capítulo 1:
Topología

La topología consiste en el estudio de las características de los espacios métricos continuos, y se basa
en la densidad de los números reales. Esta premisa significa que, entre dos números reales, siempre
hay otro número real. En el caso de este curso es fundamental su estudio, puesto que garantiza que
los espacios sobre los cuales se realizan procesos de optimización estén correctamente definidos.

Parte I: Conceptos básicos

 Definición 1.1: Bola abierta o vecindad

Dado un vector (también conocido como punto) denominado 𝑥0 en el espacio 𝑅 𝑛 , una bola
abierta 𝐵𝑟 (𝑥𝑜 ) se define como el conjunto de todos aquellos puntos que están próximos de 𝑥0
en una distancia menor a 𝑟. Formalmente, se tiene que:

𝐵𝑟 (𝑥0 ) = {𝑥 ∈ 𝑅 𝑛 / ||𝑥 − 𝑥0 || < 𝑟}

Ejemplo 1.1.1: El intervalo (1; 3) ⊂ 𝑅 (entendido como 𝑥 ∈ 𝑅 / 1 < 𝑥 < 3) se puede definir
como una bola abierta de la forma 𝐵1 (2). Esto quiere decir que el conjunto comprende a todos
los números reales alrededor de 2, en una distancia menor que 1. Así, dicho conjunto se puede
denotar formalmente de la siguiente manera: 𝐵1 (2) = {𝑥 ∈ 𝑅 / |𝑥 − 2| < 1}. Nótese que, en
este caso, la distancia entre 2 y cualquier punto del conjunto se calcula con el valor absoluto
de su diferencia.

Ejemplo 1.1.2: El caso anterior es sencillo de entender al tratarse de vectores en 𝑅 (números

reales). No obstante, se puede extender el ejemplo a mayores dimensiones. Supongamos que
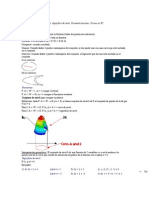
tenemos el vector 𝑥0 = (2; 2)′ ∈ 𝑅 2 , y que queremos identificar a todos los vectores que estén
a una vecindad de 1 unidad o menos de este (recordar que toda distancia es un número real no
negativo). Es decir, nuestro objetivo es determinar todos los vectores 𝑥 = (𝑥1 ; 𝑥2 )′ ∈ 𝑅 2 que
formarán parte de 𝐵1 (𝑥0 ).

¿Bajo qué condición el vector arbitrario 𝑥 formará parte de 𝐵1 (𝑥0 )? La respuesta es sencilla:
solo será parte de la bola abierta si es que la distancia entre 𝑥0 y 𝑥 es menor que 1 unidad.
Observando el Gráfico 1.1, se deduce que la distancia entre 𝑥0 y 𝑥 se puede calcular usando el
teorema de Pitágoras. En particular, se obtiene como 𝑑 = √(2 − 𝑥1 )2 + (2 − 𝑥2 )2 =
√(𝑥 − 𝑥0 )′(𝑥 − 𝑥0 ) = ||𝑥 − 𝑥0 ||. Nótese que esta última expresión es el módulo del vector de
la diferencia entre 𝑥0 y 𝑥; lo cual es análogo al valor absoluto usado en el caso de bolas abiertas
en 𝑅.

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

Gráfico 1.1
2,5

1,5

0,5

0
0 0,5 1 1,5 2 2,5

En el caso del vector 𝑥 mostrado en el gráfico, se distingue que (𝑥1 ; 𝑥2 )′ = (1; 1)′, por lo cual
se tiene que 𝑑 = √1 + 1 = √2 > 1 = 𝑟. Es decir, 𝑥 está alejado de 𝑥0 en más de 1 unidad, y
se concluye que 𝑥 ∉ 𝐵1 (𝑥0 ).

 Definición 1.2: Punto interior

Se dice que el vector 𝑥 ∈ 𝐴 ⊂ 𝑅 𝑛 es un punto interior del conjunto 𝐴 si se le puede “rodear”

por completo de otros vectores que también pertenezcan a 𝐴. Dicha proposición equivale a
decir que debe existir al menos una bola abierta centrada en 𝑥 que esté contenida en su totalidad
dentro de 𝐴. Así, basta con encontrar algún 𝑟 > 0 de tal forma que 𝐵𝑟 (𝑥) ⊂ 𝐴 para probar que
𝑥 sea un punto interior. De manera formal, se tiene que 𝑥 es un punto interior de 𝐴 si y solo si:

∃ 𝑟 > 0 / 𝐵𝑟 (𝑥) ⊂ 𝐴

Ejemplo 1.2.1: ¿Es 𝑥 = (2; 2)′ un punto interior del conjunto 𝐵2 (𝑥0 ) ⊂ 𝑅 2 , donde 𝑥0 =
(3; 3)′? En primer lugar, debemos verificar que la distancia entre el vector en cuestión y el
centro de la bola abierta sea “admisible”. La distancia es 𝑑 = √12 + 12 = √2, lo cual es menor
que el radio de la bola. No obstante, no es suficiente con esto, pues falta verificar que 𝑥 pueda
estar rodeado completamente por otros vectores de 𝐵2 (𝑥0 ). Del análisis gráfico, se desprende
que cualquier radio de magnitud 𝑟 ′ ≤ 2 − √2 permitirá que 𝐵𝑟 ′ (𝑥) ⊂ 𝐵𝑟 (𝑥0 ).

Gráfico 1.2
5

4.5

3.5

2.5

1.5

0.5

0
0 1 2 3 4 5

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

Si bien ya se tiene identificado gráficamente el radio “eficiente”, aún queda pendiente probar
que 𝐵𝑟 ′ (𝑥) ⊂ 𝐵𝑟 (𝑥0 ). Esto se conseguirá si mostramos que cualquier vector de la bola 𝐵𝑟 ′ (𝑥)
pertenece también a la bola 𝐵𝑟 (𝑥0 ). Tomemos por ejemplo 𝑥 ′ ∈ 𝐵𝑟 ′ (𝑥), un vector arbitrario
de dicho conjunto. Luego, se tiene que ||𝑥 ′ − 𝑥 || < 𝑟 ′ = 2 − √2. Haciendo algunos arreglos
a la expresión mediante la desigualdad triangular, se tiene que:

||𝑥 ′ − 𝑥 || = ||𝑥 ′ − 𝑥0 + 𝑥0 − 𝑥 || = ||𝑥 ′ − 𝑥0 − (𝑥 − 𝑥0 )|| ≥ ||𝑥 ′ − 𝑥0 || − ||𝑥 − 𝑥0 ||

→ ||𝑥 ′ − 𝑥0 || − ||𝑥 − 𝑥0 || = ||𝑥 ′ − 𝑥0 || − √2 ≤ ||𝑥 ′ − 𝑥 || < 2 − √2

→ ||𝑥 ′ − 𝑥0 || − √2 < 2 − √2 → ||𝑥 ′ − 𝑥0 || < 2

Así, queda probado que 𝐵𝑟 ′ (𝑥) ⊂ 𝐵𝑟 (𝑥0 ) y que por lo tanto 𝑥 es un punto interior de 𝐵𝑟 (𝑥0 ).

 Definición 1.3: Punto de acumulación

Se dice que 𝑥 es un punto de acumulación de 𝐴 ⊂ 𝑅 𝑛 si está lo suficientemente cerca o “en

contacto” de otros vectores del conjunto 𝐴. Visto de otra forma, si se toma cualquier valor para
𝑟 > 0, entonces para que 𝑥 sea un punto de acumulación necesariamente 𝐵𝑟 (𝑥) debe contener
al menos un vector (distinto de 𝑥) que pertenezca a 𝐴. Formalmente, se tiene que:

𝑥 𝑒𝑠 𝑝𝑢𝑛𝑡𝑜 𝑑𝑒 𝑎𝑐𝑢𝑚𝑢𝑙𝑎𝑐𝑖ó𝑛 𝑑𝑒 𝐴 ↔ ∀𝑟 > 0, {𝐵𝑟 (𝑥) − {𝑥}} ∩ 𝐴 ≠ ∅

Nótese que los puntos de acumulación de 𝑨 no necesariamente pertenecen a 𝑨. Por otro

lado, es posible definir 𝐴𝑎𝑐 como el conjunto de puntos de acumulación de 𝐴.

Finalmente, tomando en cuenta la definición 1.2, se deduce que cualquier punto interior se
puede catalogar también como punto de acumulación. Supongamos que 𝑥 es un punto interior
de 𝐴, por lo cual ∃𝑟 > 0, 𝐵𝑟 (𝑥) ⊂ 𝐴. Hasta este punto ya sabemos que existe al menos un radio
que permite que 𝑥 esté completamente rodeado de otros vectores de 𝐴. No obstante, esto no es
suficiente, pues debemos probar que todo radio arbitrario 𝑟′ permita llegar a la definición dada
líneas arriba. Así, pueden considerarse dos casos:

- 𝑟′ > 𝑟 (tomamos un radio mayor al que escogimos a partir del hecho de que 𝑥 es un punto
interior). En este caso, es sencillo notar que {𝐵𝑟 (𝑥) − {𝑥}} ⊂ ({𝐵𝑟 ′ (𝑥) − {𝑥}} ∩ 𝐴), ya
que {𝐵𝑟 (𝑥) − {𝑥}} ⊂ {𝐵𝑟 ′ (𝑥) − {𝑥}} ∧ {𝐵𝑟 (𝑥) − {𝑥}} ⊂ 𝐴, por lo cual {𝐵𝑟′ (𝑥) − {𝑥}} ∩
𝐴 ≠ ∅.
- 𝑟 > 𝑟′. En este caso, es sencillo notar que 𝐵𝑟 ′ (𝑥) ⊂ 𝐵𝑟 (𝑥) ⊂ 𝐴.

Ejemplo 1.3.1: ¿Cuáles son los puntos de acumulación de 𝐴1 = (1; 3) ∪ {4}? Nótese que, dado
que {1} y {3} están lo suficientemente cercanos a los puntos de 𝐴 dentro del intervalo (1; 3),
se les puede considerar puntos de acumulación. Asimismo, por lo mencionado previamente, el
intervalo entero (1; 3) está compuesto por puntos de acumulación, dado que todos son puntos
interiores. No obstante, es fácil mostrar que {4} no es un punto de acumulación, pues, por
ejemplo, {𝐵1 (4) − {4}} ∩ 𝐴 = ∅. Así, se concluye que 𝐴𝑎𝑐 = [1; 3].

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

 Definición 1.4: Punto frontera

Se dice que 𝑥 es un punto frontera de 𝐴 si está rodeado por vectores que pertenecen a 𝐴 y otros
vectores que no pertenecen a 𝑨. Formalmente, se tiene que:

𝑥 𝑒𝑠 𝑝𝑢𝑛𝑡𝑜 𝑓𝑟𝑜𝑛𝑡𝑒𝑟𝑎 𝑑𝑒 𝐴 ↔ ∀𝑟 > 0, 𝐵𝑟 (𝑥) ∩ 𝐴 ≠ ∅ ∧ 𝐵𝑟 (𝑥) ∩ 𝐴 ≠ 𝐵𝑟 (𝑥)

Nótese que en este caso se deja libre la posibilidad de que la única intersección entre 𝐵𝑟 (𝑥) y
𝐴 sea {𝑥}. Es decir, los vectores “aislados” también se consideran puntos frontera. Asimismo,
al igual que en la definición anterior, se deja libre la posibilidad de que un punto frontera no
necesariamente pertenezca al conjunto en cuestión.

Finalmente, puede definirse 𝐴 𝑓 como el conjunto de puntos frontera de 𝐴, y a 𝑐𝑙(𝐴) = 𝐴 ∪ 𝐴 𝑓

como la clausura de 𝐴 . Este último concepto se interpreta como una especie de
“transformación” de 𝐴, que hace que pase a incluir todos sus puntos frontera. Evidentemente,
si 𝐴 ya contenía a todos sus puntos frontera, entonces 𝑐𝑙(𝐴) = 𝐴.

Ejemplo 1.4.1: ¿Cuáles son los puntos frontera del conjunto 𝐴1 = (1; 3) ∪ {4}? Los puntos
frontera son {1; 3; 4}.

 Definición 1.5: Conjuntos cerrados y abiertos

Se dice que un conjunto 𝐴 ⊂ 𝑅 𝑛 es cerrado si contiene a todos sus puntos frontera; es decir, si
𝑐𝑙(𝐴) = 𝐴 o 𝐴 𝑓 ⊂ 𝐴. Asimismo, el conjunto es abierto cuando no contiene a ninguno de sus
puntos frontera (𝐴 𝑓 ∩ 𝐴 = ∅). Nótese que esta última proposición es similar a decir que un
conjunto es abierto si todos los vectores que lo componen son puntos interiores.

Sobre la base de estas definiciones, se pueden deducir algunas propiedades:

- Si 𝐴 ⊂ 𝑅 𝑛 es un conjunto cerrado, entonces 𝐴𝑐 = 𝑅 𝑛 − 𝐴 (es decir, el complemento de 𝐴)

es un conjunto abierto.
- Si 𝐴 ⊂ 𝑅 𝑛 es un conjunto abierto, entonces 𝐴 𝑓 = 𝑐𝑙(𝐴) ∩ 𝐴𝑐 . Esto es sencillo de probar,
pues 𝑐𝑙(𝐴) ∩ 𝐴𝑐 = (𝐴 ∪ 𝐴 𝑓 ) ∩ 𝐴𝑐 = (𝐴 ∩ 𝐴𝑐 ) ∪ (𝐴 𝑓 ∩ 𝐴𝑐 ). Por lógica se deduce que
𝐴 ∩ 𝐴𝑐 = ∅. Por otro lado, dado que 𝐴 es un conjunto abierto, no posee a ningún punto
frontera y por lo tanto 𝐴 𝑓 ⊂ 𝐴𝑐 . Esto quiere decir que 𝐴 𝑓 ∩ 𝐴𝑐 = 𝐴 𝑓 , por lo que finalmente
se tiene que 𝑐𝑙(𝐴) ∩ 𝐴𝑐 = 𝐴 𝑓 .

Ejemplo 1.5.1: Nótese que el conjunto 𝑁 = {1; 2; 3; … } (el conjunto de números naturales) es
un conjunto cerrado, pues todos sus puntos son frontera. Resulta interesante concluir que, pese
a que el conjunto es infinito, se le puede catalogar de cerrado.

 Definición 1.6: Conjunto acotado

Un conjunto 𝐴 ⊂ 𝑅 𝑛 es acotado si existe alguna abierta centrada en el origen y de radio finito

que pueda contener por completo a dicho conjunto. Es decir, si ∃𝑟 > 0 / 𝐵𝑟 (0) ⊃ 𝐴,
1
Ejemplo 1.6.1: ¿Es el conjunto 𝐴 = {𝑆1 ; 𝑆2 ; … } acotado, dado que 𝑆𝑖 = 𝑆𝑖−1 + y 𝑆1 = 1?
𝑖2

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

Para verificar si el conjunto 𝐴 es acotado, basta con analizar si la suma 𝑆𝑛 es convergente

conforme 𝑛 → ∞ . Es decir, lo único que debe hacerse es verificar que ∃𝐿 = lim 𝑆𝑛 =
𝑛→∞
1 1
lim (1 + 22 + 33 + ⋯ ). Nótese que no es necesario calcular el límite exacto, pues basta con
𝑛→∞
encontrar 𝑀 ∈ 𝑅 tal que 𝑀 > 𝐿. Si conseguimos esto, probaremos que 𝐵𝑀 (0) ⊃ 𝐴.

Si se trabaja cuidadosamente la expresión, se tiene que:

𝑛 𝑛 𝑛
1 1 1
𝑆𝑛 = ∑ 2 = 1 + ∑ 2 < 1 + ∑
𝑖 𝑖 (𝑖 − 1)𝑖
𝑖=1 𝑖=2 𝑖=2

Usando fracciones parciales, se tiene que:

𝑛 𝑛
1 1 1 1 1 1 1
𝑆𝑛 < 1 + ∑ = 1 + ∑( − ) = 1 + (1 − ) + ( − ) + ⋯ = 2 − → 2
(𝑖 − 1)𝑖 𝑖−1 𝑖 2 2 3 𝑛
𝑖=2 𝑖=2

Así, se concluye que 𝐵2 (0) ⊃ 𝐴.

 Definición 1.7: Conjunto compacto

Un conjunto 𝐴 ⊂ 𝑅 𝑛 es compacto si es cerrado y a la vez acotado. En términos simples, un

espacio compacto replica (sin importar que sea continuo o no) las características de un conjunto
finito, en donde se pueden determinar máximos y mínimos. Esta noción es sumamente
importante para cualquier formulación de optimización.

 Definición 1.8: Combinación lineal

Dados 𝑥, 𝑦 ∈ 𝑅 𝑛 , una combinación lineal es cualquier composición con una estructura como
𝑣 = 𝛼𝑥 + (1 − 𝛼)𝑦, donde 𝛼 ∈ 𝑅. En términos generales, nótese que:

(𝑣1 ; 𝑣2 ; … ; 𝑣𝑛 )′ = (𝛼𝑥1 + (1 − 𝛼)𝑦1 ; 𝛼𝑥2 + (1 − 𝛼)𝑦2 ; … ; 𝛼𝑥𝑛 + (1 − 𝛼)𝑦𝑛 )′

El conjunto de todas las combinaciones lineales 𝑣 para todo posible valor de 𝛼 ∈ 𝑅 se conoce
como línea en 𝑅 𝑛 ; y por construcción son vectores ubicados a lo largo de la recta que une a 𝑥
e 𝑦.

Por otro lado, es posible generar una combinación lineal de más de dos componentes. De
manera general, puede definirse una combinación lineal de 𝑚 elementos 𝑥𝑖 ∈ 𝑅 𝑛 de la
siguiente forma:
𝑚

𝑣 = ∑ 𝛼𝑖 𝑥𝑖
𝑖=1

Donde ∑𝑚 𝑖=1 𝛼𝑖 = 1. Finalmente, una combinación lineal convexa es aquella en donde además
se requiere 1 ≥ 𝛼𝑖 ≥ 0 ∀𝛼𝑖 . Gráficamente, esto último conlleva a que la combinación 𝑣
resultante se ubique en un lugar intermedio entre todos sus componentes. Regresando a un
ejemplo de dos elementos, se tiene que:

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

𝑣 = 𝛼𝑥 + (1 − 𝛼)𝑦

Asumiendo sin pérdida de generalidad que 𝑥 < 𝑦, se puede transformar la expresión de modo
que:

𝑣 = 𝛼𝑥 + (1 − 𝛼)(𝑦 − 𝑥 + 𝑥) = 𝛼𝑥 + (1 − 𝛼)(𝑦 − 𝑥) + (1 − 𝛼)𝑥 = 𝑥 + (1 − 𝛼)(𝑦 − 𝑥)

De dicha descomposición se distingue que, conforme 𝛼 → 1, entonces 𝑣 → 𝑥; mientras que

conforme 𝛼 → 0, entonces 𝑣 → 𝑦.

 Definición 1.9: Conjunto convexo

Se dice que un conjunto es convexo si toda combinación lineal convexa de algunos de sus
elementos también pertenece al conjunto. De manera formal:
𝑛 𝑛

𝐴 𝑒𝑠 𝑐𝑜𝑛𝑣𝑒𝑥𝑜 ↔ { 𝑥1 ; 𝑥2 ; … ; 𝑥𝑛 ∈ 𝐴 → 𝑣 = ∑ 𝛼𝑖 𝑥𝑖 ∈ 𝐴, 𝑑𝑎𝑑𝑜 1 ≥ 𝛼𝑖 ≥ 0 ∧ ∑ 𝛼𝑖 = 1}
𝑖=1 𝑖=1

En la práctica, es suficiente con tomar solo dos elementos arbitrarios del conjunto y verificar
que su combinación lineal sigue perteneciendo al mismo.

Algunas propiedades de los conjuntos convexos son las siguientes:

- La intersección de dos conjuntos convexos también es un conjunto convexo.

- La unión de dos conjuntos convexos no necesariamente es un conjunto convexo.

Ejemplo 1.9.1: Dado, 𝑃 = (𝛾1 ; 𝛾2 ; … ; 𝛾𝑛 )′ , probar que el conjunto 𝐴 = {𝑥 ∈ 𝑅 𝑛 /𝑥 ′ 𝑃 = 𝑐} es

convexo.

Tomando dos elementos arbitrarios de 𝐴, se tiene 𝑥1 ∈ 𝐴 → 𝑥1′ 𝑃 = 𝑐 ∧ 𝑥2 ∈ 𝐴 → 𝑥2′ 𝑃 = 𝑐.

Así, solo falta verificar que (𝛼𝑥1 + (1 − 𝛼)𝑥2 ) ∈ 𝐴. Reemplazando, se tiene que:

(𝛼𝑥1 + (1 − 𝛼)𝑥2 )′ 𝑃 = 𝛼𝑥1′ 𝑃 + (1 − 𝛼)𝑥2′ 𝑃 = 𝛼𝑐 + (1 − 𝛼)𝑐 = 𝑐

Por lo cual se verifica que el conjunto 𝐴 es convexo.

Parte II: Concavidad y convexidad de funciones

En términos generales, la convexidad o convexidad de una función hace alusión a la monotonicidad

de las primeras derivadas de la misma. Intuitivamente, si la pendiente de dicha función es decreciente
conforme el valor del dominio incrementa, entonces la gráfica es cóncava. Por otro lado, si la
pendiente es creciente, entonces la función es convexa.

 Definición 1.10: Desigualdad de Jensen

La idea intuitiva planteada anteriormente puede sustentarse en un análisis gráfico para una
función univariada 𝑓(𝑥): 𝐷𝑜𝑚(𝑓) → 𝑅:

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

Gráfico 1.3

Evidentemente, en este caso la función tiene pendiente creciente, por lo cual es convexa. Si se
traza un segmento que una a dos puntos cualesquiera de la función, es indudable que dicho
segmento pasará “por encima” de la gráfica. Por otro lado, si la función fuera cóncava
(pendiente decreciente), el segmento pasaría “por debajo” de la gráfica. Finalmente, si la
función fuera una línea recta, el segmento sería parte de la misma recta. Es por ello que una
función lineal se puede considerar cóncava y convexa a la vez.

De manera formal, se tiene que la función es convexa si 𝑤 ≥ 𝑓(𝑣) para 𝑥1 , 𝑥2 arbitrarios. No

obstante, es posible ir un poco más allá en la formulación de la definición. Nótese que el
segmento punteado no es más que el conjunto de todas las combinaciones lineales convexas
′ ′
posibles entre los vectores (𝑥1 ; 𝑓(𝑥1 )) y (𝑥2 ; 𝑓(𝑥2 )) . Así, se puede definir el vector (𝑣; 𝑤)′
como:
′
(𝑣; 𝑤)′ = (𝛼𝑥1 + (1 − 𝛼)𝑥2 ; 𝛼𝑓(𝑥1 ) + (1 − 𝛼)𝑓(𝑥2 )) 𝑝𝑎𝑟𝑎 𝛼 ∈ [0; 1] 𝑎𝑟𝑏𝑖𝑡𝑟𝑎𝑟𝑖𝑜

Luego, se concluye que la función en cuestión es convexa si:

𝑤 = 𝛼𝑓(𝑥1 ) + (1 − 𝛼)𝑓(𝑥2 ) ≥ 𝑓(𝑣) = 𝑓(𝛼𝑥1 + (1 − 𝛼)𝑥2 )

A esta expresión se le conoce como desigualdad de Jensen. En este caso está aplicada a la
combinación de únicamente dos elementos de la función. No obstante, es posible extender el
concepto a 𝑛 elementos de la misma. Así, se tiene el siguiente criterio, tomando 𝑥1 ; 𝑥2 ; … ; 𝑥𝑛
como valores arbitrarios del dominio:

- 𝑓(𝑥) es convexa si ∑𝑛𝑖=1 𝛼𝑖 𝑓(𝑥𝑖 ) ≥ 𝑓(∑𝑛𝑖=1 𝛼𝑖 𝑥𝑖 )

- 𝑓(𝑥) es cóncava si ∑𝑛𝑖=1 𝛼𝑖 𝑓(𝑥𝑖 ) ≤ 𝑓(∑𝑛𝑖=1 𝛼𝑖 𝑥𝑖 )

Es importante recordar que, en cualquier caso, debe cumplirse que 𝛼𝑖 ∈ [0; 1]∀𝑖 = 1; 2; … ; 𝑛
y ∑𝑛𝑖=1 𝛼𝑖 = 1, donde cada valor 𝛼𝑖 es arbitrario.

No obstante, un punto importante que se ha dejado de lado es el análisis del dominio de la

función 𝑓(𝑥) en cuestión. ¿Qué pasaría si, por ejemplo, 𝑣 = 𝛼𝑥1 + (1 − 𝛼)𝑥2 ∉ 𝐷𝑜𝑚(𝑓)? En
dicho caso, no podría analizarse la convexidad de la misma. En ese sentido, además de los
criterios descritos líneas arriba, se requiere absolutamente que 𝑫𝒐𝒎(𝒇) sea un conjunto

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

convexo. Con ello, se garantiza que cualquier combinación lineal de sus elementos siga
perteneciendo al dominio.
1
Ejemplo 1.10.1: La función hiperbólica 𝑓(𝑥) = es convexa en el dominio restringido a los
𝑥
números positivos. Por ello, utilizando la desigualdad de Jensen para 𝑛 elementos, se tiene que:

𝑛 𝑛 −1
1
∑ 𝛼𝑖 ≥ (∑ 𝛼𝑖 𝑥𝑖 )
𝑥𝑖
𝑖=1 𝑖=1

1
Más aún, tomando 𝛼𝑖 = , se tiene que:
𝑛

𝑛
1 1 𝑛 ∑𝑛𝑖=1 𝑥𝑖 𝑛
∑ ≥ 𝑛 → ≥
n 𝑥𝑖 ∑𝑖=1 𝑥𝑖 𝑛 1
𝑖=1 ∑𝑛𝑖=1
𝑥𝑖

Este resultado no es despreciable, pues es una de las grandes propiedades usadas en estadística.
Dicho resultado prueba que, en una muestra con valores positivos, el promedio aritmético (lado
izquierdo de la inecuación) de las observaciones siempre es mayor o igual que el promedio
armónico de las mismas (lado derecho de la ecuación).

Ejemplo 1.10.2: La función logarítmica 𝑓(𝑥) = ln(𝑥) es cóncava en todo su dominio. Así,
utilizando la desigualdad de Jensen para 𝑛 elementos, se tiene que:
𝑛 𝑛

∑ 𝛼𝑖 ln(𝑥𝑖 ) ≤ ln (∑ 𝛼𝑖 𝑥𝑖 )
𝑖=1 𝑖=1

1
Más aún, tomando 𝛼𝑖 = , se tiene que:
𝑛

𝑛 𝑛 1 𝑛
1 1 1
∑ ln(𝑥𝑖 ) = ∑ ln (𝑥𝑖𝑛 ) = ln(𝑥1 ∗ 𝑥2 ∗ … ∗ 𝑥𝑛 )𝑛 ≤ ln ( ∑ 𝑥𝑖 )
𝑛 𝑛
𝑖=1 𝑖=1 𝑖=1

𝑛
1 1
→ (𝑥1 ∗ 𝑥2 ∗ … ∗ 𝑥𝑛 )𝑛 ≤ ∑ 𝑥𝑖
𝑛
𝑖=1

Al igual que en el ejemplo anterior, este resultado prueba una importante relación estadística.
Dada una muestra con valores positivos, el promedio aritmético de las observaciones (lado
derecho de la ecuación) siempre será mayor o igual que el promedio geométrico de las mismas
(lado izquierdo de la ecuación).

 Definición 1.11: Criterio de la segunda derivada

Este criterio se sustenta en el concepto intuitivo planteado al inicio de esta parte del capítulo,
con respecto a la monotonicidad de las pendientes de la función bajo análisis. Partiendo de
𝜕𝑓(𝑥)
𝑓(𝑥): 𝑅 → 𝑅, la función será convexa si 𝑓 ′ (𝑥) = es una función creciente; y será cóncava
𝜕𝑥

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

𝜕𝑓(𝑥)
si 𝑓 ′ (𝑥) = es una función decreciente. Así, el criterio de la segunda derivada establece
𝜕𝑥
que:

𝜕 2 𝑓(𝑥)
- Si 𝑓 ′′ (𝑥) = ≥ 0, entonces 𝑓(𝑥) es convexa.
𝜕𝑥 2
𝜕 2 𝑓(𝑥)
- Si 𝑓 ′′ (𝑥) = ≤ 0, entonces 𝑓(𝑥) es cóncava.
𝜕𝑥 2

Extendiendo el análisis a 𝑓(𝑥; 𝑦): 𝑅 2 → 𝑅, basta con aplicar el mismo criterio tomando en
cuenta el diferencial total de la función. Así, se tiene que:

𝜕(𝑓𝑥 𝑑𝑥 + 𝑓𝑦 𝑑𝑦) 𝜕(𝑓𝑥 𝑑𝑥 + 𝑓𝑦 𝑑𝑦)

𝐷𝑓(𝑥: 𝑦) = 𝑓𝑥 𝑑𝑥 + 𝑓𝑦 𝑑𝑦 → 𝐷 2 𝑓(𝑥; 𝑦) = 𝑑𝑥 + 𝑑𝑦
𝜕𝑥 𝜕𝑦

→ 𝐷 2 𝑓(𝑥; 𝑦) = (𝑓𝑥𝑥 (𝑑𝑥)2 + 𝑓𝑦𝑥 𝑑𝑦𝑑𝑥) + (𝑓𝑥𝑦 𝑑𝑥𝑑𝑦 + 𝑓𝑦𝑦 (𝑑𝑦)2 )

= 𝑓𝑥𝑥 (𝑑𝑥)2 + 2𝑓𝑥𝑦 𝑑𝑥𝑑𝑦 + 𝑓𝑦𝑦 (𝑑𝑦)2

Si definimos 𝑑𝑣 = (𝑑𝑥; 𝑑𝑦)′ , es sencillo notar que 𝐷 2 𝑓(𝑥; 𝑦) es una forma cuadrática de la
forma 𝐷 2 𝑓(𝑥; 𝑦) = (𝑑𝑣)′ 𝐻(𝑑𝑣) , donde 𝐻 es la matriz Hessiana o matriz de segundas
derivadas de 𝑓(𝑥; 𝑦). Nótese además que 𝐷 2 𝑓(𝑥; 𝑦) = 𝐷(∇𝑓 ′ (𝑑𝑣)). Particularmente, se tiene
que:

𝑓𝑥𝑥 𝑓𝑥𝑦
𝐻=[ ]
𝑓𝑥𝑦 𝑓𝑦𝑦

Ahora, solo falta determinar el signo de 𝐷 2 𝑓(𝑥; 𝑦) = (𝑑𝑣)′ 𝐻(𝑑𝑣). Si es positivo, entonces la
pendiente total será creciente y la función 𝑓(𝑥; 𝑦) será convexa. Si es negativo, entonces la
función será cóncava. No obstante, las propiedades de las formas cuadráticas son bastante útiles
para llegar a una conclusión:

- 𝐻 𝑒𝑠 𝑑𝑒𝑓𝑖𝑛𝑖𝑑𝑎 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑎 (𝐷𝑃) ↔ 𝑥 ′ 𝐻𝑥 > 0 ∀𝑥 ∈ 𝑅 𝑛 . En este caso, 𝑓 es estrictamente

convexa.
- 𝐻 𝑒𝑠 𝑠𝑒𝑚𝑖 − 𝑑𝑒𝑓𝑖𝑛𝑖𝑑𝑎 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑎 (𝑆𝐷𝑃) ↔ 𝑥 ′ 𝐻𝑥 ≥ 0 ∀𝑥 ∈ 𝑅 𝑛 . En este caso, 𝑓 es
convexa.
- 𝐻 𝑒𝑠 𝑑𝑒𝑓𝑖𝑛𝑖𝑑𝑎 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑎 (𝐷𝑁) ↔ 𝑥 ′ 𝐻𝑥 < 0 ∀𝑥 ∈ 𝑅 𝑛 . En este caso, 𝑓 es estrictamente
cóncava.
- 𝐻 𝑒𝑠 𝑠𝑒𝑚𝑖 − 𝑑𝑒𝑓𝑖𝑛𝑖𝑑𝑎 𝑛𝑒𝑔𝑎𝑡𝑖𝑣𝑎 (𝑆𝐷𝑁) ↔ 𝑥 ′ 𝐻𝑥 ≤ 0 ∀𝑥 ∈ 𝑅 𝑛 . En este caso, 𝑓 es
cóncava.

Evidentemente, dicho análisis se puede extender a 𝑓(𝑥): 𝐷𝑜𝑚(𝑓) ⊂ 𝑅 𝑛 → 𝑅, siempre que

𝐷𝑜𝑚(𝑓) sea un conjunto convexo. Finalmente, algunas propiedades por tomar en cuenta con
respecto a la convexidad o concavidad de las funciones son las siguientes:

- Dada la función 𝐹(𝑥): 𝐴 ⊂ 𝑅 𝑛 y el conjunto 𝑋 = {𝑥 ∈ 𝐴/𝐹(𝑥) ≤ 𝑎, 𝑎 ∈ 𝑅}, si 𝐹(𝑥) es

convexa en 𝐴, entonces 𝐴 es un conjunto convexo de 𝑅 𝑛 .
- Si 𝐹(𝑥) es cóncava (convexa) y 𝐺(𝑢) es cóncava (convexa) y creciente, entonces 𝐻(𝑥) =
𝐺(𝐹(𝑥)) es cóncava (convexa).

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

- Si 𝐹(𝑥) y 𝐺(𝑥) son cóncavas (convexas), entonces 𝐻(𝑥) = min{𝐹(𝑥); 𝐺(𝑥)} (𝐻(𝑥) =
max{𝐹(𝑥); 𝐺(𝑥)}) es cóncava (convexa).

Parte III: Máximos y mínimos

La idea general de un máximo (o mínimo) es bastante intuitiva: la función 𝐹(𝑥): 𝐷𝑜𝑚(𝐹) → 𝑅

alcanza su punto máximo (o mínimo) en 𝑥 ∗ si 𝐹(𝑥 ∗ ) ≥ 𝐹(𝑥) (𝐹(𝑥 ∗ ) ≤ 𝐹(𝑥)) para cualquier valor
de 𝑥 en un determinado espacio del dominio de la función. Así, se tienen dos posibles casos: máximos
globales y máximos locales.

 Definición 1.12: Máximo local

El máximo local es aquél que se alcanza dentro de una vecindad “cercana”. Así, para una
función 𝐹(𝑥): 𝑅 𝑛 → 𝑅, se tiene que:

𝑥 ∗ 𝑒𝑠 𝑚á𝑥𝑖𝑚𝑜 𝑙𝑜𝑐𝑎𝑙 𝑑𝑒 𝐹(𝑥) ↔ ∃𝑟 > 0, 𝐹(𝑥 ∗ ) ≥ 𝐹(𝑥) ∀ 𝑥 ∈ 𝐵𝑟 (𝑥 ∗ ) ∩ 𝐷𝑜𝑚(𝐹)

La idea general es que en este caso 𝐹(𝑥 ∗ ) es el mayor valor de 𝐹(𝑥) a lo largo de valores del
dominio lo suficientemente cercanos a 𝑥 ∗ . Es decir, 𝐹(𝑥 ∗ ) es como “la cima de una de las
colinas de la cordillera”. Finalmente, nótese que si 𝐹(𝑥) alcanza un máximo local en 𝑥 ∗ ,
entonces −𝐹(𝑥) alcanza un mínimo local en 𝑥 ∗ .

 Definición 1.13: Máximo global

El máximo global es el mayor valor alcanzable por la función a lo largo de todo su dominio.
Así, para una función 𝐹(𝑥): 𝑅 𝑛 → 𝑅, se tiene que:

𝑥 ∗ 𝑒𝑠 𝑚á𝑥𝑖𝑚𝑜 𝑔𝑙𝑜𝑏𝑎𝑙 𝑑𝑒 𝐹(𝑥) ↔ 𝐹(𝑥 ∗ ) ≥ 𝐹(𝑥) ∀ 𝑥 ∈ 𝐷𝑜𝑚(𝐹)

En este caso, 𝐹(𝑥 ∗ ) es como “la cima de la montaña más alta de la cordillera”. Finalmente,
nótese que si 𝐹(𝑥) alcanza un máximo global en 𝑥 ∗ , entonces −𝐹(𝑥) alcanza un mínimo
global en 𝑥 ∗ .

 Definición 1.14: Teorema de Weiestrass

El teorema de Weiestrass busca determinar la existencia de algún óptimo (ya sea máximo o
mínimo) sin necesidad de conocer la función que se busca optimizar (sin embargo, se necesita
que esta sea continua). En ese sentido, solo se requiere conocer el dominio sobre el cual se
está trabajando, y las características del mismo. El teorema establece lo siguiente:

Sea el problema:

𝑀𝑎𝑥 𝐹(𝑥), 𝑑𝑎𝑑𝑜 𝑥 ∈ 𝐴 ⊂ 𝐷𝑜𝑚(𝐹) ⊂ 𝑅 𝑛

Donde 𝐴 es el conjunto de restricciones impuestas sobre el dominio de 𝐹, pudiendo ser

además el dominio en su totalidad.

Así, el teorema indica que, si 𝑨 es un conjunto compacto y no vacío, y además la función

𝑭(𝒙) es continua, entonces el problema tiene al menos una solución. No obstante, ¿por
qué se requiere que 𝐴 cumpla con dichas características?

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

Para responder esta interrogante, debemos recordar los dos conceptos involucrados en la
definición de conjunto compacto: i) acotado; y ii) cerrado. En primer lugar, supongamos que
el conjunto no es acotado. En ese sentido, la función podría ser creciente y extenderse
indefinidamente a lo largo de un dominio infinito, por lo cual alcanzar un máximo sería
imposible (por ejemplo, la función 𝐹(𝑥) = 𝑥 a lo largo de 𝑥 ∈ 𝑅 se extiende al infinito).

Por otro lado, supongamos que el conjunto 𝐴 no es cerrado. En particular, supongamos por
ejemplo que queremos hallar el máximo de 𝐹(𝑥) = 𝑥 a lo largo de 𝑥 ∈ (1; 2) ⊂ 𝐷𝑜𝑚(𝐹) =
𝑅. Nótese que, en este caso, el conjunto 𝐴 = (1; 2) es abierto dado que no incluye a sus
puntos frontera.

Antes de proseguir, supongamos primero que 𝐴 = [1; 2]. En este caso, es evidente que el
valor máximo de la función es 𝐹(2) = 2, y que 𝑥 ∗ = 2. No obstante, esto solo es posible
porque el valor 𝑥 = 2 pertenece al conjunto 𝐴 . Así, regresando al caso 𝐴 = (1; 2) , se
distingue que no es posible hallar un máximo en dicho intervalo; pues todos los valores
del mismo son puntos interiores de 𝑨. Es decir, cada valor posible que podamos pensar
(dentro de dicho intervalo) estará por definición rodeado de otros valores de dicho intervalo.
Así, sin importar qué número determinemos como un posible “máximo” (por ejemplo, 𝑥 =
1,99) este quedará descartado por el hecho de que siempre se podrá encontrar un número
mayor (por ejemplo, 𝑥 = 1,999). En ese sentido, no se puede definir propiamente un valor
máximo para 𝐹(𝑥) en dicho intervalo.

Finalmente, es importante notar que el Teorema de Weiestrass brinda condiciones

suficientes para determinar la existencia de un óptimo (es decir, si dichas condiciones se
cumplen, entonces necesariamente habrá un óptimo). No obstante, dichas condiciones no
son necesarias para que haya un óptimo; pues si no se cumplen, aún existe la posibilidad
de que exista un óptimo bajo otras circunstancias. Visto de otra forma, el cumplimiento
del Teorema de Weiestrass implica que existe un óptimo; pero la existencia de un óptimo no
necesariamente está delimitada a que se cumpla dicho teorema.

Ejemplo 1.14.1: El problema 𝑀𝑎𝑥 − 𝑥 2 , 𝑑𝑎𝑑𝑜 𝑥 ∈ 𝑅 se resuelve para 𝑥 ∗ = 0. No obstante,

nótese que el conjunto 𝐴 = 𝑅 es abierto y no acotado. Por ello en este caso no se verifica el
Teorema de Weiestrass; sin embargo, esto no es concluyente con respecto a si el problema
tiene una solución o no. Pese a ello, tal como ya se verificó, el máximo sí existe y se da en
𝑥∗.

Ejemplo 1.14.2: Analice si el problema 𝑀𝑎𝑥 𝐹(𝑥) = 𝑥12 + 𝑥22 − (𝑥1 𝑥2 + 3)3 , 𝑑𝑎𝑑𝑜 𝑥 ∈
𝐴 = {𝑥 ∈ 𝑅 2 , 𝑥𝑖 ≤ 10 ∧ 𝑥1 + 𝑥2 ≥ 3} admite una solución.

Se deben analizar dos proposiciones: i) 𝐹(𝑥) es continua; y ii) 𝐴 es compacto y no vacío.

Yendo paso por paso:

i) Dado que 𝐹(𝑥) es una función con estructura polinómica, entonces es continua.
ii) El espacio de restricciones no vacío, pues comprende a al menos un vector dentro de él.
Basta con notar que, por ejemplo, 𝑣 = (2; 2)′ cumple con ambas restricciones impuestas.
Por otro lado, es notorio que el conjunto es acotado. Sin pérdida de generalidad, juntando
ambas restricciones se tiene que 𝑥1 + 10 ≥ 𝑥1 + 𝑥2 ≥ 3 → 𝑥1 ≥ −7. Así, se deduce que
−7 ≤ 𝑥𝑖 ≤ 10 ∀𝑖. Finalmente, este conjunto acotado es cerrado, puesto que contiene a

Elaborado por Kevin Gershy-Damet Vargas

 Lima, 19 de marzo de 2019

todos sus puntos frontera (la desigualdad en las restricciones no es estricta). Por ende, el
conjunto es compacto.

Dado que se cumplen las premisas 𝑖) y 𝑖𝑖), se concluye que se verifica el Teorema de
Weiestrass, por lo que existe un máximo obtenible de dicho problema de optimización.

 Definición 1.15: Teorema Local-Global

El teorema Local-Global busca determinar la unicidad de un valor óptimo de la función, una

vez que se ha probado la existencia de algún valor óptimo (probablemente a partir del
Teorema de Weiestrass). Para ello, en primer lugar se requiere que el conjunto de
restricciones impuestas al dominio (o el dominio mismo en sí) sea un conjunto convexo
(además de no vacío). La necesidad de que esta premisa se cumpla se basa en que los
siguientes pasos requieren evaluar la concavidad de la función bajo análisis (para lo cual se
requiere que el dominio restringido sea convexo). Así, se tienen dos casos posibles:

- Si la función es cóncava, entonces se puede concluir que cada máximo local posible
también es un máximo global. Nótese que el hecho de que la función sea “solamente”
cóncava deja abierta la posibilidad de que sea estrictamente cóncava en algunos tramos y
lineal en otros, tal como se muestra en el gráfico 1.4. Evidentemente, en este caso la parte
lineal (que además es de pendiente nula) de la curva se centra en el valor máximo de la
función, lo cual se traduce en el hecho de que habrá múltiples máximos locales que por lo
tanto serán además máximos globales.
- Si la función es estrictamente cóncava, entonces el máximo global es único. Esto se debe
a que, dado que la pendiente es decreciente en todo su dominio, sólo se iguala a cero en un
punto del mismo, y por lo tanto la función sólo alcanza su valor máximo en un único valor
del dominio.

Gráfico 1.4

Ejemplo 1.15.1: El problema 𝑀𝑎𝑥 𝐹(𝑥) = 𝑥12 + 𝑥22 , 𝑑𝑎𝑑𝑜 𝑥 ∈ 𝐴 = {𝑥 ∈ 𝑅 2 , 𝑥𝑖 ≤ 10 ∧ 𝑥1 +

𝑥2 ≥ 3} admite una solución, análogamente al planteado en el ejemplo 1.14.2. Luego, el
conjunto 𝐴 es convexo debido a que todas las restricciones involucradas son lineales; y por
otro lado, la función 𝐹(𝑥) es, claramente, estrictamente convexa. En ese sentido se concluye,
por el teorema Local-Global, que existe un único máximo global para el problema.

Elaborado por Kevin Gershy-Damet Vargas