1

Estudio de una funcin utilizando su derivada

Sea I un intervalo en , abierto, cerrado o semicerrado (semiabierto), acotado o no.
Crecimiento y decrecimiento
Definiciones:
- Una funcin definida en I es creciente en dicho intervalo si, siendo , x y I e , cuando
x y < es ( ) ( ) f x f y s .
- Una funcin es estrictamente creciente en I si, para , x y I e , cuando x y < es
( ) ( ) f x f y < .
- Una funcin es decreciente en I si, con , x y I e , cuando x y < es ( ) ( ) f x f y > .
- Una funcin es estrictamente decreciente en I si, para x y < , es ( ) ( ) f x f y > .
Una funcin puede ser creciente y decreciente en un intervalo al mismo tiempo, siempre que
sea de valor constante.
Si ( ) y f x = es creciente en I , es ( ) 0 f x > en los puntos x I e donde tiene derivada.
En este caso, sea h positivo o negativo, es siempre
( ) ( )
0
f x h f x
h
+
> , y por tanto
0
( ) ( )
( ) lim 0
h
f x h f x
f x
h

+
= > , si existe este lmite.
Nota:
3
( ) y f x x = = es estrictamente creciente en , pero
3
1
(0) ?
3 0
f = no existe.
Igualmente, si ( ) y f x = es decreciente en I , es ( ) 0 f x s en los x I e donde es derivable.
Veremos ms adelante que, si es ( ) 0 f x > en todo x I e , entonces es ( ) y f x = creciente en
dicho intervalo, y que, si es ( ) 0 f x s en todo x I e , ser decreciente.
Por ahora slo podemos decir lo que ocurre cerca de un punto donde la derivada no se anula.
Como ya vimos, si por ejemplo es
0
( ) 0 f x > , para valores pequeos de h ,0 h o < < , debe
ser
0 0
( ) ( )
0
f x h f x
h

>

, y por tanto
0 0 0
( ) ( ) ( ) f x h f x f x h < < + .
Esto no quiere decir que en un intervalo alrededor del punto la funcin es creciente.
Contraejemplo:
La funcin
4/3
( ) f x x x sen
x
t | |
= +
|
\ .
, si 0 x = , (0) 0 f = , tiene derivada (0) 1 f = , y en los otros puntos
1/3
2/3
4
( ) 1 cos
3
f x x sen
x x x
t t t | | | |
= +
| |
\ . \ .
.
Luego ( )
3 3 2 1 2
(1/ ) 1 cos 1 ( 1)
n
f n n n n t t t
+
= = + .
Por tanto no es creciente en ningn intervalo centrado en cero, por pequeo que sea.
2
Mximos y mnimos
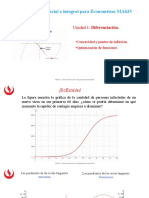
Si para un punto a I e la funcin continua ( ) y f x = , por ejemplo, crece en un intervalo a su
izquierda,( , ) c a , y decrece en un intervalo a su derecha,( , ) a b , debe ser ( ) ( ) f a f x > para cada
( , ) x c b e . Diremos que ( ) f x tiene en a un punto de mximo local. Si existe la derivada
( ) f a , tiene que ser ( ) 0 f a = , pues si fuera ( ) 0 f a > , en los puntos inmediatos a la derecha
sera ( ) ( ) f a f x < , y con ( ) 0 f a < sera ( ) ( ) f x f a > en los puntos a la izquierda de a.
Para poder expresarse con precisin son precisas varias definiciones:
- Un punto a I e es punto de mximo local de ( ) f x en I , si existe algn 0 r > tal
que ( ) ( ) f a f x > para todo ( , ) x a r a r e + que adems est en I .
- Un punto a I e es punto de mximo local estricto de ( ) f x en I , si existe algn
0 r > tal que ( ) ( ) f a f x > para todo ( , ) x a r a r e + que adems est en I y es
distinto de a.
- Un punto a I e es punto de mnimo local de ( ) f x en I , si existe algn 0 r > tal que
para todo ( , ) x a r a r e + que adems est en I , es ( ) ( ) f a f x s .
- Un punto a I e es punto de mnimo local estricto de ( ) f x en I , si existe algn
0 r > tal que, para todo ( , ) x a r a r e + , distinto de a, que adems est en I , es
( ) ( ) f a f x < .
- Un punto a I e es punto de mximo global de ( ) f x en I , si ( ) ( ) f a f x > para todo
x I e .
- Un punto a I e es punto de mximo global estricto de ( ) f x , si ( ) ( ) f a f x > para
todo x a = .
- Un punto a I e es de mnimo global de ( ) f x en I , si ( ) ( ) f a f x s para todo x I e .
- Un punto a I e es punto de mnimo global estricto de ( ) f x , si ( ) ( ) f a f x < para
todo x a = .
Los puntos de mximo o mnimo se denominan puntos extremos de la funcin en el intervalo.
Para una funcin constante ( ) ( ) y f x c c = = e , todo punto del dominio de definicin es
punto de mximo y de mnimo, local y global, pero ninguno es de tipo estricto.
Una funcin, incluso siendo continua, no tiene necesariamente puntos de mximo o mnimo,
local o global, en un intervalo.
Ejemplos:
La funcin
1
( ) f x
x
= no tiene punto de mximo en el intervalo | (
0,1 (en 0 no est definida)
donde es continua, pues dado ne, por grande que sea, es | (
1/ 0,1 ne , y (1/ ) f n n = . Y
ningn nmero real es mayor o igual que todo nmero natural.
La funcin ( ) f x x = es continua, pero no tiene punto de mnimo ni de mximo en (0, ) .
La funcin
1
( ) f x
x
= continua, salvo en 0 donde no est definida, no tiene puntos de mximo
ni mnimo global en
{ } | ) ( | 0 1 1,0 0,1 x x e < s = .
La funcin
1
( ) cos f x
x x
t | |
=
|
\ .
es continua en | (
0,1 , y (1/ ) cos
1/
f n n n
n
t | |
= =
|
\ .
, (signo +, si
n par; signo , si n impar). Luego no tiene ni mximo ni mnimo global.
3
Sin embargo, si una funcin es continua en un intervalo | | , I a b = cerrado y acotado, con
seguridad tiene puntos de mximo y mnimo, globales en dicho intervalo :
Teorema (Weierstrass): En un intervalo cerrado y acotado toda funcin continua tiene al
menos un punto de mximo y un punto de mnimo, globales.
Este teorema nos asegura, cuando se cumplen las condiciones (intervalocerrado y acotado y
funcin continua), que si buscamos los puntos extremos (de mximo o mnimo) de una
funcin ( ) f x en un intervalo, esos puntos existen. Otro asunto es cmo encontrarlos.
Para esto vamos a utilizar la derivada, ya que se verifica la siguiente propiedad.
Condicin necesaria de extremo:
Si una funcin ( ) f x tiene punto de mximo o mnimo local en un punto interior (no es uno
de sus extremos) de un intervalo, en ese punto la derivada, si existe, se anula.
En concreto si I tiene extremos , a b , y en ( ) , c a b e tiene ( ) f x un punto extremo (de
mximo o mnimo), ha de ser necesariamente ( ) 0 f c = , supuesto que existe esta derivada.
En efecto, para valores muy pequeos de h , el numerador de
( ) ( ) f c h f c
h
+
mantiene el
signo, pero el denominador es positivo o negativo. Por ello ha de ser, si existe,
0
( ) ( )
( ) lim 0
h
f c h f c
f c
h
+
= = .
Los puntos donde la derivada se anula se llaman puntos estacionarios.
Usando esta propiedad podemos demostrar un teorema importante, el Teorema del valor
medio.
Vemos primero un caso particular:
Teorema (de Rolle): Si ( ) f x es continua en | | , I a b = , derivable en ( ) , a b , y adems es
( ) ( ) f a f b = , entonces en algn ( ) , c a b e es ( ) 0 f c = .
Demostracin: Si ( ) f x k = constante, es ( ) 0 f x = en todo | | , x a b e .
En otro caso o bien el valor mximo o el mnimo de ( ) f x se alcanza en algn punto, distinto de a y de b ,
( ) , c a b e . Es ( ) 0 f c = .
Teorema del valor medio: Si ( ) f x es continua en | | , I a b = , derivable en ( ) , a b , para algn
punto ( ) , a b e es
( ) ( )
( )
f b f a
f
b a

.
Demostracin: La funcin
( ) ( )
( ) ( ) ( )
f b f a
g x f x x a
b a

tiene las propiedades de ( ) f x y adems es

( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( ( ) ( )) ( ) ( ) ( )
f b f a f b f a
g a f a a a f a f b f b f a f b b a g b
b a b a

= = = = =

Aplicando el teorema anterior, existe ( ) , a b e tal que
( ) ( )
( ) ( ) 0
f b f a
g f
b a


= =

.
4
El teorema del valor medio nos permite demostrar:
Si ( ) f x tiene derivada positiva o cero ( ( ) 0 f x > ) en todos los puntos del intervalo I , es
creciente en I .
Si ( ) f x tiene derivada negativa o cero ( ( ) 0 f x s ) en todos los puntos del intervalo I , es
decreciente en I .
Por lo tanto, si ( ) 0 f x = en todos los puntos del intervalo I , es ( ) f x C = constante.
Supuesto que ( ) 0 f x > en todo punto, si , c d I e , siendo c d < , es ( ) ( ) ( )( ) 0 f d f c f d c = > ,
luego ( ) ( ) f c f d s . Por lo tanto ( ) f x es creciente.
Si ( ) 0 f x s en todo punto, ( ) ( ) ( )( ) 0 f d f c f d c = s , siendo entonces ( ) f x decreciente
Esto permite, estudiando el signo de la derivada, localizar los puntos de mximo y mnimo
(local) de una funcin ( ) f x :
Si
0
( ) 0 f x = , y es ( ) 0 f x > en ( )
0 0
, x r x (puntos justo a la izquierda de
0
x ) , pero
( ) 0 f x s en ( )
0 0
, x x s + (puntos justo a la derecha de
0
x ), ( ) f x tiene un punto de mximo en
0
x . Crece a la izquierda y decrece a la derecha del punto de mximo.
Si
0
( ) 0 f x = , y es ( ) 0 f x s en ( )
0 0
, x r x (puntos justo a la izquierda de
0
x ) , pero
( ) 0 f x > en ( )
0 0
, x x s + (puntos justo a la derecha de
0
x ), ( ) f x tiene un punto de mnimo en
0
x . Decrece a la izquierda y crece a la derecha del punto de mnimo.
Estos cambios de signo de la derivada, cerca de un punto estacionario
0
x donde la derivada se
anula,
0
( ) 0 f x = , podemos deducirlos del valor de la derivada segunda
0
( ) f x :
Si
0
( ) 0 f x = y
0
( ) 0 f x < , entonces para valores muy pequeos de 0 h > es
0 0 0
( ) ( ) 0 ( ) f x h f x f x h > = > + , y por tanto
0
x es punto de mximo local.
Si
0
( ) 0 f x = y
0
( ) 0 f x > , entonces para valores muy pequeos de 0 h > es
0 0 0
( ) ( ) 0 ( ) f x h f x f x h < = < + , y por tanto
0
x es punto de mnimo local.
Atencin: Hay ejemplos de funciones importantes en los que en los puntos de mximo
mnimo no hay derivada.
La funcin ( ) f x x = , definida en tiene mnimo en 0, pero (0) f no existe.
Lo mismo ocurre con
2/3
( ) f x x = .
Modo de hallar los puntos de extremo en un intervalo cerrado y acotado.
Suponemos ( ) f x continua, lo que nos asegura la existencia de al menos un punto de cada
tipo. Suponemos tambin que es derivable, salvo a lo sumo en algn punto aislado.
Igualamos la derivada a cero: ( ) 0 f x = . Se calculanlas soluciones de esta ecuacin.
Dispuestos todos estos puntos en la recta real, tanto aquellos donde no es derivable la funcin
como los que anulan la funcin derivada, en los intervalos intermedios entre dichos puntos,
dentro del dominio de la funcin, la derivada mantiene constante su signo, que hemos de
determinar en cada intervalo.
Si en un punto de los sealados,
0
x , la derivada es negativa a su izquierda y positiva a su
derecha, ese punto es punto de mnimo local. Esto es cierto si
0
( ) 0 f x > , en los puntos en
que ( ) 0 f x = .
5
Si la derivada es positiva a su izquierda y negativa a su derecha, ese punto es punto de
mximo local. Esto es cierto si
0
( ) 0 f x < , en los puntos en que ( ) 0 f x = .
Si el intervalo es | | , I a b = , ser a punto de mnimo, si cumple las condiciones anteriores de
mnimo o ( ) 0 f a > y ser punto de mximo, si cumple las condiciones anteriores de mximo
o ( ) 0 f a < .
El punto b es punto de mnimo, si cumple las condiciones generales anteriores o ( ) 0 f b < , y
serpunto de mximo en las condiciones generales o si ( ) 0 f b > .
Concavidad y convexidad.
Una funcin, derivable, es convexa en un intervalo, si su derivada es creciente en dicho
intervalo.
Una funcin, derivable, es cncava en un intervalo, si su derivada es decreciente en dicho
intervalo.
Si la funcin es dos veces derivable en el intervalo, si ( ) 0 f x > en todos los puntos del
intervalo, ser convexa y, si siempre es ( ) 0 f x s , ser cncava.
Se llama punto de inflexin a todo punto,
0
x , en que cambia la funcin de cncava a convexa
o viceversa. Es decir, si existen intervalos
0
( , ) c x y
0
( , ) x d , a derecha e izquierda de
0
x , tales
que ( ) f x es cncava en uno de dichos intervalos y convexa en el otro. Esto puede ocurrir, si
0
( ) 0 f x = .
Ejemplos:
3
y x = , tiene derivadas
2
3 , 6 y x y x = = nulas en el punto 0, que es de inflexin,
pues 6 0 y x = < , si 0 x < , y 6 0 y x = > , si 0 x > .
Pero para
4 3 2
, 4 , 12 y x y x y x = = = , se anulan las dos derivadas en 0, que en este caso no es
punto de inflexin, sino punto de mnimo.
Sea ( ) y f x = derivable y convexa en I , siendo c I e . Entonces es ( ) ( ) ( )( ) f x f c f c x c > +
para todo x I e
Si, por ejemplo, c x < , es ( ) ( ) ( )( ) ( )( ) f x f c f x c f c x c = > al ser c x < <
La grfica de ( ) y f x = va por encima, en I , de las rectas tangentes en todos los puntos
( ) , ( ) c f c correspondientes.
Si es cncava en I y c I e . Entonces es ( ) ( ) ( )( ) f x f c f c x c s + para todo x I e
Si, por ejemplo, c x < , es ( ) ( ) ( )( ) ( )( ) f x f c f x c f c x c = s al ser c x < <
La grfica de ( ) y f x = va por debajo, en I , de las rectas tangentes en todos sus puntos
( ) , ( ) c f c .
6

Lmites e infinito.
La funcin
1
( ) f x
x
= , continua y decreciente (
2
1
( ) 0 f x
x

= < ) en el intervalo (0,1], no est

definida en 0 x = . Pero, adems, ningn valor, que quiera darse a (0) f , puede hacerla
continua en ese punto. Por lo tanto no existe un nmero real al que podamos llamar
0
1
lim
x
x

.
Sabemos que no tiene punto de mximo en (0,1], pues si fuese
0
0
1
( ) f x
x
= su valor mximo
(
0
x punto de mximo), tomando un nmero, incluso natural ne, tal que
0
0
1
( ) f x n
x
= < ,
es
0
1
( ) f n f x
n
| |
= >
|
\ .
siendo ( |
1
0,1
n
e : luego
0
x no es punto de mximo.
En realidad, si x (positivo) se acerca decreciendo a 0 x = ,
1
( ) f x
x
= crece indefinidamente,
tomando valores mayores que cualquier valor, por grande que sea, que hayamos fijado de
antemano: en concreto, si 0 M > es, por ejemplo,
30
10 M = , basta con que x cumpla
30
1 1
0
10
x
M
< < = , para que
30
1 1
( ) 10
1/
f x M
x M
= > = = .
Esta situacin la resumimos escribiendo
0
1
lim
x
x
+

= +.
Como los valores de x , que se acercan a 0, son slo los positivos ( 0 , x x x = + positivo),
ponemos en esta expresin, bajo lim, 0 x
+
(Lmite a la derecha). Y dado que, cuando
0 x
+
, los valores de
1
( ) f x
x
= superan cualquier valor arbitrario escribimos
0
1
lim
x
x
+
= + .
Si, con la misma funcin, x se acerca a 0 con valores negativos ( 0 , x x x = positivo),
escribiremos 0 x

, y
0
1
lim
x
x

(Lmite a la izquierda).
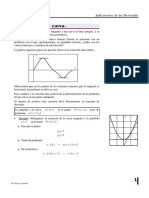
0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8
f cncava f convexa
P. inflexin
7
Pero si 0 x

,
1
( ) f x
x
= ser ms y ms negativo, y habr que escribir
0
1
lim
x
x

= .
Para
2
1
( ) f x
x
= , argumentando del mismo modo que en el caso anterior, se puede escribir
2 2
0 0
1 1
lim lim
x x
x x
+
= + = . Lo resumimos con
2
0
1
lim
x
x

= + (Lmite bilateral)
Tambin es
0
1
lim
x
x
+
= +, no teniendo sentido
0
1
lim
x
x

(No existe x si x es negativo).
Si en lugar de aplicar la funcin
1
( ) f x
x
= a nmeros pequeos en valor absoluto (prximos
a 0), se piensa en sus valores para nmeros muy grandes, positivos, la situacin se invierte.
Para todo nmero 0 c > , por pequeo que sea, es posible encontrar un nmero grande
0 M > tal que, para cualquier x M > , es
1
0 ( ) f x
x
c < = < . Por ejemplo si
15
10 c

= , siendo
15
10 M = , cuando
15
10 x M > = es
15
1 1
0 ( ) 10 f x
x M
c

< = < = = .
Se escribe entonces
1
lim 0
x
x
+
= .
Incluso podemos escribir
1
lim 0
x
x
+
+
= , pues en este caso
1
x
es siempre positivo.
Para nmeros negativos, de enorme valor absoluto, dado 0 c > , si
1
M
c
= , siendo
x M < (muy negativo) es
1 1
0 ( ) f x
x M
c c

> > = > = .

Por ello se escribe
1
lim 0
x
x

= , que podramos poner

1
lim 0
x
x
+
= .
De forma similar se justifica que
2 2
1 1
lim 0 lim
x x
x x
+
= = . (En ambos lmites 0+).
Tambin
1
lim 0
x
x
+
= . Pero,
1
lim
x
x

no tiene sentido.
Lmites infinitos.
En general, si una funcin ( ) y f x = est definida en un intervalo ( , ) a a h + , y para cualquier
0 M > , es posible hallar un nmero 0 o > , tal que cuando a x a o < < + es ( ) f x M > , se
escribe lim ( )
x a
f x
+
= +.
Si, en cambio, para todo 0 M > , es posible hallar un nmero 0 o > , tal que cuando
a x a o < < + es ( ) f x M < , se escribe lim ( )
x a
f x
+
= .
Si ( ) y f x = est definida en ( , ) a h a , y para cualquier 0 M > , es posible hallar un nmero
0 o > , tal que cuando a x a o < < es ( ) f x M > , se escribe lim ( )
x a
f x

= +.
8
lim ( )
x a
f x

= , si para todo 0 M > , es posible hallar un nmero 0 o > , tal que cuando
a x a o < < es ( ) f x M < .
Se escribe lim ( )
x a
f x

, si lim ( ) lim ( )
x a x a
f x f x
+
= .
Lmites en infinito.
Si ( ) y f x = est definida en un intervalo ( , ) a , y existe un nmero real l e tal que, dado
cualquier 0 c > , es posible hallar 0 M > , siendo ( ) l f x l c c < < + cuando x M > , se
escribe lim ( )
x
f x l
+
= .
Ejemplo
1
lim 1
x
x
x
+
+
= , pues
1 1
1 1 1 1
x
x x
c c
+
< < = + < + , siempre que
1
x M
c
> = .
Si ( ) y f x = est definida en un intervalo ( , ) b , y existe un nmero real l e tal que, dado
cualquier 0 c > , es posible hallar 0 M > , siendo ( ) l f x l c c < < + cuando x M < , se
escribe lim ( )
x
f x l

= .
Ejemplo:
1
lim 1
x
x
x

+
= , pues
1 1
1 1 1 1
x
x x
c c
+
< = + < < + , siempre que
1
x M
c

< = (Ojo!:
1 1
0
M x
c = < <

)
Con estos lmites infinitos y los lmites numricos se pueden establecer algunas reglas de
clculo, que deben usarse con ms cuidado que en el simple caso de lmites finitos.
Reglas de clculo:
Para lmites en un punto (vlidas tambin para lmites laterales):
- Si lim ( )
x a
f x c

= e, y lim ( )
x a
g x

= , es:
lim( ( ) ( ))
x a
f x g x

+ = ;
( )
lim 0
( )
x a
f x
g x

= .
- Si lim ( ) 0
x a
f x c

= > , es lim( ( ) ( ))
x a
f x g x

= ,
( )
lim
( )
x a
g x
f x

=
- Si lim ( ) 0
x a
f x c

= < , es lim( ( ) ( ))
x a
f x g x

= ,
( )
lim
( )
x a
g x
f x

=
Hay que tener especial cuidado si lim ( ) 0
x a
f x

= , lim ( )
x a
g x

= . No hay regla general para

calcular lim( ( ) ( ))
x a
f x g x

, que en muchos casos ni siquiera existe.

Ejemplo: Son
2 2
2
0
0 0 0
1 1
lim 0; lim 0; lim 0; lim
x
x x x
x x x sen
x x

| |
= = = = +
|
\ .
,
siendo
2
2 2
0
0
1 1
lim ; lim 1
x
x
x x
x x

= = . Y no existe
2
2
0 0
1 1 1
lim lim
x x
x sen sen
x x x
| | | |
=
| |
\ . \ .
Para los lmites en infinito
Sean lim ( )
x
f x c
+
= e, y lim ( )
x
g x d
+
= e, por ejemplo, entonces:
9
lim( ( ) ( ))
x
f x g x c d
+
+ = + , lim( ( ) ( ))
x
f x g x c d
+
+ = + , lim( ( ) ( ))
x
f x g x cd
+
=
Y si lim ( ) 0
x
g x d
+
= = , ser
( )
lim
( )
x
f x c
g x d
+
= .
Lmites en funciones racionales.
Si
( )
( )
( )
P x
R x
Q x
= , siendo
0
( )
n
n
P x a x a = + + polinomio de grado n ,
0
( )
m
m
Q x b x b = + +
de grado m :
,
( )
lim ,
( )
0,
n
x
n
si n P Q m
a P x
si n P Q m
Q x b
si n P Q m
+
= c > c =

= = c = c =

= c < c =

En el primer caso (n P Q m = c > c = ) el lmite es +, si ( 1) 0

n m n
m
a
b

> , siendo +, si
( 1) 0
n m n
m
a
b

< .
Ejemplos:
2
2
2
lim lim
1
3 1
3
x x
x
x
x
x
x
+ +
+
+
= = +

;
2 2
2
2
2 2
2
2
lim 1
1
2 1
lim lim
1 1 3 1 3
3 lim 3
x
x x
x
x x
x
x
x x
+
+ +
+
| |
+
+ |
+
\ .
= = =
| |

|
\ .
;
2
1
3
3 1
lim lim 0
2
2
x x
x
x
x
x
x
+ +

= =
+
+
Si es ( ) 0 Q a = , y por ello
( )
( )
( )
P x
a Dom R x Dom
Q x
e = , la funcin es continua en ese punto:
( ) ( )
lim
( ) ( )
x a
P x P a
Q x Q a

= .
Si ( ) 0 Q a = , se presenta diferentes situaciones.
1
( ) 0 ( ) ( ) ( ) Q a Q x x a Q x = = y, si a es raz de multiplicidad k , ( ) ( ) ( )
k
Q x x a q x = .
Sea j la multiplicidad de a para ( ) P x ( 0, j = si ( ) 0 P a = ), ( ) ( ) ( )
j
P x x a p x = .
( ), ( ) q x p x son polinomios , siendo ( ) 0, ( ) 0 q a p a = = .
Se presentan tres casos:
1) cuando k j < , es
( ) ( ) ( ) ( ) ( )
lim lim lim( ) 0 0
( ) ( ) ( ) ( ) ( )
j
j k
k
x a x a x a
P x x a p x p x p a
x a
Q x x a q x q x q a

= = = =

10
2) siendo k j = , es
( ) ( ) ( ) ( ) ( )
lim lim lim
( ) ( ) ( ) ( ) ( )
k
k
x a x a x a
P x x a p x p x p a
Q x x a q x q x q a

= = =

3) para k j > (en particular 0 j = ) , es

( ) ( ) ( ) 1 ( )
lim lim lim
( ) ( ) ( ) ( ) ( )
j
k k j
x a x a x a
P x x a p x p x
Q x x a q x x a q x

= = =

El signo de este ltimo lmite depende de , ( ), ( ) k j p a q a y de si x a
+
x a

.
Oj0!: si k j es par
( ) ( )
lim lim
( ) ( )
x a x a
P x P x
Q x Q x
+
= , pero si es impar
( ) ( )
lim lim
( ) ( )
x a x a
P x P x
Q x Q x
+
=
Exponenciales y logaritmos.
Idea de exponencial
Una cantidad aumenta (o disminuye) exponencialmente cuando aumenta (o disminuye) en un
factor fijo por unidad de tiempo.
Ahora bien, no es preciso que la variable independiente sea el tiempo, y en general se define:
Una funcin ( ) f x es de tipo exponencial, si el valor de la funcin es multiplicado por un
factor constante, al aumentar la variable independiente en una unidad: ( 1) ( ) f x bf x + = (b
multiplicador fijo positivo).
Si suponemos ( ) f x de tipo exponencial, definida para los nmeros enteros y (0) f C = , ha de
ser (1) f Cb = ,
2
(2) (1) f bf Cb = = ,, ( )
n
f n Cb = (n e ).
Como
2
(0) ( 1) ( 2) ( )
n
C f bf b f b f n = = = = = , debe ser ( )
n
f n Cb

= (n e ).
Los valores de ( ) f x , si x e ( x no entero), no se deducen de la propiedad ( 1) ( ) f x bf x + = .
Dados arbitrariamente los valores de ( ) f x para
| ) 0,1 x e , quedan determinados todos los
valores en . Por ejemplo, sera
3
( ) (3,14159..) (0,14159..) f f Cb f t = = .
Pero en Matemticas se utiliza el adjetivo exponencial, slo si es ( )
x
f x Cb = .
Funcin exponencial
Una funcin exponencial es de la forma ( )
x
y f x Cb = = , con 0 b > y siendo (0) C f = .
Recordamos que: dado b nmero real positivo, cuando n e , se define
n
b b b b b = , en
que n es el nmero de factores de este producto.
Si , n me se verifican las leyes de los exponentes
n m n m
b b b
+
= , y por tanto ( )
n m nm
b b = .
Para que estas leyes se mantengan, con exponentes enteros, se define
0
1 b = ,
1
n
n
b
b

= .
11
Igualmente, si
n
m
e
( , n m e e ), debe ser
( )
n
n
m n m m
b b b = = .
Es posible extender, por continuidad, estas definiciones para definir una funcin ( )
x
f x b = ,
siendo x e, que cumpla la regla de los exponentes
x y x y
b b b
+
= , para todo , x y e .
(La otra ley ( )
x y xy
b b = es consecuencia de esa regla
x y x y
b b b
+
= ).
Esta funcin es una exponencial de base b y es la nica funcin continua con esas
caractersticas y con valor b para 1 x = .
Es decir, todas las funciones continuas que cumplen la ecuacin funcional
( ) ( ) ( ) f x y f x f y + = para todo . x y e , son de esa forma:
x
b .
Si 1 b > la exponencial es estrictamente creciente en , siendo estrictamente decreciente si
1 b < .
Exponencial y derivada
Una funcin exponencial de la forma ( )
x
y f x Cb = = , 0 b > , es derivable en todo punto, pero
la expresin de su derivada no es sencilla, como veremos.
El problema est en conocer su derivada en 0, ya que:
0 0 0
1 1
( ) lim lim lim ( )
x h x h h
x x
b
h h h
Cb Cb b b
f x Cb Cb k f x
h h h
+


= = = =
siendo
0
1
lim (0)
h x
b
h
b db
k
h dx

= =
.
(0)
x
b
db
k
dx
=
, la derivada en 0 de
x
y b = , es una constante que slo depende de b .
Por lo tanto, si ( )
x
f x Cb = , su variacin instantnea ( ) f x es proporcional al valor ( ) f x :
( )
( )
b
f x
k
f x
=
constante.
Podemos por ello definir con ms precisin:
Una cantidad aumenta (o disminuye) exponencialmente cuando su tasa relativa de variacin
es constante.
(La tasa relativa de variacin es el cociente entre la tasa de variacin instantnea (derivada) y
el valor de la funcin)
La funcin exponencial natural.
Para poder expresar
(0)
x
b
db
k
dx
=
en funcin de 0 b > , vamos a utilizar un nmero de gran
importancia en las matemticas: el nmero e .
e es el nmero real positivo para el que
(0) 1
x
e
de
k
dx
= =
.
La funcin exponencial ( )
x
f x e = se llama exponencial natural y su propiedad caracterstica
es :
( )
x
x
de
f x e
dx
= =
Como
( ) 0
x
x
de
f x e
dx
= = >
, ( )
x
f x e = es una funcin estrictamente creciente. Luego es 1 e > .
2
2
( ) ( )
x x
x x
d e d de d
f x e e
dx dx dx dx
| |
= = = =
|
\ .
es siempre positiva, luego ( )
x
f x e = es convexa en .
Por ello, su grfica est por encima de todas sus rectas tangentes.
Como (0) (0) 1 y f f x x = + = + es la tangente en (0,1), es ( ) 1
x
f x e x = > + , si 0 x =
12
Siendo 1 e > , ha de ser
lim
x
x
e
+
= +
. Como 1
x x
e e

= , es
1
lim lim lim 0
x x
x
x x x
e e
e

+ +
= = =
.
Dado m e , es lim 0
m
x
x
x
e
+
= . En efecto
1
1
1
x
m
x
e
m
+
> +
+
. Luego
1
(1 )
1
x m
x
e
m
+
> +
+
, y por tanto
si x es positivo, es
1
0
(1 )
1
m m
x
m
x x
x
e
m
+
< <
+
+
, siendo finalmente, cuando x +:
1
0 lim lim 0
(1 )
1
m m
x
x x
m
x x
x
e
m
+ +
+
s s =
+
+
(El polinomio del denominador es de grado mayor que el del numerador.)
Logaritmos naturales
La funcin exponencial ( )
x
f x e = es derivable, continua, estrictamente creciente en toda la
recta real.
Al ser adems
lim 0
x
x
e

=
,
lim
x
x
e

= +
, su rango es la semirrecta (0, ) , de modo que cada
nmero real positivo y es imagen de un nico xe.
Si es
x
y e = , escribimos lny x = , que se lee logaritmo (natural o neperiano) dey igual a x .
ln
x
y e x y = =
Slo los nmeros positivos tienen logaritmo.
Por definicin:
ln
1
ln1 0, ln 1, ln , ln ,
2
x x
e e e x e x = = = = = .
Propiedades algebraicas de los logaritmos:
Como
lnx
x e = ,
lny
y e = , es tambin
ln( ) ln ln ln ln xy x y x y
e xy e e e
+
= = = , luego
ln( ) ln ln xy x y = + ( 0, 0) x y > >
De donde se deducen:
ln(1) 0 = ,
ln( ) ln( ) ln( )
x
x y
y
=
,
1
ln( ) ln( ) x
x
=
,
ln( ) ln( )
q
x q x = ( 0, ) x q > e .
En general: dado que
ln ln
( )
a x a a x
x e e = = , es ln( ) ln( )
a
x a x = ( 0, ) x a > e .
Grfica de
x
y e =
13

2 2 4
2
2
4
6
8

Grfica de ln y x =
Funcin ln y x =
La funcin ln y x = es continua, derivable, estrictamente creciente y cncava, pues su grfica
es simtrica, respecto de la recta y x = , de la grfica de la funcin exponencial
x
y e = .
Derivada de la funcin logaritmo:
Como
lnx
x e = , derivando en ambos lados de la igualdad,
ln
(ln ) (ln )
1
x
d x d x
e x
dx dx
= =
Por lo tanto
(ln ) 1 d x
dx x
= , si 0 x > .
Para 0 x = , se puede definir ln y x = , siendo su derivada
(ln )
1 1
d x d x
dx x dx x
= = .
La derivada segunda,
2
2 2
(ln ) 1
0
d x
dx x

= < , confirma que su grfica es cncava.

El nmero e.
Hemos definido e como el nmero para el que
(0) 1
x
e
de
k
dx
= =
.
Para los logaritmos con base e , ln y x = , es
(ln ) 1 d x
dx x
=
.
Como
1/
0 0
(ln ) ln(1 ) ln1
1 (1) lim lim(ln(1 ) )
h
h h
d x h
h
dx h

+
= = = +
, ha de ser
1/ 1/
0 0
lim(ln(1 ) ) ln( lim(1 ) )
1/
0
1
lim(1 ) lim 1
h h
h h
n
h h
h
h n
e e e h
n

+ +

| |
= = + = +
|
\ .
14
El ltimo lmite es la definicin ms popular del nmero e , que es un nmero irracional del
que se han calculado slo unos cientos de miles de decimales,:
2,71828182845904523536...... e =
Exponenciales y logaritmos
Siendo, para 0 b > ,
lnb
b e = , ser
ln x x b
b e = y por tanto
( )
(ln )
x
x
d b
b b
dx
= .
Luego
( )
(0) ln
x
b
d b
k b
dx
= = .
Si, para un 0 b > dado, es
z
x b = , escribimos log
b
z x = (logaritmo en base b de x ).
Ejemplos:
2
log 8 3 = , pues
3
2 8 = .
10
log (0.01) 2 = , pues
2
10 0.01

= .
Ya que
log (ln )(log ) ln
b b
x b x x
e x b e = = = , ser
ln
log
ln
b
x
x
b
= .
Adems es
(log ) 1
( )
(ln )
b
d
x
dx b x
=
Lmites importantes.
lim(ln )
x
x

=
0
limln
x
x
+

=
ln
lim lim 0
m m
m
x x
x y
x e

= =
(me). (Basta poner ln y x = , pues x y en este caso).
En 0 es de sealar :
1
1
0 0
( 1) (ln ) ( 1) (ln )
lim (ln ) lim lim 0
m m m m
m
x x y
x y
x x
x y

= = =
0
lim (ln ) 0
m
x
x x

=
Derivacin logartmica
Si ( ) y f x = es positiva y derivable, podemos derivar ln ln( ( )) z y f x = =
Ser
( )

( )
y f x
z
y f x
= = . Y por tanto: y z y =
ln( ( ))
( ) ( )
d f x
f x f x
dx
=
Ejemplo: Para derivar
x
y x = , tomando logaritmos es ln ln( ( )) ln( ) z y f x x x = = = .
Luego
1
ln 1 ln
y
z x x x
y x
= = + = + . Por lo tanto: (1 ln )
x
y x x = +