Documentos de Académico
Documentos de Profesional
Documentos de Cultura
Transformada Fourier
Transformada Fourier
Cargado por
Alonso SandovalDerechos de autor
Formatos disponibles
Compartir este documento
Compartir o incrustar documentos
¿Le pareció útil este documento?
¿Este contenido es inapropiado?
Denunciar este documentoCopyright:
Formatos disponibles
Transformada Fourier
Transformada Fourier
Cargado por
Alonso SandovalCopyright:
Formatos disponibles
Universidad Tecnica Federico Santa Mara
Departamento de Matem atica
Notas mat 023
Segundo Semestre 2012
1. La Transformada de Fourier
1.1. Denicion. Sea f : R C una funci on cualquiera, no necesariamente periodica. Si nos restringimos
al intervalo [L, L] R podemos suponer que la funci on es periodica de perodo 2L (usando su expansi on de
medio rango) y entonces, si f es lo sucientemente buena
1
, podemos expresarla en Serie de Fourier exponencial
como
(1.1) f(x) =
kZ
c(
k
, L)e
i
k
x
,
k
=
k
L
, k Z,
donde
(1.2) c(
k
, L) =
1
2L
_
L
L
f(x)e
i
k
x
dx.
Denimos la siguiente funci on
(1.3) c() =
1
2
_
f(x)e
ix
dx.
Pero, note que
(1.4) lm
L
L
c(
k
, L) = c().
Usando lo ultimo es facil notar que
(1.5) lm
L
kZ
L
c(
k
, L)e
ix
=
_
c()e
ix
d,
por lo tanto, si nuestra funci on es lo sucientemente buena (ver nota al pie), se tiene que
(1.6) f(x) =
_
c()e
ix
d, c() =
1
2
_
f(x)e
ix
dx,
JCM/jcm. juan.chavarria@usm.cl.
1
Diremos esto cuando f es absolutamente integrable, es decir
R
|f(x)|dx < y ademas si es continua por tramos.
1
o equivalentemente,
f(x) =
1
2
_
__
f(t)e
it
dt
_
e
ix
d. (1.7)
=
1
2
_
_
1
2
_
f(t)e
it
dt
_
e
ix
d. (1.8)
Lo anterior es, por tanto, un analogo de la serie de Fourier valido para funciones denidas sobre todo R. Con
esto, podemos denir lo siguiente
Definici on 1.1 Dada una funci on absolutamente integrable, continua por tramos f : R C, deniremos su
transformada de Fourier, que denotaremos por
f o F[f], a la aplicacion F : C C
(1.9)
f() = F[f]() =
1
2
_
f(x)e
ix
dx.
Ademas, denimos la transformada inversa de Fourier a la aplicacion F
1
: C C:
(1.10) f(x) = F
1
[
f ](x) =
1
2
_
f()e
ix
d.
Definici on 1.2 A la funci on F() = |
f()| se le llama espectro de la funci on f.
Ejemplo 1.1 Encontrar la transformada de Fourier de
f(x) =
_
1 si 0 x L
0 si no.
Utilizando la denicion
f() =
1
2
_
f(x)e
ix
dx =
1
2
_
L
0
1 e
ix
dx =
1
2
e
ix
i
L
0
=
1
2
_
1 e
iL
i
_
.
Con esto se muestra que, en general, la transformada de Fourier es una funci on a valores complejos.
Ejemplo 1.2 Encontrar la transformada de Fourier de
f(x) =
_
1 si L x L
0 si no.
Utilizando la denicion
f() =
1
2
_
f(x)e
ix
dx
=
1
2
_
L
L
1 e
ix
dx
=
1
2
e
ix
i
L
L
=
1
2
e
iL
e
iL
i
(usando formula de Euler) =
_
2
sen L
.
Ejemplo 1.3 Vamos a encontrar la transformada de Fourier de la funci on f(x) = e
ax
2
, a > 0.
Por denicion tenemos que
f() =
1
2
_
e
ax
2
e
ix
dx =
1
2
_
e
(ax
2
+ix)
dx.
Completamos el cuadrado x
2
+ix = a
_
x
2
+ 2
i
2a
x +
_
i
2a
_
2
_
i
2a
_
2
_
= a
_
x +
i
2a
_
2
+
2
4a
. Con esto, obtenemos
f() =
e
2
4a
2
_
e
a(x+
i
2a
)
2
dx.
2
La integral
_
e
a(x+
i
2a
)
2
dx se calcula utilizando integrales m ultiples y vale
_
a
. Por lo tanto
f() =
1
2a
e
2
4a
.
Ejemplo 1.4 Encontrar la transformada de Fourier de (x a), a R.
Esta vez tenemos una funci on absolutamente integrable. Sin embargo, ella no es seccionalmente continua
(razon?). Pero, utilizando la propiedad de integraci on de esta funci on, conseguimos calcular su transformada
de Fourier. Veamos
F[(x a)]() =
1
2
_
(x a)e
ix
dx
=
1
2
e
ia
.
En particular, si a = 0, se tiene que F[(x)]() =
1
2
llamado usualmente ruido blanco. Si ademas usamos la
denicion de transformada inversa de Fourier, tenemos que
F
1
[1()](x) =
2(x).
1.2. Propiedades. Las propiedades de la Transformada de Fourier son muy parecidas a las propiedades de
la Transformada de Laplace y se demuestran de forma similar (es decir, usando la denicion). Resumimos a
continuacion los resultados principales.
Teorema 1.1. Sean a, b R y f, g : R C tales que existen sus transformadas de Fourier
f, g. Entonces, la
transformada de Fourier es una transformacion lineal, i.e.
F[af +bg]() = aF[f]() +bF[g]()
= a
f() +b g(). (1.11)
Teorema 1.2. Sea f C
k
(R) tal que f, f
, . . . , f
(k)
son absolutamente integrables. Entonces
F[f
(n)
]() = (i)
n
F[f](), n = 0, 1, . . . , k. (1.12)
F[f(x)x
n
]() = (i)
n
d
n
d
n
F[f]() =
f
(n)
(), n = 0, 1, . . . , k. (1.13)
Teorema 1.3. (Translacion y escalamiento) Sea f absolutamente integrable y sean , a R, entonces
F[f(x +a)]() = F[f(x)]e
ia
=
f()e
ia
. (1.14)
F[f(x)e
ixa
]() = F[f(x)]( a) =
f( a). (1.15)
F[f(x)]() =
1
||
F[f(x)]
_
_
=
1
||
f
_
_
. (1.16)
F[f(x)]() = F[f(x)](). (1.17)
Recordemos ahora la denicion de producto de convoluci on para dos funciones f, g : R C, f g est a dada
por
(f g)(x) =
_
f(p)g(x p)dp.
El teorema que relaciona la transformada de Fourier con el producto de convoluci on es muy similar al resultado
de transformada de Laplace y se enuncia como sigue
3
Teorema 1.4. Sean f, g : R C continuas por tramos, acotadas y absolutamente integrables. Entonces
(1.18) F[f g]() =
2F[f]()F[g]() =
2
f() g().
Teorema 1.5. (Generalizaci on de Parseval) Sea f seccionalmente continua y de cuadrado integrable, i.e.,
f
2
=
_
R
|f|
2
dx < . Entonces
(1.19) f
2
=
f
2
2. Aplicaci on a la Resoluci on de EDPs
A continuacion, aplicaremos la transformada de Fourier para resolver un problema de Ecuaciones Diferen-
ciales Parciales (EDP).
Ejemplo 2.1 Para comenzar, consideramos la ecuaci on de transporte. Encontrar u = u(x, t) tal que
u
t
+au
x
= 0 < x < t > 0 a > 0,
u(x, 0) = f(x) < x < .
Donde u, u
x
, f son todas funciones absolutamente integrables. Para resolver, aplicaremos el siguiente procedi-
miento
Aplicamos transformada de Fourier en el espacio para obtener:
d
dt
u(, t) +ai u(, t) = 0
u(, 0) =
f().
Note que el sistema obtenido consta de una EDO lineal y homogenea de primer orden en t y una condicion
inicial. La solucion de esta ecuaci on separable es
u(, t) = c()e
iat
.
Al imponer la condicion inicial es claro que c() =
f() y luego u(, t) =
f()e
iat
. Por la propiedad
de escalamiento 1.14 se tiene que
u(x, t) = f(x at),
es decir, la informacion inicial se transmite por espacio y tiempo sin alteraciones.
Ejemplo 2.2 La siguiente Ecuaci on Diferencial Parcial modela el comportamiento de una onda que se propaga
en el espacio. Encontrar u = u(x, t) tal que
u
tt
= u
xx
, < x < , t 0.
u(x, 0) = f(x), < x < .
u
t
(x, 0) = 0, < x < .
Donde u, u
x
, f son todas absolutamente integrables.
4
Aplicamos transformada de Fourier en el espacio para obtener:
d
2
dt
2
u(, t) =
2
u(, t)
u(, 0) =
f()
d
dt
u(, 0) = 0,
Note que el sistema obtenido consta de una EDO lineal y homogenea de segundo orden con dos condiciones
iniciales. El polinomio caracterstico asociado es
p
2
+
2
= 0,
que implica que la solucion es
u(, t) = a() cos t +b() sent,
donde a(), b() son funciones que dependen de . Imponiendo la primera condicion inicial obtenemos
a() =
f().
Derivando a la solucion e imponiendo la segunda condicion inicial, es claro que
b() = 0.
Por lo tanto, la solucion en el espacio de frecuencia es
u(, t) =
f() cos t.
Al aplicar la formula de inversi on, se tiene que
u(x, t) =
1
2
f(x) F
1
[cos t](x).
La transformada inversa de cos t se obtiene por tabla y es
_
2
_
(x t) +(x + t)
_
. Luego la solucion
del problema planteado es
u(x, t) =
1
2
f(x)
_
2
_
(x t) +(x +t)
_
=
1
2
f(x)
_
(x t) +(x +t)
_
,
pero de acuerdo a la propiedad de integraci on del delta de Dirac es igual a
u(x, t) =
1
2
_
f(x t) +f(x +t)
_
,
conocida como la formula de DAlembert.
Ejemplo 2.3 Consideremos el problema de transmision de calor en una barra delgada muy larga aislada en su
supercie lateral, que es modelada por el siguiente problema de valor inicial. Encontrar u = u(x, t) tal que
u
t
= c
2
u
xx
, < x < , t > 0, c > 0;
u(x, 0) = f(x), < x < .
Donde la solucion y su derivada con respecto a x, u(x, t), u
x
(x, t) son absolutamente integrables si |x| , t >
0 y f es una funci on seccionalmente continua e integrable en todo R.
5
Sean u(, t) y
f() las transformadas de Fourier de u(x, t) y f(x) respectivamente, entonces, tras aplicar
transformada de Fourier al problema anterior obtenemos
d
dt
u(, t) = c
2
(i)
2
u(, t), < < , t > 0;
u(, 0) =
f(), < < .
La primera de las ecuaciones corresponde a la EDO lineal de primer orden
d
dt
u(, t) +c
2
2
u(, t) = 0,
con solucion u(, t) = k()e
c
2
t
2
. Luego, al imponer la condicion inicial sigue que k() =
f() con lo cual
u(, t) =
f()e
c
2
t
2
.
Utilizando la formula de convoluci on para la transformada inversa de Fourier obtenemos
u(x, t) =
1
2
f(x) F
1
[e
c
2
t
2
](x),
quedando solo por determinar la transformada inversa de e
c
2
t
2
. Esto es sencillo si recordamos el ejemplo 1.3,
que nos dice que F[e
ax
2
]() =
1
2a
e
2
4a
. Basta hacer 4a =
1
tc
2
y obtenemos F
1
[e
c
2
t
2
] =
1
c
2t
e
x
2
4tc
2
. De
esta forma:
(2.1) u(x, t) = f(x)
1
4c
2
t
e
x
2
4tc
2
,
conocida como formula de GauWeierstra. Si el dato es inicial est a dado por f(x) = (x ), entonces
u
f
(x, t) = (x )
1
4c
2
t
e
x
2
4tc
2
=
1
4c
2
t
e
(x)
2
4tc
2
. (2.2)
Para cada f(x) se tendra la solucion es la convoluci on de f con u
f
(x, t), llamada solucion fundamental para el
problema de calor.
3. Otras Representaciones en Frecuencia
Sabemos que si f es una funci on integrable entonces su transformada de Fourier est a dada por
f() =
1
2
_
f(x)e
ix
dx.
Nuestro objetivo es explotar los casos en que f posea alguna propiedad de paridad o imparidad. Para comenzar,
si f es una funci on par se tiene, utilizando la formula de Euler, que
f() =
1
2
_
f(x) cos xdx
i
2
_
f(x) sen xdx.
La segunda integral es cero en vista de la paridad de f y la simetra del intervalo (, ). Ademas, por el
mismo argumento se tiene que
(3.1)
f
c
() =
_
2
_
0
f(x) cos xdx,
6
conocida como transformada Fourier de cosenos de f(x). Por la formula de inversi on obtenemos
(3.2) f(x) =
_
2
_
0
f
c
() cos xd.
De forma similar, si f es una funci on impar, se dene la transformada de Fourier de senos como
(3.3)
f
s
() =
_
2
_
0
f(x) sen xdx,
con inversa dada por
(3.4) f(x) =
_
2
_
0
f
s
() senxd.
Ejemplo 3.1 Vamos a determinar la transformada de Fourier de cosenos de la funci on e
x
. Claramente,
tenemos
f
c
() =
_
2
_
0
e
x
cos xdx
(F ormula de Euler) =
_
2
1
1 +
2
.
Teorema 3.1. Sea f(x) continua y absolutamente integrable sobre el eje x y sea f
(x) seccionalmente continua
sobre cada intervalo nito, y sea f(x) 0 si x . Entonces,
1. F
c
[f
(x)]() =
f
s
()
_
2
f(0), y
2. F
s
[f
(x)]() =
f
c
().
Ademas, si existe f
(x) y es seccionalmente continua y absolutamente integrable sobre el eje x con f
(x) 0
si x . Entonces
3. F
c
[f
(x)]() =
2
f
c
()
_
2
(0
+
), y
4. F
s
[f
(x)]() =
2
f
s
() +
_
2
f(0
+
).
Ejemplo 3.2 Con la ayuda del ejemplo 3.1 y del resultado anterior, resolveremos la ecuaci on de Laplace en
una placa semi innita. Encontrar u = u(x, y) tal que
u
xx
+u
yy
= 0, 0 < x < , y > 0;
u(0, y) = 0, y > 0;
u(, y) = e
y
, y > 0;
u
y
(x, 0) = 0, 0 < x < .
La condicion inicial u
y
(x, 0) = 0 sugiere que usemos la tercera parte del teorema 3.1 y apliquemos transformada
de Fourier de cosenos a nuestro problema. Haciendo esto, obtenemos
u
xx
2
u
_
2
u
y
(x, 0) = 0, 0 < x < , > 0;
u(0, ) = 0, > 0;
u(, ) =
_
2
1
1 +
2
, > 0.
7
En vista de la condicion inicial u
y
(x, 0) = 0 el problema se simplica y se reduce a una ecuaci on diferencial
ordinaria de orden dos en la variable x para u(x, ) con condiciones de frontera en x = 0, x = . Resolver este
problema es sencillo y obtenemos
u(x, ) = A()e
x
+B()e
x
.
Al imponer la condicion de frontera en x = 0 obtenemos A() = B(). Usando el dato en x = encontramos
que
A() =
1
2
1
1 +
2
1
senh
.
Con lo cual
u(x, ) =
_
2
1
1 +
2
senh x
senh
.
Por lo tanto, la representacion en integral de Fourier de la solucion es
u(x, y) =
2
_
0
1
1 +
2
senh x
senh
cos y d.
Observaci on 3.1 Notemos que si la condicion inicial hubiera sido de la forma u(x, 0) = f(x), entonces es
apropiado aplicar la cuarta parte del teorema 3.1, es decir, usar transformada de Fourier de senos.
3.1. Integrales de Fourier. Denimos las funciones
A() =
_
2
f
c
() =
2
_
0
f(x) cos xdx, (3.5)
B() =
_
2
f
s
() =
2
_
0
f() sen xdx, (3.6)
como las integrales de Fourier de cosenos y senos, respectivamente. Notemos ahora que si f no es una funci on
ni par ni impar, estas integrales lucen como
A() =
1
f(x) cos xdx,
B() =
1
f() sen xdx.
En este caso, tendremos la siguiente representacion para f:
Teorema 3.2. Sea f(x) continua por tramos y absolutamente integrable en < x < , entonces f puede
ser representada como integral de Fourier como
(3.7) f(x) =
_
0
[A() cos x +B() sen x]d.
Ademas, para cada x:
_
0
[A() cos x +B() sen x]d =
1
2
_
f(x
+
) +f(x
)
_
.
Ejemplo 3.3 Vamos a encontrar la representacion en integral de Fourier del pulso unitario
f(x) =
_
1 si |x| < 1
0 si |x| > 1
8
Tenemos que
A() =
1
f(x) cos xdx =
1
_
1
1
cos xdx =
2 sen
,
B() =
1
_
1
1
senxdx = 0.
As, tenemos la representacion:
f(x) =
2
_
0
cos xsen
d.
Del teorema anterior es claro que
_
0
cos xsen
d =
_
2
si |x| < 1,
2
1+0
2
si x = 1,
0 si |x| > 1.
Esta integral es llamada factor discontinuo de Dirichlet. Al evaluar en x = 0 es claro que
_
0
sen
d =
2
.
4. Funciones Test
A continuacion daremos una breve introduccion a la llamada Teora de las distribuciones que sera utilizada
para calcular la transformada de Fourier de algunas funciones que no cumplen con la denicion usual dada en
la secci on precedente.
Definici on 4.1 (Funci on Test) Diremos que : R R es una funci on test o de prueba si y solo si C
(R
(es decir, posee innitas derivadas continuas sobre R) y si ademas existe M > 0 tal que (x) = 0, x : |x| > M.
Fig. 1. Una funcion test.
Ejemplo 4.1 Probar que
(4.1) x(x) = 0, x.
9
Sea una funci on test arbitraria. Al multiplicar por a 4.1 e integrar sobre todo R obtenemos
_
x(x)(x)dx =
_
(x)(x(x))dx
(propiedad integral de (x)) = x(x)|
x=0
= 0.
Como la igualdad anterior es valida para una funci on test arbitraria se tiene que x(x) = 0, x.
Ejemplo 4.2 Demostremos que la expresion
(4.2)
_
(x)(x)dx =
_
f(x)
(x)dx
es consecuente con la denicion ordinaria de una derivada de f(x) si f C
1
(R).
Si integramos por partes a 4.2 obtenemos
_
(x)(x)dx = f(x)(x)|
f(x)
(x)dx.
Puesto que (x) = 0, x > |M| se tiene que el primer termino es igual a cero y entonces tenemos lo pedido
_
(x)(x)dx =
_
f(x)
(x)dx.
Si f(t) es una funci on arbitraria (no necesariamente C
1
(R)) su derivada est a denida por 4.2. Por ejemplo, si
consideramos a (x a), tenemos
_
(x a)(x)dx =
_
(x)
(x a)dx
= (x a). (4.3)
Generalizando lo anterior, es posible demostrar que
(n)
(x a) = (1)
n
(n)
(x a).
Si ahora consideramos a (x a) y utilizamos 4.2, tenemos
_
(x a)(x)dx =
_
(x a)
(x)dx
=
_
a
(x)dx
= (x)|
a
= (() (a))
= (a).
Pero
(a) =
_
(x a)(x)dx.
Y luego
(4.4)
_
(x a)(x)dx =
_
(x a)(x)dx, funci on test.
Como esta ultima igualdad es valida para toda funci on test, sigue que la derivada generalizada de (x a) es
(x a).
Ejemplo 4.3 Utilicemos lo anterior para calcular la transformada de Fourier de (x a).
De acuerdo al primer teorema de traslacion, se tiene que
F[(x a)]() = F[(x)]e
ia
,
10
y todo se reduce a encontrar F[(x)]. Note que para todo x = 0 se tiene que
(x) +(x) = 1.
Para tal caso, al aplicar transformada de Fourier y usando 1.17 se tiene que
() + () =
2().
Sin embargo, no hemos considerado el caso en que x = 0. Para ello, supondremos que () = c() + A(),
donde A() es una funci on que iremos caracterizando. Con ello
() + () = c() +A() +c() +A()
= 2c() +A() +A()
=
2().
De aca se concluye que c =
_
2
y que A() debe ser impar. S olo resta determinarla. Para ello, utilizaremos la
formula de la derivada de la funci on escal on como sigue
F[(x)]() = F[
(x)] = iF[(x)]
= i
__
2
() +A()
_
(por 4.1) = iA().
Pero F[(x)]() =
1
2
. Por lo tanto
A() =
i
2
.
Finalmente obtenemos
(4.5) () =
_
2
()
i
2
.
Referencias
[1] Ordinary and Partial Dierential Equations. R. P. Agarwal & D. ORegan. Universitext, Springer Verlag, 2009.
11
También podría gustarte
- Guía # 1 Matemáticas P1 - 11° OkDocumento29 páginasGuía # 1 Matemáticas P1 - 11° OkJuan Felipe Herrera BuenoAún no hay calificaciones
- Unidad V-Servicio Comunitario - Trabajo CompletoDocumento25 páginasUnidad V-Servicio Comunitario - Trabajo CompletoNesbely PietriAún no hay calificaciones
- Trucos para EXAMENES PsicotecnicosDocumento7 páginasTrucos para EXAMENES PsicotecnicosJose VasconcelosdelaveintidosAún no hay calificaciones
- TAREA - Introduccion A La Trigonometeria EsfericaDocumento12 páginasTAREA - Introduccion A La Trigonometeria EsfericaIvan DiazAún no hay calificaciones
- Sistema Por UnidadDocumento4 páginasSistema Por UnidadJorgeMoralesAún no hay calificaciones
- Examen Algebra Lineal-2020-1 - Ok PDFDocumento2 páginasExamen Algebra Lineal-2020-1 - Ok PDFDiegoAún no hay calificaciones
- Buscadores Web y Redes Semánticas PDFDocumento8 páginasBuscadores Web y Redes Semánticas PDFHarry HallerAún no hay calificaciones
- Ejercicios ExellDocumento43 páginasEjercicios ExelljanedimejeAún no hay calificaciones
- AaaaaaaaaDocumento4 páginasAaaaaaaaaLenon Quispesivana ȻhAún no hay calificaciones
- Act 3-Estadistica DescriptivaDocumento3 páginasAct 3-Estadistica DescriptivaDaniela MeloAún no hay calificaciones
- Tema 9 GraficasDocumento30 páginasTema 9 GraficasMaria Perez GomezAún no hay calificaciones
- Tercer Parcial de Matemáticas Básicas 2-2020Documento3 páginasTercer Parcial de Matemáticas Básicas 2-2020HIDRIPAV PISCINAS OLIMPICAS CALLE 42 IBAGUEAún no hay calificaciones
- Evaluación Final Del Área Del Matematica CuartoDocumento2 páginasEvaluación Final Del Área Del Matematica CuartoAnonymous sn5lwGvUSBAún no hay calificaciones
- 7 Clase - Estructuras de Control Simple y DobleDocumento12 páginas7 Clase - Estructuras de Control Simple y DobleKeidy GómezAún no hay calificaciones
- TAREA 8 TransporteDocumento3 páginasTAREA 8 TransporteJuanjo Vivanco XDAún no hay calificaciones
- Array ListDocumento20 páginasArray Listeudys_aAún no hay calificaciones
- Balance Macroscopico de EnergiaDocumento12 páginasBalance Macroscopico de EnergiaMoises Alcocer100% (1)
- Tabla de DerivadasDocumento1 páginaTabla de DerivadasE&GAún no hay calificaciones
- Ejercicios Semana 15 D25Documento2 páginasEjercicios Semana 15 D25Nicolás Daniel AndlnAún no hay calificaciones
- Informe de Control de Equipo ScoopDocumento19 páginasInforme de Control de Equipo ScoopFrank GarciaAún no hay calificaciones
- Segundo Parcial I.ODocumento126 páginasSegundo Parcial I.OMelAún no hay calificaciones
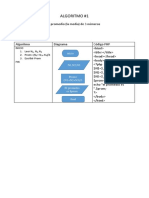
- ALGORITMODocumento5 páginasALGORITMOanthony urrutia canoAún no hay calificaciones
- Malla Curricular Emprendimiento 2017 - PrimariaDocumento9 páginasMalla Curricular Emprendimiento 2017 - PrimariaJulio Quevedo Montaña100% (6)
- Cuadernillo Actividades CBDocumento28 páginasCuadernillo Actividades CBSol MirandaAún no hay calificaciones
- Evaluación de ProyectosDocumento31 páginasEvaluación de ProyectosMarco GomLAún no hay calificaciones
- Fracciones Homogeneas y Heterogeneas para Tercer Grado de PrimariaDocumento2 páginasFracciones Homogeneas y Heterogeneas para Tercer Grado de Primariakaren.montoya305Aún no hay calificaciones
- IPER ModeloDocumento5 páginasIPER ModeloAntonioAún no hay calificaciones
- KTUC Análisis.Documento5 páginasKTUC Análisis.Tatiana Uribe clavijoAún no hay calificaciones
- Anualidad Vencida Matematica Financiera PDFDocumento28 páginasAnualidad Vencida Matematica Financiera PDFgreta179Aún no hay calificaciones
- Dialnet LasImplicaturasConversacionalesGeneralizadasYParti 5279866Documento18 páginasDialnet LasImplicaturasConversacionalesGeneralizadasYParti 5279866Manuel GranadosAún no hay calificaciones