5.

6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 406

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal)

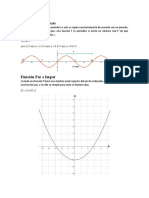
Funciones Pares e Impares

En el manejo de series de Fourier es muy útil observar dos tipos de funciones con las que
podemos hacer simplificaciones de las fórmulas de Euler-Fourier. Estas son las funciones
pares e impares que geométricamente se caracteriza por la propiedad de simetría con
respecto al eje y y el origen, respectivamente.

Se muestran algunas gráficas de dichas funciones.

2 25

20

15
cos( x ) 2
12.57 6.28 0 6.28 12.57 x
10

2
10 5 0 5 10
x x

Figura 5.6.1 Ejemplo de funciones pares tales como cos( x) y x 2

2 10

sin ( x ) x
12.57 6.28 0 6.28 12.57 10 0 10

2 10

x x

Figura 5.6.2 Ejemplo de funciones impares tales como sen( x) y x

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 407

Se dice que f es una función par si su dominio contiene al punto x , y si

f ( − x) = f ( x) (1)

Se dice que f es una función impar si su dominio contiene a − x , y si

f (− x) = − f ( x) (2)

Para cada x en el dominio de f .

La mayoría de funciones no son pares ni impares.

Teniendo un intervalo simétrico, observamos ciertas características en las operaciones con

funciones pares e impares.

• La suma, diferencia, producto y cociente de dos funciones pares es par.

• La suma y diferencia de dos funciones impares es impar.
• El producto y cociente de dos funciones impares es par.
• La suma o diferencia de una función impar y otra función par no es ni par ni impar
• El producto y cociente una función par y otra impar es impar.

De igual importancia son las siguientes dos propiedades de integrales de funciones pares
e impares

• si f es una función par entonces

a a
∫−a
f ( x)dx = 2∫ f ( x)dx
0
(3)

• si f es una función impar entonces

a
∫−a
f ( x)dx = 0 (4)

La comprobación de las afirmaciones anteriores son triviales y se deducen directamente de

las definiciones.

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 408

Ejemplo 5.6.1 Si f1 ( x ) y f 2 ( x ) son impares y además g ( x) = f1 ( x) + f 2 ( x) , comprobar

si g ( x) es impar. [1]

Revisamos de acuerdo a (2), para que sea impar entonces se debe cumplir g (− x) = − g ( x)

Si g (− x) = f1 (− x) + f 2 (− x) , ya que f1 y f 2 son impares, entonces se debe cumplir

también que

f1 (− x) = − f1 ( x) y f 2 (− x) = − f 2 ( x) , por lo tanto

g (− x) = − f1 ( x) − f 2 ( x) , factorizando el signo − [ f1 ( x) + f 2 ( x) ] = − g ( x)

De tal modo que f1 ( x ) + f 2 ( x ) también es una función impar.

Ejemplo 5.6.2 Si f1 ( x ) y f 2 ( x ) son impares y tenemos que h( x) = f1 ( x) f 2 ( x) ,

comprobar que h( x) es par

Entonces haciendo h(− x) = f1 (− x) f 2 (− x) , como son pares se debe cumplir

f1 (− x) f 2 (− x) = [ − f1 ( x) ][ − f 2 ( x) ]

Por lo que realizando operación de los signos nos queda

[ − f1 ( x)][ − f 2 ( x)] = f1 ( x) f 2 ( x) , así h(− x) = h( x)

Por lo que el producto f1 f 2 es par.

En los siguientes ejemplos determinar si la función es par o impar.

−π π
Ejemplo 5.6.3 Siendo f ( x) = cos ( x ) para valores de ≤ x < determinar si es par
2 2
o no.

Haciendo f (− x) = cos (− x) , por la identidad cos (− x) = cos ( x ) , de tal manera que

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 409

f (− x) = f ( x) , por lo tanto la función cos ( x ) es una función par.

Ejemplo 5.6.4 Siendo f ( x) = x 2 para −1 ≤ x < 1 , determinar si es par o no.

Haciendo f (− x) = (− x) 2 , entonces f (− x) = x 2 de tal manera que f (− x) = f ( x) .

Por lo tanto la función x 2 es función par.

Ejemplo 5.6.5 Determinar si f ( x) = x en el intervalo −1 ≤ x ≤ 1 es una función par o

impar

Haciendo f (− x) = −x , entonces f (− x) = − f ( x) , por lo tanto es una función par

−π π
Ejemplo 5.6.6 Determinar si la función f ( x) = sen ( x ) , en el intervalo ≤ x ≤ , es
2 2
par o impar.

Haciendo f (− x) = sen(− x) = − sen ( x ) = − f ( x)

Por lo tanto la función sen ( x ) es función impar

Serie de Cosenos

Suponga que f y f ´ son seccionalmente continuas, y que f es una función periódica

par, en el intervalo (− p, p) , de periodo 2 p .

Dado que el producto de funciones pares es par, una propiedad mencionada anteriormente,
 nπ 
entonces el producto f ( x)cos  x  es par, pues ambas son funciones pares.
 p 

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 410

 nπ 
El producto de f ( x) sen  x  es impar, como resultado de multiplicar una función par y
 p 
una impar.

De tal manera que los coeficientes de Fourier de f (siendo f par ) entonces están dados
por

2 p
p ∫0
• ao = f ( x)dx

2 p  nπ 
• an =
p ∫0
f ( x)cos 
 p
x  dx

n = 0,1, 2...

• bn = 0 n = 1, 2...

Así podemos expresar nuestra función f en términos de la serie de Fourier.

a0 ∞  nπ 
f ( x) = + ∑ an cos  x (5)
2 n =1  p 

Dado que no están presentes términos senoidales, una serie de este tipo recibe el nombre
de serie cosenoidal de Fourier .

Serie de Senos

Suponga que f y f ´ son seccionalmente continuas sobre − p ≤ x < p y que f es una

función periódica impar de periodo 2 p , de tal manera que manejando las propiedades
 nπ 
anteriores, obtenemos que f ( x)cos  x  es impar como resultado de multiplicar una
 p 
 nπ 
función impar con una par y que f ( x) sen  x  es par, dado que es el producto de dos
 p 
funciones impares

En este caso los coeficientes de Fourier de la función f son

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 411

• an = 0 n = 0,1, 2,...;

2 p  nπ 
• bn = ∫
p 0
f ( x) sen 
 p
x dx para n = 1, 2,...;


Y la serie de Fourier para la función f tiene la forma

∞
 nπ 
f ( x) = ∑ bn sen  x (6)
n =1  p 

a la cual se le conoce con el nombre de serie senoidal de Fourier dado que no existen
términos cosenos.

Ejemplo 5.6.7 Sea f ( x) = x para valores de −1 < x < 1 de periodo 2 (figura 5.6.2), la
función definida de esta manera se conoce como onda diente de sierra. Encontrar la serie
de Fourier para esta función.

1
f(x)

5 3 1 1 3 5

Figura 5.6.2 Gráfica de la figura onda diente de sierra

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 412

Como f es una función impar, ya que tiene simetría con el origen, sus coeficientes de
fourier son de acuerdo con la teoría anterior, entonces

an = 0 para n = 0,1, 2,...;

2 1  nπ 
bn = ∫ ( x ) sen  x  dx
1 0  1 

Haciendo u = x y dv = sen ( nπ x )

1
Entonces du = dx y v=− cos ( nπ x )
nπ
1
 x 1 1 
De tal manera que bn = 2  − cos ( nπ x ) − ∫ − cos ( nπ x ) dx 
 nπ 0 nπ  0

 x  1 
2
 1
Resulta bn = 2  − cos ( nπ x ) +   sen ( nπ x ) 
 nπ  nπ   0

Sustituyendo los límites de la integral resulta

 2  2    2 ( 0)  2  
bn =  − cos nπ +  
 ( nπ )2 
sen ( nπ )  −  − cos ( 0 ) +  
 ( nπ )2 
sen ( 0 )  , quedando
 nπ   
   nπ   

2
( −1)
n
bn = − (7)
nπ

Por lo tanto la serie de Fourier para f , la onda de diente de sierra es

− ( −1)
n
∞
2
f ( x) =
π
∑
n =1 n
sen ( nπ x ) (8)

Ejemplo 5.6.8 Sea f ( x) = x 2 para valores de −1 < x < 1 (figura 5.6.3), encontrar la
serie de Fourier para esta función.[1]

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 413

f(x)

x
0 5

Figura 5.6.3 f ( x) = x 2 periódica, con período p = 2

Como f es una función impar, ya que tiene simetría con el origen, sus coeficientes de
fourier son de acuerdo con la teoría anterior

an = 0 para n = 0,1, 2,...;

2 1  nπ x 
bn = ∫ ( x ) sen   dx
1 0  1 

Haciendo u = x y dv = sen ( nπ x )

1
Entonces du = dx y v=− cos ( nπ x )
nπ
1
 x 1 1 
De tal manera que bn = 2  − cos ( nπ x ) − ∫ − cos ( nπ x ) dx 
 nπ 0 nπ  0

 x  1 
2
 1
Resulta bn = 2  − cos ( nπ x ) +   sen ( nπ x ) 
 nπ  nπ   0

Sustituyendo los límites de la integral resulta

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres

5.6 Serie de Fourier de funciones pares e impares (desarrollo cosenoidal o senoidal) 414

 2  2    2 ( 0)  2  
bn =  − cosnπ +  
 ( nπ )2 
sen ( nπ )  −  − cos ( 0 ) +  
 ( nπ )2 
sen ( 0 ) 
 nπ   
   nπ   

Quedando

2
( −1)
n
bn = − (9)
nπ

Por lo tanto la serie de Fourier para f , la onda de diente de sierra es

− ( −1)
n
∞
2
f ( x) =
π
∑
n =1 n
sen ( nπ x ) (10)

Instituto Tecnológico de Chihuahua / C. Básicas Amalia C. Aguirre Parres