CAP

ITULO 1
Funciones holomorfas
1.1 INTRODUCCI

ON
La denici on y primeras propiedades de la derivaci on de funciones complejas son
muy similares a las correspondientes para las funciones reales (exceptuando, como
siempre, las ligadas directamente a la relaci on de orden en R, como por ejemplo
el teorema del valor medio). Sin embargo, iremos comprobando poco a poco que
la derivabilidad compleja es una condici on mucho m as fuerte que la derivabilidad
real, o incluso que la diferenciabilidad de las funciones de dos variables reales. La
explicaci on nal la encontraremos en resultados posteriores.
Para las primeras secciones de este captulo puede usarse como libro de con-
sulta el texto de Open University: Complex Numbers / Continuous Functions /
Differentiation. The Open University Press, Milton Keynes (1974); para las nales,
ver Duncan, J.: The elements of complex analysis. Wiley, London (1968).
1.2 DERIVABILIDAD DE LAS FUNCIONES DE VARIABLE COMPLEJA
1. Denici on y primeras propiedades.
Como C es un cuerpo y tiene sentido la divisi on, podemos imitar literalmente
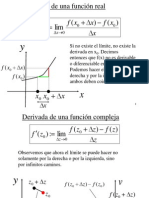
la denici on de derivabilidad de funciones reales.
Denici on. Sea abierto de C. Sea f : C y sea z
0
. Diremos que f
es derivable en z
0
si existe
lim
zz
0
f (z) f (z
0
)
z z
0
= f
/
(z
0
) C.
Al valor de dicho lmite f
/
(z
0
) lo llamaremos derivada de f en z
0
.
Observaci on. Aunque, formalmente, la denici on es como en R, la existencia
de lmite es aqu m as exigente, al tener que existir de cualquier modo que nos
acerquemos a z
0
por el plano. Esto har a que las funciones derivables en C sean
mejores que las derivables en R, y que podamos desarrollar una teora mucho m as
redonda para estas.
Para empezar, listamos las propiedades de derivabilidad que se demuestran
imitando punto por punto lo que se hace en R.
17
18 Funciones holomorfas
1. f derivable en z
0
= f continua en z
0
.
2. Si f y g son derivables en z
0
,
i) f g es derivable en z
0
y ( f g)
/
(z
0
) = f
/
(z
0
) g
/
(z
0
).
ii) f g es derivable en z
0
y ( f g)
/
(z
0
) = f
/
(z
0
)g(z
0
) g
/
(z
0
) f (z
0
).
iii) (Si f (z
0
) ,= 0), 1/f es derivable en z
0
y (1/f )
/
(z
0
) = f
/
(z
0
)/f (z
0
)
2
.
3. Regla de la cadena. Sean f :
1
C, g :
2
C con f (
1
)
2
.
Si f derivable en z
0
y g es derivable en f (z
0
), entonces g f es derivable en
z
0
, y
(g f )
/
(z
0
) = g
/
( f (z
0
)) f
/
(z
0
).
4. Derivaci on de la funci on inversa en un punto. Sea f : C inyectiva,
derivable en z
0
con f
/
(z
0
) ,= 0. Supongamos adem as que f () es abierto y
que f
1
es continua en f (z
0
). Entonces, f
1
es derivable en f (z
0
) y
( f
1
)
/

f (z
0
)

=
1
f
/
(z
0
)
.
Veamos, a modo de ejemplo, c omo este ultimo resultado se prueba igual que
para funciones reales:
La derivabilidad de f en z
0
es equivalente a la continuidad en z
0
de la funci on
g : C dada por
g(z) =

f (z) f (z
0
)
z z
0
si z ` {z
0
};
f
/
(z
0
) si z = z
0
.
Esta funci on permite escribir para todo z
f (z) f (z
0
) = g(z)(z z
0
),
y como ahora g es continua en z
0
con g(z
0
) = f
/
(z
0
) ,= 0, se vericar a g(z) ,= 0
en un entorno de z
0
. Poniendo w
0
= f (z
0
), si tomamos w f () y z = f
1
(w),
w w
0
= g

f
1
(w)

f
1
(w) f
1
(w
0
)

,
y, teniendo en cuenta que f
1
es continua en w
0
, para w en un entorno reducido
de w
0
,
1
g

f
1
(w)
=
f
1
(w) f
1
(w
0
)
w w
0
:
Funciones holomorfas 19
usando nuevamente la continuidad de f
1
en w
0
y la de g en z
0
= f
1
(w
0
), vemos
que existe
lim
ww
0
f
1
(w) f
1
(w
0
)
w w
0
=
1
f
/
(z
0
)
.
Ejemplos de funciones derivables.
1. Las funciones constantes son derivables en todo punto de C con derivada 0.
La funci on identidad es derivable en todo C y su derivada es constantemente
1.
2. Por operaciones algebraicas con funciones derivables, todo polinomio es deri-
vable en Cy su derivada tiene la misma expresi on que en R. Del mismo modo,
toda funci on racional, puesta en forma irreducible, es derivable en todo C
salvo los ceros del denominador.
1.3 CONDICIONES DE CAUCHY-RIEMANN
El problema que ahora vamos a tratar es exclusivo del contexto de C. Ya sabemos
que dar una funci onde variable compleja es dar dos funciones reales de dos variables
reales. Nos vamos a preguntar por la relaci on que existe entre la derivabilidad de
la funci on compleja y la diferenciabilidad de estas dos funciones.
En este apartado emplearemos sin m as comentarios la notaci on:
f : C, f (z) = u(z) i v(z) = u(x, y) i v(x, y),
z = x i y , z
0
= x
0
i y
0
.
Tenemos:
Teorema. f es derivable en z
0
si y solo si
i) u, v son diferenciables en (x
0
, y
0
).
ii) Se cumplen las llamadas condiciones de Cauchy-Riemann:
u
x

(x
0
,y
0
)
=
v
y

(x
0
,y
0
)
,
u
y

(x
0
,y
0
)
=
v
x

(x
0
,y
0
)
.
Demostraci on. Antes de entrar en ella, modiquemos un poco las notaciones.
Primero, es claro que f derivable en z
0
se puede escribir de la forma
lim
h0
f (z
0
h) f (z
0
) h. f
/
(z
0
)
h
= 0. (1)
20 Funciones holomorfas
Por otra parte, recordemos la noci on de diferenciabilidad. u diferenciable en
(x
0
, y
0
) signica que existe una forma lineal
L : R
2
R a (k, l) L(k, l) = ak bl
tal que
lim
(k,l)(0,0)
u(x
0
k, y
0
l) u(x
0
, y
0
) L(k, l)

k
2
l
2
= 0.
Recu erdese adem as que
a =
u
x

(x
0
,y
0
)
, b =
u
y

(x
0
,y
0
)
.
) Supongamos que f es derivable en z
0
y sea su derivada f
/
(z
0
) = i.
Escribimos h = k il para el par ametro complejo h.
(1) implica que
lim
h0
f (z
0
h) f (z
0
) h. f
/
(z
0
)
[h[
= 0. (2)
porque (2) se obtiene de (1) multiplicando por h/[h[ que es una funci on acotada.
Ahora,
f (z
0
h) f (z
0
) h. f
/
(z
0
)
[h[
=
u(x
0
k, y
0
l) u(x
0
, y
0
) (k l)

k
2
l
2
i
v(x
0
k, y
0
l) v(x
0
, y
0
) (k l)

k
2
l
2
(3)
luego, las partes real e imaginaria de esta expresi on tienen que tender a 0 cuando
h 0 (o, lo que es lo mismo (k, l) (0, 0)).
Pero esto quiere decir exactamente que u y v son diferenciables en (x
0
, y
0
)
con
u
x

(x
0
,y
0
)
= =
v
y

(x
0
,y
0
)
y
u
y

(x
0
,y
0
)
= =
v
x

(x
0
,y
0
)
.
) Si u y v son diferenciables en (x
0
, y
0
) y se cumplen las condiciones de Cauchy-
Riemann, llamamos
u
x

(x
0
,y
0
)
= =
v
y

(x
0
,y
0
)
y
u
y

(x
0
,y
0
)
= =
v
x

(x
0
,y
0
)
Funciones holomorfas 21
y se tiene que cumplir que la expresi on en (3) tiende a 0.
Por tanto, se cumple (2) y de aqu (1) (otra vez porque (1) se obtiene de (2)
multiplicando por [h[/h). As, f es derivable en z
0
con derivada f
/
(z
0
) = i.
Observaci on.
De paso, hemos visto en la demostraci on que la derivada de f se puede obtener
a partir de las derivadas parciales de u y de v,
f
/
(z
0
) =
u
x

(x
0
,y
0
)
i
u
y

(x
0
,y
0
)
=
v
y

(x
0
,y
0
)
i
u
y

(x
0
,y
0
)
=
u
x

(x
0
,y
0
)
i
v
x

(x
0
,y
0
)
=
v
y

(x
0
,y
0
)
i
v
x

(x
0
,y
0
)
.
Observaci on.
En el teorema anterior vemos que el concepto de derivabilidad compleja es
m as exigente que el de diferenciabilidad real. Si miramos a f como funci on de R
2
en R
2
, ser diferenciable signica sin m as que lo sean sus dos componentes u y v,
mientras que ser derivable exige, adem as de esto, que se cumplan las condiciones
sobre las derivadas parciales de u y v que establecen las ecuaciones de Cauchy-
Riemann. Algunas de las consecuencias de este hecho se ver an al nal del captulo.
NOTA. En Levinson, N.; Redheffer, R.M.: Curso de variable compleja. Revert e,
Barcelona (1990), p ags. 77 y ss. se da una interpretaci on fsica de las condiciones
de Cauchy-Riemann, en t erminos del estudio del ujo bidimensional de un uido
ideal.
Para una interpretaci on geom etrica de las condiciones de Cauchy-Riemann y
otras muchas consideraciones interesantes sobre la derivada y dem as conceptos,
con un enfoque muy original, v. Needham, T.: Visual Complex Analysis. Clarendon
Press, Oxford (1997).
1.4 FUNCIONES HOLOMORFAS. FUNCIONES ARM

ONICAS.
Denici on. Sea abierto de C. Sea f : C. Diremos que f es holomorfa
en un punto z
0
(o tambi en, que z
0
es un punto regular para f ) si f es derivable
en todos los puntos de un entorno de z
0
. Diremos que f es holomorfa en si f es
holomorfa en z
0
, z
0
.
Claramente, f es holomorfa en f es derivable en todos los puntos de
(pues al ser abierto, es entorno de todos sus puntos).
22 Funciones holomorfas
Denotaremos
H() = { f : C : f es holomorfa en }.
Por otra parte, recordemos el concepto de funci on arm onica.
Denici on. Sea abierto de R
2
. Sea u : R. Diremos que u es arm onica
en si u es de clase C
2
(i.e., u tiene derivadas parciales hasta el orden 2 y son
continuas) y cumple
.u =

2
u
x
2


2
u
y
2
= 0
en todo punto del abierto .
Gracias a las condiciones de Cauchy-Riemann tenemos:
Corolario. Si f H(), f = u i v, y u, v son de clase C
2
, entonces u, v son
arm onicas en .
Demostraci on. Por las condiciones de Cauchy-Riemann, se tiene

2
u
x
2
=

x

u
x

=

x

v
y

2
u
y
2
=

y

u
y

=

y

v
x

y, como u es de clase C
2
, las derivadas cruzadas coinciden y tenemos que u es
arm onica. An alogamente se razona con v.
Observaci on.
Veremos m as adelante que si f H() entonces f es indenidamente deri-
vable, lo cual implicar a que la hip otesis C
2
del corolario es innecesaria.
Las condiciones de Cauchy-Riemann nos van a permitir obtener funciones
holomorfas a partir de funciones arm onicas en abiertos de R
2
. Empecemos con la
siguiente denici on:
Denici on. Dada u arm onica en un abierto de R
2
, diremos que v es arm onica
conjugada de u en si f = u i v es holomorfa en . O, equivalentemente, por
las condiciones de Cauchy-Riemann, v satisface las condiciones
v
x
= u
y
, v
y
= u
x
en todo punto de .
Es inmediato demostrar que una funci on arm onica conjugada de otra es,
asimismo, arm onica.
Funciones holomorfas 23
Ejemplo 1.
Tomemos la funci on
u(x, y) = e
x
cos y.
Es una comprobaci on inmediata que dicha funci on es arm onica en todo R
2
. Para
tratar de encontrar una arm onica conjugada, planteamos las ecuaciones:
v
x
(x, y) = u
y
(x, y) = e
x
sen y
v
y
(x, y) = u
x
(x, y) = e
x
cos y
Es f acil resolver este sistema, obteniendo que la funci on
v(x, y) = e
x
sen y
es soluci on en todo R
2
. Por tanto, hemos obtenido que la funci on
f (z) = e
x
cos y i e
x
sen y, z = x i y
es una funci on holomorfa en todo C. Si utilizamos la notaci on polar, podemos
poner
f (z) = e
x
e
i y
Con lo que esta funci on compleja parece tener derecho a llamarse la funci on
exponencial compleja. En efecto lo ser a, aunque la introduciremos de forma ocial
con las series de potencias.
Que hayamos podido resolver el sistema en el ejemplo anterior no ha sido
casual. En efecto, vamos a ver en el siguiente resultado que para ciertos abiertos
de C, una funci on arm onica siempre tiene arm onica conjugada.
Teorema. Sea abierto estrellado de R
2
. Sea u arm onica en . Entonces, existe
v arm onica conjugada de u en .
Demostraci on. El resultado es una simple aplicaci on del lema de Poincar e para
abiertos estrellados. Recordemos que este resultado dice que toda forma diferencial
cerrada es exacta. Entonces, dada nuestra funci on u, consideramos la forma
(x, y) = u
y
(x, y)dx u
x
(x, y)dy
El ser u arm onica implica que es una forma cerrada. Entonces, es exacta, lo
cual quiere decir (por denici on) que existe una funci on v diferenciable tal que
v
x
= u
y
y v
y
= u
x
. Luego v es arm onica conjugada de u.
24 Funciones holomorfas
Observaci on.
M as adelante veremos que el teorema anterior es cierto en abiertos m as gene-
rales (los simplemente conexos). Pero, conel siguiente ejemplo, vamos a demostrar
que no es ampliable a abiertos cualesquiera.
Ejemplo 2.
Sea el abierto = C ` {0} y sea la funci on
u(x, y) =
1
2
log(x
2
y
2
)
que se comprueba sin dicultad que es arm onica en .
Esta funci on u no tiene arm onica conjugada en .
En efecto, si existiera v arm onica conjugada de u en , consideramos la
funci on de variable real
g(t ) = v(cos t, sen t ), t [0, 2].
g es una funci on continua en [0, 2] (por composici on de funciones continuas). La
derivamos por la regla de la cadena para funciones de varias variables y utilizamos
las ecuaciones de Cauchy-Riemann, obteniendo
g
/
(t ) = v
x
(cos t, sen t ) sen t v
y
(cos t, sen t ) cos t
= u
y
(cos t, sen t ) sen t u
x
(cos t, sen t ) cos t = 1.
Esto implica que g(t ) = t C, lo cual no puede ser porque g(0) = g(2).
Sin embargo, en un abierto estrellado como C ` (, 0], por el teorema ya
probado, la funci on anterior debe tener arm onica conjugada o, lo que es lo mismo,
ser la parte real de una funci on holomorfa. Esta funci on holomorfa cuya parte real
es u veremos m as adelante que es la funci on logaritmo principal.
4. Consecuencias de las condiciones de Cauchy-Riemann.
Las condiciones de Cauchy-Riemann nos permiten obtener con facilidad va-
rios resultados para funciones holomorfas, apoy andonos en el conocimiento de
funciones reales de dos variables.
1. Sea una regi on (i.e., abierto y conexo) de C. Si f es holomorfa en y
f
/
(z) = 0 para todo z , entonces f es constante.
Funciones holomorfas 25
En efecto, si f = u i v, f
/
= u
x
i u
y
= v
y
i v
x
= 0 en implica que
u
x
= u
y
= v
y
= v
x
= 0 y esto, ya sabemos que implica u, v constantes y,
por tanto f constante.
2. Sea regi on. Si f es holomorfa en y +e f (z) = C ( o `m f (z) = C) para
todo z , entonces f es constante.
En efecto, si u = ct e, entonces u
x
= u
y
= 0. Luego, por Cauchy-Riemann,
tambi en ser a v
x
= v
y
= 0, lo que implica v =cte. Por tanto, f es constante.
An alogamente se razonara si fuera constante la parte imaginaria.
3. Sea regi on. Si f es holomorfa en y [ f (z)[ = C para todo z , entonces
f es constante.
En efecto, la hip otesis es u
2
v
2
= ct e. Derivando en esta expresi on con
respecto a x e y, tenemos
2uu
x
2vv
x
= 0, 2uu
y
2vv
y
= 0.
Si utilizamos las ecuaciones de Cauchy-Riemann tendremos
2uu
x
2vu
y
= 0, 2uu
y
2vu
x
= 0
Multiplicando la primera u y la segunda v, nos da
(u
2
v
2
)u
x
= 0,
de donde u
x
= 0. De forma parecida se obtiene u
y
= v
x
= v
y
= 0. Por tanto,
u y v son constantes y en consecuencia lo es f .
Observaci on.
N otese c omo las condiciones de Cauchy-Riemann impiden que una funci on
holomorfa pueda tomar valores de forma caprichosa. Apoco que exista una ligaz on
entre las partes real e imaginaria, esta fuerza a que la funci on holomorfa sea cons-
tante.
Por ejemplo, resultados de esta naturaleza seran:
i) Si f = u i v es holomorfa en regi on y u
3
= v entonces f C.
ii) Si f = u i v es holomorfa en regi on y 5u 2v = ct e entonces f C.
Comprobamos as que la derivabilidad en Ces muy exigente, y no s olo a nivel
local.
26 Funciones holomorfas
1.5 AP

ENDICE: C

ALCULO DE ARM

ONICAS CONJUGADAS
Y M

ETODO DE MILNE-THOMSON
La Teora de funciones analticas constituye un aut entico l on
de m etodos de gran ecacia para resolver importantes problemas
de Electroest atica, Conducci on del calor, Difusi on, Gravitaci on,
Elasticidad y Flujo de corrientes el ectricas. La gran potencia del
An alisis de variable compleja en tales campos se debe, principal-
mente, al hecho de que las partes real e imaginaria de una funci on
analtica satisfacen la ecuaci on de Laplace.
Este p arrafo, tomado de LevinsonRedheffer, loc. cit., p ag. 77, da idea de que la
b usqueda de funciones holomorfas con parte real (o parte imaginaria) conocidas
es una cuesti on importante en muchas aplicaciones de la teora de funciones de
variable compleja.
Hemos visto una soluci on de este problema mediante el c alculo de funciones
arm onicas conjugadas siguiendo lo que, a falta de otro nombre mejor, podemos
denominar el m etodo real: dada una funci on u arm onica en un abierto conexo
de R
2
, nos son conocidas las derivadas parciales de su arm onica conjugada v (si
existe!) a trav es de las condiciones de Cauchy-Riemann, de manera que el c alculode
primitivas de funciones reales de una variable real [o, equivalentemente, el c alculo
de las funciones potenciales de la forma diferencial u
y
(x, y) dx u
x
(x, y) dy]
nos lleva, en casos sencillos al menos, a expresiones explcitas para la(s) funcion(es)
v. Este procedimiento es f acilmente automatizable, y resulta c omodo llevarlo a
cabo mediante programas de c alculo simb olico como Mathematica.
Esquem aticamente, podramos proceder as: dada u(x, y),
1.- calcular la derivada parcial de u respecto de x, u
x
(x, y);
2.- calcular la derivada parcial de u respecto de y, u
y
(x, y);
3.- integrar u
y
(x, y) respecto de x, es decir, obtener una primitiva W(x, y)
de u
y
(x, y) como funci on s olo de x;
4.- calcular su derivada parcial respecto de y, W
y
(x, y);
5.- calcular (y) = u
x
(x, y) W
y
(x, y)
6.- integrar (y) respecto de y, es decir, obtener una primitiva (y) de (y);
7.- calcular W(x, y) (y): esta ser a una funci on v(x, y) arm onica conjugada
de u (y las dem as diferir an de ella en la adici on de una constante real).
T engase en cuenta que Mathematica no proporciona constantes de integraci on.
Adem as, el n umero de funciones cuyas primitivas puede calcular explcitamente
es limitado.
Funciones holomorfas 27
Hay tambi en un m etodo complejo para tratar el problema, el denominado
m etodo de MILNE-THOMSON(ver Phillips, E.G.: Funciones de variable com-
pleja. Dossat, Madrid (1963), p. 1718, y Needham, T.: Visual Complex Analysis.
Clarendon Press, Oxford (1997), pp. 512513), que, aunque precise ciertas condi-
ciones restrictivas, proporciona directamente las funciones holomorfas f con parte
real prejada u. Su justicaci on se basa en resultados importantes que probaremos
posteriormente: toda funci on holomorfa es analtica (y su derivada tambi en), y dos
funciones analticas en un abierto conexo son iguales si y s olo si coinciden en
un conjunto de puntos de que tenga al menos un punto de acumulaci on dentro
de ; por ejemplo, en un segmento abierto (principio de prolongaci on analtica).
Sea, pues, un abierto conexo de R
2
que corte al eje real, con lo cual la
intersecci on de con R contendr a al menos un segmento abierto (por qu e?)
Dada entonces una funci on u arm onica en , notemos que la funci on g dada
en por f
1
(x i y) = u
x
(x, y) i u
y
(x, y) es holomorfa en (por qu e?).
Supongamos que sabemos encontrar una funci on g holomorfa en tal que g
/
(x) =
f
1
(x) = u
x
(x, 0)i u
y
(x, 0) para todo x (x, 0) R: entonces g
/
(z) = f
1
(z)
por el principio de prolongaci on analtica, y la parte real de g diere de u en una
constante real (por qu e?). La funci on f = g C, para una constante real C
adecuada, tiene como parte real u.
El m etodo de Milne-Thompson es tambi en f acilmente traducible a Mathe-
matica. Pero tanto si se usa este m etodo como el anterior, sigue siendo necesario
vericar los resultados obtenidos y valorar el alcance de los procedimientos em-
pleados, muy especialmente debido a que los programas de c alculo simb olico, en
general, no tienen en cuenta el dominio de las funciones que intervienen, mani-
pulando tan s olo nombres de funciones o funciones dadas por f ormulas, por
decirlo de alguna manera. Como ejemplo recomendamos vivamente al lector que
pruebe a aplicar los m etodos descritos a la malvada funci on u(x, y) = ln(x
2
y
2
),
denida y arm onica en R
2
`{(0, 0)}. Cu ales son sus arm onicas conjugadas, seg un
Mathematica?
NOTA. El m etodo de Milne-Thompson puede esquematizarse as: dada u(x, y),
1.- calcular la derivada parcial de u respecto de x, u
x
(x, y);
2.- calcular la derivada parcial de u respecto de y, u
y
(x, y);
3.- calcular u
x
(x, 0), es decir, sustituir y por 0 en u
x
(x, y);
4.- calcular u
y
(x, 0), es decir, sustituir y por 0 en u
y
(x, y);
5.- sustituir x por z en u
x
(x, 0) i u
y
(x, 0) para obtener f
1
(z);
6.- integrar f
1
(z) respecto de z, es decir, obtener una primitiva g(z) de f
1
(z);
7.- calcular f (z) = g(z) +e g(x
0
) u(x
0
, 0) para cualquier x
0
R.
Entonces f (z) i c, c R, son las funciones holomorfas con parte real u;
8.- si se busca una funci on arm onica conjugada de u, hallar la parte imaginaria
de f (z).