Lecci on H

Diferenciaci on e integraci on num erica

H.1. Diferenciaci on num erica

Se nos plantea ahora el problema de calcular la derivada de una funci on de la que s olo conocemos un n umero nito de datos. Dos m etodos son los m as usuales a la hora de resolver tal problema: Derivar un polinomio de interpolaci on construido mediante alguno de los m etodos estudiados en el cap tulo anterior. La funci on h_deriv denida en el libro [7], p ag. 249, permite el c alculo de las sucesivas derivadas en un punto dado del polinomio interpolante asociado a nuestros datos. Calcular directamente la derivada utilizando para ello aproximaciones de la funci on mediante los polinomios de Taylor. Las f ormulas obtenidas de esta manera reciben el nombre de f ormulas de diferencias nitas . Pr actica a Sean x,y el conjunto de datos dados debajo. Queremos estimar las sucesivas derivadas en el punto a = 0.3 utilizando la funci on h_deriv citada anteriormente, lo que signica calcular las sucesivas derivadas del polinomio interpolador asociado a x,y; para ello, ejecutamos: x=[0 0.2 0.4 0.6 0.5672 0.6982 0.7941 0.8614 derivadas=h_deriv(x,y,a) 0.8 1 0.9053]; a=0.3; ]; y=[0.3927

El resultado, en orden de derivada creciente y empezando por f 1) (0.3), es 0.6533 -0.9710 1.0406 -1.3750 1.8750 Pr actica b La denici on de derivada de una funci on f viene dada por la expresi on f (x) = l m f (x + h) f (x) h0 h (H.1)

f (x + h) f (x) con lo cual podemos decir que es una aproximaci on de f con tal de que h h sea sucientemente peque no. De hecho usando el desarrollo de Taylor para la funci on f en el punto x podemos poner 73

74

H. DIFERENCIACION E INTEGRACION NUMERICA LECCION

f (x + h) = f (x) + hf (x) + O(h) lo que signica que el error cometido al aproximar f (x) por el valor orden 1 respecto de h. Utilizando Taylor tambi en pod amos haber puesto

(H.2) f (x + h) f (x) es de h

f (x + h) = f (x)+ hf (x)+

h2 h2 f (x)+ O(h3 )f (x h) = f (x) hf (x)+ f (x)+ O(h3 ) (H.3) 2! 2!

f (x + h) f (x h) y, por tanto, f (x) = + O(h3 ). Y procediendo de forma an aloga se puede 2h obtener las siguientes f ormulas para las derivadas primera y segunda:

Derivada primera de f en x0 f1 f0 + O(h) h f1 f1 + O(h2 ) 2h f2 + 4f1 3f0 + O(h2 ) 2h f2 + 8f1 8f1 + f2 + O(h2 ) 12h

Derivada segunda de f en x0 f2 2f1 + f0 + O(h2 ) h2 f1 2f0 + f1 + O(h2 ) h2 f3 + 4f2 5f1 + 2f0 + O(h2 ) h2 f2 + 16f1 30f0 + 16f1 f2 + O(h2 ) 12h2

(H.4)

Vamos a aplicar alguna de estas f ormulas en el c alculo de la derivada de f (x) = arct x en x = 2 y con paso h = 0.1. Ejecutamos el listado x=sqrt(3); h=0.01; ex=-0.5; %ex= valor exacto de la derivada de f en x at=atanh(x); ath=atanh(x+h); at2h=atanh(x+2*h); at3h=atanh(x+3*h); atmh=atanh(x-h); atm2h=atanh(x-2*h); f2pa=(ath-at)/h; er2pa=abs(f2pa-ex); f3pc=(ath-atmh)/(2*h); er3pc=abs(f3pc-ex); f3pa=(-at2h+4*ath-3*at)/(2*h); er3pa=abs(f3pa-ex); f4pc=(-at2h+8*ath-8*atmh+atm2h)/(12*h); er4pc=abs(f4pc-ex); resultados=[f2pa,f3pc,f3pa,f4pc]; errores=[er2pa,er3pc,er3pa,er4pc]; fprintf(\t 2p. adel.\t 2p. centr.\t 3p. adel.\t 4p. centr. \n) fprintf(f(x)\t %e\t %e\t %e\t %e\n,resultados.) fprintf(error:\t %e\t %e\t %e\t %e\n,errores) En los resultados podemos comprobar que son m as exactas las f ormulas centradas y con mayor n umero de puntos que sus an alogas.

H.2.

Integraci on num erica

Los m etodos de integraci on num erica nos permiten integrar funciones que est an denidas anal ticamente o de las que s olo conocemos su tabla en un n umero nito de puntos.

 NUMERICA H.2. INTEGRACION

75

Consideremos el caso en que tenemos un conjunto de puntos a = x0 < x1 < . . . < xn = b equiespaciados y que queremos calcular la integral de determinada funci on f denida sobre el intervalo [a, b]. Podemos entonces considerar el polinomio interpolador de f respecto a los nodos xi , ver (G.11) y su integral con la esperanza de as obtener una aproximaci on a la integral de f . De hecho, tenemos
b b

f (x) dx =
a a

(f0 +

x x0 f0 + . . . h
b a

(x x0 )(x x1 ) (x xn1 ) n f0 ) dx + + n!hn

(H.5) En (x) dx

donde En es el error cometido al aproximar la funci on f por su polinomio interpolador y cuya expresi on (ver [10], p ag. 37, o [3], p ag. 291) es: En (x) = (x x0 )(x x1 ) (x xn ) f n+1) (zx ) , (n + 1)! x0 < zx < xn (H.6)

de esto u ltimo y utilizando el teorema de la media integral se deduce En (x) dx = f n+1) (zx ) (n + 1)! (x x0 )(x x1 ) . . . (x xn ) dx, x0 < zx < xn (H.7)

En particular, si aproximamos f en [a, b] fragmentariamente mediante polinomios de grado uno entonces el polinomio interpolante en el fragmento [x0 , x1 ] tiene la forma P (x) = f0 + de donde
x1

x x0 f0 h

(H.8)

f (x) dx =
x0

x1 x0 [f0

xx0 h f0 ] dx

x1 x0

E (x) dx (H.9)

= hf0 + Ahora teniendo en cuenta que concluimos que

b a b a

f (0,1 ) 3 h f (0,1 ) 3 h (f1 f0 ) h = (f0 + f1 ) h 2 12 2 12

x1 xn

=
x0

+ +
xn1

y que h(f (0,1 )) =

x1 x0

f (x) dx + o(h)

f=

h h2 [(f0 + f1 ) + (f1 + f2 ) + + (fn1 + fn )] [ 2 12 h = (f0 + 2f1 + + 2fn1 + fn ) + cT h2 + o(h2 ) 2

b a f

f (x) dx + o(h)]
a

(H.10) (H.11)

mediante el n umero T (f, h) = h 2 (f0 + 2f1 + + 2fn1 + fn ) se b 2 h denomina regla de los trapecios y a la expresi on cT h2 = f (x) dx se la denomina parte 12 a principal del error al aproximar la integral de f por la regla de los trapecios T (f, h). La regla que aproxima Nota: Para que todas las expresiones anteriores sean correctas es necesario exigir que f C 3 [a, b], es decir, que f posea derivada de orden 3 continua. Si en lugar de fragmentar el intervalo [a, b] en los subintervalos [xi , xi+1 ] utilizando aproximaciones lineales en cada uno de ellos hubi eramos fragmentado en los subintervalos [x0 , x2 ],. . . ,[x2k2 , x2k=n ]

76

H. DIFERENCIACION E INTEGRACION NUMERICA LECCION

y en cada uno de estos fragmentos hubi esemos utilizado un polinomio interpolador de orden dos respecto a los datos (xi , fi ) entonces (x x0 ) (x x0 )(x x1 ) 2 f0 + f0 h 2h2 ser a el polinomio interpolador en el primer fragmento y tendr amos P0,2 (x) = f0 +
x2

(H.12)

f=
x0 b

h h5 (f0 + 4f1 + f2 ) f 4) (zx ) 3 90

(H.13) (H.14)

f=
a

h (f0 + 4f1 + 2f2 + + 2f2k2 + 4f2k1 + fn ) + cS h4 + o(h4 ) 3

b a f

mediante el n umero S (f, h) = h 3 (f0 +4f1 +2f2 + +4f2k1 + fn ) 1 b 4) recibe el nombre de regla de Simpson y a la expresi on cS h4 = h4 f (x) dx se la denomina 90 a parte principal del error al aproximar la integral de f por la regla de Simpson S (f, h). La regla que nos aproxima Nota: An alogamente a la nota anterior, las f ormulas relacionadas con la regla de Simpson son 5 ciertas a condici on de que f C [a, b], es decir, de que f posea derivada de orden 5 continua. Es importante ahora observar que el error cometido al aproximar I = Ih = S (f, h) es f acilmente computable ya que de las relaciones I = Ih + cS h4 + o(h4 ); se obtiene, restando, Ih/2 Ih + o(h4 ) 15 I = Ih/2 + 1 cS h4 + o(h4 ) 16
b a f

por el n umero

(H.15)

Ih/2 Ih = 15cS (h/2)4 + o(h4 ), lo que nos permite concluir

y tambi en cS (h/2)4 =

(H.16)

Ih/2 Ih + o(h4 ) (H.17) 15 Esta f ormula, junto con su an aloga para el caso de los trapecios (ver (H.20)), nos permite controlar el error cometido, siempre que c = 0, al aplicar la regla de Simpson y de los trapecios en b el c alculo de la integral denida a f . En la pr actica dichas f ormulas se emplean para adaptar el paso de integraci on h de modo que el error en el fragmento donde estamos integrando sea menor que la tolerancia por nosotros admitida. De este modo surgen los m etodos adaptativos de integraci on que si est an basados en la regla de los trapecios ser a denominado m etodo adaptativo de los trapecios y si est a basado en la regla de Simpson ser a denominado m etodo adaptativo de Simpson . Se denomina regla de Runge el c alculo de la estimaci on aproximada del error seg un (H.17) al cumplirse la condici on (H.15), ver [10] p ag. 123. En general, si I Ih/2 = z = zh + chk + o(hk ) (H.18)

es la relaci on que verica el valor exacto z en funci on de su aproximaci on zh ; entonces, la regla de Runge nos dice que z zh/2 = zh/2 zh + o(hk ) 2k 1 (H.19)

 NUMERICA H.2. INTEGRACION

77

deduci endose, como caso particular, que el error de la regla de los trapecios viene dado por la relaci on I T (f, h/2) = T (f, h/2) T (f, h) + o(h2 ) 3 (H.20)

Para realizar la cuadratura o integral denida de una funci on f en el intervalo [a, b] por un m etodo adaptativo, Matlab cuenta con el comando quad. Su sintaxis es: quad(nombre_f,a,b,tol,traza) donde tol es la tolerancia global en la cuadratura y traza es un par ametro opcional, al igual que tol, que por omisi on toman los valores tol= 1e 6 y traza= 0. Si traza= 0 entonces el programa nos informa de las iteraciones y de la naturaleza de la convergencia del algoritmo. Pr actica c Matlab cuenta con la funci on trapz(x,y) que realiza la integraci on de una funci on f dada como tabla de datos mediante la regla de los trapecios. Como ejemplo consideramos la funci on f que en el intervalo [0, 1] tiene la siguiente tabla x y = f (x) 0 0 0.15 0.1494 0.35 0.3429 0.45 0.4350 0.60 0.5646 0.90 0.7833 1.00 0.8415

(H.21)

para calcular su integral en [0, 1] ejecutamos el listado x=[0 0.1500 0.3500 y=[0 0.1494 0.3429 Integral=trapz(x,y) 0.4500 0.4350 0.6000 0.5646 0.9000 0.7833 1.0000]; 0.8415];

Es tambi en f acil obtener una funci on propia, I=h_trapz(nombre_f,a,b,h) que nos calcule la cuadratura de una funci on f de nombre nombre_f en un intervalo [a, b] por la regla de los trapecios y a partir de un paso de integraci on igual a h. function I=h_trapz(nombre_f,a,b,h) n=floor((b-a)/h); hh=(b-a)/n; x=a+(0:n)*hh; y=feval(nombre_f,x); I=trapz(y)*hh; Pr actica d Ejecutando el comando doc quad se nos explica la cuadratura de una funci on por el m etodo adaptativo de Simpson empleado por Matlab para el c alculo num erico de integrales denidas. Comprobar que con el comando quad(sin,0,pi,1e-8) obtenemos la integral de la funci on seno en [0, ] con una tolerancia de 1e 8. Por u ltimo, utilizar el comando quad para el c alculo de las integrales en el intervalo [0, 1] de las funciones h10 y h15 siguientes: function f=h10(x) f=sqrt(x); function f=h15(x) f=(x.^(0.7)).*cos(x);

78

H. DIFERENCIACION E INTEGRACION NUMERICA LECCION

Pr actica e Las funciones propias denidas en el libro de Nakamura, [7] p ag. 2178, con los nombres I=h_simpsv(y,h) y I =h_simpsn(nombre_f,a,b,n) permiten el c alculo de la integral denida de una funci on y = f (x) por la regla de Simpson en sus dos posibles formas: h_simpsv lo hace cuando tenemos la funci on como una tabulaci on de valores equiespaciados a distancia h y h_simpsn lo hace a partir del nombre de f y del n umero de nodos n + 1 en que fragmentamos el intervalo [a, b]. Como ejemplo, consideramos la funci on tangente en el intervalo [0, /4], su tabulaci on con paso h = /24 es x f (x) 0 0 0.1309 0.1317 0.2618 0.2679 0.3927 0.4142 0.5236 0.5774 0.6545 0.7673
/4

0.7854 1.0000

(H.22)

de modo que podemos obtener una aproximaci on al valor 0 tg(x) dx ejecutando Int= h_simpsn(tan,0,pi/4,6) o equivalentemente ejecutando el listado y=[0 0.1317 0.2679 Int=h_simpsv(y,pi/24) 0.4142 0.5774 0.7673 1.0000];

H.3.

Integraci on num erica con l mites innitos o singulares

En este apartado seguimos lo expuesto en la secci on 5.4 de [7]. Una funci on es integrable en un dominio innito, [, ] o semiinnito, [a, ], [, b], s olo si es signicativamente distinta de cero en un dominio acotado [K, K ] y se aproxima a cero conforme la variable se aproxima a y . En denitiva, el primer paso para evaluar

I=

f (x) dx

(H.23)

consiste en sustituir los l mite innitos por l mites nitos:

K

I=
K

f (x) dx

(H.24)

donde K es un valor tan grande que la contribuci on para los valores de la x que verican x [K, K ] es menor que la tolerancia por nosotros jada. Emplearemos como m etodo m as eciente en el c alculo de la ecuaci on (H.24) el m etodo de los trapecios. Un ejemplo lo hacemos en la pr actica siguiente
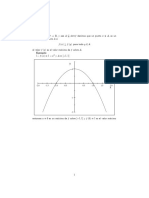
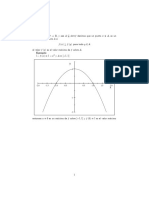
1 on h20(x) = f (x) = Pr actica f Consideramos la funci exp(x2 ) y su integral innita I = on gr aca de f para hacernos una idea f (x) dx. Primeramente hacemos una representaci de su comportamiento, digamos en el intervalo [30, 30], lo que hacemos con el listado

x=-30:0.1:30; y=(1/sqrt(pi))*exp(-x.^2); plot(x,y), grid De su gr aca observamos que f toma valores pr acticamente cero para x [4, 4]. Evaluamos la integral (H.24) con K = 4 y una magnitud de paso discreta, h = 0.5, para no hacer excesivamente largos los c alculos y vamos incrementando K en un factor de 1.5 siguiendo la sucesi on K = 4, 6, 9, 13.5, . . . para ver si un incremento en el intervalo de integraci on signica un crecimiento del valor integral (H.24), si este valor permanece sensiblemente estable entonces

 NUMERICA H.3. INTEGRACION CON L IMITES INFINITOS O SINGULARES

79

disminuimos la magnitud h hasta un n umero que estimemos conveniente para la tolerancia con que estemos trabajando y, nalmente, si el valor obtenido ahora es semejante al que ya ten amos concluimos que el valor de la integral innita de f es igual al valor estable obtenido. Aunque este proceso puede parecer laborioso en la pr actica no requiere m as de diez pruebas. En el caso que nos ocupa ejecutamos K=4; I(1)=h_trapz(h20,-K,K,0.5); KK(1)=K; for k=2:5 KK(k)=KK(k-1)*1.5; K=KK(k); I(k)=h_trapz(h20,-K,K,0.5); end; fprintf(K\t %f\t %f\t %f\t %f\t %f\n, KK.) fprintf(Integ.\t %f\t %f\t %f\t %f\t %f\n, I.) II=h_trapz(h20,-K,K,0.1) fprintf(Si converge la integral vale %f\n,II) Como resultado del listado anterior obtenemos K 4.000000 6.000000 9.000000 13.500000 20.250000 1.000000

Integ. 1.000000 1.000000 1.000000 1.000000 Si existe la integral vale 1

deduci endose que f (x) dx = 1 al menos con una tolerancia de 1e 5. El listado de la funci on f =h20 es el expresado a continuaci on function f=h20(x) f=(1/(sqrt(pi))).*exp(-x.^2);

H.3.1.

Integraci on num erica con l mites singulares

Hasta ahora s olo hemos considerado integrales de funciones en dominios innitos. En el caso de tener como dominio de integraci on el intervalo (a, b) y que alguno de los extremos sea singular para la funci on f entonces lo que hacemos es utilizar una transformaci on de coordenadas x = x(z ) de modo que el intervalo(, ) se transforme en (a, b) con el n de convertir nuestra integral
b

singular
a

f (x) dx en la integral innita

f (x(z ))

dx dz dz

(H.25)

de la que ya podemos calcular su integral utilizando el m etodo expresado anteriormente. Un ejemplo de transformaci on de coordenadas que convierte el intervalo (, ) en (1, 1) es la dada por la ecuaci on x = th( sh(z )), 2 de donde se deduce que x= x (1, 1) cuando z (, ) (H.26)

a + b + (b a) th( 2 sh(z )) (H.27) 2 es una transformaci on que convierte el intervalo (, ) en (a, b). Tal transformaci on recibir a el nombre de doble exponencial

80

H. DIFERENCIACION E INTEGRACION NUMERICA LECCION

Pr actica g Para hacernos un idea de la transformaci on doble exponencial (H.26) proponemos ejecutar el siguiente listado con el n de obtener su representaci on gr aca z=-2:0.001:2; x=tanh((pi/2)*sinh(z)); figure(1); plot(z,x); xlabel(z);ylabel(x) axis equal figure(2),plot(x,z), xlabel(x); ylabel(z), title(trans. inversa), axis equal Es f acil obtener el valor de la expresi on dx cuando x = x(z ) viene dado por (H.26), resultando dz (H.28)

dx (b a) ch(z ) = dz 4 ch2 ( 2 sh(z ))

b

y llevando esta expresi on a (H.25) tenemos que mediante la transformaci on doble exponencial la integral
a

f (x) dx se transforma en Tf (z ) dz, donde Tf (z ) = (b a) ch(z ) f (x(z )) 2 4 ch ( 2 sh(z )) (H.29)

Afortunadamente la anterior conversi on y c alculo de la integral innita est a implementada en el chero h_dblexp (ver [7], p ag. 219). La sintaxis del citado comando es h_dblexp(nombre_f,a,b,K,h,pintar) donde pintar es un par ametro opcional que si es activado, es decir si pintar es distinto del vac o, entonces se nos representan las funciones f y Tf . Adem as, h corresponde al paso de integraci on y [K, K ] al intervalo de integraci on donde calculamos la integral transformada por la regla de los trapecios. Como ejemplo sirva la siguiente pr actica Pr actica h exp(x2 ) Consideramos la funci on f (x) = , x [0, 1], de ella queremos realizar su 1 x2 integral. Para ello ejecutamos un listado semejante al de la pr actica hf

K=0.8; I(1)=h_dblexp(h40,0,1,K,0.2); KK(1)=K; for k=2:6 KK(k)=KK(k-1)*1.5; K=KK(k); I(k)=h_dblexp(h40,0,1,K,0.2); end; fprintf(K\t %f\t %f\t %f\t %f\t %f\t %f\n, KK.) fprintf(Integ.\t %f\t %f\t %f\t %f\t %f\t %f\n, I.) II=h_dblexp(h40,0,1,K,0.02) fprintf(Si converge, la integral vale %f\n,II) donde h40 es la funci on dada por el gui on

 NUMERICA H.4. INTEGRACION EN UN DOMINIO BIDIMENSIONAL function f=h40(x) f=(exp(-x.^2))/sqrt(1-x.^2); Como resultado del listado anterior obtenemos K 0.800 1.200 1.800 2.700 4.050 6.075

81

Integ. 0.820894 0.954171 1.007650 1.013213 1.013219 1.013219 Si converge, la integral vale 1.013219
1

deduci endose de todo ello que la integral impropia una tolerancia de 1e 4.

0

exp(x2 ) dx toma el valor 1.01321 con 1 x2

Si adem as queremos tener una representaci on gr aca de la funci on f (x) y de Tf (z ), ejecutamos el comando h_dblexp(h40,0,1,1.3,0.2,0) Nota: Si nos damos cuenta en el listado anterior el valor m aximo de K para el que para el K que aproximamos Tf (z ) dz mediante K f (z ) dz es para K = 6.075 la raz on de esto es que para valores un poco mayores el ordenador se desborda ya que la transformaci on doble exponencial obliga al ordenador a trabajar con n umeros m as grandes de lo que est a preparado el propio programa. Pr actica i Repetimos la pr actica anterior con la funci on h25(x) = 1/x, si x = 0 y h25(x) = 1, si x = 0. Ejecutamos, por tanto el mismo listado que en la pr actica anterior con la salvedad de que sustituimos h25 por h40 y obtenemos como resultado K 0.800 1.200 1.800 2.700 4.050 6.075

Integ. 2.799361 4.757909 9.273903 23.344968 90.440137 685.388927 Si converge, la integral vale 683.079195 de ello concluimos que 0 h25(x) dx no converge, por lo menos, hasta donde nosotros somos capaces de decidir. De hecho, la anterior integral es divergente. El listado de la funci on h25 es el expresado a continuaci on function f=h25(x) [m,n]=size(x); H=ones(m,n); R=(x==1);CR=1-R; xx=(x.*CR)+H.*R; f=1./xx;
1

H.4.

Integraci on num erica en un dominio bidimensional

El comando de Matlab dblquad permite calcular la integral doble de una funci on f (x, y ) denida sobre un rect angulo acotado [a, b] [c, d] simplemente escribiendo dblquad(@nombre_f,a,b,c,d, tol)

82

H. DIFERENCIACION E INTEGRACION NUMERICA LECCION

Si es un recinto de R2 contenido en el rect angulo [a, b] [c, d] y denota la funci on caracter stica de : 1 si (x, y ) (x, y ) = 0 si (x, y ) entonces, la igualdad f (x, y ) dx dy =
[a,b][c,d]

(x, y ) f (x, y ) dx dy

nos permitir a el c alculo de integrales dobles en dominios acotados y limitados por curvas de las que se conoce o se puede calcular, al menos aproximadamente, sus expresiones impl citas cartesianas

C2 C1 C3
la u nica precauci on ser a incluir en el chero m que dene la funci on a integrar las condiciones que denen el recinto . Como ejemplo realizamos las siguientes pr acticas Pr actica j Calcular la integral I=

sen(x + y ) dy dx

(H.30)

para el recinto de R2 limitado por las curvas C1 : x = 1; C2 : x = 3; C3 : y = 3 + ex/5 ; C4 : y = ln x

Para ello, sencillamente ejecutamos I=dblquad(@(x,y) sin(x+y).*(y-log(x)>=0).*(y-3-exp(x/5)<=0),1,3,0,10) obteniendo I= -2.6119. Pr actica k El area de un c rculo unitario es . La exactitud de un m etodo num erico para la doble integraci on puede probarse con el c alculo de la integral : Area() =

dx dy

donde es el dominio denido por los puntos (x, y ) que verican x2 + y 2 2x, regi on que es un circulo unitario de centro el punto (1, 0). Realizar la evaluaci on num erica de la doble integral anterior ejecutando

 E INTEGRACION SIMBOLICA H.5. DERIVACION I=dblquad(@(x,y) (x.^2+y.^2-2*x<=0),0,2,-1,1,tol) y observar la exactitud del resultado para diferentes tolerancias tol.

83

Pr actica l Calcular el volumen del solido situado en semiespacio z 0 y limitado por los cilindros C1 : x2 + y 2 = 1, C2 : (x 1)2 + (y 1)2 = 1 y la supercie z = xy . Ejecutamos triplequad(@(x,y,z) (x.^2+y.^2<=1).*((x-1).^2+(y-1).^2<=1).*(z<=x.*y),0,1,0,1,0,1)

lo que da como respuesta ans=0.117884 lo que supone cometer un error superior a 8 diezmil esimas, lo que es esperable en el computo num erico de una integral triple.

H.5.

Derivaci on e integraci on simb olica

Realizamos en la ventana de comandos las siguientes operaciones %creaci on %derivada %derivada %integral %integral de una funci on simb olica de f segunda de f de f definida de f en [0,2]

Pr actica m

f=3*x^3+4x^2-x-33 df=diff(f) d2f=diff(f,2) int_f=int(f) int_def_f=int(f,0,2)

H.6.

Ejercicios
(0.2 puntos) Evaluar las siguientes integrales con una tolerancia menor

Pr actica puntuable p a la mil esima

1.
0 5

dx 1 + (230x 30)2

/2

2.
0 0

sen(x) dx dx 2 + cos(x) x exp(2x) dx

0 1

3.
0 2

1 dx 2+x ln(1 + x) dx x xx dx
/4

4.
0

(2x cos(2x) (x 2)2 ) dx 5. dx 1 + sen2 (x) exp(2x) sen2 (x) dx x2 ln(x) dx 2 dx 2 x 4

4

6.
1 1

/2

7.
0 2

8. 11.
0

9.
0

10.
0 1.5

x0.001 dx

12.
0 1.6 1

tg(x) dx 2 dx 4

13.
1

14.
1 1

100 sen(10/x2 ) dx 15. x2 exp(x) dx 18.

x2

0.35

16.
0

17.
0

cos(x2 ) dx

0 3 1

19.
0

x2 (x 1)2 (x 3)2 (x 4)2 dx 20.

e2x sen(3x) dx

84

H. DIFERENCIACION E INTEGRACION NUMERICA LECCION

Pr actica puntuable q (0.2 puntos) Calcular las siguientes integrales impropias con una tolerancia menor a la mil esima

1.

exp(x2 ) dx 1 + x2 ex 1+ x2 dx

2.
0

tg(x) dx x0.7

3.
0 1 1

exp(x) 1 x2 dx 1 + x2 x3/2 sen(1/x) dx

2

4.
0

5.
0

ln(1 + ex ) dx 6. dx 1 + x4 e2x dx 5 x2 ex dx 1x dx x2 + 9 9.
0

/2

7.
0 1

cos x dx x

8.
0 1

10.
0 1

x1/4 sen x dx cos 2x dx 3 x xex

3

11.
0 1

12.
1

ln x dx 5 x1 cos x dx 1 + x2 cos x x3

13.
0 1

14.
0

15.
0

16.
0

(x

1)2

dx 17.
0

18.
1

Pr actica r De las funciones f y g conocemos sus expresiones tabulares en los puntos que se detallan m as abajo. Se pide, calcular de la forma que se estime mejor, las integrales
0.8 1

f (x) dx y
0 0

g (x) dx

a partir de los datos x f (x) 0 0 0.1 2.1220 x g(x) 0.2 3.0244 0 0.9162 0.3 3.2568 0.25 0.8109 0.4 3.1399 0.50 0.6931 0.5 2.8579 0.75 0.5596 0.6 2.5140 1.0 0.4055 0.7 2.1639 0.8 1.8358

Pr actica puntuable s (0.1 puntos) Calcular, cometiendo un error menor a la diezmil esima, las siguientes integrales bidimensionales
2 1 1

1.
0

dx
0

sen(x + y ) dy
sen x

2.
0 2

dx
0

x + y dy x + y dy

3.
0

dx
0

exp(x2 y 2 ) dy 4.
1

dx
0

20.5x

Pr actica puntuable t (0.2 puntos) Se llama polinomio de Legendre de orden n al polinomio Pn denido por la igualdad Pn (x) = 1 dn (x2 1)n 2n n! dxn (H.31)

Una relaci on importante que verican los polinomios de Legendre es la f ormula en recurrencia siguiente

H.6. EJERCICIOS 2n 1 n1 xPn1 (x) Pn2 (x) n n

85

Pn (x) =

(H.32)

1. Deducir de ella y de las igualdades P0 (x) = 1, P1 (x) = x, la denici on de una funci on propia de Matlab, Pn (x) =h_legend(n), que nos calcule el polinomio Pn (x) a partir del dato n N. 2. Realizar una representaci on gr aca, en el intervalo [1, 1], de las funciones polinomiales Pn (x), n = 3, 5, 7, 10, y de sus ceros constatando que todas ellas poseen todos sus ceros en el citado intervalo. 3. Se llaman nodos de Legendre de orden n del intervalo [1, 1] a los n puntos {p1 < p2 < . . . < pn } caracterizados por ser las n ra ces del polinomio de Legendre de orden n, Pn (x). Se pide calcular los nodos de Legendre de [1, 1] para los ordenes n = 3, 5, 7, 10. En general se llaman nodos de Legendre del intervalo [a, b] a los obtenidos por la f ormula pk = a+b ba + pk , 2 2 k = 1, 2, . . . , n (H.33)

Pr actica u 1) Considerar la funci on f (x) = 3x5 + 7x2 28x + 3 en el intervalo [1, 3]; los nodos de Legendre de orden 3 de dicho intervalo, p1 < p2 < p3 ; y el polinomio interpolador de grado 3 asociado a los datos (pi , f (pi )). Comprobar que, al menos con una tolerancia de 1e 7, se verica la igualdad
3 3

f (x) dx =
1 1

Pf (x) dx

(H.34)

La igualdad anterior es un hecho general, de hecho se verica que la integral de un polinomio de grado 2n 1 coincide con la integral de su polinomio interpolador de grado n obtenido respecto a los nodos de Legendre de orden n. 2) (apartado puntuable con 0.3 puntos) Se denomina m etodo de integraci on de GaussLegendre con n puntos a aquel que realiza los siguientes pasos con el n de obtener una aproximaci on b de a f (x) dx: Calcula los n puntos de Legendre p1 < p2 < . . . < pn del intervalo [a, b]. Calcula el polinomio interpolador Pf (x) de grado n asociado a los datos (pi , f (pi )). Aproxima
b a f (x) dx

por el valor

b a Pf (x) dx.

Pues bien, se pide denir una funci on propia, I=h_gauss(nombre_f,a,b,n) que permita b calcular la aproximaci on con n puntos de la integral a nombre_f(x) dx por el m etodo de GaussLegendre. 3) (apartado puntuable con 0.15 puntos) Utilizar la funci on propia denida anteriormente para calcular las aproximaciones con 4,8, y 16 puntos de las integrales 110 de la pr actica hp. Observar la exactitud obtenida con pocos puntos. 4) (apartado puntuable con 0.15 puntos) Como habremos observado una de las grandes ventajas del m etodo de GaussLegendre es su exactitud con pocos puntos y otra ventaja es que se puede aplicar tambi en sobre integrales singulares. En este apartado pedimos utilizar la funci on propia denida en el punto 2 para el c alculo aproximado de las integrales singulares 15 de la pr actica hq con 10 puntos observando si la exactitud obtenida es suciente.

86 Pr actica puntuable v

H. DIFERENCIACION E INTEGRACION NUMERICA LECCION (0.3 puntos) Denir una funci on propia,
b d(x)

I=h_dblgau(nombre_f,nombre_c,nombre_d,a,b,m,n) que permita aproximar la integral bidimensional a c(x) f (x, y ) dy dx por el m etodo de Gauss Legendre a partir de un mallado de m n puntos de Legendre. Utilizar la funci on propia denida para calcular las integrales 12 de la pr actica hs.