Documentos de Académico
Documentos de Profesional
Documentos de Cultura
Review of Vector Analysis
Cargado por
Jomar DadorDerechos de autor
Formatos disponibles
Compartir este documento
Compartir o incrustar documentos
¿Le pareció útil este documento?
¿Este contenido es inapropiado?
Denunciar este documentoCopyright:
Formatos disponibles
Review of Vector Analysis
Cargado por
Jomar DadorCopyright:
Formatos disponibles
Review of
Vector Analysis
EEL 3472
Review of Vector Analysis
Review of Vector Analysis
Vector analysis is a mathematical tool with which
electromagnetic (EM) concepts are most conveniently
expressed and best comprehended.
A quantity is called a scalar if it has only magnitude (e.g.,
mass, temperature, electric potential, population).
A quantity is called a vector if it has both magnitude and
direction (e.g., velocity, force, electric field intensity).
The magnitude of a vector A
is a scalar written as A or A
A
2
EEL 3472
Review of Vector Analysis
A unit vector eA along A is defined as a vector whose
magnitude is unity (that is,1) and its direction is along A
eA
A
A
A
A
( eA 1)
Thus
A A eA
which completely specifies A in terms of A and its
direction eA
EEL 3472
Review of Vector Analysis
A vector A in Cartesian (or rectangular) coordinates may
be represented as
(A x , A y , A z )
A x ex A y ey A z ez
or
where AX, Ay, and AZ are called the components of A in the
x, y, and z directions, respectively; e x , e y , and
vectors in the x, y and z directions, respectively.
are unit
EEL 3472
Review of Vector Analysis
Suppose a certain
vector V is given by
V 2ex 3ey 4ez
The magnitude or
absolute value of
the vector V is
V 22 32 42 5.385
(from the Pythagorean theorem)
EEL 3472
Review of Vector Analysis
The Radius Vector
A point P in Cartesian coordinates may be represented by
specifying (x, y, z). The radius vector (or position vector) of
point P is defined as the directed distance from the origin O
to P; that is,
r x ex y ey z ez
The unit vector in the direction of r is
er
x ex y ey z ez
x2 y2 z2
EEL 3472
Review of Vector Analysis
Vector Algebra
Two vectors A and B can be added together to give
another vector C ; that is ,
C AB
Vectors are added by adding their individual components.
Thus, if A x ex A y ey A z ez and B B x ex B y ey Bz ez
C (A x B x )ex (A y B y )ey (A z Bz )ez
EEL 3472
Review of Vector Analysis
Parallelogram
rule
Head to
tail rule
Vector subtraction is similarly carried out as
D A B A (B )
D (A x B x )ex (A y B y )ey (A z Bz )ez
8
EEL 3472
Review of Vector Analysis
The three basic laws of algebra obeyed by any given vector
A, B, and C, are summarized as follows:
Law
Commutative
Addition
AB BA
Associative
A (B C ) (A B ) C
Distributive
k(A B ) kA k B
Multiplication
kA A k
k(lA) (kl)A
where k and l are scalars
EEL 3472
Review of Vector Analysis
When two vectors A and B are multiplied, the result is
either a scalar or a vector depending on how they are
multiplied. There are two types of vector multiplication:
1. Scalar (or dot) product:
AB
2.Vector (or cross) product:
AB
The dot product of the two vectors A and B is defined
geometrically as the product of the magnitude of B and the
projection of A onto B (or vice versa):
A B AB cos AB
where AB is the smaller angle between A and B
10
EEL 3472
Review of Vector Analysis
If
and
B (BX , B Y , BZ )
then
A B A XB X A YB Y A ZBZ
which is obtained by multiplying A and B component by
component
AB B A
A (B C ) A B A C
2
A A A A 2
eX ey ey ez eZ ex 0
A (A X , A Y , A Z , )
eX ex ey ey eZ ez 1
11
EEL 3472
Review of Vector Analysis
The cross product of two vectors A and B is defined as
A B AB sin AB en
where en is a unit vector normal to the plane containing A
and B . The direction of en is determined using the righthand rule or the right-handed screw rule.
Direction of A B
and en using
(a) right-hand rule,
(b) right-handed
screw rule
12
EEL 3472
Review of Vector Analysis
If
A (A X , A Y , A Z , ) and B (BX , B Y , BZ )
ex
A B Ax
Bx
ey
Ay
By
then
ez
Az
Bz
(A yBz A zB y )ex (A zBx A xBz )ey (A xBy A yBx )ez
13
EEL 3472
Review of Vector Analysis
Note that the cross product has the following basic
properties:
(i) It is not commutative:
AB B A
It is anticommutative:
A B B A
(ii) It is not associative:
A (B C ) (A B ) C
(iii) It is distributive:
A (B C ) A B A C
(iv)
14
AA 0
(sin 0)
EEL 3472
Review of Vector Analysis
Also note that
ex ey ez
ey ez ex
ez ex ey
which are obtained in cyclic permutation and illustrated
below.
Cross product using cyclic permutation: (a) moving clockwise leads to positive results;
(b) moving counterclockwise leads to negative results
15
EEL 3472
Review of Vector Analysis
Scalar and Vector Fields
A field can be defined as a function that specifies a particular
quantity everywhere in a region (e.g., temperature
distribution in a building), or as a spatial distribution of a
quantity, which may or may not be a function of time.
Scalar quantity scalar function of position scalar field
Vector quantity vector function of position vector field
16
EEL 3472
Review of Vector Analysis
17
EEL 3472
Review of Vector Analysis
Line Integrals
A line integral of a vector field can be calculated whenever a
path has been specified through the field.
The line integral of the field V along the path P is defined as
P2
V dl V
P
18
cos dl
P1
EEL 3472
Review of Vector Analysis
19
EEL 3472
Review of Vector Analysis
Example.
The vector V is given by V Vo ex where V o
is a constant. Find the line integral
I
V dl
P
where the path P is the closed path below.
It is convenient to break the path P up into the four parts P 1,
P2, P3 , and P4.
20
EEL 3472
Review of Vector Analysis
V Voex
For segment P1, dl dx ex
x xo
V dl
x 0
P1
Thus
xo
(Vo ex ) (dx ex ) Vo (ex ex )dx Vo (xo 0) Voxo
0
For segment P2,
dl dy e y
y yo
and
V dl (V e ) (dy e ) 0
o x
P2
21
(since ex e y 0)
y 0
EEL 3472
Review of Vector Analysis
For segment P3,
dl dxex (thedifferentiallengthdlpointstotheleft)
x xo
V dl (V e ) (dx e ) - V x
o
x 0
P3
V dl 0
P4
V x
o
P1
22
P2
P3
0 Voxo 0 0 (conservat ive field)
P4
EEL 3472
Review of Vector Analysis
Example.
Let the vector field V be given by V Vo ex.
Find the line integral of V over the semicircular path shown
below
Consider the contribution of
the path segment located at
the angle
dl dl cos ex
dl sin ey
Since 90
cos cos( 90) sin
sin sin( 90) cos
dl dl sin ex
dl cos ey
ad
{ (sin ex cosey )
dl
23
EEL 3472
Review of Vector Analysis
180
(V e ) (sin e
o x
cos e y )ad
180
aVo [sin (ex ex ) cos (ex e y )]d
0
180
aVo sin d aVo (cos
0)
180
cos
0
2aVo
24
EEL 3472
Review of Vector Analysis
Surface Integrals
Surface integration amounts to adding up normal
components of a vector field over a given surface S.
The flux of
a vector
field A
through
surface S
We break the surface S into small surface elements and
assign to each element a vector ds ds en
ds is equal to the area of the surface element
en is the unit vector normal (perpendicular) to the surface
element
25
EEL 3472
Review of Vector Analysis
(If S is a closed surface, ds is by convention directed
outward)
Then we take the dot product of the vector field V at the
position of the surface element with vector ds . The result is
a differential scalar. The sum of these scalars over all the
surface elements is the surface integral.
V ds V
S
ds cos
V cos is the component of V in the direction of ds
(normal
to the surface). Therefore, the surface integral can be
viewed as the flow (or flux) of the vector field through the
surface S
(the net outward flux in the case of a closed surface).
26
EEL 3472
Review of Vector Analysis
Example.
Let V be the radius vector
V x ex y ey z ez
The surface S is defined by
zc
d x d
d y d
The normal to the surface is directed in the +z direction
Find
V ds
S
27
EEL 3472
Review of Vector Analysis
Surface S
V is not perpendicular to S, except at one point on the Z axis
28
EEL 3472
Review of Vector Analysis
V ds V ds cos
S
x 2 y 2 c2
ds dxdy
cos
c
x 2 y 2 c2
V
cos
ds
x d y d
x d
c
2
2
2
V
ds
dydx c [d (d)]dx
S
2
2
2
x y c
x d y d
x d
2dc[d - (-d)] 4d2c
29
EEL 3472
Review of Vector Analysis
Introduction to Differential Operators
An operator acts on a vector field at a point to produce
some function of the vector field. It is like a function of a
function.
If O is an operator acting on a function f(x) of the single
variable X , the result is written O[f(x)]; and means that
first f acts on X and then O acts on f.
Example.
f(x) = x2 and the operator O is (d/dx+2)
O[f(x)]=d/dx(x2 ) + 2(x2 ) = 2x +2(x2 ) = 2x(1+x)
30
EEL 3472
Review of Vector Analysis
An operator acting on a vector field O[V(x, y, z)] can produce
either a scalar or a vector.
Example. O(A) A A (the length operator), V 3y ex z ey
Evaluate O(V) at the point x=1, y=2, z=-2
O(V)
V V 9y2 z2
40 6.32 scalar
Thus, O is a scalar operator acting on a vector field.
Example. O(A) A A A 2A , V 3y ex z ey ,
x=1, y=2, z=-2
O(V) (3y ex z ey ) 9y2 z2 6y ex 2z ey
(6 ex 2ey ) 40 12ex 4 ey
49.95 ex 16.65ey vector
Thus, O is a vector operator acting on a vector field.
31
EEL 3472
Review of Vector Analysis
Vector fields are often specified in terms of their rectangular
components:
V(x, y, z) Vx (x, y, z)ex Vy (x, y, x)ey Vz (x, y, z)ez
where Vx , Vy , and Vz are three scalar features functions of
position. Operators can then be specified in terms of Vx ,
Vy , and Vz .
The divergence operator is defined as
32
Vx
Vy
Vz
x
y
z
EEL 3472
Review of Vector Analysis
Example V x2 ex y ey (2 x)ez
point x=1, y=-1, z=2.
Vx x2
Vx 2x
x
. Evaluate V at the
Vy y
Vz 2 x
Vy 1
Vz 0
y
z
V 2x 1 3
Clearly the divergence operator is a scalar operator.
33
EEL 3472
Review of Vector Analysis
1.
2.
V - divergence, acts on a vector to produce a scalar
- gradient, acts on a scalar to produce a vector
3. V - curl, acts on a vector to produce a vector
4.
2V
-Laplacian, acts on a scalar to produce a scalar
Each of these will be defined in detail in the subsequent
sections.
34
EEL 3472
Review of Vector Analysis
Coordinate Systems
In order to define the position of a point in space, an
appropriate coordinate system is needed. A considerable
amount of work and time may be saved by choosing a
coordinate system that best fits a given problem. A hard
problem in one coordinate system may turn out to be easy
in another system.
We will consider the Cartesian, the circular cylindrical, and
the spherical coordinate systems. All three are orthogonal
(the coordinates are mutually perpendicular).
35
EEL 3472
Review of Vector Analysis
Cartesian coordinates (x,y,z)
The ranges of the coordinate variables are
x
y
z
A vector A in Cartesian coordinates can be written as
(A x , A y , A z )
or
A x ex A y ey A z ez
The intersection of three
orthogonal infinite places
(x=const, y= const, and z =
const)
defines point P.
Constant x, y and z surfaces
36
EEL 3472
Review of Vector Analysis
dl dx ex dy ey dz ez
d dxdydz
Differential elements in the right handed Cartesian coordinate system
37
EEL 3472
Review of Vector Analysis
dS dydz ax
dxdz ay
dxdy az
38
EEL 3472
Review of Vector Analysis
Cylindrical Coordinates (, , z) .
- the radial distance from the z axis
0 2 - the azimuthal angle, measured from the xaxis in the xy plane
z - the same as in the Cartesian system.
A vector
in cylindrical coordinates can be written as
(A , A A z )
or
A e A e A z ez
2
A (A A A z )1 / 2
Cylindrical coordinates amount to a combination of
rectangular coordinates and polar coordinates.
39
EEL 3472
Review of Vector Analysis
Relationship between (x,y,z) and (, , z)
Positions in the x-y plane are determined by the values of
and
y
x2 y2
tan1
zz
x
40
EEL 3472
Review of Vector Analysis
Point P and unit vectors
in the cylindrical
coordinate system
e e ez
e ez e
ez e e
e e e e ez ez 1
e e e ez e e 0
41
EEL 3472
Review of Vector Analysis
semi-infinite
plane with its
edge along
the z - axis
Constant , and z surfaces
42
EEL 3472
Review of Vector Analysis
Metric coefficient
dl d ap da dz az
dv dddz
Differential elements in cylindrical coordinates
43
EEL 3472
Review of Vector Analysis
dS ddza
ddza
dd az
Cylindrical
surface
( =const)
Planar surface
( = const)
Planar surface
( z =const)
44
EEL 3472
Review of Vector Analysis
Spherical coordinates (r, , ) .
0r
014
2
43
Colatitude
( polarangle)
0 2
- the distance from the origin to the point P
- the angle between the z-axis and the radius
vector of P
- the same as the azimuthal angle in
cylindrical coordinates
45
EEL 3472
Review of Vector Analysis
er e e
e e er
e er e
er er e e e e 1
Point P and unit vectors in spherical
coordinates
er e e e e er 0
A vector A in spherical coordinates may be
written as
(Ar , A A )
or
Ar er A e A e
2
A (Ar A A )1 / 2
46
EEL 3472
Review of Vector Analysis
x y z
tan
x2 y2
z
tan1
tan-1
y
cos 1
x
x
x2 y2
z
cos1
z
r
x r sin cos
y r sin sin
z r cos
Relationships between space variables (x, y, z), (r, , ), and (, , z)
47
EEL 3472
Review of Vector Analysis
Constant
48
r, , and surfaces
EEL 3472
Review of Vector Analysis
dl dr ar rda r sin d a
dv r 2 sin drdd
Differential elements in the spherical coordinate system
49
EEL 3472
Review of Vector Analysis
dS r 2 sin d d ar
r sin dr d a
rdr d a
50
EEL 3472
Review of Vector Analysis
51
EEL 3472
Review of Vector Analysis
52
EEL 3472
Review of Vector Analysis
53
EEL 3472
Review of Vector Analysis
54
EEL 3472
Review of Vector Analysis
POINTS TO REMEMBER
1.
2.
3.
55
EEL 3472
Review of Vector Analysis
4.
5.
6.
7.
56
EEL 3472
También podría gustarte
- UNIT-1: Lecture Notes Unit 1: Transient AnalysisDocumento36 páginasUNIT-1: Lecture Notes Unit 1: Transient AnalysisRamalingeswar JAún no hay calificaciones
- SAMPLE Introductory Mathematical Analysis PDFDocumento90 páginasSAMPLE Introductory Mathematical Analysis PDFLalani Wije60% (5)
- Vector and Tensor Analysis with ApplicationsDe EverandVector and Tensor Analysis with ApplicationsCalificación: 4 de 5 estrellas4/5 (10)
- IJSO Stage-I & II - Physics Sheet-2017-18 PDFDocumento378 páginasIJSO Stage-I & II - Physics Sheet-2017-18 PDFTechnical AdvikAún no hay calificaciones
- Kalkulus 03-DerivatDocumento86 páginasKalkulus 03-DerivatFajar Nur HidayatiAún no hay calificaciones
- Interview With Greg LynnDocumento8 páginasInterview With Greg LynnbblqAún no hay calificaciones
- Vectors: Introduction of VectorDocumento9 páginasVectors: Introduction of Vectorskj6272Aún no hay calificaciones
- Laplace Transform & Inverse Laplace Transform MCQDocumento22 páginasLaplace Transform & Inverse Laplace Transform MCQShivam Pandey86% (7)
- Impacts of Water PollutionDocumento31 páginasImpacts of Water PollutionJomar Dador100% (2)
- Engr. Jeffrey T. Dellosa Information and Communications Technology (ICT) Center NormisistDocumento60 páginasEngr. Jeffrey T. Dellosa Information and Communications Technology (ICT) Center NormisistJomar DadorAún no hay calificaciones
- Energy Bands and Charge CarriersDocumento59 páginasEnergy Bands and Charge CarriersengaltarekAún no hay calificaciones
- Ee105 Fet LectDocumento61 páginasEe105 Fet LectKahMun LimAún no hay calificaciones
- CHAPTER 2 - Transducer - 2Documento73 páginasCHAPTER 2 - Transducer - 2RafaelTituzAún no hay calificaciones
- Assignment 2 NTKDocumento2 páginasAssignment 2 NTKtsegay100% (1)
- Problems: Unit - 1 Presented by Mrs. M.P.SasirekhaDocumento6 páginasProblems: Unit - 1 Presented by Mrs. M.P.SasirekhaSasirekha Kosalram0% (1)
- Book ListDocumento6 páginasBook Listdebasishmee58080% (1)
- Magnetic Fields Due To Electric CurrentDocumento18 páginasMagnetic Fields Due To Electric CurrentHrishikesh GunjalAún no hay calificaciones
- CH-1 - DC Generator Q.bank PDFDocumento2 páginasCH-1 - DC Generator Q.bank PDFjaythakar8887Aún no hay calificaciones
- QuesDocumento2 páginasQuesGmind0% (5)
- Solution:: Fig. 2 Shows The Required Common Base ConnectionDocumento9 páginasSolution:: Fig. 2 Shows The Required Common Base ConnectionSwathi Gudivada100% (1)
- EMI Class Notes Assignment 1Documento2 páginasEMI Class Notes Assignment 1Praneshvar Praneshvar50% (2)
- ConductorsDocumento62 páginasConductorsRamon Lopez Lapiña100% (1)
- PTDU Lab No. 10 Study of Real Time Operation of Bus Bars Abdul Wahab Nasir (02) Bsee 16-20Documento2 páginasPTDU Lab No. 10 Study of Real Time Operation of Bus Bars Abdul Wahab Nasir (02) Bsee 16-20Ali ArshadAún no hay calificaciones
- Transducers (Lecture Notes)Documento13 páginasTransducers (Lecture Notes)sel_d_bellAún no hay calificaciones
- Linear TransformerDocumento44 páginasLinear TransformerRonmark AbinoAún no hay calificaciones
- Analog Electronics-2 PDFDocumento20 páginasAnalog Electronics-2 PDFAbhinav JangraAún no hay calificaciones
- Chapter 1 SolutionsDocumento3 páginasChapter 1 SolutionsRicardo SudAún no hay calificaciones
- Cyclotron Angular Frequency, Problems On Magnetron: Microwave Crossed-Field Tubes: 03/12/2020 & 10:00 AM-11:00 AMDocumento18 páginasCyclotron Angular Frequency, Problems On Magnetron: Microwave Crossed-Field Tubes: 03/12/2020 & 10:00 AM-11:00 AMravi kiranAún no hay calificaciones
- Intrinsic Semiconductor: Free Electrons HolesDocumento7 páginasIntrinsic Semiconductor: Free Electrons HolesSyed Zubair ZahidAún no hay calificaciones
- TransLine 1 ConclusionDocumento2 páginasTransLine 1 ConclusionmultisporkyAún no hay calificaciones
- EE TermsDocumento26 páginasEE TermsMarry Joy AndradaAún no hay calificaciones
- EE6604-Design of Electrical Machines - QBDocumento16 páginasEE6604-Design of Electrical Machines - QBmadhu balanAún no hay calificaciones
- IntegratorDocumento38 páginasIntegratorSyed AshmadAún no hay calificaciones
- Lab 4 - Clippper and Clamper CircuitsDocumento7 páginasLab 4 - Clippper and Clamper CircuitseyobAún no hay calificaciones
- Numericals - Magnetic CircuitsDocumento10 páginasNumericals - Magnetic CircuitsdtrhAún no hay calificaciones
- Electrical Objective Questions With AnswDocumento3 páginasElectrical Objective Questions With Answasjadullah1Aún no hay calificaciones
- Chapter 5Documento38 páginasChapter 5awrexAún no hay calificaciones
- Analog Circuits SyllabusDocumento5 páginasAnalog Circuits SyllabusVilayil jestinAún no hay calificaciones
- Circuit Lab Div. B Tryout Test PDFDocumento6 páginasCircuit Lab Div. B Tryout Test PDFMadhavi VangipurapuAún no hay calificaciones
- Lecture 6-Magnetic CircuitsDocumento49 páginasLecture 6-Magnetic CircuitsMAENYA BRUCE OYONDIAún no hay calificaciones
- Okumura ModelDocumento6 páginasOkumura Modelrktiwary256034Aún no hay calificaciones
- Question Bank AECDocumento5 páginasQuestion Bank AECChandra SekharAún no hay calificaciones
- 02-Alternator On LoadDocumento12 páginas02-Alternator On Loadcooldude99344100% (1)
- Chapter 6Documento13 páginasChapter 6aregawi weleabezgiAún no hay calificaciones
- Soal-Jawab TrafoDocumento5 páginasSoal-Jawab TrafoNizar SyamsudinAún no hay calificaciones
- BETT 3414 - Lab 3 Stub MacthingDocumento12 páginasBETT 3414 - Lab 3 Stub Macthingnurin run100% (2)
- 325 Lab 3 ReportDocumento13 páginas325 Lab 3 Reportapi-241454978Aún no hay calificaciones
- Ee6501 Psa Eee VST Au Units IVDocumento24 páginasEe6501 Psa Eee VST Au Units IVManeesh K ChaudharyAún no hay calificaciones
- I DT DT DT DT: Class Notes On Electrical Measurements & InstrumentationDocumento71 páginasI DT DT DT DT: Class Notes On Electrical Measurements & InstrumentationTia Nur AmaliahAún no hay calificaciones
- Eeeb113 Circuit Analysis 1: Chapter 6: Capacitors and Inductors Sharifah Azma Syed MustaffaDocumento25 páginasEeeb113 Circuit Analysis 1: Chapter 6: Capacitors and Inductors Sharifah Azma Syed MustaffaSharifah Azma100% (1)
- ADE Lab Manual - Analog Part PDFDocumento21 páginasADE Lab Manual - Analog Part PDFJk RinkuAún no hay calificaciones
- Digital Control Systems: Introduction & Z-TransformDocumento70 páginasDigital Control Systems: Introduction & Z-TransformZeeshan RafiqAún no hay calificaciones
- Iecep GeasDocumento9 páginasIecep GeaswengAún no hay calificaciones
- GEAS Review GuideDocumento15 páginasGEAS Review GuideSanny Domingo AfableAún no hay calificaciones
- Electrical Engineering Lab ReportDocumento7 páginasElectrical Engineering Lab ReportFrancis Paul SantiagoAún no hay calificaciones
- Objective QuestionsUNIT - 3&4Documento17 páginasObjective QuestionsUNIT - 3&4Omkar Shete50% (2)
- Measuring Position and Displacement With LVDTS: 1. What Is Linear Displacement MeasurementDocumento4 páginasMeasuring Position and Displacement With LVDTS: 1. What Is Linear Displacement MeasurementJelena GavanskiAún no hay calificaciones
- EE GATE 1995 Question and AnswersDocumento6 páginasEE GATE 1995 Question and AnswersUTKAL.450% (1)
- Exercise Chapter 2Documento5 páginasExercise Chapter 2zulAún no hay calificaciones
- Ideal Transformer - PPT 5th LectureDocumento22 páginasIdeal Transformer - PPT 5th LectureAmmara RasheedAún no hay calificaciones
- 5 Year QB - EMF - 2017 PDFDocumento168 páginas5 Year QB - EMF - 2017 PDFVijay Nagendran0% (1)
- DLD - Ch.1 Notes PDFDocumento35 páginasDLD - Ch.1 Notes PDFAlradi Malak FadiAún no hay calificaciones
- Unit II 2 MarksDocumento6 páginasUnit II 2 MarksGowthamanAún no hay calificaciones
- Review Vector AnalysisDocumento54 páginasReview Vector Analysiss_eiko5Aún no hay calificaciones
- Chapter 1 - Vector AnalysisDocumento48 páginasChapter 1 - Vector AnalysisMujeeb AbdullahAún no hay calificaciones
- TESTDocumento1 páginaTESTJomar DadorAún no hay calificaciones
- Week 2 Baseband 1Documento40 páginasWeek 2 Baseband 1Jomar DadorAún no hay calificaciones
- Biomed ApplicantsDocumento2 páginasBiomed ApplicantsJomar DadorAún no hay calificaciones
- Solenoid Driver 1Documento1 páginaSolenoid Driver 1El GroneAún no hay calificaciones
- Ee321 ObjectivesDocumento3 páginasEe321 ObjectivesJomar DadorAún no hay calificaciones
- Sports Coordinator JobsDocumento3 páginasSports Coordinator JobsJomar DadorAún no hay calificaciones
- Unit 2Documento24 páginasUnit 2Thảo NguyệtAún no hay calificaciones
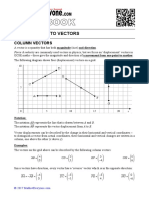
- Introduction To VectorsDocumento26 páginasIntroduction To VectorsNayem Hossain HemuAún no hay calificaciones
- Sequences and SeriesDocumento34 páginasSequences and SeriesChoy CristobalAún no hay calificaciones
- CO-1 Sessionwise ProblemsDocumento6 páginasCO-1 Sessionwise Problemsaswith Reddy. AtlaAún no hay calificaciones
- Table of Laplace Transforms PDFDocumento1 páginaTable of Laplace Transforms PDFMegaAún no hay calificaciones
- EE 470 - Signals and Systems: 3. The Laplace TransformDocumento33 páginasEE 470 - Signals and Systems: 3. The Laplace Transformmohammed alolofiAún no hay calificaciones
- M-10 Content+Previous Years QuestionDocumento65 páginasM-10 Content+Previous Years QuestionOnline Physics Care by Syed Al-NahiyanAún no hay calificaciones
- Arfken MMCH 10 S 1 e 5Documento3 páginasArfken MMCH 10 S 1 e 5QuratulainAún no hay calificaciones
- Cse M1Documento4 páginasCse M1GPNAún no hay calificaciones
- BC A Syl Lab Us and CurriculumDocumento47 páginasBC A Syl Lab Us and CurriculumRitik kumarAún no hay calificaciones
- Non Homogeneous Second Oder Linear Differential Equation PDFDocumento19 páginasNon Homogeneous Second Oder Linear Differential Equation PDFLuqman RajputAún no hay calificaciones
- E6 2014-2-Pah-Sultan Abu Bakar-ADocumento4 páginasE6 2014-2-Pah-Sultan Abu Bakar-APeng Peng KekAún no hay calificaciones
- 2016 Lecture5Documento15 páginas2016 Lecture5Rehan GamingAún no hay calificaciones
- Important Questions For CBSE Class 11 Maths Chapter 13Documento36 páginasImportant Questions For CBSE Class 11 Maths Chapter 135 Aditya Kr. 8CAún no hay calificaciones
- 05 The Uniqueness of Limits of A Function Theorem - MathonlineDocumento1 página05 The Uniqueness of Limits of A Function Theorem - MathonlineArista WibowoAún no hay calificaciones
- L5 - Methods of IntegrationDocumento32 páginasL5 - Methods of IntegrationJOHN RafaelAún no hay calificaciones
- Numerical Solution of The Fokker Planck Equation Using Moving Finite ElementsDocumento14 páginasNumerical Solution of The Fokker Planck Equation Using Moving Finite Elementsjuan carlos molano toroAún no hay calificaciones
- Limit of A Function and Limit Theorems: Mathematics 21Documento27 páginasLimit of A Function and Limit Theorems: Mathematics 21Cristan Dave ZablanAún no hay calificaciones
- SW#2 Integrals of Trigonometric FunctionsDocumento1 páginaSW#2 Integrals of Trigonometric FunctionsRachel MonesAún no hay calificaciones
- Unit2 PhysicsDocumento92 páginasUnit2 PhysicsSwapnil SahuAún no hay calificaciones
- Today:: + Cos + Sin ,:, Arg Arg + Arg +Documento20 páginasToday:: + Cos + Sin ,:, Arg Arg + Arg +IbrahimAún no hay calificaciones
- Mathematics-Ii: Prepared By: Ms. K. Rama Jyothi,: Mr. G Nagendra KumarDocumento118 páginasMathematics-Ii: Prepared By: Ms. K. Rama Jyothi,: Mr. G Nagendra KumarNithya SridharAún no hay calificaciones
- Fract Aacademic Course BookletDocumento124 páginasFract Aacademic Course BookletRavikumaar RayalaAún no hay calificaciones
- Laplace FormulasDocumento2 páginasLaplace FormulasNagendrababu VanamalaAún no hay calificaciones
- Tabela T.Laplace.192-204Documento13 páginasTabela T.Laplace.192-204Ana Luiza CamposAún no hay calificaciones