TECHNICAL

581

NOTES

distribution in the clay sidewall of the type shown in Fig. 5(b). In this case, an equivalent
beam would be fixed by the bentonite suspension 3 m above the base and be subject to a peak
pressure at 3.75 m below its simply supported top. If this pressure distribution is assumed
then conjugate beam analysis shows that the maximum horizontal deformation occurs at a
depth of 6 m and is equal to 15 mm for a clay beam 4.7 m thick, and having an assumed
modulus of elasticity of lo5 kN/m2. Correlation of the observed deformation profile in
the present instance, with the postulated existence of peak earth pressures at a depth roughly
equal to one quarter the total depth of the trench, has considerable significance in the wider
design of bentonite-supported excavations. It is well known that the occurrence of overbreak
in such excavations in weaker soils is invariably located close to the top of the excavation. If,
as seems likely, there is a causatory relationship between overbreak and the shear stresses
existing in the supported sidewall, a design approach based on the resultant pressure distribution in the wall may be a more suitable method than stability analysis.
ACKNOWLEDGEMENTS

The experimental work

with the Tunnels Division
ment of the Environment,
permission of the London

described in the Note was carried out under a research contract

of the Transport and Road Research Laboratory of the Departwith the co-operation of Messrs Mott, Hay and Anderson and by
Transport Executive.

REFERENCES
Elson, W. K. (1968). An experimental investigation of the stability of slurry trenches.
Gefofechnique 18,
No. 1, 3749.
Morgenstern, N. R. & Amir-Tahmasseb,
I. (1965). The stability of a slurry trench in cohesionless soils.
Geotechnique 15, No. 4, 387-395.
Nash, J. K. T. L. & Jones, G. K. (1963). The support of trenches using fluid mud. Proceedings of the
Symposium on Grouts and DriIling Muds in Engineering Practice.
London: Butterworth.
Terzaghi, K. & Peck, R. B. (1967). Soil mechanics in engineering practice, 2nd ed. New York: Wiley.

Laboratory determination of the coefficient of

electro-osmotic permeability of a soil
M. ARNOLD, BSc (Eng), PhD, MIE Aust, MNZIE, MASCE, AMS Afr, MICE*
INTRODUCTION

In the application of electro-osmosis to engineering projects, the coefficient of electro-osmotic

permeability k, plays an important role in the form of the ratio k,/k, where kh is the coefficient
of hydraulic permeability.
The direct measurement of k,/k, involves practical problems and
it is sometimes more convenient to measure these parameters independently.
Methods for the
determination of k,, are well established but very little attempt has been made to improve the
method for the determination of k, introduced by Casagrande (1948). This method involved
a direct measurement of the quantity of water transported by an electric current under a fixed
potential gradient and was subject to problems caused by electro-chemical effects at the
electrodes. The method proposed by Schaad (1948) based on that of Geuze et al. (1948)
involved the measurement of the rate of rise of hydrostatic head in a standpipe at the cathode
l

Senior Lecturer in Civil Engineering,

University

of Adelaide.

582

TECHNICAL
Air

Phosphor-bronze

ink

NOTES

disc

Ith silver steel confxr

Terminal with

Fig. 1.

Electra-osmotic pressure apparatus

and used the initial rate of rise for determining

the coefficient.
This method reduced the
inaccuracies caused by the gradual development of electro-chemical
effects but still retained the
disadvantages
of a considerable net flow of water through the soil specimen.
In order to overcome both problems the apparatus shown diagrammatically
in Fig. 1 was
developed on the basis of the following analytical relationships.
ANALYTICAL

EXPRESSION

The coefficient

FOR THE COEFFICIENT

of electro-osmotic

permeability

OF PERMEABILITY

(k,) was defined by Casagrande

as

s=g . . . . . , . . . *

(1)

where
n = porosity

of soil

5 = zeta potential

of soil

D = dielectric

constant

tk = viscosity

of soil water

For an open standpipe

in the following form

of soil water

measuring

h =

system the flow equations

!!$

of Geuze et al. can be rewritten

(1_e[-A~gdZt32~al)l)

where
h = head developed
E/I = potential

gradient

at cathode
applied

p = density of soil water

g = gravitational

constant

standpipe
across soil specimen

TECHNICAL

583

NOTES

d = diameter

of hypothetical

soil capillaries

A = cross-sectional

area of soil specimen

a = cross-sectional

area of standpipe

I = length of soil specimen

t = time
dh
= initial rate of increase
( dt i t=O
For a closed measuring
results from the elasticity
modified as follows

of head in cathode

standpipe

system as in Fig. 1, where the only possibility of net induced flow

of the cathode pressure chamber, equations (2) and (3) must be

where
P = pressure
R = calibration

developed
constant

in cathode

chamber

of the equipment

=-dQ
dP

Q = net flow into cathode

DETAILS

chamber

(electro-osmotic

flow minus hydraulic

reverse flow)

OF APPARATUS

General details of the apparatus,

which contained a soil sample 33 mm in diameter and
72 mm in length, are shown in Fig. 1. This was a closed pressure system where any tendency
for water to be transported through the soil specimen was opposed by a rise in pressure in the
chamber at the cathode.
This pressure was then measured by means of a balancing air pressure in the chamber on the right of the flexible diaphragm.
In practice, the needle contact was
initially set so that electrical contact was just made with atmospheric pressure on both sides of
the diaphragm.
A small excess pressure was then applied to the air pressure chamber, breaking the contact, and when the cathode chamber pressure reached this value, contact was reestablished.
Applications
of further increments
of air pressure enabled successively higher
cathode chamber pressures to be measured.
For an infinitely rigid closed pressure system, the calibration coefficient R=O, (dP/dt),=,
It is possible to measure the magnibecomes infinite and the conditions are indeterminate.
tude of the almost instantaneous
cathode chamber pressure which is developed in a very rigid,
closed pressure system at the outset of current flow, but the practical difficulties are considerable and the method introduced here is simpler and requires no sophisticated equipment.
Initially it was found that the elasticity of the sample container gave a positive value of R but
the rate of pressure rise was so great that it was necessary to introduce a means of controlling
the elasticity of the system.
This was done by introducing
a subsidiary pressure chamber at
This chamber contained
a spring-loaded
the cathode pressure chamber bleeder outlet.
diaphragm
whose rigidity could be controlled
by altering the compression
of the spring.

584

TECHNICAL

0.632
.lf

.____

H = 0.632
F

t-l

l____
I

Fig. 2.

NOTES

Time

Geometrical relationships for exponential curve

Nevertheless, when the rate of pressure rise had been reduced to an acceptable figure considerable scatter in the first few pressure measurements
was still found.
Because the determination
of the value of the coefficient k, depended on an accurate determination
of the initial tangent
modulus (dP/dt), = o it became necessary to develop a method of increasing the accuracy of this
determination.
METHOD

Equation

OF ANALYSIS

OF PRESSURE

RISE DATA

(4) can be written

P = M(l-e-t)

and

dp= Mae-at
dt

(6)

(7)

(8)

It will be seen that the parameters M and 01are extremely complex, with some factors that
are indeterminate
or difficult to measure and hence must be determined empirically.
Rather
involved methods already exist for the determination
of the parameters
of an exponential
relationship
of this form, but the method outlined below has been found to be the most direct
and suitable for routine evaluations of k, from pressure rise data.
Using the concept of a time constant as in electrical systems, it will be seen from equation
(6) that when t = l/et, P= O-632 M and dP/dt = O-368 Ma and hence a simple, graphical method
can be established for determining the time constant, l/a.

TECHNICAL

585

NOTES

From the geometrical

relationships

of Fig. 2, where the line FAC is tangent

to the curve at A

GA = H = Q-632 M
GB = 1.582 H = M
OF = 0.264 M = 0.418 H
OG = l/a = BC (time constant)
tan 0 = HjOG

= O-632 MCZ

= 1.582 tan 0
Thus it will be seen that if the time constant, determined by the tangent point A, can be
accurately established, the parameters M and Q and the initial tangent modulus are immediately
obtainable.
The procedure adopted to establish the time constant is as follows
(a)
(b)
(c)
(d)

any point A on the curve is selected

the ordinate GA = H is measured
point F on the P-axis is established such that OF=0*418 H
line FAC is drawn; if the line FAC is tangential to the curve at A then that point has
been correctly chosen and the abscissa of A represents the time constant; if not, a
further trial is necessary.
(e) with the tangent point correctly located
M = 1.582 H

= l-582 tan 0
(f) Check along the horizontal

THE EFFECT

OF INCORRECT

at M that EB = EC

LOCATION

OF THE TANGENT

POINT

As the proposed method of establishing the initial tangent modulus for use in the determination of k, depends on the visual selection of the correct tangent point A, it is necessary to assess
Fig. 3 shows the tangent point
the effects of incorrect choice of the location of that point.
located such that the time constant is in error with a factor q=O.8 and q= 1.2 and it will be
seen that in each case the line FAC is clearly not tangent to the curve at A. Thus it is evident
that the time constant can easily be selected within of:20% of the correct value.
If the value of the time constant has been incorrectly determined at q(l/a) the value of P at
the incorrect time constant becomes
H = M(l-eW4)
From this an incorrect

value of M will be derived, i.e.

M = 1.582 H = l-582 M(I -e-)

The incorrect

form of the exponential

expression

will now become

P = M(1 _,-(aiQ)t)
= 1.582 M(l -eWq)(l -e-(rrlq)t)
or

P/M = 1*582(1 -emq)(l -e-(aq)c)

TECHNICAL

!!
If

,
= 09371
---

0.

T
0
A

o*,

--

0.264 nr= 0,230

-_----

0.
t--.

,,axzo.5
(a)

i
~

q=04

+
i

I
----

----

---------_c_____
C

I.0

0.8

I
i

0,6

P
3I
0.4

F
0.2

--A_-_

i
i
i

a = 2.0

--

i
k

I/a=04
*=

P)

152

I
0

Fig. 3.

I-0

Ttme

Effect of incorrect location of tangent point

2.0

1
3.0

NOTES

TECHNICAL

NOTES

587

..__.
__---

_.-.._..

Jf

=I.s82(l-t)

a=

1-O

qzo.9
qzO.8

----_----_---_---_

_.-.*_

.._.._

20

2.0

340

Time

Fig. 4.

Effect of incorrect determination of time constant

This has been plotted in Fig. 4 for values of q= O-8 to q= 1.2 and it will be seen that the
error is barely discernible up to a value of P/M=0*65.
The initial tangent moduli are incorrect by + 9% for q=O*S and - 5% for q= 1.2. These errors are negligible.
EXAMPLE

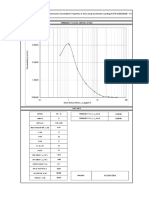
Figure 5 shows a typical pressure-time relationship for a bentonite clay (Volclay) at the
liquid limit with an applied potential gradient of 1.4 V/cm. From the figure, tan B=O.264
kgf/cm2/min. For the apparatus and specimen used, R/A(E/l) = 0.0121 cm4/kgf/V
R
k, = 1.582 A(E,I) tan 0
= 8.4 x 10e5 cm/s/V/cm

A direct flow test made immediately after the pressure rise test gave
k, = 7-3 x 10S5 cm/s/V/cm
CONCLUSIONS

This method of determining the coefficient of electro-osmotic permeability of a soil is simple,

straightforward, requires no sophisticated apparatus and involves a short test duration.

588

TECHNICAL NOTES
E614A
0
----

Experimental
Derived

valuer

relationship

= 0417kg/cm2

/r&l.

t=o

I'0

2.0

3-o

Time:

Fig.5.

min.

Typical experimental evaluation

Although the method relies on the determination

of the initial tangent modulus of the pressuretime curve, this is established from the secant modulus at a short time after the start of the test.
This avoids the consistent scatter of the early pressure-time
readings, but still establishes the
required parameters
before significant disturbing
effects can occur, such as gassing at the
electrodes and other electro-chemical
effects.
This method has been used for the routine determination
of the coefficient of electro-osmotic
permeability involving several hundreds of specimens and in only a few isolated cases was it not
possible to establish the point of tangency with sufficient accuracy.
The apparatus shown in Fig. 1 can easily be adapted for the measurement
of hydraulic
permeability.
It may be noted that the exponential
relationship
y=M(l - emarX)is sometimes in closer
agreement with the stress/deformation
characteristics of a soil (particularly at low strains) than
is the hyperbolic relationship
introduced by Kondner (1963). For these cases the relevant
parameters can also be determined by the method outlined here.
REFERENCES
Casagrande, L. (1948). Electra-osmosis.
Proc. 2nd Int. ConJ Soil Mech., Rotterdam 1,218.
Geuze, E. C. W. A., de Bruyn C. M. A. & Joustra, K. (1948). Results of laboratory investigation of the
electrical treatment of soils. Proc. 2nd Int. Conf. Soil Mech., Rotterdam 3, 153.
Kondner, R. L. (1963). Hyperbolic stress-strain response: cohesive soils. Jnl Soil Mech. Fdns Div. Am. Sot.
Civ. Engrs 89, SMl, 115.
Schaad, W. (1948). Electrical treatment of soils. Proc. 2nd. Znt. Conf. Soil Mech., Rotterdam 5, 85.