Documentos de Académico
Documentos de Profesional
Documentos de Cultura
Conservation! Of! Mass!: The Equations Governing Fluid Motion!
Cargado por
Raul CondoyTítulo original
Derechos de autor
Formatos disponibles
Compartir este documento
Compartir o incrustar documentos
¿Le pareció útil este documento?
¿Este contenido es inapropiado?
Denunciar este documentoCopyright:
Formatos disponibles
Conservation! Of! Mass!: The Equations Governing Fluid Motion!
Cargado por
Raul CondoyCopyright:
Formatos disponibles
Computational Fluid Dynamics
http://www.nd.edu/~gtryggva/CFD-Course/!
The
Equations
Governing
Fluid Motion!
Computational Fluid Dynamics
Outline!
Derivation of the equations governing fluid flow in
integral form!
!Conservation of Mass!
!Conservation of Momentum!
!Conservation of Energy!
Differential form!
Summary!
Incompressible flows!
Inviscid compressible flows!
Grtar Tryggvason!
Spring 2011!
Computational Fluid Dynamics
Computational Fluid Dynamics
Conservation of Mass!
In general, mass can be added or removed:!
Conservation!
of!
Mass!
time t+t!
time t!
The conservation law must be stated as:!
Final!
Original!
Mass! Mass!
=!
+!
-!
Mass!
Mass!
Added! Removed!
Computational Fluid Dynamics
Conservation of Mass!
Rate of
Net influx
increase of =!
of mass!
mass!
We now apply this statement to
an arbitrary control volume in an
arbitrary flow field!
Computational Fluid Dynamics
Conservation of Mass!
Control
volume V!
The rate of
change of
total mass in
the control
volume is
given by:!
Control
surface S!
dv
t V
Rate of
change!
Total
mass!
Computational Fluid Dynamics
Conservation of Mass!
Control
volume V!
Computational Fluid Dynamics
Conservation of Mass!
Select a small rectangle outside the boundary
such that during time t it flows into the CV:!
Control
surface S!
Ut!
Density !
Velocity Ux!
A!
time t! time t+t!
To find the mass flux through!
the control surface, lets examine!
a small part of the surface where
the velocity is normal to the surface!
where Ux = -un!
Computational Fluid Dynamics
Conservation of Mass!
The sign of the normal component of the velocity
determines whether the fluid flows in or out of the
control volume. We will take the outflow to be positive:!
un<0
Inflow!
The net in-flow through the boundary of the control
volume is therefore:!
Negative since
this is net inflow!
Integral over
the boundary!
Mass flow
through the
boundary
A during t
is: !
U x tA
u n ds
S
Mass flow normal
to boundary!
Computational Fluid Dynamics
Computational Fluid Dynamics
Conservation of Mass!
Conservation of Mass Equation in Integral Form!
dv = S u n ds
t V
Rate of change
of mass!
Computational Fluid Dynamics
Conservation of momentum!
Momentum per volume: !
Conservation!
of!
momentum!
Net inflow of mass!
Momentum in control volume: !
u dv
Rate of
Net influx of
+! Body +! Surface
increase of =!
momentum!
forces!
forces!
momentum!
Computational Fluid Dynamics
Rate of change of momentum!
Computational Fluid Dynamics
In/out flow of momentum!
Control
volume V!
Control
surface S!
The rate of
change of
momentum
in the control
volume is
given by:!
Select a small rectangle outside the boundary
such that during time t it flows into the CV:!
Density !
Uxt!
Velocity u!
A!
time t! time t+t!
u dv
t V
Rate of
change!
( u )U x tA
Ux"
Ux = -un so the net influx of momentum
per unit time (divided by t ) is:!
Total
momentum!
Computational Fluid Dynamics
Body force!
Body forces,
such as
gravity act on
the fluid in the
control
volume.!
Control
volume V!
The viscous
force is given
by the dot
product of the
normal with
the stress
tensor T!
f!
f dv
Control
surface S!
ds
Tn!
T n dS
S
Total body force!
Total stress force!
Computational Fluid Dynamics
Viscous flux of momentum!
Stress Tensor!
T = ( p + u )I + 2 D
Deformation Tensor!
1
D = (u + uT )
2
Whose components are:!
1 u u
Dij = i + j
2 x j xi
uu n ds
Computational Fluid Dynamics
Viscous force!
Control
volume V!
dv
Momentum
flow through
the boundary
A during t is:!
Computational Fluid Dynamics
Pressure force!
For
incompressible
flows!
u=0
And the stress
tensor is!
T = pI + 2D
Control
volume V!
The pressure
produces a
normal force
on the control
surface. The
total force is:!
Control
surface S!
ds
pn!
pn dS
Total pressure force!
Computational Fluid Dynamics
Conservation of Momentum!
Computational Fluid Dynamics
Gathering the terms!
u dv = uu n ds Tn ds + f dv
t
Conservation!
of!
energy!
T = pI + 2D
Substitute for the stress tensor!
u dv = uu n ds pn ds + 2 D n ds + f dv
t
Net inflow of
Rate of
momentum!
change of
momentum!
Total
pressure!
Total
viscous
force!
Total
body
force!
Computational Fluid Dynamics
Conservation of energy!
Computational Fluid Dynamics
The energy equation in integral form!
Net inflow of
kinetic+internal
energy!
Rate of change of
kinetic+internal
energy!
1
1
e + u 2 dv = e + u 2 u n ds
t
2
2
+ u f dv +
n (uT)ds n q ds
V
Net work
done by
the stress
tensor!
Work
done by
body
forces!
Differential Form!
of!
the Governing Equations!
Net heat
flow!
Computational Fluid Dynamics
Differential form!
Computational Fluid Dynamics
Differential form!
Start with the integral form of the mass conservation equation!
The Divergence or Gauss Theorem can be used to
convert surface integrals to volume integrals!
a dv = a n ds
V
dv = S u n ds
t V
Using Gausss theorem!
u n ds = ( u)dv
S
The mass conservation equations becomes!
dv = V ( u)dv
t V
Computational Fluid Dynamics
Differential form!
Computational Fluid Dynamics
Differential form!
Rearranging!
dv + V (u)dv = 0
t V
Since the control volume is fixed, the derivative can be
moved under the integral sign!
dv + V ( u)dv = 0
t
+ (u) dv = 0
t
This equation must hold for ANY control volume, no
matte what shape and size. Therefore the integrand
must be equal to zero!
+ ( u) = 0
t
Rearranging!
+ (u) dv = 0
t
Computational Fluid Dynamics
Differential form!
The differential form of the momentum equation is
derived in the same way:!
Start with!
Expanding the divergence term:!
(u) = u + u
The mass conservation equation becomes:!
+ (u) =
+ u + u
t
t
or!
where!
D
+ u = 0
Dt
D() ()
=
+ u ()
Dt t
Computational Fluid Dynamics
Differential form!
Rewrite as:!
u dv = f dv + (T uu )dv
To get:!
u
= f + (T uu)
t
Convective
derivative!
Computational Fluid Dynamics
Differential form!
Using the mass conservation equation the
advection part can be rewritten:!
u
+ uu =
t
u
u
+ u u +
+ u u =
t
t
Du
Du
u + u +
=
t
Dt
Dt
=0, by mass
conservation!
u dv = f dv + (nT u(u n))ds
Computational Fluid Dynamics
Differential form!
The momentum equation equation!
u
= f + (T uu)
t
Can therefore be rewritten as!
where!
Du
= f + T
Dt
Du
= + u u
t
Dt
Computational Fluid Dynamics
Differential form!
Computational Fluid Dynamics
Differential form!
The mechanical energy equation is obtained by taking
the dot product of the momentum equation and the
velocity:!
The energy equation equation can
be converted to a differential form in
the same way. It is usually simplified
by subtracting the mechanical
energy !
u
u
+ u u = f + T
t
The result is:!
u2
u 2
= u + u fb + u ( T)
t 2
2
The mechanical energy equation!
Computational Fluid Dynamics
Differential form!
Computational Fluid Dynamics
Differential form!
The final result is!
Subtract the mechanical energy equation from the
energy equation!
The final result is!
De
T u + q = 0
Dt
where!
Using the constitutive relation presented earlier for
the stress tensor and Fouries law for the heat
conduction:!
De
+ p u = + kT
Dt
= ( u) 2 + 2D D
is the dissipation function and is the rate at which
work is converted into heat.!
T = ( p + u )I + 2 D
Generally we also need:!
p = p(e, ); T = T (e, );
q = kT
and equations for ! ,
Computational Fluid Dynamics
, k
Computational Fluid Dynamics
Integral Form!
Summary!
of!
governing equations!
dv = u n ds
S
u dv = f dv + (nT u(u n))ds
t
1
1
(e + u 2 )dv = u f dv + n (uT (e + u 2 ) q)ds
t
2
2
Computational Fluid Dynamics
Computational Fluid Dynamics
Conservative Form!
Convective Form!
+ ( u) = 0
t
D
+ u = 0
Dt
u
= f + (T uu)
t
1
(e + u 2 )=
t
2
Du
= f + T
Dt
De
= T u q
Dt
Special Cases!
Compressible inviscid flows!
Incompressible flows!
!Stokes flow!
Not in this course!!
!Potential flows!
1
(e + u 2 )u uT + q
Computational Fluid Dynamics
Computational Fluid Dynamics
Inviscid, compressible flows!
= 0 and = 0
T = ( p + u )I + 2 D
Inviscid compressible
flows!
T = pI
D
+ u = 0
Dt
Du
= f p
Dt
De
= p u
Dt
Computational Fluid Dynamics
Computational Fluid Dynamics
U E F G
+
+
+
=0
t x y z
U=
u
v
w
E
E=
u
u 2 + p
uv
uw
( E + p ) u
F=
v
uv
v 2 + p
vw
( E + p ) v
G=
p = RT; e = c v T; h = c p T; = c p /c v
cv =
R
( 1)e
; p = ( 1)e; T =
;
1
R
vw
w 2 + p
( E + p ) u
u
uw
Incompressible flow!
Computational Fluid Dynamics
Incompressible flows:!
D
+ u = 0
Dt
Computational Fluid Dynamics
Objectives:!
The 2D Navier-Stokes Equations for incompressible, !
homogeneous flow:!
D
=0
Dt
u=0
Navier-Stokes equations (conservation of momentum)!
u = uu- P + fb + (u + T u)
t
For constant viscosity!
u + u u = -P + fb + 2u
t
u
u
u
1 P 2 u 2 u
+u +v =
+
+
t
x
y
x x 2 y 2
v
v
v
1 P 2 v 2 v
+u +v =
+
+
t
x
y
y x 2 y 2
u v
+
=0
x y
Computational Fluid Dynamics
Computational Fluid Dynamics
Pressure and Advection!
Incompressibility (conservation of mass)!
u n ds = 0
Advection:!
!Newtons law of motion: In the absence of forces,
a fluid particle will move in a straight line!
Navier-Stokes equations (conservation of momentum)!
udV = uu ndS + u ndS 1 pn x dS
S
S
S
t V
vdV = Svu ndS + Sv ndS 1 S pny dS
t V
The role of pressure:!
Needed to accelerate/decelerate a fluid particle:
Easy to use if viscous forces are small!
Needed to prevent accumulation/depletion of fluid
particles: Use if there are strong viscous forces!
Computational Fluid Dynamics
Computational Fluid Dynamics
Pressure!
Pressure!
The pressure opposes local accumulation of fluid. For
compressible flow, the pressure increases if the
density increases. For incompressible flows, the
pressure takes on whatever value necessary to
prevent local accumulation:!
Increasing pressure slows the fluid down and
decreasing pressure accelerates it!
Pressure
increases!
High Pressure!
u < 0
Low Pressure!
u > 0
Slowing down!
Pressure
decreases!
Speeding up!
Computational Fluid Dynamics
Computational Fluid Dynamics
Viscosity!
Diffusion of fluid momentum is the result of friction
between fluid particles moving at uneven speed. The
velocity of fluid particles initially moving with different
velocities will gradually become the same. Due to
friction, more and more of the fluid next to a solid wall
will move with the wall velocity.!
Computational Fluid Dynamics
Nondimensional Numbers!
u
u
u
1 P 2 u 2 u
+u +v =
+
+
t
x
y
x x 2 y 2
u,v
x, y Ut
u,v =
; x, y =
; t=
U
L
L
U 2 u
u
u
1 P U 2 u 2 u
+ u + v
=
+
+
L t
x
y
L x L2 x 2 y 2
u
u
u
L 1 P L U 2 u 2 u
+ u + v = 2
+
+
t
x
y
U L x U 2 L2 x 2 y 2
Computational Fluid Dynamics
Nondimensional Numbers!
The momentum equations are:!
u
u
u
P 1 2 u 2 u
+ u + v =
+
+
t
x
y
x Re x 2 y 2
v
v
v
P 1 2 v 2v
+ u + v =
+
+
t
x
y
y Re x 2 y 2
The continuity equation is unchanged!
u v
+
=0
x y
Nondimensional
Numbersthe Reynolds
number!
Computational Fluid Dynamics
Nondimensional Numbers!
u
u
u
L 1 P L U 2 u 2 u
+ u + v = 2
+
+
t
x
y
U L x U 2 L2 x 2 y 2
L 1 P
1 P P
=
=
2
U L x U 2 x x
L U
1
=
=
2 2
U L UL Re
where!
where!
P
P =
U 2
Re =
UL
Computational Fluid Dynamics
Outline!
Derivation of the equations governing fluid flow in
integral form!
!Conservation of Mass!
!Conservation of Momentum!
!Conservation of Energy!
Differential form!
Summary!
Incompressible flows!
Inviscid compressible flows!
También podría gustarte
- Ip-Opgaver 10.8Documento13 páginasIp-Opgaver 10.8Tarique Hasan KhanAún no hay calificaciones
- CFD Advection-Diffusion EquationDocumento8 páginasCFD Advection-Diffusion Equationneurolepsia3790Aún no hay calificaciones
- Formelsammlung Strömungslehre PDFDocumento8 páginasFormelsammlung Strömungslehre PDFmaildesantiagoAún no hay calificaciones
- 4 SnappyHexMeshDocumento35 páginas4 SnappyHexMeshJesthyn VCAún no hay calificaciones
- AC Power Control With Triac and PIC Microcontroller 16F628ADocumento6 páginasAC Power Control With Triac and PIC Microcontroller 16F628ABảo BìnhAún no hay calificaciones
- CH 01Documento6 páginasCH 01MagehartAún no hay calificaciones
- Matlab ExerciseDocumento8 páginasMatlab ExerciseabvibAún no hay calificaciones
- OFcheat SheetDocumento1 páginaOFcheat SheetmimiAún no hay calificaciones
- Numerical Methods For Parabolic Equations-IDocumento11 páginasNumerical Methods For Parabolic Equations-IPrasad BairyAún no hay calificaciones
- Batch MeshDocumento23 páginasBatch MeshjibharatAún no hay calificaciones
- J. B. Barlow, W. H. Rae, JR, A. Pope-Low Speed Wind Tunnel Testing. (1999)Documento724 páginasJ. B. Barlow, W. H. Rae, JR, A. Pope-Low Speed Wind Tunnel Testing. (1999)Dipanjan BarmanAún no hay calificaciones
- Separator SizingDocumento18 páginasSeparator SizingmkwendeAún no hay calificaciones
- 2013 Lecture 6Documento11 páginas2013 Lecture 6emir_delic2810Aún no hay calificaciones
- 2011 Lecture 1Documento7 páginas2011 Lecture 1Balaji BaluAún no hay calificaciones
- Solving Euler EquationsDocumento8 páginasSolving Euler EquationsRaul Martinez JardonAún no hay calificaciones
- Chapter 10 LectureDocumento22 páginasChapter 10 LectureBala MuruganAún no hay calificaciones
- Numerical Methods For Elliptic EquationsDocumento12 páginasNumerical Methods For Elliptic Equationsatb2215Aún no hay calificaciones
- Call MATLAB Functions - MATLAB & SimulinkDocumento5 páginasCall MATLAB Functions - MATLAB & SimulinkLuis Enrique Carmona GutierrezAún no hay calificaciones
- FM 2e SI Chap11 LectureDocumento70 páginasFM 2e SI Chap11 Lecturesyafiq hashimAún no hay calificaciones
- Assembly Program's FileDocumento30 páginasAssembly Program's FileHirdesh80% (5)
- Semaphore ExercisesDocumento18 páginasSemaphore ExercisesGheorghe Cotleţ0% (1)
- Liquid State Theory PDFDocumento79 páginasLiquid State Theory PDFAlejandro Vega100% (1)
- FFTReal Version 2.11Documento5 páginasFFTReal Version 2.11Budi PrastyoAún no hay calificaciones
- C++ Programmierung (Benjamin Buch, Wikibooks - Org)Documento257 páginasC++ Programmierung (Benjamin Buch, Wikibooks - Org)stefano rossiAún no hay calificaciones
- Simulink Collate 290321Documento109 páginasSimulink Collate 290321TiniAún no hay calificaciones
- German Hannover Kronsberg A141428Documento28 páginasGerman Hannover Kronsberg A141428Azman SamerAún no hay calificaciones
- Partial Differential Equation of Parabolic TypeDocumento15 páginasPartial Differential Equation of Parabolic TypeDionysios Zelios100% (1)
- CFD Workshop: Day Two and Three Backward Facing StepDocumento24 páginasCFD Workshop: Day Two and Three Backward Facing StepAckim MvulaAún no hay calificaciones
- Finite Volume MethodDocumento21 páginasFinite Volume MethodmekwonuAún no hay calificaciones
- G SimpleDocumento72 páginasG SimpleantoniobarbaAún no hay calificaciones
- Mathcad's Keyboard Shortcuts (Page 1)Documento2 páginasMathcad's Keyboard Shortcuts (Page 1)ajakukAún no hay calificaciones
- Implement Multiphase Chalmers Student ProjectDocumento23 páginasImplement Multiphase Chalmers Student ProjectJack WeatherittAún no hay calificaciones
- Tractor Seat DesignDocumento5 páginasTractor Seat Designsln_rjAún no hay calificaciones
- Digital Signal Processing Lab: Bachelor of Technology in Electronics and Communication EngineeringDocumento13 páginasDigital Signal Processing Lab: Bachelor of Technology in Electronics and Communication Engineeringvivek nuniaAún no hay calificaciones
- Chemcad 5: The Book of ExamplesDocumento66 páginasChemcad 5: The Book of Examplesdanan widjanarkoAún no hay calificaciones
- Thermolib UserManualDocumento334 páginasThermolib UserManualSarmad HussainAún no hay calificaciones
- Numerical Methods ProgrammingDocumento9 páginasNumerical Methods ProgrammingMudit SrivastavaAún no hay calificaciones
- Backtracking: Sum of Subsets and KnapsackDocumento36 páginasBacktracking: Sum of Subsets and KnapsackShilpa BhatiaAún no hay calificaciones
- AdvancedPython PartI PDFDocumento44 páginasAdvancedPython PartI PDFabuobidaAún no hay calificaciones
- Cs-101: Computer Systems: Introduction To Programming Using MatlabDocumento60 páginasCs-101: Computer Systems: Introduction To Programming Using MatlabnicksoldenAún no hay calificaciones
- Cubic Spline CodeDocumento3 páginasCubic Spline CodeSanjana KarpeAún no hay calificaciones
- Turbulence Y+Documento4 páginasTurbulence Y+kakadeabhiAún no hay calificaciones
- Physics of FluidsDocumento76 páginasPhysics of FluidsGeorge ShyamAún no hay calificaciones
- Formelsammlung Strömungslehre PDFDocumento8 páginasFormelsammlung Strömungslehre PDFmaildesantiagoAún no hay calificaciones
- STEALLA Tutorial - How To Build A Model in STELLADocumento11 páginasSTEALLA Tutorial - How To Build A Model in STELLAguslarAún no hay calificaciones
- OctaveDocumento122 páginasOctaveTarik ZiadAún no hay calificaciones
- Gray Simple Profile ResumeDocumento1 páginaGray Simple Profile ResumeshivaAún no hay calificaciones
- Dynamic Programming - Subset Sum ProblemDocumento4 páginasDynamic Programming - Subset Sum ProblemUttam SinghAún no hay calificaciones
- WIP January February 2013Documento52 páginasWIP January February 2013Orlando BarriosAún no hay calificaciones
- Journal hp28s 1987 08Documento40 páginasJournal hp28s 1987 08PaulKajzerAún no hay calificaciones
- RecursiveDocumento44 páginasRecursiveezzatulakmmaAún no hay calificaciones
- UK MICHELIN X MULTI Z - PRODUCT SHEET - UKversion - Mar17 v2 PDFDocumento2 páginasUK MICHELIN X MULTI Z - PRODUCT SHEET - UKversion - Mar17 v2 PDFJeanAún no hay calificaciones
- Practice - Visualization Using OpenStreetMap DataDocumento48 páginasPractice - Visualization Using OpenStreetMap Datatek bahadur katuwalAún no hay calificaciones
- Journal Pre-Proofs: Applied Thermal EngineeringDocumento40 páginasJournal Pre-Proofs: Applied Thermal EngineeringDedi AfandiAún no hay calificaciones
- A Genetic Algorithm For The Flexible Job-Shop Scheduling ProblemDocumento11 páginasA Genetic Algorithm For The Flexible Job-Shop Scheduling ProblemSilvia Adelina MateescuAún no hay calificaciones
- Mach4 Mill GCode ManualDocumento60 páginasMach4 Mill GCode Manualsahiljain_146Aún no hay calificaciones
- CPLEX User Manual PDFDocumento952 páginasCPLEX User Manual PDFUlises ArayaAún no hay calificaciones
- Blood Flow - MatlabDocumento6 páginasBlood Flow - Matlaba_minisoft2005Aún no hay calificaciones
- Autoregressive-Moving Average (ARMA) ModelsDocumento34 páginasAutoregressive-Moving Average (ARMA) Modelsflaviorochaavila100% (1)
- Exercices Corrigesd AnalysepremiereanneeuniversitaireDocumento131 páginasExercices Corrigesd AnalysepremiereanneeuniversitaireccccAún no hay calificaciones
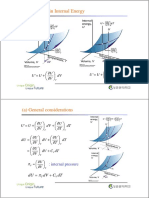
- 2.11 Changes in Internal Energy: DV V U U U DT T U U UDocumento6 páginas2.11 Changes in Internal Energy: DV V U U U DT T U U UHyeon Chang NoAún no hay calificaciones
- Conservation Laws of Fluid Motion: 2.1 Governing Equations of Fluid Flow and Heat TransferDocumento16 páginasConservation Laws of Fluid Motion: 2.1 Governing Equations of Fluid Flow and Heat TransferkantscribdAún no hay calificaciones
- Heat ExchangerDocumento29 páginasHeat ExchangeragvassAún no hay calificaciones
- Lubricated Plug Valves: Price List #3119 - Effective: 3/1/19Documento16 páginasLubricated Plug Valves: Price List #3119 - Effective: 3/1/19nurhadiAún no hay calificaciones
- Water QualityDocumento21 páginasWater QualityLakshmi NarayanAún no hay calificaciones
- Process Equipment Design by Brownell Young PDF DownloadDocumento2 páginasProcess Equipment Design by Brownell Young PDF DownloadBrylian Rizky Pratama17% (6)
- TopGas Technical InformatioDocumento34 páginasTopGas Technical Informatiosbiv28fbxhunavvd7cAún no hay calificaciones
- MembranesionoDocumento16 páginasMembranesionoمحمد ازواديAún no hay calificaciones
- WASTE DISPOSAL TREATMENT and RECYCLINGDocumento4 páginasWASTE DISPOSAL TREATMENT and RECYCLINGKimo KenoAún no hay calificaciones
- Installation ManualDocumento20 páginasInstallation ManualHasan GüleryüzAún no hay calificaciones
- Load Sensing HydraulicsDocumento12 páginasLoad Sensing HydraulicsKishore Kandikunta100% (2)
- MCQ Thermal PDFDocumento6 páginasMCQ Thermal PDFpriya dharshiniAún no hay calificaciones
- Industrial Hydraulic Valves - EUROPE PDFDocumento864 páginasIndustrial Hydraulic Valves - EUROPE PDFconimecAún no hay calificaciones
- O - Brien Julien ASCE88Documento11 páginasO - Brien Julien ASCE88NINGSIAR BRAULIO LIMA USNAYOAún no hay calificaciones
- Use of Superposition To Describe Heat TransferDocumento59 páginasUse of Superposition To Describe Heat TransferHezekiah AntonanoAún no hay calificaciones
- Coiled Tubing OperationsDocumento44 páginasCoiled Tubing OperationsPabel LemaAún no hay calificaciones
- D. Chapter 10Documento18 páginasD. Chapter 10halongvanAún no hay calificaciones
- Boiler Efficiency Calculation:-: 2. Indirect MethodDocumento3 páginasBoiler Efficiency Calculation:-: 2. Indirect MethodVISHAL GANGWARAún no hay calificaciones
- LEVAPOR Step Feed IFAS ProcessDocumento9 páginasLEVAPOR Step Feed IFAS ProcessAmit ChristianAún no hay calificaciones
- Absorption Cooling: Datasheet 07 FEB 2012Documento3 páginasAbsorption Cooling: Datasheet 07 FEB 2012mohamadAún no hay calificaciones
- Ersatzteilliste KolbenhubpumpeDocumento59 páginasErsatzteilliste KolbenhubpumpealiwaAún no hay calificaciones
- Moving Bed ProcessorsDocumento11 páginasMoving Bed ProcessorsWaqar AhmedAún no hay calificaciones
- Ashrae Ic 90.1-2016-1Documento2 páginasAshrae Ic 90.1-2016-1widiantoekoAún no hay calificaciones
- Chapter-1: Fundamental Concepts Set-B: Page 1 of 2Documento2 páginasChapter-1: Fundamental Concepts Set-B: Page 1 of 2SWAGATAM BAZAún no hay calificaciones
- Unit 2. Absorption & StrippingDocumento22 páginasUnit 2. Absorption & StrippingThabo ThaboAún no hay calificaciones
- Vertical Pumps PDFDocumento3 páginasVertical Pumps PDFsiva242245Aún no hay calificaciones
- Compilation of Brayton Cycle ProblemsDocumento1 páginaCompilation of Brayton Cycle ProblemsJohn JacobsAún no hay calificaciones
- Question Paper Code:: Nitro PDF Software 100 Portable Document Lane WonderlandDocumento3 páginasQuestion Paper Code:: Nitro PDF Software 100 Portable Document Lane WonderlandBIBIN CHIDAMBARANATHANAún no hay calificaciones
- Opi Marine DDC r2021Documento9 páginasOpi Marine DDC r2021Ozan EgemenAún no hay calificaciones
- SESSION 3 - Presentation GBDocumento37 páginasSESSION 3 - Presentation GBMarko KorenićAún no hay calificaciones