Documentos de Académico
Documentos de Profesional
Documentos de Cultura
Nonlinear Smectic Elasticity of Helical State in Cholesteric Liquid Crystals and Helimagnets
Cargado por
Danay ManzoTítulo original
Derechos de autor
Formatos disponibles
Compartir este documento
Compartir o incrustar documentos
¿Le pareció útil este documento?
¿Este contenido es inapropiado?
Denunciar este documentoCopyright:
Formatos disponibles
Nonlinear Smectic Elasticity of Helical State in Cholesteric Liquid Crystals and Helimagnets
Cargado por
Danay ManzoCopyright:
Formatos disponibles
PHYSICAL REVIEW E 83, 051701 (2011)
Nonlinear smectic elasticity of helical state in cholesteric liquid crystals and helimagnets
Leo Radzihovsky
Department of Physics, University of Colorado, Boulder, Colorado 80309, USA
T. C. Lubensky
Department of Physics, University of Pennsylvania, Philadelphia, Pennsylvania 19174, USA
(Received 3 February 2011; published 2 May 2011)
General symmetry arguments, dating back to de Gennes, dictate that at scales longer than the pitch, the
low-energy elasticity of a chiral nematic liquid crystal (cholesteric) and of a Dzyaloshinskii-Morya (DM) spiral
state in a helimagnet with negligible crystal symmetry elds (e.g., MnSi, FeGe) is identical to that of a smectic
liquid crystal, thereby inheriting its rich phenomenology. Starting with a chiral Frank free energy (exchange and
DM interactions of a helimagnet) we present a transparent derivation of the fully nonlinear Goldstone mode
elasticity, which involves an analog of the Anderson-Higgs mechanism that locks the spiral orthonormal (director
or magnetic moment) frame to the cholesteric (helical) layers. This shows explicitly the reduction of three
orientational modes of a cholesteric down to a single-phonon Goldstone mode that emerges on scales longer than
the pitch. At a harmonic level our result reduces to that derived many years ago by Lubensky and collaborators.
DOI: 10.1103/PhysRevE.83.051701 PACS number(s): 61.30.Cz
I. INTRODUCTION
Dating back to the original cholesterol liquid crystal
discovered by Reinitzer, chirality plays a central role in
modern study of liquid crystals [1]. It is equally important for
understanding helical states of noncentrosymmetric magnets
(e.g., MnSi) [24], driven by a chiral Dzyaloshinskii-Morya
(DM) interaction [5].
Among a wealth of induced phenomena [1] chirality
converts uniformnematic and ferromagnetic phases into states
in which the orientational (nematic or spin) eld twists
periodically, thereby leading to a variety of spatially modulated
phases, such as the cholesteric, two- and three-dimensional
Blue phases [1,6,7] and recently discovered Skyrmion line
crystals in the MnSi helimagnet [8]. These spontaneously
break the translational and rotational symmetries, forming
liquid-crystalline structures that are periodic along one, two, or
three dimensions. Cholesteric and helical phases are the most
ubiquitous of these, characterized by a biaxial order with
n
0
(r) = x
1
cos(q r) + x
2
sin(q r), (1)
breaking the translational symmetry along a single, sponta-
neously selected axis, x
3
z, where x
1
, x
2
, x
3
x
1
x
2
form
an orthonormal triad that is constant in the ground state.
General symmetry arguments [1] and an explicit derivation
at a harmonic level [9] applied to this spontaneously layered
helical state predict that at scales longer than the helical pitch,
the low-energy (Goldstone mode) elasticity is identical to that
of a smectic liquid crystal [1]. The three orientational degrees
of freedom dening the cholesteric at short scales thereby
reduce to a single smectic-like phonon mode, which emerges
on scales longer than the pitch. The associated enhanced
uctuations in Refs. [10,11] and disordering of these states
leads to rich phenomenology [1,12] and in the case of MnSi is
believed to be associated with the striking observation of the
non-Fermi liquid behavior [13].
Although by now quite familiar, the symmetry breaking of
the helical state falls outside the conventional G/H paradigm
[12]. Despite fully breaking the O(3) rotational symmetry
of the Euclidean group the state is characterized by only a
single U(1) Goldstone mode, , the spirals phase related
to the smectic phonon u = /q
0
. As we will show below,
the absence of the two additional orientational Goldstone
modes is best understood as a mathematical equivalent of the
Anderson-Higgs mechanism [1,12,14] that gaps them out.
In this paper we explicitly show how this single low-
energy helical mode emerges and derive its nonlinear smectic
energy functional, expected from the underlying rotational
symmetry [1,12]. Because the latter leads to harmonic phonon
uctuations that diverge in three dimensions and below, the
inclusion of nonlinearities is essential for a sensible and self-
consistent description, as anticipated long ago by Lubensky
et al. [9] and Grinstein and Pelcovits [10] (see also Ref. [11]).
With the neglect of crystalline anisotropy all of our cholesteric
results apply equally well to the description of the low-energy
bosonic modes of the helical state in the DM helimagnets such
as MnSi [24].
II. FROM A CHOLESTERIC TO A SMECTIC
The helical texture n
0
(r) minimizes the chiral Frank-Oseen
free-energy density of a chiral nematic [1,12,15]
H =
1
2
K
s
( n)
2
+
1
2
K
b
( n n)
2
,
+
1
2
K
t
( n n +q
0
)
2
, (2a)
=
1
2
K
(
i
n
j
)
2
+2q
0
n n +q
2
0
, (2b)
where in the second form we focused on the isotropic limit,
K
s
= K
b
= K
t
K, and dropped the total derivative saddle-
splay (Gaussian curvature) contribution, which reduces the
Hamiltonian to that of DM ferromagnet in the absence of
crystal symmetry-breaking elds [3,5]. Within this approxi-
mation the space-spin (r n) coupling enters only through
the chiral (second) term, with the elastic (rst) piece explicitly
exhibiting independent rotational invariances of space r and
of the director n (spin in the MnSi magnet context).
051701-1 1539-3755/2011/83(5)/051701(3) 2011 American Physical Society
LEO RADZIHOVSKY AND T. C. LUBENSKY PHYSICAL REVIEW E 83, 051701 (2011)
We now look at long-wavelength, low-energy Goldstone
mode excitations about the helical ground state n
0
(r). A
general state is described by
n(r) = e
1
(r) cos[q r +(r)] + e
2
(r) sin[q r +(r)], (3)
where e
1
(r), e
2
(r), e
3
(r) e
1
(r) e
2
(r) now constitute a spa-
tially dependent orthonormal frame, describing the orientation
of the local director (spin) helical plane, that is, independent
of the helical axis set by q r +(r) = const. The phase
(r) = q
0
u(r) of the chiral helix also denes the phonon
eld u(r) of the helical layers, which on scales longer than
the pitch a = 2/q
0
dene the smectic-like displacement of
these helical phase fronts. Thus, altogether on the intermediate
scales there are three independent orientational degrees of
freedom, (r) and e
3
(r). The azimuthal angle (r), dening
the orientation of the e
1,2
around e
3
, is redundant to (r),
as it can be eliminated in favor of it via a local gauge-like
transformation on e
1,2
. Although naively, the low-energy coset
space is isomorphic to (S
1
S
2
)/Z
2
= RP
3
, as we will see
below, only a single Goldstone mode (r) will survive this
helical symmetry breaking.
Substituting n(r) from Eq. (3) into the free energy of the
chiral nematic (helimagnet), Eq. (2b), and using
i
n
j
= (q
i
+
i
)[ e
1j
sin(q r +) + e
2j
cos(q r +)]
+
i
e
1j
cos(q r +) +
i
e
2j
sin(q r +), (4)
together with
i
e
1j
= a
i
e
2j
+c
1i
e
3j
, (5a)
i
e
2j
= a
i
e
2j
+c
2i
e
3j
, (5b)
and gauge eld spin connections
a
i
= e
2
i
e
1
, (6a)
c
1i
= e
1
i
e
3
, (6b)
c
2i
= e
2
i
e
3
, (6c)
we nd
H =
K
2
{(a
i
e
2j
+c
i
e
3j
) cos(q r +) +(a
i
e
1j
+c
2i
e
3j
) sin(q r +) +(q
i
+
i
)[ e
1j
sin(q r +)
+ e
2j
cos(q r +)] +q
0
( e
2i
e
3j
e
3i
e
2j
) cos(q r +) +q
0
( e
3i
e
1j
e
1i
e
3j
) sin(q r +)}
2
, (7a)
=
K
2
( +a +q q
0
e
3
)
2
+
K
4
(c
1
+q
0
e
2
)
2
+
K
4
(c
2
q
0
e
1
)
2
. (7b)
In obtaining Eq. (7b), we dropped the constant and
oscillatory parts, which average away upon spatial integration.
We rst note that the requirement of well-dened helical
phase fronts, i.e., the absence of dislocations and disclinations
in the layer structure, can be enforced by the compatibility
condition a = 0, consistent with the Mermin-Ho relation
[16]. This allows us to take a = and thereby shift (gauge)
away (r) in favor of (r), according to (r) +(r) (r).
Without loss of generality, we next take q = q
0
z with z
dening the orientation of the helical axis in the laboratory
coordinate system x, y, z. The long-wavelength free-energy
density, reexpressed in terms of the smectic-like phonon eld
u(r) and the local nematic helical frame orientation e
3
, then
reduces to
H =
Kq
2
0
2
(u + e
3
z)
2
+
K
4
c
2
1
+c
2
2
+
Kq
0
2
(c
1
e
2
c
2
e
1
). (8)
Clearly the rst term above accounts for the energetic cost
of the deviation of the local nematic frame e
3
from the
local orientation of the helical layers. A minimization of
this term [or equivalently at long wavelengths, in a statistical
mechanical treatment integrating out the independent e
3
(r)
degree of freedom], at low energies locks the orientations of
the cholesteric layers and the nematic frame. In a perturbative
treatment this leads to the expected relation
u e
3
, (9)
which is an example of a Higgs-like mechanism (akin to
thermotropic smectic liquid crystals [1,12,17]), that at long
scales effectively gaps out the orientational Goldstone modes.
The exact minimization over the unit vector e
3
(r) can also
be carried out using a Lagrange multiplier to impose the
constraint e
3
e
3
= 1. Minimization over e
3
(r) gives
u + e
3
z = e
3
, (10)
with the solution
+1 =
(u z)
2
=
1 2u
zz
, (11a)
e
3
= ( z u)/
1 2u
zz
, (11b)
where
u
zz
=
z
u
1
2
(u)
2
(12)
is the standard fully nonlinear smectic strain tensor, which
encodes the full rotational invariance of the helical state [10,
12]. Using Eqs. (1) to eliminate and e
3
(r) in favor u
zz
(valid
at long scales), we nd
H =
Kq
2
0
2
(
1 2u
zz
1)
2
+
K
4
[( e
1
i
e
3
)( e
1
i
e
3
)
+( e
2
i
e
3
)( e
2
i
e
3
)] +
Kq
0
2
e
1i
e
2j
(
i
j
u
j
i
u),
(13a)
B
2
u
2
zz
+
K
2
(
i
j
u)
2
, (13b)
B
2
z
u
1
2
(u)
2
2
+
K
2
(
2
u)
2
, (13c)
051701-2
NONLINEAR SMECTIC ELASTICITY OF HELICAL STATE . . . PHYSICAL REVIEW E 83, 051701 (2011)
where to obtain our main result, Eq. (13c), we used the
condition of well-dened helical layers with no dislocations
in u(r), i.e., a single-valued phase eld (r), neglected the
boundary terms, expanded to lowest order in the nonlinear
strain tensor u
zz
, and dened the compressional and bending
elastic moduli
B = Kq
2
0
, K = K/2. (14)
III. SUMMARY AND CONCLUSIONS
Thus, as advertised, we have demonstrated that on scales
longer than the helical pitch 2/q
0
, the low-energy deforma-
tions (Goldstone modes) of the helical state are characterized
by a fully rotationally invariant, nonlinear smectic elastic
theory [1,10,12]. The latter can be derived by spontaneously
ordering the density (r) of the isotropic uid into a one-
dimensional periodically modulated state (smectic), character-
ized by (r) =
0
+
q
cos[(q r q
0
u)] [10]. Alternatively,
the above nonlinear compressional form [rst term in (13a)]
emerges directly from the de Genness gauge theory of the
smectic [1], after condensing
q
= |
q
|e
i(r)
to give
H
sm
=
1
2
B( n)
2
+
1
2
K( n)
2
, (15)
and then minimizing over the unit director n(r) as in (10)(12).
We note that as required, Hin Eq. (13a) is a function of the
fully nonlinear strain u
zz
as it must to preserve full rotational
invariance. Furthermore, it is a nonlinear function of this strain,
which reduces to the familiar harmonic nonlinear form [10]
in Eq. (13c) only for small u
zz
. It is worth observing that
through the introduction of the phase eld = z +u, this
nonlinear in u
zz
term in (13a) can be written as (|| 1)
2
.
This formhas been used in recent analyses of various nonlinear
properties of smectics [18].
Our result in Eq. (13c) then in turn implies that the helical
state inherits all the novel nonlinear elastic effects previously
discovered in the context of conventional, thermotropic, and
lyotropic smectic liquid crystals and other spontaneously
layered states that emerge from an isotropic state. These
include thermal uctuations [10,11,19] and heterogeneous
[20,21] anomalous elasticity effects, the undulation instability
[22], and many others.
One important distinction from a conventional smectic,
however, is the underlying chirality of the helical layered state.
Although as in the chiral smectic the effective Anderson-Higgs
mechanism expels the expression of chirality (e.g., twist)
inside the helical state (as the magnetic ux density [twist of the
vector potential] is expelled fromthe Meissner state) [1,12,17],
inclusion of the chiral terms [encoded in the departure from
the a = 0 condition used to get to (8)] is essential to
understanding the topological defects and melting of the
helical state [23].
We acknowledge nancial support through the NSF DMR-
1001240, MRSEC DMR-0820579 (LR) and NSF-DMR-
0804900 (TL).
[1] P. deGennes and J. Prost, The Physics of Liquid Crystals
(Clarendon Press, Oxford, 1993).
[2] Y. Ishikawa et al., Solid State Commun. 19, 525 (1976).
[3] P. Bak and M. H. Jensen, J. Phys. C (Solid State) 13, L88
(1980).
[4] D. Belitz, T. R. Kirkpatrick, and A. Rosch, Phys. Rev. B 73,
054431 (2006).
[5] I. E. Dzyaloshinskii, Sov. Phys. JETP 19, 960 (1964); T. Moriya,
Phys. Rev. 120, 91 (1960).
[6] R. M. Hornreich, M. Kugler, and S. Shtrikman, Phys. Rev. Lett.
54, 2099 (1985).
[7] D. C. Wright and N. D. Mermin, Rev. Mod. Phys. 61, 385 (1989).
[8] S. Muehlbauer et al., Science 323, 915 (2009).
[9] T. C. Lubensky, Phys. Rev. A 6, 452 (1972); Phys. Rev. Lett. 29,
206 (1972).
[10] G. Grinstein and R. A. Pelcovits, Phys. Rev. Lett. 47, 856 (1981).
[11] L. Golubovic and Z. G. Wang, Phys. Rev. Lett. 69, 2535 (1992).
[12] P. M. Chaikin and T. C. Lubensky, Principles of Condensed
Matter Physics (Cambridge University Press, Cambridge UK,
1995).
[13] C. Peiderer et al., Nature (London) 414, 427 (2001).
[14] T. C. Lubensky, S. G. Dunn, and J. Isaacson, Phys. Rev. Lett.
47, 1609 (1981).
[15] This is a valid description on intermediate and longer scales,
where the magnitude of the nematic order parameter Q can be
taken to be a constant.
[16] N. D. Mermin and T. L. Ho, Phys. Rev. Lett. 36, 594 (1976).
[17] P. G. deGennes, Solid State Commun. 10, 753 (1972).
[18] R. D. Kamien and C. D. Santangelo, Geometriae Dedicata 120,
229 (2006); C. D. Santangelo and R. D. Kamien, Proc. R. Soc.
London A 461, 2911 (2005).
[19] J. Als-Nielsen, J. D. Litster, R. J. Birgeneau, M. Kaplan, C. R.
Sanya, A. Lindegaard-Andersen, and S. Mathiesen, Phys. Rev.
B 22, 312 (1980).
[20] L. Radzihovsky and J. Toner, Phys. Rev. Lett. 78, 4414 (1997).
[21] L. Radzihovsky and J. Toner, Phys. Rev. B 60, 206
(1999).
[22] N. A. Clark and R. B. Meyer, Appl. Phys. Lett. 22, 493
(1973).
[23] L. Radzihovsky and J. Toner (unpublished).
051701-3
También podría gustarte
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDe EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryCalificación: 3.5 de 5 estrellas3.5/5 (231)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)De EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Calificación: 4.5 de 5 estrellas4.5/5 (120)
- Grit: The Power of Passion and PerseveranceDe EverandGrit: The Power of Passion and PerseveranceCalificación: 4 de 5 estrellas4/5 (588)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDe EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaCalificación: 4.5 de 5 estrellas4.5/5 (266)
- The Little Book of Hygge: Danish Secrets to Happy LivingDe EverandThe Little Book of Hygge: Danish Secrets to Happy LivingCalificación: 3.5 de 5 estrellas3.5/5 (399)
- Never Split the Difference: Negotiating As If Your Life Depended On ItDe EverandNever Split the Difference: Negotiating As If Your Life Depended On ItCalificación: 4.5 de 5 estrellas4.5/5 (838)
- Shoe Dog: A Memoir by the Creator of NikeDe EverandShoe Dog: A Memoir by the Creator of NikeCalificación: 4.5 de 5 estrellas4.5/5 (537)
- The Emperor of All Maladies: A Biography of CancerDe EverandThe Emperor of All Maladies: A Biography of CancerCalificación: 4.5 de 5 estrellas4.5/5 (271)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDe EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeCalificación: 4 de 5 estrellas4/5 (5794)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDe EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyCalificación: 3.5 de 5 estrellas3.5/5 (2259)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDe EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersCalificación: 4.5 de 5 estrellas4.5/5 (344)
- Rise of ISIS: A Threat We Can't IgnoreDe EverandRise of ISIS: A Threat We Can't IgnoreCalificación: 3.5 de 5 estrellas3.5/5 (137)
- Team of Rivals: The Political Genius of Abraham LincolnDe EverandTeam of Rivals: The Political Genius of Abraham LincolnCalificación: 4.5 de 5 estrellas4.5/5 (234)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDe EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreCalificación: 4 de 5 estrellas4/5 (1090)
- Joy To The WorldDocumento4 páginasJoy To The WorldFrancois du ToitAún no hay calificaciones
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDe EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceCalificación: 4 de 5 estrellas4/5 (895)
- Her Body and Other Parties: StoriesDe EverandHer Body and Other Parties: StoriesCalificación: 4 de 5 estrellas4/5 (821)
- The Perks of Being a WallflowerDe EverandThe Perks of Being a WallflowerCalificación: 4.5 de 5 estrellas4.5/5 (2101)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDe EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureCalificación: 4.5 de 5 estrellas4.5/5 (474)
- NaturalDocumento23 páginasNaturalthenjhomebuyer100% (1)
- The Unwinding: An Inner History of the New AmericaDe EverandThe Unwinding: An Inner History of the New AmericaCalificación: 4 de 5 estrellas4/5 (45)
- Significance of Rosary in SikhismDocumento9 páginasSignificance of Rosary in SikhismhansrabAún no hay calificaciones
- The Yellow House: A Memoir (2019 National Book Award Winner)De EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Calificación: 4 de 5 estrellas4/5 (98)
- On Fire: The (Burning) Case for a Green New DealDe EverandOn Fire: The (Burning) Case for a Green New DealCalificación: 4 de 5 estrellas4/5 (73)
- Bare AnalysisDocumento22 páginasBare AnalysisBrendan Egan100% (2)
- Zealot by Reza Aslan, ExcerptDocumento19 páginasZealot by Reza Aslan, ExcerptRandom House Publishing Group86% (7)
- Plato's Theory of ImitationDocumento2 páginasPlato's Theory of ImitationAnkitRoy82% (17)
- Egyptian Origin of Greek MagicDocumento8 páginasEgyptian Origin of Greek MagicAdrian StanAún no hay calificaciones
- Nick Herbert Dossier: Ong's HatDocumento4 páginasNick Herbert Dossier: Ong's HatJoseph Matheny0% (1)
- MCQ On Testing of Hypothesis 1111Documento7 páginasMCQ On Testing of Hypothesis 1111nns2770100% (1)
- 2) - William Grabe PDFDocumento11 páginas2) - William Grabe PDFJalal Zbirat67% (3)
- Solucionario Tipler 6 EdicionDocumento6 páginasSolucionario Tipler 6 EdicionLubeck Abraham Huaman Ponce25% (4)
- ChaucerDocumento22 páginasChaucerZeeshanAhmad100% (1)
- Organizational Development InterventionsDocumento57 páginasOrganizational Development InterventionsAmr YousefAún no hay calificaciones
- PYPX PlannerDocumento4 páginasPYPX PlannerhgendiAún no hay calificaciones
- Ultrathin Electrospun PANI Nanofibers For Neuronal Tissue EngineeringDocumento10 páginasUltrathin Electrospun PANI Nanofibers For Neuronal Tissue EngineeringDanay ManzoAún no hay calificaciones
- Electrical Properties of Electrospun Fibers of PANI-PMMA CompositesDocumento7 páginasElectrical Properties of Electrospun Fibers of PANI-PMMA CompositesDanay ManzoAún no hay calificaciones
- Journal of NanomaterialsDocumento5 páginasJournal of NanomaterialsDanay ManzoAún no hay calificaciones
- Polymers 09 00453Documento12 páginasPolymers 09 00453Danay ManzoAún no hay calificaciones
- Ultrathin Electrospun PANI Nanofibers For Neuronal Tissue EngineeringDocumento10 páginasUltrathin Electrospun PANI Nanofibers For Neuronal Tissue EngineeringDanay ManzoAún no hay calificaciones
- Electrospinning Nanofibers of PANI/PMMA BlendsDocumento6 páginasElectrospinning Nanofibers of PANI/PMMA BlendsDanay ManzoAún no hay calificaciones
- Eletrospunnanomatirials For Ultrasensitive SensorsDocumento12 páginasEletrospunnanomatirials For Ultrasensitive SensorsDanay ManzoAún no hay calificaciones
- Development and Characterization of Gas Sensors Using Thin Films of Polyaniline As Active LayerDocumento9 páginasDevelopment and Characterization of Gas Sensors Using Thin Films of Polyaniline As Active LayerDanay ManzoAún no hay calificaciones
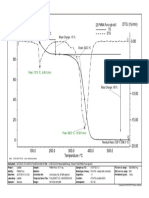
- TG /% DTG / (%/min) : Onset: 130.3 °C Mass Change: - 15 %Documento1 páginaTG /% DTG / (%/min) : Onset: 130.3 °C Mass Change: - 15 %Danay ManzoAún no hay calificaciones
- Ultrathin Electrospun PANI Nanofibers For Neuronal Tissue EngineeringDocumento10 páginasUltrathin Electrospun PANI Nanofibers For Neuronal Tissue EngineeringDanay ManzoAún no hay calificaciones
- Toward Innovations of Gas Sensor TechnologyDocumento13 páginasToward Innovations of Gas Sensor TechnologyDanay ManzoAún no hay calificaciones
- ApartaDocumento1 páginaApartaDanay ManzoAún no hay calificaciones
- Nano Porosity in GaSb Induced by SHIIDocumento5 páginasNano Porosity in GaSb Induced by SHIIDanay ManzoAún no hay calificaciones
- Development of Porous Structures in GaSb by Ion IrradiationDocumento4 páginasDevelopment of Porous Structures in GaSb by Ion IrradiationDanay ManzoAún no hay calificaciones
- PhysRevE 67 061709Documento11 páginasPhysRevE 67 061709Danay ManzoAún no hay calificaciones
- Coulombic Charge Ice: Phys. Rev. 102 1008 1956Documento15 páginasCoulombic Charge Ice: Phys. Rev. 102 1008 1956Danay ManzoAún no hay calificaciones
- Alexis Karpouzos - The Mathematics of ImaginationDocumento4 páginasAlexis Karpouzos - The Mathematics of ImaginationAlexis karpouzos100% (2)
- Seminar Slides HRM Application Blanks Group 1Documento13 páginasSeminar Slides HRM Application Blanks Group 1navin9849Aún no hay calificaciones
- Theoretical Framework For Conflict ResolDocumento9 páginasTheoretical Framework For Conflict ResolAAMNA AHMEDAún no hay calificaciones
- Local Networks: Prepared By: Propogo, Kenneth M. Burce, Mary Jane PDocumento20 páginasLocal Networks: Prepared By: Propogo, Kenneth M. Burce, Mary Jane PPatricia Nicole Doctolero CaasiAún no hay calificaciones
- A Human Rights Approach To Prison Management: Handbook For Prison StaffDocumento169 páginasA Human Rights Approach To Prison Management: Handbook For Prison StaffAldo PutraAún no hay calificaciones
- The Downfall of The Protagonist in Dr. FaustusDocumento13 páginasThe Downfall of The Protagonist in Dr. FaustusRaef Sobh AzabAún no hay calificaciones
- The Anthropocene Review 1 2Documento95 páginasThe Anthropocene Review 1 2bordigaAún no hay calificaciones
- 50 Interview QuestionsDocumento5 páginas50 Interview QuestionsСтрахиња АрсићAún no hay calificaciones
- Fear and Foresight PRTDocumento4 páginasFear and Foresight PRTCarrieAún no hay calificaciones
- International Journal of Children's SpiritualityDocumento15 páginasInternational Journal of Children's SpiritualityМаксим КоденевAún no hay calificaciones
- MS AldayDocumento41 páginasMS AldayRogelio Lupian ElemiaAún no hay calificaciones
- PepsiCo Mission Statement Has Been Worded by CEO Indra Nooyi AsDocumento2 páginasPepsiCo Mission Statement Has Been Worded by CEO Indra Nooyi AsSyarifah Rifka AlydrusAún no hay calificaciones
- NCP 31Documento14 páginasNCP 31Arunashish MazumdarAún no hay calificaciones
- Vector Calculus NotesDocumento10 páginasVector Calculus NotesNarendra SinghAún no hay calificaciones
- Master of Education (Instructional Technology)Documento2 páginasMaster of Education (Instructional Technology)Abel Jason PatrickAún no hay calificaciones
- Chapter 1-Law and Legal ReasoningDocumento9 páginasChapter 1-Law and Legal Reasoningdimitra triantosAún no hay calificaciones
- EBS The Effects of The Fall of ManDocumento12 páginasEBS The Effects of The Fall of ManAlbert A. MaglasangAún no hay calificaciones