Documentos de Académico
Documentos de Profesional
Documentos de Cultura
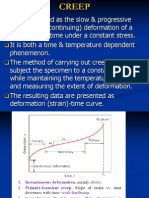
Creep
Cargado por
V DhinakaranDescripción original:
Derechos de autor
Formatos disponibles
Compartir este documento
Compartir o incrustar documentos
¿Le pareció útil este documento?
¿Este contenido es inapropiado?
Denunciar este documentoCopyright:
Formatos disponibles
Creep
Cargado por
V DhinakaranCopyright:
Formatos disponibles
KL Murty MSE 450 page 1
Creep and Stress Rupture :
Ch. 13 : 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 15(optional)
Definition of Creep and Creep Curve : (13-3)
def. Creep is the time-dependent plastic strain at constant stress and temperature
Creep curve : Fig. 13-4
steady-state creep-rate (D
s
or simply D
) : Temperature and Stress Dependencies
- Fig. 13-6 Fig. 13-8
- total creep curve : =
o
+
p
+
s
o
= instantaneous strain at loading (elastic, anelastic and plastic)
s
= steady-state creep strain (constant-rate viscous creep ) = D
s
t
p
= primary or transient creep : Andrade- flow (or 1/3 rd law) : t
1/3
primary or transient creep :
Andrade- flow (or 1/3 rd law) :
p
= t
1/3
problem as t 0
Garofalo / Dorn Equation :
p
=
t
(1 - e
-rt
) , r is related to
s
i
>
>
(~1-20)
Dorn Both primary and steady-state follow similar kinetics
- temperature compensated time ( = t e
- Q
c
/RT
)
- single universal curve with t replaced by
or
s
t
Or, creep strain
-
o
=
t
(1 - e
-
D
s
t
) + D
s
t see Sherby-Dorn (Al), Murty (Zr)
Sherby-Dorn -parameter
Creep curves for Al at Sherby & Dorn (1956) A single curve demonstrating the
(3,000 psi) and at three different temperatures validity of -parameter
KL Murty MSE 450 page 2
s
t
Creep data in Zircaloy at varied temperatures (F)
and stresses (ksi) fall into a single curve
demonstrating the validity of Dorn equation
(Murty et al 1976)
(K. L. Murty, M.S. Thesis, 1967)
Zener-Holloman :
RT Q
e Z
/
D =
Stress Rupture Test : (13-4) vs t
r
Representation of engineering creep / rupture data (13-12, 13-13)
- Figs. 13-17, 13-18
Sherby-Dorn Parameter : P
S-D
= t e
-Q/RT
Larson-Miller Parameter : P
L-M
= T (log t + C) Fig. 13-19-21
Manson-Haferd Parameter : P
M-H
=
T - T
a
log t - log t
a
--- these parameters are for a given stress and are functions of (Fig. 13-20) ---
Monkman-Grant : =
r s
t C
Eq. 13-24
Demonstration of Monkman-Grant
Relationship in Cu (Feltham and Meakin 1959)
KL Murty MSE 450 page 3
Creep Under Multiaxial Loading
(text 14-14)
Use Levy-Mises Equations in plasticity
eff
=
1
2
(
1
-
2
)
2
+ (
2
-
3
)
2
+ (
3
-
1
)
2
and d
1
=
d
eff
eff
[
1
-
1
2
(
2
+
3
) ] ,
since creep is plastic deformation 1/2 appears as in plasticity.
Similarly, d
2
and d
3
.
Dividing by dt, get the corresponding creep-rates,
D
1
=
eff
eff
[
1
-
1
2
(
2
+
3
) ], etc.
One first determines the uniaxial creep-rate equation,
D
s
= A
n
e
-Q/RT
and assume the same for effective strain-rate : D
eff
= A
n
eff
e
-Q/RT
so that
1
= A
n-1
eff
e
-Q/RT
[
1
-
1
2
(
2
+
3
)] etc.
Stress Relaxation
As noted in section 8-11, the stress relaxation occurs when the deformation is held
constant such as in bolt in flange where the constraint is that the total length of the
system is fixed.
t
=
E
+
creep
= const. Here,
E
=
E
.
Thus
d
t
dt
= 0 =
1
E
d
dt
+ D
s
Or,
d
dt
= - E D
s
= - E A
n
@ fixed T
Integration from o to t gives,
f
d
n
= - E A
o
t
dt = - E A t
) 1 /( 1 1
] ) 1 ( 1 [
) (
+
=
n n
o
o
final
t n AE
t or
5000 4000 3000 2000 1000 0
20
40
60
80
100
Data from "HW #8-8"
time, hr
KL Murty MSE 450 page 4
Deformation / Creep Mechanisms :
Introduction - structural changes (13-5)
- Slip (difficult to observe slip lines / folds etc are usually noted)
Subgrains
GBS
- excess (deformation induced) vacancies
Two important relationships :
Orowan equation : D =bv and Taylor equation : =
2
G
2
b
2
Thermally Activated Dislocation Glide (at low T and/or high strain-rates)
D
= A e
B
e
-
Q
i
/RT
where Q
i
is the activation energy for the underlying mechanisms
Peierls mechanism (bcc metals) Intersection mechanism (fcc and hcp metals)
Dislocation creep - (lattice) diffusion controlled glide and climb
Diffusion creep - (viscous creep mechanisms mainly due to point defects) - at low
stresses and high temperatures
Grain-Boundary Sliding - (GBS) - intermediate stresses in small grained
materials and ceramics (where matrix deformation is difficult)
Many different mechanisms may contribute and the total strain-rate :
parallel mechanism series mechanisms
(fastest controls / dominates) (slower controls / dominates)
D
=
i
D
i
D
=
1
1
i
Slip following creep deformation in -iron
Uncrept specimen Crept at 5500 psi to 21.5% strain
(K.L. Murty, MS thesis, Cornell University, 1967)
KL Murty MSE 450 page 5
Dislocation Creep :
Pure Metals / Class-M alloys: Experiments :
D
= A
n
e
-Q
c
/RT
,n ! 5, Q
c
! Q
L
(Q
D
)
(edge ) glide - climb model Weertman-Climb model (Weertman Pill-Box Model)
sequential processes
L
= average distance a dislocation glides
t
g
= time for glide motion
h = average distance a dislocation climbs
t
c
= time for climb
FR L
h
Lomer-Cottrell
Barrier
= strain during glide-climb event =
g
+
c
!
g
= b L
t = time of glide-climb event = t
g
+ t
c
! t
c
=
h
v
c
, v
c
= climb velocity
D
=
t
=
b L
h/v
c
= b (
L
h
) v
c
where v
c
C
v
e
-E
m
/kT
, E
m
= activation energy for vacancy migration
Here, C
v
= C
+
v
- C
-
v
= C
o
v
e
V/kT
- C
o
v
e
-
V/kT
= C
o
v
2 Sinh(
V
kT
)
D
= b (
L
h
) v
c
= b (
L
h
) C
o
v
e
-E
m
/kT
2 Sinh(
V
kT
)
At low stresses, Sinh() ! so that
D
= A
1
b (
L
h
) C
o
v
e
-E
m
/kT
V
kT
D
= A
1
b (
L
h
) D
L
V
kT
! A
2
(
L
h
) D
L
Or D A
3
= D natural creep-law
Weertman:
L
h
1.5
, D
= A
4.5
D as
experimentally observed in Al
In general D
= A(T)
n
Power-law
- n is the stress exponent
{f(xal structure, )}
Garofalo Eqn.
D
= A D (sinhB)
n
also known as Nortons Equation
(n is Norton index)
At high stresses ( " 10
-3
E), Sinh(x) ! e
x
, D
= A
H
e
B
D (Power-law breakdown)
KL Murty MSE 450 page 6
Experimental Observations - Dislocation Creep
Fig. 13-13 (Dieter) (Sherby)
What happens if we keep decreasing the stress, say to a level at and below the
FR
?
As is decreased reach a point when #
FR
,
dislocation density would become constant (independent of ): D
- viscous creep known as Harper-Dorn creep
Harper-Dorn creep occurs at
E
# b
! 10
-5
,
o
! 10
6
cm
-2
H-D creep is observed in large grained
materials (metals, ceramics, etc.)
D
HD
= A
HD
D
L
ln
ln
2
1
Characteristics of Climb Creep (Class-M) :
large primary creep regions
subgrain formation (
1
)
dislocation density
2
independent of grain size
KL Murty MSE 450 page 7
Effects of Alloying : (class-A)
Solid-solution - decreases rate of glide A glide controlled creep although
annihilation due to climb still occurs (micro-creep / viscous glide creep)
viscous glide controlled creep : (decreased creep-rates)
D
g
= A
g
D
s
3
, D
s
is solute diffusion
little or no primary creep
no subgrain formation
2
grain-size independent
5
3
1
1
class-M
class-A
log(stress)
(Al)
(Al-3Mg)
At low stresses (for large grain sizes), Harper-Dorn creep dominates
what happens as grain size becomes small
As grain-size decreases (and at low stresses) diffusion creep due to point defects
becomes important : (due to migration of vacancies from tensile boundaries to
compressive boundaries)
Nabarro-Herring Creep (diffusion through the lattice) : D
NH
= A
NH
D
L
d
2
Coble Creep (diffusion through grain-boundaries) : D
Co
= A
Co
D
b
d
3
Nabarro-Herring Creep vs Coble Creep :
Coble creep for small grain sizes and at
low temperature
NH creep for larger grain sizes and at
high temperatures
at very large grain sizes, Harper-Dorn
creep dominates
3
2
1
1
log (grain-size)
N-H
Coble
Harper-Dorn
At small grain-sizes, GBS dominates at intermediate stresses and temperatures :
D
GBS
= A
GBS
D
b
2
d
2
superplasticity
KL Murty MSE 450 page 8
Effect of dispersoids : Dispersion Strengthening / Precipitate Hardening
- recall Orowan Bowing
at high temperatures, climb of dislocation loops around the precipitates
controls creep D
ppt
= A
ppt
D
8 - 20
Rules for Increasing Creep Resistance
Large Grain Size
(directionally solidified superalloys)
Low Stacking Fault Energy
(Cu vs Cu-Al alloys)
Solid Solution Alloying
(Al vs Al-Mg alloys)
Dispersion Strengthening
(Ni vs TD-Ni)
Formability Improvement
Small (stable) Equiaxed Grain Size
(superplasticity)
Strengthen Matrix
(i.e., increase GBS - ceramics)
Stoichiometry
(especially Ceramics)
KL Murty MSE 450 page 9
Summary of Creep Mechanisms: D
t
= D
N-H
+ D
Coble
+ D
H-D
+D
GBS
+
1
1 1
+
g c
Dorn Equation :
n
E
A
DEb
kT
=
Mechanism D n A
Climb of edge dislocations D
L
5 6x10
7
(Pure Metals and class-M alloys) (n function of Xal structure & )*
Low-temperature climb D
7 2x10
8
Viscous glide (Class-I alloys - microcreep) D
s
3 6
Nabarro-Herring D
L
1 14 (
b
d
)
2
Coble D
b
1 100 (
b
d
)
3
Harper-Dorn D
L
1 3x10
-10
GBS (superplasticity) D
b
2 200 (
b
d
)
2
D
L
= lattice diffusivity; D
s
= solute diffusivity; D
= core diffusivity;
D
b
= Grain-Boundary Diffusivity; b = Burgers vector; d = grain size;
= subgrain size = 10
Gb
and =
2
G
2
b
2
where G is the shear modulus
*
n increases with decreasing (stacking-fault energy)
KL Murty MSE 450 page 10
Deformation Mechanism Maps
Visual picture of the domains (, T) where various mechanisms dominate
Ashby-Map
Lead pipes on a 75-year-old building in southern England
The creep-induced curvature of these pipes is typical
of Victorian lead water piping. (Frost and Ashby)
Other examples :
W filament (light bulbs)
turbind blade {Ni-based alloy DS by Ni
3
(Ti,Al)}
KL Murty MSE 450 page 11
WEERTMAN PILL-
BOX MODEL
Pure Metals - Glide faster
Climb-controlled creep (n!5)
t
=
1
c
+
1
g
1
Alloys - Glide slower
Glide-controlled creep (n!3)
Solid Solution Alloys
Pb 9Sn
d = 0.25 mm
I
II
III
IV
ln
(
k T
D b
)
ln
(
)
10
-6
10
-5
10
-4
10
-3
10
-2
10
-16
10
-14
10
-12
10
-10
10
-8
10
-6
Creep Transitions for Alloy Class Murty and Turlik (1992)
También podría gustarte
- Strength of Materials FinalDocumento11 páginasStrength of Materials FinalRenel Alucilja100% (6)
- Introduction To Tribology: Lesson 8Documento30 páginasIntroduction To Tribology: Lesson 8V Dhinakaran100% (2)
- Geh 6676 Power System Stabilizer For EX2100 Excitation ControlDocumento48 páginasGeh 6676 Power System Stabilizer For EX2100 Excitation ControlSupolAún no hay calificaciones
- RKB Proper Lubricant Selection For Rolling Bearing Applications PDFDocumento8 páginasRKB Proper Lubricant Selection For Rolling Bearing Applications PDFJako MishyAún no hay calificaciones
- Thermal StressDocumento5 páginasThermal StressmdmarufurAún no hay calificaciones
- Steam TurbineDocumento76 páginasSteam TurbineV DhinakaranAún no hay calificaciones
- PPAP ChecklistDocumento4 páginasPPAP ChecklistHirbod HirmandAún no hay calificaciones
- PumpDocumento116 páginasPumpV Dhinakaran67% (3)
- Creep & FatigueDocumento20 páginasCreep & Fatiguegaspardo123Aún no hay calificaciones
- ETBX Stress-Life Fatigue Analysis ModuleDocumento11 páginasETBX Stress-Life Fatigue Analysis ModuleLeonardo Da Rosa Gonçalves100% (1)
- Principles of Fracture MechanicsDocumento49 páginasPrinciples of Fracture MechanicsgodzillafoodAún no hay calificaciones
- Optimization Design of The U-Shaped Metal BellowsDocumento5 páginasOptimization Design of The U-Shaped Metal BellowsdaymonAún no hay calificaciones
- AS 3600-2018 RC-PN Example 001Documento4 páginasAS 3600-2018 RC-PN Example 001Aashu chaudharyAún no hay calificaciones
- 2 Chemical Reactor To Reactor Safety PDFDocumento41 páginas2 Chemical Reactor To Reactor Safety PDFV DhinakaranAún no hay calificaciones
- 03 PT12 CycleAnaly 61Documento61 páginas03 PT12 CycleAnaly 61Mhammad Yaser Najjar100% (1)
- Vent SizingDocumento13 páginasVent SizingClarence AG Yue100% (1)
- Hardness Conversion TableDocumento3 páginasHardness Conversion TableNisarg PandyaAún no hay calificaciones
- Testing and Evaluation of Engineering MaterialsDocumento5 páginasTesting and Evaluation of Engineering MaterialsFAHED AYYAD100% (1)
- Conditional Chart PDFDocumento1 páginaConditional Chart PDFeduardo menesesAún no hay calificaciones
- Stress Corrosion Crack Growth Behavior of Cold Worked Austenitic Stainless Steel in High Temperature WaterDocumento7 páginasStress Corrosion Crack Growth Behavior of Cold Worked Austenitic Stainless Steel in High Temperature Wateramd mhmAún no hay calificaciones
- A Study of The Collapsing Pressure of Thin-Walled CylindersDocumento86 páginasA Study of The Collapsing Pressure of Thin-Walled CylindersLucas YiewAún no hay calificaciones
- HardeningDocumento15 páginasHardeningபென்ஸிஹர்Aún no hay calificaciones
- An Assesment of The High Temperature Oxidation Behaviour of Fe-Cr Steels in Water Vapour and SteamDocumento15 páginasAn Assesment of The High Temperature Oxidation Behaviour of Fe-Cr Steels in Water Vapour and SteammogirevansAún no hay calificaciones
- Solucao OxfordDocumento12 páginasSolucao OxfordLeonardo DuarteAún no hay calificaciones
- ch4-6 SlipDocumento5 páginasch4-6 SlipAyesha Farooq100% (1)
- Creep and FatigueDocumento20 páginasCreep and Fatiguecheveresan123100% (2)
- 3 2 CreepDocumento7 páginas3 2 CreepB Bala Venkata GaneshAún no hay calificaciones
- Creep and High Temperature Failure: OutlineDocumento6 páginasCreep and High Temperature Failure: OutlineAravind PhoenixAún no hay calificaciones
- 2.1 Testing MachineDocumento3 páginas2.1 Testing MachinekoushipriyathamAún no hay calificaciones
- Creep SlidesDocumento52 páginasCreep SlidesiJordanScribdAún no hay calificaciones
- Verification of Allowable Stresses in Asme Section Iii, Subsection NH For Grade 91 SteelDocumento143 páginasVerification of Allowable Stresses in Asme Section Iii, Subsection NH For Grade 91 SteelHarish TokiAún no hay calificaciones
- Heat Transfer LecturesDocumento200 páginasHeat Transfer LecturesdnkindrajithAún no hay calificaciones
- Binder CreepDocumento29 páginasBinder CreepettypasewangAún no hay calificaciones
- Heat and Mass Transfer Heat Transfer For PDFDocumento7 páginasHeat and Mass Transfer Heat Transfer For PDFEinar TverangerAún no hay calificaciones
- Heat Transfer by Radiation: Prof. Eckehard SpechtDocumento45 páginasHeat Transfer by Radiation: Prof. Eckehard Specht一然 曹Aún no hay calificaciones
- Deformation of Single CrystalsDocumento52 páginasDeformation of Single CrystalsNitinAún no hay calificaciones
- Advanced Metallura Y Materials: Al-Mustansiryia University College of Engineering Materials Engineering DepartmentDocumento8 páginasAdvanced Metallura Y Materials: Al-Mustansiryia University College of Engineering Materials Engineering DepartmentroseAún no hay calificaciones
- VI. Auxiliary FunctionsDocumento21 páginasVI. Auxiliary FunctionsAnshu Kumar Gupta100% (4)
- Result: 500 MM 50 MM Specimen W, LoadDocumento21 páginasResult: 500 MM 50 MM Specimen W, LoadamirulfahmieAún no hay calificaciones
- Fatiguea Ssignement Strength of Materials 3Documento15 páginasFatiguea Ssignement Strength of Materials 3Etienne CierenbergAún no hay calificaciones
- 3 2 Creep PDFDocumento7 páginas3 2 Creep PDFAZMI 333625Aún no hay calificaciones
- Strength of MaterialsDocumento7 páginasStrength of Materialsletter_ashish4444100% (1)
- AerodynamicsDocumento284 páginasAerodynamicsCaptRavi PooniaAún no hay calificaciones
- Uniaxial Tension Compression Tests and Cyclic BendingDocumento10 páginasUniaxial Tension Compression Tests and Cyclic Bendingmodestboy110Aún no hay calificaciones
- Linear Elastic Fracture Mechanics Report PDFDocumento13 páginasLinear Elastic Fracture Mechanics Report PDFLisa RobertsAún no hay calificaciones
- ME346A Lecture Notes Win2012Documento183 páginasME346A Lecture Notes Win2012Moises RomeroAún no hay calificaciones
- Fatigue Failure CriteriaDocumento17 páginasFatigue Failure CriteriaAmrMashhourAún no hay calificaciones
- Full Elementary Aerodynamics Course by MITDocumento158 páginasFull Elementary Aerodynamics Course by MIT34plt34Aún no hay calificaciones
- Diffusion in Solids PDFDocumento72 páginasDiffusion in Solids PDFrantiana27100% (1)
- Mak 214 Soru 3Documento3 páginasMak 214 Soru 3skeletonkey11Aún no hay calificaciones
- Heat NotesDocumento216 páginasHeat NotesSaswata Pradhan100% (1)
- Creep Properties PDFDocumento23 páginasCreep Properties PDFMehmet Soysal100% (1)
- Me1303-Gas Dynamics and Jet Propulsion PDFDocumento58 páginasMe1303-Gas Dynamics and Jet Propulsion PDFNarayana SamyAún no hay calificaciones
- ENGG1500 Study Guide S1 2018 PDFDocumento137 páginasENGG1500 Study Guide S1 2018 PDFKatty TsaiAún no hay calificaciones
- Chapter 9: Fluid Dynamics: A. The Equation of Continuity - Conservation of MassDocumento12 páginasChapter 9: Fluid Dynamics: A. The Equation of Continuity - Conservation of MassLorenzo Miguel GonzalesAún no hay calificaciones
- Measurement of A Thermal Expansion Coefficient For A Metal by Diffraction Patterns From A Narrow SlitDocumento5 páginasMeasurement of A Thermal Expansion Coefficient For A Metal by Diffraction Patterns From A Narrow SlitHamza QayyumAún no hay calificaciones
- Problems-2 4012 PDFDocumento5 páginasProblems-2 4012 PDFjonthemes100% (1)
- What Is FractureDocumento36 páginasWhat Is FractureMona AwadAún no hay calificaciones
- AR02 Fracture Mechanics As A Tool in Failure Analysis - Prospects and LimitationsDocumento87 páginasAR02 Fracture Mechanics As A Tool in Failure Analysis - Prospects and LimitationsmaddogoujeAún no hay calificaciones
- 6 Mechanical Behaviour of MaterialsDocumento44 páginas6 Mechanical Behaviour of MaterialsArjun MahendraAún no hay calificaciones
- Problem Set 1 SolutionsDocumento4 páginasProblem Set 1 SolutionsAnshu Kumar GuptaAún no hay calificaciones
- BruchM Aufgabenheft - enDocumento28 páginasBruchM Aufgabenheft - enIlham HakikiAún no hay calificaciones
- Creep and Stress RuptureDocumento11 páginasCreep and Stress RuptureprakrthiAún no hay calificaciones
- Ch4c CreepDocumento2 páginasCh4c Creepazizieh5701Aún no hay calificaciones
- Fracture: KL Murty MSE 450Documento9 páginasFracture: KL Murty MSE 450azizieh5701Aún no hay calificaciones
- Strengthening Mechanism3 PDFDocumento78 páginasStrengthening Mechanism3 PDFAmber WilliamsAún no hay calificaciones
- Structural Geology FormulaeDocumento2 páginasStructural Geology FormulaePrayas DuttaAún no hay calificaciones
- NEEP 541 - Hardening: Fall 2002 Jake BlanchardDocumento41 páginasNEEP 541 - Hardening: Fall 2002 Jake BlanchardezekingsAún no hay calificaciones
- Isentropic Flow PDFDocumento8 páginasIsentropic Flow PDFV DhinakaranAún no hay calificaciones
- Introducing Object-Oriented Programming (OOP) : CSCI N201: Programming ConceptsDocumento23 páginasIntroducing Object-Oriented Programming (OOP) : CSCI N201: Programming ConceptsV DhinakaranAún no hay calificaciones
- Scanned by CamscannerDocumento41 páginasScanned by CamscannerV DhinakaranAún no hay calificaciones
- Philip Hofmann Wiley-VCH Berlin: Isbn-10: 3527412824, ISBN-13: 978-3527412822Documento56 páginasPhilip Hofmann Wiley-VCH Berlin: Isbn-10: 3527412824, ISBN-13: 978-3527412822V DhinakaranAún no hay calificaciones
- Friction Stir Welding 4 3 V52Documento5 páginasFriction Stir Welding 4 3 V52V DhinakaranAún no hay calificaciones
- 0708 Conduction Convection RadiationDocumento23 páginas0708 Conduction Convection RadiationBella LimAún no hay calificaciones
- Vibration EndDocumento2 páginasVibration EndV DhinakaranAún no hay calificaciones
- Green EnergyDocumento36 páginasGreen EnergyV DhinakaranAún no hay calificaciones
- Rocket PropulsionDocumento41 páginasRocket PropulsionV DhinakaranAún no hay calificaciones
- Alphabets of This New Literature Called Gas DynamicsDocumento9 páginasAlphabets of This New Literature Called Gas DynamicsV DhinakaranAún no hay calificaciones
- Auto SystemsDocumento27 páginasAuto SystemsV DhinakaranAún no hay calificaciones
- Prop FluidDocumento46 páginasProp FluidV DhinakaranAún no hay calificaciones
- Quota SamplingDocumento6 páginasQuota SamplingKeking Xoniuqe100% (1)
- Notes On Absolutely Continuous Functions of Several VariablesDocumento16 páginasNotes On Absolutely Continuous Functions of Several VariablesSufyanAún no hay calificaciones
- MATH 9 Module 2 Week 6Documento13 páginasMATH 9 Module 2 Week 6Henry Kahal Orio Jr.Aún no hay calificaciones
- PIDE Presentation Part 1 PDFDocumento7 páginasPIDE Presentation Part 1 PDFGilmar DemenekAún no hay calificaciones
- SootblowerDocumento9 páginasSootblowerVan LudwigAún no hay calificaciones
- Tut-sheet-2-PHL120-13 With Final Answers PDFDocumento2 páginasTut-sheet-2-PHL120-13 With Final Answers PDFjgrgpt33Aún no hay calificaciones
- Solved Multiple Choice Questions of DataDocumento40 páginasSolved Multiple Choice Questions of Datamini projectAún no hay calificaciones
- Abstract Classes Versus Interfaces: C# (And Other Languages) Polymorphism Explained To Young PadawansDocumento4 páginasAbstract Classes Versus Interfaces: C# (And Other Languages) Polymorphism Explained To Young Padawanssridevishinas100% (1)
- Eklavya Central Shool, Saharsa: Holiday HomeworkDocumento3 páginasEklavya Central Shool, Saharsa: Holiday HomeworkChitrakumariAún no hay calificaciones
- Unit 4 - Lesson 2Documento3 páginasUnit 4 - Lesson 2api-243891235Aún no hay calificaciones
- Syllabus Jan09 MAT183Documento2 páginasSyllabus Jan09 MAT183Mike ZakwanAún no hay calificaciones
- Open Set ProofDocumento2 páginasOpen Set Proofsagetbob43Aún no hay calificaciones
- Aits 2021 FT Ix Jeem.Documento16 páginasAits 2021 FT Ix Jeem.Atharv AtoleAún no hay calificaciones
- ASB-410 JQL in Jira Service Desk Slides and NotesDocumento198 páginasASB-410 JQL in Jira Service Desk Slides and NotesCarlos GarciaAún no hay calificaciones
- Maths Y8 4Documento2 páginasMaths Y8 4s100% (1)
- New Microsoft Office Word DocumentDocumento7 páginasNew Microsoft Office Word DocumentMangisetty SairamAún no hay calificaciones
- Real Time DC Motor Speed Control Using Pid in Labview With ArduinoDocumento3 páginasReal Time DC Motor Speed Control Using Pid in Labview With ArduinoabsalnabiAún no hay calificaciones
- CA-course FileDocumento12 páginasCA-course FileSivagami ManiAún no hay calificaciones
- Latent Graph Diffusion A Unified Framework For Generation and Prediction On GraphsDocumento21 páginasLatent Graph Diffusion A Unified Framework For Generation and Prediction On GraphslinkzdAún no hay calificaciones
- Quarter: First Quarter Month: March 2021 QF010-A - ELEMENTARY - Goldfield ESDocumento5 páginasQuarter: First Quarter Month: March 2021 QF010-A - ELEMENTARY - Goldfield ESJocelyn BuslotanAún no hay calificaciones
- Ludwig Wittgenstein - A Mind On Fire - New StatesmanDocumento14 páginasLudwig Wittgenstein - A Mind On Fire - New StatesmanzentropiaAún no hay calificaciones
- Modelacion Calida Agua Parte 1Documento14 páginasModelacion Calida Agua Parte 1Gisell AguilarAún no hay calificaciones
- Tutorial Letter 001/3/2021: Complex AnalysisDocumento19 páginasTutorial Letter 001/3/2021: Complex AnalysisKyle MaharajAún no hay calificaciones
- Final Quiz 2 4Documento4 páginasFinal Quiz 2 4Erick GarciaAún no hay calificaciones