Libro Mates

Matemticas
Los propietarios del tiene reservados todos los derechos. Cualquier reproduccin, total o parcial de este texto, por cualquier medio, o soporte sonoro, visual o informtico, as como su utilizacin fuera del mbito estricto de la informacin del alumno comprador, sin la conformidad expresa por escrito de los propietarios de los derechos, ser perseguida con todo el rigor que prev la ley y se exigirn las responsabilidades civiles y penales, as como las reparaciones procedentes. Matemticas Autor: ISBN: Depsito Legal: Imprime: SEAS, Estudios Superiores Abiertos S.A. 84-8422-791-X Z-122-2004 El depositario, con autorizacin expresa de SEAS, S.A.
NDICE ASIGNATURA
UNIDAD 1. EL CONJUNTO DE LOS NMEROS MATEMTICOS

1.1. DIFERENTES CONJUNTOS DE NUMEROS 1.2. ORDEN Y VALOR ABSOLUTO EN LOS NMEROS REALES 1.2.1. ORDEN 1.2.2. VALOR ABSOLUTO 1.2.3. PROPIEDADES DEL VALOR ABSOLUTO 1.2.4. INTERVALO EN LA RECTA 1.3. POTENCIAS DE NMEROS REALES 1.3.1. OPERACIONES CON POTENCIAS 1.4. RADICALES 1.4.1. OPERACIONES CON RADICALES 1.5. LOGARITMOS 1.5.1. PROPIEDADES DE LOS LOGARITMOS
Matemticas
UNIDAD 2. SISTEMAS DE COORDENADAS.

2.1. EJES DE COORDENADAS CARTESIANOS 2.1.1. COORDENADAS DE UN PUNTO 2.1.2. CUADRANTES 2.2. DISTANCIA ENTRE DOS PUNTOS 2.2.1. PUNTO MEDIO DE UN SEGMENTO 2.3. VECTORES 2.3.1. COMPONENTES DE UN VECTOR 2.3.2. MDULO E INCLINACIN DE UN VECTOR
UNIDAD 3. RECTAS EN EL PLANO.

3.1. ECUACIN DE LA RECTA 3.1.1. ECUACIN DE UNA RECTA QUE PASA POR DOS PUNTOS 3.1.2. ECUACIN PUNTO-PENDIENTE 3.1.3. ECUACIN EXPLCITA DE LA RECTA 3.1.4. ECUACIN GENERAL DE LA RECTA 3.2. SITUACIN DE UNA RECTA EN EL PLANO 3.2.1. SIGNO DE LA PENDIENTE 3.2.2. RECTAS HORIZONTALES Y VERTICALES 3.3. INCIDENCIA DE RECTA Y RECTA 3.3.1. RECTAS PARALELAS Y PERPENDICULARES
UNIDAD 4. TRIGONOMETRA
4.1. TRIGONOMETRA 4.1.1. MEDIDAS DE NGULOS 4.2. RAZONES TRIGONOMTRICAS DE UN NGULO 4.2.1. EN UN TRINGULO RECTNGULO 4.2.2. EN UNA CIRCUNFERENCIA 4.2.3. RELACIONES ENTRE LAS RAZONES TRIGONOMTRICAS DE UN NGULO 4.2.4. RAZONES EXACTAS DE NGULOS 4.2.5. LNEAS Y SIGNOS DE LAS RAZONES TRIGONOMTRICAS 4.2.6. RAZONES TRIGONOMTRICAS DE UN NGULO CUALQUIERA RELACIONADAS CON UN NGULO DEL 1 CUADRANTE 4.3. APLICACIONES DE LA TRIGONOMETRIA 4.3.1. RESOLUCIN DE TRINGULOS RECTNGULOS 4.3.2. RESOLUCIN DE TRINGULOS CUALESQUIERA 4.4. FUNCIONES TRIGONOMTRICAS DIRECTAS E INVERSAS 4.4.1. DIRECTAS 4.4.2. INVERSAS 4.4.3. OTRAS FRMULAS
Matemticas
UNIDAD 5. NMEROS COMPLEJOS.

5.1. UNIDAD IMAGINARIA Y NMEROS COMPLEJOS 5.1.1. LA UNIDAD IMAGINARIA 5.1.2. NMEROS COMPLEJOS 5.1.3. REPRESENTACIN GRFICA DE UN NMERO COMPLEJO 5.2. FORMAS DE EXPRESAR UN NMERO COMPLEJO 5.3. NMEROS CONJUGADOS Y OPUESTOS DE OTRO COMPLEJO 5.4. POTENCIAS DE LA UNIDAD IMAGINARIA 5.5. OPERACIONES FUNDAMENTALES CON NMEROS COMPLEJOS 5.5.1. SUMA Y RESTA 5.5.2. PRODUCTO 5.5.3. COCIENTE 5.5.4. POTENCIA DE UN COMPLEJO 5.5.5. RAZ DE UN COMPLEJO
UNIDAD 6. FUNCIN REAL DE VARIABLE REAL

6.1. FUNCIN Y DOMINIO 6.2. GRFICA DE UNA FUNCIN 6.2.1. DOMINIOS Y GRFICAS DE FUNCIONES ELEMENTALES 6.3. LMITES 6.3.1. DEFINICIN 6.3.2. LMITES LATERALES 6.3.3. LMITES INFINITOS 6.3.4. PROPIEDADES DE LOS LMITES 6.3.5. INDETERMINACIONES 6.4. CONTINUIDAD DE UNA FUNCIN 6.4.1. PROPIEDADES 6.4.2. DISCONTINUIDAD
Matemticas
UNIDAD 7. DERIVADAS DE FUNCIONES.

7.1. CONCEPTO DE DERIVADA 7.1.1. DEFINICIN 7.1.2. INTERPRETACIN GEOMTRICA DE LA DERIVADA 7.1.3. DERIVABILIDAD Y CONTINUIDAD 7.2. CLCULO DE FUNCIONES DERIVADAS 7.2.1. DERIVADAS DE LAS FUNCIONES ELEMENTALES 7.2.2. COMPOSICIN DE FUNCIONES DERIVABLES. LA REGLA DE LA CADENA. 7.2.3. DERIVADA DE UNA FUNCION POTENCIAL- EXPONENCIAL 7.2.4. DERIVADAS SUCESIVAS 7.3. FUNCIONES CRECIENTES Y DECRECIENTES 7.3.1. DEFINICIONES 7.3.2. CRECIMIENTO Y DERIVADA DE LA FUNCIN 7.4. MXIMOS Y MNIMOS DE LAS FUNCIONES 7.4.1. DEFINICIONES 7.4.2. CARACTERIZACIN DE MXIMOS Y MNIMOS 7.4.3. APLICACIONES A PROBLEMAS 7.5. CURVATURA Y PUNTOS DE INFLEXIN 7.5.1. CARACTERIZACIN DE CONCAVIDAD Y CONVEXIDAD 7.5.2. PUNTOS DE INFLEXIN
UNIDAD 8. INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA.

8.1. CONCEPTO DE INTEGRAL INDEFINIDA 8.1.1. PROPIEDADES 8.2. INTEGRALES INMEDIATAS 8.3. MTODOS DE INTEGRACIN 8.3.1. INTEGRACIN POR PARTES 8.3.2. INTEGRACIN POR CAMBIO DE VARIABLE 8.4. INTEGRALES CUMPLIENDO CONDICIONES 8.5. INTEGRAL DEFINIDA 8.5.1. DEFINICIN 8.5.2. PROPIEDADES DE LA INTEGRAL DEFINIDA 8.6. APLICACIONES DE LA INTEGRAL DEFINIDA 8.6.1. CLCULO DE UNA LONGITUD DE ARCO 8.6.2. CLCULO DE REAS DE REVOLUCIN 8.6.3. VOLMENES DE REVOLUCIN
Matemticas
MATEMTICAS
1
EL CONJUNTO DE LOS NMEROS MATEMTICOS
M065(01)
Matemticas
NDICE
OBJETIVOS .................................................................................................3 INTRODUCCIN ..........................................................................................4 1.1. Diferentes Conjuntos de Numeros .......................................................5 1.2. Orden y Valor Absoluto en los Nmeros Reales ................................9 1.2.1. Orden ................................................................................................9 1.2.2. Valor absoluto ...................................................................................9 1.2.3. Propiedades del valor absoluto .......................................................10 1.2.4. Intervalo en la recta.........................................................................11 1.3. Potencias de nmeros reales .............................................................13 1.3.1. Operaciones con potencias.............................................................14 1.4. Radicales ..............................................................................................18 1.4.1. Operaciones con radicales..............................................................19 1.5. Logaritmos............................................................................................21 1.5.1. Propiedades de los logaritmos ........................................................22 RESUMEN..................................................................................................25
Unidad 1. El Conjunto de los Nmeros Matemticos
Matemticas
OBJETIVOS
Tras el estudio de la presente unidad didctica el alumno debe:
Conocer y diferenciar los principales conjuntos numricos, N, Z, Q, R y saber

clasificar los nmeros en dichos conjuntos.
Comprender y manejar la representacin de los nmeros en la recta real y

ordenar los nmeros reales.
Definir y manejar el concepto de valor absoluto. Comprender las definiciones de intervalo abierto y cerrado. Saber operar con potencias y radicales. Entender el concepto de logaritmo, el nmero irracional e y los logaritmos
neperianos. Conocer y aplicar sus propiedades.
Formacin Abierta
INTRODUCCIN
El concepto de nmero que ahora nos resulta tan familiar se ha ido elaborando a travs de la historia muy lentamente. Para poder contar, medir distintos objetos, distancias necesitamos usar nmeros escritos de muy diversas formas. En este primer tema vamos a recordar los conjuntos en que se clasifican los nmeros que normalmente usamos. Para ello veremos sus distintos tipos, sus propiedades principales y las relaciones que existen entre ellos. Desde el punto de vista matemtico se utilizan los nmeros naturales para medir con la unidad, los nmeros racionales para medir con partes de la unidad, los irracionales que aparecen en distintas situaciones y completan la recta de los reales. Intuitivamente sobre la recta real entendemos los conceptos de orden y distancia entre los nmeros y los puntos. Vamos a formalizar esta idea intuitiva y conocer el valor absoluto y sus propiedades. Tambin veremos y recordaremos las operaciones de potenciacin, radicacin, y la funcin logartmica. Los clculos con potencias aparecen muchas veces cuando queremos hallar el rea de una figura o el volumen de algn recipiente. De la misma forma, las operaciones con radicales aparecen al aplicar el teorema de Pitgoras, al resolver ecuaciones de segundo grado... La funcin logartmica, el clculo de logaritmos es la forma de hallar exponentes cuando los datos conocidos son la base y el resultado de la potencia. De todos modos, las aplicaciones de los logaritmos van mucho ms all porque tienen unas propiedades que resultan muy tiles para simplificar ciertas operaciones.
Matemticas
1.1. DIFERENTES CONJUNTOS DE NUMEROS

Cuando se empieza a numerar pginas en un libro, o empezamos a contar objetos de cualquier tipo, usamos los nmeros naturales, 1,2,3,4,...y designamos con N a la coleccin de todos ellos. Sobre estos nmeros existe un orden y que podemos realizar operaciones como la suma y el producto cuyo resultado siempre ser otro nmero natural. Si se intenta contar cuntos nmeros naturales hay, se observa que a cada nmero natural le sigue otro y que esta cadena no tiene final, as aparece la nocin matemtica de infinito. Hay bastantes situaciones en que los nmeros naturales resultan insuficientes para expresar la realidad, por ejemplo las temperaturas bajo cero, gastos en un presupuesto...faltan nmeros negativos, y aparecen los nmeros enteros que designamos por Z. Z = {....-4, -3, -2, -1, 0, 1, 2, 3, 4....}. Los enteros contienen a los nmeros naturales o enteros positivos y a los enteros negativos. Los podemos representar grficamente sobre una recta donde vemos claramente el orden entre ellos.
-3 -2 -1
0 1
Figura 1.1. Los nmeros enteros sobre la recta.
Hay una notacin especfica para los conjuntos. Si queremos expresar que un elemento, en este caso un nmero, pertenece a un conjunto, usaremos el smbolo , por ejemplo, -3 Z . Si queremos indicar que un elemento no pertenece al conjunto lo haremos escribiendo , por ejemplo, -3 N . Luego los smbolos , , expresan la pertenencia o no de un elemento a un conjunto. Si lo que queremos es indicar que un conjunto est contenido o incluido en otro, usaremos el smbolo . Por ejemplo N Z. El smbolo , indica lo contrario, no est incluido o contenido, y , indica est contenido o es igual, o coincide.
Formacin Abierta
Estos smbolos , , se usan para expresar la inclusin, o no o inclusin o coincidencia entre conjuntos. Si queremos unir dos conjuntos A y B, la notacin ser A B que ser el conjunto formado por todos los elementos de A y de B. Conjunto unin. La interseccin de dos conjuntos A y B est formada por los elementos que tienen en comn, los que pertenecen a la vez a A y a B, y se escribe A B. Las operaciones que podemos realizar dentro de los enteros son la suma y el producto, como en los naturales, solo que al sumar un nmero negativo lo que hacemos es lo mismo que restar un positivo. Al dividir nmeros enteros o naturales, aparecen los nmeros fraccionarios o fracciones. Las fracciones no son nmeros enteros.
Se entiende como fraccin la expresin
a , donde a y b son b
distintos de cero, son enteros y se interpreta como tomar a veces la unidad
1 . b
Llamamos fracciones equivalentes a aquellas que tienen el mismo valor y definen un nmero racional.
3 2 1 12 13 , , , , ,.... } son todas fracciones equivalentes y representan al 6 4 2 24 26 1 nmero racional . 2

{ Los nmeros racionales tambin tienen un orden y sobre ellos podemos definir las operaciones de suma, producto y cociente. Al conjunto de los nmeros racionales se le llama Q. Los racionales tambin se representan sobre la recta y contienen a los enteros Z Q .
Expresin decimal de los nmeros racionales. Los nmeros racionales se expresan de forma decimal mediante la divisin del numerador por el denominador, y siempre nos encontramos en uno de los siguientes casos:
Matemticas
1) La divisin es un nmero entero, o sea el numerador es un mltiplo del denominador. Ejemplo:
54 = 9 = 9,000 6
2) La divisin es un decimal exacto, cuando el denominador es producto de los factores primos 2 y 5. Ejemplo:
67 = 1,34 50
3) La divisin no es un decimal exacto, si el denominador contiene factores primos distintos de 2 y 5. Se llaman decimales peridicos puros o peridicos mixtos. Ejemplo:
) 11 = 1,83333 = 1,83 6
Todo nmero racional se puede expresar en forma decimal peridica y todo nmero decimal peridico se puede expresar en forma racional.
Con los nmeros racionales y los enteros no est llena la recta, hay nmeros que no pertenecen al conjunto de los racionales ni los enteros, nmeros cuya expresin decimal es infinita no peridica. Se llaman nmeros irracionales y se representan con la letra I. Por ejemplo, si calculamos la longitud de la diagonal del cuadrado de lado la unidad , usando el teorema de Pitgoras, obtenemos d = 1 + 1 =
2 2
d= 2 L=1
L=1
Figura 1.2. Diagonal del cuadrado de lado la unidad
Formacin Abierta
Hay nmeros irracionales muy importantes, por ejemplo el nmero , es el resultado de dividir la longitud de una circunferencia por su dimetro y su valor es =3,1416..... Un nmero irracional muy usado es el nmero e. Su valor decimal, se puede obtener en la calculadora, es 2,718281828459045.... Aparece en muchos fenmenos de crecimiento de especies vegetales y animales y en la frmula de la curva llamada catenaria. Es la curva que describe un hilo flexible que cuelga sujeto solo por sus extremos, por ejemplo, los cables de cualquier tendido elctrico. Si representamos los nmeros irracionales sobre la recta si que la llenamos completamente, y es la que normalmente se conoce como la recta real o recta de nmeros reales. Los nmeros reales son el conjunto de nmeros constituido por la unin de los racionales y los irracionales, y se designa por la letra R. Cul es el primer nmero real?, El ms pequeo? y Cul es el ms grande?. Los nmeros reales forman un conjunto no acotado, lo que quiere decir que se extienden de a + . N: Conjunto de los nmeros naturales. Z: Conjunto de los nmeros enteros. Q: Conjunto de los racionales. I: Conjunto de los irracionales. R: Conjunto de los nmeros reales. Y como hemos ido viendo unos conjuntos engloban a otros, eso lo expresaremos utilizando la notacin de los conjuntos de la siguiente manera:
N Z QR
Matemticas
1.2. ORDEN Y VALOR ABSOLUTO EN LOS NMEROS REALES

Intuitivamente la idea de orden, la de distancia o separacin entre dos nmeros o dos puntos de la recta real son conceptos que todos entendemos. En este apartado trataremos cmo expresar estos conceptos usando la notacin matemtica.
1.2.1. ORDEN
Tal y como hemos visto en el apartado 1.1, los nmeros reales se representan sobre la recta, esta representacin ya nos da una idea muy clara sobre el orden en el conjunto R, un nmero es mayor que otro si est situado a la derecha del mismo. Vamos a definir un poco ms concretamente este concepto de orden. Dados dos nmeros a y b, se dice que a es menor que b, y se escribe a<b si b-a es positivo. Si usamos el smbolo a b , estamos expresando a es menor o igual que b.
1.2.2. VALOR ABSOLUTO

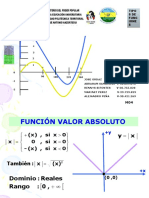
El valor absoluto de un nmero real expresa la distancia del nmero al cero, al origen. As, el valor absoluto de un nmero real positivo es l mismo y el de un nmero real negativo es su opuesto. El valor absoluto de un nmero a, se simboliza con a . Definimos el valor absoluto de un nmero real a, como:
a =a
si
a>0
a = a
si
a<0
Y el valor absoluto de cero, es cero. 0 = 0
Formacin Abierta
Ejemplos:
5,78 = 5,78 3,987 = 3,987

El concepto de valor absoluto como distancia, nos lleva a poder definir la distancia entre dos puntos cualesquiera de la recta real como el valor absoluto de su diferencia. Se llama distancia entre dos puntos de la recta real, x1 y x2, al valor absoluto de su diferencia, es decir:
x1 x2
1.2.3. PROPIEDADES DEL VALOR ABSOLUTO

Por la propia definicin de valor absoluto es fcil darse cuenta de que un nmero y su opuesto tienen el mismo valor absoluto, as, por ejemplo, la ecuacin x = 3 , tiene dos soluciones, 3 y 3. Aplicando la definicin y esta simple conclusin, se demuestran fcilmente las siguientes propiedades del valor absoluto.
a = a ab = ba
a + b a + b Desigualdad triangular
a b = a b
a a = b b
10
Matemticas
Para comprobarlas sobre distintos ejemplos, puede usar los siguientes:
Calcular:
2 , 4 5 , 8,98 10,675 7
1.2.4. INTERVALO EN LA RECTA

Si a y b son dos nmeros reales, el intervalo limitado por ellos en la recta real es el conjunto de nmeros comprendidos entre a y b. A los nmeros a y b se les llama extremos del intervalo. Llamamos intervalo abierto y se designa (a,b) al conjunto de nmeros reales que estn situados entre a y b, sin incluirlos a ellos, sin incluir los extremos. En notacin matemtica: (a,b) = {x R, tal que a < x < b Vemoslo sobre un dibujo:
a
Figura 1.3.
b
Intervalo abierto de extremos a, b.
Llamamos intervalo cerrado y lo designamos [a,b] al conjunto de nmeros reales que estn situados entre a y b, incluyndolos a ellos, incluyendo los extremos. En notacin matemtica: [a,b] = {x R, tal que a x b Sobre el dibujo:
a
Figura 1.4.
b
Intervalo cerrado de extremos a,b.
As es lo mismo escribir 3 x 5 , que poner [-3, 5], nos referimos exactamente al mismo conjunto de nmeros. Los nicos valores con los que nunca aparece el intervalo cerrado son con y con + . Cuando alguno de estos dos valores sea el extremo de algn intervalo, en ese extremo siempre el intervalo ser abierto.
11
Formacin Abierta
Si queremos expresar en forma de intervalo los nmeros que cumplen x 5 , deberamos escribir ( ,5] .
Intervalos y valor absoluto Si nos encontramos con la expresin x 9 6 hemos de darnos cuenta que lo que indica es que x es cualquier nmero que se encuentre a una distancia de 9 que sea menor o igual que 6. As, si queremos expresar este mismo conjunto de nmeros utilizando un intervalo, tendremos que buscar sus extremos. Sumamos y restamos 6, que es la distancia mxima, a 9, que va a ser el centro del intervalo, y obtenemos los extremos que sern 3 y 15. Luego x [3,15] x 9 6 Si nos encontramos con un intervalo y queremos expresarlo con valor absoluto deberemos proceder al revs. El intervalo (-2, 6). Empezaremos por calcular el punto medio del intervalo, el punto medio siempre se puede calcular como la suma de los extremos dividida entre 2. En este caso
2+6 = 2. 2
distancia a un extremo,
Luego
2 6 = 2 ( 2 ) = 4 , este valor es la distancia mxima a la que
calcularemos
la
los puntos se pueden encontrar del centro. Luego tendramos la expresin:
x2 4
12
Matemticas
1.3. POTENCIAS DE NMEROS REALES

Las operaciones suma, (diferencia), producto y cociente de nmeros reales son las bsicas en este conjunto, el resultado de cualquiera de ellas es siempre otro nmero real. Cmo operar y las propiedades de estas operaciones son conocidas por todos. Vamos a centrarnos en las potencias de nmeros reales y explicar cmo operar con ellas. Potencias de la misma base, potencias del mismo exponente y distinta base, exponentes positivos y negativos y exponentes fraccionarios. Si a es un nmero real cualquiera y n un nmero natural:
a n = a a a a......a (n veces)
a0 = 1 a1 = a an = 1 an
Hemos visto en esta definicin qu representan las potencias de exponente natural y de exponente entero, as como el exponente nulo y la unidad. Veamos algunos ejemplos.
4 4 4 43 64 4 = = 3 = 3 3 3 3 27 3 2340 = 1 3 2 = 1 1 = 32 9
( 2)4 = ( 2) ( 2) ( 2) ( 2) = 16
13
Formacin Abierta
1.3.1. OPERACIONES CON POTENCIAS

Veamos ahora cmo hacer productos, cocientes...de potencias enteras. Producto de potencias de la misma base.
an am = an+m
El producto de potencias de la misma base es otra potencia de la misma base y exponente la suma de los exponentes. Si alguno de los exponentes es negativo la operacin se realiza igual. Veamos algunos ejemplos.
52 5 3 = 52 + ( 3 ) = 51 = 2 2 2 = 7 7 7
Cociente de potencias de la misma base
4 5 4+5
1 5
9
2 = 7
El cociente de potencias de la misma base es otra potencia de la misma base y exponente la diferencia entre el exponente del numerador y el del denominador.
an = anm m a
En realidad es un caso particular del producto donde una de las potencias tiene exponente negativo y la expresamos como inversa de una con exponente positivo. Veamos unos ejemplos.
76 1 = 7 6 8 = 7 2 = 2 8 7 7 5 = 51 ( 3 ) = 54 5 3
14
Matemticas
Potencia elevada a otra potencia
Si hay que elevar una potencia a otra potencia el resultado es una potencia de la misma base y exponente el producto de los exponentes. O sea, para elevar una potencia a otra potencia se deja la misma base y se multiplican los exponentes.
(a ) (2 )
5 3
n m
= a nm
= 25(3) = 215
Factores y cociente con el mismo exponente.
Para multiplicar o dividir potencias con distinta base y el mismo exponente se mantiene el exponente y se multiplican o dividen las bases.
a n b n = (a b ) an a = bn b
n
Tambin podramos expresarlo al revs, para elevar un producto a una potencia se eleva cada uno de los factores a la potencia. De la misma forma con el cociente, y sera leer las igualdades de izquierda a derecha.
7 3 33 = 213 28 2 8= 5 5
8
Teniendo clara esta forma de operar, podremos resolver cualquier expresin en que intervengan potencias, productos o cocientes de potencias enteras. Hagamos un pequeo resumen.
15
Formacin Abierta
Operaciones con potencias:
a0 = 1 an = 1 an
Producto de potencias de la misma base:
an am = an+m
Cociente de potencias de la misma base:
an = anm m a
Elevar una potencia a otra potencia:
(a )
n m
= a nm
Factores y cociente con el mismo exponente:
n
Cuando queremos escribir nmeros grandes que son potencia de 10 o nmeros con muchos decimales a menudo se usan las potencias de 10 con exponente positivo o negativo. Es una cuestin de comodidad y algo que aparece en las calculadoras cientficas. Por ejemplo en lugar de escribir 3.000.000 se escribe 3 106 .
3.250.000 = 3,25 10 0,0000025 = 25 10
6
En la calculadora no aparece el 10, solamente aparecen arriba y en pequeo los nmeros que son el exponente de 10 y para introducirlos se hace con la tecla EXP.
16
Matemticas
Hay algunas potencias que aparecen a menudo en los clculos y que quiz sea mejor verlas aparte. Alguna ya la hemos comentado, las potencias con exponente nulo.
a0 = 1
a a + a
a =
a = 0
1 = in det er min acin 0 , 0 = in det er min acin
17
Formacin Abierta
1.4. RADICALES
Hallar una raz de ndice n es hacer la operacin inversa a calcular una potencia de exponente n. Vemoslo.
A un nmero a cuya potencia n-sima (ensima) es otro nmero conocido b, se le llama su raz ensima y se expresa:
n
b = a an = b
n es el ndice de la raz. b es el radicando
Si el ndice es 2, se llama raz cuadrada y si es 3 se llama raz cbica, que son expresiones ms usadas que raz de ndice 2 3.
Si tenemos una raz de ndice par, una raz cuadrada por ejemplo de un nmero real positivo nos encontramos con que hay dos soluciones posibles, una positiva, y otra negativa.
9 = 2 9 = 3
4
16 = 2
Sin embargo la raz de ndice par de un nmero real negativo es una operacin que no tiene solucin en el conjunto de los nmeros reales. Para buscar estas soluciones tendremos que conocer los nmeros complejos, a los que les dedicamos otro captulo.
Si estamos resolviendo una raz de ndice impar no aparecen estas situaciones, la raz de ndice impar es un nico valor, con el mismo signo que el radicando. Luego la raz de ndice impar de un nmero negativo, existe, es nica y tiene signo negativo tambin.
3 5
27 = 3 1 = 1 1 32 = 2 25 = 5
18
Matemticas
Potencias de exponente racional
Veamos cmo expresar un radical cualquiera como el radicando elevado a un exponente racional.
n
am = a
De lo que fcilmente se deduce:

n
( a ) =a
n m n
am = a
= b bn = a m
m nm m ya que a n = a n = a m n
Para multiplicar y dividir potencias de la misma base que tengan exponente racional se acta de la misma forma que con los exponentes enteros. En general todo lo que se ha visto para operar con potencias de exponente entero es vlido cuando el exponente es racional.
1.4.1. OPERACIONES CON RADICALES

De todos modos, vamos a especificar como operar con radicales aunque siempre podamos escribirlos en forma de potencia y aplicar las reglas aprendidas para ello.
Producto y cociente de races con igual ndice
El producto (cociente) de races de igual ndice es otra raz del mismo ndice y radicando el producto (cociente) de los radicandos.
n n n
a n b = n a b a n a = b b
Si hemos de multiplicar o dividir radicales de distinto ndice pero con el mismo radicando, lo ms sencillo y rpido es escribirlos como potencias racionales y sumar o restar los exponentes.
19
Formacin Abierta
3 4
5 3 3 = 3 15
4
24 4 = 4 6
1 2
3 5
3 3 32 = 3 33 = 3 5 7 52 = 5 5 5
7
=5
( 15 )+ 2 7
=5
7 +10
35
=5
17
35
= 35 517
Si nos encontramos con radicales de distinto ndice y distinto radicando, los reduciremos a dos radicales del mismo ndice y multiplicaremos o dividiremos los radicandos transformados. Vemoslo en un ejemplo.
2 2 5 = 6 22 6 53 = 6 4 125 = 6 500
Para poner los dos radicales con el mismo ndice, hallamos el mnimo comn mltiplo de los ndices, este valor ser el ndice comn, y los radicandos se elevan al resultado de dividir ese ndice comn por el de la raz en que se encuentran. Quiz sea ms fcil reduciendo a comn denominador los exponentes racionales correspondientes.
Raz de una raz
La raz de una raz es otra raz de ndice el producto de los ndices, y como radicando el mismo radicando. Es equivalente a hallar la potencia de una potencia.
m n
a = nm a
3 3 5
5 =65 6 = 15 6
20
Matemticas
1.5. LOGARITMOS
En ocasiones conocemos la base de una potencia y el resultado de elevarla a un exponente que desconocemos. Lo que precisamente queremos es hallar ese exponente. Para ello la operacin que hemos de realizar es un logaritmo.
Logaritmacin: Decimos que el logaritmo de b en base a es igual a n si se cumple que a elevado a n es igual a b.
log a b = n a n = b
Luego el resultado de un logaritmo es siempre un exponente que puede ser cualquier nmero real.
Dado un nmero a, perteneciente a los reales positivos y distinto de la unidad, se llama funcin logartmica a una aplicacin de los reales positivos en los reales tal que a cada x corresponder una imagen y = log a x .
+
le hace
log 2 8 = 3 log 5 25 = 2 log10 10000 = 4 log10 0'001 = 3

Existencia del logaritmo Como la base a es positiva, a>0 , entonces los nicos posibles valores de b para los que puedo hallar el logaritmo, para los que existe el logaritmo, son los reales positivos + . Por ejemplo, el logaritmo en base 2 de 4 no existe, ya que no hay ningn valor que cumpla que 2 elevado a l sea igual a 4. Logaritmos ms usuales Los logaritmos que ms se emplean, los que aparecen en las calculadoras, son el logaritmo con base 10 o logaritmo decimal que se escribe log y el logaritmo en base e o logaritmo neperiano que se escribe ln..
21
Formacin Abierta
Es evidente que log10 = 1 y lne = 1.
1.5.1. PROPIEDADES DE LOS LOGARITMOS

Los logaritmos tienen ciertas propiedades que hacen que resulte muy prctico trabajar con ellos cuando queremos facilitar ciertos clculos. Vemoslas.
Logaritmo del producto
El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
log a (C D ) = log a C + log a D

Luego si aplicamos un logaritmo a un producto podemos transformarlo en una suma de logaritmos. A veces se dice: Los logaritmos transforman productos en sumas.
Logaritmo del cociente
El logaritmo de un cociente es igual al logaritmo del dividendo o numerador menos el logaritmo del divisor o denominador.
C log a = log a C log a D D

Transformamos entonces una divisin o un cociente en una resta.
log(3 ) = log 3 + log ln (4e ) = ln 4 + ln e = (ln 4) + 1
log
6 = log 6 log11 11 e ln = ln e ln 10 = 1 ln 10 10
22
Matemticas
Logaritmo de una potencia y de una raz
El logaritmo de una potencia es igual al exponente por el logaritmo de la base. El logaritmo de una raz es igual al logaritmo del radicando dividido por el ndice de la raz. Como antes, la raz la expresamos como potencia racional y aplicamos el logaritmo de una potencia.
log a C n = n log a C log a n C = 1 log a C n
( )
Veamos que al aplicarle el logaritmo a una potencia la transformamos en un producto de dos factores y una divisin en un cociente. Luego conseguimos operaciones ms sencillas.
log 5 63 = 3 log5 6 log 20 2 4 log10 = 4 log10 = 4 log 20 = ln e

2 3
= 2 ln e = 2 3 3
El logaritmo es una operacin o funcin relacionada con la potenciacin como ya hemos visto. Veamos ahora desde el punto de vista de los logaritmos esos casos particulares de potencias que a veces quedaban indeterminadas.
log1 = ln 1 = 0 log 0 = ln 0 = log = ln = log( ) = ln ( ) no existen
23
Matemticas
RESUMEN
Los distintos conjuntos de nmeros , los naturales , los enteros , los
racionales Q, los irracionales I y los reales estn incluidos unos en otros de la siguiente forma: Q
Los nmeros reales los representamos sobre una recta infinita, ( ,+ )

en la que cada punto corresponde con un nmero real y viceversa. Los reales estn ordenados y siempre que comparamos dos de ellos podemos concluir cual es mayor o menor que el otro o si son iguales.
El valor absoluto o mdulo de un nmero se puede interpretar como la

distancia de ese punto, de ese nmero, al valor o al punto cero, el origen. Y como consecuencia de ello, la distancia entre dos puntos o dos nmeros la podemos definir como el mdulo o valor absoluto de su diferencia
Las propiedades del valor absoluto son:

a = a ab = ba
a + b a + b Desigualdad triangular
a b = a b
a a = b b
Intervalos abiertos y cerrados sobre la recta real.

Llamamos intervalo abierto y se designa (a,b) al conjunto de nmeros reales que estn situados entre a y b, sin incluirlos a ellos, sin incluir los extremos. En notacin matemtica: (a,b) = {x R, tal que a < x < b
25
Formacin Abierta
Llamamos intervalo cerrado y lo designamos [a,b] al conjunto de nmeros reales que estn situados entre a y b, incluyndolos a ellos, incluyendo los extremos. En notacin matemtica: [a,b] = {x R, tal que a x b
Las operaciones con potencias y races de nmeros reales.

a0 = 1 an =
1 an
Producto de potencias de la misma base:
an am = an+m
Cociente de potencias de la misma base:
an = anm m a
Elevar una potencia a otra potencia:
(a )
n m
= a nm
Factores y cociente con el mismo exponente:
n
Las races siempre podemos ponerlas en forma de potencia con exponente racional y operar como acabamos de ver con ellas.
n
am = a
26
Matemticas
Algunas potencias reseables:

a0 = 1
a = a a + a
a = 0
1 = in det er min acin 0 , 0 = in det er min acin
Logaritmos
Logaritmacin: Decimos que el logaritmo de b en base a es igual a n si se cumple que a elevado a n es igual a b.
log a b = n a n = b
Propiedades de los logaritmos

Logaritmo del producto y del cociente
log a (C D ) = log a C + log a D C log a = log a C log a D D

Logaritmo de una potencia y una raz
log a C n = n log a C log a n C = 1 log a C n
( )
27
MATEMTICAS
2
SISTEMAS DE COORDENADAS CARTESIANAS. VECTORES
Matemticas
NDICE
OBJETIVOS .................................................................................................3 INTRODUCCIN ..........................................................................................4 2.1. Ejes de coordenadas cartesianos ........................................................5 2.1.1. Coordenadas de un punto.................................................................6 2.1.2. Cuadrantes........................................................................................7 2.2. Distancia entre dos puntos ...................................................................8 2.2.1. Punto medio de un segmento ...........................................................9 2.3. Vectores ................................................................................................10 2.3.1. Componentes de un vector .............................................................10 2.3.2. Mdulo e inclinacin de un vector ...................................................11 RESUMEN..................................................................................................13
Unidad 2. Sistemas de Coordenadas.
Matemticas
OBJETIVOS
El alumno debe alcanzar los siguientes objetivos tras el estudio de la presente unidad didctica:
Representar en el plano puntos y vectores dados por sus coordenadas

cartesianas.
Obtener las coordenadas de un vector del que se conocen sus

componentes y las coordenadas de uno de sus representantes.
Calcular ciertas medidas geomtricas como distancias y puntos medios,

con apoyo de los procedimientos propios de la geometra analtica del plano.
Formacin Abierta
INTRODUCCIN
En esta unidad se ven conceptos que suponemos conocidos ya por todos, ejes cartesianos, coordenadas de un punto.... Nos sirven para situar puntos, vectores, segmentos... en el plano. Tener un sistema de referencia para calcular distancias y puntos medios de los segmentos, la misma funcin que hace un mapa cuando nos trasladamos por tierra, por mar... algo que ha resultado imprescindible en el desarrollo de la humanidad y es bsico para el desarrollo del temario. Por ello, planteamos un recordatorio de estos conceptos sencillos que aparecen de una forma u otra a lo largo de todo el temario desarrollado.
Matemticas
2.1. EJES DE COORDENADAS CARTESIANOS

En esta unidad se va a aprender a representar puntos y vectores en el plano, lo primero que hay que tener es una referencia, un lugar desde donde empezar a medir. Este sistema de referencia ser el formado por los ejes cartesianos. En el plano se consideran dos rectas perpendiculares, una horizontal y otra vertical. La recta horizontal se llama eje OX o eje de abscisas, y a la recta vertical se le llama eje OY o eje de ordenadas. El punto de corte de ambas rectas de llama Origen de coordenadas, representa el valor cero del eje OX y del eje OY. Veamos el dibujo:
OY 3 2 1 0 -3 -2 -1 -1 -2 -3 1 2 3 OX
Figura 2.1.
Ejes de coordenadas
Del origen de coordenadas a la derecha se encuentran los valores positivos del eje OX y a la izquierda los valores negativos. En el eje vertical OY, los valores positivos estn situados hacia arriba del origen y los valores negativos se sitan del origen hacia abajo. Vamos a ver cmo establecer una correspondencia entre los puntos del plano y pares de nmeros reales.
Formacin Abierta
2.1.1. COORDENADAS DE UN PUNTO

Se considera un punto P cualquiera del plano, se trazan las rectas paralelas a los ejes que pasan por el punto. Estas dos rectas cortan a los ejes, al eje OX en el punto a, y al eje OY en el punto b. Estos puntos o lugares a y b, representan la distancia del punto P al origen, medida sobre los ejes.
OY
P (a , b)
OX
Figura 2.2.
Punto P(a,b)
Al par de nmeros reales (a,b) se les llama coordenadas del punto P. La primera coordenada, el primer nmero del par, a, se llama abscisa de P o coordenada x de P. El segundo nmero b se corresponde con la coordenada y del punto, u ordenada del punto P. As, cualquier par de nmeros reales P(a,b) tiene una representacin grfica en el plano, se corresponde con un punto del plano. Y cualquier punto del plano puede representarse por un par de nmeros reales (a,b).
Veamos varios puntos representados en el plano y las coordenadas correspondientes
Matemticas
OY
Z (-4 , 7)
P (2 , 3)
OX
W (-6 , -2) V (6 , -3)
2.1.2. CUADRANTES
Como se puede observar los signos de las coordenadas determinan claramente la posicin que ocupan stos respecto a los ejes. Los ejes dividen el plano en cuatro partes que llamamos cuadrantes. Los cuadrantes se numeran de la siguiente forma:
2 CUADRANTE
1er CUADRANTE
3er CUADRANTE 4 CUADRANTE
Figura 2.3. Numeracin de los cuadrantes.
Luego los puntos del primer cuadrante tienen ambas coordenadas positivas (+a,+b), los del segundo cuadrante, la x negativa y la y positiva (-a,+b), en el tercero sern las dos coordenadas negativas (-a,-b) y por ltimo en el cuarto la abscisa positiva y la ordenada negativa (+a,-b).
Formacin Abierta
2.2. DISTANCIA ENTRE DOS PUNTOS

La distancia entre dos puntos se define como la longitud de la recta que los une. Para calcular esta distancia veremos una frmula que se basa en el teorema de Pitgoras.
Y2
d
P2 ( X 2 , Y 2 )
Y2 Y1
Y1
P1 ( X 1 , Y1 )
X 2 X1
X1
Figura 2.4.
X2
Teorema de Pitgoras aplicado en el clculo de la distancia existente entre dos puntos.
Sean dos puntos P1 y P2, con coordenadas P1 (x1,y1) y P2 (x2,y2). La distancia entre ellos viene dada por la siguiente frmula:
D = P1 P 2 =
(x 1 x 2 )2 + ( y 1 y 2 )2
Por supuesto siempre tomaremos el valor positivo de la raz, una distancia es algo siempre no negativo. Veamos cmo se aplica esta frmula en algunos ejemplos: La distancia entre (2,5) y (7,17) es D = La distancia entre (1,4) y (5,2) es D =
(2 7 )2 + (5 17 )2
= 169 = 13
(1 5)2 + (4 2)2
= 20 = 2 5
Matemticas
2.2.1. PUNTO MEDIO DE UN SEGMENTO

Ahora trataremos de encontrar las coordenadas del punto medio M(x,y) del segmento que une dos puntos P1(x1,x2) y P2(x1,x2).
Y2
Y
P1 ( X 1 , Y1 )
M ( X ,Y )
P2 ( X 2 , Y2 )
Y1
X1
Figura 2.5.
X2
Punto medio de un segmento
Las coordenadas (x,y) de ese punto medio M del segmento que une P1(x1,x2) y P2(x1,x2) vienen dadas por la siguiente frmula:
x=
x1 + x 2 2
y=
y1 + y 2 2
Vamos a ver unos ejemplos:
El
punto
medio
del
segmento
que
une
(2,9)
(4,3)
es
2 + 4 9 + 3 , = (3,6) 2 2
El punto medio entre (-5,1) y (1,4) es
5 5 +1 1+ 4 , = 2, 2 2 2
Formacin Abierta
2.3. VECTORES
Visto y entendido el concepto de punto y segmento en un plano, vamos a definir lo que es un vector. Un vector no solo indica una posicin en el plano, digamos que determina un movimiento, un desplazamiento en el plano.
Un vector es un segmento orientado en el plano. Por lo tanto est caracterizado por su punto origen y su extremo o por la longitud del segmento, su direccin y su sentido.
Una de las formas de determinar un vector es conociendo los puntos que marcan sus extremos dados en orden. Un desplazamiento tiene un punto de partida y un destino. La direccin del vector es la de la recta que une los dos puntos dados y el sentido depende del orden en que se den los puntos, cual es el origen y cual el extremo. Situndonos en el plano, conocemos dos puntos, uno de ellos es el origen y otro el extremo del vector. Las coordenadas de estos puntos nos sirven para hallar las componentes del vector.
2.3.1. COMPONENTES DE UN VECTOR

Sean los puntos P1(x1,y1) y P2(x2,y2), el vector P1 P2 = V = ( v1 , v 2 ) , las
componentes son v1, v2, y la forma de hallarlas es
v1 = x 2 x 1 y
v 2 = y 2 y1 .
V (V1 ,V2 )
P2 ( X 2 , Y2 )
P1 ( X 1 , Y1 )
x 2 x1 = V 1
Figura 2.6. Componentes de un vector
10
Matemticas
Las componentes del vector que tiene por extremos P1(2,-3) y P2(1,4) son P1 P2 = V = (1 2, 4 3) = ( 1,7) . Las componentes del vector que tiene por extremos P1(-1,6) y P2(0,-1) son P1 P2 = V = ( 1 0, 6 1) = ( 1,7) . Observar que hay dos vectores con las mismas componentes pero distintos puntos extremos. Estos dos vectores del ejemplo son vectores equipolentes, o sea, el mismo vector, solo que situado en distinto lugar del plano. Todos los vectores que tienen sus componentes iguales son equipolentes, indican el mismo desplazamiento. Conociendo las componentes de un vector y uno de los puntos que lo determinan, origen o extremo, es muy sencillo calcular el punto que falta sin ms que despejar de la frmula de las componentes.
2.3.2. MDULO E INCLINACIN DE UN VECTOR

Otra forma de caracterizar vectores es conociendo su mdulo y el ngulo que forman con el eje OX.
Figura 2.7.
Mdulo y ngulo de un vector.
El mdulo o norma de un vector se define como la longitud del segmento que une los puntos origen y extremo de un vector y se denota V Para calcularlo nos basaremos en la frmula vista para hallar la distancia entre dos puntos.
11
Formacin Abierta
Sean los puntos P1(x1,y1) y P2(x2,y2), el vector P1 P2 = V = ( v1 , v 2 ) , entonces

2 V = v1 + v 2 = 2
(x 1 x 2 )2 + ( y 1 y 2 )2 .
La inclinacin de un vector se determina midiendo el ngulo que forma el mismo con la parte positiva del eje OX. En una de las siguientes unidades, la dedicada a trigonometra, se trata con mayor detenimiento el tema de los ngulos, sus medidas, sus razones trigonomtricas y en la unidad dedicada a los nmeros complejos se vuelve al tema de vectores, con su mdulo e inclinacin. El ngulo buscado es aquel cuya tangente vale
v2 . v1
As, en esta unidad, solamente se pretende que quede claro que una forma de determinar un vector es conociendo su mdulo y el ngulo que forma con el eje OX midindolo desde la parte positiva.
12
Matemticas
RESUMEN
Sobre el plano se consideran dos rectas perpendiculares entre s, una
horizontal y otra vertical, forman un conjunto de dos ejes que llamamos ejes cartesianos. El punto de corte de los dos ejes es el Origen de coordenadas.
El eje horizontal es el eje de abscisas o eje OX, y el vertical es el eje de

ordenadas o eje OY.
Partiendo de este sistema de referencia podemos hacer corresponder a

cada punto del plano un par de n reales, que llamaremos coordenadas y a cada par de reales le corresponde un punto del plano.
Al par de nmeros reales (a,b) se les llama coordenadas del punto P.

La primera coordenada, el primer nmero del par, a, se llama abscisa de P o coordenada x de P. El segundo nmero b se corresponde con la coordenada y del punto, u ordenada del punto P.
Grficamente vemos de forma clara el valor de las coordenadas y los

cuadrantes en que dividen los ejes al plano.
+
2 CUADRANTE 1er CUADRANTE P(a , b)
3er CUADRANTE
4 CUADRANTE
13
Formacin Abierta
Sean dos puntos P1 y P2, con coordenadas P1 (x1,y1) y P2 (x2,y2). La distancia entre ellos viene dada por la siguiente frmula:
D = P1 P 2 =
(x 1 x 2 )2 + ( y 1 y 2 )2
Las coordenadas (x,y) de ese punto medio M del segmento que une
P1(x1,x2) y P2(x1,x2) vienen dadas por la siguiente frmula:
x=
x1 + x 2 2
y=
y1 + y 2 2
Un vector es un segmento orientado en el plano. Por lo tanto est

caracterizado por su punto origen y su extremo o por la longitud del segmento, su direccin y su sentido.
Las componentes de un vector las determinamos a partir de los puntos

origen P1(x1,y1) y extremo P2(x2,y2) del mismo, P1 P2 = V = ( v1 , v 2 ) las componentes las componentes son v1, v2, y la forma de hallarlas es
v1 = x 2 x 1 y v 2 = y 2 y1 .
El mdulo o norma de un vector es la longitud del segmento

determinado por sus extremos. Podemos hallarlo partiendo de sus componentes o de las coordenadas de los puntos aplicando la siguiente frmula:
2 V = v1 + v 2 = 2
(x 1 x 2 )2 + ( y 1 y 2 )2
La inclinacin de un vector se determina midiendo el ngulo que

forma el mismo con el eje OX.
14
MATEMTICAS
3
RECTAS EN EL PLANO
Matemticas
NDICE
OBJETIVOS .................................................................................................3 INTRODUCCIN ..........................................................................................4 3.1. Ecuacin de la recta ..............................................................................5 3.1.1. Ecuacin de una recta que pasa por dos puntos ..............................5 3.1.2. Ecuacin punto-pendiente ................................................................6 3.1.3. Ecuacin explcita de la recta ..........................................................7 3.1.4. Ecuacin general de la recta.............................................................8 3.2. Situacin de una recta en el plano .......................................................9 3.2.1. Signo de la pendiente .......................................................................9 3.2.2. Rectas horizontales y verticales......................................................10 3.3. Incidencia de recta y recta ..................................................................11 3.3.1. Rectas paralelas y perpendiculares ................................................12 RESUMEN..................................................................................................15
Unidad 3. Rectas en el Plano.
Matemticas
OBJETIVOS
El alumno debe alcanzar los siguientes objetivos:
Conocer diferentes tipos de ecuacin de una recta en funcin del

conocimiento de algn elemento que la determine.
Resolver situaciones geomtricas sencillas con el apoyo de las

coordenadas de los puntos, los vectores y las ecuaciones de las rectas.
Saber determinar la posicin relativa de un par de rectas dadas o decidir

sobre la pertenencia de un punto a una recta determinada.
Formacin Abierta
INTRODUCCIN
En la unidad anterior hemos visto los ejes de coordenadas cartesianas en el plano, la forma de representar un punto cualquiera por un par de nmeros reales, los vectores, la distancia entre dos puntos cualesquiera... En esta unidad veremos las rectas en el plano.Geomtricamente todos sabemos que la recta es el camino ms corto entre dos puntos, pero adems de esta idea sencilla e intuitiva, una recta sobre un plano representa infinitos puntos que cumplen una determinada condicin. Es interesante conocer bien la forma de representar una recta a travs de sus ecuaciones puesto que numerosos fenmenos en la naturaleza se pueden representar de esta manera. Por ejemplo, el espacio recorrido por un mvil que lleva una velocidad constante en funcin del tiempo que transcurrido desde su partida, se representa con una recta en el plano. El eje OX se identificar con el tiempo t, y sobre el eje OY se localizarn los valores correspondientes al espacio s, recorrido por el mvil. Si dibujamos los pares de puntos (t,s) correspondientes a cada instante considerado, la figura resultante es una recta. Con muchos otros fenmenos fsicos y econmicos ocurre lo mismo, luego el estudio de las ecuaciones de las rectas ser muy prctico en campos bien distintos.
Matemticas
3.1. ECUACIN DE LA RECTA

Intuitivamente todos sabemos lo que es una recta, pero vamos a dar una definicin desde el punto de vista matemtico:
Una recta es el lugar geomtrico de los puntos del plano, alineados con un punto dado A y segn una direccin dada por un vector V.
La forma analtica de representar una recta es mediante una ecuacin lineal, los infinitos puntos que cumplen la condicin dada por la ecuacin son los puntos de la recta. La forma de saber si un punto pertenece o no a una recta es sustituir las coordenadas del punto en la ecuacin de la recta, si satisfacen la ecuacin, el punto pertenece a la recta, y si no la satisfacen, no se cumple la ecuacin es que el punto no pertenece a la recta considerada. Para determinar la ecuacin de una recta es necesario tener siempre dos condiciones, puede ser saber que la recta pasa por dos puntos determinados o conocer un punto y la inclinacin de la recta. Dependiendo de qu es lo que conocemos escribiremos la ecuacin de una u otra forma.
3.1.1. ECUACIN DE UNA RECTA QUE PASA POR DOS PUNTOS

Si las condiciones que tenemos para determinar la ecuacin de la recta son las coordenadas de dos puntos por los que pasa, plantearemos la ecuacin de la siguiente forma.
y
P1 ( X 1 , Y1 )
P2 ( X 2 , Y2 )
0
Figura 3.1.
Representacin de una recta que pasa dos puntos.
Formacin Abierta
Sean P1(x1,y1) y P2(x2,y2) dos puntos por los que pasa una recta, la ecuacin de la misma viene dada por:
x x1 y y1 Ecuacin de una recta que pasa por dos puntos = x 2 x 1 y 2 y1

Escribir la ecuacin de una recta que pasa por los puntos (2,3) y (-2,5).
x2 y3 x 2 y3 = = 2(x 2 ) = 4(y 3) 22 53 4 2 1 1 x +1 = y 3 y = x + 4 2 2
Dejando despejada la variable dependiente, y.
3.1.2. ECUACIN PUNTO-PENDIENTE

Cuando los datos conocidos sean un punto y la pendiente de la recta, plantearemos la ecuacin de otra manera. Antes de esto recordaremos qu es la pendiente de una recta. La pendiente de una recta es una magnitud que refleja o mide la inclinacin de la misma. Est relacionada con el ngulo que forma la recta con el eje OX, a ese ngulo le llamaremos .
y
P2 ( X 2 , Y2 )
y2 y1
P1 ( X 1 , Y1 )
x2 x1 x
Figura 3.2.
Representacin de la pendiente de una recta.
Matemticas
La
pendiente
viene
dada
por:
m=
(x 2 , y 2 ) cualquiera
y1 y 2 , x1 x 2
siendo
(x 1 , y1 )
dos puntos de la recta. Como se ver en la unidad de
trigonometra este valor m es el valor de la tangente del ngulo formado por la recta y la parte positiva del eje OX. Entonces, si la informacin de la que disponemos es un punto de la recta (x 1 , y1 ) y su pendiente m, la forma de plantear la ecuacin es:
y y1 = m(x x 1 ) Ecuacin punto-pendiente

Plantea la ecuacin de una recta que pasa por el punto (5,-3) y tiene pendiente m=2.
y (3) = 2( x 5) y + 3 = 2 x 10 y = 2 x 13
3.1.3. ECUACIN EXPLCITA
DE LA RECTA
Partiendo de cualquier ecuacin se puede despejar la y, variable dependiente, como se ha hecho en los dos ejemplos, y la expresin queda de la forma: Y=mx+b Ecuacin explcita de la recta Las dos constantes que aparecen en esta ecuacin tienen mucho significado, m es la pendiente de la recta b es la ordenada en el origen, o sea, el valor que toma y, cuando x=0 En el ejemplo anterior la ecuacin explicita es y=2x-13. Donde m=2, la pendiente y b=-13, la ordenada en el origen.
Formacin Abierta
3.1.4. ECUACIN GENERAL DE LA RECTA

Partiendo de cualquiera de las ecuaciones anteriores, podemos despejar y poner todos los trminos igualados a cero, esa es la expresin que se llama ecuacin general de la recta. Ax+By+Cz=0 Ecuacin general de la recta En el ejemplo, la ecuacin general sera: y-2x+13=0. La pendiente de una recta dada en forma general la hallaramos partiendo de los coeficientes aplicando m =
A B
Matemticas
3.2. SITUACIN DE UNA RECTA EN EL PLANO

La pendiente es algo fundamental en el estudio de las rectas. La pendiente caracteriza a las rectas horizontales, verticales, nos habla de su inclinacin y determina las rectas paralelas o perpendiculares a una dada.
3.2.1. SIGNO DE LA PENDIENTE

Si una recta tiene pendiente positiva, m>0 indica que su inclinacin es como en la figura y el ngulo es menor de 90.
m>0
Figura 3.3.
Pendiente positiva.
Si la pendiente es negativa, m<0 , el ngulo es mayor de 90 y la inclinacin de la recta es como en la figura:
m<0
0 x
Figura 3.4.
Pendiente negativa.
Formacin Abierta
3.2.2. RECTAS HORIZONTALES Y VERTICALES

Las rectas horizontales son paralelas al eje OX y tienen por pendiente m=0. Las rectas verticales, paralelas al eje OY tienen por pendiente m = .
y y
m= m=0
Figura 3.5.
Rectas paralelas a los ejes OX e OY.
10
Matemticas
3.3. INCIDENCIA DE RECTA Y RECTA

Geomtricamente hay tres posibilidades para la posicin relativa de dos rectas en el plano R1 y R2: Secantes, si se cortan en un nico punto, coincidentes, si tienen infinitos puntos en comn, o sea, son la misma recta y paralelas, si no se cortan en ningn punto.
R1
P ( x, y )
R2
R1 R2
R1 R2
Figura 3.6.
Posiciones relativas de dos rectas en un plano.
Analticamente, o sea fijndonos en las ecuaciones de las rectas, estas posibilidades se corresponden con las siguientes situaciones. Consideramos el sistema de dos ecuaciones con dos incgnitas formado por las ecuaciones de ambas rectas, las rectas sern: Secantes El sistema de ecuaciones tiene una nica solucin Coincidentes El sistema tiene infinitas soluciones, ecuaciones proporcionales Paralelas El sistema no tiene solucin. Determinar la posicin relativa de las dos rectas siguientes:
r 2 x 3y + 6 = 0 s 2x + y 10 = 0
Para ello lo que haremos es solucionar el sistema de ecuaciones formado, al hacerlo, queda como ejercicio para el alumno, obtenemos un nica solucin, x=3, y=4. Luego son dos rectas secantes y el punto de corte es P(3,4). Hacer lo mismo con las rectas:
r 2x + y = 20 s 10x + 5y = 100
11
Formacin Abierta
Vemos claramente que son dos ecuaciones proporcionales, si multiplicamos la primera por cinco, obtenemos la segunda. Eso indica que representan a la misma recta, o sea, son dos rectas coincidentes. Si resolvemos el sistema vemos que tiene infinitas soluciones, situacin que implica que las dos rectas son coincidentes. Y la posicin relativa de las siguientes rectas:
r 5x + 6 y 7 = 0 s 10 x + 12 y + 8 = 0
Al resolver el sistema, ejercicio que debe realizar el alumno, resulta un sistema incompatible, sin solucin, lo que indica que las rectas son paralelas. Si calculamos la pendiente de ambas, ejercicio propuesto para el alumno, se comprueba que son iguales.
3.3.1. RECTAS PARALELAS Y PERPENDICULARES

Todas las rectas paralelas a una dada tienen en comn con ella la pendiente, o sea, todas las rectas paralelas a una dada tienen la misma pendiente. Luego, para comprobar si dos rectas son o no paralelas sin dibujarlas y sin solucionar el sistema de ecuaciones correspondiente, bastar con que comparemos sus pendientes. Sean dos rectas R1 y R2, con pendientes m1 y m2, entonces R1 y R2 son paralelas m1 = m 2
12
Matemticas
Comprobar si las siguientes rectas son paralelas:
x 3 y 1 = y 2x + y 1 = 0 2 1
Despejando y en las dos ecuaciones, localizamos el coeficiente de x que es la pendiente y se ve que m=2 en ambas rectas. Luego son paralelas.
La condicin que cumplen dos rectas perpendiculares es que sus pendientes son opuestas e inversas. Dos rectas son perpendiculares si al cortarse forman un ngulo recto, un ngulo de 90. Sean dos rectas R1 y R2, con pendientes m1 y m2, entonces son perpendiculares si se cumple m1 =
1 . m2 1 m2
R1 y R2 perpendiculares m1 =
Es evidente que la perpendicularidad entre rectas es un caso particular de rectas secantes, se cortan en un nico punto y el ngulo que forman al cortarse es un ngulo recto,90.
Las
rectas
R1: y = 2 x + 3
R2: y =
1 x+3 2
son
perpendiculares, por la forma de las pendientes, y su punto de corte, se halla solucionando el sistema de ecuaciones. El punto es P(0,3)
13
Matemticas
RESUMEN
Una recta es el lugar geomtrico de los puntos del plano, alineados con
un punto dado A y segn una direccin dada por un vector V.
La forma de saber si un punto pertenece o no a una recta es sustituir

las coordenadas del punto en la ecuacin de la recta, si satisfacen la ecuacin, el punto pertenece a la recta, y si no la satisfacen, no se cumple la ecuacin es que el punto no pertenece a la recta considerada.
Para determinar la ecuacin de una recta es necesario tener siempre

dos condiciones, puede ser saber que la recta pasa por dos puntos determinados o conocer un punto y la inclinacin de la recta. Hemos visto distintas expresiones para la ecuacin de una recta:
x x1 y y1 Ecuacin de una recta que pasa por dos puntos = x 2 x 1 y 2 y1 y y1 = m(x x 1 ) Ecuacin punto-pendiente
Y=mx+b Ecuacin explcita de la recta Ax+By+Cz=0 Ecuacin general de la recta
La pendiente de una recta, m, representa la inclinacin de la recta

respecto a la parte positiva del eje OX. Est relacionada con el ngulo que forma la recta con el eje OX, a ese ngulo le llamaremos .
Como se ver en la unidad de trigonometra este valor m es el valor de la

tangente del ngulo formado por la recta y la parte positiva del eje OX. Las rectas horizontales son paralelas al eje OX y su pendiente es m=0. Las rectas verticales, paralelas al eje OY tienen por pendiente m = .
15
Formacin Abierta
Si una recta tiene pendiente positiva, m>0 indica que el ngulo es

menor de 90. Si la pendiente es negativa, m<0, el ngulo es mayor que 90.
Posicin relativa de dos rectas en el plano. Secantes, si se cortan en

un nico punto, coincidentes, si tienen infinitos puntos en comn, o sea, son la misma recta y paralelas, si no se cortan en ningn punto. Secantes El sistema de ecuaciones tiene una nica solucin Coincidentes El sistema tiene infinitas soluciones, ecuaciones proporcionales Paralelas El sistema no tiene solucin.
Todas las rectas paralelas a una dada tienen en comn con ella la
pendiente, o sea, todas las rectas paralelas a una dada tienen la misma pendiente. R1 y R2 son paralelas m1 = m 2
La condicin que cumplen dos rectas perpendiculares es que sus

pendientes son opuestas e inversas.
R1 y R2 perpendiculares m1 =
1 m2
16
MATEMTICAS
4
TRIGONOMETRA
Matemticas
NDICE
OBJETIVOS .................................................................................................3 INTRODUCCIN ..........................................................................................4 4.1. Trigonometra .........................................................................................5 4.1.1. Medidas de ngulos ..........................................................................5 4.2. Razones trigonomtricas de un ngulo...............................................7 4.2.1. En un tringulo rectngulo ................................................................7 4.2.2. En una circunferencia .......................................................................9 4.2.3. Relaciones entre las razones Trigonomtricas de un ngulo .........10 4.2.4. Razones exactas de ngulos ..........................................................11 4.2.5. Lneas y signos de las razones trigonomtricas .............................12 4.2.6. Razones trigonomtricas de un ngulo cualquiera relacionadas con un ngulo del 1 cuadrante.......................................................14 4.3. Aplicaciones de la trigonometria........................................................19 4.3.1. Resolucin de tringulos rectngulos .............................................19 4.3.2. Resolucin de tringulos cualesquiera ...........................................21 4.3.2.1. Teorema del seno........................................................................21 4.3.2.2. Teorema del coseno....................................................................23 4.4. Funciones trigonomtricas directas e inversas................................27 4.4.1. Directas ...........................................................................................27 4.4.2. Inversas...........................................................................................30 4.4.3. Otras frmulas.................................................................................30 RESUMEN..................................................................................................33
Unidad 4. Trigonometra
Matemticas
OBJETIVOS
Tras el estudio de la presente unidad didctica el alumno debe saber:
Expresar medidas angulares en grados o en radianes y calcular las

equivalencias entre ellas.
Calcular las razones trigonomtricas de los ngulos agudos de un

tringulo rectngulo. Obtencin de ngulos y distancias en situaciones cotidianas.
Calcular las razones trigonomtricas de un ngulo si se conoce una

cualquiera de ellas.
Obtener las razones trigonomtricas de un ngulo con ayuda de las de

otro que pertenece al primer cuadrante o con las de otros que estn relacionados con l.
Resolver tringulos cualesquiera mediante la utilizacin del teorema de los

senos y del teorema del coseno .
Calcular reas de tringulos y figuras poligonales mediante una previa

triangulacin, si fuera necesario, y la aplicacin de las herramientas trigonomtricas apropiadas a cada caso.
Conocer las funciones trigonomtricas directas e inversas.
Formacin Abierta
INTRODUCCIN
Para comprender el universo, el sistema solar, predecir eclipses, conocer la distancia de la tierra al sol, hay que medir distancias entre objetos no accesibles. La parte de las matemticas que surgi a raz de estas necesidades y que estudia estos problemas es la trigonometra. El origen de la trigonometra se atribuye a Hiparco de Nicea (190-125 a.c.), que la aplic a sus clculos astronmicos y confeccion las primeras tablas trigonomtricas. En este tema, nos vamos a ocupar de medir alturas de faros, de torres o en general de objetos a los que no podemos acceder directamente para ello. Utilizaremos las distancias que si que podamos medir y los ngulos bajo los que observamos los objetos. Dado que la trigonometra trabaja con ngulos, son necesarios instrumentos para medirlos, como el teodolito, el gonimetro..Quiz lo ms habitual en nuestro entorno es que en cualquier actividad de construccin nos encontremos a un topgrafo tomando medidas de ngulos.
Matemticas
4.1. TRIGONOMETRA
ngulo: parte del plano comprendido entre dos rectas que se cortan.
B
Figura 4.1. ngulo entre dos rectas
0 s
4.1.1. MEDIDAS DE NGULOS

Para medir ngulos se emplean como: Unidades principales: Angulo completo, ngulo llano y ngulo recto.
ngulo completo ngulo llano ngulo recto
90 180 360
Figura 1.1.
Unidades principales de un ngulo.
Sistemas de unidades:
Angulo completo Sistema sexagesimal Sistema basado en radianes Angulo llano Angulo recto
360 2
180
90 /2
Formacin Abierta
1 radio 1 rad
Figura 1.2.
Representacin de un radin.
Radian es la medida de un ngulo central cuyo arco mide igual que un arco de la circunferencia. Grado sexagesimal es cada una de las 360 partes iguales en las que dividimos un ngulo completo. Para hallar los radianes que tiene un ngulo completo razonaremos as: La longitud de la circunferencia es L = 2r =2 radios. Cada radio de arco implica un radin en el ngulo central. Luego el ngulo completo son 2 radianes. Expresar en radianes un ngulo de 135.360 radianes. 2
360 135
x =
2 ra d ia n e s x ra d ia n e s 2 1 3 5 3 = ra d ia n e s 360 4
Si observas, hemos aplicado una sencilla regla de tres, para obtener la equivalencia de grados y radianes. Expresar en grados sexagesimales 2,4 radianes.
2
2 ,4
360 y
y =
432 2 ,4 3 6 0 = g ra d o s 2
Matemticas
4.2. RAZONES TRIGONOMTRICAS DE UN NGULO

Las vamos a definir de dos formas, en primer lugar partiendo de un tringulo rectngulo y luego sobre una circunferencia dibujada en el plano cartesiano.
4.2.1. EN UN TRINGULO RECTNGULO

-Son las distintas proporciones que se establecen entre los lados de un tringulo rectngulo:
Notacin universal: Los lados del tringulo se nombran con la misma letra que su ngulo opuesto pero en minscula. Como se ve en la figura siguiente.
C a b A
a = hipotenusa b = opuesto de B o contiguo de C c = opuesto de C o contiguo de B
-Las razones se definen para un ngulo agudo, menor de 90, menor que el ngulo recto Seno de un ngulo es su cateto opuesto partido por la hiipotenusa b / a = senB = cosC Coseno de un ngulo es su cateto adyacente partido por su hipotenusa. c / a = cosB = senC
Formacin Abierta
Tangente de un ngulo es su cateto opuesto partido por su cateto adyacente b / c = tgB = cotgC Cosecante de un ngulo es la hipotenusa partido por el cateto opuesto. a / b = cosecB = secC Secante de un ngulo es la hipotenusa dividida por el cateto adyacente. a / c = secB = cosecC Cotangente de un ngulo es el cateto adyacente partido por el cateto opuesto. c / b = cotgB = tgC
En un tringulo rectngulo los catetos miden 8m. y 6m. Hallar las razones trigonomtricas del menor de sus ngulos. Como se puede ver en la figura anterior, el ngulo menor se opone al lado menor. Por el teorema de Pitgoras, la medida de la hipotenusa ser
a = 16 + 36 = 10m.
Aplicando las frmulas y las definiciones que acabamos de ver. sen B= 6/10= 3/5 Cos B= 8/10= 4/5 Tg B= 6/8= Cosec B= 10/6= 5/3 Sec B= 10/8= 5/4 Cotg B= 8/6= 4/3.
Matemticas
El teorema de Pitgoras nos da una frmula que permite relacionar la longitud de la hipotenusa y los dos catetos de un tringulo rectngulo. En un tringulo rectngulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos. Frmula: a2 = b2 + c2
C a b A
4.2.2. EN UNA CIRCUNFERENCIA

Para ello recordaremos primero el concepto de coordenadas cartesianas en el plano. Coordenadas cartesianas: Estn en funcin de las medidas de los ejes de coordenadas. Coordenada X es la medida sobre el eje de abscisas (el eje horizontal) y coordenada Y que es la medida sobre el eje de ordenadas (el eje vertical). En un sistema de coordenadas cartesianas dibujamos una circunferencia con centro en el origen y radio r. Tomando como lado origen el semieje positivo de abscisas construimos un ngulo agudo .
y C
= r
c=x
b=y
Formacin Abierta
Por el punto C, donde ese lado extremo corta a la circunferencia, trazamos la perpendicular al eje de abscisas y se forma un tringulo rectngulo OCA. Ahora definiremos las razones trigonomtricas de este ngulo basndonos en este tringulo, donde la hipotenusa a = r es el radio de la circunferencia, el cateto opuesto b =y es la ordenada del punto C y el cateto adyacente es c= x la abscisa del punto C. Para cualquier ngulo en la circunferencia, definiremos sus razones trigonomtricas por medio del radio r, y las coordenadas del punto C (x,y) , punto en el que el lado extremo del ngulo corta a la circunferencia.
Seno de es la ordenada en el punto C partido por el radio de la Sen = y/r circunferencia Coseno de es la abscisa del punto C partida por el radio de la Cos = x/r circunferencia Tangente de es la ordenada del punto C partido por su abscisa Tg = y/r
Cosecante de es el radio de la circunferencia partido por la ordenada en Cosec= r/y el punto C Secante de es el radio de la circunferencia partido por la abscisa del punto Sec = r/x C. Cotangente de es la abscisa del punto C partido por la ordenada de C Cotg = x/y
4.2.3. RELACIONES ENTRE LAS RAZONES TRIGONOMTRICAS

DE UN NGULO Como habrs observado las razones trigonomtricas de un ngulo estn muy relacionadas entre si. Vamos a escribir esas relaciones. Cosec =
1 sen
Sec =
1 cos
10
Matemticas
Cotg =
1 tg
Tg =
sen cos
Aparte de estas cuatro que son muy fciles de comprobar casi solamente mirando los dibujos, hay otras tres relaciones ms de tipo cuadrtico, que son muy interesantes. 1 = sen2 + cos2 Cosec2 = 1+ cotg2 Sec2 = 1 + tg2 Todas estas frmulas nos sern de utilidad para deducir las razones trigonomtricas de un ngulo del que conocemos una de ellas y para resolver tringulos.
4.2.4. RAZONES EXACTAS DE NGULOS

En esta tabla aparecen las razones trigonomtricas de los ngulos ms usados, sabindonos estos valores podremos hallar fcilmente las razones de otros ngulos relacionados con ellos. Luego veremos cmo.
0 Sen Cos Tg Cosec Sec Cotg
0/2
1/0
1/0
30
1/2
3/2
3/3
2 3 /3
45
2/2
2/2
60 90 180
3/2
1/2 0 -1
2 3 /3
2 1/0 -1
3/3
1 0
1/0 0
1 1/0
0 1/0
11
Formacin Abierta
Para ver cmo relacionar las razones trigonomtricas de unos ngulos con otros y para aprender algo ms sobre las mismas vamos a desarrollar otro apartado sobre las lneas y los signos de las razones.
4.2.5. LNEAS Y SIGNOS DE LAS RAZONES TRIGONOMTRICAS

A) Lneas trigonomtricas. Vamos a construir ahora una circunferencia como la de antes, pero con radio la unidad, r = 1.
SENO y C COSENO y C
0 B
0 B
sen =
CB OC
= CB
cos =
OB = OB OC
OC = 1 = Radio
Figura 1.3.
Circunferencia de radio 1, seno y coseno del ngulo
As, es fcil ver que el seno de un ngulo coincide con el cateto opuesto del tringulo y su coseno con el cateto adyacente del mismo.
Una circunferencia de radio la unidad, se llama circunferencia goniomtrica.
B) Signos de las razones trigonomtricas.

Basndonos en el apartado anterior, vamos a ver los signos de las distintas razones trigonomtricas de un ngulo cualquiera. Nos bastar con saber los signos del seno y el coseno porque los del resto de razones se deducen directamente de ellos usando las relaciones ya vistas.
12
Matemticas
Los signos de seno y coseno dependern del cuadrante en el que est situado el ngulo. El signo del seno ser el del eje de ordenadas, eje vertical, o sea, positivo en el primer y segundo cuadrante y negativo en el tercero y en el cuarto. El signo del coseno ser el del eje de abscisas, eje horizontal, positivo en el primer y cuarto cuadrante y negativo en el segundo y tercero.
SENO Y COSEC
COS Y SEC 90
TG Y COTG 90
180
++ - 0 180 y
- + - +
270
0 ; 360
- + + y x
Conociendo los signos de las razones trigonomtricas de un ngulo y las relaciones entre las mismas, podremos conocer todas ellas partiendo de una sola y del cuadrante en que se encuentra el ngulo.
Vemoslo en un ejemplo. Ejercicio 1 Sabiendo que senX = 0,3 y que 90< X <180, hallar las restantes razones trigonomtricas de X.
13
Formacin Abierta
Solucin
Signos: El ngulo pertenece al 2 cuadrante, luego su coseno ser

negativo
Valores:
Cosec x = 1 1 = 0,3 sen x
Sen 2 x + Cos 2 x = 1 0,32 + Cos 2 x = 1 Cos 2 x = 1 - 0,09 = 0,91 cos x = 0,91 y como sabemos que es negativo, tomaremos el valor negativo de la raiz. 1 1 Sec x = =cosx 0,91 Tgx = senx 0,3 = cosx 0,91 1 - 0,91 = tgx 0,3
cotgx =
Hallar las restantes razones trigonomtricas de un ngulo x tal que sec x= 2 y sabemos que 0< x < /2
4.2.6. RAZONES TRIGONOMTRICAS DE UN NGULO

CUALQUIERA RELACIONADAS CON UN NGULO DEL 1 CUADRANTE Ya conocemos los valores de las razones trigonomtricas de los ngulos ms usuales en el primer cuadrante, vamos a aprender a deducir las razones de ngulos relacionados con ellos. O aunque no conozcamos exactamente el valor de las razones, poder relacionar las razones de un ngulo cualquiera con las de un ngulo de primer cuadrante.
14
Matemticas
A. Dos ngulos que suman 180, ngulos suplementarios, en el 1 cuadrante y lgicamente situado en el 2 cuadrante.
Y
y A
x 0
x A
y X
y' = y x = -x
Como se ve en la figura, x = -x, y = y, luego las relaciones entre las razones de los ngulos suplementarios y las podremos deducir de estas igualdades de segmentos.
sen =
y' y = = sen r r x' - x cos = = = - cos r r
Conociendo el seno y el coseno de , ya sabramos deducir el valor de la tangente, secante.... Conclusin: Las razones del ngulo son iguales en valor absoluto a las razones de y los signos son los que corresponden al 2 cuadrante.
Tg 120 = - tg 60 = - 3 . Sec 135 = - sec 45 = - 2
B. Cuando y difieren en 180. - = 180, luego est situado en el 3 cuadrante.
15
Formacin Abierta
A y C x
0 x A
y X
y' = -y x = -x
Podemos ver en el dibujo que , x = -x , y = - y, igual que en el caso anterior podremos ver las razones de basndonos en estas igualdades entre los segmentos.
sen =
y' - y = = sen r r x' - x cos = = = - cos r r
El resto de las razones, como antes se deducen de stas. Conclusin: Las razones trigonomtricas del ngulo son iguales en valor absoluto a las de y los signos sern los del 3 cuadrante.
Cos 225 = - cos 45 =
- 2 2
Tg 240 = tg 60 =
C. Cuando y suman 360. ngulos opuestos. en el primer cuadrante, como siempre y estar en el cuarto cuadrante.
16
Matemticas
y x x y C X
y' = -y x = x
Podemos ver en el dibujo que , x = x , y = - y, procederemos igual que en los casos anteriores.
sen =
y' - y = = sen r r x' x cos = = = cos r r
Conclusin: las razones de un ngulo del 4 cuadrante, opuesto a son iguales en valor absoluto a las de y los signos del cuarto cuadrante.
Sen 330 = - sen30 = -1/2.
D. Cuando y difieren 360.

Y
C = C
x = x A
y= y X
y' = y x = x
17
Formacin Abierta
Como vemos en el dibujo, los ngulos coinciden sobre el primer cuadrante, Conclusin: Las razones de y son idnticas en valor y signo.
Tg 2655 = tg 135 = -tg 45 = -1. Sen(- 2730) = sen (-210) = sen150 = sen 30 = 1/2
Para transformar un ngulo mayor de 360 en otro que se encuentre en la circunferencia, o sea, menor que 360, no tenemos ms que dividir el ngulo que nos den entre 360 y quedarnos con el valor del resto de dicha divisin, este resto es el ngulo que buscamos. Para entendernos, el resultado de la divisin es el nmero de vueltas completas que damos y el resto indica el lugar donde pararamos. Un ngulo negativo no es ms que un ngulo medido en el sentido de giro opuesto al normal. El habitual, el que consideramos positivo es el contrario a las agujas del reloj y el negativo es el de las agujas horarias.
18
Matemticas
4.3. APLICACIONES DE LA TRIGONOMETRIA

Vamos a ver cmo aplicar estos conocimientos a problemas reales. Utilizaremos lo visto hasta ahora y veremos tambin algunos teoremas que completaran nuestro conocimiento y recursos para resolver problemas.
4.3.1. RESOLUCIN DE TRINGULOS RECTNGULOS

Resolver un tringulo rectngulo consiste en encontrar las medidas de sus seis elementos, tres lados y tres ngulos.
C a b 90 B c A
Recuerde que los tres ngulos de cualquier tringulo siempre suman 180.
1.Por ser un tringulo rectngulo sabemos que uno de sus ngulos es recto, o sea A = 90.Los otros dos ngulos restantes sumarn por tanto 90. B + C = 90. 2. Los lados, por el teorema de Pitgoras: a2 = b2 + c2. 3. Las razones trigonomtricas que relacionan lados y ngulos. Sen B = b/a, cos B = c/a, tg B = b/c, y lo mismo con el ngulo C.
19
Formacin Abierta
CASO 1: Conocidos dos lados:
Una escalera de tres metros de largo est apoyada sobre una pared, se apoya en el suelo a 1,5 m. de la misma. Qu ngulo forma la escalera con el suelo?
3m
1,5m
Tenemos un tringulo rectngulo. Conocemos la hipotenusa y el cateto adyacente del ngulo que buscamos. La razn trigonomtrica que relaciona cateto adyacente e hipotenusa es el coseno. Luego el ngulo que buscamos tiene un cos = 1,5/3 = = 0,5. Debemos encontrar un ngulo agudo que tenga coseno igual a 0,5, y ese ngulo sabemos que es 60. = 60 forma la escalera con el suelo.
Utilizando la calculadora tambin podemos hallar el valor del ngulo. Tendremos que usar la funcin cos-1 y aplicarla al valor 0,5.
Aplicando el teorema de Pitgoras podremos sacar fcilmente la longitud del otro lado del tringulo, la altura que alcanza la escalera en la pared. Igual que se ha hecho en el ejemplo del apartado 2.2.1. El ngulo que falta conocer es evidentemente 30.
20
Matemticas
CASO 2: Conocidos un lado y un ngulo.

C
70m
b 30 B c 90 A
Conocemos la hipotenusa y un ngulo, podemos usar tanto el seno como el coseno para resolver el tringulo. Usaremos el seno. Sabemos que sen 30 = = 0,5 = b/70 b = 70 0,5 = 35m. Igual que antes ya podemos fcilmente obtener las medidas del lado y ngulo que faltan.
4.3.2. RESOLUCIN DE TRINGULOS CUALESQUIERA 4.3.2.1. TEOREMA DEL SENO

Los lados de un tringulo cualquiera son proporcionales a los senos de los ngulos opuestos. Es decir:
a b c = = senA senB senC

Vemoslo sobre una figura.
C b h A
Al trazar la altura del tringulo obtenemos dos tringulos rectngulos: ACD y BCD. Vamos a trabajar sobre ellos.
21
Formacin Abierta
SenA =
h h = b senA b h h = a senB a
SenB =
Luego b senA = a senB
a b = senA senB
De la misma forma se obtiene
b c = senB senC
El teorema del seno permite resolver tringulos cualesquiera, no necesariamente rectngulos como en el caso anterior, en los que conozcamos: a) Dos lados y el ngulo opuesto a uno de ellos. b) Dos ngulos y un lado.
En el tringulo de la figura , hallar el ngulo B.
C 10m 30 A c B 8m
Solucin:
8 10 b a = = senB senA sen30 senB
22
Matemticas
senB =
10 sen30 5 = B = arco cuyo seno vale 5/8. 8 8
Con estos datos y aplicando el teorema del seno, tambin podramos hallar el lado c y el ngulo C. Este problema que se nos plantea de hallar un ngulo conociendo alguna de sus razones trigonomtricas lo resolveremos definiendo las funciones trigonomtricas inversas. Es el apartado 2.4 del tema.
4.3.2.2. TEOREMA DEL COSENO

El cuadrado de un lado es igual a la suma de los cuadrados de los otros dos, menos el doble producto de stos por el coseno del ngulo que forman. a2 = b2 + c2 2bc . cosA
C
C a b B D x A c
b h A
x c
Tringulo oblicungulo
Tringulo acutngulo
Consideramos en las figuras anteriores los tringulos rectngulos ACD y BCD. Entonces, en el tringulo oblicungulo: h2 = b2 x2 h2 = a2 (x+c)2 b2 x2 = a2 (x+c)2 b2 x2 = a2 x2- c2- 2xc a2 = b2 + c2 + 2xc
23
Formacin Abierta
Como x = - b. CosA (ya que por estar en el 2 cuadrante el cosA es negativo), resulta a2 = b2 + c2 2bc cosA. Y en el tringulo acutngulo: h2 = b2 x2 h2 = a2 (c - x)2 b2 x2 = a2 (c - x)2 b2 x2 = a2 x2 - c2 + 2xc a2 = b2 + c2 - 2xc Como x = b. CosA (ya que por estar en el 2 cuadrante el cosA es negativo), resulta a2 = b2 + c2 2bc cosA. El teorema del coseno permite cualesquiera cuando se conocen: resolver tringulos
a) Dos de sus lados y el ngulo comprendido entre ellos. b) Los tres lados.
Si las dos ramas de un comps forman un ngulo de 60 y su longitud es de 12 cm. Hallar la distancia a la que se encuentran las puntas.
60 b = 12 c = 12
24
Matemticas
Aplicando el teorema del coseno: a2 = b2 + c2 2bc . cosA a2 = 122 + 122 - 2 12 12 cos 60 a 2 = 144 a = 12 cm. Luego el tringulo formado por el comps tiene todos sus lados iguales, es un tringulo equiltero. Para la resolucin de tringulos cualesquiera, lo primero que tenemos que hacer es saber de qu tipo es el tringulo que nos proponen. Si es un tringulo rectngulo podremos aplicar: Relacin entre ngulos. Suman 180. Relacin entre los lados. Teorema de Pitgoras. Relacin entre lados y ngulos. Razones trigonomtricas. Si el tringulo no es rectngulo. Relaciones entre ngulos. Suman 180. Teorema del seno. Teorema del coseno.
El resolver tringulos sirve tambin para calcular el rea de los mismos. La frmula para calcular el rea de un tringulo es Area =
base altura . El poder 2
hallar el rea de cualquier tringulo a partir de datos de ngulos y lados, servir para hallar el rea de cualquier polgono o figura geomtrica que podamos dividir en tringulos.
Calcular el rea del tringulo siguiente:
25
Formacin Abierta
c = 10 cm h 30 B x a
b = 6 cm
C a-x
sen30 = cos 30 =
h 1 = h = 5cm 10 2 3 x = 2 10
Solucin: La altura divide al tringulo en dos tringulos rectngulos. En ellos podremos aplicar directamente las definiciones de las razones trigonomtricas y el teorema de Pitgoras.
Sen 30 =
h 1 = h = 5cm 10 2
Por otro lado, se necesita saber lo que vale a, la base del tringulo para poder hallar el rea. Podemos hallar su valor hallando los dos segmentos en que queda dividida por la altura, x, a-x.
Cos 30 =
x 3 = x = 5 3cm . 2 10
Y para hallar a-x, usaremos el teorema de Pitgoras.
62 = 52 + (a x ) (a x ) = 36 25 = 11 a x = 11cm
2 2
Luego la base del tringulo mide:
11 + 5 3cm = 11,9768cm
base altura a h 11,9768 5 = rea = = = 29,942cm 2 2 2
26
Matemticas
4.4. FUNCIONES TRIGONOMTRICAS DIRECTAS E INVERSAS

En este apartado vamos a ver la representacin grfica y las caractersticas ms relevantes de las funciones trigonomtricas ms usadas.
4.4.1. DIRECTAS
Y = sen X Esta funcin peridica es una aplicacin del conjunto de los ngulos en un intervalo de los nmeros reales, el intervalo [ 1,1] .
Se dice que es peridica porque los valores que toma se repiten cada 360, cada giro completo. El seno de 45 es igual al de 405.
sen x
F:A x
Y
R [-1,1]
1 0
0 0
3 2
-1 -1
Figura 1.4.
Representacin grfica de la funcin seno.
Caractersticas: 1.Campo de existencia: Existe para cualquier nmero real, ( ,+ ) 2.Continuidad: Es una funcin continua en todo el campo de existencia. 3.Cuadro de valores:
27
Formacin Abierta
X Sen X
0 0
90 1
180 0
270 -1
360 0
Y = Cos X La funcin peridica Y = Cos X es una aplicacin del conjunto de ngulos en el intervalo de los reales [ 1,1] .
F:A x
Y
cos x
R [-1,1]
-1 1
0 0
3 2
Figura 1.5.
Representacin grfica de la funcin coseno.
Caractersticas: 1.Campo de existencia: Existe para cualquier nmero real, ( ,+ ) 2.Continuidad: Es una funcin continua en todo el campo de existencia. 3.Cuadro de valores:
X Cos X 0 1 90 0 180 -1 270 0 360 1
28
Matemticas
Y = Tg X La funcin peridica Y = Tg X es una aplicacin del conjunto de los ngulos en el conjunto de los nmeros reales ( ,+ ) .
F:A x
Y
yR
0 0
3 2
-1
-2
Figura 1.6.
Representacin grfica de la funcin tangente
Caractersticas: 1.Campo de existencia: Existe para cualquier nmero real, salvo los que hacen cero a la funcin cos X. 2.Continuidad: Es una funcin continua salvo donde cos X = 0. Estos valores son los ngulos X = (2n 1)90, donde n = 1, 2, 3,.....
29
Formacin Abierta
3.Cuadro de valores:
X Tg X 0 0 90 180 0 270 360 0
4.4.2. INVERSAS
Al igual que ocurri en la resolucin de un tringulo rectngulo del que conocamos dos de sus lados, en ocasiones el valor que podemos obtener es el de una razn trigonomtrica y a partir de l hemos de averiguar el valor del ngulo al que corresponde. Las funciones trigonomtricas inversas son las que nos sirven para hallar el valor de un ngulo conociendo alguna de sus razones trigonomtricas. Y = arc sen X Leeremos Y es igual al arco cuyo seno vale X, y evidentemente es la funcin inversa del seno. Para hallar los valores del ngulo Y acudiremos a los valores de los ngulos ms usuales que ya conocemos o a la funcin sen-1 de la calculadora. Y = arc cos X, Y = arc tg X Se definen de forma anloga a la anterior y el clculo de valores tambin se hace de la misma manera. En la calculadora las funciones sern, cos 1 y tg-1.
4.4.3. OTRAS FRMULAS

Aqu hay otras frmulas que no vamos a explicar y servirn como referencia si se aplican en algn tema posterior.
Razones del ngulo suma Razones del ngulo diferencia
Sen ( + ) = sen cos + cos sen Cos ( + ) = cos cos + sen sen
Tg( + ) = tg + tg 1- tg tg
Sen ( ) = sen cos cos sen Cos ( ) = cos cos + sen sen
Tg( ) = tg tg 1 + tg tg
30
Matemticas
Razones del ngulo doble
Razones del ngulo mitad

1 cos Sen( ) = 2 2 1 + cos Cos( ) = 2 2
Sen2 = sen ( + ) = 2sen cos
Cos2 = cos ( + ) = cos 2 sen 2
Tg2 = tg( + ) =
2tg 1 tg 2
1 cos Tg( ) = 2 1 + cos
Razones que transforman el producto en sumas
Sen ( + ) + Sen ( ) = 2sen cos

A+ B A B cos 2 2
SenA + senB = 2 sen
Cos ( + ) + Cos ( ) = 2cos cos

A+ B A B cos 2 2
CosA + cos B = 2cos
Razones que transforman el producto en resta

SenA senB = 2cos A+ B A B sen 2 2
CosA cos B = 2 sen
A+ B A B sen 2 2
31
Matemticas
RESUMEN
Concepto de ngulo y medidas de los ngulos. Grados sexagesimales y
radianes. Radian es la medida de un ngulo central cuyo arco mide igual que un arco de la circunferencia. Grado sexagesimal es cada una de las 360 partes iguales en las que dividimos un ngulo completo.
Concepto de razn trigonomtrica. Hemos aprendido a calcularlas a

partir de un tringulo rectngulo y una circunferencia en el plano.
En el tringulo:
Seno de un ngulo es su cateto opuesto partido por la hiipotenusa Coseno de un ngulo es su cateto adyacente partido por su hipotenusa. Tangente de un ngulo es su cateto opuesto partido por su cateto adyacente Cosecante de un ngulo es la hipotenusa partido por el cateto opuesto. Secante de un ngulo es la hipotenusa dividida por el cateto adyacente. Cotangente de un ngulo es el cateto adyacente partido por el cateto opuesto.
Signos de las razones trigonomtricas de un ngulo cualquiera.

Conocemos los signos de las distintas razones sin ms que localizar el cuadrante en que de encuentra el ngulo.
33
Formacin Abierta
Relaciones entre las razones trigonomtricas de un ngulo.

1 sen
Cotg =
Cosec =
1 tg
Sec =
1 cos
Tg =
sen cos
1 = sen2 + cos2
Cosec2 = 1+ cotg2
Sec2 = 1 + tg2
Valores de las razones trigonomtricas de los ngulos ms usuales.

0 Sen Cos Tg Cosec Sec Cotg
0/2
1/0
1/0
30
1/2
3/2
3/3
2 3 /3
45
2/2
2/2
60 90 180
3/2
1/2 0 -1
2 3 /3
2 1/0 -1
3/3
1 0
1/0 0
1 1/0
0 1/0
Resolucin de tringulos rectngulos. Teorema de Pitgoras.

Aplicacin de las razones trigonomtricas.En un tringulo rectngulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos. Frmula: a2 = b2 + c2
34
Matemticas
Resolucin de tringulos cualesquiera. Teorema del seno y del coseno.

Los lados de un tringulo cualquiera son proporcionales a los senos de los ngulos opuestos. Es decir:
a b c = = senA senB senC

El cuadrado de un lado es igual a la suma de los cuadrados de los otros dos, menos el doble producto de stos por el coseno del ngulo que forman. a2 = b2 + c2 2bc . cosA
35
MATEMTICAS
5
NMEROS COMPLEJOS
Matemticas
NDICE
OBJETIVOS .................................................................................................3 INTRODUCCIN ..........................................................................................4 5.1. Unidad imaginaria y nmeros complejos ............................................5 5.1.1. La unidad imaginaria.........................................................................5 5.1.2. Nmeros complejos ..........................................................................6 5.1.3. Representacin grfica de un nmero complejo...............................7 5.2. Formas de expresar un nmero complejo...........................................8 5.3. Nmeros conjugados y opuestos de otro complejo ........................11 5.4. Potencias de la unidad imaginaria .....................................................13 5.5. Operaciones fundamentales con nmeros complejos.....................14 5.5.1. Suma y resta ...................................................................................14 5.5.2. Producto..........................................................................................14 5.5.3. Cociente ..........................................................................................16 5.5.4. Potencia de un complejo .................................................................18 5.5.5. Raz de un complejo .......................................................................19 RESUMEN..................................................................................................21
Unidad 5. Nmeros Complejos.
Matemticas
OBJETIVOS
Los objetivos que debe alcanzar el alumno tras el estudio de la presente unidad didctica son:
Escribir un nmero complejo en todas las formas conocidas sabiendo

pasar de una de ellas a otra cualquiera y representarlo en el plano.
Realizar operaciones con nmeros complejos expresando el resultado

tanto en su forma binmica como en su forma polar.
Calcular todas las races, tanto reales como complejas, de ecuaciones

reales.
Formacin Abierta
INTRODUCCIN
Como ya vimos en la unidad didctica 1, hay races de nmeros reales que no se pueden calcular, que no existen en la recta real. Como ya se indic para resolver esas races hemos de recurrir a otro tipo de nmeros, los nmeros complejos, que no pueden representarse sobre la recta real. Los nmeros complejos como veremos se representan sobre los ejes cartesianos, sobre el plano, luego nos servirn para indicar posiciones en el plano adems de para resolver ecuaciones que no tengan solucin en los nmeros reales. Aparecern en problemas de fsica o electricidad, para calcular impedancias o con la corriente alterna.
Matemticas
5.1. UNIDAD IMAGINARIA Y NMEROS COMPLEJOS

En el mbito de los nmeros reales hay ciertas operaciones que no tienen sentido, las races cuadradas de nmeros negativos, y en general las races de ndice par de cualquier real menor que cero.
Ejemplos:
9 , (-3)3/4 , log (-1)
Estos nmeros suelen aparecer como soluciones a ecuaciones del tipo: X2 + 1 = 0, donde obtenemos un valor para X = 1 . Para poder resolver este tipo de problemas hemos de ampliar el concepto de nmero a un conjunto ms amplio que es el conjunto de los nmeros complejos.
5.1.1. LA UNIDAD IMAGINARIA

En el caso de una raz cuadrada de cualquier real negativo a, actuaremos de la forma siguiente:
a = a -1
La unidad imaginaria es 1 = i , la raz de ( 1) la representaremos con la letra i, y cumple que i2 = -1, por tanto:
a =
a i
el concepto de
A partir de esta unidad imaginaria i vamos a entender nmero complejo.
Formacin Abierta
5.1.2. NMEROS COMPLEJOS

Un nmero complejo Z es un par ordenado de nmeros reales (a,b) a, b R. Donde los nmeros a y b representan: a= 1 componente o componente real. b= 2 componente o componente imaginaria.
El nmero expresado en funcin de la unidad imaginaria, sera a + bi. Por lo tanto es fcil entender: Z1= (a,0) es un nmero real. Z2= (0,b) es un nmero imaginario puro. Z3=(a,b) es un nmero complejo. Z4=(0, 1) es la unidad imaginaria.
Resolver la ecuacin x2 2x + 5 = 0.
Recordemos la frmula general para solucionar una ecuacin de 2 grado del tipo ax2 + bx + c = 0. X tiene en general dos soluciones que vienen dadas por
x=
b b 2 4ac 2a
Luego las soluciones a la ecuacin planteada, sern:
x=
( 2)2 4 1 5
2
= 1
16 4i = 1 = 1 2i 2 2
Matemticas
Luego las soluciones son dos complejos 1 + 2i, 1 - 2i. Estos nmeros complejos se llaman conjugados, ms adelante explicaremos ms despacio este trmino.
5.1.3. REPRESENTACIN GRFICA DE UN NMERO COMPLEJO

Un nmero complejo Z=(a,b) se representa por un punto del plano P=(a,b). Tomando como coordenadas la parte real y la parte imaginaria del nmero complejo. Este punto P del plano que representa al nmero complejo, se llama afijo del complejo. El eje horizontal es el eje real. El eje vertical es el eje imaginario.
Im Z(a,b) b
a
Figura 5.1.
Re
Representacin de un complejo en los ejes cartesianos
Formacin Abierta
5.2. FORMAS DE EXPRESAR UN NMERO COMPLEJO

1. Forma vectorial o par ordenado Z=(a,b) 2. Forma binmica Z = a + bi 3. Forma polar Z = r Para entender esta forma polar hemos de explicar los conceptos de mdulo y argumento de un complejo. El mdulo de un nmero complejo Z es r y es la raz cuadrada de la suma de los cuadrados de la componente real y la componente imaginaria.
r = a 2 + b2
El argumento del nmero complejo Z es y es el ngulo que forma el nmero complejo Z con el eje real (en sentido positivo). = arc tg
b a
Im Z(a,b) b
r
0
Figura 5.2.
Re
Mdulo y argumento de un nmero complejo
Matemticas
4. Forma trigonomtrica o mdulo argumental
Z = r (cos + isen )
b a
r = a 2 + b2
= arc tg
Resolver la ecuacin: x2 + 2x +4 = 0 y expresar las soluciones obtenidas de las cuatro formas explicadas.
Solucin: Por la frmula de la ecuacin de 2 grado.
x=
2 4 - 16 2 12 = 2 2
12 = 12i = 2 3i
Luego las soluciones expresadas en forma binomial sern:
1 + 3i , 1 - 3i
Ya podemos expresar estas soluciones tambin en forma cartesiana. (1,
3 ) , (1, - 3 )
Para pasar a la forma polar y la trigonomtrica tendr que hallar el mdulo y el argumento correspondientes a las dos soluciones. Tomamos la primera de ellas. X1 = 1+ Hallemos su mdulo:
3i
m1 =
12 + ( 3 ) 2 = 2
Formacin Abierta
Y el argumento:
1 = arc tg
Forma binmica
3 = 60 1
1+ 260 2
3i
Forma Polar Forma trigonomtrica
( cos60 + i sen60 )
Con la otra solucin haga lo mismo, el mdulo es el mismo y el argumento es 300.
Se ve claramente que cambiar de forma cartesiana a binomial es inmediato. Igual que ocurre con la forma polar y la trigonomtrica.
10
Matemticas
5.3. NMEROS CONJUGADOS Y OPUESTOS DE OTRO COMPLEJO

Dado un complejo Z = a + bi , su conjugado ( Z ) tiene la misma parte real y opuesta la parte imaginaria. Fjate, las dos soluciones del ejemplo anterior son conjugadas.
Z = a - bi
El complejo opuesto de Z = a + bi es -Z y tiene opuestas las componentes real e imaginaria de Z.
- Z = -a - bi
Im a + bi
Re
-a - bi opuesto
Figura 5.3.
a - bi conjugado
Conjugado y opuesto de un complejo.
Como se ve en la figura y claramente se puede comprobar, el mdulo de un complejo, de su conjugado y de su opuesto son iguales. El mdulo es la longitud del vector que representa el complejo en el plano independientemente de su posicin.
Encontrar dos nmeros complejos conjugados, sabiendo que la suma de sus componentes reales es 10, y que la suma de sus mdulos es 26.
Solucin:
11
Formacin Abierta
Por ser dos complejos conjugados los representamos a + bi, a- bi. Si la suma de sus componentes reales es 10, a+a = 10, luego a = 5, la parte real es 5. Dos nmeros complejos tienen el mismo mdulo, como hemos visto. Luego el mdulo de cada uno ser 13.
13 = a 2 + b 2 = 25 + b 2 169 = 25 + b 2 b 2 = 144 b = 12 .
Luego los nmeros buscados son: 5 + 12i, 5 12i.
12
Matemticas
5.4. POTENCIAS DE LA UNIDAD IMAGINARIA

Para elevar la unidad imaginaria a una potencia cualquiera basta con conocer el valor de las cuatro primeras potencias de la misma.
Como cualquier nmero, si lo elevo a cero, el resultado es uno, y para resolver el resto de las potencias trabajaremos con
i0 = 1 i1 = i = - 1 i 2 = 1 i3 = i i4 = 1
Cuando el exponente es superior a 4 se divide ste entre 4, y se eleva i al resto de la divisin.
i n = i 4c + r = i 4c i r = (i 4 ) i r = i r
c
Calcular i 36 ,i 23 . 36/4 =9 y el resto es cero, luego i 36 = i 0 = 1 23/4 = 5 y el resto es 3, luego i 23 = i 3 = i
13
Formacin Abierta
5.5. OPERACIONES FUNDAMENTALES CON NMEROS COMPLEJOS

5.5.1. SUMA Y RESTA
La suma (resta) de dos nmeros complejos es otro nmero complejo, cuya parte real es la suma (diferencia) de las partes reales de los nmeros dados y cuya parte imaginaria es la suma (diferencia) de las partes imaginarias de los nmeros dados.
Z1 + Z2 = (a + bi) + (c + di) = (a + c) + (b + d)i Z1 Z2 = (a + bi) (c + di) = (a c) + (b d)i

(3 + 5i) + (2 3 i) = (5 + 2i ). (3 + 5i) - (2 3 i) = (1+ 8i ). (2,-5) + (-6,1) = (-4,-4) (2,-5) - (-6,1) = (8,-6)
Para sumar y restar nmeros complejos es necesario representarlos en forma binomial o cartesiana.
5.5.2. PRODUCTO
El producto de complejos es una operacin que se hace de distinto modo dependiendo de la forma en que est representado el complejo. Forma binmica Se aplica la propiedad distributiva:
Z1Z2 = (a + bi)(c + di) = ac + iad + ibc + i 2 bd = (ac bd) + (bc + ad)i
14
Matemticas
Es inmediato pasar a forma cartesiana. Calcular (2 + 3i)(3 + 3i). Aplicando directamente la frmula anterior obtenida de aplicar la propiedad distributiva = (6 9) + (9 + 6)i = -3 + 15i
Forma polar Es muy sencillo y rpido, no hay ms que multiplicar los mdulos y sumar los argumentos:
Z1Z2 = (r1 ) (r2 ) = (r1r2 )
Es tambin inmediato pasar a expresar este resultado en forma trigonomtrica, pero hagamos el desarrollo a partir de los complejos expresados de esta forma para comprobarlo. Forma trigonomtrica Se aplica la distributiva y las frmulas trigonomtricas de la adicin de ngulos. (Ver en el tema 2). Z1 = r1 (cos + i sen ) Z2 = r2 (cos + i sen) Z1Z2 = r1 r2 (cos + i sen) (cos + i sen) = r 1 r2
cos cos + i2 sen sen + i ( sen cos + cos sen)
Y aplicando las frmulas trigonomtricas queda Z1Z2 = r1 r2 [cos ( + ) + i sen( + )]
15
Formacin Abierta
Z1 = 260 Z2 = 330. Z1Z2 = 690 = 6 (cos90 + i sen90) Resulta ms rpido y sencillo hacer las operaciones con complejos en forma polar y expresar el resultado en forma trigonomtrica si as nos interesa. A partir de ahora, si hemos de elegir entre forma polar y trigonomtrica, por comodidad y sencillez, operaremos siempre en forma polar.
Producto de un nmero real por un nmero complejo
k R
kZ1 = k(a + bi) = Ka + Kbi
Si pensamos en la forma polar, el mdulo quedara multiplicado por el nmero real y el argumento no cambiara.
k.r = (kr )
Ejemplo: 2 (8 3i ) = 16 6i = (16,6 )
En forma polar:
3 430 = 1230
5.5.3. COCIENTE
Igual que el producto, el cociente de nmeros complejos se expresa en funcin de la forma en que vengan representados los mismos.
16
Matemticas
Forma binomial
Z1 a + bi (a + bi)(c di) (ac + bd) + (ad + bc)i (ac + bd) + (ad + bc)i = = = = Z 2 c + di (c + di)(c di) c2 + d 2 c2 + d 2
Z1 = 1 + 3i Z2 = 3 4i
Z1 1 + 3i 15 + 13i = = Z 2 3 + 4i 25
Forma polar
Z1 (r1 ) r1 = = Z 2 (r2 ) r2
Z1 = 260 Z2 = 330.
Z1 2 = = 0,6630 Z 2 3 60 30
El inverso de un nmero complejo es un caso particular de la divisin donde el numerador o dividendo es el nmero real 1, y el denominador o divisor es el nmero complejo de que se trate.
1 1 1(a bi) a b 2 = = 2 = 2 i 2 2 Z a + bi a +b a +b a + b2
Ejemplo
1 1 (4 + 3i ) 4 3 = 2 = + i 2 4 3i 4 +3 25 25
17
Formacin Abierta
5.5.4. POTENCIA DE UN COMPLEJO

Forma binomial Se aplica la frmula del binomio de Newton que recordamos a continuacin, ya aplicada a calcular el cuadrado de un nmero complejo.
2 Z1 = (a + bi) 2 = a 2 + (bi) 2 + 2abi = a 2 + b 2 + 2abi = (a 2 b 2 ) + 2abi
Calcular (2 + 3i ) = 4 + 2 2 3i 9 = 5 + 12i .
2
Si
me
pidieran
2
hallar
(2 + 3i )3 ,
podra
hacerlo
como (2 + 3i ) (2 + 3i )
Forma polar El resultado de elevar un complejo a una potencia n es un n complejo que tiene como mdulo el del complejo de la base elevado a la potencia y como argumento el del complejo de la base multiplicado por la potencia.
(r )n = (r )n
Hallar (2 +3i)2
Visto el resultado obtenido del binomio de Newton: (2 +3i)2 = (4 9) + 12i = -5 + 12i Hallar (530 ) = 12590
3
18
Matemticas
5.5.5. RAZ DE UN COMPLEJO

La raz n-sima de un nmero complejo z, es otro nmero complejo r que elevado a la potencia n coincide con z.
r = n z rn = z
Forma polar Aprenderemos a hacer races de un complejo cuando est expresado en forma polar, si nos los dan de cualquier otra forma, tendremos que pasarlo a forma polar para hacer la raz. El mdulo de r ser la raz ensima del mdulo de Z. Su argumento es
+ 360k , siendo el argumento de Z. n
Resolver la ecuacin x 6 + 243 = 0
Solucin: Despejando x, resulta x = 6 - 243 , -243 es un nmero real negativo del que no podemos hallar una raz de ndice par en los reales. Tendremos que expresarlo como un nmero complejo para poder resolver la ecuacin. -243 = -243 + 0i en forma binomial, tendremos que ponerlo en forma polar. Mdulo: m =
(- 243 )
+ 02 = 243
Argumento: = arc tg
0 = arc tg (0) - 243
El ngulo cuya tangente vale cero puede ser o 180, para averiguarlo representaremos grficamente el complejo y nos damos cuenta que su afijo, el punto que lo representa, se encuentra en el 2 cuadrante, luego el ngulo que le corresponde es 180.
19
Formacin Abierta
Luego lo que tenemos es x = 6 - 243180 . Entonces, Mdulo de x =

6
243 = 3 + 360k 180 + 2k = 30 + k . Con K = = 6 n 6
Argumento de x = 1,2,3,... Entonces para: k = o x = 330 k = 1 x = 390 k = 2 x = 3150
Luego tendremos infinitas soluciones todas con el mismo mdulo y argumentos que difieren entre s 60 =
rad. 3
20
Matemticas
RESUMEN
La unidad imaginaria i es la raz cuadrada de 1, i = - 1 . Nos sirve para
definir el concepto de nmero complejo como un par de nmeros reales ordenados (a,b) que representan el binomio a + bi.
Los nmeros complejos podemos representarlos grficamente en el plano

y a partir de ah definir su mdulo y su argumento. Mdulo r = argumento = arc tg .
a 2 + b2 y
b a
Estos dos conceptos nos permitirn expresar cualquier nmero complejo en forma polar Z = r y trigonomtrica Z = r (cos + isen ) . Hemos de saber calcular las cuatro potencias fundamentales de la unidad
imaginaria y saber lo que es el conjugado y el opuesto de un complejo.
Operaciones con complejos: Suma, diferencia, multiplicacin, divisin,

potencia y raz.
21
MATEMTICAS
6
FUNCIN REAL DE VARIABLE REAL. LMITES Y
CONTINUIDAD
Matemticas
NDICE
OBJETIVOS .................................................................................................3 INTRODUCCIN ..........................................................................................4 6.1. Funcin y dominio .................................................................................5 6.2. Grfica de una funcin ..........................................................................8 6.2.1. Dominios y grficas de funciones elementales .................................9 6.3. Lmites...................................................................................................15 6.3.1. Definicin ........................................................................................15 6.3.2. Lmites laterales ..............................................................................16 6.3.3. Lmites infinitos ...............................................................................17 6.3.4. Propiedades de los lmites ..............................................................19 6.3.5. Indeterminaciones...........................................................................20 6.4. Continuidad de una funcin................................................................22 6.4.1. Propiedades ....................................................................................24 6.4.2. Discontinuidad.................................................................................25 RESUMEN..................................................................................................27
Unidad 6. Funcin Real de Variable Real
Matemticas
OBJETIVOS
Tras el estudio de la presente unidad didctica el alumno debe ser capaz de:
Hallar el dominio de cualquier funcin a partir de su expresin algebraica. Representar funciones elementales partiendo de su expresin algebraica. Conocer el concepto de lmite de una funcin. Lmites laterales y
propiedades de los lmites.
Saber calcular lmites de expresiones funcionales sencillas, identificar las

indeterminaciones y saber qu herramientas usar para evitarlas.
Conocer el concepto de continuidad de una funcin, saber estudiarla y

distinguir las discontinuidades evitables de las inevitables.
Formacin Abierta
INTRODUCCIN
Los distintos objetos y fenmenos que observamos en la naturaleza estn relacionados unos con otros en la mayora de los casos, son interdependientes. Algunas de estas relaciones no son perfectas, no se rigen por una frmula, por ejemplo, la altura y el peso de una persona son dos medidas, dos variables que estn relacionadas, pero sin embargo conociendo la altura de una persona no puedo conocer su peso, ni a la inversa. En otras ocasiones, esa relacin se puede expresar con una expresin algebraica o frmula que nos permite asegurar cual es el valor de una de las variables conociendo la otra. Por ejemplo, la relacin entre la longitud del lado de un cuadrado, L, y su rea, A, se expresa como A=L2. Conociendo el lado tenemos perfectamente determinada el rea del cuadrado. El ser humano conoce desde hace tiempo muchas de estas relaciones, en los fenmenos fsicos, por ejemplo, la velocidad a la que cae un mvil sabiendo la altura a la que se encuentra cuando empieza su cada. Correspondencias de este estilo dieron origen al concepto de funcin, que en esencia es una frmula algebraica que relaciona los valores de algunas variables, dndonos un medio para obtener el valor de una de ellas conociendo el valor de la otra. En esta unidad y en algunas de las siguientes se estudiarn las funciones y sus propiedades.
Matemticas
6.1. FUNCIN Y DOMINIO

Decimos que una cantidad Y, es funcin de otra cantidad X, si el valor de Y queda determinado por el valor que tome X. Si denotamos f a la funcin, la dependencia entre Y y X se expresa con la frmula y = f (x ) .
El espacio recorrido Y por un mvil que circula a una velocidad constante V= 65 km/h, se puede expresar en funcin del tiempo transcurrido X a travs de la funcin Y=65X.
Y es la variable dependiente o valor de la funcin. X es la variable independiente o argumento de la funcin. Si ambas variables son nmeros reales, tendremos una funcin real de variable real. Se llama funcin real de variable real a cualquier aplicacin f : D , siendo D un subconjunto de los reales, D . Al conjunto D = x f (x ) funcin. El dominio de una funcin es el conjunto de valores reales para los que existe la funcin, a los que se puede aplicar la funcin. El rango de una funcin es el conjunto de valores que la funcin asocia al dominio. La funcin f ( x ) = x 2 tiene como dominio todos los nmeros reales, y como rango los reales no negativos. Es una funcin que existe, que est bien definida para todos los reales y la imagen de cualquier nmero real ser siempre otro real pero positivo salvo para el cero que la imagen ser cero.
se denomina dominio de la
Formacin Abierta
El dominio pueden especificarlo con la funcin o, como pasa en general hemos de saber hallarlo partiendo de la expresin algebraica de la funcin. As, los casos ms comunes son: Dominio de una funcin racional:
f (x ) g(x )
Esta funcin existir para cualquier valor del numerador y denominador salvo para aquellos valores de x que anulen el denominador. Luego el dominio sern todos los reales salvo los que hagan cero el denominador. Sea la funcin f (x
)=
3x
2 x , es una funcin 4x 4
racional, luego el dominio ser el conjunto de todos los reales salvo las races del denominador. Si solucionamos la ecuacin de segundo grado
3x 2 4x 4 = 0 obtenemos dos soluciones

luego el dominio lo expresaremos como:
x = 2, x =
2 3
2 D = - 2, 3
Esta notacin entre llaves incluye solamente los nmeros especificados, no intervalos de nmeros reales que se expresan entre parntesis o corchetes. Otro caso bastante frecuente es el de las funciones irracionales. Dominio de una funcin irracional y = n f (x )
En este caso, el dominio depende del valor del ndice de la raz. Si n es impar, raz cbica por ejemplo, la funcin existe en todos los puntos del dominio de f(x). Sin embargo si es una raz de ndice par, solamente existe para aquellos valores en los que f(x) 0 .
Matemticas
Sea f ( x ) = 4 3x 2 4 x 4 , por ser una raz de ndice par solo existe para los valores de x que hagan al polinomio positivo o nulo. Hallamos sus races y estudiamos en que intervalo se cumple esta condicin.
2 D = , [2,+ ) 3
Veamos tambin el caso de las funciones logartmicas. Dominio de log f(x) y ln f(x) Como se vio en la unidad de los nmeros matemticos, tanto los logaritmos decimales como los neperianos tienen por base un nmero positivo, luego existirn para los valores de x que hagan f(x)>0. En esa misma unidad tambin se indic que cualquier nmero elevado a es igual a cero, luego el logaritmo de cero en cualquier base es igual a que no se considera nmero real. Por lo tanto, no son del dominio los puntos donde f(x)=0. Y= ln (x-1) Los valores que hacen x-1>0, son el dominio de la funcin.
D = (1,+ )
Y por ltimo, las funciones exponenciales. Dominio de e f ( x ) , a f ( x ) con a
La funcin exponencial existe para cualquier valor del exponente, luego estas funciones existirn para todos los puntos del dominio de f(x). El dominio de una funcin exponencial coincide con el dominio de su exponente.
Formacin Abierta
6.2. GRFICA DE UNA FUNCIN

Las funciones reales de variable real se representan en los ejes de coordenadas cartesianos. Los valores de x sobre el eje de abscisas y los de y sobre el de ordenadas.
Se llama grfica de una funcin y = f(x) cuyo dominio es D, al conjunto de puntos del plano de la forma (x, f(x)) con x .
Uno de los objetivos de este tema es saber representar grficamente las funciones. Veamos unos ejemplos. Las rectas en el plano, las funciones ms sencillas, se vieron en una unidad anterior. Grfica de la funcin y = 3 x , cuyo dominio son todos los reales.
y
y=3 x
1 -1 1 -1
Tambin es interesante aprender a representar funciones afectadas por el valor absoluto. Hemos de escribir su valor expresado sin las barras del valor absoluto, siempre se obtendr una funcin definida de forma diferente segn el intervalo.
Matemticas
Funcin y = x Escrita sin la expresin del valor absoluto es:
x si x 0 y= - x si x < 0
Luego es la representacin de dos rectas.
y
y= x
1
-1 1
6.2.1. DOMINIOS Y GRFICAS DE FUNCIONES ELEMENTALES

Ya conocemos el concepto de dominio de una funcin y hemos aprendido a calcularlo en las funciones ms comunes. A continuacin vamos a hacer un pequeo recordatorio de los dominios de ciertas funciones, completado con las grficas de algunas de ellas. Funcin potencial Es de la forma y = x con . Su grfica y dominio dependen de .
Formacin Abierta
Funcin polinmica Es de la forma y = a0 + a1 x + a2 x 2 + ... + an x n con ai . Su dominio son todos los nmeros reales. La grfica es una recta si el polinomio es de grado menor o igual que 1 y una parbola de eje vertical si el polinomio es de grado 2.
y
y = x2
x -3 -2 2 3
Funcin racional Es de la forma y =
P ( x) siendo P(x) y Q(x) polinomios. El dominio son todos Q( x)
los nmeros reales excepto las races del polinomio Q (x). Funcin irracional Es de la forma y = n
P ( x) siendo P(x) y Q(x) polinomios y n un nmero Q( x)
natural. Su dominio depende de si n es par o impar; en el caso de que n sea impar son todos los nmeros reales excepto las races de Q(x), si n es par son todos los nmeros reales tales que negativos.
P( x) exista y tome valores no Q ( x)
10
Matemticas
Funcin exponencial Es de la forma y = a x con a y a > 0. Su dominio son todos los nmeros reales.
y y
y = ax
1 x 1
a<1
a>1
La funcin exponencial ms utilizada es y = e x . Funcin logartmica Es la funcin inversa a la exponencial, se denota y = log a x con a y a > 0. Su dominio son todos los nmeros reales positivos.
y y
y = log a x
y = log a x
1 1 x x
a<1
a>1
La funcin logartmica ms utilizada es y = ln x que es la funcin inversa de
y = ex .
11
Formacin Abierta
Funciones trigonomtricas
y = senx
Su dominio es y est acotada.
y = senx
0
0 0
3 2
-1
y = cos x
Su dominio es y est acotada.
y = cos x
0 0
3 2
12
Matemticas
y = tgx
Su dominio son todos los nmeros reales excepto los que anulan el coseno, es decir, (2k + 1)
k } y no est acotada.
3 2
3 2
Funciones inversas de las funciones trigonomtricas. Las funciones trigonomtricas son biyectivas si se consideran definidas en un subconjunto de su dominio. Por ejemplo, la funcin seno es biyectiva en
2 , 2 , la funcin coseno en [0, ] y la funcin tangente en 2 , 2 .
y = arcsenx se define en [ 1,1] y toma valores en , 2 2
13
Formacin Abierta
x -1 1
y = arccos x se define en [ 1,1] y toma valores en [0, ]

y
x -1 1
y = arctgx se define en y toma valores en , 2 2

y
14
Matemticas
6.3. LMITES
Es ste un concepto muy importante en el estudio de las funciones.
6.3.1. DEFINICIN
Si f(x) es una funcin, se dice que lim x a f ( x ) = L si el valor de f(x) se aproxima mucho a L, cuando x se aproxima mucho a a. Por ejemplo,
lim x 3 x 2 = 9 , ya que x 2 se aproxima mucho a 9 cuando x se aproxima

mucho a 3. Decimos que el lmite de una funcin f(x) es L, cuando x se aproxima a a y se denota lim x a f ( x ) = L , si y solo si, para cualquier n > 0, tan pequeo como queramos, existe un > 0 , que cumple que 0< x a < , entonces f (x ) L < . a puede no pertenecer al dominio de f(x). Vemoslo representado en una figura.
x a a
(i)
f (x)
a + L
(ii)
L+
Calcular lim x 2
x2 4 x2
Esta funcin en principio no existe para x=2, no es un punto de su dominio ya que anula al denominador, pero intentemos simplificarla
x 2 4 (x 2) (x + 2 ) = = x + 2 x 2 4 x2 x2
Luego lim x 2
x2 4 =4 x2
15
Formacin Abierta
6.3.2. LMITES LATERALES

En la recta real, si decimos que x se aproxima a a, x a , no especificamos si se acerca por la derecha, o sea, por valores mayores que a, o por la izquierda por valores menores que a. En el concepto de lmite lateral tiene cabida esta distincin. Lmite lateral derecho, o lmite por la derecha de f(x) cuando x a , es el valor del lmite de la funcin teniendo en cuenta que nos aproximamos a a por valores mayores que a. Se denota lim x a + f ( x ). Lmite lateral izquierdo o lmite por la izquierda es exactamente lo mismo pero aproximndonos por valores ms pequeos que a. Se denota lim x a f ( x ). Los lmites laterales se tienen que calcular cuando la funcin esta definida solamente en un intervalo a la derecha de a, o en un intervalo a la izquierda de a. Si f (x ) =
x , entonces f est definida solo a la derecha de
cero, para valores mayores que cero, luego en este caso solamente podremos hallar el lmite lateral derecho que vale cero. En este caso el lmite coincide con el lmite lateral.
lim x 0 x = lim x 0+
x =0
En otras funciones, definidas a ambos lados del nmero a, se pueden calcular ambos lmites laterales. Se deben calcular cuando se sospecha que el valor del lmite puede variar dependiendo de que nos acerquemos al punto por la derecha o la izquierda. En este caso, para poder decir que existe el lmite es necesario que existan ambos lmites laterales y que adems coincidan. Ese valor de coincidencia ser el valor del lmite.
16
Matemticas
Calcular lim x 0 x . Por la definicin de esta funcin, antes representada, sabemos que no se expresa de la misma forma para los valores mayores que 0, a la derecha de 0 o para los menores que 0, a la izquierda de 0.
x si x 0 f (x) = - x si x < 0
Para hallar el lmite que nos piden tendremos que calcular los dos laterales y comprobar que coinciden. En este ejemplo, es sencillo ver que as sucede y que
lim x 0 x = lim x 0+ x = lim x 0 x = 0

Hay otras funciones que por su propia definicin est claro que en algunos puntos hay que hallar lmites laterales. Son las funciones definidas de distinto modo para distintos intervalos de los reales. Por ejemplo:
x 1 x ( ,1) f (x ) = 2 x + 2 x [1,+ )
Para calcular lim x 1 f ( x ) , tendremos que calcular lmites laterales.
lim x 1 f ( x ) = lim x 1 ( x 1) = 0
lim x 1+ f (x ) = lim x 1 x 2 + 2 = 3
Como los lmites laterales no coinciden, el lmite buscado no existe.
6.3.3. LMITES INFINITOS

No todos los lmites son nmeros reales, ni todos los lmites existen o podemos determinar su valor. A veces el resultado de un lmite es el valor + o .Lo que indica que la funcin no est acotada, crece o decrece sin lmite. Es decir si
lim x a f ( x ) = + significa que cuando x se acerca a a, f(x) se hace

infinitamente grande y positiva. Anlogamente con .
17
Formacin Abierta
Con los lmites laterales puede pasar lo mismo, por supuesto.
lim x 0
1 1 = + = + 2 x 0 1 1 = + = + 2 (x 1) 0 x+3 3 = + = + x2 0
lim x 1
lim x 0
3 x + 4 = + 1 = + lim x 1 2 (x 1) 5
En estos ejemplos con la simbologa 0+, indicamos que se llega al valor cero pero siempre a travs de valores positivos. Vamos a ver un ejemplo donde este matiz es algo fundamental para el resultado.
lim xo
1 Vamos a ver como en esta funcin hace falta hallar x

1 1 = + = + x 0 1 1 = = x 0
los lmites laterales.
lim x o + lim x o
Los lmites laterales no coinciden, la funcin crece indefinidamente si me acerco a 0 por la derecha y decrece infinitamente si es por la izquierda. Evidentemente el lmite que se est buscando no existe. Ocurre lo mismo al calcular lim x 0 e
1 x
, si se calcula el lmite
lateral derecho el resultado es e + = + y sin embargo el izquierdo vale
e =
1 = 0 . Los lmites laterales no e
coinciden, luego el lmite de la funcin cuando x se acerca a cero no existe
18
Matemticas
Adems tambin podemos intentar saber qu pasa con la funcin cuando x se aproxima a los infinitos de la recta real. Los conceptos de lmite mencionados pueden extenderse de forma obvia al caso en que la variable tiende a + o , expresndose lim x + f ( x ) = L o lim x f ( x ) = L . Veamos algunos ejemplos.
2 2 lim x = 3 3
1 lim x 2 x
x x3
x2
=0
ya que
2 <1 3
= 0 =
1 = + 0 +
1 1 lim x = 2 2
= 2 + = +
6.3.4. PROPIEDADES DE LOS LMITES

Lmite de una funcin constante: Si f(x)=c, una constante, entonces
lim xa f ( x) = c .
Para
los
siguientes
cinco
teoremas,
se
asume
que
lim xa f ( x) = A y
lim xa g ( x) = B .
Lmite del producto de una constante por una funcin:

lim x a c f ( x) = c lim x a f ( x) = cA .
Lmite de la suma de dos funciones:
lim xa [ f ( x) g ( x)] = lim xa f ( x) lim xa g ( x) = A B .
Lmite del producto de dos funciones:
lim xa [ f ( x) g ( x)] = lim xa f ( x) lim xa g ( x) = A B .
19
Formacin Abierta
Lmite del cociente de dos funciones:

f ( x) lim xa f ( x) A lim xa = , si B 0. g ( x) = lim B xa g ( x )
Lmite de la raz de una funcin:

lim xa n f ( x) = n lim xa f ( x) = n A , si n A est definida .
6.3.5. INDETERMINACIONES
Existen casos en los que no se puede asegurar a priori el valor del lmite de una operacin con funciones. Estas situaciones se conocen con el nombre de indeterminaciones y representadas simblicamente son:
+ ; 0 ;
0 ; ; 0 ; 0 y 1 0
3 1 3x 2 1 1.- lim x 0 4 2 = = lim x 0 = + x x4 x
La indeterminacin + se elimina realizando la diferencia. 2.lim x
1 + x2 x 1 + x2 x En este caso la indeterminacin + se elimina multiplicando y dividiendo por el conjugado de la expresin.
1 + x + x = = lim x
2
1 + x2 + x
)(
1 + x2 x
) = lim
1 + x2 x2
x
1 =0 +
3.- lim x 3
( x 3)
( 3 x ) = 0 () = lim x 3
( x 3)
4 = 0
Esta indeterminacin 0 se resuelve simplificando 3-x, simplificacin vlida pues 3-x es no nulo dado que x se acerca a 3 pero no toma dicho valor.
3 x 3 x 1 32 x = lim x+ 1 2 x = 3 4.- lim x+ x 1 3 + 3 x 3 +3

El primer paso consiste en dividir el numerador y el denominador por 3x , en el segundo se ha tenido en cuenta que lim x+ 32 x = 0
20
Matemticas
1 1 3 x2 1 0 5.- lim x + = = lim x + x x = =0 3 1 1 3x 3 3 x3
Esta indeterminacin
se resuelve dividiendo numerador y denominador
por x3 que es la mayor potencia de x que aparece.
6.- lim x
x3 t 3 1 = limt + 2 = limt + = 2 1 1 x 1 t 1 3 t t
Se ha realizado el cambio de variable t = x .
7.- lim x
1 3x
3
4 x 8x 3
= lim x
3
1 3 3 x = 2 4 8 2 x
En este caso la indeterminacin se resuelve dividiendo numerador y denominador por x. 8.- lim x f ( x) g ( x ) = 1 e
lim x x 2x + 1 lim x =e 3 + 2x x2
lim x g ( x ) [ f ( x ) 1]
2 x +1 1 3+ 2 x
=e
2 lim x x 2 3+ 2 x
= e + = +
21
Formacin Abierta
6.4. CONTINUIDAD DE UNA FUNCIN

La idea intuitiva de continuidad de una funcin es algo muy sencillo, una funcin es continua cuando al dibujar su grfica no tengo que levantar el lpiz del papel. La lnea de la grfica no tiene cortes o saltos. Las funciones que verifican que a variaciones infinitesimales de la variable independiente corresponden variaciones infinitesimales de la variable dependiente, son las funciones continuas. Para expresar este concepto de forma matemtica veremos la siguiente definicin. Una funcin se define como continua en a si existe la imagen de a, existe el lmite de la funcin cuando x a , y ambos valores coinciden. f es continua en a
f ( a ) , lim x a f ( x ) , f ( a ) = lim x a f ( x )
La primera condicin, la existencia de imagen, implica que una funcin solo puede ser continua en los puntos de su dominio. a D . Por ejemplo, f(x)=x2+1 es una funcin continua en x=2, es muy fcil de comprobar. La comprobacin queda para el alumno. Estudiar la continuidad de la siguiente funcin
f (x ) =
1 en el punto x=2. x2
Se tienen que comprobar las condiciones de la definicin. En este caso, 2 D , la funcin no est definida en el punto 2, y
lim x 2+
1 = + , x2
lim x 2
1 = , luego no existe el lmite. La x2
funcin no es continua en el punto 2. Vamos a ver la representacin grfica.
22
Matemticas
0 x 2
Se dice que una funcin f(x) es continua en un conjunto A si es

continua para todos los puntos de A.
Se dice que una funcin f(x) es continua si es continua para todos los
reales, si es continua x . Hay funciones definidas por intervalos, como si dijramos por trozos, para ver si estas funciones son continuas o no, se tendr que estudiar cada una de las funciones en el intervalo que estn definidas y luego ver la continuidad en el punto donde se unen esos intervalos. Vemoslo en un ejemplo.
x 2 + 2 si x < 0 Dada f ( x ) = x + 3 si x 0
Las dos funciones son polinomios, luego son continuas en los intervalos en los que estn definidas. Hay que estudiar entonces la continuidad en el punto x=0, que es donde puede haber problemas, para calcular el lmite de la funcin tendremos que calcular lmites laterales, puesto que la funcin se define de distinta manera a la derecha y a la izquierda del punto cero. Calculando los lmites laterales, se ve que por la izquierda el lmite es 2, y por la derecha es 3, f(0)=3, luego no hay coincidencia, la funcin no es continua en x=0.
23
Formacin Abierta
6.4.1. PROPIEDADES
Hay numerosas propiedades que cumplen las funciones continuas y muchos teoremas y resultados matemticos vlidos para funciones continuas. En esta unidad nos limitaremos a ver los ms sencillos y de ms inmediata aplicacin. 1. Si f(x) y g(x) son continuas en a la funcin f+g es tambin continua en a.La suma de funciones continuas es una funcin continua. 2. Si f(x) y g(x) son continuas en a la funcin fg es tambin continua en a.El producto de funciones continuas es una funcin continua. 3. Si f(x) y g(x) son continuas en a la funcin f/g es tambin continua en asalvo para los puntos que hacen g(x)=0. El cociente de funciones continuas es una funcin continua salvo para los puntos que anulan la funcin que est en el denominador. 4. Sea f(x) una funcin continua en a,
n
f ( x) es continua en a
siempre que est definida. La raz de ndice n de una funcin continua es continua siempre que est definida. En particular, todos los polinomios son funciones continuas para cualquier x , luego cualquier suma o producto de polinomios ser una funcin continua, y el cociente de polinomios es una funcin continua salvo en las races del denominador. Estudiar la continuidad de f ( x ) =
1 + x3 + x2 + 1 x2
Esta funcin es suma de un polinomio, funcin continua para todos los reales, y un cociente. Para estudiar la continuidad de la funcin suma es suficiente con examinar la funcin cociente. Como se ha visto antes no es continua en x=2, luego la funcin suma es continua para todos los reales salvo para x=2.
24
Matemticas
6.4.2. DISCONTINUIDAD
Se dice que f(x) es discontinua en un punto a, cuando no es continua en dicho punto. Se dice que f(x) es discontinua evitable en a si existe
lim xa f ( x) y se dice discontinua inevitable si no existe lim xa f ( x) .

Si la funcin es discontinua porque no existe la imagen del punto, pero si existe el lmite de la funcin al acercarse al punto la discontinuidad se dice evitable porque siempre se puede definir la imagen del punto como el valor del lmite. La funcin f ( x ) =
x2 1 es discontinua evitable en x=1, ya x 1 x2 1 = 2 , para evitar la x 1
que no existe f(1), pero lim x 1
discontinuidad se redefine la funcin de la siguiente forma:
x2 1 f ( x) = x 1 2
si x 1 si x = 1
Cuando se estudia la continuidad de una funcin y se ven los puntos de discontinuidad es conveniente clasificar tambin el tipo de discontinuidad, evitable o inevitable, as el estudio ser ms completo.
25
Matemticas
RESUMEN
Se llama funcin real de variable real a cualquier aplicacin f : D ,
siendo D un subconjunto de los reales, D .
Al conjunto D = {x f (x )} se denomina dominio de la funcin. Es el

conjunto de los puntos para los que existe la funcin.
Para hallar el dominio de cualquier funcin hay que tener en cuenta los
casos estudiados, races de ndice par que solo existen cuando el radicando es cero o mayor que cero, cocientes que no existen para los puntos que anulan el denominador y logaritmos decimales o neperianos que existen solo para valores positivos.
El rango de una funcin es el conjunto de valores que la funcin asocia al

dominio.
Se llama grfica de una funcin y = f(x) cuyo dominio es D, al conjunto

de puntos del plano de la forma (x, f(x)) con x .
Decimos que el lmite de una funcin f(x) es L, cuando x se aproxima a

a y se denota lim x a f ( x ) = L , si y solo si, para cualquier n
> 0, tan pequeo como queramos, existe un > 0 ,

dominio de la funcin.
que
cumple
que
0< x a < , entonces f (x ) L < . El punto a puede no pertenecer al
Los lmites laterales son los lmites que hallamos teniendo en cuenta si
nos acercamos al punto a, por la derecha o por la izquierda, por nmeros ms grandes o ms pequeos. Para que exista el lmite de una funcin en un punto es necesario que existan los dos lmites laterales y que ambos coincidan.
27
Formacin Abierta
Al calcular lmites de funciones pueden aparecer indeterminaciones,

hemos aprendido a evitar algunas de ellas manipulando la funcin, simplificndola, multiplicado por el conjugado del denominador...
Una funcin se define como continua en a si existe la imagen de a, existe

el lmite de la funcin cuando x a , y ambos valores coinciden.
f ( a ) , f es continua en a lim x a f ( x ) , f ( a ) = lim x a f ( x )
Hay bastantes propiedades y teoremas que verifican las funciones

continuas, en esta unidad solamente se han visto los de ms inmediata aplicacin. Si f(x) y g(x) son continuas en a la funcin f+g es tambin continua en a.La suma de funciones continuas es una funcin continua. Si f(x) y g(x) son continuas en a la funcin fg es tambin continua en a.El producto de funciones continuas es una funcin continua. Si f(x) y g(x) son continuas en a la funcin f/g es tambin continua en asalvo para los puntos que hacen g(x)=0. El cociente de funciones continuas es una funcin continua salvo para los puntos que anulan la funcin que est en el denominador. Sea f(x) una funcin continua en a,
n
f ( x) es continua en a
siempre que est definida. La raz de ndice n de una funcin continua es continua siempre que est definida.
Cuando una funcin no es continua en un punto se dice que es

discontinua, dentro de las discontinuidades distinguimos las evitables de las inevitables. Las discontinuidades evitables son aquellas en las que no existe la imagen del punto pero si el lmite en el punto, y se puede redefinir la funcin dndole a la imagen el valor del lmite.
28
MATEMTICAS
7
DERIVADAS DE
FUNCIONES
Matemticas
NDICE
OBJETIVOS .................................................................................................3 INTRODUCCIN ..........................................................................................4 7.1. Concepto de derivada............................................................................5 7.1.1. Definicin ..........................................................................................5 7.1.2. Interpretacin geomtrica de la derivada ..........................................6 7.1.3. Derivabilidad y continuidad ...............................................................7 7.2. Clculo de funciones derivadas ...........................................................9 7.2.1. Derivadas de las funciones elementales...........................................9 7.2.2. Composicin de funciones derivables. La regla de la cadena. .......10 7.2.3. Derivada de una funcion potencial- exponencial ............................13 7.2.4. Derivadas sucesivas .......................................................................14 7.3. Funciones crecientes y decrecientes ................................................16 7.3.1. Definiciones.....................................................................................16 7.3.2. Crecimiento y derivada de la funcin ..............................................17 7.4. Mximos y mnimos de las funciones................................................20 7.4.1. Definiciones.....................................................................................20 7.4.2. Caracterizacin de mximos y mnimos..........................................21 7.4.3. Aplicaciones a problemas ...............................................................22 7.5. Curvatura y puntos de inflexin .........................................................25 7.5.1. Caracterizacin de concavidad y convexidad .................................25 7.5.2. Puntos de inflexin..........................................................................26 RESUMEN..................................................................................................29
Unidad 7. Derivadas de funciones.
Matemticas
OBJETIVOS
El alumno debe ser capaz de alcanzar los objetivos siguientes:
Saber derivar las funciones elementales. Entender la interpretacin

geomtrica de la derivada.
Obtener la derivada de una funcin definida como combinacin lineal,

producto o cociente de funciones elementales.
Aplicar la regla de la cadena para la obtencin de la derivada de una

funcin compuesta por dos funciones elementales.
Obtener la funcin derivada de una funcin de tipo potencial- exponencial. Estudiar los intervalos de monotona de una funcin, determinar sus
mximos y mnimos usando la primera y segunda derivadas.
Estudiar el tipo de curvatura de una funcin y determinar sus puntos de

inflexin mediante las derivadas primera y segunda.
Aplicar el clculo de mximos y mnimos de una funcin a la resolucin de

problemas de optimizacin.
Formacin Abierta
INTRODUCCIN
En la unidad anterior se estudi el concepto de funcin, las posibilidades de representar fenmenos fsicos o de cualquier otro tipo a travs de funciones y cmo se puede determinar el valor de una variable dependiente conociendo el valor de la independiente. En esta unidad se va a profundizar en el conocimiento de las funciones, nos interesa saber cuando crecen o decrecen, si existe un punto en el que alcancen un valor mximo o mnimo. Si conseguimos expresar el consumo de energa en funcin de cualquier otra variable que nosotros podamos controlar directamente, ser interesante poder hallar el valor de la variable para el que ese consumo se hace mnimo o mximo. Para esto, la derivada de la funcin nos va a ser de mucha utilidad.
Matemticas
7.1. CONCEPTO DE DERIVADA

La derivabilidad de una funcin y = f(x) permite conocer, con mayor precisin que la continuidad, la variacin infinitesimal de la variable dependiente y, respecto de la variacin infinitesimal de la variable independiente x.
7.1.1. DEFINICIN
Dada la funcin f : D y x0 D , se dice que f es derivable en x0 si existe el siguiente lmite lim x x0
f ( x) f ( x0 ) y es un nmero real. x x0
Si la funcin f es derivable en x0 , se llama derivada de f en x0 al valor
f ( x0 ) = lim x x0
f ( x) f ( x0 ) . x x0
de la x,
Llamando
incremento
x = x x 0
de
e la
incremento derivada
de queda
y, y = f ( x0 + x) f ( x0 ) ,
expresin
f ( x0 ) = lim x 0
f ( x0 + x) f ( x0 ) y = lim x 0 . x x
Dada f ( x) = x 2 , veamos si es derivable en x=2. Calculamos
lim x 2
( x 2) ( x + 2) f ( x) f (2) x2 4 =4 = lim x 2 = lim x2 x2 x2 x2
Luego la funcin es derivable en x=2 y el valor de la derivada de la funcin en ese punto es 4, f (2) = 4 Si decimos que una funcin f es derivable en un intervalo (a,b) estamos diciendo que es derivable para todos los puntos de ese intervalo. Y llamamos funcin derivada de f a la funcin f tal que asocia a cada n real x, el valor de la derivada de la funcin en ese punto
Formacin Abierta
7.1.2. INTERPRETACIN GEOMTRICA DE LA DERIVADA

La derivada de una funcin en un punto coincide con la pendiente de la recta tangente a la funcin en ese punto.
y Recta tangente a y = f ( x) en x0 f ( x0 + x)
f ( x0 + x ) f ( x0 )
f ( x0 ) x
x0
x0 + x
Si f es derivable en x0 , la ecuacin de la recta tangente en ese punto es
y f ( x 0 ) = f ( x0 ) ( x x0 ) , es la ecuacin punto pendiente de una recta.

En un ejemplo vamos a ver cmo conseguir esta ecuacin de la recta tangente a una curva en un punto, hallando la derivada de la funcin de la curva en dicho punto. La ecuacin de la recta tangente a la curva f ( x) = x 2 en x=3, es y f (3) = f (3)( x 3) . Luego la ecuacin de la recta queda y 9 = 6( x 3) . El clculo de la derivada queda para el alumno.
Matemticas
7.1.3. DERIVABILIDAD Y CONTINUIDAD

Al igual que en continuidad, hay muchos teoremas y proposiciones que se cumplen para funciones derivables, pero el objetivo fundamental de esta unidad es aprender a derivar, as que solo vamos a indicar la relacin entre continuidad y derivabilidad. Si f es una funcin derivable en x0 entonces f es continua en
x0 .
Esto es equivalente a decir que si una funcin es discontinua en un punto, no es derivable en dicho punto. Luego derivabilidad implica continuidad, pero no al revs, una funcin puede ser continua en un punto y no ser derivable en dicho punto. Veamos un ejemplo de este ltimo caso. En la unidad anterior se vio que la funcin y = f ( x) = x es una funcin continua en x=0, para comprobarlo hubo que hallar los lmites laterales. Como es continua puede que sea derivable, vamos a comprobarlo.
x si x 0 f ( x) = , para calcular la derivada habr que hacerlo por la - x si x < 0

derecha y por la izquierda, como para la continuidad. La funcin ser derivable en 0, si los lmites laterales calculados coinciden.
lim x 0+
f ( x) f (0) x0 = lim x 0+ =1 x0 x0 f ( x) f (0) x0 = lim x 0 = 1 x0 x0
lim x0
Los lmites no coinciden, no existe la derivada de la funcin en x=0, luego la funcin y = f ( x ) = x no es derivable en el punto x=0. Grficamente en el cero la funcin presenta un pico.
Formacin Abierta
y= x
1
-1 1
Comprobar si la siguiente funcin es continua y derivable en x=2.
1 x 2 si x (- 3,2] f ( x) = si x > 2 - x -1
Como antes es continua pero no derivable en x=2
Matemticas
7.2. CLCULO DE FUNCIONES DERIVADAS

Como se ha definido en el primer apartado, se llama funcin derivada f (x) de una funcin dada f (x) , a aquella a que a cada punto le hace corresponder el valor de la derivada en ese punto.
7.2.1. DERIVADAS DE LAS FUNCIONES ELEMENTALES

Veamos en un cuadro las derivadas de las funciones ms utilizadas.
Derivadas de las funciones elementales FUNCIN Potencial SIMPLE DERIVADA
y = xn y = ex
y = n x n 1 y = e x y = a x Ln a y = 1 x
Exponencial
y = ax y = Ln x
Logartmica
y = Log a x
y =
1 Ln a x
Seno Coseno Tangente
y = sen x y = cos x
y = tg x
y = cos x y = sen x y = 1 + tg 2 x =
y = 1 1 x2
1 cos 2 x
Arco seno
y = arc sen x
Arco coseno
y = arc cos x
y = arc tg x
y =
1 1 x2
Arco tangente
y =
1 1+ x2
Adems las funciones derivables tienen ciertas propiedades que nos sirven para poder calcular fcilmente las derivadas de las sumas, productos o cocientes de las funciones elementales.
Formacin Abierta
Propiedades de las funciones derivables. La suma, producto por un escalar, producto y cociente de funciones derivables en un intervalo (a , b) y sus funciones derivadas son: 1.- ( f + g ) ( x ) = f ( x ) + g ( x ), x (a, b ) . 2.- (t f ) ( x ) = t f ( x ), t x (a, b ) . 3.- ( f g ) ( x ) = f (x )g ( x ) + f ( x )g (x ), x (a, b ) .
f f ( x )g ( x ) f (x )g ( x ) 4.- ( x ) = , x (a, b ) tal que g ( x ) 0 . g g 2 ( x)

Algunos ejemplos sencillos.
y = x 3 y = 3x 2 y = 3 x 4 + 4 x y = 12 x 3 + 4 y = (3 x + 4)e x y = 3e x + (3x + 4)e x = e x (3x + 7) y= x3 1 ( x 2 5) 2 x ( x 3) y = x2 5 ( x 2 5) 2
y = e x + x 4 senx y = e x + 4 x 3 cos x
7.2.2. COMPOSICIN DE FUNCIONES DERIVABLES. LA REGLA DE LA CADENA.

Composicin de funciones es lo que se suele expresar como una funcin de otra funcin. Por ejemplo, una exponencial que tiene por exponente un polinomio. Para derivarla habr que tener en cuenta las dos funciones, exponencial y polinmica. La llamada regla de la cadena es la aplicada para calcular estas derivadas de funciones compuestas. En el siguiente cuadro aparecen las derivadas de funciones compuestas, obtenidas aplicando la regla de la cadena.
10
Matemticas
Derivadas de las funciones elementales FUNCIN Potencial Exponencial COMPUESTA DERIVADA
y = f ( x) n y = e f ( x) y = a f ( x) y = Ln f( x)
y = n f ( x) n 1 f ( x) y = f ( x)e f ( x ) y = f ( x)a f ( x ) Ln a y = y = f ( x) f ( x)
Logartmica
y = Log a f (x)
Seno Coseno Tangente Arco seno
f ( x) Ln a f ( x)
y = sen f( x) y = cos f( x) y = tg f( x)
y = f ( x) cos f( x) y = f ( x) sen f( x) y = f ( x)(1 + tg 2 f ( x) )

y =
y = y =
y = arc sen f( x)
y = arc cos f( x)
y = arc tg f( x)
f ( x) 1 f ( x) 2
f ( x) 1 f ( x) 2 f ( x) 1 + f ( x) 2
Arco coseno
Arco tangente
Veamos algunos ejemplos resueltos:
y = e senx y = (senx ) e senx = cos x e senx

y = sen ( x 3 + 3x ) y = cos( x 3 + 3x ) ( x 3 + 3x ) = = (3x 2 + 3) cos( x 3 + 3x ) 2x 2 senx 2x cos x 2(senx x cos x ) y= y = = senx sen 2 x sen 2 x y = cos(e 3 x ) y = sen (e 3x ) (e 3x ) = sen (e 3 x ) 3(e 3x ) = 3e 3x sen (e 3x )
11
Formacin Abierta
Es importante ser ordenado a la hora de derivar funciones, simplificar lo mximo posible las expresiones de las derivadas y ordenar el resultado de forma que no pueda dar lugar a confusiones. Cuando hay que derivar un cociente donde el numerador es un valor constante, cualquier nmero real, y el denominador es una funcin, es ms rpido expresarlo como una potencia negativa y luego hacer la derivada de una potencia. La derivada de una potencia es ms corta a la hora de calcular que la de un cociente. Los cocientes que se puedan expresar como potencias negativas conviene expresarlos as antes de hacer la derivada.
Veamos la derivada de la funcin y =
2 , se puede hacer como la x +4

2
derivada de un cociente, se deja como ejercicio para el alumno, y se puede hacer de la siguiente forma, que nosotros recomendamos:
2 = 2( x 2 + 4) 1 y = 2 (1) ( x 2 + 4) 2 ( x 2 + 4) = 2( x 2 + 4) 2 (2x ) = x +4 4x = 2 ( x + 4)2 y=

2
Este es el mismo resultado que el que habra que haberse obtenido derivando como cociente.
El alumno debe elegir el mtodo que le resulte ms fcil y rpido, ya que ambos son correctos.
Algunos ejemplos ms.
y = ln(senx 2 ) y =
(senx 2 ) cos x 2 ( x 2 ) 2 x cos x 2 = = senx 2 senx 2 senx 2
y = ( x 2 + cos x ) ln x y = ( x 2 + cos x ) ln x + ( x 2 + cos x )(ln x ) = 1 (2 x senx ) ln x + ( x 2 + cos x ) x
12
Matemticas
A veces la notacin de las funciones trigonomtricas y la potencial puede dar lugar a confusin. Hemos de distinguir bien si la potencia afecta a la funcin trigonomtrica o a sus argumentos, o sea, a lo de dentro. La expresin: y = senx 2 es equivalente a y = sen( x 2 ) , o sea, lo que est afectado por la potencia es el argumento, la x, lo de dentro. Sin embargo la expresin:
y = sen 2 x es equivalente a
y = (senx ) 2 , lo que est afectado por la potencia es la funcin

trigonomtrica, no el argumento, no la x. Las derivadas de ambas funciones son distintas, ahora las haremos.
y = sen 2 x y = 2 senx cos x y = senx 2 y = cos x 2 (2 x ) = 2 x cos x 2
7.2.3. DERIVADA DE UNA FUNCION POTENCIAL- EXPONENCIAL

Hay un caso en el que no aplicamos directamente la regla de la cadena, si no que transformamos la funcin antes de derivarla aplicando entonces la regla de la cadena. Este caso es el de las funciones de tipo potencial-exponencial.
y = [f ( x )]
g(x)
Vamos a ver qu mtodo seguir para derivar funciones de este tipo. Iremos desarrollando los pasos sobre un ejemplo para entenderlo mejor. Sea la funcin:
y = ( x 2 + x ) senx
Primero: transformacin de la funcin mediante logaritmos. As, aplicando las propiedades de los logaritmos vistas en la primera unidad, se consigue pasar a un producto de funciones.
ln y = ln( x 2 + x ) senx = (senx ) ln(x 2 + x )
13
Formacin Abierta
Segundo: derivacin del logaritmo y derivacin del producto de funciones.
(ln y) =
y = y 2x + 1 x2 + x
(senx ) ln(x 2 + x ) + (senx ) (ln(x 2 + x )) = cos x ln(x 2 + x ) + senx
Tercero: Obtencin de la derivada buscada. El resultado del paso anterior no es la derivada de la funcin y, sino la derivada de la funcin lny. Tendremos que despejar partiendo de la expresin anterior de la siguiente manera:
2x + 1 2x + 1 2 senx 2 y = y cos x ln(x 2 + x ) + senx 2 = ( x + x ) cos x ln(x + x ) + senx x 2 + x x + x
Donde hemos sustituido y por su valor, la funcin potencial-exponencial de la que partamos.
7.2.4. DERIVADAS SUCESIVAS

Hemos visto cmo calcular la derivada de una funcin cualquiera, la primera derivada o derivada de primer orden. Esta funcin obtenida se puede volver a derivar, obteniendo la segunda derivada o derivada de segundo orden y as sucesivamente. Hay funciones que se pueden derivar infinitamente y nunca se anulan, cualquier exponencial e x , por ejemplo. Sin embargo, cualquier funcin polinmica si derivamos sucesivamente siempre llega un momento en que se anula. La notacin de estas derivadas sucesivas, ser: f , f , f ...y escrito en nmeros romanos f iv , f v , f vi ... para las
derivadas de orden mayor que tres, se expresa ese orden en el superndice
14
Matemticas
Calcular las 2 y 3 derivadas de las funciones f ( x ) = e 3 x y
f ( x ) = x 2 5x + 3 .
f ( x ) = e 3x f ( x ) = 3e 3 x f ( x ) = 9e 3x = 3 2 e 3 x f ( x ) = 27e 3 x = 33 e 3 x f ( x ) = x 2 5x + 3 f ( x ) = 2x 5 f ( x ) = 2 f ( x ) = 0
15
Formacin Abierta
7.3. FUNCIONES CRECIENTES Y DECRECIENTES

Intuitivamente o viendo la grfica de una funcin es muy sencillo identificar si la funcin crece o decrece en un intervalo determinado.
y
y = x2
decreciente
4
creciente
x -3 -2 2 3
7.3.1. DEFINICIONES
Veamos las definiciones matemticas de estos conceptos. Se dice que una funcin f(x) es creciente en un intervalo si se cumple que para cualquiera dos puntos del intervalo tales que
x 1 < x 2 , sus imgenes cumplen que f ( x 1 ) < f ( x 2 ) .

De igual forma, f(x) es decreciente en un intervalo si se cumple que para cualquiera dos puntos del intervalo tales que
x 1 < x 2 , sus imgenes cumplen que f ( x 1 ) > f ( x 2 ) .

Si queremos estudiar el crecimiento o decrecimiento de una funcin en un intervalo determinado o sobre la recta real podemos dibujar la grfica y observarlo directamente o ir haciendo comprobaciones. Ninguno de estos mtodos es rpido.
16
Matemticas
7.3.2. CRECIMIENTO Y DERIVADA DE LA FUNCIN

Vamos a ver cmo las derivadas de las funciones son muy tiles para caracterizar el crecimiento y decrecimiento de stas. Si la derivada de una funcin f es positiva en un intervalo, entonces la funcin f es creciente en dicho intervalo. Si la derivada de una funcin f es negativa en un intervalo, entonces la funcin f es decreciente en dicho intervalo.
f > 0 f creciente f < 0 f decreciente

Para poder aplicar estos resultados es necesario que la funcin sea continua en el intervalo en que se estudia. Si queremos saber si una funcin es creciente o decreciente en un intervalo determinado no tendremos ms que sustituir en la derivada de la funcin el valor de cualquier elemento del intervalo, ver el signo del resultado y ya podemos saber si la funcin crece o decrece. Esto es bastante prctico por ejemplo en una funcin que represente el beneficio de una empresa en funcin de la inversin realizada. Nos conviene saber para qu intervalo de valores de inversin la funcin beneficio es creciente o decreciente. Ahora, lo que nos podemos preguntar es cmo saber que en un intervalo determinado la funcin pasa de creciente a decreciente o a la inversa. Cmo determinar intervalos donde la funcin es siempre creciente o decreciente, estos son los que nos interesa estudiar. Para esto tambin va a resultar muy prctico conocer la funcin derivada. Si la funcin pasa de ser creciente a decreciente o a la inversa, la derivada pasa de ser positiva a negativa o al revs, luego, como la funcin es contina y derivable, no puede haber saltos, la derivada tiene que alcanzar el valor nulo, ha de haber un momento en que tome valor cero. Estos valores de x donde la derivada se anula son los que van a marcar los intervalos de crecimiento y decrecimiento de la funcin.
17
Formacin Abierta
Si queremos delimitar los intervalos donde una funcin continua crece o decrece procederemos de la siguiente forma: 1. Comprobar que la funcin es continua y calcular la derivada de la funcin. 2. Igualarla a cero y sacar las soluciones de la ecuacin que resulte. Estas soluciones se llaman puntos crticos. 3. Dividir la recta real en los intervalos obtenidos con los puntos crticos hallados. Estos sern los intervalos de crecimiento y decrecimiento de la funcin. 4. Sustituir en la primera derivada un punto cualquiera de cada intervalo para ver el signo que toma y poder decir si la funcin es creciente o decreciente. Vamos a ver en un ejemplo cmo estudiar el crecimiento o decrecimiento de una funcin. A veces tambin se dice estudio de la monotona de una funcin. La funcin representada en la figura anterior, es y = x 2 , grficamente se ve claro que es decreciente desde hasta x=0, y creciente desde x=0 hasta + . Vamos a comprobar que coincide lo que vemos grficamente con el resultado hallado con la primera derivada. 1. La funcin es un polinomio, luego es continua para todos los reales. Calculamos la derivada
y = x 2 y = 2x
2.
y = 0 2 x = 0 x = 0 es la abscisa del punto

crtico. El punto crtico es (0,0).
3. Los intervalos en que queda dividida la recta real son:
( , o ) (0,+ )
Sern los intervalos de crecimiento y
decrecimiento de la funcin.
18
Matemticas
4.
y = 2x sustituida en un punto cualquiera del primer

intervalo tomar siempre un valor negativo, luego la funcin ser decreciente ese primer intervalo ( , o ) . Anlogamente, la funcin y = 2 x en el intervalo
(0,+ )
tomar valor positivo en cualquiera de sus
puntos, luego la funcin ser creciente. Muchas veces para expresar toda esta informacin de manera clara y conjunta se escribe una tabla como la siguiente.
Intervalos Signo f Crecimiento de f
(,0)
(0, +)
Decreciente
+
Creciente
Hay funciones que son crecientes o decrecientes para todos los reales, su primera derivada nunca se anula. Al igualar la primera derivada a cero se obtiene una ecuacin sin solucin, eso quiere decir que el intervalo de crecimiento o decrecimiento es toda la recta real. Como ejercicio para el alumno queda el demostrar que la funcin
f ( x ) = x 5 + 20x 6 es una funcin creciente para todos los valores de x.
19
Formacin Abierta
7.4. MXIMOS Y MNIMOS DE LAS FUNCIONES

Al igual que con el crecimiento y decrecimiento, la idea intuitiva de mximo y mnimo es muy sencilla, grficamente tambin son fciles de identificar los puntos donde la funcin alcanza un mnimo o un mximo.
7.4.1. DEFINICIONES
Veamos tambin una definicin matemtica de estos conceptos.
Sea y=f(x) una funcin continua en un dominio D, y sea x 0 D un punto del dominio, se dice que f tiene un mximo relativo o local en x 0 si existe un intervalo alrededor de x 0 para el que se cumple que si x es un punto de ese intervalo, entonces f (x ) f (x 0 ) .
Anlogamente funcin.
f (x ) f (x 0 ) , se define mnimo relativo o local de una
pero
con
la
condicin
de
que
El mximo o mnimo es global cuando las desigualdades se verifican para cualquier punto del dominio de la funcin, x D . El mximo o mnimo es estricto si se verifica la desigualdad estricta. Para hablar indistintamente de mximos o mnimo hablaremos de ptimos o valores extremos de la funcin.
Cmo localizar los puntos donde se pueden dar estos valores extremos de la funcin, cmo buscar los mximos y mnimos. Los candidatos a mximos y mnimos son los puntos crticos encontrados al igualar a cero la primera derivada. Hay otros puntos a tener en cuenta en este estudio, son los puntos de discontinuidad, donde tambin se puede encontrar algn ptimo. Lgicamente, en los puntos crticos la funcin pasa de creciente a decreciente o al revs, est claro, y si no grficamente se ve, que la funcin alcanza en estos casos un mximo local o un mnimo local respectivamente.
20
Matemticas
Mximo local
Mximo local
y = senx
0
0 0
3 2
Mnimo local
7.4.2. CARACTERIZACIN DE MXIMOS Y MNIMOS

Ahora ya tenemos los posibles ptimos, veamos como comprobar si verdaderamente lo son y cmo distinguir si son mximos o mnimos. Podemos hacerlo usando la informacin que nos da la primera derivada de la funcin, o calculando la segunda derivada y estudiando los valores que toma en los puntos crticos. Utilizando la primera derivada Con la informacin organizada como hemos visto en la tabla es fcil identificar los mnimos como los puntos donde la funcin pasa de decreciente a creciente, por lo tanto la primera derivada pasar de negativa a positiva. Los mximos son los puntos donde pasa justo lo contrario. Y los puntos crticos donde la funcin no cambia su crecimiento, o sea, donde la primera derivada no cambia de signo, no son ni mximos ni mnimos. Utilizando la segunda derivada Sea x 0 el valor de la abscisa de un punto crtico, para determinar si corresponde a un mximo, a un mnimo o a ninguno de ellos, procederemos de la siguiente manera:
21
Formacin Abierta
1. Calcular la segunda derivada f ( x ) , sin ms que derivar la primera derivada f ( x ) . 2. Sustituir el valor x 0 en la expresin de la segunda derivada, entonces si
f ( x 0 ) < 0 La funcin f alcanza un mximo en x 0 . f ( x 0 ) > 0 La funcin f alcanza un mnimo en x 0 . f ( x 0 ) = 0 No se alcanza ni mximo ni mnimo en x 0 .
Vamos a verlo sobre un ejemplo.
Dada f ( x ) = x 3 x 2 x + 2 , estudiar la monotona y calcular sus extremos. Calculamos la primera derivada, f ( x ) = 3x 2 2 x 1 La igualamos a cero y obtenemos los puntos crticos, x 1 = 1 y
1 x2 = . 3
Pongamos la tabla con los intervalos y estudiemos el signo de la primera derivada.
Intervalos f f
1 , 3
1 ,1 3
(1, )
+ Creciente
+ Creciente
Decreciente
22
Matemticas
7.4.3. APLICACIONES A PROBLEMAS

En ocasiones lo interesante es hallar un mximo o un mnimo de una funcin que no nos dan de forma explcita, nos hablan de una magnitud que se quiere optimizar y de las condiciones que se han de cumplir. Hemos de plantear el problema, expresar esa magnitud en funcin de las variables necesarias y tener en cuenta las condiciones que se han de cumplir. Planteado as, solo quedar aplicar las tcnicas aprendidas para localizar los ptimos. La parte escrita de la pgina de un libro ocupa 400 cm2, los mrgenes superior e inferior deben ser de 3 cm y los laterales de 2 cm.Cules deben ser las dimensiones de la pgina para que el coste del papel fuera mnimo?
Viendo la figura
3 b
2 3
Figura 7.1.
Dimensiones de la pgina
La funcin a minimizar es la del rea de la pgina, la podemos expresar como:
f (a , b ) = (a + 6 ) (b + 4 )
Es una funcin de dos variables, a y b. Hemos aprendido a calcular los ptimos de las funciones de una variable, funcin real de variable real, luego tendremos que expresar esta funcin dependiendo solo de una variable. Para ello utilizaremos la restriccin o condicin que nos plantean.
23
Formacin Abierta
La parte escrita de la pgina ocupa 400cm2 , esto se puede expresar:
a b = 400 a =
400 b
As, en la funcin a minimizar, que llamamos funcin objetivo, sustituimos a por lo que vale en funcin de b.
1600 400 f (b ) = + 6 (b + 4) = + 6b + 424 b b

Que es nuestra nueva funcin objetivo, la que tenemos que minimizar, que est en funcin de una sola variable b. Empezaremos entonces por calcular su primera derivada y sus puntos crticos como se ha aprendido.
f (b ) =
1600 800 +6=0 b = = 16,32cm 2 3 b
Tenemos entonces un punto crtico b = 16,32 ya que no tiene sentido una distancia negativa. Hemos de comprobar que es un mnimo y lo haremos calculando la segunda derivada.
f (b ) =
3200 3200 f (16,32 ) = > 0 MINIMO 3 b (16,32)3
Entonces es lo que estbamos buscando.
b = 16,32 a =
400 = 24,49cm b
Y las dimensiones que piden son
(a + 6) (b + 4) 30,49cm 20,32cm
24
Matemticas
7.5. CURVATURA Y PUNTOS DE INFLEXIN

Adems de estudiar el crecimiento o decrecimiento de una funcin, tambin vamos a estudiar su curvatura, el ver si es cncava o convexa. No daremos las definiciones de concavidad y convexidad nos limitaremos a entender estos conceptos sobre una representacin grfica. Las curvas convexas son aquellas que quedan por encima de cualquier recta tangente a un punto de ellas.
Las curvas cncavas son aquellas que quedan por debajo de cualquier recta tangente a un punto de ellas.
La mayora de las curvas tienen zonas de concavidad y de convexidad. Luego las rectas tangentes quedarn por encima o por debajo de la curva en determinados intervalos.
7.5.1. CARACTERIZACIN DE CONCAVIDAD Y CONVEXIDAD

Veamos cmo conocer la curvatura de una funcin sin ver su grfica, y para ello necesitamos calcular y conocer la segunda derivada de la funcin.
25
Formacin Abierta
Si la segunda derivada de la funcin f(x) es positiva en un intervalo (a,b), entonces la grfica de la funcin f(x) es convexa en ese intervalo (a,b). O sea Si f ( x ) > 0 x (a , b) f ( x ) es convexa en (a,b) Si la segunda derivada de la funcin f(x) es negativa en un intervalo (a,b), entonces la grfica de la funcin f(x) es cncava en ese intervalo (a,b). Si f ( x ) < 0 x (a, b) f(x) es cncava en (a,b) Igual que nos pasaba con la monotona, los intervalos de crecimiento y decrecimiento, hemos de localizar los intervalos de concavidad y convexidad. Para determinar estos intervalos veremos en qu puntos se anula la segunda derivada. Estos puntos se llaman puntos de inflexin.
7.5.2. PUNTOS DE INFLEXIN

Puntos de inflexin de una funcin son aquellos en los que la grfica de la funcin pasa de ser cncava a ser convexa o al revs. Estos puntos de inflexin son evidentemente los que marcan los intervalos de concavidad y convexidad, igual que los puntos crticos marcan los intervalos de crecimiento y decrecimiento. Para localizar estos puntos igualaremos la segunda derivada de la funcin a cero, y hallaremos las soluciones de la ecuacin que resulte. Para verificar que estos puntos candidatos, son o no verdaderos puntos de inflexin hay dos caminos, uno usando la segunda derivada y otro calculando la tercera derivada.
Usando la segunda derivada Con los posibles puntos de inflexin hallados se plantean los intervalos de concavidad y convexidad, en cada intervalo se estudia la curvatura de la funcin (sustituyendo en la segunda derivada), y los puntos donde realmente se compruebe que hay cambio de signo, que hay cambio de curvatura esos si son puntos de inflexin.
26
Matemticas
Usando la tercera derivada Para comprobar si un punto que anula la segunda derivada es un verdadero punto de inflexin, calcularemos la tercera derivada y sustituimos en ella el punto, si la tercera derivada sustituida es distinta de cero, el punto es un verdadero punto de inflexin. Si la tercera derivada sustituida en el punto es igual a cero, no podemos asegurar que sea punto de inflexin, habr que comprobar por el criterio anterior. Sea f ( x ) = x 3 f ( x ) = 3x 2 f ( x ) = 6 x = 0 x = 0 , en (0,0) hay un posible punto de inflexin, vamos a comprobar que realmente lo es. Los intervalos de concavidad y convexidad seran: (,0) (0,+) , la segunda derivada sustituida en cualquier punto del primer intervalo da siempre un valor negativo, luego la funcin ser cncava en ese intervalo; y en el segundo intervalo pasa lo contrario, la segunda derivada en cualquiera de los puntos es positiva, luego la funcin es convexa en ese intervalo. Luego hay cambio en el punto cero de concavidad a convexidad, (0,0) es un punto de inflexin. Vamos a comprobarlo tambin con el criterio de la tercera derivada. f ( x ) = 6 0 luego la tercera derivada es distinta de cero, es un punto de inflexin. La grfica de esta funcin como ya se vio en la unidad 6 es:
y
1 x 1
-1
(0,0) Punto de inflexin

-1
Se propone como ejercicio para el alumno buscar los intervalos de concavidad y convexidad para la funcin f ( x ) = x 4 . El resultado es una funcin convexa para todos los reales y el punto (0,0), no es un punto de inflexin.
27
Matemticas
RESUMEN
Definicin de la derivada de una funcin en un punto y su interpretacin
geomtrica. Si la funcin f es derivable en x0 , se llama derivada de f en
x0 al valor f ( x0 ) = lim x x0
f ( x) f ( x0 ) . La derivada de una funcin en x x0
un punto coincide con la pendiente de la recta tangente a la funcin en ese punto.
Si f es una funcin derivable en x0 entonces f es continua en x0 . Esto es

equivalente a decir que si una funcin es discontinua en un punto, no es derivable en dicho punto.
Cuadro de derivadas de las operaciones fundamentales y de las funciones

compuestas. Derivadas de las funciones elementales
FUNCIN Potencial SIMPLE DERIVADA COMPUESTA DERIVADA
y = xn y = ex
y = n x n 1 y = e x y = a x Ln a y =
y = f ( x) n y = e f ( x) y = a f ( x) y = Ln f( x)
y = n f ( x) n 1 f ( x) y = f ( x)e f ( x ) y = f ( x)a f ( x ) Ln a y = f ( x) f ( x)
Exponencial
y = ax y = Ln x
Logartmica
1 x
y = Log a x
Seno Coseno
y =
1 Ln a x
y = Log a f ( x)
y =
f ( x) Ln a f ( x)
y = sen x y = cos x
y = cos x
y = sen x
y = sen f( x)
y = cos f( x)
y = f ( x) cos f( x)
y = f ( x) sen f( x)
29
Formacin Abierta
Derivadas de las funciones elementales

FUNCIN Tangente SIMPLE DERIVADA COMPUESTA DERIVADA
y = tg x
y = 1 + tg 2 x =
1
1 cos 2 x
y = tg f( x) y = arc sen f( x)
y = f ( x)(1 + tg 2 f ( x) ) y = f ( x)
Arco seno
y = arc sen x
y =
1 x2 1 1 x2
1 f ( x) 2 f ( x) 1 f ( x) 2
f ( x) 1 + f ( x) 2
Arco coseno
y = arc cos x
y =
y = arc cos f( x)
y =
Arco tangente
y = arc tg x
y =
1 1+ x2
dy dy dx = dt dx dt
y = arc tg f( x)
y =
La regla de la cadena se expresa
La derivada de una funcin potencial-exponencial hay que hacerla

transformando primero la funcin mediante logaritmos y luego aplicando las reglas de derivacin en ambos miembros.
Se dice que una funcin f(x) es creciente en un intervalo si se cumple

que para cualquiera dos puntos del intervalo tales que imgenes cumplen que f ( x 1 ) < f ( x 2 ) .
x 1 < x 2 , sus
De igual forma, f(x) es decreciente en un intervalo si se cumple que para

cualquiera dos puntos del intervalo tales que cumplen que f ( x 1 ) > f ( x 2 ) .
x 1 < x 2 , sus imgenes
Para calcular los intervalos de crecimiento y decrecimiento, hay que hallar

los puntos crticos, aquellos que anulan la primera derivada, dividir la recta real por esos valores y ver qu signo toma la primera derivada en un punto cualquiera de ellos.
30
Matemticas
f > 0 f creciente f < 0 f decreciente
Para caracterizar los ptimos, o sea los puntos mximos o mnimos de

la funcin, partimos de los puntos crticos y podemos emplear la primera derivada, viendo los cambios de monotona de la funcin o estudiar el valor de la segunda derivada en esos puntos crticos.
f ( x 0 ) < 0 La funcin f alcanza un mximo en x 0 . f ( x 0 ) > 0 La funcin f alcanza un mnimo en x 0 . f ( x 0 ) = 0 No se alcanza ni mximo ni mnimo en x 0 .
La concavidad y convexidad de una funcin se estudian en la segunda

derivada. Para hallar los intervalos de concavidad y convexidad hay que igualar a cero la segunda derivada obteniendo los posibles puntos de inflexin. Son los puntos donde la funcin cambia su curvatura.
Si la segunda derivada de la funcin f(x) es positiva en un intervalo

(a,b), entonces la grfica de la funcin f(x) es convexa en ese intervalo (a,b). O sea Si f ( x ) > 0 x (a , b) f ( x ) es convexa en (a,b)
Si la segunda derivada de la funcin f(x) es negativa en un intervalo

(a,b), entonces la grfica de la funcin f(x) es cncava en ese intervalo (a,b). Si f ( x ) < 0 x (a, b) f(x) es cncava en (a,b)
Para comprobar si un punto es verdadero punto de inflexin hay dos

posibilidades. Una estudiando con los signos de la segunda derivada los puntos donde realmente cambia la curvatura. Y otra, calculando la tercera derivada y sustituyendo los valores, si esta derivada no se anula, los puntos son puntos de inflexin.
31
MATEMTICAS
8
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES
Matemticas
NDICE
OBJETIVOS .................................................................................................3 INTRODUCCIN ..........................................................................................4 8.1. Concepto de integral indefinida ...........................................................5 8.1.1. Propiedades ......................................................................................6 8.2. Integrales inmediatas ............................................................................7 8.3. Mtodos de integracin.......................................................................10 8.3.1. Integracin por partes .....................................................................10 8.3.2. Integracin por cambio de variable .................................................14 8.4. Integrales cumpliendo condiciones ...................................................17 8.5. Integral definida ...................................................................................18 8.5.1. Definicin ........................................................................................18 8.5.2. Propiedades de la integral definida.................................................19 8.6. Aplicaciones de la integral definida ...................................................23 8.6.1. Clculo de una longitud de arco......................................................25 8.6.2. Clculo de reas de revolucin .......................................................26 8.6.3. Volmenes de revolucin................................................................28 RESUMEN..................................................................................................31
Unidad 8. Integral indefinida e integral definida.
Matemticas
OBJETIVOS
Los objetivos que se persiguen con el estudio de la presente unidad didctica son:
Obtener la integral indefinida de funciones sencillas utilizando

integrales inmediatas y los mtodos de integracin.
las
Saber escoger entre las diferentes primitivas aquella que cumple una
condicin inicial determinada.
Calcular integrales definidas mediante la aplicacin de la regla de Barrow. Aplicar el clculo integral a la resolucin de problemas como el clculo de
reas planas, volmenes, superficies de revolucin y longitudes de arco.
Formacin Abierta
INTRODUCCIN
Uno de los problemas que ocup la mente de los matemticos durante una poca fue el clculo de reas de figuras planas. Si se dispona de frmulas para determinar el rea de algunas de estas figuras, como el tringulo, cuadrado, rectngulo...no ocurra lo mismo para las figuras ms generales. Ni siquiera haba una definicin formal de rea. La resolucin de este problema requera introducir un concepto nuevo: el de integral definida, que posteriormente dio lugar al Clculo Integral.
Matemticas
8.1. CONCEPTO DE INTEGRAL INDEFINIDA

En la unidad anterior hemos aprendido a derivar funciones, calcular la integral de una funcin es realizar la operacin inversa, buscar una funcin que al derivarla obtengamos la funcin de la que se parte. Llamamos primitiva de una funcin f, a otra funcin g cuya derivada sea justamente f. g es primitiva de f g = f Por ejemplo, dada la funcin f ( x ) = x 2 , una primitiva es por ejemplo
g( x ) =
x3 x3 , pero la funcin h ( x ) = + 2 tambin es primitiva de la funcin f. 3 3 x3 + C , siendo C un nmero 3
En general cualquier funcin de la forma G ( x ) = real, es una primitiva de la funcin f.
Despus de entender este concepto de primitiva de una funcin, surgen dos cuestiones: Qu funciones tienen primitivas?, Todas o solo algunas? En caso de tener primitivas, Cuntas tienen?
Aunque no lo demostraremos, si diremos que si una funcin es continua, entonces admite primitivas. Es el Teorema Fundamental del Clculo Integral: Si una funcin f es continua en el intervalo [a,b], entonces admite una funcin primitiva en dicho intervalo, es decir, existe una funcin F tal que
F(x ) = f ( x ).
Y como se puede deducir del ejemplo, si una funcin tiene una primitiva, tiene infinitas primitivas. No hay ms que sumar cualquier nmero real para encontrar otra primitiva.
Formacin Abierta
Se llama integral indefinida de una funcin f(x), al conjunto formado por todas sus primitivas y se denota por:
f (x)dx
Luego si C
f (x )dx = {Primitivas de f(x)} = {F(x) + C , donde F(x) = f(x)}
Por ejemplo, la integral indefinida de f(x)=sen x ser F( x ) = cos( x ) + C , el alumno puede comprobar que para cualquier valor real de la constante C al hacer la derivada de F(x) se obtiene f(x).
8.1.1. PROPIEDADES
Las propiedades que cumplen las integrales indefinidas son las siguientes: La integral de la derivada de una funcin es la propia funcin.
f (x )dx = f (x ) + C
La integral de una constante por una funcin es igual a la constante por la integral de la funcin.
k f (x )dx = k f (x )dx
La integral de una suma (diferencia) es igual a la suma (diferencia) de las integrales.
( f (x ) g (x ))dx = f (x )dx g (x )dx

Las dos ltimas propiedades afirman que la integral indefinida es lineal, y se pueden englobar en una sola, de la siguiente manera:
(m f (x ) n g (x ))dx = m f (x )dx n g (x )dx
Matemticas
8.2. INTEGRALES INMEDIATAS

Se llaman integrales inmediatas a las integrales de las derivadas de las funciones elementales, esto es, de las funciones polinmicas, racionales, exponenciales, logartmicas y trigonomtricas. Es como si le diramos la vuelta al cuadro de derivadas de funciones elementales.
INTEGRALES INMEDIATAS
FUNCIN Potencial PRIMITIVA SIMPLE
n x dx =
PRIMITIVA COMPUESTA
x n +1 +C n +1
f f n dx =
f n +1 +C n +1
e
Exponencial
dx = e x + C ax +C Ln a
f e
dx = e f + C af +C Ln a
x a dx =
f a f dx =
Logartmica
x dx = Ln x + C
f dx = Ln f + C f
Seno Coseno
cos xdx = senx + C

senxdx = cos x + C
f cos fdx = senf + C

f senfdx = cos f + C
(1 + tg x )dx = tgx + C
2
f (1 + tg f )dx = tgf + C
2
Tangente
cos
sen
1
2
1
2
dx = tgx + C
cos sen
f
2
f
2
f
2
dx = tgf + C
(1 + cot g x )dx = cot gx + C f (1 + cot g f )dx = cot gf + C

2
Cotangente
dx = cot gx + C
dx = arc senx + C
f
2
dx = cot gf + C
dx = arc senf + C
dx = arc cos x + C dx = arc tgf + C
+1 1 x2
+ f 1 f
f 1 f
2
Arco seno
Arco coseno
1 1 x2
dx = arc cos x + C
Arco tangente
1+ x
dx = arc tgx + C
1+ f
Formacin Abierta
Es importante memorizar o entender muy bien casi todas las integrales de este cuadro, hay integrales que no son inmediatas pero que se resuelven fcilmente vindolas como semejantes a una inmediata. En los siguientes ejemplos se ve cmo hacerlo.
(2x
=2
+ 3x + 1 dx = 2 x 2 dx + 3 xdx + dx =
x2 x3 +3 +x+C 2 3 4 3 3 1 (2 x + 1) 1 (2x + 1) dx = 2 2 (2x + 1) dx = 2 4 + C
Para hacer esta segunda integral se han seguido los pasos siguientes. Faltaba en la integral la derivada de la base de la potencia para tener dentro la derivada completa de la potencia de una funcin. Hemos multiplicado dentro de la integral por esa constante que nos falta y dividido por ella fuera para que el valor total no cambie. As conseguimos una integral inmediata.
3x
dx =
1 1 3x 3x 3e dx = 3 e + C 3 1 1
cos(2x + 1)dx = 2 2 cos(2x + 1)dx = 2 sen(2x + 1) + C

1 1 1 + x 1 dx = ( x 2 x 2 + x 1 )dx = 2 x x 1 1 1 1 12 = x x + ln x + C = x 1 2x 2 + ln x + C 1 1 2
Al igual que para derivar recomendamos el poner los cocientes como potencia negativa, para integrar funciones esta recomendacin sigue siendo vlida. A la hora de integrar es ms sencillo expresar los cocientes como potencia negativa, y las races como potencias racionales. As se tiene que calcular la integral de una potencia que es bastante sencilla, solamente habr que localizar la derivada de la base.
Matemticas
Hay que tener siempre en cuenta que
x dx = x
dx = ln x + C , la integral
de esta potencia de exponente negativo, es el logaritmo neperiano, todas las dems se integran como potencias.
sen x 3 + 1 dx =
1 1 2 3 3 3x sen x + 1 dx = 3 cos x + 1 + C 3
Formacin Abierta
8.3. MTODOS DE INTEGRACIN

No siempre podemos calcular la integral de una funcin dada, aunque sepamos seguro que existe. Ahora bien, el procedimiento para calcular una integral consiste en reducir, mediante transformaciones que no alteren su valor, la integral dada en otra u otras que sepamos resolver. Aqu veremos solamente las transformaciones o mtodos de integracin ms sencillos: Integracin por partes. Integracin por cambio de variable.
8.3.1. INTEGRACIN POR PARTES

Este mtodo se emplea cuando se quieren integrar ciertos productos de funciones. Lo que se har es una transformacin que se basa en la expresin de la derivada de un producto de funciones. Sean dos funciones u, v.
(u v ) = u v + u v
Escrito con diferenciales
d (u v ) = du v + u dv
Integrando en ambos lados de la igualdad:
d(u v) =
du v + u dv
u v = v du + u dv
Y despejando:
udv = uv vdu
Que es la frmula que se conoce para la integracin por partes.
10
Matemticas
El procedimiento para aplicar esta frmula ser: 1. Identificar en la integral que tenemos que calcular la parte que se corresponder con u, y la parte que se corresponder con dv. Siempre identificaremos con dv la funcin que al integrarla no aumente de grado o se complique ms. Funciones como la exponencial, o las trigonomtricas senos y cosenos. E identificaremos con u la funcin que al derivarla quede ms sencilla, ms fcil de integrar. 2. Calcular
dv ,
derivar u para conseguir v, du.
3. Sustituir en la frmula y calcular la integral sencilla que la integral
vdu , que ha de ser ms
udv .
A continuacin veremos cmo aplicar este mtodo a ejemplos concretos:
1.- Resolver la siguiente integral:
(2 x + 1 )sen (x )d (x )
e
x
2.- Resolver la siguiente integral:
cos xdx
Resolucin del ejemplo 1. Segn lo dicho anteriormente, tenemos:
(2 x + 1)sen(x )d (x ) =
du ( x ) = 2dx v( x ) = sen( x )d ( x ) = cos x
dv(x ) = sen( x )d ( x )
u ( x ) = (2 x + 1)
A continuacin aplicamos la frmula de integracin por partes:
(2 x + 1)sen(x )d (x ) = (2 x + 1)( cos x ) ( cos x )2d (x ) =

= (2 x + 1)( cos x ) + 2 senx + C
11
Formacin Abierta
Resolucin del ejemplo 2. Siguiendo las indicaciones tenemos:
u ( x ) = e x du ( x ) = e x dx e x cos xdx = dv( x ) = cos xdx v( x ) = senx

Entonces:
cos xdx = e x (senx ) e x senxdx [*]
Nuevamente integrando por partes obtenemos que:
e senxdx = e
x
cos x + e x cos xdx
Entonces sustituyendo en [*] llegamos a la siguiente igualdad:
cos xdx = e x (senx ) + e x (cos x) e x cos xdx
Si llamamos I = e x cos xdx obtenemos la integral pedida:
I = e x senx + e x cos x I 2 I = e x senx + e x cos x I =

INTEGRACIN POR PARTES
Un polinomio por senos o cosenos
e x senx + e x cos x +C 2
P (x )senf (x )dx
n
u (x ) = Pn ( x ) dv( x ) = senf ( x )dx u ( x ) = Pn (x ) f (x ) dv( x ) = e dx u (x ) = Log ( f ( x )) dv( x ) = Pn (x )dx u ( x ) = e f ( x ) dv( x ) = sen g (x )dx
Un polinomio por una funcin exponencial
P (x )e
n
f (x )
dx
Un polinomio por una funcin logartmica
P (x )Log ( f (x ))dx
n
Una funcin exponencial por senos o cosenos
f (x )
sen g ( x )dx
12
Matemticas
3.- Resolver la siguiente integral utilizando la integracin por partes:
x e dx
2 x
4.- Resolver la siguiente integral mediante la integracin por partes:
(x
+ x 1 Ln x dx
Resolucin del ejemplo 3. Como se trata del producto de un polinomio por una exponencial, tenemos:
u ( x ) = x 2 du( x ) = 2 xdx x e dx = x x x dv( x ) = e dx v(x ) = e dx = e

e2 x
Aplicando la frmula de integracin por partes obtenemos:
x e dx = (x e ) 2 xe dx =(x e ) 2 xe dx
2 x 2 x
x
2 x
Para calcular la integral
xe
x
aplicamos otra vez la integracin por partes:
xe dx = (xe ) e dx = xe
x x x
e x =e x ( x + 1)
Por tanto:
x e dx = (x e ) 2e (x 1) = e (x
2 x 2 x
x x
x +1
Resolucin del ejemplo 4. En este caso, tenemos el producto de un polinomio por un logaritmo:
dx u ( x ) = Ln x du ( x ) = x x 2 + x 1 Ln x dx = 3 2 dv( x )dx = x 2 + x 1 v(x ) = x + x x 3 2
13
Formacin Abierta
Aplicando la frmula de integracin por partes obtenemos:
dx x3 x2 x3 x 2 Ln x + x = + (x + x 1)Ln x dx = 3 2 x x 3 2
2
x3 x2 x3 x2 = + x Ln x + x + C 9 3 2 4
8.3.2. INTEGRACIN POR CAMBIO DE VARIABLE

Este mtodo consiste en transformar la integral de partida, que est en funcin de x, por otra integral equivalente expresada en funcin de otra variable t, de forma que esta segunda integral sea ms fcil de resolver. Tendremos un cambio de variable x = g(t ) , y por la regla de la cadena
dx = g (t )dt , as que la integral quedar
f (x)dx = f (g(t ))g (t )dt
Este mtodo de resolucin de integrales se puede aplicar a gran cantidad de casos, algunos de ellos complicados. Nosotros nos limitaremos a algunos ejemplos sencillos como los que exponemos a continuacin. 5.-Resuelve la siguiente integral mediante un cambio de variable:
dx 5x 2
6.-Resuelve la siguiente integral mediante un cambio de variable:
x 1dx
Resolucin del ejemplo 5. Para resolver esta integral empleamos el cambio t = 5 x 2 dt = 5dx .
dx 5x 2
dt 5 t
1 2 2 t +C= 5 5
(5x 2) + C
14
Matemticas
Resolucin del ejemplo 6.
x (t
2 5
t = x 1 x 1dx = = (t + 1) t dt = dt = dx
32
+ t 1 2 dt =
t5 2 t3 2 2 2 52 23 + = ( x 1) + ( x 1) = 52 32 5 3
(x 1)5 + 2 3 (x 1)2 + C
3
7.- Resuelve la siguiente integral mediante un cambio de variable:
x e
2 x3
dx
dx 1 x2
Resolucin del ejemplo 7.

3 et 1 t 1 x3 t = x x e dx = = dt = e + C = e + C 2 3 3 3 dt = 3x dx 2 x3
Resolucin del ejemplo 8. Para resolver esta integral utilizaremos el cambio de variable: x = sen t
x = sen t cos t dt cos t dt = = = dt = t + C = arc sen x + C 2 1 x cos 2 t dx = cos t dt 1 sen t dx

2
sen x cos x dx
3
xdx 1 + x2
15
Formacin Abierta
Resolucin del ejemplo 9. De nuevo utilizaremos el cambio t = sen x
sen x cos x dx = {sen x = t} = t

3 3 t dt =
cos x
dt = cos x
(sen x ) + C t4 +C = 4 4
4
Resolucin del ejemplo 10. En este caso consideramos el cambio de variable: t = x 2 .
xdx
1+ x
= x2 = t =
xdt dt = = 1+ t + C 2x 1 + t 2 (1 + t )
16
Matemticas
8.4. INTEGRALES CUMPLIENDO CONDICIONES

Hemos visto que hay infinitas funciones primitivas para algunas funciones, y a ese conjunto de primitivas lo llamamos integral indefinida de la funcin. En las integrales indefinidas siempre aparece una constante C que puede tomar el valor de cualquier nmero real. En ocasiones podemos encontrarnos con que nos pidan determinar el valor de esa constante C, dndonos una condicin que ha de cumplir la primitiva o integral de la funcin. Hallar la ecuacin de la curva que pasa por el punto (3,2) y tiene por derivada la funcin 5x 2 x + 1 . Empezaremos por calcular la integral de la funcin
2 (5x x + 1)dx = 5
x3 x2 +x+C 3 2
Ahora ya tenemos la ecuacin de infinitas curvas que solamente difieren en el valor de una constante C
x3 x2 y=5 +x+C 3 2
De estas curvas hemos de elegir la que pasa por el punto (3,2), luego a esta ecuacin le impondremos esta condicin:
2=5
33 3 2 83 +3+ C C = 3 2 2
Luego la ecuacin buscada es
y=5
x3 x2 83 +x 3 2 2
Que es una ecuacin concreta, no depende de ninguna constante.
17
Formacin Abierta
8.5. INTEGRAL DEFINIDA

8.5.1. DEFINICIN
La integral definida de la funcin f en el intervalo [a,b] coincide con el rea del recinto R, limitado por la grfica de la funcin f, el eje OX y las rectas x=a y x=b.
y=f(x)
R
x=a
Figura 8.1.
x=b
rea del recinto R
Aparecen ahora dos cuestiones, cmo calcular estas reas y su relacin con la integral indefinida y las primitivas de la funcin f. La Regla de Barrow es la que nos plantea la solucin a estas dos cuestiones. Regla de Barrow Sea f una funcin continua en el intervalo [a,b]. Entonces la integral definida de f entre a y b es igual al valor de que toma una primitiva F en b, menos el valor que toma F en a, es decir:
b
f (x)dx = F(b) F(a)

a
Los valores a y b se llaman lmites de integracin. As, cuando queramos calcular el rea encerrada entre una funcin continua y el eje de abscisas, en un intervalo [a,b], tendremos que calcular la integral indefinida de una funcin y sustituirla en los extremos del intervalo dado.
18
Matemticas
Calcular el rea limitada por la curva f ( x ) = x 2 y el eje de abscisas en el intervalo [0,1].
x3 1 1 x dx = = 0 = 3 0 3 3 0
1 2
A x -1 1
La constante C desaparece al restar las dos primitivas, por eso ni siquiera se pone. Cuando se ha calculado la integral indefinida y solo queda sustituir por los extremos del intervalo, se indica con el corchete y los extremos del intervalo como subndice y superndice, como est en este ejemplo.
8.5.2. PROPIEDADES DE LA INTEGRAL DEFINIDA

Vamos a sealar las principales propiedades de la integral definida, aunque no vamos a demostrarlas. Lo importante es saber aplicarlas y entender su significado geomtrico. Si c es un nmero entre a y b, esto es a < c < b, entonces se verifica lo siguiente:
f = f + f
a c
19
Formacin Abierta
y=f(x)
R1
R2
Figura 8.2. Propiedad
El significado geomtrico de esta propiedad es claro. El rea que est bajo la grfica de la funcin f entre los puntos a y b es igual al rea comprendida entre x=a y x=c ms el rea comprendida entre x=c y x=b. Si a=b, entonces:
f = f =0
a
Si permutamos los lmites de integracin, entonces la integral cambia de signo. Pueden aparecer resultados negativos que no tienen ningn sentido real si los interpretamos cmo reas.
f = f
b
La integral de la suma (diferencia) de dos funciones f y g es igual a la suma (diferencia) de las integrales. Esto es:
a ( f
b
g) = f g
b b a a
La integral del producto de una constante k por una funcin f es igual a la constante por la integral de la funcin:
a (k f ) = k a f
b b
20
Matemticas
reas por debajo del eje OX Cuando una curva se encuentra por debajo del eje de abscisas y calculamos el rea que encierra entre dos puntos, el resultado al aplicar la regla de Barrow es un nmero negativo. Pero no tiene ningn sentido real el expresar el rea de un recinto como algo negativo. En ocasiones, las curvas pueden limitar con el eje OX unas reas por encima del eje y otras por debajo, como se ve en la siguiente figura. En estos casos, en los que la funcin f , entre a y b, asume tanto valores positivos como negativos, entonces
f (x )dx
a
es la diferencia entre la suma de las reas por
encima del eje y la suma de las reas que estn por debajo del eje y dan lugar a integrales con valor negativo.
A1
a
0 0
A3
X
A2
f (x )dx = A
a
A 2 + A 3 , este resultado no coincide con el que queremos
hallar. Para poder conseguir la suma de las tres reas habr que proceder calculando por separado sus valores, de la siguiente manera. Observar que los intervalos de integracin quedan determinados por los puntos de corte de la curva con el eje OX. Todos los puntos de corte que se encuentren entre los valores a y b.
A 1 + A 2 + A 3 = f ( x )dx f ( x )dx + f ( x )dx = f ( x )dx + f ( x )dx + f ( x )dx

a c d a d d
21
Formacin Abierta
Por lo que si lo requerido es el clculo de el rea encerrada entre una curva y el eje OX habr que dibujar primero la curva para delimitar los intervalos de integracin con los puntos de corte con el eje. Calcular el rea limitada por la curva f ( x ) = senx y el eje OX en el intervalo [0,2] . Sabemos que la funcin f ( x ) = senx toma valores positivos y negativos en el intervalo [0,2] , luego tendremos que hacer la representacin grfica y determinar los puntos de corte con el eje.
A1
0 0
A2 3 2
El rea buscada es A 1 + A 2 , para calcularla habr que calcular las integrales siguientes:
A 1 + A 2 = senxdx senxdx = cosx ] (cosx)] =

2 0 0
cos + cos 0 [ cos 2 + cos ] = 1 + 1 + 1 + 1 = 4

En este caso en el que se ve claramente que A 1 = A 2 , tambin se puede calcular A 1 + A 2 = 2 A 1 = 2 senxdx
0
22
Matemticas
8.6. APLICACIONES DE LA INTEGRAL DEFINIDA

Ya se ha visto la integral definida como un instrumento para determinar reas encerradas bajo una curva y el eje OX. Basndonos en este concepto podemos encontrar otras aplicaciones. Consideremos la regin que aparece en la siguiente figura. Est limitada a la izquierda por el eje de ordenadas y a la derecha por una curva x = g ( y) , para calcular ese rea procederemos de forma anloga pero intercambiando el papel de x por el de y.
y
x = g (y)
d
A x
Area = g ( y)dy
c
Calcular el rea de la regin limitada a la derecha por la parbola x = 4 y 2 , a la izquierda por el eje de ordenadas y por encima y por debajo, por y=2, y=-1.
y
2 1
x 1 -1 2 3 4 5
-2
Area =
1 (4 y )dy = 4y 3 y ]
2 2
3 2 1
=9
23
Formacin Abierta
Otra posible aplicacin de la integral definida es para calcular el rea encerrada entre dos curvas. reas entre curvas Sean f y g funciones continuas tales que g ( x ) f ( x ) para a x b . Entonces, la curva y=f(x) queda por encima de y=g(x) entre x=a y x=b, El rea A de la regin entre las dos curvas y que queda entre a y b se calcula con la frmula:
A = (f ( x ) g ( x ) )dx
a
Vamos a verlo sobre la grfica: Realmente lo que se est haciendo es restar el rea que queda por debajo de f(x) y el rea que queda por debajo de g(x), grficamente se ve que este resultado es el rea A buscada.
y = f(x)
A
y = g(x)
0 0
A = f ( x )dx g ( x )dx = (f ( x ) g ( x ))dx

a a a
Por supuesto, en estos casos habr que tener en cuenta tambin si la regin cuya rea se quiere determinar est situada por encima o por debajo del eje OX para cambiar los signos necesarios.
24
Matemticas
Hallar el rea de la regin situada bajo la recta y =
1 x+2, 2
encima de la parbola y = x 2 y entre el eje de ordenadas y x=1.

y
x 1 2
1 1 1 A = x + 2 x 2 dx = x 2 + 2 x x 3 2 4 3 0
1 0
23 12
8.6.1. CLCULO DE UNA LONGITUD DE ARCO

En ocasiones lo que interesa es calcular la longitud de una curva determinada entre dos puntos en lugar de calcular el rea encerrada por ella y el eje. Para resolver esta cuestin tambin aplicaremos la integral definida.
y
x b
Sea una funcin f(x), derivable en (a,b), para calcular la longitud de la curva y=f(x) entre los valores x=a y x=b, hay que aplicar la siguiente frmula:
25
Formacin Abierta
L = 1 + (f ( x )) dx = 1 + ( y ) 2 dx
2 a a
Tendremos que derivar la funcin, elevar la derivada al cuadrado y calcular la integral que aparece en la frmula. Calcular la longitud de arco L de la curva y = x hasta x=5. Primero derivamos la funcin:
3
desde x=0
y =
3 12 3 x = x 2 2
Elevamos la derivada al cuadrado
( y )2
9 x 4
Calculamos la integral definida de la frmula:
4 9 9 2 4 2 9 9 2 L = 1 + x dx = 1 + x dx = 1 + x 9 0 4 4 9 3 4 4 0 335 = 27
]5 = 0
Si nos imaginamos que el arco de una curva gira sobre el eje OX, lo que se forma en el espacio es un cuerpo de revolucin. Este cuerpo de revolucin tiene un determinado volumen y una superficie que llamaremos volumen y superficie o rea de revolucin.
8.6.2. CLCULO DE REAS DE REVOLUCIN

Vamos a ver cmo poder calcular esta rea o superficie de revolucin., engendrada al girar la curva que representa a la funcin alrededor del eje OX.
26
Matemticas
y = f(x)
Sea f una funcin continua en [a,b] y derivable en (a,b), tal que f ( x ) 0 para
a x b , entonces el rea o superficie de revolucin S generada al girar la grfica de f(x) en [a,b] sobre el eje OX, se calcula aplicando la siguiente frmula: S = 2 f ( x ) 1 + (f ( x ) ) dx
2 a b
Determinar la superficie del paraboloide, engendrada por la revolucin alrededor del eje OX de un arco de la parbola
y 2 = 2x , desde x=0 hasta x=a.
Para aplicar la frmula primero hemos de tener y como funcin de x, luego tendremos que despejar y, y = f ( x ) =
2x = (2x ) 2 .
1
27
Formacin Abierta
Tambin aparece la derivada de la funcin y = f ( x ) , en este caso la derivada de una raz, y = f ( x ) =

1 1 1 (2x ) 2 2 = (2x ) 2 = 1 . 2 2x
Aplicando la frmula que nos da la superficie: S = 2 f ( x ) 1 + (f ( x ) ) dx
1 1 1 S = 2 (2 x ) 2 1 + dx = 2 2 x 1 + dx = 2 2 x + 1dx = 2 (2 x + 1) 2 dx 2x 2x 0 0 0 0 1 3 3 2 1 2 (2a + 1) 2 1 = 2 (2 x + 1) 2 = 3 20 3 a
8.6.3. VOLMENES DE REVOLUCIN

Otra de las aplicaciones de la integral definida es el clculo de los volmenes de los cuerpos engendrados al girar reas sobre el eje OX. Volmenes de revolucin engendrados al girar un rea determinada por cualquier curva y el eje.
y = f(x)
Hay distintos mtodos para calcular estos volmenes segn nos basemos en funcin de las reas de secciones paralelas, mtodo de las capas cilndricas, mtodo de Washer o de arandelas, pero aplicaremos la frmula general para el clculo de volmenes que es la siguiente:
V = y 2 dx = [f (x )] dx
2 a a
28
Matemticas
Esta frmula resulta ms sencilla de plantear que las anteriores porque no es necesario calcular la derivada de la funcin. Veamos un ejemplo. Estudiemos el volumen del cuerpo de revolucin engendrado por la rotacin del rea determinada por la curva y = las rectas x=a, x=b.
1 2 x y 3
Aplicando la frmula:
1 1 1 V = x 2 dx = x 4 dx = x 5 3 9a 9 5 a
5 4 b a4 9
Siendo b y a cualquiera dos valores de x que se consideren.
29
Matemticas
RESUMEN
Llamamos primitiva de una funcin f, a otra funcin g cuya derivada sea justamente f. g es primitiva de f g = f
Si una funcin es continua, entonces admite primitivas. Si una funcin

tiene primitivas, estas son un conjunto de infinitas funciones que solo difieren en el valor de una constante C que puede tomar el valor de cualquier nmero real.
Se llama integral indefinida de una funcin f(x), al conjunto formado por

todas sus primitivas y se denota por:
f (x)dx
Las integrales indefinidas cumplen las siguientes propiedades
La integral de la derivada de una funcin es la propia funcin.
f (x )dx = f (x ) + C
La integral de una constante por una funcin es igual a la constante por la integral de la funcin.
k f (x )dx = k f (x )dx
La integral de una suma (diferencia) es igual a la suma (diferencia) de las integrales.
( f (x ) g (x ))dx = f (x )dx g (x )dx

Las dos ltimas propiedades afirman que la integral indefinida es lineal, y se pueden englobar en una sola, de la siguiente manera:
(m f (x ) n g (x ))dx = m f (x )dx n g (x )dx
31
Formacin Abierta
A las integrales de las funciones elementales se les llama integrales

inmediatas, son las siguientes:
INTEGRALES INMEDIATAS FUNCIN PRIMITIVA SIMPLE PRIMITIVA COMPUESTA
Potencial
x n +1 x dx = n + 1 + C
n
f f n dx =
f n +1 +C n +1
e
Exponencial
dx = e x + C ax +C Ln a
f e
dx = e f + C af +C Ln a
x a dx =
f a f dx =
Logartmica
x dx = Ln x + C
f dx = Ln f + C f
Seno
cos xdx = senx + C

senxdx = cos x + C (1 + tg x )dx = tgx + C
2
f cos fdx = senf + C

f senfdx = cos f + C f (1 + tg f )dx = tgf + C
2
Coseno
Tangente
1 cos 2 x dx = tgx + C
2
f cos 2 f dx = tgf + C
2
(1 + cot g x )dx = cot gx + C f (1 + cot g f )dx = cot gf + C

Cotangente
sen
Arco seno
1
2
dx = cot gx + C
sen
f
2
dx = cot gf + C
+1 1 x2 1 1 x
2
dx = arc senx + C
+ f 1 f f 1 f
2 2
dx = arc senf + C
Arco coseno
dx = arc cos x + C
dx = arc cos x + C
Arco tangente
1+ x
dx = arc tgx + C
1+ f
dx = arc tgf + C
32
Matemticas
El mtodo de integracin por partes se aplica para integrar ciertos

productos de funciones. Es muy importante elegir las partes de la forma adecuada, tal y como se ha indicado en los distintos casos, si no, podemos complicar ms la integral. La frmula de integracin por partes es
udv = uv vdu
La integracin por cambio de variable se aplica en integrales de muy

diverso tipo, en el texto hay bastantes ejemplos. Expresaremos x en funcin de otra variable t, o al revs, a una expresin en funcin de x la llamaremos t.
Para poder elegir una de las infinitas primitivas de una funcin hay que
concretar el valor de la constante C, para ello hay que tener una condicin inicial que sea de obligado cumplimiento par la funcin primitiva.
La integral definida de la funcin f en el intervalo [a,b] coincide con el

rea del recinto R, limitado por la grfica de la funcin f, el eje OX y las rectas x=a y x=b.
Regla de Barrow: Sea f una funcin continua en el intervalo [a,b].

Entonces la integral definida de f entre a y b es igual al valor de que toma una primitiva F en b, menos el valor que toma F en a, es decir:
f (x)dx = F(b) F(a)

a
Propiedades de la integral definida:

Si c es un nmero entre a y b, esto es a < c < b, entonces se verifica lo siguiente:
f = f + f
a c
Figura 8.3.
Propiedad
33
Formacin Abierta
El significado geomtrico de esta propiedad es claro. El rea que est bajo la grfica de la funcin f entre los puntos a y b es igual al rea comprendida entre x=a y x=c ms el rea comprendida entre x=c y x=b. Si a=b, entonces:
f = f =0
a
Si permutamos los lmites de integracin, entonces la integral cambia de signo. Pueden aparecer resultados negativos que no tienen ningn sentido real si los interpretamos cmo reas.
f = f
b
La integral de la suma (diferencia) de dos funciones f y g es igual a la suma (diferencia) de las integrales. Esto es:
( f g) =
b a
f g
a
La integral del producto de una constante k por una funcin f es igual a la constante por la integral de la funcin:
(k f ) = k
b a
Se ha visto tambin cmo calcular el rea encerrada entre dos curvas sin
ms que integrar la diferencia de las funciones que las representan. Hay que tener en cuenta qu curva se encuentra por encima de la otra.
Tambin hay que tener en cuenta que si hacemos la integral definida de

una funcin cuya curva se encuentre por debajo del eje OX , el resultado obtenido es un n negativo que no puede representar un rea o superficie, por lo que hay que tenerlo en cuenta y cambiarle el signo.
34
Matemticas
Otra importante aplicacin de la integral definida es el clculo de la

longitud de un arco de curva entre dos puntos dados, en un intervalo [a,b]. La frmula a emplear es la siguiente:
b b
L = 1 + (f ( x )) dx = 1 + ( y ) 2 dx
2 a a
Tambin se pueden calcular reas de revolucin y volmenes de

revolucin, engendrados al girar cualquier curva alrededor del eje OX. Las frmulas respectivas son las siguientes:
b
S = 2 f ( x ) 1 + (f ( x ) ) dx
2 a b b
V = y 2 dx = [f (x )] dx
2 a a
35

Libro Mates

Cargado por

Información del documento

Derechos de autor

Formatos disponibles

Compartir este documento

Compartir o incrustar documentos

Opciones para compartir

¿Le pareció útil este documento?

¿Este contenido es inapropiado?

Copyright:

Formatos disponibles

Libro Mates

Cargado por

Copyright:

Formatos disponibles

Matemticas

UNIDAD 1. EL CONJUNTO DE LOS NMEROS MATEMTICOS

UNIDAD 2. SISTEMAS DE COORDENADAS.

UNIDAD 3. RECTAS EN EL PLANO.

UNIDAD 5. NMEROS COMPLEJOS.

UNIDAD 6. FUNCIN REAL DE VARIABLE REAL

UNIDAD 7. DERIVADAS DE FUNCIONES.

UNIDAD 8. INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA.

Unidad 1. El Conjunto de los Nmeros Matemticos

Conocer y diferenciar los principales conjuntos numricos, N, Z, Q, R y saber

Comprender y manejar la representacin de los nmeros en la recta real y

Unidad 1. El Conjunto de los Nmeros Matemticos

Unidad 1. El Conjunto de los Nmeros Matemticos

1.1. DIFERENTES CONJUNTOS DE NUMEROS

Figura 1.1. Los nmeros enteros sobre la recta.

Unidad 1. El Conjunto de los Nmeros Matemticos

Se entiende como fraccin la expresin

distintos de cero, son enteros y se interpreta como tomar a veces la unidad

3 2 1 12 13 , , , , ,.... } son todas fracciones equivalentes y representan al 6 4 2 24 26 1 nmero racional . 2

Unidad 1. El Conjunto de los Nmeros Matemticos

1) La divisin es un nmero entero, o sea el numerador es un mltiplo del denominador. Ejemplo:

Unidad 1. El Conjunto de los Nmeros Matemticos

Unidad 1. El Conjunto de los Nmeros Matemticos

1.2. ORDEN Y VALOR ABSOLUTO EN LOS NMEROS REALES

1.2.2. VALOR ABSOLUTO

Y el valor absoluto de cero, es cero. 0 = 0

Unidad 1. El Conjunto de los Nmeros Matemticos

5,78 = 5,78 3,987 = 3,987

1.2.3. PROPIEDADES DEL VALOR ABSOLUTO

Unidad 1. El Conjunto de los Nmeros Matemticos

Para comprobarlas sobre distintos ejemplos, puede usar los siguientes:

1.2.4. INTERVALO EN LA RECTA

Unidad 1. El Conjunto de los Nmeros Matemticos

2 6 = 2 ( 2 ) = 4 , este valor es la distancia mxima a la que

los puntos se pueden encontrar del centro. Luego tendramos la expresin:

Unidad 1. El Conjunto de los Nmeros Matemticos

1.3. POTENCIAS DE NMEROS REALES

Unidad 1. El Conjunto de los Nmeros Matemticos

1.3.1. OPERACIONES CON POTENCIAS

Unidad 1. El Conjunto de los Nmeros Matemticos

Potencia elevada a otra potencia

Factores y cociente con el mismo exponente.

Unidad 1. El Conjunto de los Nmeros Matemticos

Operaciones con potencias:

Producto de potencias de la misma base:

Factores y cociente con el mismo exponente:

Unidad 1. El Conjunto de los Nmeros Matemticos

1 = in det er min acin 0 , 0 = in det er min acin

Unidad 1. El Conjunto de los Nmeros Matemticos

n es el ndice de la raz. b es el radicando

Unidad 1. El Conjunto de los Nmeros Matemticos

Potencias de exponente racional

De lo que fcilmente se deduce:

1.4.1. OPERACIONES CON RADICALES

Unidad 1. El Conjunto de los Nmeros Matemticos

Unidad 1. El Conjunto de los Nmeros Matemticos

log 2 8 = 3 log 5 25 = 2 log10 10000 = 4 log10 0'001 = 3

Unidad 1. El Conjunto de los Nmeros Matemticos

Es evidente que log10 = 1 y lne = 1.

1.5.1. PROPIEDADES DE LOS LOGARITMOS

El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

log a (C D ) = log a C + log a D

C log a = log a C log a D D

log(3 ) = log 3 + log ln (4e ) = ln 4 + ln e = (ln 4) + 1