Run Run Shaw Library

Copyright Warning
Use of this thesis/dissertation/project is for the purpose of private study or scholarly research only. Users must comply with the Copyright Ordinance. Anyone who consults this thesis/dissertation/project is understood to recognise that its copyright rests with its author and that no part of it may be reproduced without the authors prior written consent.

CITY UNIVERSITY OF HONG KONG

A Study on Efficient Chaotic Image Encryption Schemes

Submitted to Department of Electronic Engineering in Partial Fulfillment of the Requirements for the Degree of Master of Philosophy

by

Kwok Sin Hung

September 2007

Abstract
With the advancements of mobile communication technologies, the utilization of audio-visual information in addition to textual information becomes more prevalent than the past. Cryptographic approaches are therefore necessary for secure multimedia content storage and distribution over open networks such as the Internet. A traditional way to resist statistical and differential cryptanalyses is to employ permutation and diffusion alternatively. Recently, research on image encryption using chaos theory has been emerged. Some chaotic image encryption schemes use a multi-dimensional chaotic map for pixel permutation in the spatial domain while taking another one-dimensional (1D) chaotic map for keystream generation in the diffusion function. Various image encryption schemes under this architecture have been proposed in the literature. There are still two realization constraints of the above architecture which hinder the system performance. First, the confusion and diffusion effect is solely contributed by the permutation and the diffusion stage, respectively. Consequently, more overall rounds than necessary are required to achieve a certain level of security. Second, in particular to diffusion stage, real-valued chaotic sequence is commonly treated as a pseudo-random keystream. However, a considerable amount of computation load is sacrificed for real-valued computation and consequent integer quantization. In this thesis, the typical structure of chaos-based image encryption schemes has been studied. The concept of introducing certain diffusion effect in the confusion stage by simple sequential Add-and-then-shift operations is proposed. The purpose is to mix the pixel values over the entire image to achieve similar effect of diffusion. The explicit diffusion function then contributes the second level diffusion effect which leads to fewer overall rounds and hence a faster encryption. Moreover, a more efficient diffusion function using simple table lookup techniques as a light-weight replacement to real-valued chaotic

ii

maps is also suggested. Instead of floating point computation, the diffusion process is accomplished by mutual lookup of a static two-dimensional (2D) permutation table and a dynamic 2D diffusion table. Both the position and the value of each permuted image pixel are used to locate a secret mask. Eventually, each permuted pixel value is added to the random mask drawn from the table. Simulation results show that at a similar performance level, the proposed cryptosystem requires around one-third the encryption time of an existing cryptosystem. The effective acceleration of the encryption speed is therefore achieved which is then more applicable to real-time image encryption.

iii

Acknowledgements
First and foremost, I would like to express my deepest gratitude to my supervisor, Dr. K.W. Wong for his patient guidance and support during my research. Dr. Wongs kind encouragement and insightful advice have helped me to overcome many challenges and guided me to complete this thesis. In addition, I sincerely appreciate the fruitful collaborations with my colleagues, Mr C.W. Lee and Mr K.P. Man, in various research projects. They have made my study life more enjoyable. I would especially like to thank City University of Hong Kong for providing financial support and an ideal environment for my research. Finally, I am very grateful to my family for their great love, support and understanding at all times, especially during the most difficult periods of my research and thesis writing.

iv

Contents
List of Figures .....................................................................................................vi List of Tables .......................................................................................................x List of Symbols ...................................................................................................xi List of Abbreviations ........................................................................................ xii Chapter 1 Introduction .........................................................................................1 1.1 Motivation and Objective .......................................................................1 1.2 Outline of the Thesis...............................................................................3 Chapter 2 Fundamentals of Cryptography ...........................................................5 2.1 Background .............................................................................................5 2.2 Private-key Cryptography.......................................................................8 2.2.1 The Encryption Process .................................................................8 2.2.2 Typical Private-key Cryptosystems .............................................10 2.2.3 Brief Review on Some Existing Image Encryption Schemes......12 2.3 Public-key Cryptography ......................................................................14 2.3.1 Principle of Public-key Encryption..............................................14 2.3.2 Typical Public-key Cryptosystems ..............................................16 2.4 Summary ...............................................................................................17 Chapter 3 Chaotic Cryptography .......................................................................19 3.1 Introduction to Chaotic Maps ...............................................................20 3.1.1 One-dimensional Chaotic Maps...................................................20 3.1.2 Two-dimensional Chaotic Maps ..................................................22 3.2 The Important Properties of Chaotic Maps...........................................25 3.2.1 Sensitive Dependence on Initial Conditions ................................25 3.2.2 Sensitive Dependence on System Parameters..............................26 3.2.3 Ergodicity.....................................................................................26 3.3 Relationship between Cryptosystems and Chaotic Systems.................27 3.4 Chaotic Encryption Schemes for Digital Images..................................30 3.4.1 Review of Some Existing Chaotic Image Encryption Schemes ..31 3.4.2 Architecture of Generic Chaos-based Image Cryptosystems ......33 3.4.3 Other Issues in Chaos-based Image Cryptosystems ....................37 3.4.4 Cryptanalysis of Chaos-based Image Cryptosystems ..................40 3.5 Summary ...............................................................................................42

Chapter 4 Chaotic Confusion Process for Image Encryption ............................43 4.1 Overview of an Image Encryption Scheme Using 2D Standard Map ..44 4.2 Some Observations ...............................................................................46 4.3 Modified Confusion Process with Pixel Value Mixing ........................49 4.3.1 Investigation of Some Possible Operations on Pixel Value.........49 4.3.2 Encryption Procedure...................................................................56 4.3.3 Decryption Procedure ..................................................................58 4.3.4 Hardware Implementation ...........................................................58 4.4 Security Analysis ..................................................................................61 4.4.1 Histogram.....................................................................................61 4.4.2 Key Space ....................................................................................62 4.4.3 Differential Analysis with Time Performance.............................63 4.4.4 Correlation Analysis of Two Adjacent Pixels .............................67 4.5 Summary ...............................................................................................70 Chapter 5 Efficient Image Diffusion Using Table Operations...........................71 5.1 Diffusion Algorithms Based on 1D Logistic map ................................72 5.1.1 Diffusion Techniques Based on XOR plus mod Operations....72 5.1.2 Diffusion Techniques Based on XOR with Substitutions............73 5.2 Practical Problems of the Algorithms ...................................................74 5.3 The Proposed Cryptosystem .................................................................79 5.3.1 Diffusion Based on Table Lookup and Entries Swapping...........79 5.3.2 The Overall Encryption Procedure ..............................................85 5.3.3 Hardware Implementation ...........................................................89 5.4 Experimental Results and Analysis ......................................................90 5.4.1 Diffusion Key Analysis................................................................92 5.4.2 Correlation Analysis of Two Adjacent Pixels .............................94 5.4.3 NPCR & UACI Analyses.............................................................95 5.5 Summary ...............................................................................................98 Chapter 6 Conclusion and Further Developments .............................................99 6.1 Conclusion ............................................................................................99 6.2 Further Developments.........................................................................101 6.2.1 Joint Compression-encryption Approach to Reduce Cipher Image Size................................................................................101 6.2.2 Extension to Chaos-based Video Encryption ............................102 6.2.3 Incorporation of Public-key with Private-key Schemes ............102 References ........................................................................................................104 List of Publications ..........................................................................................109

vi

List of Figures
Figure 2.1 Figure 2.2 Figure 2.3 Figure 3.1 Figure 3.2 The encryption process performed by Caesar cipher...................... 6 Private-key cryptography scenario.................................................. 8 Public-key cryptography scenario................................................. 15 A plot of the tent map with parameter a = 3 ................................. 21 4 A plot of the logistic map with parameter b = 3.999. ................... 22

Figure 3.3 An illustration of baker map in the unit square (a) before action; (b) being stretched and (c) being folded. ...................................... 23 Figure 3.4 Figure 3.5 Figure 3.6 An illustration of cat map in the unit square. ................................ 24 Cobweb diagram of logistic map with (a) x0=0.7, (b) x0=0.700001. ................................................................................ 25 Variation in trajectories of the logistic map due to minor differences in system parameter b = 3.999999 and b = 3.999998........................................................................................ 26 A typical distribution of trajectory of the logistic map after 104 iterations........................................................................................ 27 (a) plain image containing many areas with identical or similar gray levels, and (b) its corresponding encrypted image by Advanced Encryption Standard (AES) with both key size and block size 128-bit long running in the ECB mode........................ 30 (a) A test image of Lena; the resultant images (b) and (c) after applying the discretized baker map once and nine times, respectively, with N = (8, 8, 32, 64, 32, 32, 32, 32, 64, 64, 32, 64, 32, 8, 8). .................................................................................. 35

Figure 3.7 Figure 3.8

Figure 3.9

Figure 3.10 The results of test image Lena (a) and (b) after applying the discretized cat map once and nine times, respectively, with a = 5 and b = 9..................................................................................... 35 Figure 3.11 The results of test image Lena (a) and (b) after applying the discretized standard map once and nine times, respectively, with k = 1750................................................................................. 36

vii

Figure 3.12 A generic architecture of image encryption systems based on 2D chaotic permutations. .............................................................. 37 Figure 3.13 An illustration of key generation and distribution proposed in [9]. ................................................................................................. 39 Figure 4.1 Figure 4.2 The chaotic image cryptosystem proposed by Lian et al. in [9]. .. 45 Plaintext sensitivity test: (a) original image, (b) and (c) cipher images ( m=n=2 ) whose corresponding plain images have one pixel difference only; (d) difference between cipher images (b) and (c) in gray scale(upper) and binary colour(lower), (e) and (f) cipher images ( m=n=4 ) with the same corresponding plain images as (b) and (c), respectively ; (g) difference between cipher images (e) and (f) in gray level. ......................................... 48 Architecture of the proposed chaotic image cryptosystem. .......... 57 An illustration of Add-and-then-shift operation on pixels in permutation. .................................................................................. 57 The proposed hardware configuration. ......................................... 59 Main modules of the proposed hardware implementation: (a) Standard Map Computation Unit; (b) Add-and-then-shift Unit and (c) Logistic Map Computation Unit. ...................................... 60 (a) Plain Lena image; (b) Histogram of the plain image; (c) Intermediate cipher image using Lian et al.s confusion; (d) Histogram of the intermediate cipher image shown in (c); (e) Intermediate cipher image using the proposed confusion; (f) Histogram of the intermediate cipher image given in (e). ............ 62 (a) Plain Cameraman image; (b) and (c) cipher images whose corresponding plain images have one pixel difference only; (d) difference between cipher images shown in (b) and (c). .............. 64 Performance of the proposed and Lian et al.s cryptosystems in terms of (a) number of pixels change rate (NPCR); and (b) unified average changing intensity (UACI) at different overall rounds (m) with 4 permutation rounds in each confusion stage (n = 4)............................................................................................ 65

Figure 4.3 Figure 4.4 Figure 4.5 Figure 4.6

Figure 4.7

Figure 4.8

Figure 4.9

viii

Figure 4.10 Correlation analyses of two horizontally adjacent pixels in (a) the plain Peppers image; (b) the cipher image obtained using the proposed scheme. .................................................................... 69 Figure 5.1 Figure 5.2 A plot of pixel value and mask value using the diffusion method employed in [9]. ............................................................... 76 Diffusion performance on plain-image: (a) 256 256 Cameraman image; (b) and (c) diffused image by 1 round of Algorithm 5.1.1 and 5.1.2, respectively; (d) and (e) diffused image by 9 rounds of Algorithm 5.1.1 and 5.1.2, respectively; (f) and (g) Histograms of results in (d) and (e), respectively........ 77 Diffusion performance on plain-image: (a) 512 512 Elaine image; (b) and (c) diffused image by 1 round of Algorithm 5.1.1 and 5.1.2, respectively; (d) and (e) diffused image by 9 rounds of Algorithm 5.1.1 and 5.1.2, respectively; (f) and (g) Histograms of results in (d) and (e), respectively. ........................ 78 An illustration of encoding method for Pi-1 and Ci-1. .................... 81 A block diagram of table lookup based on information of pixel position permutation. .................................................................... 82 Graphical representation of swapping entries (s,t) and (x4,y4). .. 83 An illustration of the dynamic update of the 2D lookup table...... 84 Flowchart of the proposed diffusion algorithm............................. 85 Architecture of the proposed chaos-based image cryptosystem. .. 86

Figure 5.3

Figure 5.4 Figure 5.5 Figure 5.6 Figure 5.7 Figure 5.8 Figure 5.9

Figure 5.10 The proposed hardware configuration. ......................................... 89 Figure 5.11 Main modules of the proposed hardware implementation: (a) Standard Map Computation Unit and (b) 2D Table Operation Unit................................................................................................ 90 Figure 5.12 Performance of diffusion function collaborated with different 2D chaotic maps (a) - (c) permutated image using baker map, cat map and standard map, respectively; (d) - (f) completely encrypted images of images (a) - (c) after diffusion process, respectively; (g) - (i) histograms of images (d) - (f). .................... 91

ix

Figure 5.13 Key sensitivity test 1: (a) plain-image; (b) encrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 90); (c) encrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 91); (d) difference image............................................................................ 93 Figure 5.14 Key sensitivity test 2: (a) plain-image; (b) encrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 90); (c) decrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 90); (d) decrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 91). ................................................................................................ 93 Figure 5.15 Correlations of two horizontally adjacent pixels in (a) the plain Lena image; (b) the encrypted image by the proposed scheme (m=2,n=1)...................................................................................... 95

List of Tables
Table 3.1 A comparison of some features characterized by chaotic systems and traditional cryptosystems........................................................... 28 Table 3.2 Comparison of the parameter space of baker map, cat map and standard map after discretization. .................................................... 38 Table 4.1 Percentage of pixel change on different test images with overall rounds m=n=2 and m=n=4. .............................................................. 47 Table 4.2 Time required to perform Algorithms 4.3.1 (a) (f). ...................... 51 Table 4.3 Test on permuting Lena image with Algorithms 4.3.1 (a) (f) (MN: Mean; SD: Standard Deviation; MDN: Median). .................. 52 Table 4.4 Test on permuting homogenous black square with Algorithms 4.3.1 (a) (f) (MN: Mean; SD: Standard Deviation; MDN: Median). ........................................................................................... 54 Table 4.5 Test on permuting homogenous white square with Algorithms 4.3.1 (a) (f) (MN: Mean; SD: Standard Deviation; MDN: Median). ........................................................................................... 55 Table 4.6 Probability of no shift on some test images.................................. 56 Table 4.7 Execution time and performance indices NPCR and UACI of the proposed and Lian et al.s schemes, for some selected values of m and n. ............................................................................................ 67 Table 4.8 Correlation coefficients of adjacent pixels of different images. ...... 68 Table 5.1 Time required for different diffusion algorithms to process an image of size 512 512. .................................................................. 75 Table 5.2 Content of the proposed 2D Diffusion table: (a) initial state (b) updated after processing the entire image........................................ 88 Table 5.3 The configuration and results of key sensitivity test........................ 94 Table 5.4 Correlation coefficients of adjacent pixels in two images ............... 94 Table 5.5 Encryption time and performance indices NPCR and UACI of the proposed, Chen et al.s and Lian et al.s scheme, for some selected values of m and n................................................................ 97

xi

List of Symbols
<< >> left shift right shift exclusive-or scalar multiplication modulus operator closed interval between a and b N-tuple of n members list of elements ai with i being the index selected pre-image of a plain image P value of ith pixel in a cipher image C inverse of function E number of pixels N in one row ranged from 0 to N-1 value of ith pixel in a plain image P Real number domain value of the 1D chaotic map iteration at the nth cycle random scan couple 1D vector with elements s and t absolute value of number x upper bound of the logistic map lower bound of the logistic map

mod [a, b] (a1 , a 2 ,L , a n ) {ai}

C

Ci E
-1

N 0N 1

Pi R

n
(rx, ry) s t |x| Xmax Xmin

xii

List of Abbreviations
AES CBC CFB CKBA DCT DES ECB ECC ECDH ECDLP HCIE IDEA IFP KDC LFSR MDN MN NIST NPCR OFB PGP RSA SD UACI XNOR XOR Advanced Encryption Scheme Cipher Block Chaining Mode Cipher Feedback Mode Chaotic Key-based Algorithm Discrete Cosine Transform Data Encryption Scheme Electronic Code Book Mode Elliptic Curve Cryptography Elliptic Curve Diffie-Hellman Protocol Elliptic Curve Discrete Logarithm Problem Hierarchical Chaotic Image Encryption International Data Encryption Algorithm Integer Factorization Problem Key Distribution Center Linear Feedback Shift Register Median Mean National Institute of Standards and Technology Number of Pixels Change Rate Output Feedback Pretty Good Privacy Rivest-Shamir-Adleman Standard Deviation Unified Average Changing Intensity Bitwise Exclusive-NOR Bitwise Exclusive-OR

Chapter 1

Introduction
1.1 Motivation and Objective
In recent years, audio-visual information sharing has become more prevalent under the rapid development of Internet. Real-time multimedia applications are also made possible with the advancement of mobile communication technologies. However, in open networks, there is a potential risk of making sensitive information such as military and medical images vulnerable to unauthorized interceptions. The development of robust cryptographic schemes is thus essential to the provision of multimedia security. For textual information, it can be satisfied with the direct application of many well-established encryption schemes such as Data Encryption Scheme (DES)[1], International Data Encryption Algorithm (IDEA) [2] and Advanced Encryption Scheme (AES) [3]. However, the case of multimedia information in real-time communication is different and hard to be accomplished by traditional schemes.

This is because the intrinsic properties of audio-visual information such as bulk data capacity, strong pixel correlation and high redundancy, lower the encryption performance. Since traditional encryption schemes are not fit for modern multimedia requirement, many researches have been devoted to investigate better solutions for image and video encryptions. In particular, application of chaos theory in multimedia encryption is one of the important research directions. The field of chaotic cryptography has undergone tremendous growth over the past few decades. The primary motivation of employing chaotic systems is its simplicity in form and complexity in dynamics. According to the classification of chaotic systems, the security application of chaos can be divided into analog chaotic secure communications utilizing continuous dynamical systems [4, 5] and digital chaotic cryptosystems utilizing discrete dynamical systems [6 - 8]. For todays computer technology, the way realizing chaos in digital domain is more vital to security application running in finite precision machines. In response to the aforementioned challenges in protecting multimedia content, the objective of this research work is specially oriented towards analyzing chaos-based image encryption schemes. Many existing schemes under this category are found to merely achieve moderate or even low security. Only a few of them [9 - 11] promise to achieve sufficient security, but without maintaining a satisfactory speed performance. Our work is to modify and optimize some existing chaotic image encryption schemes so as to uplift the efficiency required for real-time operation purpose. In this regards, two enhancement measures in the system efficiency have been proposed to the main components of typical chaos-based image cryptosystems: chaotic confusion and pixel diffusion processes. The superior results of numerical and security analysis justify the feasibility of such proposed schemes in real-time communication environment.

1.2 Outline of the Thesis

Chapter 2 covers the fundamentals and terminologies of cryptography, including the issues of private-key cryptography and public-key cryptography. Note that the chaotic image encryption schemes under study fall into the category of private-key cryptosystems. In order to have a clear background for the remaining chapters, the type of ciphers and mode of operations in private-key cryptosystems will explicitly be highlighted. In addition, some modern cryptographic standards such as DES, AES and RSA will be discussed. Chapter 3 introduces an overview of chaotic cryptography. The illustration of chaos theory will start with some widely studied one-dimensional (1D) and two-dimensional (2D) chaotic maps. Given the backgrounds of chaotic properties, the similarities and differences between chaotic maps and cryptosystems will then be analyzed. Based on the above established relationships, a more detail description on existing chaotic image encryption schemes will be given together with the issue of design considerations and list of particular cryptanalysis. Chapter 4 presents a modified approach to the confusion process in typical chaotic image cryptosystems through a special review on an image encryption scheme using 2D chaotic standard map. The principle of this approach including the encryption and decryption procedures will be explained in detail. The security evaluations on the proposed scheme will be provided after the design principle. In Chapter 5, our attention turns to the effectiveness of the diffusion process which is another important component in image cryptosystems. The goal is to investigate a light weight replacement for the concerned process which commonly requires real-valued computation and consequent integer quantization. The problems will be elaborated by two practical examples of existing schemes based on 1D logistic map. With suitably use of table lookup techniques, a new diffusion approach will be proposed. The corresponding image encryption scheme together with security consideration will be provided.

Finally, we conclude our work in this thesis and give some remarks on future research in Chapter 6.

Chapter 2

Fundamentals of Cryptography
In this chapter, the basic principles of cryptography will be introduced as a foundation for the remaining chapters of this thesis. In Section 2.1, the background of cryptography and some terminologies will be covered. The issues of private-key cryptography will be presented in Section 2.2, while the introduction of public-key cryptography will be provided in Section 2.3. A summary will finally be given in Section 2.4.

2.1 Background
Confidential communication has long been a common practice in the social life. However, as information can be communicated electronically, it is exposed in public domain and unavoidably resulted in interceptions. A scientific approach to respond the demands on achieving the sense of security is cryptography. The term cryptosystem, also called cipher, is often used in cryptography. Intuitively, its meaning is clear enough which refers to an encryption system. The central

idea of encryption is to transform the message in which its original information can only be reconstructed by a designated recipient. By definition, a message in its original form is known as plaintext P and the information concealed in an unintelligible form is known as ciphertext C. The encryption process consists of an algorithm and a key. It is generally described as C = E(P, ke), where ke is the encryption key and E( ) is the encryption algorithm. Therefore, the ciphertext C can be transmitted over public channels without exposing the information it represents. Similarly, a corresponding decryption process is the reverse of encryption which is based on the ciphertext C with decryption key kd for the reconstruction of the original plaintext: P = D(C, kd), where D( ) = E-1( ). The principle of encryption process is depicted in Figure 2.1. As an illustration, Caesar cipher is chosen which is the simplest and most classical cipher attributed to Julius Caesar [12].

encryption key ke=3 plaintext P eg. CITYU ciphertext C eg. FLWBX Encryption public channel

decryption key kd=3 plaintext P eg. CITYU

Decryption

Figure 2.1 The encryption process performed by Caesar cipher.

In this example, the encryption algorithm is to shift each plain letter forward by ke letter positions, while the decryption algorithm is similar to the encryption one, but reverse shift with kd letter positions. The keys ke and kd in this example are predefined as 3. For instance, the letter A is replaced by D, the letter B is replaced by E and consequently CITYU would be replaced by FLWBX. Since then, a confidential communication between the sender and the receiver can be realized. Obviously, it is possible to complicate the encryption algorithm by incorporating with some additional operations such as replacing each letter by another letter or multiple letters. Such approach is known as a

substitution and examples of early substitution ciphers include Affine cipher, Vigenere cipher and Playfair cipher [13]. Indeed, the substitution-based approach is still employed in many modern complex cryptosystems to be presented in Section 2.2. According to Kerckhoffs principle of secure cryptosystem [14], the security should depend on the secrecy of the key, not the secrecy of the encryption/decryption algorithm that was used. In other words, it is assumed that the algorithm is publicly known, yet decryption of message is infeasible on the basis of the ciphertext in addition to knowledge of the algorithm. Shannon pointed out two fundamental operations required for cipher design, namely confusion and diffusion [15]. The former refers to a transformation which obscures the statistical dependence between the plaintext and the ciphertext in a sense that the possibility of key discovery will be frustrated. This can be achieved by using complex substitution algorithms. The latter means dissipating the statistical structure of the plaintext by spreading it out over the ciphertext. That is, every ciphertext block is affected by many (ideally all) plaintext blocks. Collectively, with respect to the cryptographic key relationship of ke and kd, two important classes of cryptography are derived: private-key cryptography and public-key cryptography. For a private-key cryptosystem, ke and kd are either the same or one can easily be deduced from the other, whereas a pair of separate keys is required in public-key cryptosystem, i.e. ke kd. Typically, it is also impractical to seek a relationship between the keys without the knowledge of some additional information. As of todays information security, both two branches of cryptosystems have a significant importance and one cannot substitute another. A more detailed discussion on these two cryptosystems will be given in the following sections.

2.2 Private-key Cryptography

In brief, the principle of private-key cryptography, as shown in Figure 2.2, is based on the fact that the sender and receiver agree on a common secret key k before they can communicate securely. Similar to the generic encryption model described in Figure 2.1, the ciphertext C is unintelligible without the aid of the secret key k. Such an unintelligible piece of information can finally be transformed back into the original plaintext P by the receiver possessing the same key. However, it should be stressed that a secure channel between the parties for key agreement is critical but practically inconvenient to follow. This refers to the key distribution problem. As a remedy, key distribution center (KDC) together with some associated protocols is suggested for the secret key establishment.

secret key k

secure channel ciphertext C recovered plaintext P Receiver Decryption

Sender

plaintext P Encryption

public channel

Figure 2.2 Private-key cryptography scenario.

2.2.1 The Encryption Process Information is represented by a sequence of bits for storage and manipulation. In private-key cryptography, the structure of ciphers can generally be divided into two types, namely, block cipher and stream cipher.

i. Block cipher In the course of block encryption, a fixed-length block of bits is operated at a time. Each block is encrypted into another block with the same size. The block

size determines the security and complexity of the cipher. For a simple block cipher, each plaintext block is usually processed independently by the same key. In addition, there is a need for padding short last block of plaintext with certain zero bits. The way the cipher operates is called Electronic Code Book (ECB) mode [16]. In ECB mode, repeated plaintext blocks will transform to the same corresponding ciphertext blocks. The ECB mode is particularly insecure to those highly structured plaintext. To overcome this problem, three other modes of operation, namely, Cipher Block Chaining (CBC), Cipher Feedback (CFB) and Output Feedback (OFB) are defined. In CBC mode, each plaintext block being encrypted will perform Exclusive-OR (XOR) operation with its previous ciphertext block. This overcomes the problem of ECB mode by the fact that the same plaintext blocks turn out with different ciphertext blocks. On the other hand, each plaintext block is linked together in encryption operation. Under this circumstance, a single bit change in one plaintext block will propagate to the corresponding ciphertext block and all subsequent ciphertext blocks. Because of its added security, CBC is the most commonly used block cipher mode. The same effect can also be achieved by the CFB mode. With CFB mode, a shift register is required in such a way that its content together with a certain number, say j, of bits of the previous ciphertext as an encryption input. The output of encryption function appears to be pseudorandom which is then XORed with j-bit plaintext. The difference between OFB mode and CFB mode is that the content of shift register in OFB is operated with the previous output of encryption function instead of the ciphertext. The length of j in CFB and OFB modes can be any value up to the block size. Compared with CBC mode, it is possible to encrypt data in units smaller than the block size of the ciphers in CFB and OFB modes.

ii. Stream cipher In contrast to block ciphers, which operate on large plaintext blocks, stream ciphers operate on smaller units of data at a time. Typically, a random bit stream is required to serve as a keystream. It is then XORed with the plaintext stream to

10

accomplish the encryption process. The keystream can generally be produced by two types of generators, namely, synchronous and self-synchronous. In the former, the keystream generated is independent of the plaintext stream. A bit lost in transmitting ciphertext stream will cause a problem in decryption. When this happens, the keystream must be resynchronized for correct decryption. Compared with its synchronous counterparts, the basic difference of a selfsynchronous stream cipher is that the keystream is computed from knowledge of the previous n ciphertext bits. For the case of bit lost in transmission, such keystream will resynchronize itself after obtained sufficient number of correct ciphertext bit. This can be easily realized by the use of a linear feedback shift register (LFSR) [12]. Owing to its simplicity, the encryption speed of stream ciphers is faster than that of block ciphers. They are more applicable for telecommunications and real-time data transmission such as video streaming.

2.2.2 Typical Private-key Cryptosystems All of the notably known private-key cryptosystems exhibit the cryptographic properties desired in a block cipher. Some of them have become the cryptographic standards in the past few decades. In this sub-section, three typical cryptosystems will briefly be covered.

i. Data Encryption Standard Data Encryption Standard (DES) [1] was developed by IBM researchers and has been adopted by the National Institute of Standards and Technology (NIST) in 1977. As a private-key block cipher, DES operates on 64-bit blocks of plaintext, while the block encryption is governed by a 56-bit key. Aiming at achieving the confusion and diffusion properties, DES undergoes a Feistel cipher-like implementation which iteratively performs 16 rounds of permutation and substitution transformations called S-boxes and P-boxes, respectively. In this case, key schedule is specified to generate 16 sub-keys used in each round. However, people have recognized that the key space of DES is insufficient to

11

resist against brute-force attacks using todays powerful computer. Other than brute-force attacks, differential cryptanalysis [17] and linear cryptanalysis [18] have also been carried out successfully by investigating some specific plaintextciphertext pairs of DES in early 1990s.

ii. International Data Encryption Algorithm In 1990, Lai and Massey proposed the International Data Encryption Algorithm (IDEA) cryptosystem which is designed to be stronger against differential cryptanalysis than DES [2]. The security relies on employing a 128bit secret key and interleaving group of operations such as modular addition and multiplication. It is adopted as a message encryption algorithm in a hybrid encryption packages called Pretty Good Privacy (PGP). However, the patent practice and commercialization of IDEA greatly limit its deployment in the community.

iii. Advanced Encryption Standard Since the security deficits are found in DES, the need for a stronger alternative has been officially declared by NIST. After calls for proposal, a Belgian cipher, Rijndael [19] has eventually been adopted as the Advanced Encryption Standard (AES), a successor of DES in 2001. It is also an iterated block cipher with a scalable key length which can be 128, 192 or 256 bits. In the core of AES algorithm, there is no Feistel cipher-like structure. However, the entire block of input data can be processed in parallel and intertwined with operations such as substitutions, row shifting, column mixing and round key additions. In this regard, the new AES with an expanded key length has many potential advantages over other block ciphers by offering a more secure and faster implementation. Many recent security applications have been migrated to meet this new standard.

12

2.2.3 Brief Review on Some Existing Image Encryption Schemes In general, the confidentiality of multimedia data such as digital image and video can be safeguarded by means of private-key cryptography. Those techniques mentioned in previous sub-section are considered as general-purpose encryption methods. Besides, some encryption techniques particularly dedicated to image indeed form the basis for video encryption. As an extension of the related topics, a few advanced private-key image encryption techniques will be covered in the following context.

i. Selective Bitplane Encryption To achieve a fast encryption, image encryption schemes are often designed not to encrypt the entire images completely, but a portion only. In this way, the amount of computation is reduced and this approach is regarded as selective image encryption [20]. Gray level images are usually composed of eight bitplanes. The higher-order bitplanes contain the majority of visually significant and strong correlation data of the plainimage, whereas the remainings contribute to more subtle details in the image. Based on this observation, a selective bitplane encryption scheme is proposed [21]. AES is selected as the functional encryption in this scheme. Undoubtedly, the underlying security is subject to the portions of bitplane to be encrypted. Through the experiments, it is not suggested to merely encrypt the most significant bitplane which can be reconstructed from those unencrypted residual bitplanes. However, there seems to be no convincing method to determine the portions of bitplane encryption for encryption.

ii. SCAN-based Image Encryption A formal language (SCAN) is intended to describe and generate multiple of two-dimensional (2D) spatial accessing order from a short set of simple ones [22]. It is first employed for image encryption in [23]. The plain image is initially serialized to one dimensional data stream which is then described by the SCAN language. Several scanning orders are expressed into the corresponding SCAN

13

letters. Different SCAN strings (combinations of SCAN letters) form different kinds of secret images. The SCAN string is served as an encryption key bound to a given 2D image array. The encryption procedure is to rearrange image into a final sequential representation. Each assembled secret image in process of SCAN string is combined by the insertion of additive noises at particular image points. Since no one except the intended user can obtain the correct SCAN combinations, the original image is therefore considered confidential.

iii. Embedding Image Compression into Encryption The abovementioned schemes are devoted to the uncompressed image data. For compressed images, some special measures are required before strictly combining encryption and compression directly. In [24], a framework is proposed for fast encryption by entropy encoders such as Huffman coder. In entropy coding, the statistical model is used to decode the compressed bit stream. It is therefore suggested that multiple statistical models are used alternately in certain secret order to encode the input symbol stream. Through security analyses, the proposed scheme is proved to be applied effectively on both multiple Huffman coding tables of Huffman coder and multiple state indices of QM coder. However, it should be noted that the original image can be correctly reconstructed only if its input is identical to the output of the encoder. There is also a concern about codec dependence of such kind of scheme [25]. Nevertheless, the potential for integrating encryption with multimedia compression at a low computation is promised.

iv. Chaotic Image Encryption Recently, a widely studied example of image encryption is based on chaos theory which is well established, simple but with complicated dynamics. In [26], a symmetric encryption scheme based on two-dimensional chaotic maps is proposed. A two or higher dimensional discretized chaotic map is adopted for pixel permutation together with another one-dimensional (1-D) map for diffusion. The superiorities of such kinds of chaos-based approaches are mainly relatively

14

large block size and a high encryption rate. More detailed investigations on chaotic image encryption schemes will be discussed in the following chapters.

2.3 Public-key Cryptography

Apparently, key establishment protocol and KDC server can be utilized to deal with the key distribution problem caused by private-key cryptography. However, due to the requirement of online presence of KDC, the server becomes a single point of failure once it goes down in the network. The approach of centralization is probably not a complete solution to key distribution problem. The true solution was not available until the proposal of public-key cryptography introduced by Diffie and Hellman in 1976 [27]. In the following, the idea of public-key cryptography will be explained.

2.3.1 Principle of Public-key Encryption Unlike private-key cryptography, secret keys are not shared via a secure channel. Instead, each party has a pair of keys, called private key and public key. Typically, the public key for encryption is announced openly, while the private key for decryption is kept strictly secret. More importantly, it is computationally infeasible to derive the private key from the corresponding public key. Thus, all communications involve public key only, but not private key. The communication model of public-key cryptography is illustrated in Figure 2.3. Initially, each concerned party is associated with a key pair in the form of <public key, private key>, denoted by <Ksend, ksend> for the sender and <Krecv, krecv> for the receiver. The public keys of both parties are assumed to be publicly accessible to all parties throughout their communication.

15

Receivers public key Krecv ciphertext C Sender plaintext P Encryption public channel

Receivers private key krecv recovered plaintext P Receiver Decryption

Figure 2.3 Public-key cryptography scenario.

To establish a confidential communication as shown in Figure 2.3, the sender first encrypts the plaintext P using receivers public key and obtain the ciphertext C = E(P, Krecv), where E( ) is the encryption function. When C is available at the receiver side, it is decrypted by the receiver using its private key and transformed back into the original plaintext P = D(C, krecv), where D( ) is the decryption function. For eavesdroppers who sniffed the key Krecv and the encrypted message C, it is still insufficient to determine the original message as long as no one, except the receiver, has the knowledge of krecv. The ciphertext C can be transmitted publicly without exposing the information it represents. Since the secrecy of krecv is never disclosed over public channels, public-key cryptosystem is said to be free from the key distribution problem. In addition, it also provides some significant cryptographic functions for data origin authentication in digital signatures, non-repudiation services and session key distribution services in an efficient way. Mathematically, the arrangement of a key pair can be described as a one way trapdoor function. Using this kind of function, it is easy to compute in one direction, but its reverse is infeasible without the presence of some additional information. Very often, the encryption function controlled by the public key acts as a one way function, while the private key forms a decryption trapdoor. In other words, the security of public-key cryptosystems is entirely related to its underlying mathematical problem of computing a private key from the matched public key. The more complex the mathematical problem, the more secure the cryptosystem. Although there is no absolute one way trapdoor function proved,

16

some known mathematical problems are considered to be computationally hard in the scope of current computing means. Examples are the Integer Factorization Problem (IFP) and the Elliptic Curve Discrete Logarithm Problem (ECDLP). The mathematical basis of public-key cryptosystems will be explored in the next sub-section.

2.3.2 Typical Public-key Cryptosystems

i. RSA RSA [28] was developed by three MIT researchers Rivest, Shamir and Adleman shortly after the discovery of public-key cryptography. It relies on discrete logarithm and factorization of large prime numbers. To get the scheme started, a pair of keys is initiated with the steps of choosing large prime numbers p and q say of 100 digits and then multiplying them together to get the product n, i.e. n = pq. The sender determines numbers e and d such that
ed =1

(mod( p 1)(q 1) ),

(2.1)

where e is relatively prime to ( p 1)(q 1) , d is the multiplicative inverse of e modulo ( p 1)(q 1) . In this way, the public key denoted by e, n is publicly issued, while the private key denoted by d , p, q is kept secret. In RSA, the plaintext is encrypted block by block. It is divided into k-bit blocks where 2k < n. The encryption and decryption are formulated by Eqs. (2.2) and (2.3), respectively C = Pe (mod n), P = Cd = (Pe)d = P k(p-1)(q-1)+1 = P (mod n), by Eulers Theorem (2.2) (2.3)

where P is plaintext block, C is ciphertext block and k is an integer. The integer factorization problem here is assumed that given only n, it is not computationally feasible to find ( p 1)(q 1) without having knowledge of p and q. Over

decades, the factorization problem has been challenged by many trial attacks

17

such as Number Field Sieve (NFS). As of today, 512-bit RSA keys, which were formerly considered as adequate for use, are now questionable.

ii. Elliptic curve cryptosystem Elliptic curve cryptosystem (ECC) is based on Elliptic Curve Discrete Logarithm Problem (ECDLP) in which the entities are points on certain parts of an elliptic curve. The use of elliptic curves for public-key cryptographic schemes is suggested by Koblitz [29] and Miller [30] independently in 1985. The mathematical problem behind is all about two points P and Q on the curve such that Q = kP where k is scalar. With the knowledge of points k and P, it is easy (at least not hard) to obtain the scalar multiplication of point kP. Interestingly, the inverse of finding k given P and kP is intractable. In such a system, P and kP can be made public whereas k is the decryption trapdoor which must be kept secret. Theoretically, ECC is the best alternative to the RSA system since it possesses a higher security with shorter key length. As in its application, ECC devices require less memory storage and power than others. It is particularly for the deployment of those constrained platforms, such as wireless devices, PDA and smart cards.

2.4 Summary
In this chapter, the goals and common terminologies of cryptography are explained with the aid of the well-known Caesar cipher. Following the ideas of Kerckhoff and Shannon, some important issues of cipher design are outlined. Moreover, by defining the use of cipher keys, two cryptographic schemes, namely private-key cryptosystems and public-key cryptosystems and their encryption techniques are discussed. As aforementioned, public-key cryptography overcomes the key distribution problem found in private-key cryptography. However, public-key cryptosystems are derived from complex mathematical systems and thus more computationally intensive than its private-

18

key counterparts. In general, private-key cryptosystem is mainly utilized for data confidentiality services. Other than those traditional schemes such as DES, IDEA and AES, some specific private-key variants are also proposed as enhancements to the traditional one [20]. In particular, attempts to integrate chaotic dynamics and cryptosystems have been made [6, 7 & 26]. An investigation of this new research direction and its application for multimedia security will be discussed in the following chapters.

19

Chapter 3

Chaotic Cryptography
Chaos in nature is multidisciplinary which broadly covers physics, mathematics, communications, engineering and so on. The first notion of applying chaos to encryption appeared in Shannons famous paper of cryptography in 1949 [15]. As the principle of contemporary cryptographic design, he pointed out that: In a good mixing transformation functions are complicated, involving all variables in a sensitive way. A small variation of any one (variable) changes (all the outputs) considerably. This refers to the concept of confusion and diffusion, which can be connected to the fundamental properties of chaotic systems such as ergodic and sensitivity to initial conditions. Recall that traditional cryptographic schemes mainly rely on complicated algebraic operations. Interestingly, chaotic systems exhibit attractive complex dynamics but exist in a relatively simple form. In this sense, it is feasible to employ chaos theory in cryptographic aspect. Over the past decades,

20

the field of chaos-based cryptography has become more and more popular in the research literature. In this chapter, an overview of chaotic cryptography will be presented. Section 3.1 will illustrate the concept of chaos theory by some widely studied chaotic maps. In Section 3.2, the fundamental properties of chaotic systems will be described as a background for the following sections. The similarities and differences between chaotic systems and cryptosystems will then be investigated in Section 3.3. In particular, the issue of chaotic image encryption will be discussed in Section 3.4, while summary will be given in Section 3.5.

3.1 Introduction to Chaotic Maps

In a scientific context, one general description of chaos is an unpredictable and random-like long-term evolution that results from deterministic nonlinear systems. The simplest class of chaotic dynamic systems is one-dimensional chaotic map which is a difference equation of the form x n +1 = f ( x n , ) , n = 0, 1, 2, 3, (3.1)

where the state variable x and the system parameter are scalars, i.e., x, R, and f is a mapping function defined in the real domain R R. As for an introductory purpose from here on, only one- and two-dimensional chaotic maps are briefly discussed.

3.1.1 One-dimensional Chaotic Maps

From Eq (3.1), it can be seen that one-dimensional (1D) chaotic maps refer to those with the relation where the value of xn+1 is determined only by xn. More specifically, this is known as recurrence relation. In chaotic dynamics, iteration is involved, which means to evaluate the map f over and over. The first example considered is the tent map which is described as follows [31]:

21

x n +1

= a (1 2 x
1 2

1 2

) = 2ax1 x 2a (
n

if 0 x n 1 ; 2 1 if 2 < x n 1.

(3.2)

where a >

and x n [0,1] . In addition, the tent map is a piecewise-linear map

while the trajectory of map is shown in Figure 3.1. In the figure, the map parameter is chosen as a =
3 4

that is confined to the interval [0, 1].

Figure 3.1 A plot of the tent map with parameter a =

3 4

Another example is called logistic map which is originally proposed to describe population growth model [32]. The map is quadratic and thus nonlinear with the following expression: x n +1 = bx n (1 x n ) , (3.3)

where b is the control parameter governing the chaotic behavior. To ensure xn in the range [0, 1], parameter b has to be in the range [0, 4]. Figure 3.2 shows the trajectory of the map with b = 3.999. Both the tent and the logistic maps exhibit a maximum at x n = 1 . In the next section, the logistic map is explicitly chosen as 2 a typical study case of chaotic behavior.

22

Figure 3.2 A plot of the logistic map with parameter b = 3.999.

3.1.2 Two-dimensional Chaotic Maps

The simplest possible case of a multi-dimensional map is a twodimensional (2D) map. Some well-studied examples to be covered in this subsection include the baker map, the cat map and the standard map. They also possess those superior properties found in chaos, but are often described geometrically. More importantly, the nature of 2D maps is more favourable for chaotic image encryption than the 1D counterpart studied in last sub-section.

i. Baker map The baker map is a one-to-one map of the unit interval [0, 1] into itself and is given by [33]: xn +1 = 2 xn (mod1) 1 y = 2 yn n +1 1 ( yn + 1) 2

if 0 xn < 1 , 2 1 if 2 xn 1,

(3.4)

where ( x n , y n ) [0,1] and x mod 1 refers the fractional parts of a real number x. One characteristic found in the map can resemblance to the stretch-and-fold

23

mechanism as shown in Figure 3.3. An interval is elongated twice itself horizontally, then split into half and piled up. In such a way, the map is considered as topologically mixing.

Figure 3.3 An illustration of baker map in the unit square (a) before action; (b) being stretched and (c) being folded.

ii. Cat map Another most studied example is Arnold cat map or simply cat map, named after Russian mathematician Vladimir Arnold, who discovered it using an image of a cat [34]. It is described by:
x n +1 1 1 x n y = 1 2 y mod 1, n n +1

(3.5)

Of particular observation in the study of 2D invertible maps is the property of area preserving. This property is also found in the cat map as the determinant of its transform matrix is equal to 1. Similar to the baker map, Figure 3.4 explains the stretch-and-fold mechanism behind the cat map in a geometrical way.

24

Figure 3.4 An illustration of cat map in the unit square.

iii. Standard map The standard map is a perturbed twist map which results from periodic impulsive kicking of the rotor written in the form [31, 35]:
n +1 = ( n + J n ) mod 2 , J n +1 = J n + k sin n +1 mod 2 ,

(3.6)

where ( J n , n ) [0,2 ] and k (> 0) is kicking strength. Note that the maps mentioned above belong to the category of a coupled map. In geometry, the two equations of the map are dependent on each other in how they act on the coordinates of a point. In [36], it has also been proved that the map preserves area in ( J , ) -space by calculating the Jacobian of the map as follows:
n det n +1 J n +1 n n +1 J n 1 1 = 1. = det k cos J n +1 J n 1 + k cos n +1 n +1

(3.7)

The above mathematical proof implies that the map in Eq. (3.6) is also bijection onto itself in the unit space. The application of the three invertible chaotic maps will be extensively described in Section 3.4.

25

3.2 The Important Properties of Chaotic Maps

This section will step more closely to some important properties characterized by chaotic maps. They include sensitive dependence on initial conditions, sensitive dependence on system parameters and mixing in phase space. To facilitate the discussion, the logistic map is used as an example to illustrate the following properties.

3.2.1 Sensitive Dependence on Initial Conditions

High sensitivity to its initial conditions is commonly considered as the hallmark of chaos. To illustrate the point, two Cobweb diagrams, as shown in Figure 3.5, are used to illustrate the effect of perturbing the initial values of logistic map with x0 = 0.7 and x0 = 0.700001 under the same parameter b = 3.999999. In the figure, the trajectories after 100 iterations are computed. As observed, even a tiny perturbation (< 10-6) in the initial value x0 turns out to be tremendous difference in trajectory and output in long-term.

(a)

(b)

Figure 3.5 Cobweb diagram of logistic map with (a) x0=0.7, (b) x0=0.700001.

26

3.2.2 Sensitive Dependence on System Parameters

In chaotic domain, the sensitive dependence is not limited to its initial values, but also in system parameters. Figure 3.6 plots two trajectories of a logistic map which are specified with b = 3.999999 and b = 3.999998.

Figure 3.6 Variation in trajectories of the logistic map due to minor differences in system parameter b = 3.999999 and b = 3.999998.

Since the studied maps are configured with arbitrarily small different parameters, it is naturally expected that their trajectories should somehow pass through the phase space in a similar way. In the figure, the similarity in trajectories appears to happen only in the first few iterations, but diverge themselves exponentially over iterations.

3.2.3 Ergodicity

Ergodic property of chaotic system is often linked with the concept of mixing. Roughly speaking, this means that any trajectory of the map will not be restricted within a small region of phase space wherever the arbitrary point x in the space they start from. In this regard, certain amount of distributions of

27

logistic trajectories iterating for 104 times with random initial values and random system parameters (b > 3) were investigated. Apart from the transient effect in the first few iterations, it is found that all the distributions spread evenly in the phase space and are quite close to each other. Figure 3.7 depicts the typical distribution of trajectory of the logistic map.

Figure 3.7 A typical distribution of trajectory of the logistic map after 104 iterations.

3.3 Relationship between Cryptosystems and Chaotic Systems

In the literature, it has been investigated that there exists a close relationship between traditional cryptosystems and chaotic systems (maps) in many aspects [26, 36 & 37]. It is suggested that the chaotic system experiences many superior dynamical properties which can analogously correspond to those required in cryptosystems. According to the investigation made in [37], the common relationship which promotes chaos theory into practical cryptographic design are summarized in Table 3.1. In particular, the notion of confusion in traditional cryptosystems causes plaintext transforming to random ciphertext such that there should be no repeated

28

pattern in the ciphertext. By the same token, the trajectories of chaotic systems pass through all points of the phase space generally with uniform distribution. In other words, it is very difficult to predict the final position of one point from its initial position. It is indeed the concept of ergodicity which can be associated with confusion in cryptosystems.
Chaotic systems Ergodicity Sensitivity to initial condition and system parameters Parameters Iterations Traditional cryptosystems Confusion Diffusion Encryption key Cipher rounds

Table 3.1 A comparison of some features characterized by chaotic systems and traditional cryptosystems.

To develop a good cryptosystem, another essential design principle is the property of diffusion. By doing so, a totally different ciphertext is resulted no matter how one bit of key or plaintext is changed. This implies that the system is sensitive to plaintext and its encryption key. On the other hand, recall that the chaotic systems highly depend on initial conditions and parameters. A small variation in any of the system parameters or initial point leads to the trajectory diverged significantly. In this regard, chaotic systems and cryptosystems can naturally benefit from each other. With the security consideration, cryptosystems confuse and diffuse plaintext by numbers of cipher rounds. Similarly, for chaotic systems, the initial region is ultimately scattered over the entire phase space via iterations. It is therefore expected that chaos theory can be exploited in the field of cryptography by taking such system parameters and initial condition as secret keys while considering the iterations of chaotic map equivalent to rounds of the encryption function.

29

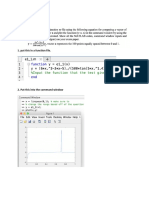
An elaborative example for the concept of chaos-based cryptography was given in [38]. For illustrative purpose, 1D chaotic map is assumed while the secret key is introduced to the initial condition as follows. Suppose be a 1D chaotic map to be employed in such a way that:

: [0,1] [0,1] ,

(3.8)

while P (0,1) be a plaintext to encrypt, and the ciphertext C is the output of the encryption. Given the secret key k and a natural number n for iterations of the map, we obtain: C = n ( P) = ( (L ( P ))) , (3.9)

where C are some selected pre-image of P under the map n . Then for encryption, k is incorporated to be an initial condition of the map which is formulated by

C = C + k (mod 1).
Decryption is the reverse of encryption procedure described as: P = n (C k ).

(3.10)

(3.11)

It is clear that the aforementioned example is too simple, without fully utilizing those chaotic properties to resist strong cryptanalysis. However, this provides some insights, to certain extent, about the cryptographic design incorporated with chaos theory. For example, even the property of sensitivity to initial conditions can considerably complicate the nature of encryption. It should also be stressed that the use of chaos is defined over real numbers, unlike traditional cryptosystems that are defined over the integer set [37, 39]. Some studies on phase space problem and possible supplementary measures such as defining approximate transformation functions have been carried out [40]. Nevertheless, by comparing the nature of these two systems, traditional cryptographic algorithms usually involve series of complicated substitution and permutation, whereas the one used in chaos only relies on simple equations. Over

30

the past few decades, chaotic cryptography has received much attention for the reasons discussed [6, 7 & 41].

3.4 Chaotic Encryption Schemes for Digital Images

In the preceding section, an integration of chaos-based techniques to data encryption has been briefly introduced. In practice, large-scale data encryption (or more precisely, multimedia encryption) seems to be rather difficult and slow to obtain a real data permutation and diffusion by conventional means such as DES, IDEA and AES [42]. An example is a digital image characterized with bulk data capacity and strong correlation among pixels. In this sense, a direct extension from document encryption to digital image may not be efficient without special modifications. Worse still, it would pose a problem as depicted in Figure 3.8 if conventional block ciphers are applied unwisely. Because of high redundancy for the area with the same or similar colour in Figure 3.8(a), it leads to the identical repeated patterns as shown in Figure 3.8(b) when a block cipher is used in the ECB mode. The source code of the block cipher proposed in [43] is implemented here.

(a)

(b)

Figure 3.8 (a) plain image containing many areas with identical or similar gray levels, and (b) its corresponding encrypted image by Advanced Encryption Standard (AES) with both key size and block size 128-bit long running in the ECB mode.

31

It is clear that image encryption has its own requirements in contrast to textual one. Alternatively, the well-established chaos theory and the simplicity of discretized chaotic maps make chaos-based techniques even more suitable for image encryption than many traditional encryption schemes. The plain image can be swiftly shuffled and diffused by the application of chaotic maps usually derived from simple equations. Thus, it can provide a relatively fast and secure means for real-time data transmission over high speed networks.

3.4.1 Review of Some Existing Chaotic Image Encryption Schemes

To deal with the challenges of image protection, an increasing number of attentions have been turned to the chaotic approaches. In the general chaotic cryptographic design, the illustrative example is given in Section 3.3. For the purpose of better image encryption, the chaotic map is indeed more than simply a functional block in the cipher. Alternatively, the map is commonly suggested to be a pseudorandom bit generator as a part of secret encryption operations [44], or to scramble the entire image pseudorandomly [45 - 47] or both [9 11, 26 & 48 50]. The former encrypts the pixels with chaotic key streams to achieve the similar security of classical stream ciphers. However, the latter focus on the effective permutation of pixel position rather than their values, usually shuffling the whole image in a single step. In particular, an inspiring concept of permutation realized by discrete version of 2D chaotic maps has been pointed out earlier in a paper by Pichler and Scharinger in 1994 [47]. Since then, dedicated chaotic image encryption schemes have been emerged in the literature. A few years later, in 1998, Fridrich [26] extended the work of Pichler and Scharinger by suggesting a more generalized approach adapting an invertible 2D chaotic map on a torus or on a square to create a symmetric block encryption scheme. In her design, an example based on the 2D baker map was given to illustrate the steps of cipher construction. The steps include choosing a chaotic map, generalizing it by introduction of some parameters, discretizing the map and extending the discretized map to three-dimensional composed with a simple

32

diffusion mechanism. The detail of the steps will be described in next subsection. On the other hand, Scharinger further proposed an encryption scheme based on chaotic Kolmogorov flow [48]. The basic idea is to take the whole image as a single block and then permute through a chaotic system based on the Kolmogorov flow. In addition, a substitution based on a pseudorandom number generator formed by shift registers is performed, which renders the statistical information of the encrypted image. Generally speaking, the two combination schemes under study can provide a more structural framework and more importantly perform faster than the classical schemes such as DES [26]. In 1999, a permutation-only image cipher called Hierarchical Chaotic Image Encryption (HCIE) was proposed by Yen and his research group [45]. As the name implied, HCIE undergoes certain levels of encryption: (1) permuting image blocks, and (2) permuting pixels in each image block in four different directions. These can be accomplished by a pseudorandom permutation matrix controlled by the binary sequence of chaotic logistic map. The scheme provides the ease of implementation and thus achieves a fast operation. In 2000, another chaotic image encryption scheme called Chaotic Key-based Algorithm (CKBA) was proposed by the same group [44]. The scheme first generates a binary sequence based on the logistic map. According to the binary sequence generated, image pixels are rearranged and pseudorandomly XOR or XNOR operated with a sub-key in the predefined set. Unfortunately, the two schemes were later criticized in [51] and [52], respectively, and are proven that either the use of permutation in fashion or chaotic binary stream encryption is insecure at all. More recently, some other chaos-based image encryption schemes have been proposed. Guan et al. employed the 2D chaotic cat map [49] while Lian et al. employed the 2D standard map [9] for their cryptographic implementation. A detailed analysis of Lian et al.s will be provided in the next chapters. In general, the said schemes here mainly follow Fridrichs framework adapting 2D permutation together with simple diffusion process. In 2004, some of mostly used 2D chaotic maps have also been spatially extended to higher-dimensional versions such as 3D cat map [10], 3D baker map [11] and 3D standard map [50].

33

Since higher degree of chaotic properties is expected, the maps achieve better permutation on image pixels and thus fewer cipher rounds are required. A distinct step to such modification is to pile up the 2D plain image into a 3D cube which do consume a certain computational time. Meanwhile a chaotic diffusion process, namely XOR plus modulo operation is performed in [10, 11]. Such diffusion process will be explicitly explained in Chapter 5.

3.4.2 Architecture of Generic Chaos-based Image Cryptosystems

For image encryption, 2D or higher-dimensional chaotic maps are naturally employed for a reason that the image can be considered as a 2D array of pixels [53]. In the previous sub-section, some related examples [9 11, 26 & 48 - 50] have been shown which all operated under Fridrichs framework. The properties of the framework provide a more stable speed performance with a higher degree of security. This greatly influences the design of chaos-based cryptosystems hereafter. For a comprehensive study, the procedures of Fridrichs generalization [26] are summarized as follows: Assuming that the size of the plain image is N N, while the number of gray levels is L. The recommended construction includes the following four steps.

i. Choosing the chaotic map and generalizing it by introduction of parameters This step intends to define a high-dimensional chaotic map to perform pixel permutation. It is suggested that the 2D map f which is a chaotic bijection of the unit square I I, where I = [0,1) should be chosen. Such a bijective requirement is known as the measure-preserving property of chaotic maps so that one-to-one mapping is guaranteed in the processes of encryption and decryption. It seems that a rich variety of chaotic maps are satisfied for cryptographic purposes. In practice, only simple ones are preferred for fast encryption process. Apart from simplicity, the parameterization of the chaotic map chosen should also be considered as well. A set of parameters can be introduced into the map to

34

constitute a portion of the secret key. Those 2D chaotic maps previously described in Section 3.1.2 are examples to be chosen.

ii. Discretizing the chaotic map Since images are composed of finite lattice called pixels, the domain of the map f is changed from the unit square I I to the discretized form N 0N 1 N 0N 1 , where

N 0N 1 = [0, N-1]. In doing so, such discretized map F maps an image pixel to
another bijectively. As emphasized in [26], the discretization in this step must fulfill the asymptotic property formulated by:
N 0i , j < N

lim max f (i / N , j / N ) F (i, j ) = 0 ,

(3.12)

where f is the continuous map chosen and F is the discretized form. This means that the discretized map will be getting closer to the continuous counterpart when the number of pixels tends to infinity. It could then preserve the basic properties of its continuous one. The discretization of the 2D chaotic baker map [47], cat map and standard map [26] are presented in Eqs. (3.13) (3.15), respectively.
N N = ( x k N i ) + y k mod , ni ni

x k +1 y k +1

n0 + n1 + K + nt = N , N = n + n + K + n , i 0 1 i with N 0 = 0, ni N x = [ N , N + n ), = y k y k mod + N i , i i i +1 k ni N y k = [0, N ).

(3.13)

a xk x k +1 1 y = b ab + 1 y mod N , k k +1

(3.14)

x k +1 = ( x k + y k ) mod N , x 2 y k +1 = y k + t sin k +1 mod N . N

(3.15)

where (xk, yk) and (xk+1, yk+1) are current and next chaotic state in each of the maps, and other symbols are the corresponding system parameters. Figures 3.9

35

3.11 illustrate the results of applying three discretized chaotic maps in Eqs. (3.13) (3.15) to the test image Lena once and nine times.

(b)

(a)

(c) Figure 3.9 (a) A test image of Lena; the resultant images (b) and (c) after applying the discretized baker map once and nine times, respectively, with N = (8, 8, 32, 64, 32, 32, 32, 32, 64, 64, 32, 64, 32, 8, 8).

(a)

(b)

Figure 3.10 The results of test image Lena (a) and (b) after applying the discretized cat map once and nine times, respectively, with a = 5 and b = 9.

36

(a)

(b)

Figure 3.11 The results of test image Lena (a) and (b) after applying the discretized standard map once and nine times, respectively, with k = 1750.

iii. Composing a diffusion mechanism

So far, an apparently unrecognized image can be achieved through shuffling the position of image pixels. However, the histogram of the resultant image remains the same as that of the plain image. The permutation-based cipher is still vulnerable to the statistical and chosen-plaintext-type attacks. It is necessary to introduce a diffusion mechanism after the permutation stage. The idea is to spread the influence of every single pixel over the entire image. In general, the gray scale of pixels can be alternated sequentially by the pseudorandom output of a 1D chaotic map.

iv. Evaluating the overall performance (security and complexity)

The security level is a fundamental issue of all kinds of ciphers. A strong cipher refers to those which is capable of resisting any kind of cryptanalytic attacks including brute-force attack, statistical attack, known-plaintext attack and chosen-plaintext attack. Therefore, a cipher of high key and plaintext sensitivity together with a large key space is preferable. On the other hand, complexity evaluation is important to image encryption as well since it always indicates the feasibility of encryption schemes. Some special attentions should be given in terms of computational speed, size and quality of the encrypted images.

37

Plain image

P1

2D Pixel value Permutation diffusion

2D Pixel value Permutation diffusion

P2 = C1 Kp1 Ks1 Kp2 Ks2

P3 = C2

2D Pixel value Permutation diffusion

Encrypted image

Pn = Cn-1 Kpn Ksn

Cn

Figure 3.12 A generic architecture of image encryption systems based on 2D chaotic permutations.

In accordance with the above cipher constructions, the basis of the generic image encryption is thereby modeled and presented in Figure 3.12. Similar to traditional block ciphers, the studied architecture is composed of two processes: chaotic confusion and pixel diffusion. The former is also called permutation which shuffles a whole plain image with a 2D chaotic map, and the latter modifies the value (gray-level) of each pixel one by one. In the confusion process, the parameters of the chaotic map can be regarded as the confusion key

Kp; in the diffusion process, parameters such as the initial values and control
parameters of the diffusion function can be regarded as the diffusion key Ks. For security enhancement reasons, the confusion and diffusion processes are often repeated for n times.

3.4.3 Other Issues in Chaos-based Image Cryptosystems

i. Ineffective confusion problems in corner pixel

As seen from the mathematical form of the 2D maps in Eqs. (3.13) (3.15), some pixels at the corner of the image merely map to their original position. In the case of baker map, the affected pixels are at (0, 0) and (N-1, N-1), while the problem of origin (0, 0) are also found in both cat map and standard map. The information leakage is insignificant, but undesirable in cryptographic design. As

38

rectified by [9, 54], the permutation can be improved by changing the scan order of the process. This means scanning a random pixel (rx, ry) other than the origin first in the course of permutation process.

ii. Parameter space analysis of common 2D chaotic maps

It is clear that parameter space of the chaotic map determines the degree of cipher security to a certain extent. As investigated in [54], the parameter spaces of three common maps are listed in Table 3.2. Consider an image of size N N, the investigation suggested that parameter space of cat map is the smallest, while standard map has the largest parameter space ((N2)!). Their spaces will be enlarged in proportional if distinct value for Kp is used for n different iterations.
2D Chaotic maps Parameter space (use the same key for n different iterations) Parameter space (use the different key for n different iterations) Baker map 2N-1 2n(N-1) Cat map N2 N2n Standard map (N2)! [(N2)!]n

Table 3.2 Comparison of the parameter space of baker map, cat map and standard map after discretization.

iii. Key generation for iterative ciphers

As pointed out in [54], distinct sub-keys for confusion and diffusion processes are essential to the security enhancement on cryptosystems. To this end, a key generator should be presented for the purpose of sub-key generation and distribution. In [9], Lian et al. proposed a scalable key scheming which is based on a chain of 1D chaotic maps as outlined in Figure 3.13. To obtain n subkeys, the secret key of the cryptosystem can be divided into n groups Xi and Ki, where i = [1, m] representing the ith of m cipher rounds. Xi is served as the initial conditions of the map, while Ki is served as the system parameter of the map with respect to Xi. In this scheme, any tiny change in the secret key will influence the consequent sub-keys substantially. As a result, the key sensitivity requirement of cryptosystems is therefore satisfied.

39

X1 K1 X2 K2

1D Map K1 1D Map K2

1D Map

X1m-1 K1

1D Map

X1m

1D Map

X2m-1 K2

1D Map

X2m

Xn Kn

1D Map Kn

1D Map

Xnm-1 Kn

1D Map

Xnm

Figure 3.13 An illustration of key generation and distribution proposed in [9].

iv. Typical preprocessing in integer and real domains

In many 1D chaotic maps or some other chaotic systems, the chaotic sense is observed in real number field. In computer programming, one is required to deal with decimal fractions and integers when a real-valued chaotic system is incorporated with the process of pixel value modification. There are many methods to approximate decimal fractions to binary integer or vice versa. For example, a typical approximation function de2bi() suggested for C++ programming can be found in [49] B = de2bi(mod((Abs(Xi)-Floor(Abs(Xi))) 1014, 256) (3.16)

where Xi is a decimal fraction obtained by the chaotic system, Abs() is the absolute function, Floor() is the round-up function to the nearest integers less than or equal to the defined value. The function assumed that the 256 gray scale image and double data type (15-digit precision) are used. On the contrary, the conversion from binary integer to decimal fractions can be realized as follows: D = bi2de(v) = v / max(v), (3.17)

where max(v) is the amplitude of input v. When a real-valued chaotic map such as logistic map is used, one should expect some overheads from preprocessing decimal and integer values in the whole encryption scheme. In this case, a tradeoff between functional simplicity and complexity in the change of domains

40

is readily different from particular cipher designs and should be thoroughly balanced in the implementation.

3.4.4 Cryptanalysis of Chaos-based Image Cryptosystems

Chaotic cryptosystems, like any other cryptosystems, should have strong ability to frustrate all kinds of cryptanalytic efforts. From the cryptographic point of view, resistance against attacks is a good measure for evaluating the performance of a cryptosystem. A typical classification of the attacks is based on the different scenarios the extra information required by a cryptanalyst. They are listed as follows: Ciphertext only attack - the cryptanalyst only has a number of ciphertext; Known plaintext attack - the cryptanalyst has some matched plaintext and ciphertext pairs; Chosen plaintext attack - the cryptanalyst can choose any plaintext and obtain the corresponding ciphertext. In other words, the cryptanalyst can choose plaintext at will, and obtain the corresponding ciphertext. This added facility can help in breaking a cipher. Chosen ciphertext attack - the cryptanalyst can choose some ciphertexts and obtain the corresponding plaintexts. In the four kinds of typical attacks, the cryptanalyst intends to determine the key that was used. It is expected that ciphertext only attack is the most difficult, yet chosen plaintext attack is the easiest to the cryptanalyst, due to the auxiliary information he or she obtains. The abovementioned attacks are generally applicable to all types of cryptosystems. In particular, some specific attacks are based on the structural characteristics of multimedia data such as image and video [55]. For image encryption, statistical and differential attacks are the two most well-known yet important security issues. The former is a variant of ciphertext-only attack. In this case, the cryptanalyst try to learn or

41

recognize some pattern if the plain image is not available. The pattern or similar information may be exposed from the histograms of some encrypted images or correlations between certain pairs of adjacent image pixels. In the latter case, the cryptanalyst try to choose two images which differ in one pixel, and then compare the encryption results. Repeating the procedure with other pixels, part of or the whole pixel position mapping in the permutation stage can be reconstructed. A more detail discussion will be covered in Chapters 4 and 5. For a comprehensive study, some particular cryptanalyses on chaotic image encryption schemes in Section 3.4.1 are outlined which is worthwhile paying attentions in the future design. For a permutation-only image cipher such as [45], it has been pointed out in [51] that when such a cipher encrypts images in the spatial domain, a pixel at the position (i, j) will be secretly relocated to another fixed position (i, j) while keeping pixel value unchanged. No matter how complicated the permutation is, by comparing a number of known plain images and the corresponding encrypted images, it is possible for the cryptanalyst to reconstruct the secret permutations of all pixels. The approach is definitely incapable of providing a sufficiently high degree of security withstanding known/chosen plaintext attacks. In [52], Yen et al.s CKBA encryption scheme is found to have some serious security loopholes. First, since sub-keys are used to encrypt more than one block of plaintext, the key set together with binary sequence can be possibly reconstructed through only one pair of known or chosen plain image and encrypted image. Therefore, it cannot resist the chosen and known plaintext attacks. In addition, its security against brute force attack [12] is also overestimated by the author due to the fact that the total key length is not fully utilized in the actual encryption. From such point of view, the secret key should never be reused in all cases. In particular, the combination of permutation and diffusion schemes has been reported with some fundamental weaknesses. Wang et al. criticized the 3D cat map based image encryption scheme [10]. Although the scheme resists statistical and differential attacks, it is still likely breakable with chosen plaintext

42

attack. According to [56], firstly, chaotic 3D permutation is meaningless if a homogenous plain image with identical pixel values is encrypted. In this case, security of the scheme relies merely on a simple diffusion process. Moreover, if a pixel value in the plain image is 0, then the underlying diffusion operation is also useless. As a result, a key recovery attack is proposed in such a way that recovers the initial condition of logistic maps according to the gray code. Apparently, the encryption of homogenous plain image is an arbitrarily insufficient issue. However, in [10], this leads to the problem that the scheme is eventually broken with chosen plaintext attack discussed.

3.5 Summary
In this chapter, the concept of chaos was shown through examples of chaotic maps and introduction of their dynamical properties. An investigation on chaotic maps and cryptosystems reveal that they share some common properties. Since then, many researchers pursued their efforts in chaotic cryptography. As mentioned in last chapter, traditional cryptographic schemes are mainly based on discrete mathematics composed with many complicated algebraic operations, while chaotic cryptographic schemes rely on the complex dynamics of nonlinear maps which are deterministic but simple. Indeed, the nice and distinct properties of chaos, such as ergodicity, sensitivity dependence on initial conditions and system parameters, favour the application of chaos theory in both document and multimedia data encryption. In this thesis, chaotic encryption scheme for digital images is particularly interested. The typical architecture and some important issues of chaotic image cryptosystems including the cryptanalysis techniques are intensively studied as a background of algorithm developments in the following chapters.

43

Chapter 4

Chaotic Confusion Process for Image Encryption

As discussed in the preceding chapter, the architecture of many chaosbased image encryption schemes mainly consists of image pixel permutation stage and pixel value diffusion stage. Generally speaking, the confusion effect is contributed by permutation-only stage, while the diffusion effect is merely found in the pixel value diffusion stage. However, for some encryption schemes, the required number of permutation-diffusion rounds is unnecessarily large to achieve a certain level of security. The efficiency of the encryption process is thus downgraded. In this chapter, the overview of an image encryption scheme using 2D chaotic standard map will be given in Section 4.1. It is considered as a reference scheme. Some observations in this reference scheme will be described in Section 4.2. Based on the observations, a modified approach of the permutation stage will be proposed to improve the performance of the reference scheme. The principle of this approach including the encryption and decryption procedures

44

will be presented in Section 4.3. Finally, security analysis and summary will be provided in Section 4.4 and Section 4.5, respectively.

4.1 Overview of an Image Encryption Scheme Using 2D Standard Map

As stated in Section 3.4.3, Lian et al. [9] pointed out the existence of weak keys for ciphers using the 2D chaotic cat and baker maps. Furthermore, the key space of both maps is smaller than the standard map. This section introduces the image encryption scheme based on 2D standard map proposed by Lian et al. [9]. It is considered as a reference model to an enhanced confusion process proposed in the following sections. Similar to the typical architecture of chaotic image cryptosystems shown in Figure 3.12, two iterative stages, namely permutation and diffusion, are also found in Lian et al.s scheme. However, to guarantee high security, they suggested iterating a chaotic map in the permutation stage for multiple times before entering the diffusion stage. Their scheme is depicted in Figure 4.1. There are n permutation rounds in the confusion stage with n 1. The whole permutation-diffusion round, also known as overall round, should be performed

m (where m 1) times to achieve a satisfactory level of security. The parameters

of the chaotic maps used are assigned differently in each overall round. They are obtained from a round key generator using skew tent map with a seed secret key as input.

45

m rounds n rounds Confusion (Pixel Permutation) Key Generator Diffusion (Sequential Pixel Value Modification)

Plain Image Secret Key

Cipher Image

Figure 4.1 The chaotic image cryptosystem proposed by Lian et al. in [9].

In Figure 4.1, the confusion process is performed solely by permuting pixel positions without pixel value mixing. It adopts an invertible discretized 2D standard map with the introduction of random scan couple (rx, ry) for cornerpixel confusion, as given by Eq. (4.1).
x k +1 = (x k + y k + rx + ry )mod N , 2 x k +1 y k +1 = y k + ry + K C sin mod N , N (4.1)

where (xk, yk) and (xk+1, yk+1) is the original and the permuted pixel position of an N N image, respectively. The standard map parameter KC is a positive integer. Since the standard map is iterated with the same key for every n permutations, it is not necessary to compute Eq. (4.1) repeatedly after n = 1 and so the permutation mode is introduced to reduce the computational complexity [9]. The permutation mode consists of position calculation (to obtain the destination position via Eq. (4.1)) and n times of pixel moving (to move the pixel data from the original position to the destination one). In practice, the permutation mode is operated by 2D table restoring. In the diffusion stage, each pixel of the 2D permuted image is scanned in sequential manner, which usually starts from the upper left corner. The diffusion effect in this stage is realized by Eq. (4.2).

46

C 1 = K d C i = Vi q[ f (C i 1 ), L]

(4.2)

where Vi is the value of the ith pixel of the permuted image, Ci-1 and Ci is the value of the (i-1)th and the ith pixel of the diffused image, respectively. The seed of the diffusion function is C-1 which is obtained from the diffusion key KD. The nonlinear function f( ) is the logistic map given by Eq. (4.3). f (C i 1 ) = 4C i 1 (1 C i 1 ) (4.3)

The quantization function q( ) takes the L bits just after the decimal point, as defined by Eq. (4.4). q( X , L) = 2 L X (4.4)

where X = 0.b1b2b3 bL is the binary representation of X and bi is either 0 or 1. For example, the value of L is 8 for gray-scale images. The new pixel value is obtained by Exclusive-OR (XOR) the current pixel value Vi of the permuted image with an L-bit sequence obtained from the logistic map taking the previous diffused pixel value Ci-1 as input. As the previous diffused pixel will influence the current one, a tiny change in the original image is reflected in more than one pixel in the cipher image and hence the diffusion effect is introduced in this stage.

4.2 Some Observations

A detail study reveals that Lian et al.s scheme is particularly vulnerable to plaintext sensitivity attack when taking insufficient permutation-diffusion rounds. To further illustrate the observation, various images have been employed for plaintext sensitivity test. For image encryption schemes, the plaintext sensitivity can be reflected by encrypting two images which have only one pixel difference. In this test, the center pixel value of the images is changed to value 0. Table 4.1 lists the performance on five test images obtained from USC-SIPI Image Database [57]. It is clear that taking m=n=2 is insufficient to generate large

47

differences. This cryptosystem probably cannot withstand such sensitivity-based attacks. The result is consistent with Lian et al.s recommendation that a satisfactory level of security is reached when m=n=4. This leads to a total of 16 permutation rounds and 4 diffusion rounds.

Image Cameraman Resolution chart Lena Chemical plant Peppers

Percentage of Pixel Change (%) m=n=2 0.89 0.24 0.99 0.47 0.21 m=n=4 98.91 99.56 99.27 99.32 98.66

Table 4.1 Percentage of pixel change on different test images with overall rounds m=n=2 and m=n=4.

For example, the center pixel value of plain Peppers image of size 512 512 is 30 which is then alternated to be 0. The plain image, the 4 encrypted images taking m=n=2 and m=n=4 are depicted in Figures 4.2 (b) and (c), (e) and (f), respectively. Figures 4.2 (d) and (g) are the difference images between (b) and (c), (e) and (f), respectively. Taking m=n=2, the sensitivity to the predefined difference covers only 553 pixels (out of a total of 262144 pixels). As expected, the sensitivity raises to 98.66% (258644 out of 262144 pixels) when m=n=4. The black region in Figures 4.2(d) and (g) refers to the same pixel value found in two encrypted images.

48

(a)

Normal gray scale image

(b)

(c)

Binay image (d)

(e)

(f)

(g)

Figure 4.2 Plaintext sensitivity test: (a) original image, (b) and (c) cipher images ( m=n=2 ) whose corresponding plain images have one pixel difference only; (d) difference between cipher images (b) and (c) in gray scale(upper) and binary colour(lower), (e) and (f) cipher images ( m=n=4 ) with the same corresponding plain images as (b) and (c), respectively ; (g) difference between cipher images (e) and (f) in gray level.

49

4.3 Modified Confusion Process with Pixel Value Mixing

As observed in Section 4.2, the diffusion process under study has little contribution to the performance of the whole scheme. Consequently, the (4, 4) overall rounds is recommended [9], which leads to a total of 16 permutation rounds and 4 diffusion rounds. Indeed, measures such as pre-computation of permutation mode and mask table are adopted to reduce the computational complexity. Apart from the above special measures, this section provides a more general perspective to accelerate the encryption speed of Lian et al.s scheme and other schemes based on the iterative confusion-diffusion processes. The main principle of the proposed approach is to introduce certain diffusion effect in the confusion process so that this effect is not solely contributed by the diffusion process. To this end, both the permutation on position and change of the pixel value are performed simultaneously in the confusion stage. On one hand, the pixel is relocated by Eq (4.1). On the other hand, the pixel value is modified with some simple operations. It is expected that the same level of security is achieved in fewer overall rounds. The consideration of possible operations on the pixel value is first given in the following subsection.

4.3.1 Investigation of Some Possible Operations on Pixel Value

Clearly, the operations to modify the pixel value during the position relocation should be as simple as possible. Otherwise, it will pose a complexity burden to the scheme. With this consideration, six possible operations on the pixel value mixing have been undergone study as follows. Denote Pi be the value of the (Pi)th pixel in the plain image, L be the total number of gray levels of the image, Ci-1 and Ci be the values of (Ci-1)th and Cith pixel after permutation, bs be the number of bit to be shift, tmp be a temporary storage.

50

Algorithm 4.3.1 (a) modular addition method Ci ( Pi + Ci-1 ) mod L Algorithm 4.3.1 (b) Exclusive-OR (XOR) method Ci Pi ^ Ci-1 Algorithm 4.3.1 (c) Add-and-then-shift method bs Ci-1 & 7 Pi ( Pi + Ci-1 ) mod L Ci ( Pi >> bs ) | (Pi << ( 8 - bs ) ) Algorithm 4.3.1 (d) XOR-and-then-shift method bs Ci-1 & 7 Pi Pi ^ Ci-1 Ci ( Pi >> bs ) | (Pi << ( 8 - bs ) ) Algorithm 4.3.1 (e) Shift-and-then-add method bs Ci-1 & 7 tmp ( Ci-1 >> bs ) | (Ci-1 << ( 8 - bs ) ) Ci ( Pi + tmp ) mod L Algorithm 4.3.1 (f) Shift-and-then-XOR method bs Ci-1 & 7 tmp ( Ci-1 >> bs ) | (Ci-1 << ( 8 - bs ) ) Ci Pi ^ tmp

51

Note that Algorithm 4.3.1 (e) and (f) can shift Pi instead of Ci-1. However, when Pi =0, Ci = Ci-1 = C-1, which is simply the seed value. This appears to be relatively insecure. Table 4.2 lists the processing time required for the six different algorithms with L = 256. From the table, the time for Algorithms 4.3.1(a) and 4.3.1(b) are very close to the normal operation of pixel moving. To enhance the execution speed, the mod 256 operation is replaced by the bitwiseAND & 0xFF operations equivalently in our program. Algorithm 4.3.1(c) (f) are the advanced versions of Algorithms 4.3.1(a) and 4.3.1(b). It turns out that more execution time is required. Algorithm 4.3.1 (e) which cyclic shifts Ci-1 and then modular-add to Pi takes the longest time. It is slower than the normal operation by 0.4951 ms.
Algorithm Time (ms) Normal 4.4915 (a) 4.5391 (b) 4.5388 (c) 4.9241 (d) 4.9199 (e) 4.9866 (f) 4.9253

Table 4.2 Time required to perform Algorithms 4.3.1 (a) (f).

To facilitate the comparison, the following test dedicated to the six algorithms has been carried out. The results are the histograms of intermediate images after performed 1 to 3 rounds of permutation with different pixel value mixing algorithms. In this experiment, plain Lena image, homogenous black square and homogenous white square are used. The corresponding results are listed in Tables 4.3 4.5, respectively. The size of all 3 test images is standardized to 512 512. The value of seed is kept consistent in the 3 tests and is distinct in different permutation rounds. For a natural image such as Lena, the first-round histogram of Algorithms 4.3.1 (e) and (f) is much fluctuated when compared to others. A satisfactory effect of pixel value mixing can be achieved with 2 runs of all algorithms as observed in Table 4.3. Although the number of test rounds is small, a reasonably flat distribution can be found using Algorithms 4.3.1(a) (d).

52

Algorithm (a) Add

n=1

n=2

MN127.45 SD73.86 MDN128 (b) Xor

MN127.70 SD73.96 MDN128

MN128.41 SD74.08 MDN130 (c) Add-andthen-shift MN125.56 SD74.15 MDN125 (d) Xor-andthen-shift MN 127.26 SD 74.09 MDN 128 (e) Shift-andthen-add MN127.68 SD78.94 MDN127 (f) Shift-andthen-xor MN132.08 SD75.98 MDN137

MN127.31 SD73.94 MDN127

MN127.74 SD73.66 MDN128

MN127.74 SD73.86 MDN128

MN128.34 SD72.92 MDN129

MN126.91 SD73.43 MDN126

Table 4.3 Test on permuting Lena image with Algorithms 4.3.1 (a) (f) (MN: Mean; SD: Standard Deviation; MDN: Median).

53

Two extended tests are performed to further investigate the effectiveness of the algorithms by using homogenous white and black images, respectively. Table 4.4 lists the results on black image whose value is 0. The results obtained are rather different to that on Lena, as listed in Table 4.3. It shows that the mixing property of Algorithm 4.3.1(b) is greatly affected by black image or at the region of black (pixel value 0). However, a flat and regular pattern can be obtained by Algorithm 4.3.1(a) which is the best among others. According to the performance of algorithms with cyclic shift, Algorithms 4.3.1(c) and (e) which utilize modular-addition are more suitable than the ones using XOR operations such as Algorithms 4.3.1(d) and (f). This is because more gray scale value spreading (i.e. area of black region in the histogram) can be found in Algorithms 4.3.1 (c) and (e). Beside black image, the homogenous white image is also employed for pixel value mixing test. The results are illustrated in Table 4.5. It is noted that Algorithm 4.3.1 (a) at n=2 as well as n=1 is perfectly uniform. This is a result of constant change among neighboring pixels by modular addition. However, there is an obvious sub-key exposure problem (peak pixel value belongs to the seed of the 3rd round) in the histogram at n=3. The abnormal frequency of peak value is formed due to the sensitivity of modular-addition operations to certain round numbers and certain repeated patterns such n=1 and n=2. From the cryptographic point of view, the uncertainty of Algorithm 4.3.1 (a) is not desirable. Similar to the observations in black image test, Algorithms 4.3.1(c) and (e) exhibit a better pixel value mixing effect than Algorithms 4.3.1 (d) and (f) while a poor performance is also found in Algorithm 4.3.1(b).

54

Algorithm (a) Add

n=2

n=3

MN127.00 SD73.90 MDN126 (b) Xor

MN127.00 SD73.90 MDN126

MN63 SD29 MDN34 (c) Add-andthen-shift MN129.54 SD73.80 MDN122 (d) Xor-andthen-shift MN 102.67 SD 82.44 MDN 95 (e) Shift-andthen-add MN152.6 SD74.45 MDN184 (f) Shift-andthen-xor MN137.12 SD63.86 MDN139

MN191 SD41.63 MDN170

MN124.99 SD74.21 MDN124

MN 123.51 SD 69.99 MDN 125

MN126.28 SD72.58 MDN126

MN127.15 SD75.97 MDN126

Table 4.4 Test on permuting homogenous black square with Algorithms 4.3.1 (a) (f) (MN: Mean; SD: Standard Deviation; MDN: Median).

55

n=2 (a) Add

n=3

MN127.50 SD73.90 MDN127 (b) Xor

MN 127.75 SD73.95 MDN128

MN127.50 SD70.72 MDN 92 (c) Add-andthen-shift MN135.73 SD74.32 MDN148 (d) Xor-andthen-shift MN73.59 SD63.02 MDN45 (e) Shift-andthen-add MN139.22 SD69.15 MDN146 (f) Shift-andthen-xor MN144.55 SD80.09 MDN175

MN128.50 SD75.92 MDN136

MN127.66 SD73.75 MDN127

MN128.11 SD71.29 MDN129

MN125.24 SD74.56 MDN124

MN125.85 SD72.30 MDN123

Table 4.5 Test on permuting homogenous white square with Algorithms 4.3.1 (a) (f) (MN: Mean; SD: Standard Deviation; MDN: Median).

56

As analyzed through some specific test images, the modular-addition only approach performs the best in terms of mixing effect and complexity. However, it suffers from the problem of leakage of sub-key information when applied on homogenous white color (i.e. value 255). Apart from the processing time and Lena test, Add-and-then-shift or its inverse, Shift-and-then-add both have good performance in the test. Strictly speaking, the overall performance of Add-andthen-shift is relatively suitable to be employed. When performing cyclic shift, the number of shifts depends on the three least significant bits of the previous pixel Ci-1. One may concern the probability of no shift which is ineffective to the scheme. A short test is done to illustrate the concern by counting the case of no shift with different size of several images selected from [57].

Image Cameraman Resolution chart Lena Elaine Peppers Airplane (U2)

Size 256 256 256 256 512 512 512 512 512 512 1024 1024

No. of no shift cases 8360 8738 36404 33296 32982 131676

Percentage % 12.75 13.33 13.89 12.70 12.58 12.56

Table 4.6 Probability of no shift on some test images.

From the experimental results, the probability of no shift case is around 13% which roughly matches the theoretical value 1/8. These 1/8 pixel of the whole image still undergo mixing by the addition operations. There is no contradiction to the objective of proposed scheme.

4.3.2 Encryption Procedure

Based on the findings in the above subsections, we propose an improved cryptosystem with architecture shown in Figure 4.3. Following the concept outlined at the beginning of this section, our new confusion stage is composed of

57

position permutation and simple pixel value modification. Algorithm 4.3.1(c), i.e., Add-and-then-shift, is adopted in the operations of the pixel value modification. An example is illustrated in Figure 4.4. Given two neighboring pixels a and b (a is located prior to b) of the source image, each of them is processed by position permutation together with value modification. In this way, operated pixel A is relocated whose value is 00001101(2). The steps of position permutation can be referred to Eq. (4.1). When this process continues, pixel b (00101010(2)) first undergoes a modular addition operation with the previously operated pixel A (00001101(2)). Its intermediate (00110111(2)) then performs cyclic right shift by the number of bits specified by the 3 least significant bits of pixel A, i.e. 101(2). The operated pixel B is finally permuted with a new value (10111001(2)). Initially, the seed KS of the Add-and-then-shift process is obtained from the key generator. It should be (0, 255] and distinct at different rounds. For the diffusion process, it remains unchanged, as described in Section 4.1.
m rounds n rounds
Position Permutation Simple Pixel Value Modification

Plain Image Secret Key

Diffusion (Sequential Pixel Value Modification)

Cipher Image

Key Generator

Figure 4.3 Architecture of the proposed chaotic image cryptosystem.

a b A a = 10111010 b = 00101010

A = 00001101 B = 10111001

Figure 4.4 An illustration of Add-and-then-shift operation on pixels in permutation.

58

4.3.3 Decryption Procedure

Since the pixel value mixing depends on the value of the previously processed pixel, the order of operations cannot be alternated. This may pose a problem in the reversed confusion process required in decryption. A solution is to make the first decryption round (n=1) perform the reversed position permutation only. Next, both reverse of position permutation and pixel value change are performed from the second decryption round (n=2). The reverse pixel value change is shown as follows. Inverse of Algorithm 4.3.1 (c) Add-and-then-shift method bs Ci-1 & 3 Pi ( Ci << bs ) | (Ci >> ( 8 - bs ) ) Pi ( Pi - Ci-1 + L) mod L where Pi be the value of the (Pi)th pixel in the plain image, L be the total number of gray levels of the image, Ci-1 and Ci be the values of the (Ci-1)th and (Ci)th pixel after permutation, bs be the number of bits to shift. In this manner, an additional decipher round is required for the reverse of pixel value change. It includes the simple Add-and-then-shift operation and adds only little cost to the overall decryption procedures. Other parts of the decryption procedure are similar to the encryption ones except reversing the order and operating with the encrypted image.

4.3.4 Hardware Implementation

In image processing, vast amounts of data are involved such that cryptosystems with high processing speed are more practical in todays application. Apart from software implementation, it would be valuable to analyze the possible hardware realizations for the proposed scheme. A potential configuration for hardware implementation is outlined in Figure 4.5. In this configuration, there are modules for logical operations governed by

59

the Control Unit and three types of arithmetic operations, namely, Standard Map Computation Unit, Add-and-then-shift Unit and Logistic Map Computation Unit. Additionally, two image buffers are required for storage of the resultant images after the proposed permutation and diffusion stages.

Standard Map Computation

Add-andthen-shift Unit

Image Buffer 1

Control Unit

Image Buffer 2

Logistic Map Computation

Figure 4.5 The proposed hardware configuration.

Figure 4.6(a) depicts the architecture of the Standard Map Computation Unit which is used to compute the new position of the pixel data initially from Image Buffer 1 in the permutation stage. This module consists of a 3-input adder, a 4-input adder, a modular operator, a subtractor, a multiplexer together with a pre-computed sine table with 256 double bytes entries. In Figure 4.6(b), a multiplexer, an adder, an 8-bit shift register as well as a temporary data register constructed the Add-and-then-shift Unit. It aims to alternate the values of permuted pixels obtained from the output of the Standard Map Computation Unit. The result is then passed to Image buffer 2. Figure 4.6(c) shows the hardware architecture of the Logistic Map Computation Unit adopted in diffusion stage. Since floating point computation is involved, two real number multipliers are mainly required, together with other components such as a data multiplexer and register as well as a 8-bit quantization processing element. The resultant image frame of the system is finally stored back to Image buffer 1. Apart from the needs of real number multipliers, the abovementioned hardware configuration

60

mainly utilizes simple logic gates and registers which should be feasible and available for the system deployment.

control signal kth position x y rx Random scan ry N 4-in Adder 256 x 1 Sin Table M U X 3-in Adder % k+1th position xk+1, yk+1 [log2N..0], [log2N..0]

(a)

control signal N init [7..0] Pixel to be permuted M U X Add

tmp x(n+1) [2..0] 8-bit Left cyclic x(n+1) [7..0]

(b)
control signal 1 Delay

x(n-1) Diffusion Key x(0) 4

M U X

Sub M U L Quan x(n) [7..0]

MUL

(c) Figure 4.6 Main modules of the proposed hardware implementation: (a) Standard Map Computation Unit; (b) Add-and-then-shift Unit and (c) Logistic Map Computation Unit.

61

4.4 Security Analysis

In this section, a detail analysis of the proposed image encryption scheme has been undergone and the results are summarized in the following subsections. In the analysis, the proposed scheme is compared with its similar scheme proposed by Lian et al. [9] which is claimed by the authors as a secure and low cost encryption scheme. The comparison results suggest that, at a similar level of security, the proposed cryptosystem leads to a higher encryption speed than Lian et al.s.

4.4.1 Histogram

The histogram of the confusion methods in Lian et al.s and our schemes are compared. The image Lena of size 512 512 and 256 gray levels is employed as the plain image. It is shown in Figure 4.7(a) while its histogram is given in Figure 4.7(b). After three rounds of the confusion process, the intermediate cipher image obtained by Lian et al.s confusion method is shown in Figure 4.7(c). As only pixel position is permuted by their confusion, the corresponding statistical information depicted in Figure 4.7(d) is exactly the same as that of the plain image. Figures 4.7(e) and Figure 4.7(f) are the cipher image and the corresponding histogram obtained by the proposed confusion scheme, respectively. For security consideration, a good pixel value mixing is crucial to make statistical attack infeasible. Figure 4.7(f) indicates a promising degree of pixel value mixing in only 3 confusion rounds.

62

(a)

(b)

(c)

(d)

(e) (f) Figure 4.7 (a) Plain Lena image; (b) Histogram of the plain image; (c) Intermediate cipher image using Lian et al.s confusion; (d) Histogram of the intermediate cipher image shown in (c); (e) Intermediate cipher image using the proposed confusion; (f) Histogram of the intermediate cipher image given in (e).

4.4.2 Key Space

As mentioned in Kerckhoff's principle in Section 2.1, the security of a cryptosystem should be determined by the secrecy of its key prior to the strength

63

of encryption algorithm. In the proposed scheme, all parameters used in both modified permutation and diffusion stage constitute the key space. These parameters include standard map parameter KC, random scan couple (rx, ry), seed of pixel value modification algorithm KS and initial value of diffusion KD. Following the computational expression of key space in [9], the available parameter space is (5 10 4 N N 255) 256
n

. When the image size N

increases, the size of key space increases accordingly. For N = 32, m = 2 and n = 2, its space equals to 8.181054 which is already larger than that of todays AES128 standard (key space of 128 bits = 2128 or 3.41038). This shows the security of the proposed scheme on images with reasonable small size is capable of withstanding brute force attacks using todays computer.

4.4.3 Differential Analysis with Time Performance

In order to withstand the known-plaintext attack and the chosen-plaintext attack, a tiny change in the plain image should cause a significant change in the cipher image. According to the proposed scheme, the diffusion effect introduced in the confusion process supplements that contributed by the explicit diffusion function. Therefore our cryptosystem achieves a similar performance in fewer cipher rounds than Lian et al.s. This can be supported by two performance indices introduced in [10, 11], number of pixels change rate (NPCR) and unified average changing intensity (UACI). The former means the percentage of the number of pixels between the cipher images whose corresponding plain images are at one pixel difference. The latter refers the average intensity of differences between these two images. First, denote two cipher images, whose corresponding plain-images has one-pixel difference, be C1 and C2, respectively. Moreover, C1(i,j) and C2(i,j) be the gray scale values of the pixels at (i,j) of C1 and C2, respectively. Then NPCR and UACI are defined as follows NPCR =

i, j

D(i, j )

W H

100% ,

(4.5)

64

UACI =

1 C1 (i, j ) C 2 (i, j ) 100% , W H i, j 255

(4.6)

where W and H is respectively the width and height of C1 and C2, D(i,j) is a bipolar array of the same size as C1 and C2 with the following definition.
1, C1 (i, j ) = C 2 (i, j ) D (i, j ) = 0, C1 (i, j ) C 2 (i, j )

(4.7)

Figure 4.8 shows the difference between two cipher images C1 and C2 whose plain images have a pixel difference at their lower right corner.

(a)

(b)

(c)

(d)

Figure 4.8 (a) Plain Cameraman image; (b) and (c) cipher images whose corresponding plain images have one pixel difference only; (d) difference between cipher images shown in (b) and (c).

The trend of these two performance indices at different overall rounds with n fixed to 4 is plotted in Figures 4.9(a) and (b), respectively. The graphs show

65

that both indices rise rapidly in our proposed scheme, which indicate good confusion and diffusion effect.

(a)

(b) Figure 4.9 Performance of the proposed and Lian et al.s cryptosystems in terms of (a) number of pixels change rate (NPCR); and (b) unified average changing intensity (UACI) at different overall rounds (m) with 4 permutation rounds in each confusion stage (n = 4).

66

In addition to the performance indices, Table 4.7 shows the encryption/decryption time required in the proposed and Lian et al.s schemes at different combinations of permutation (n) and overall (m) rounds using the 512 512 Lena image in 256 gray levels. The two mentioned indices are also provided in the same table. As observed from the table, the proposed scheme only requires one overall round with three permutation rounds in each confusion stage, i.e., m=1 and n=3 to achieve a similar performance of Lian et al.s recommended cryptosystem (m=n=4) [9]. The corresponding encryption time is 20.79 ms which is slightly higher than one-fifth of Lian et al.s (95.81 ms). When a higher performance such as NPCR > 0.996 and UACI > 0.334 is desired, Lian et al.s requirement is m=6 and n=3 while the proposed scheme only needs m=2 and n=2. It also shows that our encryption time (31.55 ms) is slightly higher than one quarter of Lian et al.s (116.33 ms). Such significant acceleration in encryption speed is gained from reducing the number of overall rounds m. On the other hand, the additional computation complexity of the simple add-and-shift operation in the modified confusion stage is insignificant. It results, on the average, an extra encryption time of only 0.45 ms per permutation. Because of the programming arrangement, the decryption time for both the proposed and Lian et al.s schemes consume a slightly longer time than the corresponding encryption time. However, as computed from the decryption time data listed in Table 4.7, the increase is acceptable, only 0.5% to 3.6% in Lian et al.s scheme and 5.5% to 9.7 % (for an explanation of the difference in percentage, please refer to Section 4.3.3) in our scheme.

67

m,n 1,2 1,3 1,4 2,1 2,2 2,3 2,4 3,1 3,2 3,3 3,4 3,5 4,1 4,2 4,3 4,4 4,5 5,1 5,2 5,3 5,4 5,5 6,1 6,2 6,3 6,4

Encryption Time (ms) Proposed 15.65 20.79 25.63 21.45 31.55 41.26 50.97 32.08 47.00 61.85 76.77 91.64 42.94 62.74 82.56 102.44 122.22 53.71 78.48 103.35 127.94 152.79 64.49 94.19 123.80 153.67 Lian et al 14.80 19.39 24.13 20.63 29.62 38.69 48.04 30.93 44.64 58.15 72.02 85.43 41.52 59.29 77.58 95.81 113.69 51.59 74.35 96.88 119.69 142.25 62.24 89.50 116.33 143.53

Decryption Time (ms) Proposed 16.95 22.37 27.14 23.93 34.48 44.09 54.17 37.10 51.15 66.47 81.59 96.76 47.80 68.10 88.43 108.63 129.03 60.38 85.27 110.77 136.15 160.95 72.74 103.38 132.14 163.23 Lian et al 15.35 19.78 24.27 21.73 30.77 39.77 48.75 32.55 46.14 59.84 73.17 86.71 43.42 61.43 79.96 97.90 116.16 54.66 76.94 99.56 122.39 144.78 65.45 92.45 119.53 146.72

NPCR Proposed 0.686642 0.99437 0.99604 0.684105 0.996086 0.996014 0.996014 0.995319 0.996353 0.996063 0.995911 0.996086 0.996078 0.996025 0.996178 0.996143 0.996239 0.996002 0.996124 0.996243 0.995956 0.99604 0.996021 0.996304 0.996181 0.996082 Lian et al 0.000179 0.000252 0.000423 0.002464 0.009903 0.019802 0.031902 0.085651 0.44632 0.647816 0.748901 0.21764 0.771065 0.984406 0.99091 0.992676 0.960281 0.992588 0.995815 0.995861 0.995892 0.995693 0.996037 0.996109 0.995865 0.996101

UACI Proposed 0.208793 0.328191 0.334905 0.211273 0.334273 0.334172 0.334896 0.330637 0.334267 0.335562 0.335196 0.334668 0.334048 0.334703 0.333724 0.334972 0.334382 0.334821 0.334286 0.334087 0.334679 0.333184 0.334316 0.334044 0.334865 0.335055 Lian et al 0.00004 0.000061 0.000093 0.000486 0.002623 0.005082 0.008362 0.021158 0.121025 0.176647 0.205962 0.05957 0.212241 0.300348 0.311426 0.317068 0.280655 0.316712 0.329292 0.33097 0.333018 0.327371 0.332429 0.333748 0.334197 0.334517

Table 4.7 Execution time and performance indices NPCR and UACI of the proposed and Lian et al.s schemes, for some selected values of m and n.

4.4.4 Correlation Analysis of Two Adjacent Pixels

Note that adjacent pixels of most plain images have the property of high correlation. One of the requirements of an effective image encryption scheme is to make the cipher image with sufficiently low correlation of adjacent pixels. In this regard, the correlations between two adjacent pixels in horizontal, vertical and diagonal directions are calculated to demonstrate the effectiveness of our cryptosystem. Throughout the test, four images, namely, a 256 gray scale plain

68

Peppers image of size 512 512, the cipher images obtained using the proposed scheme (m = 2 and n = 2) and Lian et al.s scheme (m = 6 and n = 3), and a randomly generated test image are employed. This test as stated in [10, 11] is to randomly select 1000 pairs of two adjacent pixels in the above directions, from both the plain-image and the cipher image. The correlation coefficient of the pixel pair is then calculated as
rxy = cov( x, y ) , D( x) D( y )

(4.8)

where x and y represent gray-scale values of two adjacent pixels in the image, the discrete definition of D(), E() and cov() are listed, respectively, as

D( x) = E ( x) =

1 N 1 N

( x E ( x)) ,
2 i =1 N i

(4.9) (4.10)
E ( y )), (4.11)

x ,
i =1 i

cov( x, y ) =

1 N

( x E ( x))( y
i =1 i

Table 4.8 illustrates the correlation coefficients of adjacent pixels of the four images. The data for the two cipher images are in the same order of magnitude as those for the random image. This implies that adjacent pixels of the plain image are effectively decorrelated by the application of both schemes.

Plain Peppers Image Horizontal Vertical Diagonal 0.982208 0.977046 0.978133

Cipher image by the proposed scheme (m=n=2) 0.002637 0.009177 0.003429

Cipher image by Lian et al.s scheme (m=6, n=3) 0.002453 0.004864 0.007525

Random image 0.001562 0.005922 0.004006

Table 4.8 Correlation coefficients of adjacent pixels of different images.

69

Moreover, the correlation distribution of two horizontally adjacent pixels of the plain image and the cipher image obtained using the proposed scheme is chosen as an example shown in Figures 4.10(a) and (b), respectively.

(a)

(b) Figure 4.10 Correlation analyses of two horizontally adjacent pixels in (a) the plain Peppers image; (b) the cipher image obtained using the proposed scheme.

70

4.5 Summary
In this chapter, the image encryption scheme based on 2D standard map has been studied. Similar to some other schemes, the confusion effect is solely contributed by the permutation stage while the diffusion effect is merely found in the pixel value diffusion stage. By performing common differential analysis, it is found that the diffusion part has little contribution to the whole scheme. This causes the cryptosystem requiring more overall cipher rounds than necessary. As a remedy, it is suggested to introduce certain diffusion effect in the confusion stage by simple operations on pixel values. An investigation of some possible operations on pixel value mixing has been carried out. It is found that Add-andthen-shift operation has the best overall performance with acceptable additional amount of complexity. To realize the proposed approach, both the pixel positioning permutation and value mixing are performed simultaneously in the confusion process. The pixel value modification is to add previous permuted pixel value to the current pixel value of the plain image and then perform a cyclic shift. In the confusion stage, since every computed pixel value depends on previous permuted pixel, the diffusion effect is obtained. As a result, the proposed scheme offers two levels of diffusion effect contributed separately by the confusion and diffusion stages, so that fewer overall rounds and hence a fast encryption resulted. Experimental results show that at a similar level of security, the proposed scheme requires slightly higher than one quarter the encryption time of the original scheme. The purpose of effective encryption acceleration is successfully achieved.

71

Chapter 5

Efficient Image Diffusion Using Table Operations

In the literature, 1D chaotic maps are particularly in interested for the design of chaos-based document cryptosystem. Similarly, by recalling the background introduced in Chapter 3, the same approach is applied to image encryption for diffusion probably because of the ease of implementation. Many chaotic image cryptosystems using a 2D or high-dimensional chaotic map together with a discrete 1D map have been proposed [9 - 11]. For pixel diffusion, it is observed that the chaotic map commonly in use is a real-valued function in the interval [0,1] which usually requires floating point arithmetic. The speed performance of this kind of schemes can consequently be affected because the computational complexity of floating point operations is higher than integer operations. To tackle the above-mentioned problem, in this chapter, our attention will turn to the effectiveness of diffusion approach dedicated to image encryption system. Firstly, two existing schemes based on 1D logistic map will be explored

72

in Section 5.1. In Section 5.2, the problems of these schemes will be discussed. Making use of simple table operations, a new diffusion approach has been developed to address the mentioned problems. Then, the corresponding image encryption scheme and its security analysis will be presented in Section 5.3 and Section 5.4, respectively. A summary is given in Section 5.5.

5.1 Diffusion Algorithms Based on 1D Logistic map

In this section, a review of two existing diffusion algorithms will be provided. As pointed out in Section 3.4, 2D permutation composed of the diffusion mechanism should be involved in secure image encryption schemes. A common way is to XOR a chaotic key stream with each pixel between every adjacent permutation rounds. Two related examples are the one proposed by Chen et al./Mao et al. [10, 11] and the other one proposed by Lian et al. [9]. The underlining concept of the algorithms is outlined as follows.

5.1.1 Diffusion Techniques Based on XOR plus mod Operations

To perform the diffusion step, Chen et al. [10, 11] suggested that each pixel should be processed by three operations, namely, XOR, plus and mod operations. Suppose I(k) is the kth pixel of the permuted image, C(k) and C(k-1) is the kth and (k-1)th pixel of diffused image, respectively, and L is the total number of gray scale levels. The implementation is summarized as follows.
C (k ) = (k ) { [ I (k ) + (k )] mod L} C (k 1),

(5.1)

( k ) = L

x(k ) x min x max x min

mod L ,

(5.2) (xmin,

where I(0) is obtained from the diffusion key Kd. the typical subinterval valued sequence x(k) obtained from iterating a 1D logistic map. x(0) = S,

xmax) of the chaotic map is (0.2, 0.8). (k ) is a quantization function of the real-

73

x(k+1) = 4x(k)[1-x(k)].

(5.3)

where the initial value x(0) is the seed S in (0,1). The iteration of Eq. (5.3) continues until the sequence x(k) obtained lies in (0.2, 0.8). Moreover, the value of x(k) has to be alternated slightly when it is equal to 0.5. Below is an example of the implementation of the algorithm. Algorithm 5.1.1
unsigned char dec; unsigned char init = Kd; unsigned char L = 256; double X = S; double xmax = 0.8; double xmin = 0.2; do{ if (init==0.5) init+=0.000001;

init = 4 * init * (1-init); }while((init < xmin) || (init > xmax)); dec = (unsigned char) (L*(init-xmin)/(xmax-xmin) % L); dataOut[0] = dec ^ ( (dataIn[0]+dec) % L ) ^ init;

for (i=1; i < N*N; i++) { do{ if (init==0.5) init+=0.000001;

init = 4 * init * (1-init); }while((init < xmin) || (init > xmax)); dec = (unsigned char) (L*(init-xmin)/(xmax-xmin) % L); dataOut[i] = dec ^ ( (dataIn[i]+dec) % L ) ^ dataOut[i-1]; }

5.1.2 Diffusion Techniques Based on XOR with Substitutions

Besides exploiting XOR plus mod, a variant approach proposed by Lian et al. [9] (please refer to Section 4.1) is to associate the chaotic key stream with

74

the previous diffused pixel. By recalling Eq. (4.2), the logistic map input is the previous diffused pixel Ci-1. Unlike the one described in Section 5.1.1, this key stream can be viewed as a substitution output. It is because a fixed input (Ci-1) leads to a fixed output (key stream). Since the key stream transformation is static, a masking table of size L, say 256, can be constructed before the diffusion step. It is expected that the key stream is generated quickly by means of table lookup without the need of iterating the logistic map. The corresponding algorithm is shown as follows: Algorithm 5.1.2
unsigned char init = Kd; unsigned char L = 256; unsigned char logtable[L]; unsigned char dec; double X; for (int i=0;i<256;i++) { X = i / 256.0; dec = (unsigned char) ((4 * X * (1-X) * L)%L); logtable[i] = dec; } dataOut[0] = dataIn[0] ^ logtable[init]; for (int j=0; j < N*N; j++) { dataOut[j] = dataIn[j] ^ logtable[dataOut[j-1]]; }

5.2 Practical Problems of the Algorithms

Although both chaotic cryptographic algorithms described above rely on the iterations of logistic map, the time and security performance of these schemes vary substantially. Obviously, the complexity of Algorithm 5.1.1 is much higher, due to the great demand on iterating the logistic maps. Table 5.1

75

lists a comparison of the time required by Algorithm 5.1.1 and Algorithm 5.1.2. In this experiment, the PC configuration is the same as the one mentioned in Section 4.3.1. As observed from the table, the time required for diffusing an image of size 512 512 using Algorithm 5.1.1 and 5.1.2 (direct computation of logistic map) is 22.49ms and 18.85ms, respectively. When the memory space is not constrained, a logistic map table can be built and the time required by Algorithm 5.1.2 is only 2.32ms. The main reason of the speed gain is that the number of iterations of the logistic map is reduced to 256, whereas Algorithm 5.1.1 still needs to iterate the map for at least 262,144 times (a total of 512*512 pixels). This explains a large scale of floating point arithmetic consumes a considerable processing time. Compared to Chen et al.s, Lian et al.s diffusion algorithm is extraordinarily fast.

Time required (ms) Algorithm 5.1.1 Algorithm 5.1.2 (without logistic map table) Algorithm 5.1.2 (with logistic map table) 22.49 18.85 2.32

Table 5.1 Time required for different diffusion algorithms to process an image of size 512 512.

For a reliable cryptosystem, the encryption speed and security are equally important. In the following, the diffusion effect of the two concerned algorithms will be investigated. As mentioned in the previous section, the output (key stream) of Lian et al.s diffusion is constant and dependent on the fixed input (Ci-1). A plot of pixel value input and chaotic mask using Eq (4.2 - 4.4) is depicted in Figure 5.1. Under finite precision of the machine, many pixel input (approximately 112 144) is noted to condense to a small range of mask value (252 - 255). Suppose the chosen plaintext attack is feasible, with probability of different mask outputs, opponents may perform statistical attack more easily to find some information from the encrypted images.

76

Figure 5.1 A plot of pixel value and mask value using the diffusion method employed in [9].

In addition, Figures 5.2 (a) - (g) and 5.3 (a) - (g) show the performance of the concerned diffusion algorithms on two gray scale images Cameraman of size 256 256 and Elaine of size 512 512, respectively. Throughout the above experiments, the step of pixel permutation is omitted. All results are only contributed by the diffusion algorithms described in Section 5.1. After some diffusion rounds, the image encrypted by Chen et al.s algorithm becomes hardly recognized, while the corresponding histogram shows a satisfactory level of pixel value mixing. In contrast, for Algorithm 5.1.2 proposed by Lian et al., visual appearances are persevered after performing one round or even nine rounds of diffusion process. This is explained as follows. Consider the typical example with the pixel value sequence p as given by p = 132 132 132 132 132 132 132 132 132 132 Below is the computed sequence d1 obtained using Lian et als diffusion with seed value C-1=89. d1 = 221 252 139 122 123 123 123 123 123 123

77

Related to the finite precision problem described in Figure 5.1 earlier, the identical value (123) is appeared after the forth element. As seen in Figures 5.2(c), (e) and 5.3(c), (e), even though all pixel value has been changed by the scheme, it still poses an undesirable security problem that human eyes are sensitive to the significant features.

(a)

(b)

(c)

(d)

(e)

(f) (g) Figure 5.2 Diffusion performance on plain-image: (a) 256 256 Cameraman image; (b) and (c) diffused image by 1 round of Algorithm 5.1.1 and 5.1.2, respectively; (d) and (e) diffused image by 9 rounds of Algorithm 5.1.1 and 5.1.2, respectively; (f) and (g) Histograms of results in (d) and (e), respectively.

78

(a)

(b)

(c)

(d)

(e)

(f)

(g)

Figure 5.3 Diffusion performance on plain-image: (a) 512 512 Elaine image; (b) and (c) diffused image by 1 round of Algorithm 5.1.1 and 5.1.2, respectively; (d) and (e) diffused image by 9 rounds of Algorithm 5.1.1 and 5.1.2, respectively; (f) and (g) Histograms of results in (d) and (e), respectively.

79

Moreover, when there is an error introduced to the sequence p, an error sequence p1 which is one pixel difference in sequence p and its corresponding sequence d2 by Lian et al.s diffusion are listed as follows: p1 = 61 132 132 132 132 132 132 132 132 132 d2 = 100 119 122 123 123 123 123 123 123 123 The number of pixel influences resulted from the error is 4, which is not as substantial as expected in a secure cryptosystem. The security level of Lian et al.s system may consequently be reduced to that of the pixel position permutation, which is vulnerable to chosen-plaintext attack. Although the diffusion process in the scheme performs the pixel value mixing quickly, it is relatively not strong to resist some existing attacks.

5.3 The Proposed Cryptosystem

In the previous section, several practical problems of designing diffusion algorithms were critically discussed. However, these problems can be avoided or alleviated by means of a careful design. This section presents the concept of an alternative diffusion approach based on table lookup and entries swapping techniques. By introducing fast table operations to the diffusion process, the proposed cryptosystem is more favourable for practical use.

5.3.1 Diffusion Based on Table Lookup and Entries Swapping

When implementing the aforementioned diffusion algorithms using finite computing precision, one can see that the steps for real-valued computation and consequent integer quantization consumed much computation time. Instead of iterating the real-valued chaotic map throughout the encryption, we propose another fast approach to exhibit the required diffusion effect. The proposed idea is a hybrid approach to utilize a dynamic table lookup and the information of 2D chaotic map available in permutation. As motivated by Wongs approach for

80

document encryption [8], a diffusion lookup table can be extended to be a 2D version such that the difficulty associated with any cryptanalysis can be further increased. In the diffusion stage, pixels are masked with an entry of diffusion table. The entry lookup method is based on the spatial information of 2D chaotic map obtained from pixel permutation rounds. To maintain the dynamicity of table, entry swapping is required. Hence, no direct iteration of chaotic map is needed in the course of diffusion steps. Lesser computation complexity is achieved and thus speeds up the cryptosystem. The proposed algorithm is operated as follows: Assuming that a gray scale plain image of size NN and its corresponding encrypted version is P = {P0 , P1 , K, PN N 1 } and C = {C 0 , C1 ,K , C N N 1 }, in which each element is the 8-bit gray level value of the pixel, respectively.

i. 2D Diffusion lookup table construction Construct a 1616 diffusion table DT = {(x, y); x, y = 0,1,2,,15}. Each table entry (x, y) is a unique integer drawn from the integer set [0, 255] so as to represent all the possible 8-bit gray levels of an image pixel. The initial table arrangement is key-dependent and should be kept secret.

ii. Parameter configuration Prepare three 8-bit sub-keys Kx, Ky and Kr: the first two are paired up as an initial position of table entry (x, y) while the other is relative index (rx, ry) for diffusion table.

iii. Table lookup using information of pixel position permutation As observed in preceding chapters, different chaotic maps or systems are often employed in the position permutation and diffusion stage. In the proposed scheme, during pixel permutation, each pixel is uniquely relocated by iterating a chaotic map such as cat map, baker map or standard map. The mapping information from iteration of that chaotic map, as denoted by CM( ), is

81

persevered after permutation rounds, and can be transformed to suitable geometrical information for 2D table lookup in diffusion rounds. After the permutation rounds, the cryptosystem proceeds to the diffusion step. For the encryption of the permuted pixel Pi, both diffusion round key, the previously processed pixel Pi-1 and its encrypted version Ci-1 are involved. To avoid potential chosen plaintext attack and known plaintext attack, the byte values of Pi-1 and Ci-1 are firstly encoded by some means before encryption. A simple encoding way is to associate their values with the corresponding entries of the table, as shown in Figure 5.4. It can be defined by Pi-1 = DT( U(Pi-1), L(Pi-1) ), Ci-1 = DT( U(Ci-1), L(Ci-1) ), where U( ) and L( ) is respectively the upper and lower 4-bit of pixel value. (5.4) (5.5)

Figure 5.4 An illustration of encoding method for Pi-1 and Ci-1.

The table lookup method is based on the iteration of 2D chaotic map in the position permutation step. In Figure 5.5, the encoded Pi-1 and Ci-1 are the initial conditions (x, y) of the 2D map. Due to the reuse of the chaotic map, the new chaotic state (x, y) can be obtained quickly without direct computation. As the new chaotic state (x, y) is a (log2N+log2N)-bit tuple, where N is the image width, a proper scaling is required for locating the mask in the 2D table. By the modulo 16 operation, the tuple (x4, y4) is scaled from (log2N+log2N)-bit to

82

(4+4)-bit one. The new lookup mask is XORed with pixel Pi subsequently as follows. (x4, y4) = CM(Pi-1, Ci-1) mod 16, Ci = Pi XOR DT(x4, y4). (5.6) (5.7)

Initial state (x, y)

8, 8

New state 2D chaotic map, (x, y) CM( ), for a NN image permutation log2N , log2N modulo 16

Mask to be XORed with Pi

1616 diffusion table, DT( )

4, 4

Scaled state (x4, y4)

Figure 5.5 A block diagram of table lookup based on information of pixel position permutation.

Since the encrypted pixel Ci is chained with its previously encrypted pixel Ci-1, a change in the pixel is most likely to influence all encrypted pixels after the change. The diffusion effect is thus achieved. The initial value P-1 and C-1 are chosen from sub-keys Kx and Ky in Part ii. iv. Diffusion table updates For security considerations, the content of 2D lookup table is necessarily updated throughout the diffusion process. This is realized by entry swapping and relative indexing. To update the table content effectively, it can depend on the encoded values of Pi-1 and Ci-1, and the mask. The update is performed by swapping an entry pair (s,t) and (x4,y4). Figure 5.6 illustrates the details of the swapping entries (s,t) and (x4,y4) in the lookup table. The former, i.e. (s,t), is constituted by the lower 4-bit of the encoded Pi-1 and Ci-1 in Eqs. (5.4) and (5.5) , respectively. This entry is then swapped with the new chaotic state (x4,y4) in Eq. (5.6). The definition of (s,t) is formulated as:

83

s = L(Pi-1), t = L(Ci-1) .

(5.8) (5.9)

Figure 5.6 Graphical representation of swapping entries (s,t) and (x4,y4).

Note that (s,t) and (x4,y4) may have identical values. In this case, the swapping is considered as ineffective. To solve this problem, the diagonal neighboring entry (s+1,t+1) will swap with (x4,y4) instead. In order to enhance the above mentioned dynamicity, relative indexing (rx,ry) is adopted in addition to explicit entry swapping. It intends to guarantee that the table content is completely distinct to the one for next pixel. One of the possible methods is to shift the entire table by certain rows and columns. Instead of direct table shifting, it can be implicitly done by adding the relative index (rx,ry) to (x4,y4). In this manner, the mask entry drawn from the table looks much dynamic. Initially, the value of (rx,ry) can be derived from sub-key Kr in Part ii. Afterwards, the next relative index (rx,ry) can be simply assigned to the last mask entry (x4,y4), and is therefore kept updating throughout all image pixels. Figure 5.7 outlines the 2D lookup table before and after update. Suppose the white square represent one swapping entry (s,t), while the black square is another swapping entry (x4,y4). To update the table content in the left figure, the white square and the black square are first swapped. Then, the position of the black square becomes the new relative index (rx,ry) with respect to the next pixel.

84

After these two steps, the table becomes the figure at right, which is simply a totally different one. Since the table update is governed by both plaintext and ciphertext, this further leads to the diffusion effect and is similar to the hashing function for document encryption [58].

Figure 5.7 An illustration of the dynamic update of the 2D lookup table.

A flowchart of the proposed diffusion algorithm is given in Figure 5.8. All operations required in proposed diffusion algorithm are simple XOR operations, bitwise-AND operations and some memory load operations which can be performed in high speed. Note that in the reversed procedure of pixel permutation, the chaotic map is inversely used to move permuted pixel back to the original position, whereas the map information for diffusion has to be the same at both cipher and decipher. For this reason, the information in the reversed permutation is required to remap the inversed chaotic map. It results in the allocation of additional 256256 memory space for two 8-bit inputs, Pi-1 and Ci-1. The allocation has very little effect on the speed of decryption operations. Apart from that, the decryption procedure is similar to the encryption one but operating on the encrypted image.

85

Encode Pi-1, Ci-1 by 2D Diffusion Table New Pi-1, Ci-1

Iterate 2D chaotic map and calculate (x, y) x = (x + rx) mod 16, y = (y + ry) mod 16 rx = x ry = y Lookup 2D Diffusion Table by (x, y) 8-bit of diffusion mask s = L(Pi-1), t = L(Ci-1) (s,t)= (x, y)? yes Swap table entries (s, t) and (x, y) no s=s+1 t=t+1

XOR and output

8-bit of input pixel

Figure 5.8 Flowchart of the proposed diffusion algorithm.

5.3.2 The Overall Encryption Procedure

In the beginning of this section, a diffusion algorithm based on table operations has been developed. This subsection will focus on the overall architecture of the proposed cryptosystems as illustrated in Figure 5.9. In the proposed scheme, there is a tight relationship between permutation and diffusion stages. It is because the lookup method in diffusion stage relies on the chaotic map utilized in the pixel permutation stage. The detail procedures are described as follows:

86

m rounds n rounds
Pixel Permutation Diffusion by 2D Lookup Table

Plain Image Secret Key

Cipher Image

Key Generator

Figure 5.9 Architecture of the proposed chaos-based image cryptosystem.

Step 1: From the encryption key, set the system parameters for pixel permutation and diffusion processes such as Kx, Ky and Kr (please refer to Section 5.3.1). All sub-keys can be synthesized by key generator using simple chaotic maps [9 - 11]. Step 2: Shuffle every element in the set P = {P0 , P1 , K, PN N 1 } using 2D or higher-dimensional discretized chaotic map such as Baker map, Cat map or Standard map with sub-key parameters obtained in Step 1. p p' q' = B q (mod N ), p, q = 0,1,2, K, N 1 (5.10)

where (p, q) and (p, q) are respectively the coordinates of the pixels in set P and the resultant intermediate set I. Iterate Eq. (5.10) until all elements in set I is established. In this way, there exists N N position mapping information which can be re-used in the diffusion step. By recalling the algorithm design in pervious sub-section, it is noticed that the required initial conditions (x, y) of the 2D map are in [0, 255] which implies the useful position mapping information is just 256 256. Suppose after shuffling an image, say of size 512 512, position mapping information is obtained which must be the same size as the image. With the consideration of the range refer to initial conditions, only a quarter (256 256) of the entire position mapping information is useful in the diffusion stage.

87

Based on the above arguments, the secrecy of the choice of 256 256 position mapping information in N N permutation is considered as a security enhancement issue. In this regard, two additional sub-keys Ktrow and Ktcol are suggested to control the choice of the region to be preserved. If N 256, the region covers the chaotic map information from (Ktrow, Ktcol) to (Ktrow+256, Ktcol+256). A modulo operation (mod) should be carried out when the region exceeds the size N N. On the contrary, if N < 256, 256 256 chaotic map information should be computed even larger than the necessary size in permutation. Step 3: Perform a diffusion operation using the 2D lookup table and the chosen position information according to the sub-keys Kx, Ky, Kr, Ktrow and Ktcol in Step 2. Encrypt all pixels in set I and hence output an encrypted image data set C = { C 0 , C1 ,K , C N N 1 } sequentially. An example of table content update before and after diffusion on an image of 256 256 is shown in Table 5.2. Step 4: Repeat the above steps several times with different sub-keys to satisfy the security requirements.

88

0 0 1 2 3 4 5 6 7 8 9 A B C D E F 4 94 FA 23 81 61 D2 DD 6E F8 29 71 33 90 1 7C

1 5B E7 46 F3 D0 B E AF C 27 52 C0 DF F0 6A BF

2 99 1F 7B 80 98 26 34 8C C8 6D 40 5C 97 D4 2 C1

3 3E 44 79 88 64 3D 56 E5 62 69 E2 50 89 60 A2 D8

4 35 1C 78 F6 C9 D1 3B E4 4A 63 0 E6 48 10 C7 F1

5 21 18 38 C2 D7 E1 82 B1 6B BB 6C EF AC 66 FB 17

6 ED B9 DA 15 AB CD D9 C4 E0 A3 B6 8 9F C6 96 92

7 76 2D 1E B7 51 BD 1A FE 8A 58 6 F2 4B D 4E 54

8 F9 7 55 9C BE 31 70 95 2A 91 DE 19 AE AA E9 EE

9 6F 9D 2B FC 8D 5E 7A 87 1D C5 11 DB 9A 30 C3 84

A 14 A1 75 F 45 BA 7F A0 A6 9B 5A 28 8B 7D 67 2E

B 83 2F 9 A5 D3 F4 A4 B0 B5 25 F7 5 B3 77 9E 8F

C 53 73 3 BC 16 85 B2 EC D6 CC 32 86 EB 41 43 3A

D 5F 2C 59 93 A 74 8E A9 24 42 68 47 4D F5 CF 1B

E CA 12 D5 49 20 39 A8 22 3C 65 AD FF DC 36 37 5D

F 4F CB 72 57 13 EA 7E 4C E3 A7 FD CE B8 3F B4 E8

(a)

0 0 1 2 3 4 5 6 7 8 9 A B C D E F 33 BE BC D7 C5 88 FA D4 8C 23 7 9 83 7E 7F DA

1 38 A2 41 9B FE 8A E0 3A B0 53 F9 74 FD 2A 21 B5

2 F8 6D A7 98 E6 A1 BB 7A 17 7B B7 18 63 52 DB AD

3 75 1E 50 1B DD F2 D B3 39 29 32 C9 47 22 BF A8

4 3C 66 30 C 8F CC 54 EC F7 78 90 ED 46 96 2D 44

5 2F 59 58 82 C3 E5 B4 B8 8 D8 4B AA E4 35 D5 5E

6 AF FF 91 92 C6 55 FB 9D EE 2 64 D0 A6 99 76 CB

7 24 A5 E9 D1 3F 19 BA 31 36 11 A3 E1 93 CD 8D 86

8 5D 5A 51 D6 4F 79 57 9E DC 6A EB 25 CF 0 65 6C

9 E3 9A DF B 14 56 40 B2 B1 95 1 6F 62 9F E7 4E

A FC D9 C1 CE F 89 70 5F D2 3D F1 8E 71 37 2E B6

B A4 A0 C4 27 8B 49 AE 45 81 1A C7 12 4A A9 69 72

C AB 5B 43 42 B9 F6 6E 68 2C 1C 5C 9C D3 1F 94 DE

D 67 C0 F5 6B 3B E8 F3 3E 60 85 73 61 F4 4C AC 87

E 1D C8 13 EF 48 7C 34 E 28 84 6 26 CA 3 80 20

F 10 16 7D 4D 97 2B EA 15 C2 F0 4 A BD E2 5 77

(b) Table 5.2 Content of the proposed 2D Diffusion table: (a) initial state (b) updated after processing the entire image.

89

5.3.3 Hardware Implementation

As stated in Section 4.3.4, there is a need for hardware realization. A possible hardware implementation is configured in Figure 5.10. Following the typical architecture of image cryptosystem, the proposed hardware configuration is similar to the one shown in Figure 4.5. The main difference is on their diffusion function. Instead of the Logistic Map Computation Unit, a 2D Table Operation unit is used in the proposed hardware implementation. To realize the table lookup operations, two memory storages are required which is denoted by Memory Unit 1 and 2, respectively. The former is allocated for the 256 256 log2N bits Permutation Table, whereas the latter is used to store the 16 16 bytes Diffusion Table. Figure 5.11(a) is the modified modules depicted in Figure 4.6(a) with the use of Permutation Table at the output of the Standard Map Computation unit. In Figure 5.11(b), the configuration of the 2D Table Operation Unit is composed of a data multiplexer and a de-multiplexer, a modular operator, two data registers, a delay flip-flop and an XOR gate. The control signal at the input of the system will select one of the three data signals, namely, lookup value from Permutation Table, pixel stream (i.e. permuted plain stream Pi) generated from permutation stage and the feedback of the system (i.e. cipher stream Ci). In this regard, a proper delay is essential for controlling the flow of signals. Nevertheless, the proposed algorithm is feasible to be realized with simple hardware.

Standard Map Computation Image Buffer 1

Memory Unit 1 Image Buffer 2

Control Unit

2D Table Operation

Memory Unit 2

Figure 5.10 The proposed hardware configuration.

90

control signal kth position x y rx Random scan ry 4-in Adder 256 x 1 Sin Table M U X 3-in Adder Store pixel position N % k+1th position xk+1, yk+1 [log2N..0], [log2N..0]

256 x 256 log2N bit Permutation Table

(a)
[log2N..0], [log2N..0] % init DeMux Diffusion Key x(0) x(n-1) tmp 2 Delay M U X [7..0] tmp 1 [3..0] [7..4] 16 x 16 byte Diffusion Table

256 x 256 log2N bit Permutation Table

XOR

x(n) [7..0]

(b) Figure 5.11 Main modules of the proposed hardware implementation: (a) Standard Map Computation Unit and (b) 2D Table Operation Unit.

5.4 Experimental Results and Analysis

This section gives some experimental results and analysis to show the performance of the above scheme using the proposed diffusion mechanism. In Chapter 3, some widely used 2D chaotic maps have been explored. Theoretically, they can also be collaborated with the proposed approach. Following the proposed architecture shown in Figure 5.9, three different 2D maps, namely, cat

91

map, baker map and standard map are considered. The performance of the scheme using m = 1 and n = 3 is summarized in Figure 5.12.

(a) Permuted image (Baker map)

(b) Permuted image (Cat map)

(c) Permuted image (Standard map)

(d) Encrypted image (Baker map)

(e) Encrypted image (Cat map)

(f) Encrypted image (Standard map)

(g) Histogram (Baker map)

(h) Histogram (Cat map)

(i) Histogram (Standard map)

Figure 5.12 Performance of diffusion function collaborated with different 2D chaotic maps (a) - (c) permutated image using baker map, cat map and standard map, respectively; (d) - (f) completely encrypted images of images (a) - (c) after diffusion process, respectively; (g) - (i) histograms of images (d) - (f).

In this simulation, the size of test image is 512 512 and the system parameters of 2D maps are selected as follows: for baker map, k = {64, 64, 128, 128, 64, 32, 32}; for cat map, p = 3 and q = 8 while k = 1500 for standard map. The proposed diffusion algorithm can be collaborated with the three different chaotic maps successfully. As indicated in the figures, the proposed algorithm can mix the pixel values of encrypted images into a uniform distribution. It also reflects that the choice of the maps adopted in permutation stage has no direct implication on the performance of the proposed diffusion algorithm. For testing consistency with Lian et als scheme stated in the beginning of this chapter, all

92

the following experiments will make use of 2D standard map for pixel permutation.

5.4.1 Diffusion Key Analysis

In the proposed scheme, all initial values and system parameters in permutation and diffusion mechanisms are considered as secret keys. Reviewing the proposed diffusion, all Kx, Ky, Kr, Ktrow and Ktcol and 16 16 2D diffusion table are kept secret and can be used to constitute the key. The key space from diffusion can be enlarged when N is large. For example, it is equal to 28 28 28 N N 256! , i.e., 3.4310520 when N = 512. If the parameters in the permutation stage are also taken into consideration, the key space of the proposed cryptosystem would far exceed that of the strongest AES-256 standard (key space of 256 bits = 2256 or 1.161077) and make brute-force attack infeasible. On the other hand, the key space testing has been performed. Basically, the security of the proposed diffusion approach rely on 5 important sub-keys namely Kx, Ky, Kr, Ktrow and Ktcol. In this experiment, a 512 512 test image is encrypted by using a predefined test key. Meanwhile, the encryption procedures are carried out again but using another key which is 1 bit different from the predefined test key. All other parameters (including those used in the permutation process as well as the initial state of diffusion table) remain unchanged. The two encrypted images by the two slightly different diffusion keys are compared in terms of pixel gray scale values. Suppose the predefined test key is Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 90, while the slightly different key is Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 91, with the value of Ktcol changed from 90 to 91. The results of using these two test keys are provided in Figures 5.13 (b) and (c). Figure 5.13 (d) is the difference image between (b) and (c) which is found 99.62% dissimilar to each other. In addition, the use of decryption key with 1-bit difference with the predefined one is also tested. Figure 5.14 shows the experimental results. As observed from the figure, the decrypted image is totally different from the plain-

93

image. Similar results for other keys Kx, Ky, Kr and Ktrow are tabulated in Table 5.3.

(a)

(b)

(c)

(d)

Figure 5.13 Key sensitivity test 1: (a) plain-image; (b) encrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 90); (c) encrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 91); (d) difference image.

(a)

(b)

(c)

(d)

Figure 5.14 Key sensitivity test 2: (a) plain-image; (b) encrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 90); (c) decrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 90); (d) decrypted image (Kx = 123, Ky = 34, Kr = 56, Ktrow = 78, Ktcol = 91).

94

Key 1: Original value Kx Ky Kr Ktrow Ktcol 123 34 56 78 90

Key 2: Modified value 122 35 57 79 91

Pixel difference in encryption 99.6128% 99.5899% 99.6044% 99.6048% 99.6174%

Pixel difference in decryption 99.6155% 99.6063% 99.6105% 99.6120% 99.6098%

Table 5.3 The configuration and results of key sensitivity test.

5.4.2 Correlation Analysis of Two Adjacent Pixels

In this experiment, the same configurations are adopted as in Section 4.4.3. The correlation of two horizontally adjacent pixels in the plain image and the encrypted image by the proposed scheme (n=1) is illustrated in Figures 5.15 (a) and (b), respectively. Their correlation coefficients are 0.975103 and 0.003828, respectively. Similar trends in other directions are found and tabulated in Table 5.4. These results are close to zero correlation which indicate that almost all neighboring pixels of the plain image can be decorrelated by the proposed scheme.

Plain Lena image Horizontal Vertical Diagonal 0.975103 0.988925 0.96704

Encrypted image (m=2,n=1) 0.003828 -0.001135 0.001023

Table 5.4 Correlation coefficients of adjacent pixels in two images.

95

(a)

(b) Figure 5.15 Correlations of two horizontally adjacent pixels in (a) the plain Lena image; (b) the encrypted image by the proposed scheme (m=2,n=1).

5.4.3 NPCR & UACI Analyses

To quantify the resistance against differential attacks, NPCR and UACI as previously introduced, are adopted. These experiments are also considered in the proposed cryptosystem. The testing configurations are the same as in Section 4.4.2. Table 5.5 shows the performance of the proposed, Chen et al.s and Lian et al.s scheme with different combinations of permutation (n) and overall (m)

96

rounds. One can see that there is a fluctuation between the two schemes in the first overall round (m=1). Since only one diffusion step is performed, the degree of differential influence is subject to the position of a pixel change. Diffusion effect can only be experienced on all encrypted pixels after the changed pixel. This accounts for the fluctuation caused. For other overall rounds (m>1), the performance indices of the proposed and Chen et al.s schemes stay at a very high rate (NPCR=0.996, UACI=0.334). More importantly, the proposed scheme is relatively faster (41% gain on average in encryption time) than Chen et al.s which are based on real-valued chaotic map. In addition to programming realization factors, a slight difference in decryption time of the proposed scheme also comes from the mapping conversion in the reversed procedure of pixel permutation which leads to 3.7% to 6.6% increment. Nevertheless, the encryption-decryption time is shorter (39% gain on average in total time) than that of Chen et al.s scheme. On the other hand, the performance indices of Lian et al.s scheme (m=2, n=1) are at a low rate (NPCR=0.002464, UACI=0.000486) which is unsatisfactory to resist the general cryptanalysis. The security level of Lian et al.s scheme shows more acceptable when the recommended overall and permutation rounds (m=n=4) are reached. The performance indices of the scheme raises to a sufficiently high rate (which is the closest to the rate NPCR=0.996 and UACI=0.334 with the shortest encryption time in the table) when m=6 and n=3. However, similar security level can be achieved by the proposed scheme with m=2 and n=1 only. The corresponding encryption time (39.39 ms) is around one-third the encryption time required by Lian et al.s scheme (116.33 ms). Meanwhile, the corresponding decryption time (41.53 ms) is just higher than one third of Lian et al.s (119.53 ms). Since the proposed diffusion approach only involves those naturally fast operations such as memory load and XOR, it is comparatively effective than the other two reference approaches using real-valued chaotic map.

m,n Proposed Chen et al. Lian et al. Chen et al. 0.38147 0.067055 0.772881 0.994343 0.334788 0.335223 0.335238 0.334199 0.334508 0.334134 0.334949 0.335248 0.334782 0.334585 0.334328 0.334931 0.992676 0.960281 0.992588 0.995815 0.996159 0.995941 0.996124 0.996075 0.996101 0.996216 0.996181 0.995861 146.72 0.996113 0.995861 0.996094 0.995861 0.995892 0.995693 0.996037 0.996109 0.995865 0.996101 0.334347 0.334779 0.334266 0.333991 0.333831 0.334605 0.333785 0.335647 0.334438 0.333489 0.334204 0.333375 0.333943 0.333972 0.334955 0.334831 0.335269 0.335085 0.334972 0.335109 0.333993 0.334519 0.334811 0.334858 0.334953 0.334732 0.334362 0.334192 0.334838 0.334108 0.334261 0.335093 0.333841 0.996086 0.996334 0.996044 0.996227 0.996174 0.996273 0.996147 0.995987 0.996231 0.995827 0.995857 0.99609 0.996265 0.996101 0.996418 0.771065 0.984406 0.99091 0.21764 0.748901 0.647816 0.44632 0.085651 0.031902 0.019802 0.009903 0.002464 0.334532 0.000423 0.258499 0.38805 0.000252 0.02225 0.033624 0.000179 0.127498 0.191643 0.00004 0.000061 0.000093 0.000486 0.002623 0.005082 0.008362 0.021158 0.121025 0.176647 0.205962 0.05957 0.212241 0.300348 0.311426 0.317068 0.280655 0.316712 0.329292 0.33097 0.333018 0.327371 0.332429 0.333748 0.334197 0.334517 Lian et al. Chen et al. Lian et al. 25.16 35.78 40.32 44.75 62.44 0.996117 0.996178 0.995991 0.996136 0.99593 0.996201 0.995918 0.996281 0.996105 0.995975 0.996059 0.996181 0.996166 0.996124 0.99614 0.996277 0.996342 0.996166 0.996105 71.82 81.35 90.31 93.77 107.50 121.31 134.66 148.46 125.27 143.35 161.57 179.41 199.94 156.36 178.91 202.16 225.14 247.18 187.66 215.46 242.42 269.92 119.53 92.45 65.45 144.78 122.39 99.56 76.94 54.66 116.16 97.90 79.96 61.43 43.42 86.71 73.17 59.84 46.14 32.55 48.75 39.77 30.77 21.73 24.27 0.769768 19.78 0.066723 15.35 29.75 34.28 41.53 50.55 60.19 69.02 62.63 76.62 90.37 103.49 117.29 84.44 101.72 120.46 138.47 156.31 104.84 127.90 150.52 173.33 195.46 126.34 153.65 180.52 208.58 0.37994 Proposed Proposed 14.80 19.39 24.13 20.63 29.62 38.69 48.04 30.93 44.64 58.15 72.02 85.43 41.52 59.29 77.58 95.81 113.69 51.59 74.35 96.88 119.69 142.25 62.24 89.50 116.33 143.53

Encryption Time (ms)

Decryption Time(ms)

NPCR

UACI

Proposed Chen et al. Lian et al.

1,2

24.20

35.14

1,3

28.67

39.36

1,4

33.01

44.39

2,1

39.39

61.44

2,2

48.52

70.41

2,3

57.30

79.78

2,4

66.22

88.39

3,1

59.14

92.14

3,2

72.58

105.62

3,3

86.07

119.55

3,4

99.29

132.91

3,5

112.77

146.34

4,1

79.21

122.88

4,2

97.00

140.97

4,3

114.95

159.17

4,4

132.26

177.39

4,5

150.05

195.81

5,1

99.19

153.17

5,2

121.90

176.15

5,3

143.65

198.98

5,4

166.03

222.42

5,5

188.16

244.10

6,1

119.18

184.11

6,2

145.87

211.74

6,3

172.29

238.38

6,4

199.64

265.82

97

Table 5.5 Encryption time and performance indices NPCR and UACI of the proposed, Chen et al.s and Lian et al.s scheme, for some selected values of m and n.

98

5.5 Summary
In this chapter, some diffusion algorithms using 1D chaotic map are thoroughly analyzed. Since the 1D map adopted is usually a real-valued function, time consuming floating point computation and subsequent integer quantization are involved in the process. It is found that the studied techniques used to achieve the diffusion effect vary considerably in terms of encryption time and security performance. From the aforementioned analysis, a simple yet effective diffusion algorithm is deliberately designed. The approach is to operate a dynamic 2D lookup table which is inspired by Wongs document encryption [8]. The position and the value of each permuted image pixel are used to lookup in the table so as to obtain a new 8-bit value to add on the permuted pixel value. Since the way of table entry swapping depends on the plain image, this leads to the diffusion effect and is similar to the hashing function for document encryption. Experimental results show that at a similar security level, the proposed method requires a shorter encryption time than the studied techniques using real-valued 1-D chaotic map for diffusion (40% speed gain from Chen et al.s [10, 11] and 66% speed gain from Lian et al.s [9]). This is because the table lookup and swapping operations are much faster than the floating-point arithmetic operations. A significant enhancement on the algorithms under study is thus achieved regarding the time and security considerations.

99

Chapter 6

Conclusion and Further Developments

In this chapter, a conclusion of this thesis and some suggestions for further development will be provided in Section 6.1 and Section 6.2, respectively.

6.1 Conclusion
In this thesis, issues of efficient chaos-based image encryption schemes have been investigated. Our work described here is achieved by modifying and optimizing some existing chaotic cryptographic schemes. Collectively speaking, the underlying principle of the work covers chaos and cryptography. In this regards, an overview of cryptography is firstly presented for a foundation. For a good cipher design, the properties of confusion and diffusion are explained so as to empower us to evaluate cryptosystems. Owing to the differences in mechanisms and cryptographic properties discussed in Chapter 2, it is found that the roles of public-key cryptography and private-key cryptography are

100

complement to, but not substitute, one another. Over the last decade, more and more specific private-key variants are proposed to enhance traditional ones. Chaotic cryptography is definitely one of them. For completeness, fundamentals of chaos theory are described in Chapter 3, before developing the notion of chaotic cryptography. It is found that chaotic maps and cryptography have a close relationship. The cryptographic properties of confusion and diffusion are analogous to ergodicity and sensitivity to system parameters and initial conditions of chaotic maps. Since the field of chaotic cryptography is broad, our attention mainly focuses on chaotic image encryption. In the literature, a typical approach is to perform pixel position permutation and gray-scale value diffusion processes alternatively [26]. From aforementioned, only a few schemes with recommended, but usually large number of iterations, promise to achieve adequate security and thus result in unsatisfactory encryption speed. From our analysis, the problem is mainly due to the following two realization constraints: 1. The confusion and diffusion effect is solely contributed by the permutation and the diffusion stage, respectively. Consequently, more overall rounds than necessary are required to achieve a certain level of security. 2. For keystream generation in diffusion stage, the iteration of a real-valued 1D map is a common practice. However, much computation load is required for floating point computation and the subsequent integer quantization. To deal with problem 1, a modified approach for chaos-based permutation is proposed in Chapter 4. The method is to introduce certain diffusion effect in the confusion stage by simple operations on pixel values. This can be done by adding previous permuted pixel value to the current pixel value of the plain image and then perform a cyclic shift. The additional diffusion effect contributed by the proposed scheme leads to fewer overall rounds and hence higher encryption speed. Simulation results show that at a similar level of security, the

101

proposed scheme only requires an encryption time slightly higher than one quarter of the reference scheme [9]. Secondly, a fast diffusion algorithm based on 2D table lookup and entry swapping is proposed. The approach is to operate a dynamic 2D lookup table which is an extension of Wongs document encryption scheme [8]. In the diffusion stage, both the position and the value of each permuted image pixel are used to determine a secret 8-bit mask. This mask is then added to the permuted pixel value. The table lookup and swapping operations are much faster than the floating-point arithmetic operations. Experimental results show that at a similar security level, the proposed method performs better than existing techniques using real-valued 1D chaotic map for diffusion. This is justified by 40% and 66% speed gain to Chen et al.s [10, 11] and Lian et al.s [9] approaches, respectively. This forms a practical solution to problem 2. To conclude, this thesis presents two improved approaches to a typical structure of chaotic image encryption schemes [26], so as to uplift the system efficiency in two different aspects: pixel position permutation process and pixel value diffusion process.

6.2 Further Developments

Apart from the above mentioned, further developments of the work presented in this thesis will be discussed in the following three directions.

6.2.1 Joint Compression-encryption Approach to Reduce Cipher Image Size

In image storage or transmission, lossless or lossy compression is usually applied so as to reduce the information to be stored or transmitted. Similarly, it is also expected that a reduction of cipher image size by joint compressionencryption techniques should increase the encryption efficiency [24, 59]. For instance, image compression techniques such as transform coding using Discrete Cosine Transform (DCT) can be incorporated with the proposed schemes to have

102

a small encrypted cipher image. Instead of permuting the plain image pixels, quantized DCT coefficients of the plain image can be permuted and then encrypted [24]. However, one should deliberately evaluate the complexity of compression algorithms in use. In general, the compression part should consume considerably small time in the whole process.

6.2.2 Extension to Chaos-based Video Encryption

Video data are basically in the form of three-dimensional (3D) structure with spatial and temporal redundancy. Due to the close relationship between videos and images, it is possible to extend the proposed techniques for video encryption. In practice, video data exist more often in a compressed format which involves intra frame compression and motion compensation. The extended cipher could be designed to operate on I(ntra) frames, P(redicted) frames, and B(i-predictive) frames of the compressed video. Besides, selective encryption techniques on video have long been considered as an attractive research direction. Its basic concept is to encrypt only a portion of the entire plain video to protect from illegal attempt to reconstruct the video [60]. Theoretically, the speed is further accelerated by encrypting only significant data such as low frequency DCT coefficients, I-frames, header of P-frames and motion vectors. .
6.2.3 Incorporation of Public-key with Private-key Schemes

All private-key cryptosystems, including the encryption schemes proposed in this thesis, suffer from the key distribution problem. For a more practical image security solution, public-key cryptography can be included to form a hybrid cryptosystem. Under this framework, public-key encryption is expected to solve the key distribution problem, while leaving chaos-based symmetric encryption to do bulk encryption for efficiency. For instance, public-key module may be supported by Elliptic Curve Cryptosystem (ECC) when resource utilization is a critical concern. The secret key required in chaotic encryption

103

module can be exchanged among the communication parties by making use of Elliptic Curve Diffie-Hellman (ECDH) protocol. The applicability of the image encryption scheme can be enhanced accordingly.

104

References
[1] [2] Data Encryption Standard, NIST FIPS PUB 46-2, U.S. Department of Commerce, 1993. X. Lai, J. Massey, A Proposal for a New Block Encryption Standard, Proc. of Advances in Cryptology-EUROCRYPT 90, Springer-Verlag, pp. 389404, 1991. [3] [4] [5] Advanced Encryption Standard, NIST FIPS PUB 197, U.S. Department of Commerce, 2001. Z. Li, D. Xu, A Secure Communication Scheme Using Projective Chaos Synchronization, Chaos, Solitons and Fractals 22(2), pp. 477-481, 2004. J. Y. Chen, K. W. Wong, L. M. Cheng, J. W. Shuai, A Secure Communication Scheme Based on the Phase Synchronization of Chaotic Systems, Chaos 13(2), pp. 508-514, 2003. [6] T. Habutsu, Y. Nishio, I. Sasase, S. Mori, A Secret Key Cryptosystem by Iterating a Chaotic Map, Proc. of Advances in Cryptology-CRYPTO 91, Springer-Verlag, pp. 127-140, 1991. [7] [8] [9] M. S. Baptista, Cryptography with Chaos, Phys. Lett. A 240, pp. 50-54, 1998. K.W. Wong, A Fast Chaotic Cryptographic Scheme with Dynamic Lookup Table, Phys. Lett. A 298(4), pp. 238-242, 2002. S.G. Lian, J. Sun, Z. Wang, A Block Cipher Based on a Suitable Use of Chaotic Standard Map, Chaos, Solitons and Fractals 26(1), pp. 117-129, 2005. [10] G. Chen, Y.B. Mao, C.K. Chui, A Symmetric Image Encryption Scheme Based on 3D Chaotic Cat Maps, Chaos, Solitons and Fractals 12, pp. 749761, 2004.

105

[11] Y.B. Mao, G. Chen, S.G. Lian, A Novel Fast Image Encryption Scheme Based on the 3D Chaotic Baker Map, Int. J. Bifurcat. Chaos 14(10), pp. 3613-3624, 2004. [12] B. Schneier, Applied Cryptography: protocols, algorithms, and source code in C, 2nd ed. New York: Wiley, 1996. [13] D. Kahn, The Codebreakers: The Story of Secret Writing, New York: Macmillan, 1967. [14] Kerckhoff, la Cryptographie Militaire, Journel des Sciences militaries, 9th series, IX, English trans. by Warren T. McCready of the University of Toronto, 1964. [15] C.E. Shannon, Communication Theory of Secrecy System, Bell Syst. Tech. J. 28, pp. 656-715, 1949. [16] DES Modes of operation, NIST FIPS PUB 81, U.S. Department of commerce, 1981. [17] E. Biham, A. Shamir, Differential Cryptanalysis of the Data Encryption Standard, New York: Springer-Verlag, 1993. [18] M. Matsui, Linear Cryptanalysis Method for DES Cipher, Proc. of Advances in Cryptology-EUROCRYPT 93, Springer-Verlag, pp. 386-397, 1994. [19] J. Daemen, V. Rijmen, The Block Cipher Rijndael, Lecture Notes in Computer Science 1820, pp. 288-296, 2000. [20] B. Furht, D. Socek, A.M. Eskicioglu, Fundamentals of Multimedia Encryption Techniques, in B. Furht and D. Kirovski (Eds.), Multimedia Security Handbook, Ch. 3, CRC Press, 2005. [21] M. Podesser, H.-P. Schmidt, A. Uhl, Selective Bitplane Encryption Scheme for Secure Transmission of Image Data in Mobile Environments, Proc. of the 5th IEEE Nordic Signal Processing Symposium (NORSIG02), Trondheim, Norway, October 2002. [22] C. Alexopoulos, SCAN, A Language for 2-D Sequential data accessing, PhD. thesis, University of Patras, Greece, 1989.

106

[23] N. Bourbakis, C. Alexopoulos, Picture Data Encryption using SCAN Patterns, Pattern Recognition 25(6), pp. 567-581, 1992. [24] C.P. Wu, C.C. Kuo, Design of Integrated Multimedia Compression and Encryption Systems, IEEE Trans. Multimedia 7(5), pp. 828-839, 2005. [25] T. Xiang, K.W. Wong, X. Liao, Selective Image Encryption using Spatiotemporal Chaotic System, Chaos 17(2), paper 023115, June 2007. [26] J. Fridrich, Symmetric Ciphers Based on Two-dimensional Chaotic Maps, Int. J. Bifurcat. Chaos 8(6), pp. 1259-1284, 1998. [27] W. Diffie, M.E. Hellman, New Directions in Cryptography, IEEE Trans. Information Theory 22, pp. 644-654, 1976. [28] R.L. Rivest, A. Shamir, and L. Adleman, A Method for Obtaining Digital Signatures and Public Key Cryptosystems, Comm. ACM 21, pp. 120-126, 1978. [29] N. Koblitz, Elliptic Curve Cryptosystems, Math Comp. 48, pp. 203-209, 1987. [30] V. Miller, Uses of Elliptic Curves in Cryptography, Proc. of Advances in Cryptology-CRYPTO85, Springer-Verlag, pp. 417-426, 1986. [31] S. Neil-Rasband, Chaotic Dynamics of Nonlinear Systems, John Wiley & Sons Inc., 1990. [32] A. B. Campbell, Applied Chaos Theory: A paradigm for complexity, Academic Press Inc., pp. 81-125, 1993. [33] H. Hasagawa, C. Saphir, Unitarity and Irreversibility in Chaotic Systems, Phys. Review A 46, p7401-7423, 1992. [34] E.A. Arnold, A. Avez, Ergodic Problems of Classical Mechanics, Benjamin, W. A.: New Jersey, 1968. [35] E. Ott, Chaos in Dynamical Systems, Cambridge University Press, 1993. [36] R. Brown, L.O. Chua, Clarifying Chaos: Examples and counterexamples, Int. J. Bifurcat. Chaos 6(2), pp. 219-242, 1996. [37] L. Kocarev, Chaos-based Cryptography: A brief overview, IEEE Circ. Syst. Mag. 3, pp. 6-21, 2001.

107

[38] Z. Kotulski, J. Szczepanski, Discrete Chaotic Cryptography (DCC): New method for secure communication, Proc. of 11th Workshop on Nonlinear Evolution Equations and Dynamical Systems (NEEDS97), June 1997. [39] L. Kocarev, G. Jakimovski, Chaos and Cryptography: From chaotic maps to encryption schemes, IEEE Trans. Circ. Syst.I 48(2), pp. 163-169, 2001. [40] S. Li, Q. Li, W. Li, X. Mou, Y. Cai, Statistical Properties of Digital Piecewise Linear Chaotic Maps and Their Roles in Cryptography and Pseudo-Random Coding, Proc. of IMA - C&C 2260, Springer-Verlag, pp. 205-221, December 2001. [41] R. Matthews, On the Derivation of a Chaotic Encryption Algorithm, Cryptologia 8(1), pp. 29-41, 1989. [42] S. Li, G. Chen, X. Zheng, Chaos-based Encryption for digital images and videos, in Furht B and Kirovski D (Eds.), Multimedia Security Handbook, Ch. 4, CRC Press, 2005. [43] G. Anescu, A C++ Implementation of the Rijndael Encryption/Decryption method 2001, http://www.codeproject.com/cpp/aes.asp. [44] J.C. Yen, J.I. Guo, A New Chaotic Key-based Design for Image Encryption and Decryption, Proc. of IEEE Int. Symposium Circ. Syst. 4, pp. 49-52, May 2000. [45] J.I. Guo, J.C. Yen, The Design and Realization of a New Hierarchical Chaotic Image Encryption Algorithm, Proc. of Int. Symposium Comm., pp. 210-214, 1999. [46] F. Belkhouche, I. Pitas, Binary Image Encoding Using 1D Chaotic Maps, Proc. of Annual conference of IEEE Region 5, pp. 39-43, 2003. [47] F. Pichler, J. Scharinger, Ciphering by Bernoulli Shifts in Finite Abelian groups, Proc. of Linz Conference, pp. 465-476, 1994. [48] J. Scharinger, Fast Encryption of Image Data Using Chaotic Kolmogorov Flows, J. Electronic Imaging 7(2), pp. 318-325, 1998. [49] Z.H. Guan, F.J. Huang, W.J. Guan, Chaos-based Image Encryption Algorithm, Phys. Lett. A 346, pp. 153-157, 2005.

108

[50] S.G. Lian, Y.B. Mao, Z. Wang, 3D Extensions of Some 2D Chaotic Maps and Their Usage in Data Encryption, Proc. of the Fourth ICCA 2003, pp. 819-823, 2003. [51] S. Li, C. Li, G. Chen, G. Bourbakis, K.T. Lo, A General Cryptanalysis of Permutation-Only Multimedia Encryption Algorithms, available in IACR's ePrint Archive: Report 2004/374, http://eprint.iacr.org/2004/374. [52] S. Li, X. Zheng, Cryptanalysis of a Chaotic Image Encryption Method, Proc. of IEEE Int. Symposium Circ. Syst. 2, pp. 708-711, 2002. [53] Y.B. Mao, G. Chen, Chaos-based Image Encryption, in E. BaycoCorrochano (Eds.), Handbook of Computational Computing, Ch. 8, Heidelberg:Springer-Verlag, 2004. [54] S.G. Lian, J. Sun, Z. Wang, Security Analysis of a Chaos-based Image Encryption Algorithm, Physica A 351, pp. 645-661, 2005. [55] C. Li, Cryptanalyses of Some Multimedia Encryption schemes, MSc. thesis, Zhejiang University, Hangzhou, China, 2005. [56] K. Wang, W.J. Pei, L.H. Zou, A. Song, Z. He, On the Security of 3D Cat Map Based Symmetric Image Encryption Scheme, Phys. Lett. A 346, pp. 153-157, 2005. [57] The USC-SIPI Image Database, http://sipi.usc.edu/database/. [58] K.W. Wong, A Combined Chaotic Cryptographic and Hashing Scheme. Phys. Lett. A 307(5-6), pp. 292-298, 2003. [59] R. Bose, S. Pathak, A Novel Compression and Encryption Scheme Using Variable Model Arithmetic Coding and Coupled Chaotic System, IEEE Trans. Circ. Syst.I 53(4), pp.848-857, April 2006. [60] F. Chiaraluce, L. Ciccarelli, E. Gambi, P. Pierleoni, M. Reginelli, A New Chaotic Algorithm for Video Encryption, IEEE Trans. Consumer Electron. 48(4), pp. 838-844, 2002.

109

List of Publications
1. K.W. Wong, S.H. Kwok, W.S. Law, A Fast Image Encryption Scheme Based on Chaotic Standard Map, submitted to Physics Letters A, also available in arXiv.org e-Print archive cs/0609158 http://arxiv.org/abs/cs.CR/0609158. 2. K.W. Wong, S.H. Kwok, An Efficient Diffusion Approach for Chaos-based Image Encryption, Proceedings of the Third International IEEE Scientific Conference on Physics and Control (PhysCon 2007), Potsdam, Germany, September 3-7, 2007. 3. K.W. Wong, W.S. Law, S.H. Kwok, An Efficient Baptista-type Chaotic Cryptographic Scheme, Proceedings of the Third Shanghai International Symposium on Nonlinear Sciences and Applications (Shanghai NSA07), June 6-10, 2007.