A

Apendice

APNDICE
A.1.

Regla de Leibnitz para la derivar dentro de una integral

d
dx

2 (s)

F (x, s)dx =
1 (s)

2 (s)
1 (s)

F
d1 (s)
d2 (s)
dx + F (1 (s), s)
F (2 (s), s)
x
ds
ds

Para el caso en que 1 = a y 2 = b son constantes, nos queda:

d
dx

A.2.

F (x, s)dx =
a

b
a

F
dx
x

La funcin Gamma

La funcin gamma es una generalizacin de la funcin factorial y se define como:

(p) =
ex xp1 dx
0

Cuando p R , el clculo de la funcin gamma se realiza usando tcnicas numricas y

mediante la siguiente frmula de recurrencia:
(p + 1) = p(p)
Una frmula til, conocida como la frmula de reflexin de Euler, es:
(p)(1 p) =
371

sin(p)

372

APNDICE A. APNDICE

De donde se obtiene: ( 12 ) =
(n + 12 ) =

. En general, se puede demostrar que:

(1)n
(2n 1)!

1 =
2n
(n + 2 )

para n = 1, 2, 3, . . .

Cuando p = n N, se tiene que (n) = (n 1)!. Dado que (1) =

se sigue que: (1) = 0! = 1.

ex dx = 1, entonces

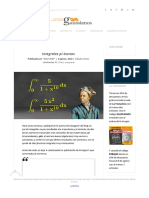
La figura A.2 muestra la grfica de la funcin gamma. Puede verse que presenta asntotas
en los puntos p = 1, 2, 3, 4, . . ., mientras que la funcin es continua para p > 0.

!(x)

10

-5

-4

-3

-2

-1

-10

Figura A.1: Funcin Gamma

Una aproximacin asinttica importante, conocida como la frmula de Stirling1 para factoriales grandes, es:
n n 1
n n

1
1
1
n! = 2n
e 12n 360n3 + 1260n5 1680n7 +... 2n
e
e
La derivada n-sima de la funcin Gamma est dada por:

dn
(p) =
ex xp1 lnn (x)dx
n
dp
0
1

En honor al matemtico escocs James Stirling(1692-1770).

A.3. NMEROS DE BERNOULLI

373

De donde un resultado importante, conocido como constante de Euler-Mascheroni o simplemente constante de Euler es:

(1) =
ex ln(x)dx = = 0.577215664901532860606
0

Descubierta en 1734 por Euler, originalmente se escribe como:

1
1
1
=
ln 1 +
= lm
ln(n)
n
k
k
k
k=1
k=1
La funcin Gamma se puede escribir en trminos de productos infinitos, as:

ep
p 1 p
(p) =
1+
en
p n=1
n

La siguiente frmula, es conocida como teorema de multiplicacin de la funcin gamma:

n1
1
1
2
n1
(x) x +
x+
x +
= n 2 nx (2) 2 (nx)
n
n
n
Una expansin en series de Taylor interesante del binomio de Newton en trminos de la funcin
Gamma es:

( + 1)
(1 + x) =
xn para |x| < 1
(n
+
1)(n

)
n=0

Un producto sucesivo se puede escribir en forma general para cualquier valor de p = 1, 2, 3, . . .

en trminos de la funcin gamma, as:
(z)n =

n1

i=0

(p + i) = p(p + 1)(p + 2)(p + 3) (p + i) (p + n 1) =

(p + n)
(p)

Donde (z)n es conocido como el smbolo de Pochhammer2 .

A.3.

Nmeros de Bernoulli

LLamados as en honor a Jakob Bernoulli, los nmeros de Bernoulli, denotados como Bn ,

surgieron al intentar obtener un resultado para la suma de potencias de nmeros naturales
m1
n
k . Tambin resultan a partir de la expansin de tangente y tangente hiperblica en series
k=0

Leo August Pochhammer (1841-1920): matemtico prusiano, conocido por su trabajo sobre funciones
especiales.

374

APNDICE A. APNDICE

B0

B1

B2

B3

B4

B5

B6

B7

B8

B9

B10

B11

B12

B13

12

1
6

1
30

1
42

1
30

5
66

691
2730

7
6

3617
510

43867
798

174611
330

854513
138

236364091
2730

Tabla A.1: Nmeros de Bernoulli

de Taylor. Los nmeros de Bernoulli tienen profundas conexiones con la funcin Zeta Riemann
en la teora de nmeros y se pueden generar a partir de la frmula recursiva:
B0 = 1 ,

Bn =

m1

k=0

m
Bk
k m+1k

Los nmeros de Bernoulli de ndices impares son cero, y los no nulos cambian de signo alternadamente. Normalmente se escriben slo los no nulos como valores absolutos. La tabla A.1
muestra algunos nmeros de Bernoulli, obviando los impares.
Una forma alterna de obtener los nmeros de Bernoulli es mediante:

(2n)! 1
(2n)!
1
1
Bn = 2n1 2n
= 2n1 2n 1 + 2n + 2n + . . .
2
k=1 k 2n
2

2
3

4n2n (e)2n n
para n grande (frmula asinttica)
Los nmeros de Bernoulli tambin se definen mediante las series:

xn
x
=
Bn
ex 1 n=0
n!
tan(x) =

para |x| < 2

(4)n (1 4n )
n=0

(2n)!

B2n x2n1

para |x| <